Magnetic Levitation Belt Conveyor Control System Based on Multi-Sensor Fusion

Abstract

Belt conveyors are critical in coal transportation systems; however, they are supported by rollers, which incur high energy costs. Magnetic levitation support is adopted. The measurement of a magnetic levitation air gap is important, and a displacement sensor is usually used in real-time. To address the problems of poor linearity and low measurement stability of single displacement sensors in magnetic levitation systems, a magnetic levitation support system based on multi-sensor data fusion is proposed. First, an industrial camera sensor is used to collect images, and the suspended air gap is obtained through image processing. Second, using an extended Kalman filter, the photoelectric position sensor and industrial camera sensor are fused to the suspension air gap value in the process of suspension. The electromagnet current is controlled by the PID (proportion integration differentiation) control algorithm, and experiments are carried out. Experimental results showed that, compared with an estimation of the suspension state of two sensors before and after EKF fusion, the root mean square error is reduced by 0.0597 and 0.0081, respectively, compared with the measurement value of a single sensor. Moreover, the fusion data were more robust, thereby meeting the requirements of magnetic levitation control.

1. Introduction

Belt conveyors have been widely used in modern high-yield efficient mines owing to their long conveying distance, large transportation volume, high productivity, and stable operation [1]. However, the energy consumption related to idlers in traditional belt conveyors accounts for approximately 70% [2] of the total energy consumption of the entire conveyor system. With the emergence of intelligent construction in coal mines, the intelligence degree of the belt conveyor—the key equipment of the main coal transportation system—directly affects the efficiency of coal transportation and the level of intelligent construction in coal mines [3]. Therefore, a magnetic suspension belt conveyor that uses magnetic suspension support instead of a roller support is proposed herein. The structural diagram of the magnetic levitation belt conveyor is shown in Figure 1.

Owing to its advantages of no contact, no friction, and long service life, magnetic levitation technology has been widely used in various industries, such as magnetic levitation trains, magnetic levitation bearings, and high-speed magnetic levitation motors [4,5,6]. Compared with permanent magnet suspension, electromagnetic levitation has the advantage of easy control. The real-time operation and the accuracy of the air gap displacement signal are crucial for controlling the magnetic levitation system stability. To date, eddy-current, capacitive, and photoelectric displacement sensors have been often used to measure the magnetic suspension air gap. However, they have some shortcomings, such as a large volume, poor stability, and poor linearity. Therefore, in order to overcome the limitations of sensor-based approaches, numerous researchers have devoted their efforts to sensorless magnetic levitation systems [7,8,9,10,11,12]. For instance, Bobtsov et al. [7]. addressed the state observation problem in sensorless control of magnetic levitation systems by only measuring the voltage and current of the power supply to adjust the position of the levitated object. Kim [11] proposed a solution to the position stabilization problem in nonlinear magnetic levitation systems using only position measurements. However, it is evident from the aforementioned sensorless research that sensors still need to be employed in conjunction with complex mathematical models. To reconcile the contradiction between sensorless approaches and the complexity of model solving, we adopt a multi-sensor scheme that exhibits transitional characteristics. Compared with a single sensor, multi-sensor fusion [13,14,15] has advantages, such as fault tolerance, complementarity, real-time performance, and economy. This approach is therefore used in various fields, such as robotics, medical applications, and target tracking. With the advancement of machine vision measurement technology, its application [16,17,18] in dimensional measurement provides high measurement efficiency. Meanwhile, industrial cameras are small, easy to install and display, and have no special requirements for the detection surface, which thus resolves some of the limitations of traditional sensors. Industrial cameras can not only assist in detecting clearances but also transmit a wealth of measurement information, including material flow and other conveyor measurements. Furthermore, even the replacement of sensors could be achieved in the future. Therefore, the integration of multiple sensor information from traditional displacement sensors and industrial cameras not only effectively addresses the aforementioned issues but also enhances the stability and reliability of the system, laying the foundation for the intelligent and diversified development of conveyors

Due to their strong nonlinearity and open-loop instability, electromagnetic levitation systems typically require displacement sensors to detect the suspension air-gap displacement in real-time and perform closed-loop feedback control. To address the issues of the traditional single displacement sensor, such as the nonlinear and temperature drift characteristics of eddy current sensors, the authors of [19] replaced the eddy current sensor with a machine vision sensor and used a convolutional neural network to complete the measurement of the suspension air gap. A new method was thus provided for the measurement of the suspension air gap. In principle, the fusion of multi-sensor data has significant advantages over data from a single source. In [20], a vehicle detection method was proposed based on the fusion of millimeter-wave radar and machine vision. This method effectively realizes the information fusion of the radar and vision detection results, and the detection effect is superior to that of the single-sensor algorithm. In [21], inertial measurement units and real-time dynamic differential positioning technology were used to measure the tilting state of the tower in the leveling process. The data fusion was more robust after a Kalman filter was used for the fusion. The authors in [22] proposed an algorithm based on a Kalman filter for data fusion of multiple sensors. More accurate and stable feedback data were obtained by fusing the data.

In this study, a magnetic levitation system based on multi-sensor fusion was designed based on a single-degree-of-freedom magnetic levitation ball system. An extended Kalman filter algorithm was used for fusion, and the PID algorithm was used to control the electromagnet current according to the fused data to realize the stable suspension state of the steel ball. A mathematical model of the magnetic levitation ball system of the control object was first established. Then, the air gap value of the industrial camera sensor was obtained by an image processing method. Next, the data were fused and controlled by the extended Kalman filter. Finally, the steel ball was suspended on a single degree-of-freedom magnetic levitation ball experimental platform [23], and the effectiveness of the proposed method was verified.

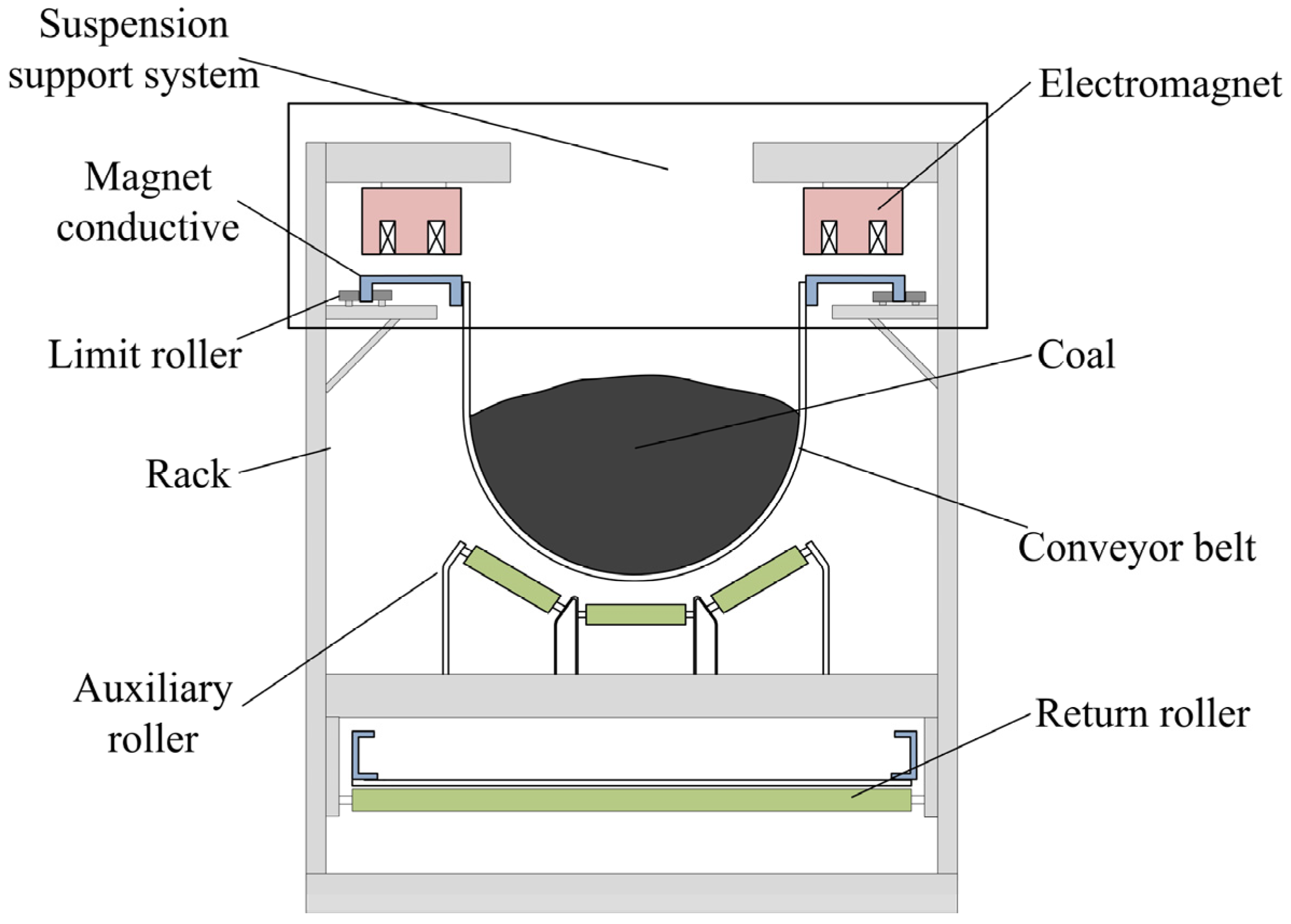
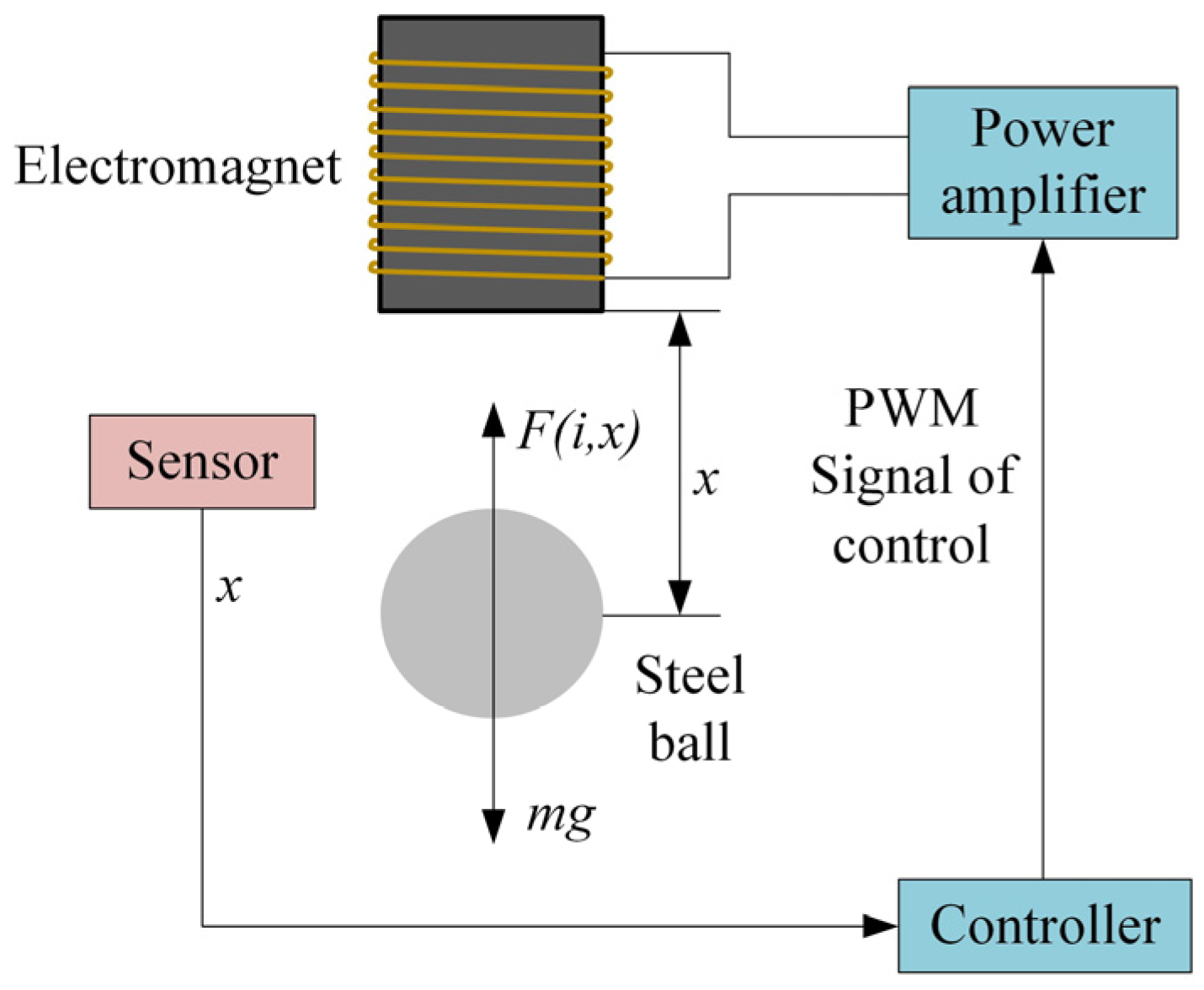
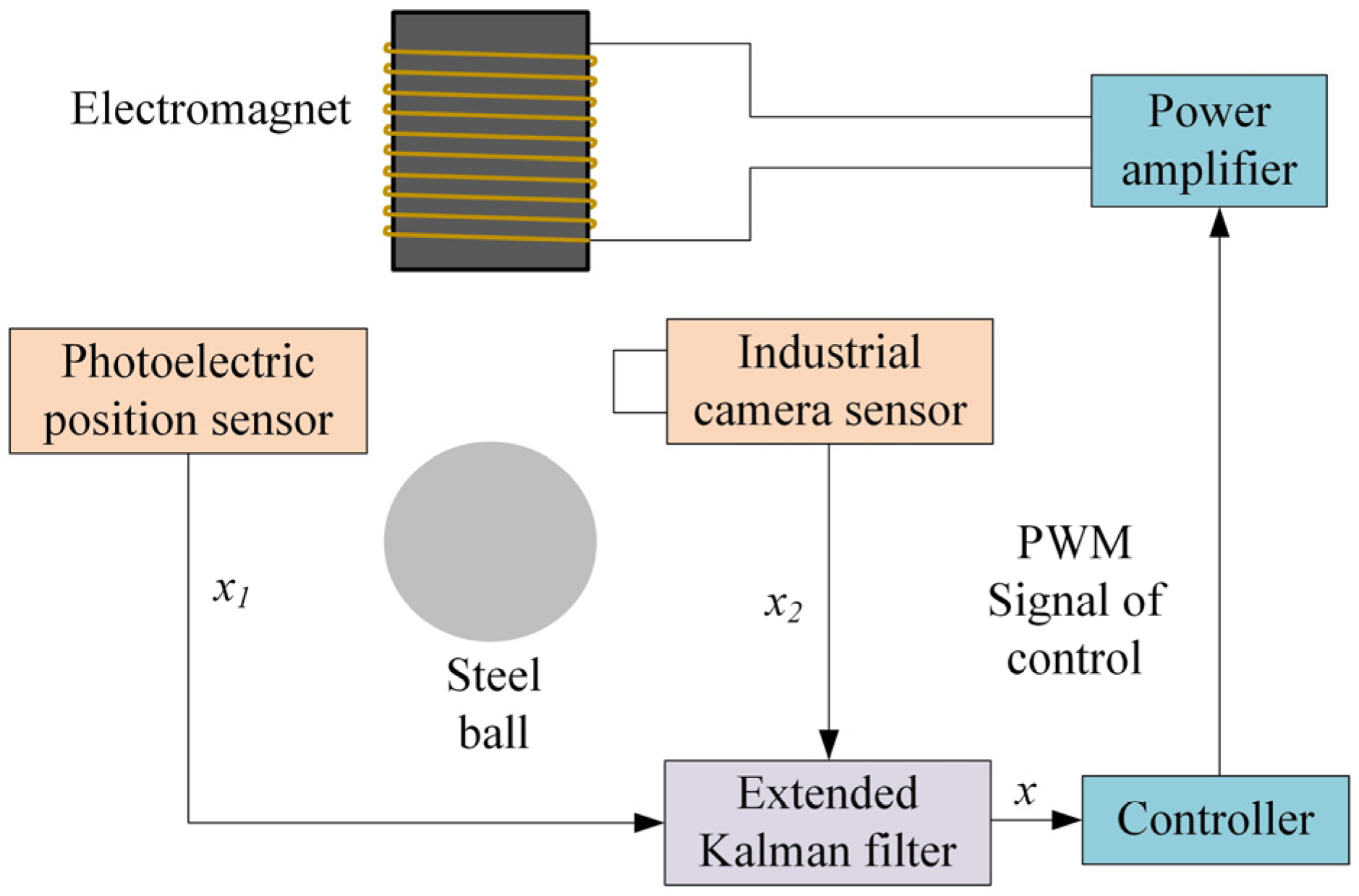
2. System Model

The magnetic levitation ball device mainly consists of electromagnets, photoelectric position sensors, a power supply, amplification and compensation devices, data acquisition cards, control objects (steel balls), and other components. The magnetic levitation ball system is a typical suction-floating levitation system. The basic structure of the system is shown in Figure 2. The electromagnetic force F(i,x) is generated by passing a certain current through the electromagnet winding. Under the condition that the current in the electromagnet winding is controlled such that the generated electromagnetic force is balanced with the gravity mg of the steel ball, the steel ball can be suspended in air and in equilibrium.

Assuming that the levitating object is not subjected to other disturbing forces, and the force analysis of the object is only subjected to vertical downward gravity mg and its reverse electromagnetic force F(i,x), then x is the distance from the center point of the steel ball to the lower edge of the electromagnet.

To simplify the derivation process, the following assumptions are typically made:

• Neglecting the magnetoresistance in the steel ball and the electromagnet, the magnetoresistance of the magnetic circuit consisting of the electromagnet and the steel ball is concentrated in the suspended air gap.
• The leakage flux is neglected, where the flux passes through the air gap of the external pole of the electromagnet.
• The magnetic flux is uniformly distributed at the air gap, thus neglecting the edge effects.

Based on the above assumptions, the mathematical model of the electromagnetic levitation ball system is obtained as follows [24]:

$$\{\begin{array}{l}m\frac{d^{2}x(t)}{d{t}^2}=F(i,x)+mg\\ F(i,x)=\frac{{\mu }_{0}A{N}^2}{4}{\left(\frac{i}{x}\right)}^2=K{\left(\frac{i}{x}\right)}^2\\ U(t)=Ri(t)+\frac{{\mu }_{0}A{N}^2}{2x}\frac{di}{dt}-\frac{{\mu }_{0}A{N}^{2}i}{2x^2}\frac{dx}{dt}\\ F(i_0,x_0)+mg=0\end{array}$$

(1)

where m is the mass of the ball, x is the levitation distance of the ball, i is the electromagnet current, F(i,x) is the electromagnetic suction force, g is the acceleration due to gravity, u₀ is the vacuum permeability, A is the core area, N denotes the number of turns in the electromagnet coil, U(t) represents the voltage across the electromagnet coil, and R is the resistance of the electromagnet coil. Additionally, i₀ and x₀ are the electromagnetic current and levitation air gap at the equilibrium point, respectively.

It can be observed that this levitation system is a typical nonlinear system, and its nonlinear part must be linearized first. Equation (1) is linearized near the equilibrium operating point (i₀,x₀) using Taylor series expansion. Accordingly, the approximate linearized model is obtained as

$$m\frac{d^{2}x}{d{t}^2}=\frac{2K{i}_0}{x_0{}^2}i-\frac{2K{i}_0{}^2}{x_0{}^3}x$$

(2)

The input quantity of the system object is defined as the input voltage of the power amplifier, which is the control voltage U_in. Moreover, the output voltage reflected by the output quantity of the system object x is U_out (sensor output voltage). According to Equation (2), the system state variables are taken to be $x_1=u_{out}$, $x_2={\dot{u}}_{out}$, respectively, and the equation of the state of the system in continuous time is obtained according to the state space theory as

$$\{\begin{array}{l}\dot{x}=Ax+BU\\ y=Cx\end{array}$$

(3)

where $A=\left[\begin{array}{cc}0& 1\\ \frac{2g}{x_0}& 0\end{array}\right]$, $B=\left[\begin{array}{c}0\\ -\frac{2g\cdot K_s}{i_0\cdot K_a}\end{array}\right]$, $C=\left[\begin{array}{cc}1& 0\end{array}\right]$.

The open-loop pole of the system is $s=\pm \sqrt{2g/x_0}$. At this time, the system has two poles, positive and negative, and an open-loop pole is located on the right side of the complex plane; therefore, the maglev ball system is an open-loop unstable system in nature.

The controllability matrix of the system is as follows:

$$M=[B⋮AB]=\left[\begin{array}{cc}0& -\frac{2g\cdot K_s}{i_0\cdot K_a}\\ -\frac{2g\cdot K_s}{i_0\cdot K_a}& 0\end{array}\right]$$

(4)

The observability matrix of the system is as follows:

$$N=\left[\begin{array}{c}C\\ CA\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

(5)

From Equations (4) and (5), we can observe that Rank(M) = Rank(N) = 2. From the above, it is apparent that the rank of the state complete controllability matrix of the system is equal to the dimensionality of the system state variables, and the rank of the output complete controllability matrix of the system is equal to the dimensionality of the system output vector. Thus, the magnetic levitation experimental system is both controllable and observable.

3. Method

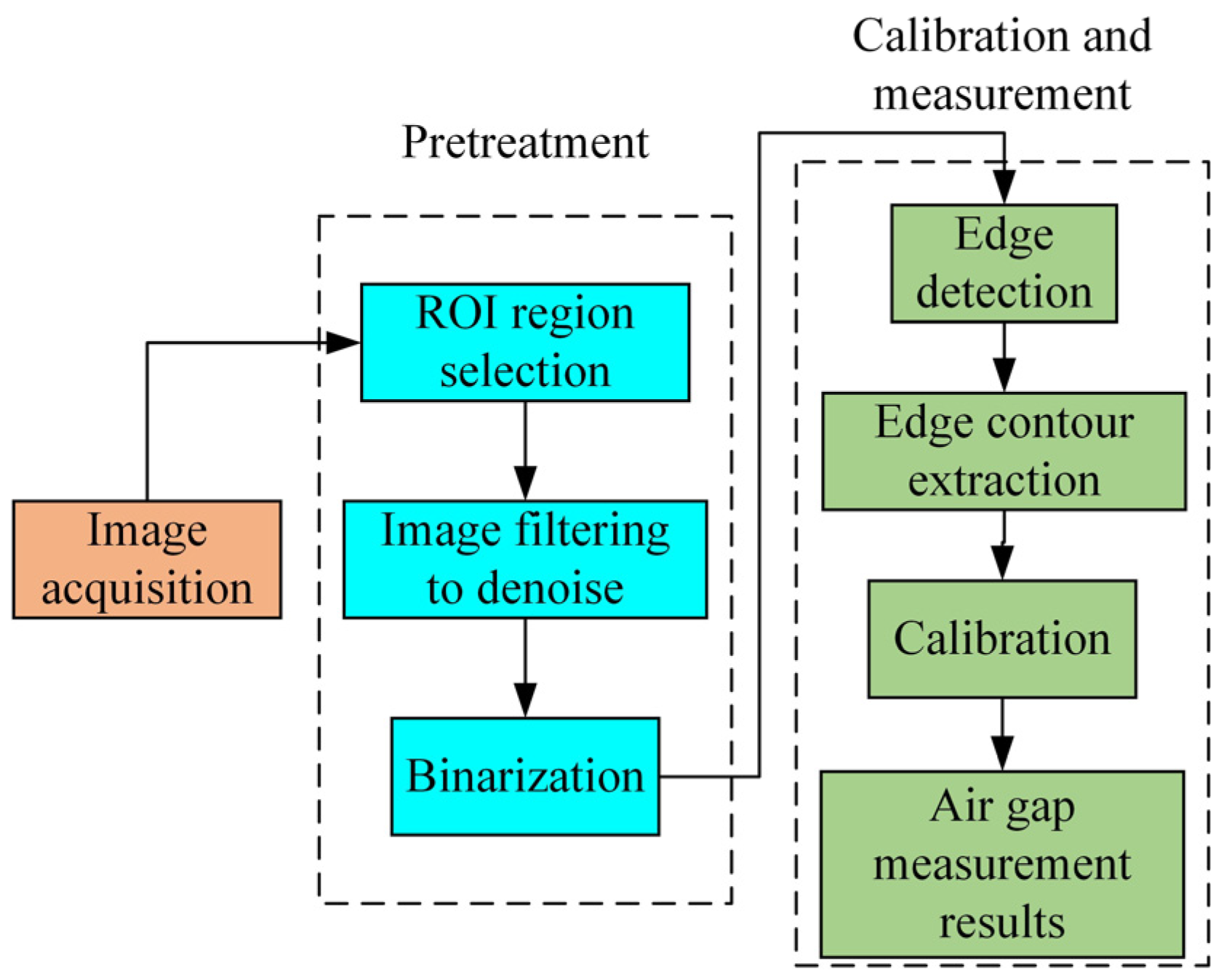
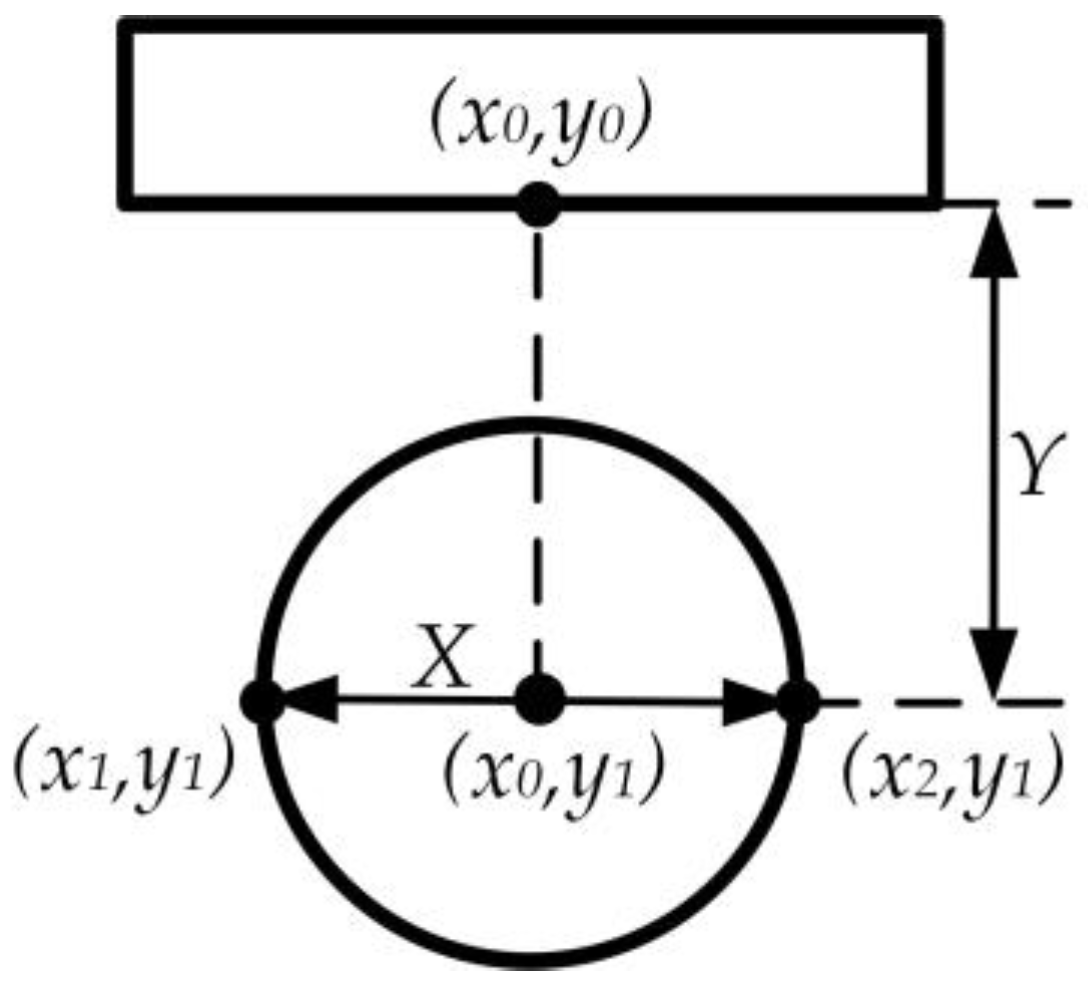
3.1. Industrial Camera Measurement Algorithm

The image processing technology is applied to the magnetic suspension clearance measurement to solve some problems of the traditional displacement sensor. The measurement algorithm is based on image preprocessing, edge detection, contour extraction, and calibration. An image processing flowchart is shown in Figure 3.

In the process of information acquisition, transmission, and terminal processing, the original image is easily affected by noise, light, and other factors, resulting in some degradation of image quality. This degradation affects the processing of subsequent images and makes it difficult to obtain accurate results. To enhance the visual quality of the image and the accuracy of the image processing, it is necessary to preprocess the image before image processing.

Image preprocessing includes region of interest (ROI) selection, image filter denoising, binarization processing, and so on. The black-and-white images obtained by the camera are shown in Figure 4a. To reduce the computational load and increase the algorithm operation speed to fulfill the real-time processing requirements, the ROI region in the middle of the suspended air gap in Figure 4a was preferentially selected in this study during image processing, as shown in Figure 4b.

The edge features extracted from part of the ROI represent the characteristics of the magnetic levitation air gap in the whole field of vision. Then, the image is smoothed and filtered. In 1998, Smith et al. proposed a nonlinear filtering algorithm, i.e., bilateral filtering [25,26], on the basis of Gaussian filtering and Yaroslavsky neighborhood filtering. The traditional Gaussian filtering method directly convolves the Gaussian weight coefficient with the image information, and it only considers the spatial distance between pixels, resulting in an unclear image. The bilateral filtering algorithm optimizes the Gaussian filtering weight coefficient in the product of the Gaussian function and image brightness information. The optimized weight coefficient is then convolved with the image information to account for the similarity between pixels. Accordingly, the obtained image edges are smoother. The filtering effect is shown in Figure 4c.

The template weights of the bilateral filter are formulated as follows:

$$w\left(i,j,k,l\right)=\exp \left[-\frac{{\left(i-k\right)}^2+{\left(j-l\right)}^2}{2{\sigma }_d^2}-\frac{{\Vert I\left(i,j\right)-I\left(k,l\right)\Vert }^2}{2{\sigma }_r^2}\right]$$

(6)

where σ_d and σ_r are the smoothing parameters, and I(i,j) and I(k,l) are the intensities of pixels (i,j) and (k,l), respectively. After calculating the weights, they are normalized as follows:

$$I_D\left(i,j\right)=\frac{{\displaystyle {\sum }_{k,l}I\left(k,l\right)w\left(i,j,k,l\right)}}{{\displaystyle {\sum }_{k,l}w\left(i,j,k,l\right)}}$$

(7)

where I_D is the denoising intensity of pixel (i,j).

Image binarization is conducive to highlighting the image contour under testing. The most effective method for binarization is threshold segmentation. The Online Teaching Support Unit (OTSU) is used to binarize the edge and background of the suspended air gap image to obtain a complete edge and background segmentation image, as shown in Figure 4d.

Before extracting the contour features of the object, edge detection of the image should be performed to obtain the object boundary, and the features of the boundary region should be extracted to calculate the image contour feature parameters. Common edge detection operators include the Roberts, Sobel, Prewitt, Laplacian, and Canny operators. The Sobel edge detection algorithm [27,28] is relatively simple and especially suitable for fields with high real-time requirements. In practical applications, its efficiency is higher than that of Canny edge detection. Because the image edge in the suspended air-gap ROI region in this study was relatively simple, Sobel edge detection was the first choice. Sobel edge detection is usually directional and can detect only vertical or vertical edges, or both. The Sobel operator uses two horizontal and vertical templates to perform plane convolution of the image, thereby achieving the approximate value of the gray difference in the image brightness. The effect of processing is illustrated in Figure 5.

Horizontal gradient:

$$G_x=\left[\begin{array}{ccc}-1& 0& +1\\ -2& 0& +2\\ -1& 0& +1\end{array}\right]$$

(8)

Vertical gradient:

$$G_{\mathrm{y}}=\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ +1& +2& +1\end{array}\right]$$

(9)

At each point in the image, the approximate gradient is determined by combining the above two results.

$$G=\sqrt{G_x^2+G_y^2}$$

(10)

As shown in Figure 6.As the diameter of the steel ball is known, X is set, Y is set as the suspension air gap value, and the real suspension air gap is calculated according to the ratio of pixels in the image to the actual length. By programming under the electromagnet the boundary center (x₀,y₀), steel ball left boundary (x₁,y₁) and right boundary (x₂,y₁), it is concluded that using the center of the ball (x₀,y₁), the diameter of steel ball, the image pixel distance for |x₂ − x₁|, suspended air gap of the pixel distance for |y₁ − y₀|, the actual value of suspension air gap can be written as

$$Y=\left|y_1-y_0\right|\cdot \frac{X}{\left|x_2-x_1\right|}$$

(11)

3.2. Extended Kalman Filtering Principle

The Kalman filter is an optimized autoregressive data processing method. It can estimate the next state according to the estimated value of the previous state under the action of the system noise, measured value, and measured noise. It can then obtain the best estimated value of the next state. Since the Kalman filter is only applicable to linear systems and cannot directly solve the estimation problem of nonlinear systems, the extended Kalman filter [29] was adopted for this system. First, a Taylor series was used to linearize the system, and then the discrete Kalman filter algorithm was used to estimate the displacement state.

The system model is expressed in the following general form of the state procedure and the observation equation of a nonlinear discrete system:

$$\{\begin{array}{c}{x}_k=f\left(x_{k-1},u_{k-1},{\omega }_{k-1}\right)\\ z_k=h\left(x_k,v_k\right)\end{array}$$

(12)

where x_k is the state quantity, z_k is the measurement value, u_k is the input vector, ω_k is the system process white noise obeying the Gaussian distribution, v_k is the system measurement white noise obeying the Gaussian distribution, and Q and R are their respective covariance matrices. Their probability distributions are P(w) ∈ N(0,Q) and P(v) ∈ N(0,R).

The specific steps of extended Kalman filter estimation are as follows:

$$\{\begin{array}{l}{\widehat{x}}_k=f\left({\widehat{x}}_{k-1},u_{k-1},0\right)\\ P^{-}{}_k=A{P}_{k-1}{A}^T+W{Q}_k{W}^T\\ K_k=P_k^{-}{H}^T{\left[H{P}_k^{-}{H}^T+VR{V}^T\right]}^{-1}\\ {\widehat{x}}_k={\widehat{x}}_k^{-}+K_k\left[z_k-h\left({\widehat{x}}_k,0\right)\right]\\ P_k=\left(I-K_{k}H\right)P_k^{-}\end{array}$$

(13)

where A is the state transition matrix after partial derivation, and H is the measurement matrix after partial derivation.

3.3. Multi-Sensor Fusion Algorithm

Multi-sensor fusion is the fusing and complementing of data from multiple sensors. The state quantity obstructed by noise and external disturbances is a random quantity, and the sensor cannot measure the exact value. Compared with a single sensor, multi-sensor fusion can quickly and accurately identify and judge the surrounding scenario, which compensates for the shortcomings of a single sensor, increases the accuracy and fault tolerance of measurement, and improves the reliability of data. In this study, the Kalman filter was used to estimate the suspended air gap of the target object. A structural diagram of the multi-sensor fusion maglev ball system is shown in Figure 7.

The algorithm reads the corresponding voltage value of the suspension air gap from the photoelectric position sensor and calculates the air gap value using a conversion formula. On the other hand, the pixel value of the suspension air gap measured by the sensor of an industrial camera is also calculated according to the conversion formula, and the data transmitted by multiple sensors are processed asynchronously. Different mathematical observation models of the industrial camera sensor and the photoelectric position sensor were established to eliminate the measurement error, and the weighted fusion of the two observation equations was conducted to obtain the final optimal estimate. Accordingly, the extended Kalman filter could be applied to the magnetic suspension control system.

The effectiveness of the system was verified by a simulation, and two types of noise interference signals of different degrees were added to the original signal, with noise amplitudes of 0.5 and 0.2, respectively. The Kalman filter was used to fuse the two signals. The results are shown in Figure 8.

As shown in Figure 8, the basic fluctuation range of the fusion signal remains within 0.01 mm at 0.3 s, and the fusion signal is stable without large fluctuation, which is basically consistent with the original signal, and thus verifies the feasibility of this method.

4. Results and Discussion

To verify the effectiveness of the above algorithm, the classical proportional-integral-derivative (PID) control algorithm was adopted, and a magnetic levitation ball system experiment platform based on semi-physical simulation was used to verify the test.

Table 1. Magnetic levitation ball system parameter description.

Parameter Numerical	Value
Ball mass m/g	100
Core diameter/mm	22
Number of electromagnet turns N	2450
Amplification factor Ka	9.776
Sensor coefficient Ks Balance position x0/mm	−467.4 34
Equilibrium position current i0/A	1.17

lists the primary parameters of the magnetic levitation ball system.

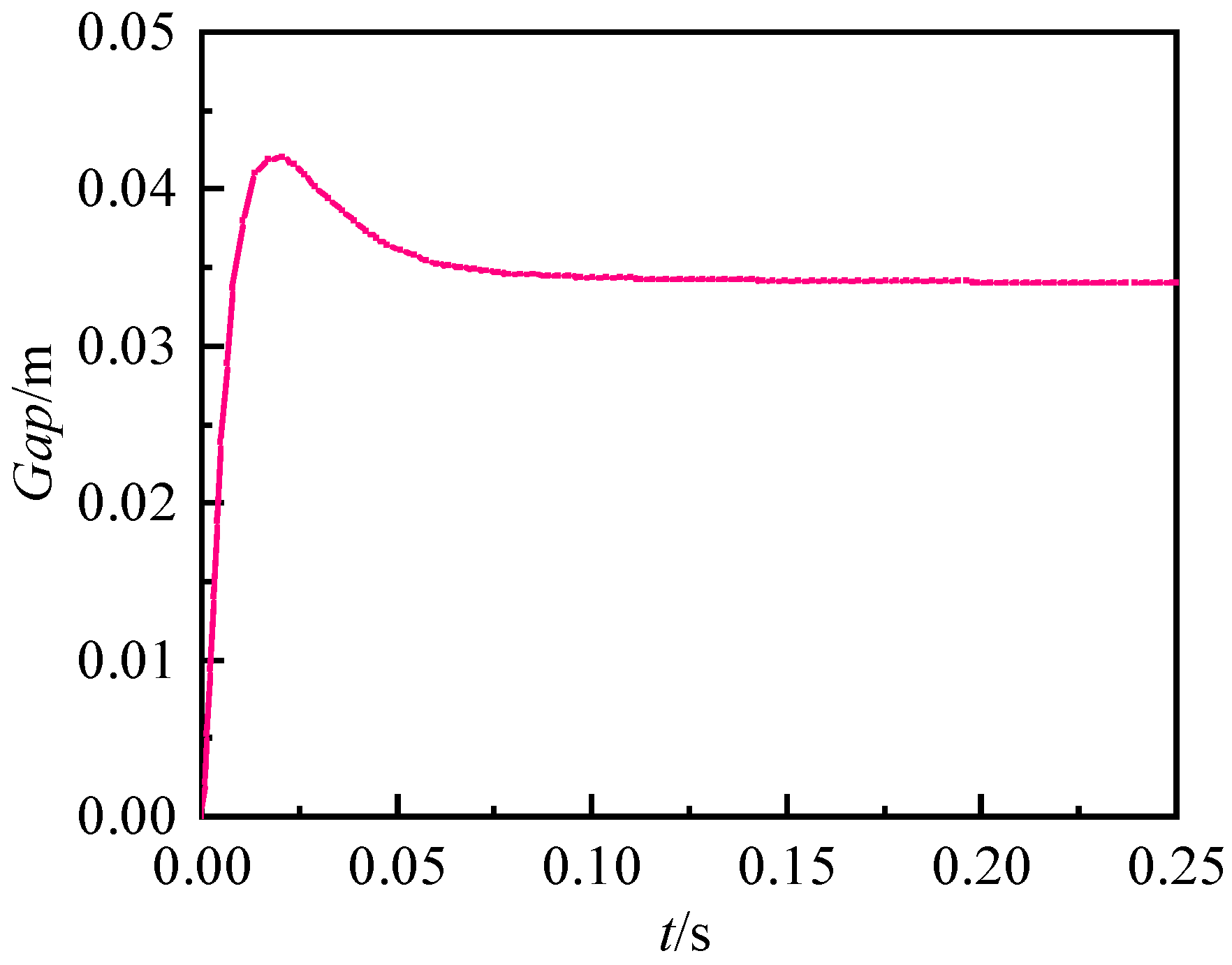
4.1. PID Simulation Analysis

In industrial control, the most widely used and mature controller is the PID controller, which is a linear controller that directs the controlled object by linearly combining the proportional, integral, and differential deviations of the given and actual values to form the control deviation. The control law of the PID controller is as follows:

$$u(t)=K_p\left[e(t)+\frac{1}{T_i}{\displaystyle {\int }_0^{t}e}(t)d_t+T_d\frac{de(t)}{dt}\right]$$

(14)

where u(t) is the control quantity output from the PID controller, K_p is the proportionality coefficient, e(t) is the difference between the given value of the system and the output value of the system (i.e., the error signal), T_i denotes the integration time constant, and T_d is the differential time constant.

The step simulation results of the PID control system based on MATLAB/Simulink established for the maglev ball are shown in Figure 9.

As observed in Figure 9, the time required for the system to reach stability is 0.12 s, and the steady-state error is 0; the steel ball realizes stable suspension, and the system responds quickly and stably. It shows satisfactory dynamic and steady-state performance. Considering that the parameters of the PID control algorithm are not optimal, the performance of the system can be further enhanced through continuous optimization and modification of the parameters.

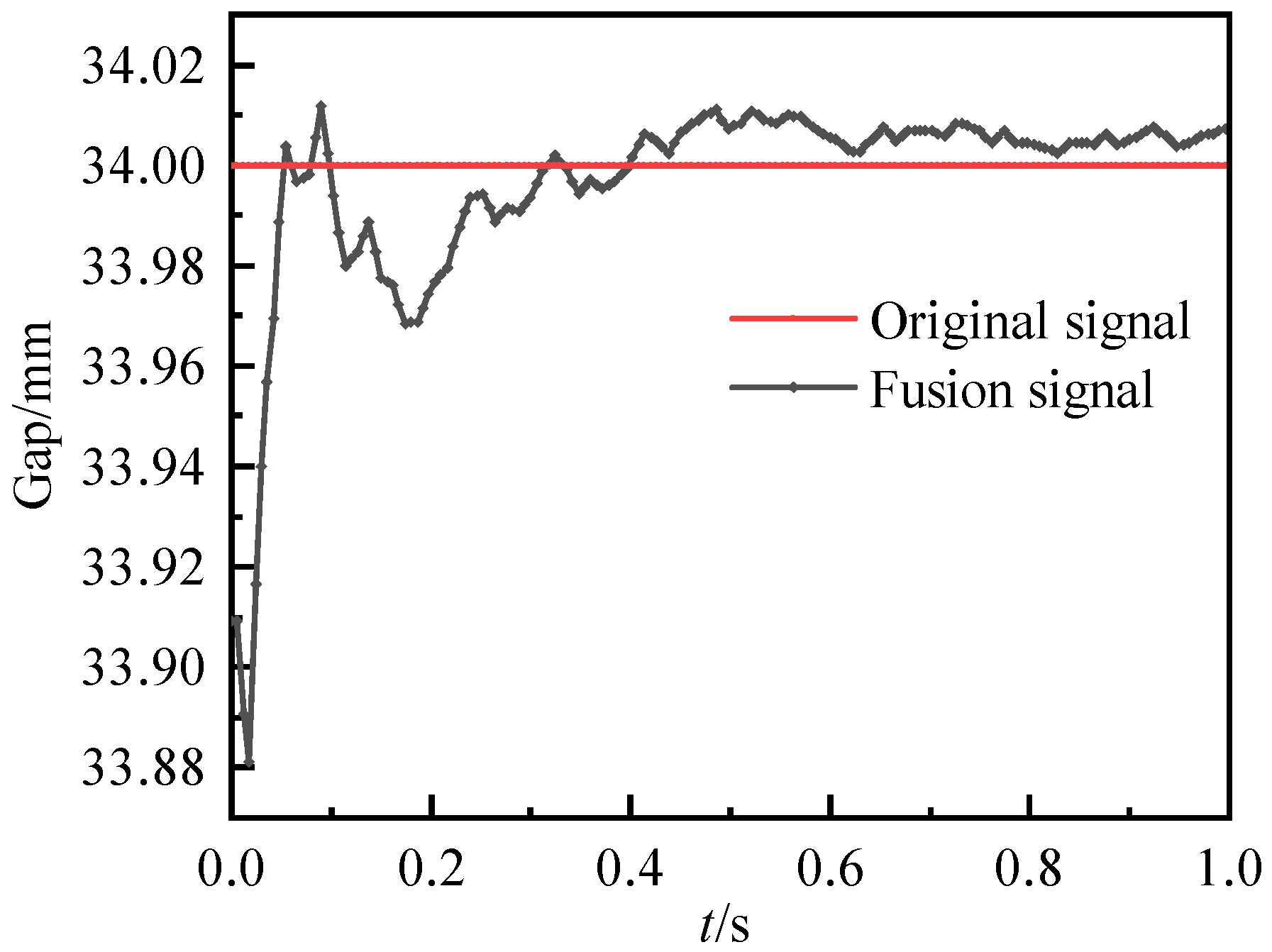
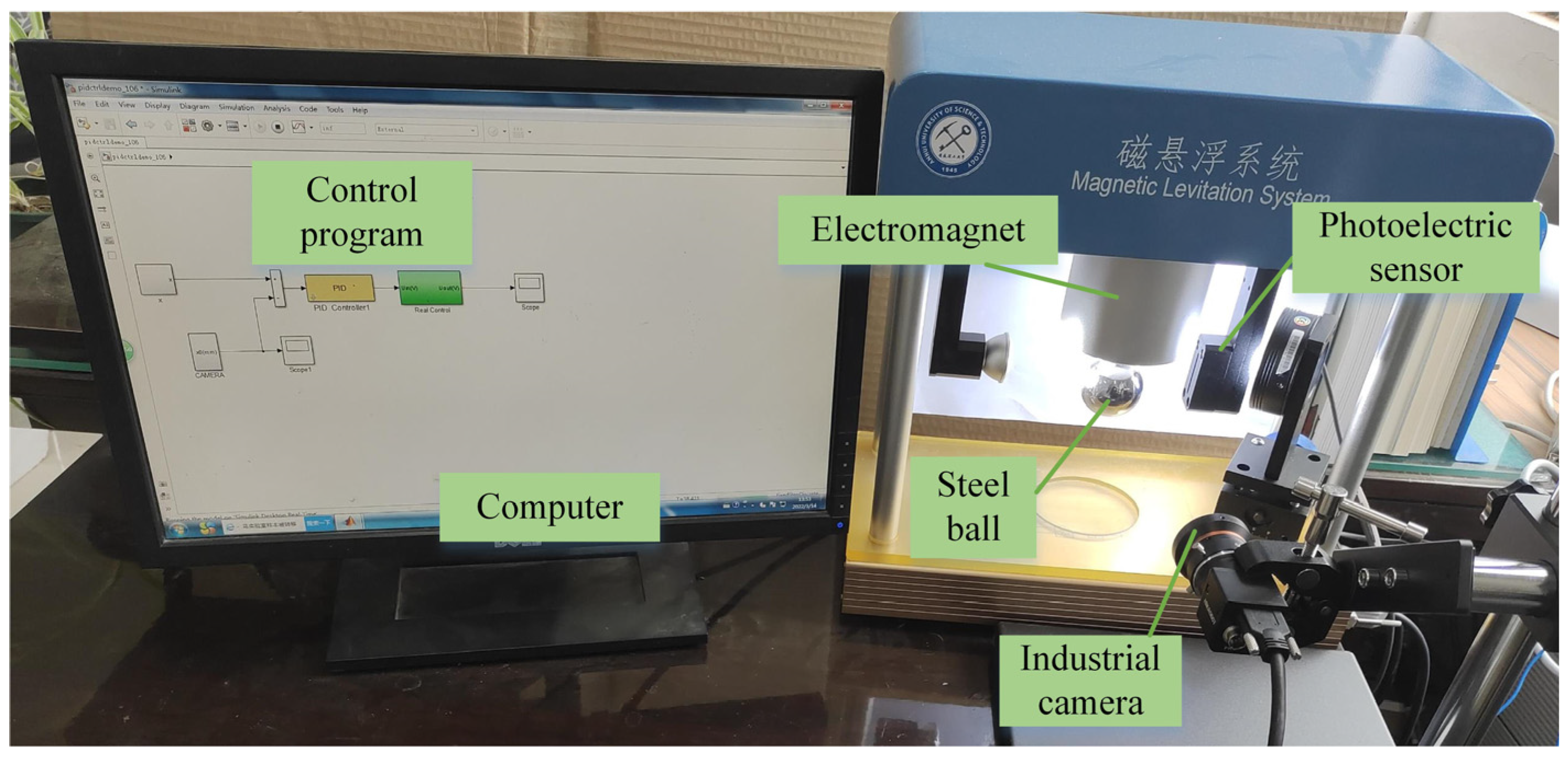
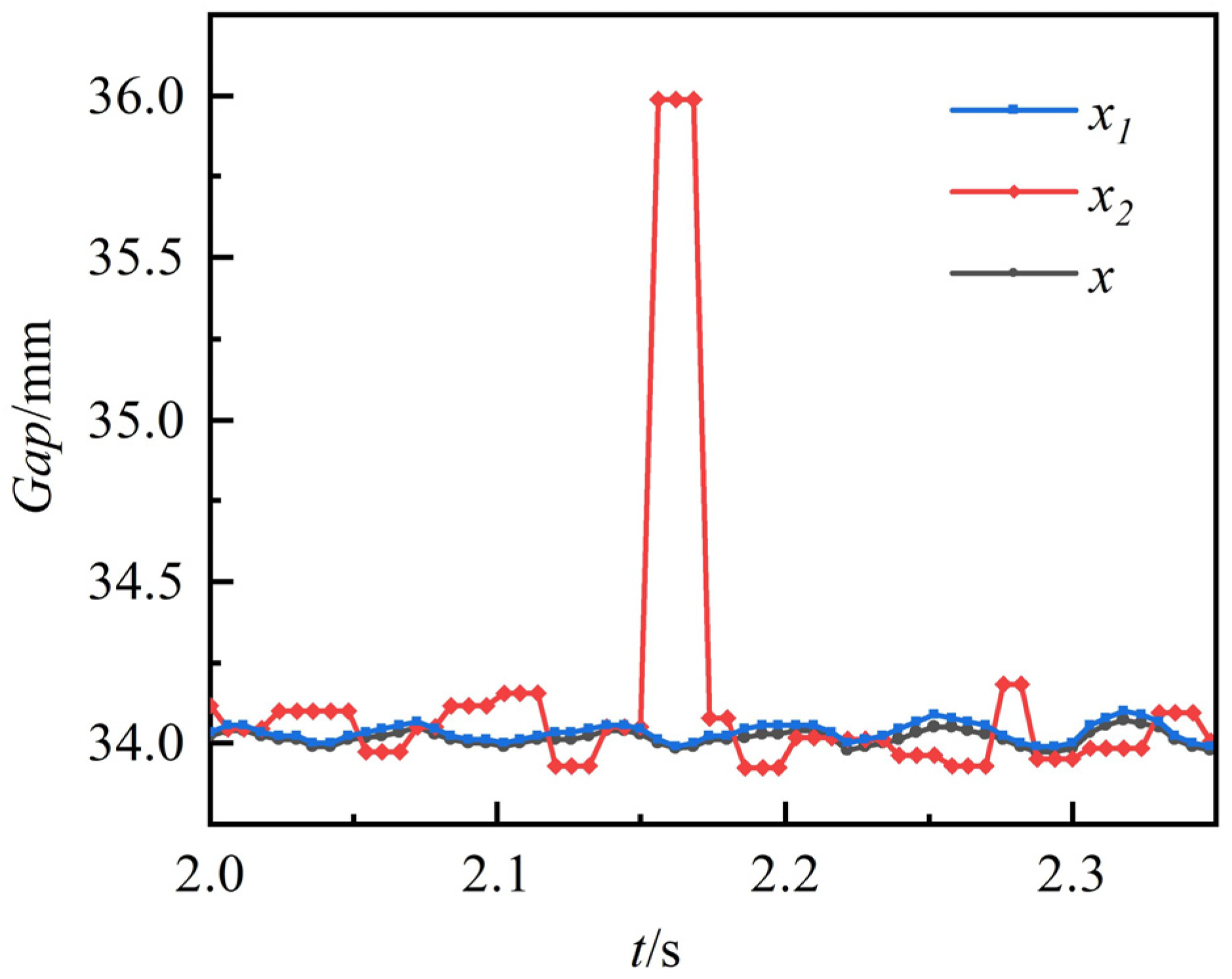
4.2. Experimental Verification

The industrial camera was connected to a computer via USB [30]. At the computer side, the camera call, image acquisition, and image processing were completed using Python-opencv, and the suspended air gap values were output to MATLAB in real-time. Meanwhile, the Simulink model of the real-time controller was also run in MATLAB, and the photoelectric position sensor measurements were fused with the two data using Kalman filtering. The experimental platform is shown in Figure 10. The fused values were passed through the PID control algorithm to control the magnitude of the solenoid current to enable the steel ball to be stably suspended. The PID algorithm parameters K_p = 23, K_i = 10, and K_d = 75 were set, and the obtained measurement results before and after fusion with the extended Kalman filter are shown in Figure 11. The anti-interference diagram is shown in Figure 12.

It can be seen from Figure 12 that at around 2.15 s, the measured value of industrial camera changes abruptly due to external interference, but the fusion value remains stable. In Figure 11, excluding the values with abrupt changes, it can be concluded that the fluctuation range of output data of the industrial camera sensor is 0.43 mm, that of the photoelectric position sensor is 0.20 mm, and that of the fusion data is 0.16 mm. Compared to the single sensor, the accuracy is improved by 0.27 and 0.04 mm, respectively. The Kalman filter was used to stabilize the data returned by the sensor. It is also observed in

Table 2. Measurement estimation error comparison.

Measurement Method	Photoelectric Sensor Value x1	Industrial Camera Value x2	Fusion Value x
Root-mean-square error/mm	0.0374	0.0890	0.0293

that the root-mean-square error of the fusion value is the smallest (0.0293). The root-mean-square errors of the industrial camera and photoelectric sensor values are 0.0890 and 0.0374, respectively. The root mean square error is reduced by 0.0597 and 0.0081, respectively. Thus, the fused data are more stable and robust.

It is feasible to apply the measurement technology of machine vision and the Kalman filter to measure the suspension air gap of the maglev system. However, it was found in the experiment that the anti-interference ability of the suspension system using machine vision ranging is poor, and it is easy to cause suspension instability owing to interference from the external environment. Meanwhile, it was verified that multi-sensor fusion has stronger robustness than single-sensor measurements. When one sensor is affected by external interference, the measured value changes significantly, and fusion technology using the extended Kalman filter can better maintain the stability of the data.

5. Conclusions

The control system of a magnetic levitation belt conveyor is not easy to control in real-time, and the stability of a single traditional displacement sensor is low. To address these problems, a magnetic levitation support system based on multi-sensor fusion was proposed. To verify the effect of the above algorithm, a single-point magnetic levitation system was used for a simulation analysis and experiment. The conclusions outlined below were drawn from the analysis:

• A magnetic levitation air-gap measurement system based on image processing was proposed. By preprocessing, edge detecting, and calibrating industrial camera images, the real suspension air-gap value was obtained, which increased the reliability of the sensor measurement.
• A system model based on multi-sensor fusion was established. The data measured by the two sensors were fused using an extended Kalman filter, and then the control algorithm was used to achieve stable suspension.
• A control test was conducted using a magnetic levitation ball system. The experimental results showed that the data fusion method accurately measured the suspension air gap, and the measurement results were not easily affected by the external environment. The fusion data were more robust, and the suspension system was stably suspended by PID control. It thus met the requirements of maglev control and improved the stability and anti-interference ability of the system.