The Thermal Analysis and Heat Dissipation Structure Optimization of a Propeller Driver System
Abstract
:1. Introduction
2. Thermal Analysis of Propeller Driver
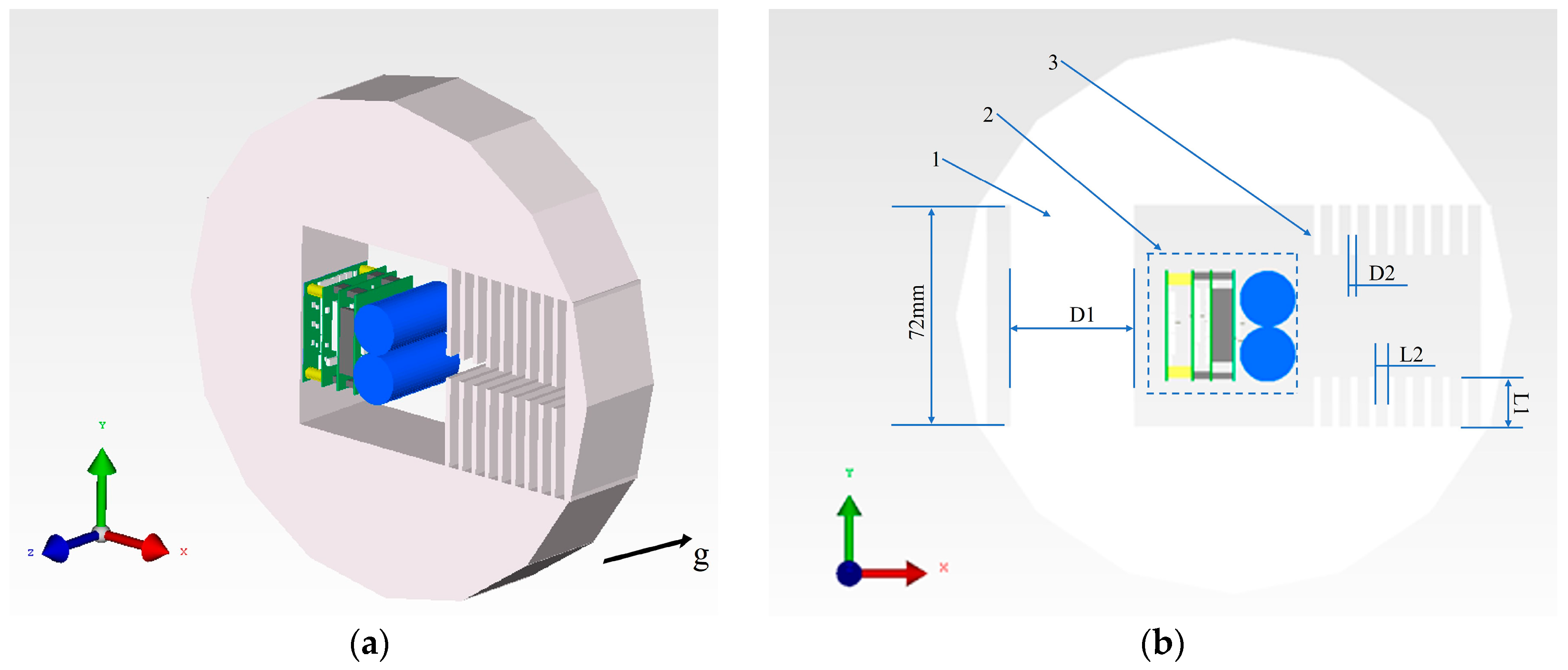
2.1. Numerical Model Description
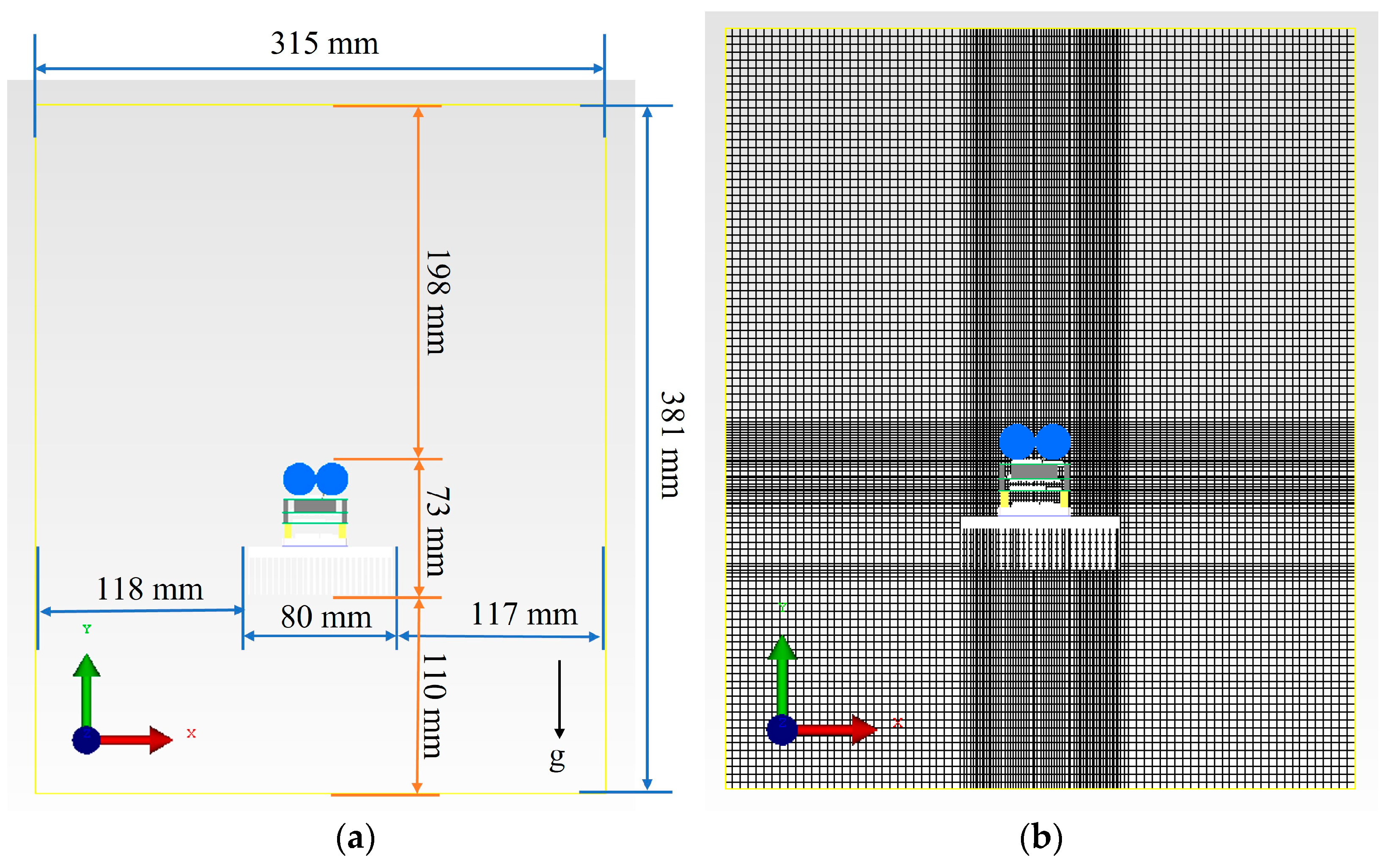
2.2. Boundary Condition Settings
2.3. Grid and Solution Domain Setting
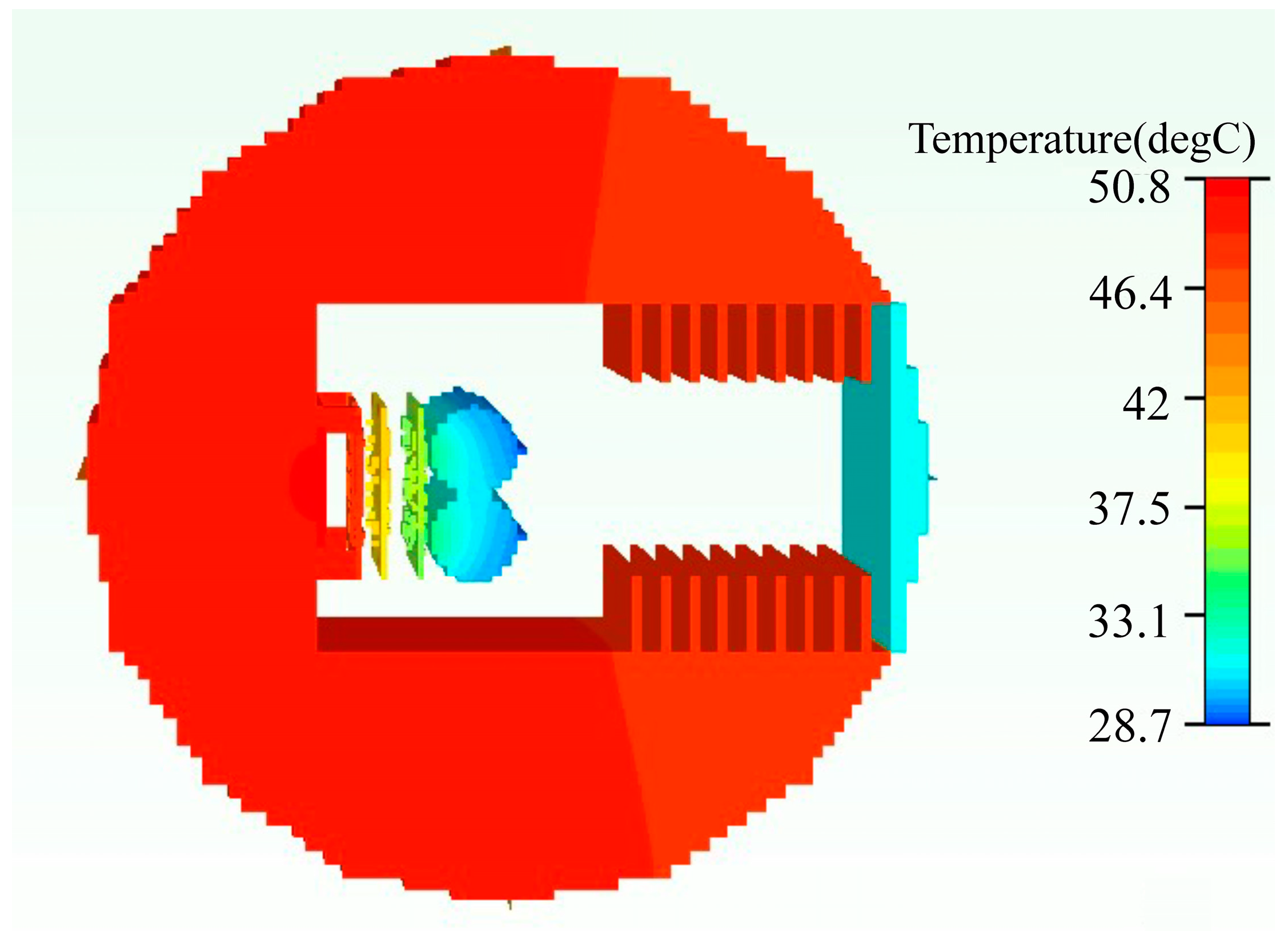
2.4. The Simulation Results and Discussion
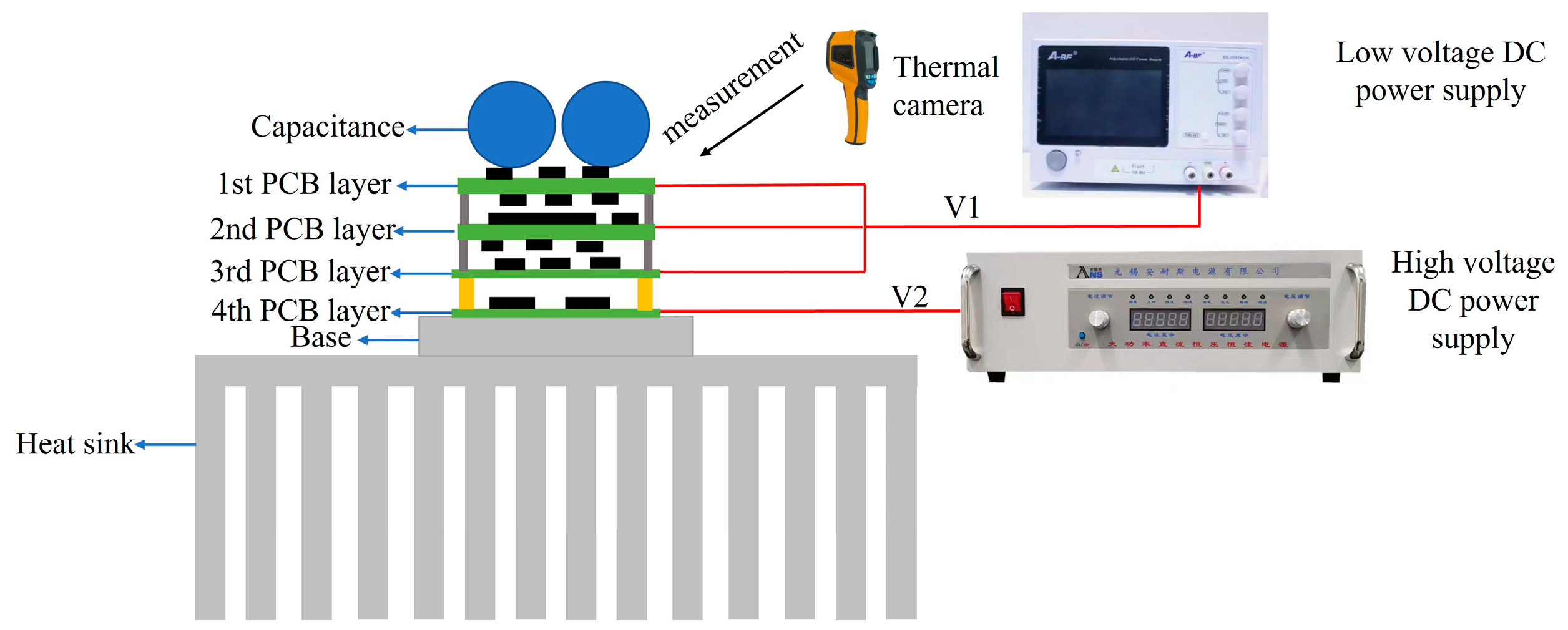
2.5. Model Experiment Verification
3. Thermal Analysis and Optimization of Heat Sink Based on Sealed Cabin
3.1. Influences of Heat Sink Geometry on Heat Dissipation
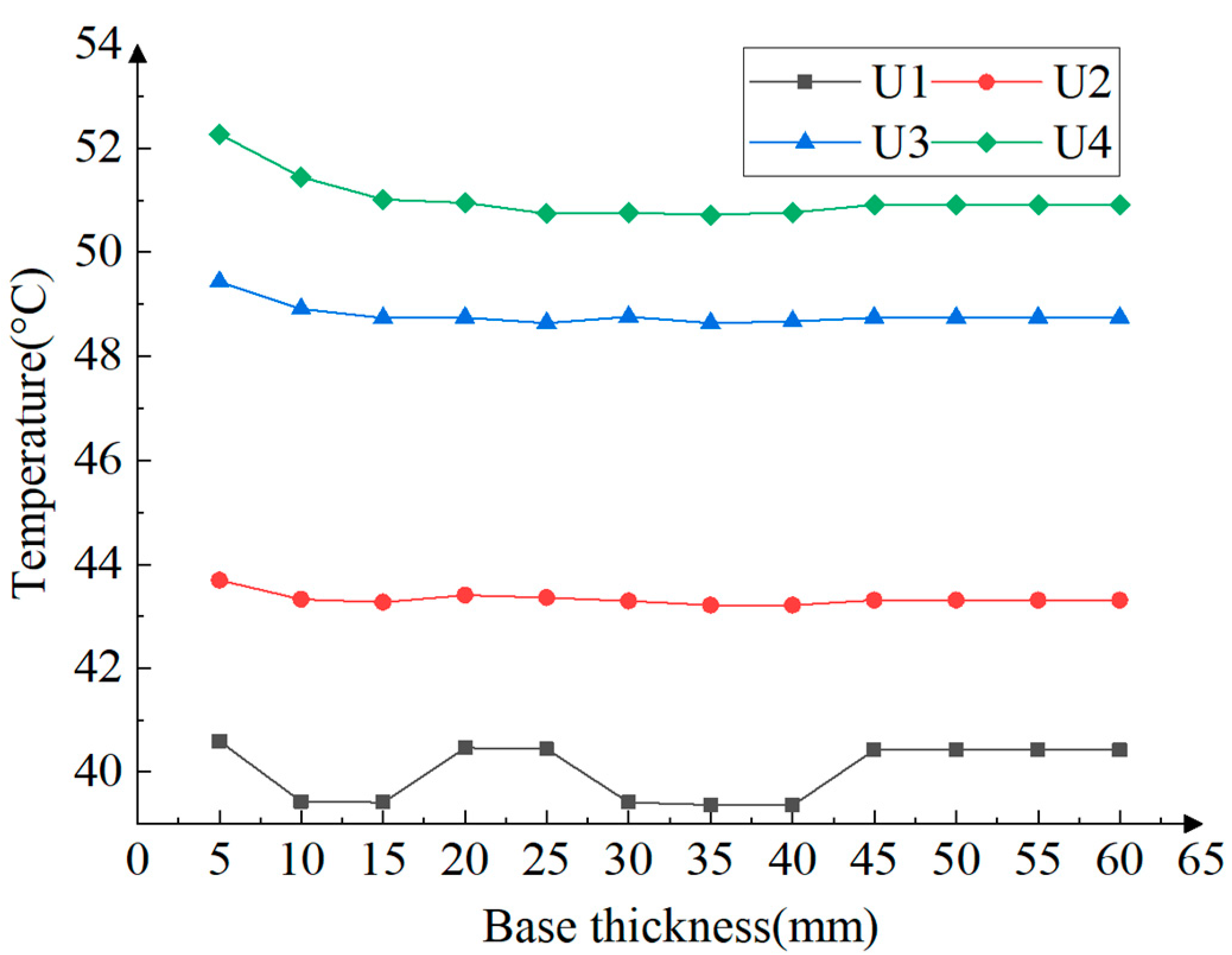
3.2. The Influences of Base Thickness on Thermal Performance
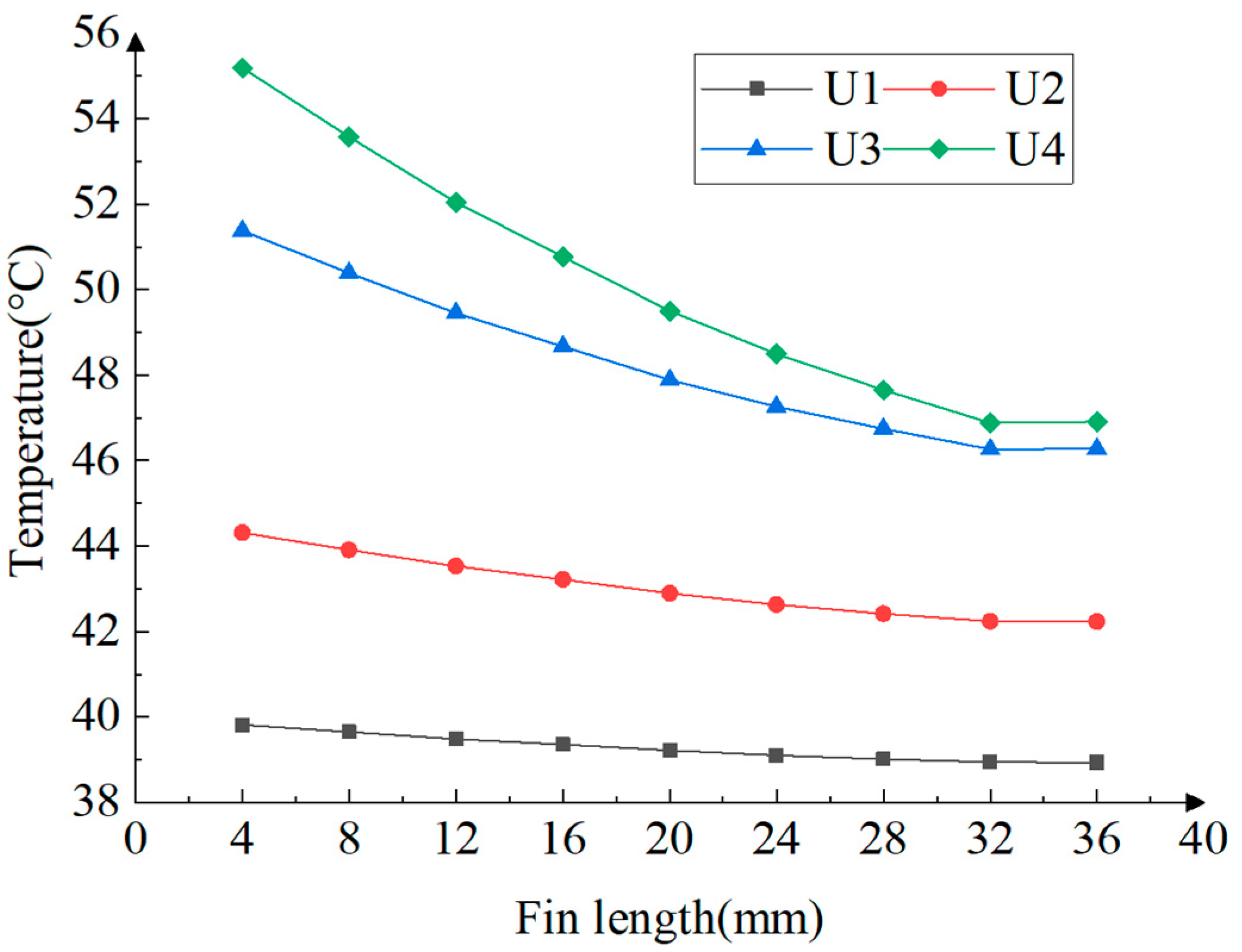
3.3. The Influences of Fin Length on Thermal Performance
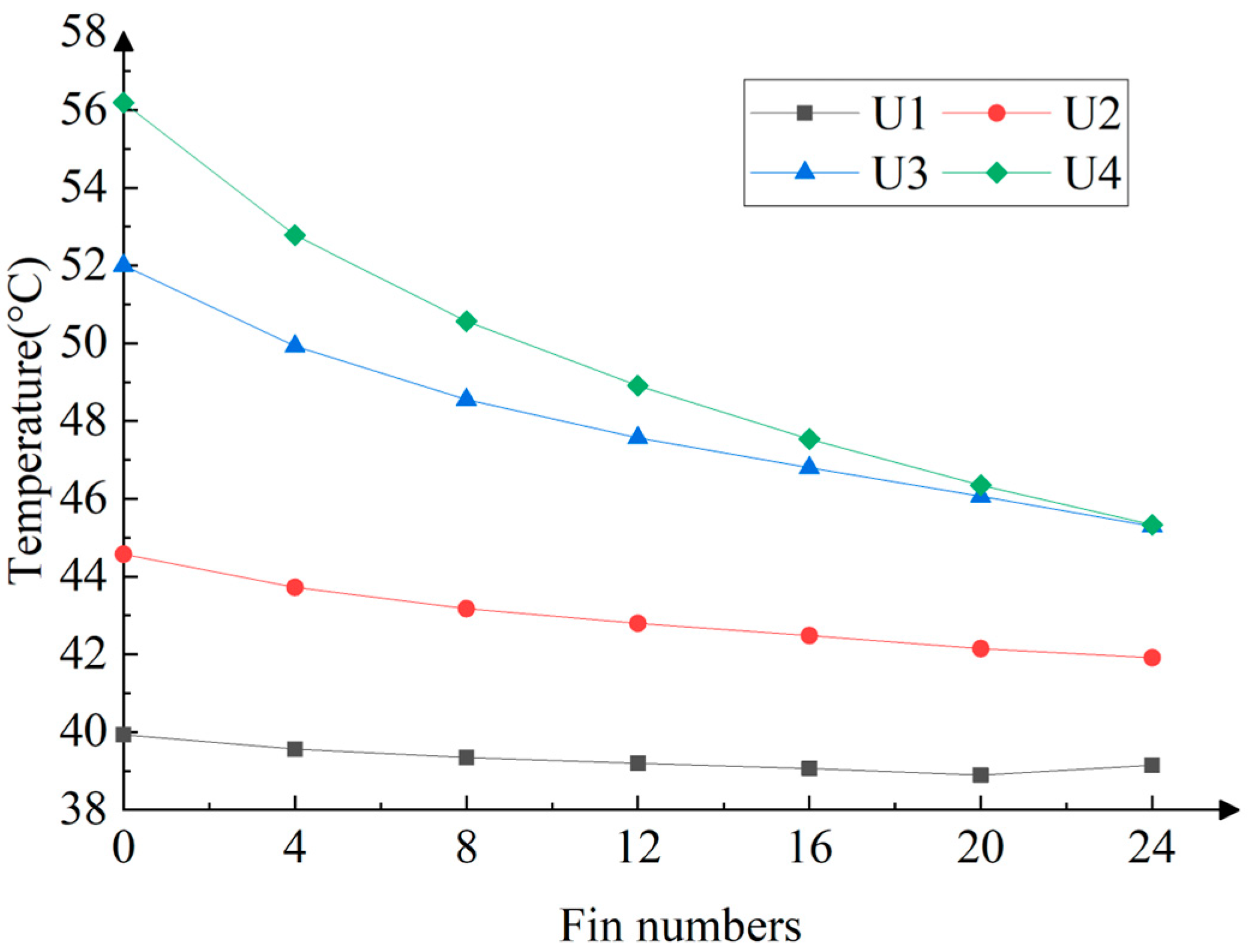
3.4. The Influences of Fin Numbers on Thermal Performance
4. Orthogonal Experiments
5. Conclusions
- (1)
- Compared to the initial straight-board heat sink, the cylindrical heat sink structure has a good heat dissipation ability. Under the same working conditions, the maximum temperature of the propeller driver can be reduced by 22.3%.
- (2)
- For the studied cylindrical heat sink, 29 simulation cases are carried out to analyze the influences of driver structure variables, such as base thickness, fin length, and fin numbers. It is shown that, generally speaking, the heat dissipation performance is strengthened by the increases in base thickness and fin length, as did the fin numbers. Considering the economics, there is an optimal solution for the cylindrical heat sink, that is, the heat sink with a base thickness of 40 mm, a fin length of 32 mm, and a fin number of 24.
- (3)
- Through orthogonal experiments, the base thickness has a very small impact on the working temperature of the driver. The fin numbers and the fin length have relatively greater impacts on the working temperature of the driver.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | surface area (m2) |
| a | thermal expansion coefficient (1/K) |
| cp | Specific heat capacity (J/(kg·K)) |
| F | Buoyancy force |
| Gr | Grashof number |
| g | acceleration of gravity (m/s2) |
| h | convection heat transfer coefficient |
| l | geometrically set dimensions (m) |
| p | pressure (Pa) |
| Pr | Prandtl number |
| Q | heat transfer rate (J/s) |
| Ra | Rayleigh number |
| τ | Time(s) |
| t | temperature(°C) |
| tref | boundary temperature(°C) |
| u | velocity in the x-direction (m/s) |
| v | velocity in the y-direction (m/s) |
| w | velocity in the z-direction (m/s) |
| fluid density (kg/m3) | |
| ST | viscous dissipation term |
| Su | momentum source terms in the u-velocity direction |
| Sv | momentum source terms in the v-velocity direction |
| Sw | momentum source terms in the w-velocity direction |
| kinematic viscosity (m2/s) | |
| λ | thermal conductivity (W/(m·K)) |
| internal heat source | |
| Δt | temperature difference |
| Acronyms | |
| 3D | Three-dimensional |
| DC | Direct current |
| LED | light-emitting diode |
| PCM | phase change materials |
| PCB | Printed circuit board |
References
- Zhao, M.; Zhou, J.; Sun, H.; Wu, B.H. Si-Based Embedded GaAs Chip Packaging Technology and Its Thermal Analysis. Chin. J. Electron Devices 2020, 43, 477–481. [Google Scholar]
- Pi, X.L.; Li, R.L.; Wang, L.P. Simulation Study on Heat Dissipation Efficiency Calculation of High Power Semiconductor Rectifier Chip. Comput. Simul. 2020, 37, 66–69. [Google Scholar]
- Ma, J.; Xu, N. Research on Thermal Analysis Method of Chip Based on GPU. Appl. Res. Comput. 2018, 35, 773–776. [Google Scholar]
- Niu, F.; Zhao, X.M.; Huang, S.P.; Huang, X.Y.; Wu, L.J.; Fang, Y.T. Heat dissipation optimization of high power density motor driver. Electr. Mach. Control 2022, 26, 58–67. [Google Scholar]
- Sun, F.Y. Numerical Simulation and Experiment Study on Heat Sink with Heat Pipe for Chips. Power Electron. 2021, 55, 153–156. [Google Scholar]
- Wu, H.; Chen, M.; Gao, L.M.; Li, M. Effect of Solder Layer Voids on the Thermal Resistance of Power Device Package. Semicond. Optoelectron. 2013, 34, 226–230. [Google Scholar]
- Wei, N.; Liu, S.Y.; Wan, W.J.; Sun, W.F. A New Method for Measuring Thermal Resistance of Power MOSFET. Microelectronics 2014, 44, 131–134. [Google Scholar]
- Liu, P.H.; Su, M.Y.; Li, J.; Zhou, M.H. Research on Microchannel Heat Dissipation Based on High Power Density Chip Application. Power Electron. 2021, 55, 129–132. [Google Scholar]
- Zhang, R.P.; Sun, J.; Wang, H.P.; Feng, Q. Numerical Simulation of Heat Dissipation for Multiple Electronic Chips Under Forced Air Convection Cooling Conditions. Cryog. Supercond. 2015, 43, 61–65. [Google Scholar]
- Pan, Y.; Liu, X. Experimental Investigation on Flow and Heat Transfer of High Power Electronics Radiator. Power Electron. 2020, 54, 10–12. [Google Scholar]
- Wang, D.C.; Yang, X.Y.; Yang, F.S.; Hu, R.; Wang, Z.K.; Chen, X. Thermal Research and Optimization Design of High Voltage and High Power Chip Package. Microelectronics 2018, 48, 850–854. [Google Scholar]
- Coudrain, P.; Souare, P.; Colonna, J.P.; Vivet, P.; Prieto, R.; Ben-Jamaa, H.; Le Pailleur, L. Experimental insights into thermal dissipation in TSV-based 3D integrated circuits. IEEE Des. Test Comput. 2016, 1, 1. [Google Scholar]
- Timbs, K.; Khatamifar, M.; Antunes, E.; Lin, W. Experimental study on the heat dissipation performance of straight and oblique fin heat sinks made of thermal conductive composite polymers. Therm. Sci. Eng. Prog. 2021, 22, 100848. [Google Scholar] [CrossRef]
- Arshad, A.; Jabbal, M.; Sardari, P.T.; Bashir, M.A.; Faraji, H.; Yan, Y. Transient simulation of finned heat sinks embedded with PCM for electronics cooling. Therm. Sci. Eng. Prog. 2020, 18, 100520. [Google Scholar] [CrossRef]
- Hu, X.; Gong, X.; Zhu, F.; Xing, X.; Li, Z.; Zhang, X. Thermal analysis and optimization of metal foam PCM-based heat sink for thermal management of electronic devices. Renew. Energy 2023, 212, 227–237. [Google Scholar] [CrossRef]
- Mozafari, M.; Lee, A.; Mohammadpour, J. Thermal management of single and multiple PCMs based heat sinks for electronics cooling. Therm. Sci. Eng. Prog. 2021, 23, 100919. [Google Scholar] [CrossRef]
- Zhu, K.; Liu, Z.K.; He, W.; Chai, X. Optimal Design of CPU Water-cooled Radiator in a Data Center Server. J. Refrig. 2019, 40, 36–42. [Google Scholar]
- Yang, D.; Wang, Y.; Ding, G.; Jin, Z.; Zhao, J.; Wang, G. Numerical and experimental analysis of cooling performance of single-phase array microchannel heat sinks with different pin-fin configurations. Appl. Therm. Eng. Des. Process. Equip. Econ. 2017, 112, 1547–1556. [Google Scholar] [CrossRef]
- Wang, F.Y.; Fan, X.B. Calculation and Simulation of Heat Dissipation Efficiency of High Power Semiconductor Rectifier Chip. Sci. Technol. Eng. 2018, 18, 225–231. [Google Scholar]
- Wang, H.; Yuan, L.; Wang, C.; Wang, R.Z. Structural design and heat dissipation performance of periodic shunt microchannels. Acta Phys. Sin. 2021, 70, 200–211. [Google Scholar]
- Zhang, R.P.; Chen, C.; Wang, Y.F. Numerical study of electronic cooling based on phase change heat transfer of heat pipe. Cryog. Supercond. 2016, 44, 88–92. [Google Scholar]
- Yang, Z. Performance study of U—Shape flow channel water cooling radiator in data center server. Cryog. Supercond. 2019, 47, 91–96. [Google Scholar]
- Wu, L.W.; Lu, T.; Chen, J.J.; Wang, M.Y. A Study of Bionic Micro-channel Topology for Chip Cooling. Acta Electron. Sin. 2018, 46, 1153–1159. [Google Scholar]
- He, W.; Zhang, J.; Guo, R.; Pei, C.; Li, H.; Liu, S.; Wang, Y. Performance analysis and structural optimization of a finned liquid-cooling radiator for chip heat dissipation. Appl. Energy 2022, 327, 120048. [Google Scholar] [CrossRef]
- Song, G.; Kim, D.H.; Song, D.H.; Sung, J.B.; Yook, S.J. Heat-dissipation performance of cylindrical heat sink with perforated fins. Int. J. Therm. Sci. 2021, 170, 107132. [Google Scholar] [CrossRef]
- Bello-Ochende, T.; Liebenberg, L.; Meyer, J.P. Constructal cooling channels for micro-channel heat sinks. Int. J. Heat Mass Transf. 2007, 50, 4141–4150. [Google Scholar] [CrossRef]
- Khalid, S.U.; Hasnain, S.; Ali, H.M.; Bano, S.; Nasir, M.A.; Abbas, N. Experimental investigation of aluminum fins on relative thermal performance of sintered copper wicked and grooved heat pipes. Prog. Nucl. Energy 2022, 152, 104374. [Google Scholar] [CrossRef]
- Krstic, M.; Pantic, L.; Djordjevic, S.; Radonjic, I.; Begovic, V.; Radovanovic, B.; Mancic, M. Passive cooling of photovoltaic panel by aluminum heat sinks and numerical simulation. Ain Shams Eng. J. 2023; in press. [Google Scholar]
- Nemati, H. A general equation based on entropy generation minimization to optimize plate fin heat sink. Eng. J. 2018, 22, 159–174. [Google Scholar] [CrossRef]
- Zhu, Y.M.; Zheng, H.; Luo, X.B. Thermal Performance Study of a Novel Automotive Headlamps LED Module With Double Substrates. J. Eng. Thermophys. 2016, 37, 390–393. [Google Scholar]
- Holman, J.P. Heat Transfer; China Machine Press: Beijing, China, 2005. [Google Scholar]
- Li, B. FloTHERM Software Foundation and Application Example; China Water & Power Press: Beijing, China, 2014. [Google Scholar]
- Li, H.Q.; Wei, L.P.; Zhuang, Z.X.; Zheng, M.S. Temperature Control Characteristics And Heat Dissipation Structure Optimization Design Of Photovoltaic Phase Change System. Acta Energ. Sol. Sin. 2022, 43, 57–62. [Google Scholar]








| Layer Name | Size (mm) | Main Heating Component | Power of the Main Heating Component (W) | Quantity of the Main Heating Component |
|---|---|---|---|---|
| 1st PCB layer | 36 × 30 × 0.8 | U1 | 0.15 | 1 |
| 2nd PCB layer | 36 × 30 × 0.8 | U2 | 0.1 | 1 |
| 3rd PCB layer | 36 × 33 × 0.4 | U3 | 0.35 | 1 |
| 4th PCB layer | 36 × 33 × 0.4 | U4 | 1 | 6 |
| Component Name | Material | Thermal Conductivity (W/(m·K)) |
|---|---|---|
| U1 | silicon | 419 |
| U2 | silicon | 419 |
| U3 | silicon | 419 |
| U4 | silicon | 419 |
| Driving plate | FR4 | 0.3 |
| Base | Al6063 | 201 |
| Heat sink | Al6063 | 201 |
| Column | Plastic Package | 5 |
| Column | Cu | 385 |
| Maximum Grid Size (mm) | Number of Grids | Monitoring Point Temperature (°C) |
|---|---|---|
| 4 | 2,405,352 | 54.84 |
| 3 | 4,225,221 | 55.61 |
| 2.5 | 6,341,556 | 55.34 |
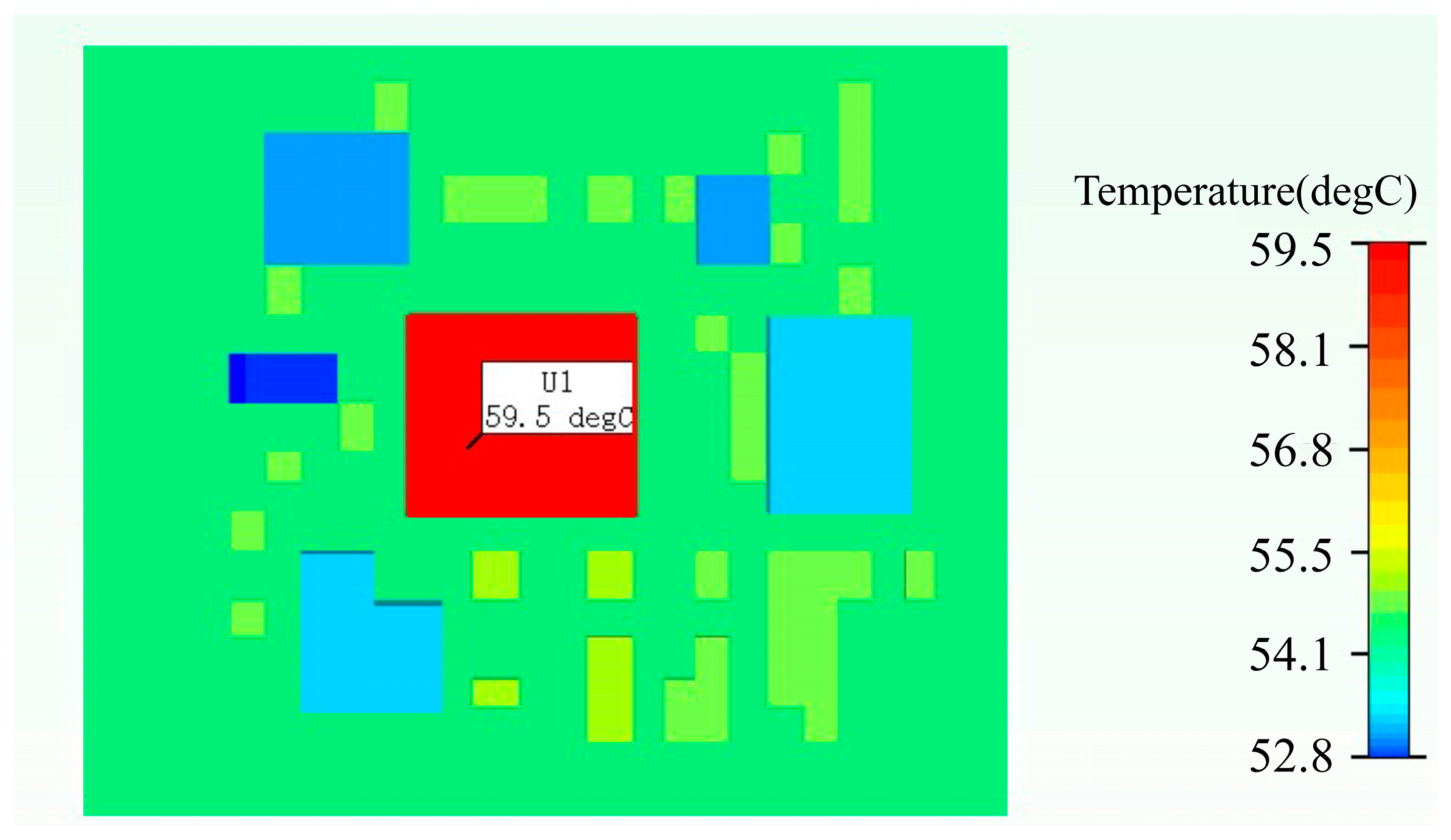
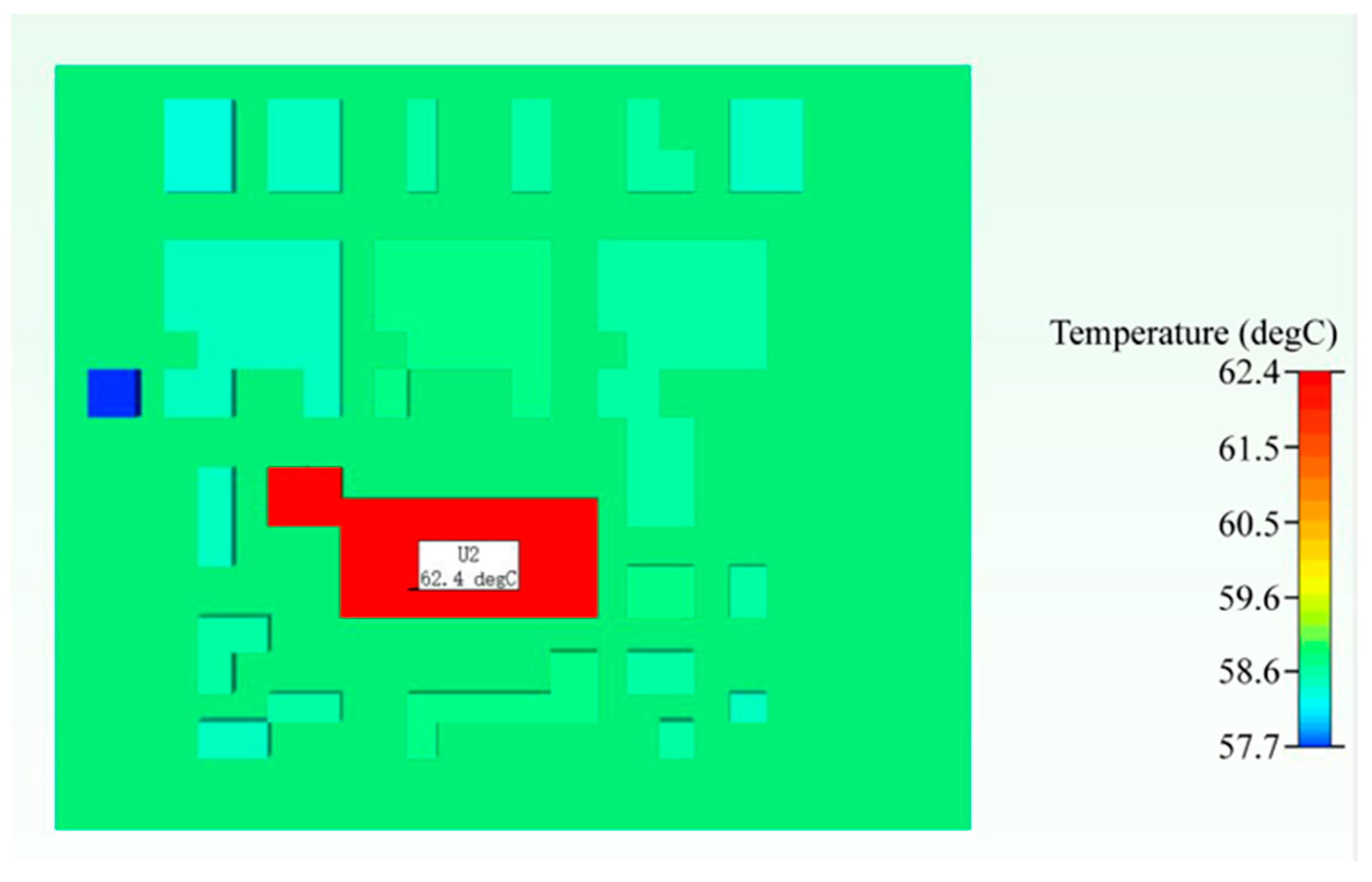
| Temperature Measurement Position | 1st PCB Layer | 2nd PCB Layer | 3rd PCB Layer | The Connection between the Base and Heat Sink |
|---|---|---|---|---|
| Simulation results/°C | 59.5 | 62.4 | 65.6 | 63.8 |
| Experimental results/°C | 59.6 | 64.4 | 66 | 63.3 |
| No. | Base Thickness/mm | Fin Number | Fin Length/ mm | Maximum Temperature/°C |
|---|---|---|---|---|
| 1 | 20 | 4 | 12 | 54.1 |
| 2 | 20 | 8 | 24 | 49.4 |
| 3 | 20 | 12 | 36 | 45.9 |
| 4 | 30 | 4 | 24 | 51.7 |
| 5 | 30 | 8 | 36 | 47.6 |
| 6 | 30 | 12 | 12 | 51.1 |
| 7 | 40 | 4 | 36 | 50.6 |
| 8 | 40 | 8 | 12 | 52.6 |
| 9 | 40 | 12 | 24 | 47.2 |
| Maximum Temperature | Maximum Temperature/°C | |||
|---|---|---|---|---|
| Variable 1 | Variable 2 | Variable 3 | Variance | |
| Factor 1 | 49.80 | 50.13 | 50.13 | 0.0363 |
| Factor 2 | 52.13 | 49.87 | 48.07 | 4.1385 |
| Factor 3 | 52.60 | 49.43 | 48.03 | 5.4823 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, N.; Lv, M.; Pan, H. The Thermal Analysis and Heat Dissipation Structure Optimization of a Propeller Driver System. Appl. Sci. 2023, 13, 7495. https://doi.org/10.3390/app13137495
Lai N, Lv M, Pan H. The Thermal Analysis and Heat Dissipation Structure Optimization of a Propeller Driver System. Applied Sciences. 2023; 13(13):7495. https://doi.org/10.3390/app13137495
Chicago/Turabian StyleLai, Ningchuan, Ming Lv, and Huachen Pan. 2023. "The Thermal Analysis and Heat Dissipation Structure Optimization of a Propeller Driver System" Applied Sciences 13, no. 13: 7495. https://doi.org/10.3390/app13137495
APA StyleLai, N., Lv, M., & Pan, H. (2023). The Thermal Analysis and Heat Dissipation Structure Optimization of a Propeller Driver System. Applied Sciences, 13(13), 7495. https://doi.org/10.3390/app13137495





