The Kinematic Investigation of the Stephenson-III Spherical Mechanism with a Spherical Slider Containing a Spherical Prismatic Pair
Abstract
:Featured Application
Abstract
1. State-of-the-Art in Studying Spherical Mechanisms
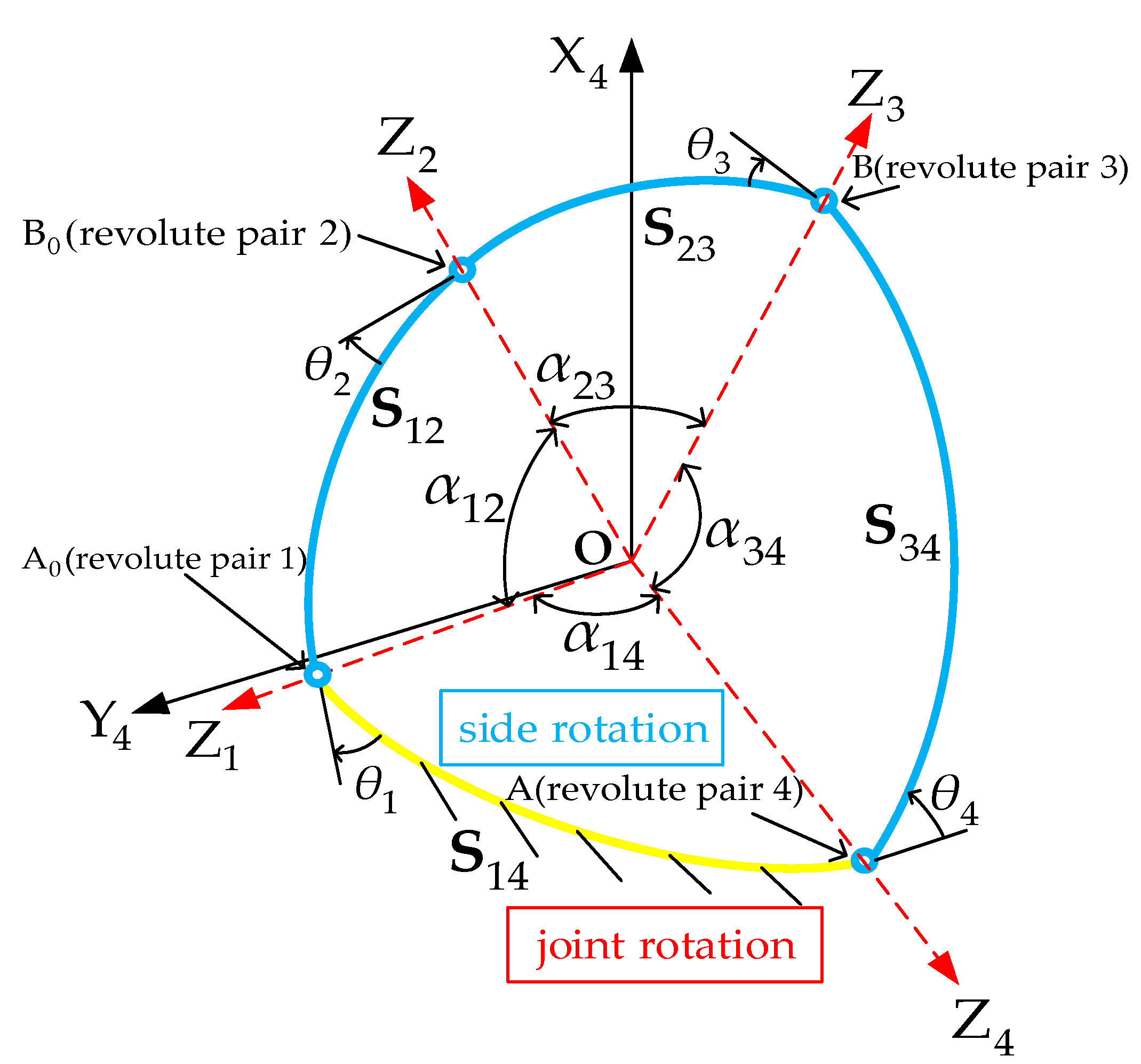
2. The Loop Equation of the Single-DOF Spherical Kinematic Chain with Only Revolute Pairs
3. Kinematics of the Stephenson-III Spherical Mechanism with a Spherical Slider Containing a Spherical Prismatic Pair
3.1. The Loop Equation
3.2. The Branch Graph of the Proposed Spherical Mechanism
3.2.1. The Type-One Branch Graph
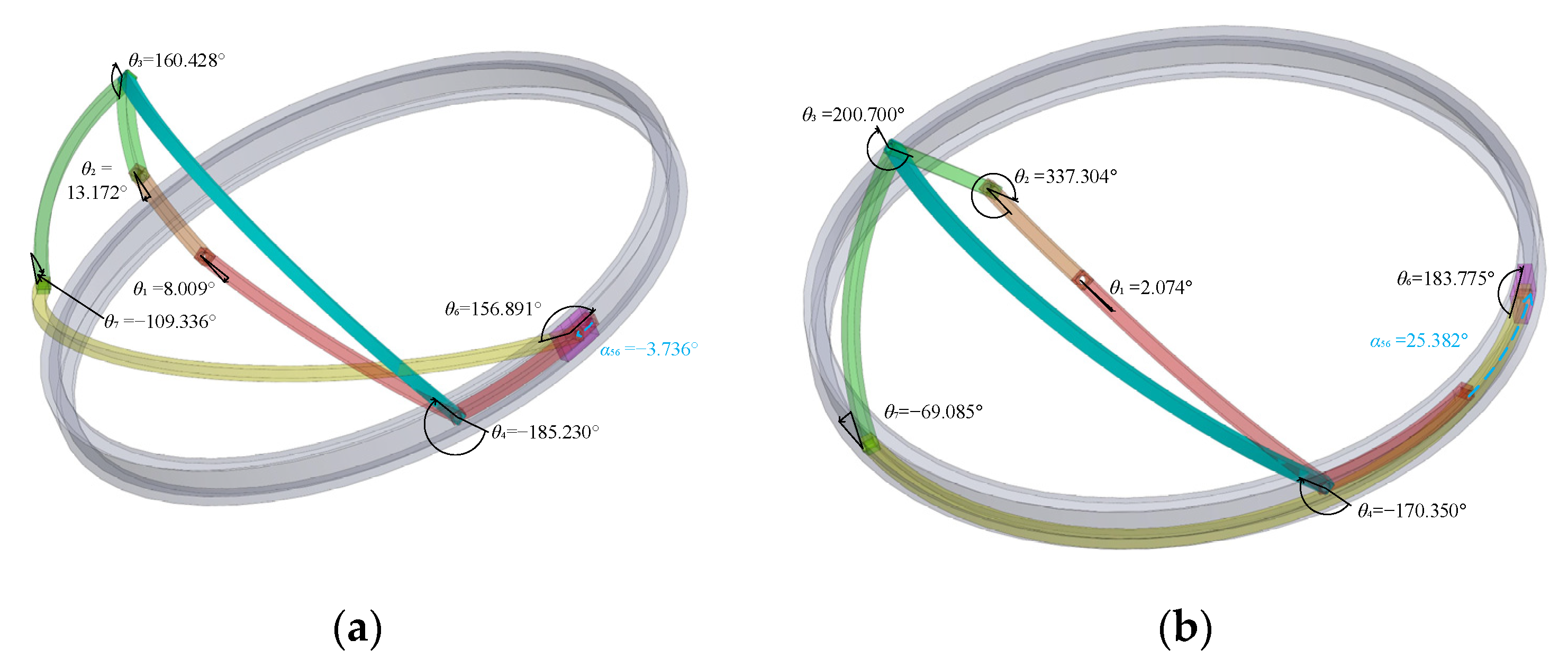
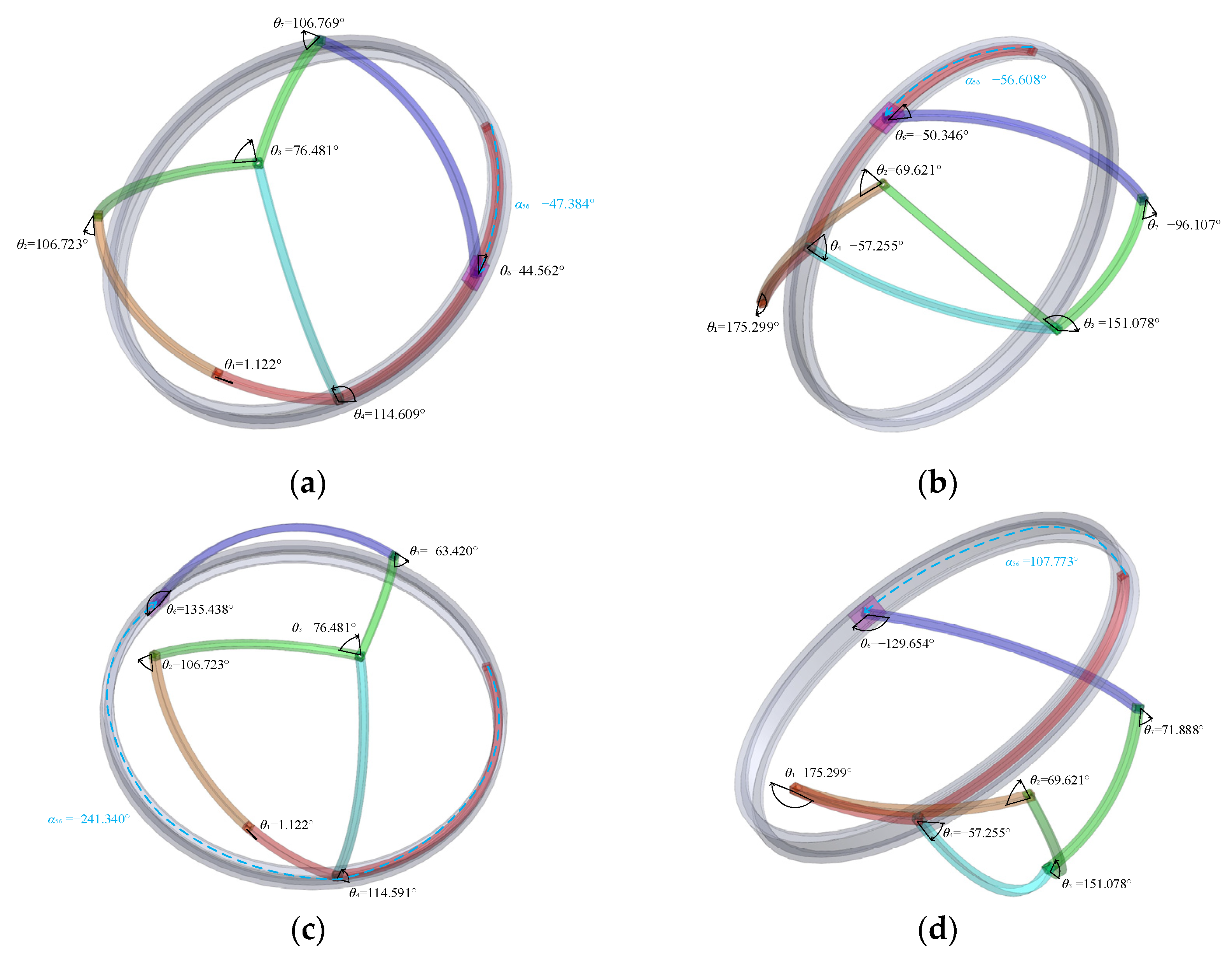
3.2.2. The Type-Two Branch Graph
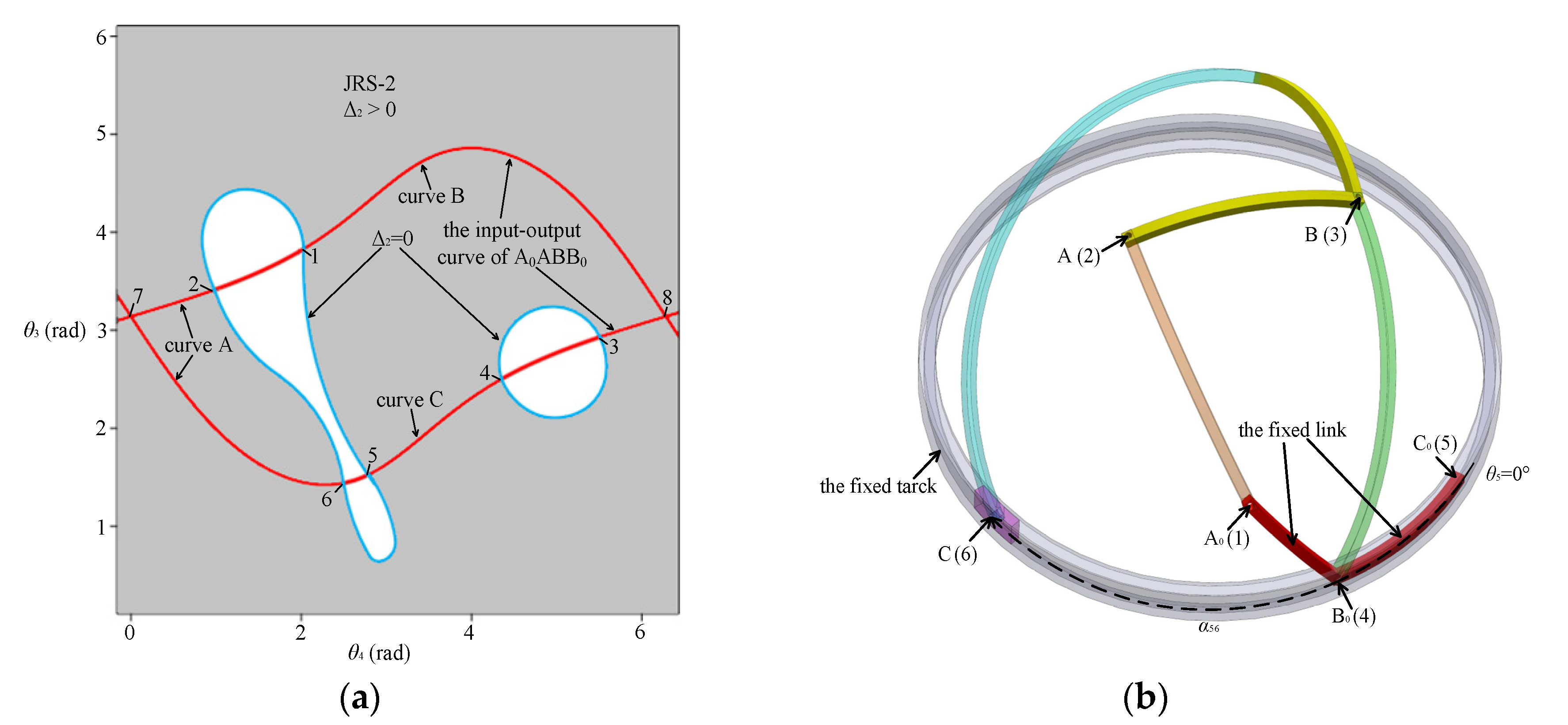
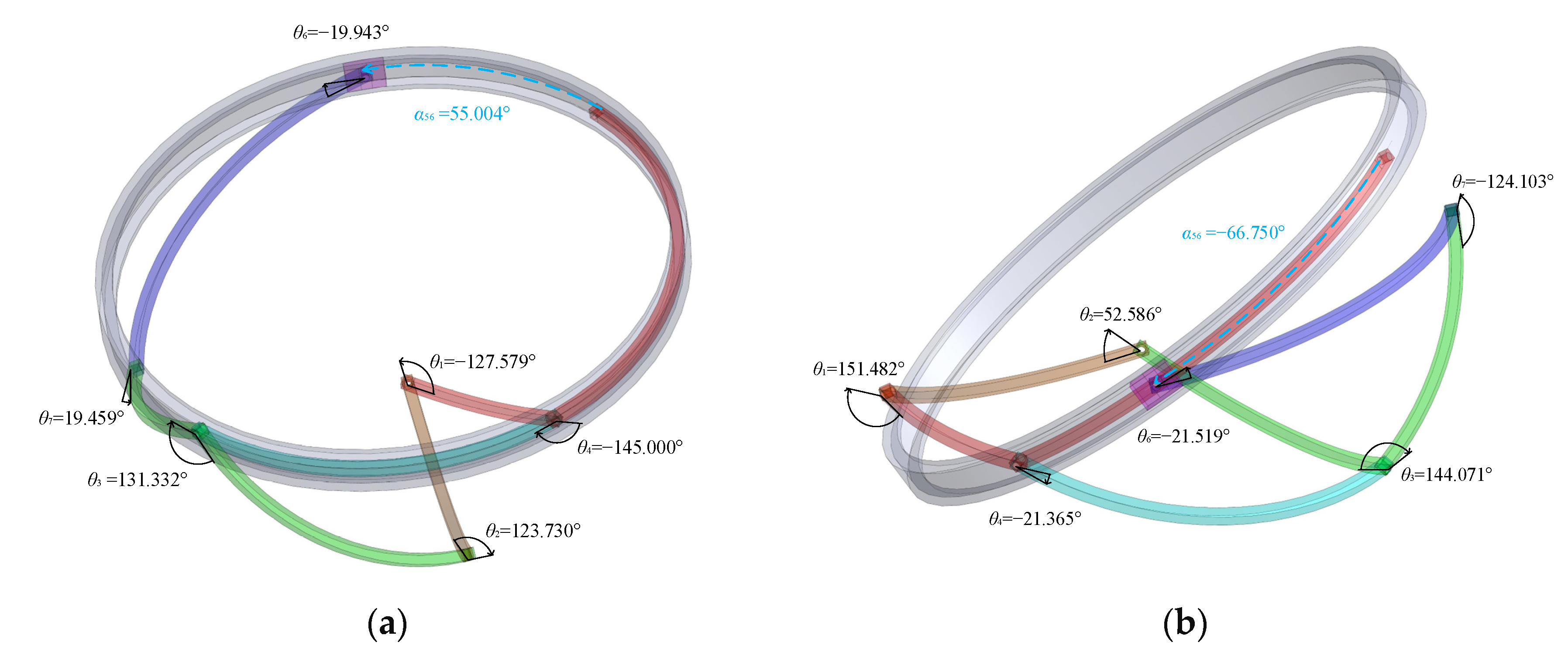
3.2.3. The Special Type-One Branch Graph
4. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nelson, C.A.; Laribi, M.A.; Zeghloul, S. Multi-robot system optimization based on redundant serial spherical mechanism for robotic minimally invasive surgery. Robotica 2019, 124, 1202–1213. [Google Scholar] [CrossRef]
- Castro, M.N.; Rasmussen, J.; Wang, Y.; Andersen, M.S.; Bai, S. A compact 3-DOF shoulder mechanism constructed with scissors linkages for exoskeleton applications. Mech. Mach. Theory 2019, 132, 264–278. [Google Scholar] [CrossRef]
- Ting, K.L.; Liu, Y.W. Rotatability laws for n-bar kinematic chains and their proof. J. Mech. Des. 1991, 113, 32–39. [Google Scholar] [CrossRef]
- Liu, Y.W.; Ting, K.L. On the rotatability of spherical n-bar chains. J. Mech. Des. 1994, 116, 920–923. [Google Scholar] [CrossRef]
- Ting, K.L. On the input joint rotation space and mobility of linkages. J. Mech. Des. 2008, 130, 092303. [Google Scholar] [CrossRef]
- Wang, J.; Ting, K.L.; Xue, C. Discriminant method for the mobility identification of single degree-of-freedom double-loop linkages. Mech. Mach. Theory 2010, 4, 740–755. [Google Scholar] [CrossRef]
- Wang, J.; Nie, L.; Wang, Q.; Sun, J.; You, Y.; Zhao, D.; Ting, K.L. Singularity analysis of planar multiple-DOF linkages. In Proceedings of the ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014; paper no: DETC2014-34213, V05AT08A051. ASME: New York, NY, USA, 2014. [Google Scholar]
- Ting, K.L.; Wang, J.; Xue, C.; Currie, K.R. Full rotatability and singularity of six-bar and geared five-bar linkages. J. Mech. Robot. 2010, 2, 298–300. [Google Scholar] [CrossRef]
- Ting, K.L.; Dou, X. classification and branch identification of Stephenson six-bar chains. Mech. Mach. Theory 1996, 31, 283–295. [Google Scholar] [CrossRef]
- Nie, L.; Wang, J.; Ting, K.L.; Zhao, D.; Wang, Q.; Ren, J.; Sun, J. Branch identification of spherical six-bar linkages. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; paper no. DETC2016-59018, V05BT07A072. ASME: Charlotte, NC, USA, 2016. [Google Scholar]
- Nie, L.; Ding, H.; Kecskemethy, A.; Gan, J.; Wang, J.; Ting, K.L. Singularity and branch identification of a 2 degree-of-freedom (DOF) seven-bar spherical parallel mechanism. Mech. Sci. 2020, 11, 381–393. [Google Scholar] [CrossRef]
- Hsu, K.L.; Lai, P.Y. Kinematic and mechanical error analysis of serial spherical linkages using a modular approach. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2022, 236, 9504–9526. [Google Scholar] [CrossRef]
- Essomba, T.; Vu, L.N. Kinematic analysis of a new five-bar spherical decoupled mechanism with two-degrees-of-freedom remote center of motion. Mech. Mach. Theory 2017, 119, 184–197. [Google Scholar] [CrossRef]
- Essomba, T.; Vu, L.N.; Wu, C.T. Optimization of a spherical decoupled mechanism for neuro-endoscopy based on experimental kinematic data. J. Mech. 2020, 36, 133–147. [Google Scholar] [CrossRef]
- Essomba, T.; Hsu, Y.; Arevalo, J.S.S.; Laribi, M.A.; Zeghloul, S. Kinematic optimization of a reconfigurable spherical parallel mechanism for robotic-assisted craniotomy. J. Mech. Robot. 2019, 11, 060905. [Google Scholar] [CrossRef]
- Valderrama-Rodriguez, J.I.; Rico, J.M.; Cervantes-Sanchez, J.J. A screw theory approach to compute instantaneous rotation axes of indeterminate spherical linkages. Mech. Based Des. Struct. Mach. 2020, 50, 2836–2876. [Google Scholar] [CrossRef]
- Sun, J.; Liu, W.; Chu, J. Synthesis of spherical four-bar linkage for open path generation using wavelet feature parameters. Mech. Mach. Theory 2018, 128, 33–46. [Google Scholar] [CrossRef]
- Danaei, B.; Arian, A.; Masouleh, M.T.; Kalhor, A. Dynamic modeling and base inertial parameters determination of a 2-DOF spherical parallel mechanism. Multibody Syst. Dyn. 2017, 41, 367–390. [Google Scholar] [CrossRef]
- Wu, G.; Bai, S. Design and kinematic analysis of a 3-RRR spherical parallel manipulator reconfigured with four bar linkages. Robot. Comput. Integr. Manuf. 2019, 56, 55–65. [Google Scholar] [CrossRef]
- Palpacelli, M.; Palmieri, G.; Carbonari, L.; Corinaldi, D. Sensitivity analysis and model validation of a 2-DOF Mini Spherical Robot. J. Intell. Robot. Syst. 2018, 91, 155–163. [Google Scholar] [CrossRef]
- Elgolli, H.; Houidi, A.; Mlika, A.; Romdhane, L. Analytical analysis of the dynamic of a spherical parallel mechanism. Int. J. Adv. Manuf. Technol. 2019, 101, 859–871. [Google Scholar] [CrossRef]
- Hhan, N.H.K.; Tung, V.D.; Kheylo, S.; Victor, G. Oscillations and control of spherical parallel manipulator. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419846394. [Google Scholar]
- Ma, X.; Zhang, K.; Dai, J. Novel spherical-planar and Bennett-spherical 6R metamorphic linkages with reconfigurable motion branches. Mech. Mach. Theory 2018, 128, 628–647. [Google Scholar] [CrossRef]
- Wang, J.; Kong, X. A geometric approach to the static balancing of mechanisms constructed using spherical kinematic chain units. Mech. Mach. Theory 2019, 140, 305–320. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, C. Design and analysis of a novel reconfigurable parallel manipulator with Kirigami-inspired Bennett Plano-spherical linkages and angular pouch motors. J. Mech. Robot. 2021, 13, 040911. [Google Scholar] [CrossRef]
- Chen, G.; Yu, W.; Wang, H.; Wang, J. Design and kinematic analysis of a spherical parallel manipulator using concurrent planar parallelogram linkages. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2019, 233, 2491–2501. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Wang, Y.; Bai, S. Kinematic design and analysis of a 6-DOF spatial five-bar linkage. Mech. Mach. Theory 2021, 158, 104227. [Google Scholar] [CrossRef]
- Wang, R.; Song, Y.; Dai, J.S. Reconfigurability of the Origami-inspired integrated 8R kinematotropic metamorphic mechanism and its evolved 6R and 4R mechanisms. Mech. Mach. Theory 2021, 161, 104245. [Google Scholar] [CrossRef]
- Kumar, S.; Bongardt, B.; Simnofske, M.; Kirchner, F. Design and kinematic analysis of the novel almost spherical parallel mechanism active ankle. J. Intell. Robot. Syst. 2019, 94, 303–325. [Google Scholar] [CrossRef]
- Bai, S.; Li, X.; Angeles, J. A review of spherical motion generation using either spherical parallel manipulators or spherical motors. Mech. Mach. Theory 2019, 140, 377–388. [Google Scholar] [CrossRef]
- Chen, X.; Sun, C. Dynamic Modeling of Spatial Parallel Mechanism with Multi-Spherical Joint Clearances. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419875910. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liang, F.; Zhou, H.; Yang, M.; Wang, Q. Analysis of position, pose and force decoupling characteristics of a 4-UPS/1-RPS parallel grinding robot. Symmetry 2022, 14, 825. [Google Scholar] [CrossRef]
- Enferadi, J.; Tootoonchi, A.A. A novel spherical parallel manipulator: Forward position problem, singularity analysis, and isotropy design. Robotica 2009, 27, 663–676. [Google Scholar] [CrossRef] [Green Version]
- Saiki, N.; Tadakuma, K.; Watanabe, M.; Takane, E.; Nobutoki, M.; Suzuki, S.; Konyo, M.; Tadokoro, S. 2-DOF spherical parallel mechanism capable of biaxial swing motion with active arc sliders. IEEE Robot. Autom. Lett. 2021, 6, 4680–4687. [Google Scholar] [CrossRef]
- Saiki, N.; Tadakuma, K.; Wantanabe, M.; Abe, K.; Konyo, M.; Tadokoro, S. Experimental study of the Mechanical properties of a spherical parallel link mechanism with arc prismatic pairs. IEEE Robot. Autom. Lett. 2022, 7, 11221–11227. [Google Scholar] [CrossRef]
- Hou, Y.; Hu, X.; Zeng, D.; Zhou, Y. Biomimetic shoulder complex based on 3-PSS/S spherical parallel mechanism. Chin. J. Mech. Eng. 2015, 28, 29–37. [Google Scholar] [CrossRef]
- Sun, J.; Lu, H.; Chu, J. Variable step-size numerical atlas method for path generation of spherical four-bar crank-slider mechanism. Inverse Probl. Sci. Eng. 2014, 23, 256–276. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Z.; Liu, W.; Sun, J.; Lu, H. Dimensional synthesis of a spherical linkage crank slider mechanism for motion generation using an optimizing algorithm. Mech. Sci. 2023, 14, 125–142. [Google Scholar] [CrossRef]

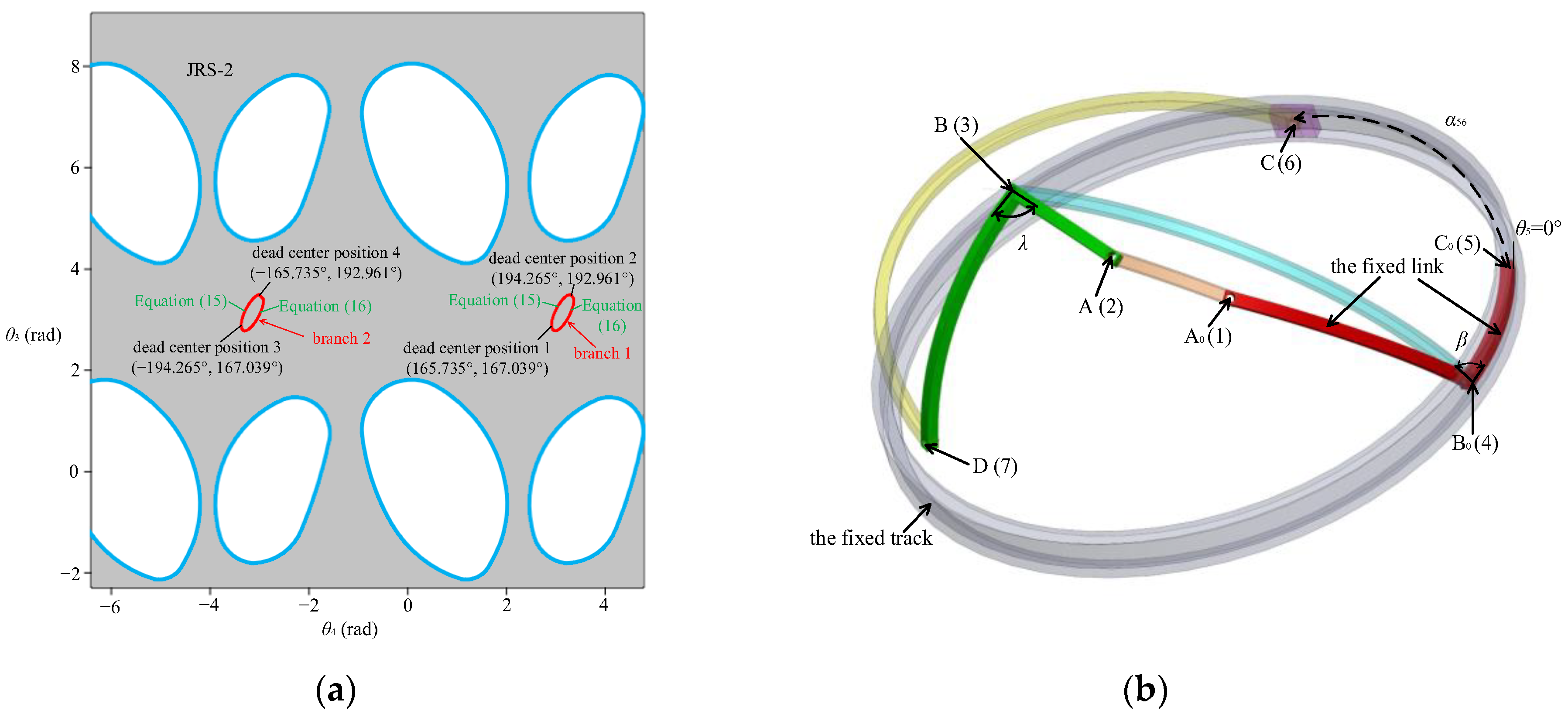




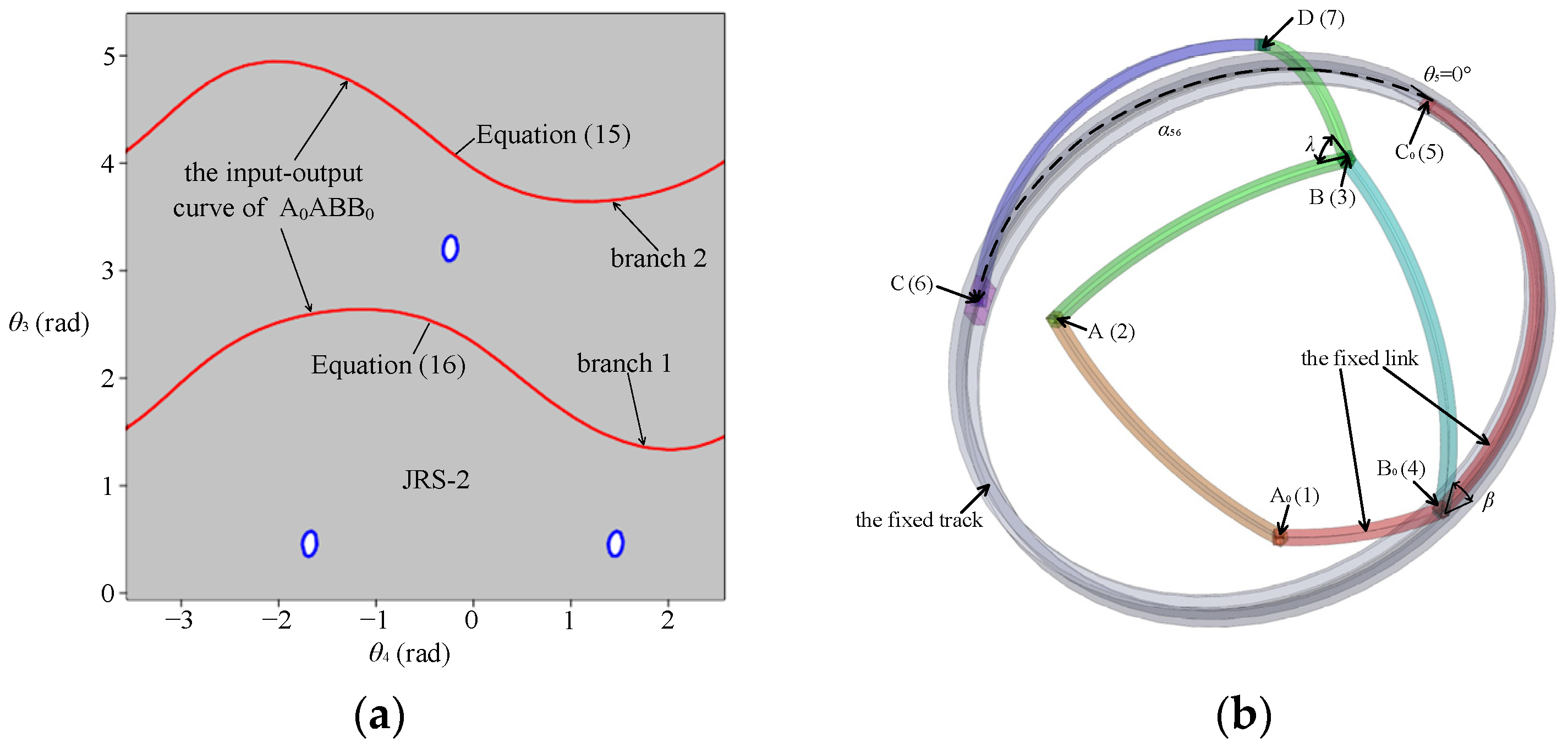
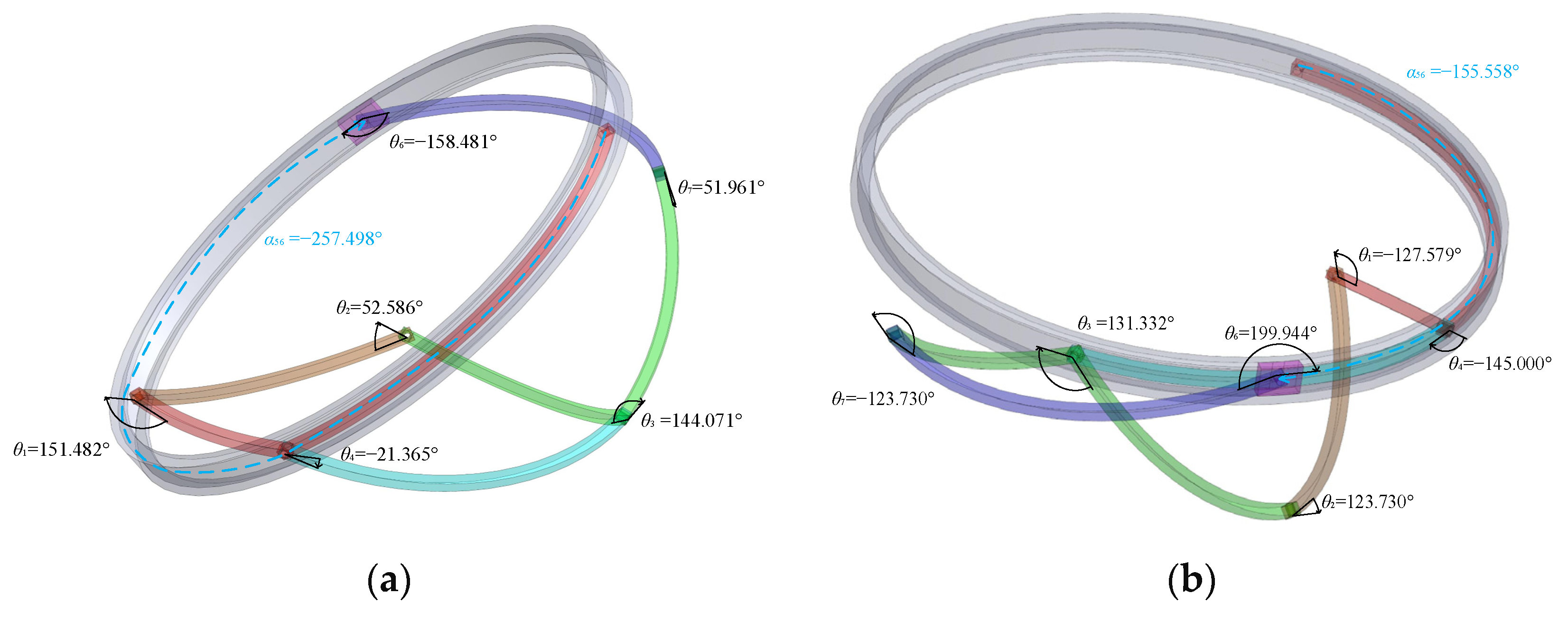
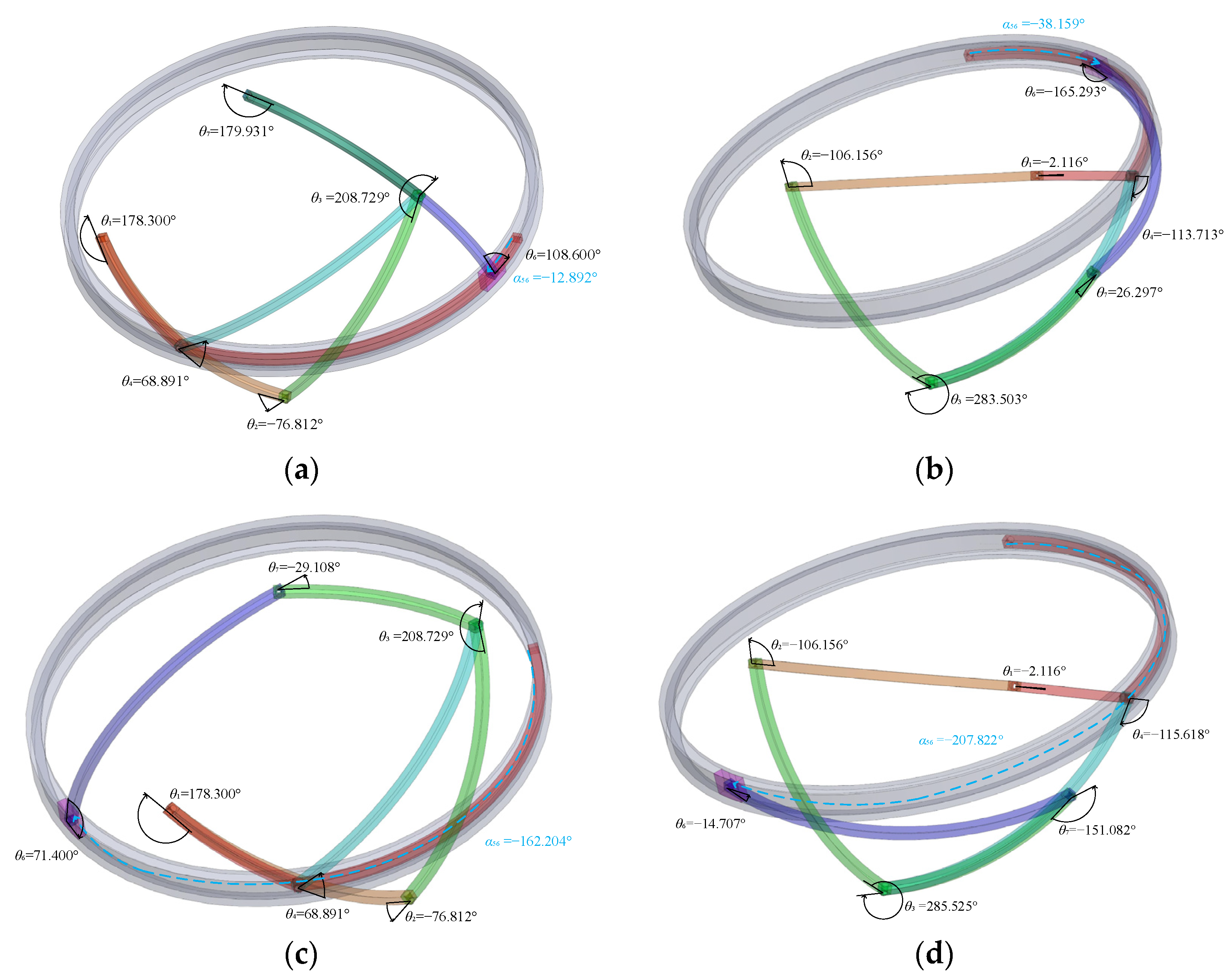

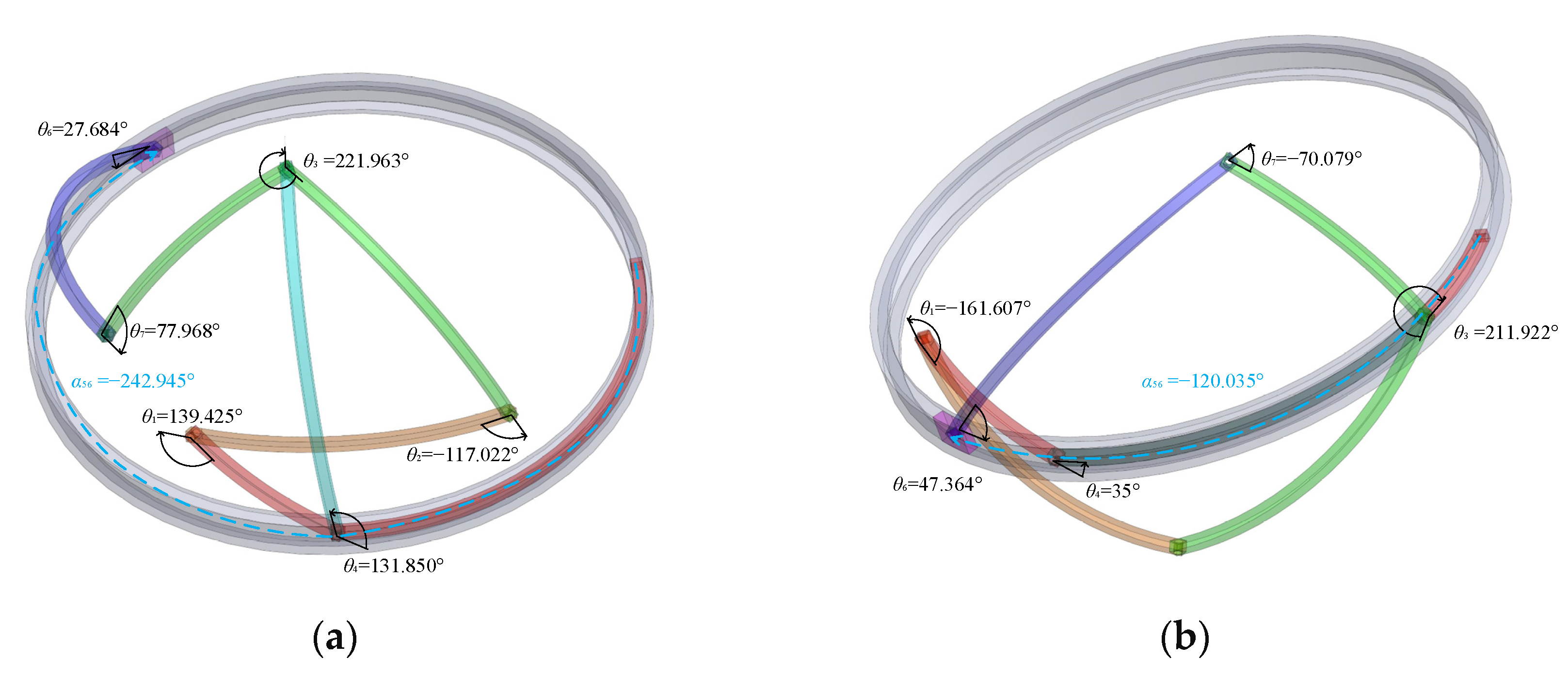
| parameters | α41 | α12 | α23 | α34 | α45 | α67 | α73 | θ5 | β | λ |
| values | 54.1° | 22.5° | 25° | 100° | 30° | 140° | 50° | 0° | 55° | 95° |
| Joint | θ3 | θ4 |
|---|---|---|
| Dead center position 1 | 165.735° | 167.039° |
| Dead center position 2 | 194.265° | 192.961° |
| Dead center position 3 | 165.735° | 192.961° |
| Dead center position 3 | 194.265° | 167.039° |
| parameters | α41 | α12 | α23 | α34 | α45 | α67 | α73 | θ5 | β | λ |
| values | 30° | 60° | 50° | 80° | 35° | 130° | 50° | 0° | 55° | 95° |
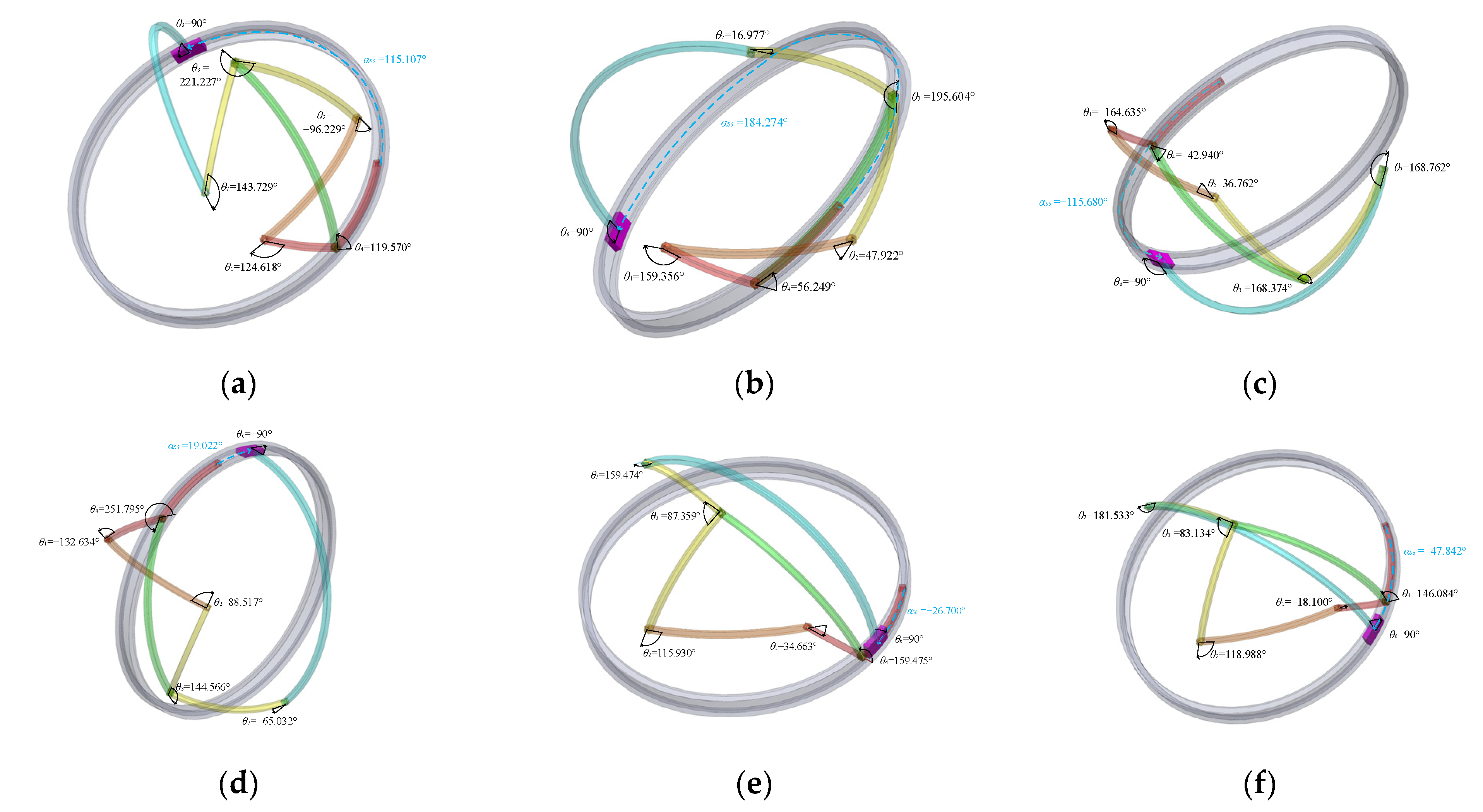
| Branch Points | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| θ3 | 221.227° | 195.604° | 168.374° | 144.566° | 87.359° | 83.134° |
| θ4 | 119.570° | 56.249° | 317.060° | 251.795° | 159.475° | 146.084° |
| α56 | 115.107° | 184.274° | 115.680° | 19.022° | 26.700° | 47.842° |
| θ1 | 124.618° | 162.090° | 164.635° | 132.634° | 34.663° | 18.100° |
| θ2 | 96.229° | 47.922° | 36.762° | 88.517° | 115.903° | 118.988° |
| θ6 | 90° | 90° | 90° | 90° | 90° | 90° |
| θ7 | 143.729° | 16.977° | 168.762° | 65.032° | 159.474° | 181.533° |
| parameters | α41 | α12 | α23 | α34 | α45 | α67 | α73 | θ5 | β | λ |
| values | 34° | 63° | 67° | 77° | 100° | 85° | 50° | 0° | 35° | 105° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Yang, M.; Huang, Y. The Kinematic Investigation of the Stephenson-III Spherical Mechanism with a Spherical Slider Containing a Spherical Prismatic Pair. Appl. Sci. 2023, 13, 7454. https://doi.org/10.3390/app13137454
Wang J, Yang M, Huang Y. The Kinematic Investigation of the Stephenson-III Spherical Mechanism with a Spherical Slider Containing a Spherical Prismatic Pair. Applied Sciences. 2023; 13(13):7454. https://doi.org/10.3390/app13137454
Chicago/Turabian StyleWang, Jun, Mingquan Yang, and Yizhe Huang. 2023. "The Kinematic Investigation of the Stephenson-III Spherical Mechanism with a Spherical Slider Containing a Spherical Prismatic Pair" Applied Sciences 13, no. 13: 7454. https://doi.org/10.3390/app13137454
APA StyleWang, J., Yang, M., & Huang, Y. (2023). The Kinematic Investigation of the Stephenson-III Spherical Mechanism with a Spherical Slider Containing a Spherical Prismatic Pair. Applied Sciences, 13(13), 7454. https://doi.org/10.3390/app13137454






