Loads on the Knee Joint Ligaments during Stair Climbing
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
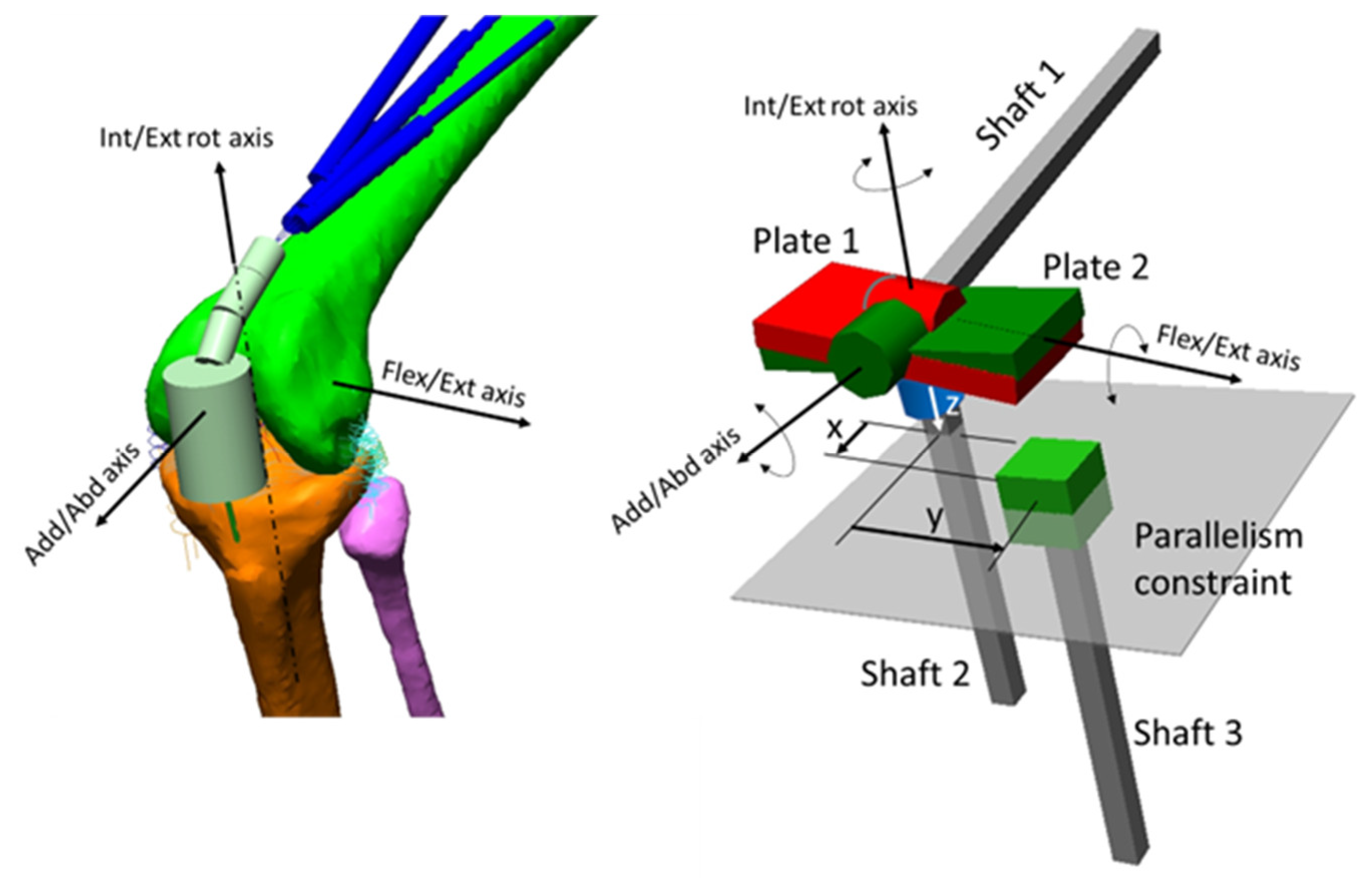
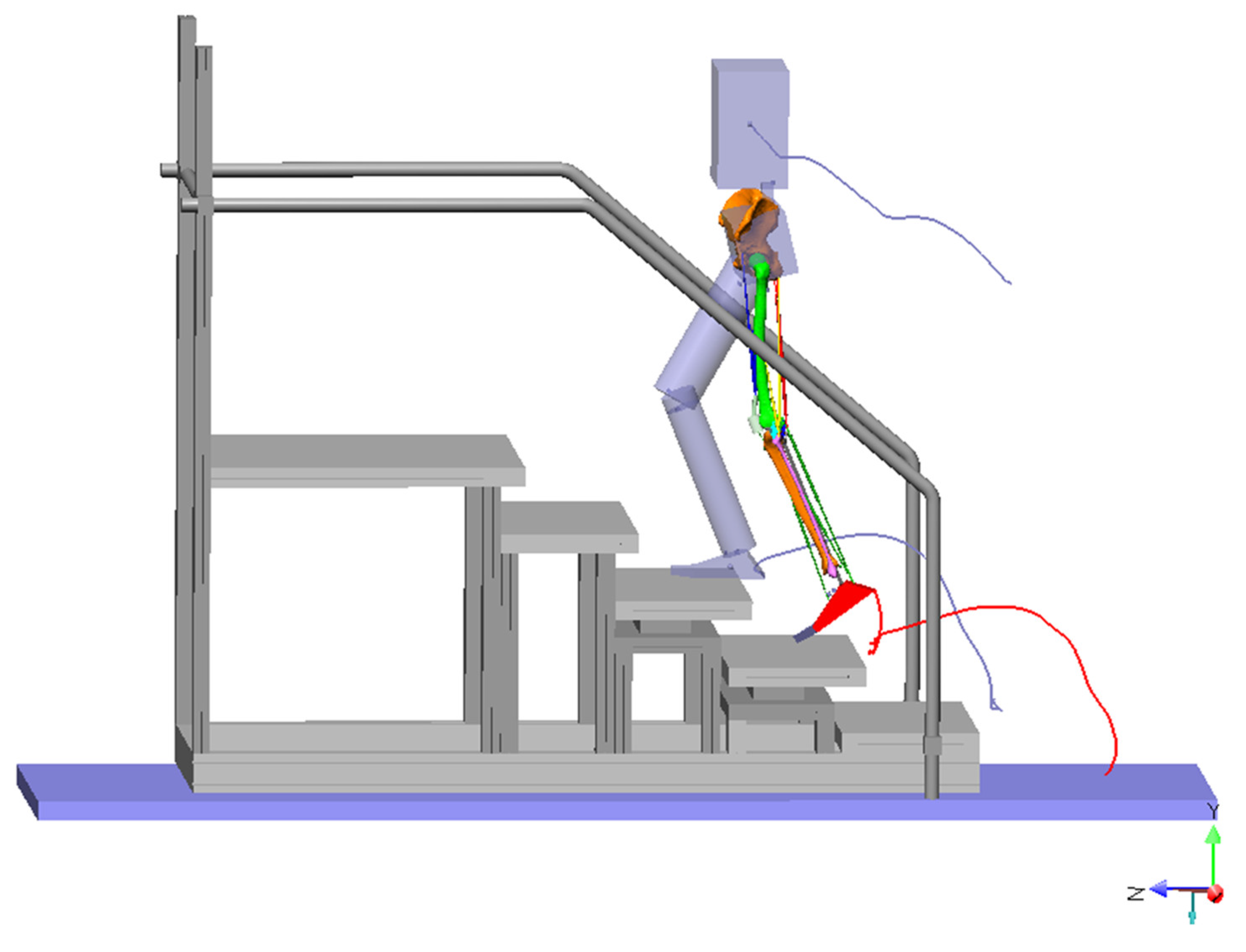
2.1. The Model
2.1.1. The Driving Model
2.1.2. The Musculoskeletal Model
2.2. The Inputs to the Model
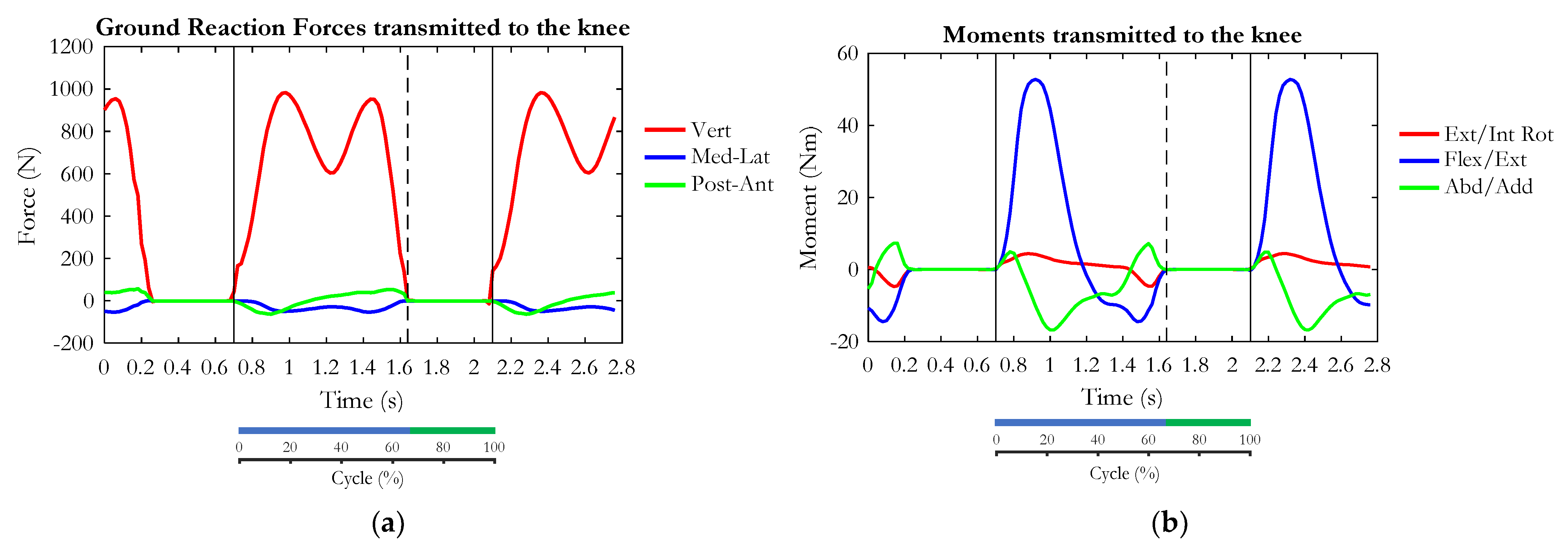
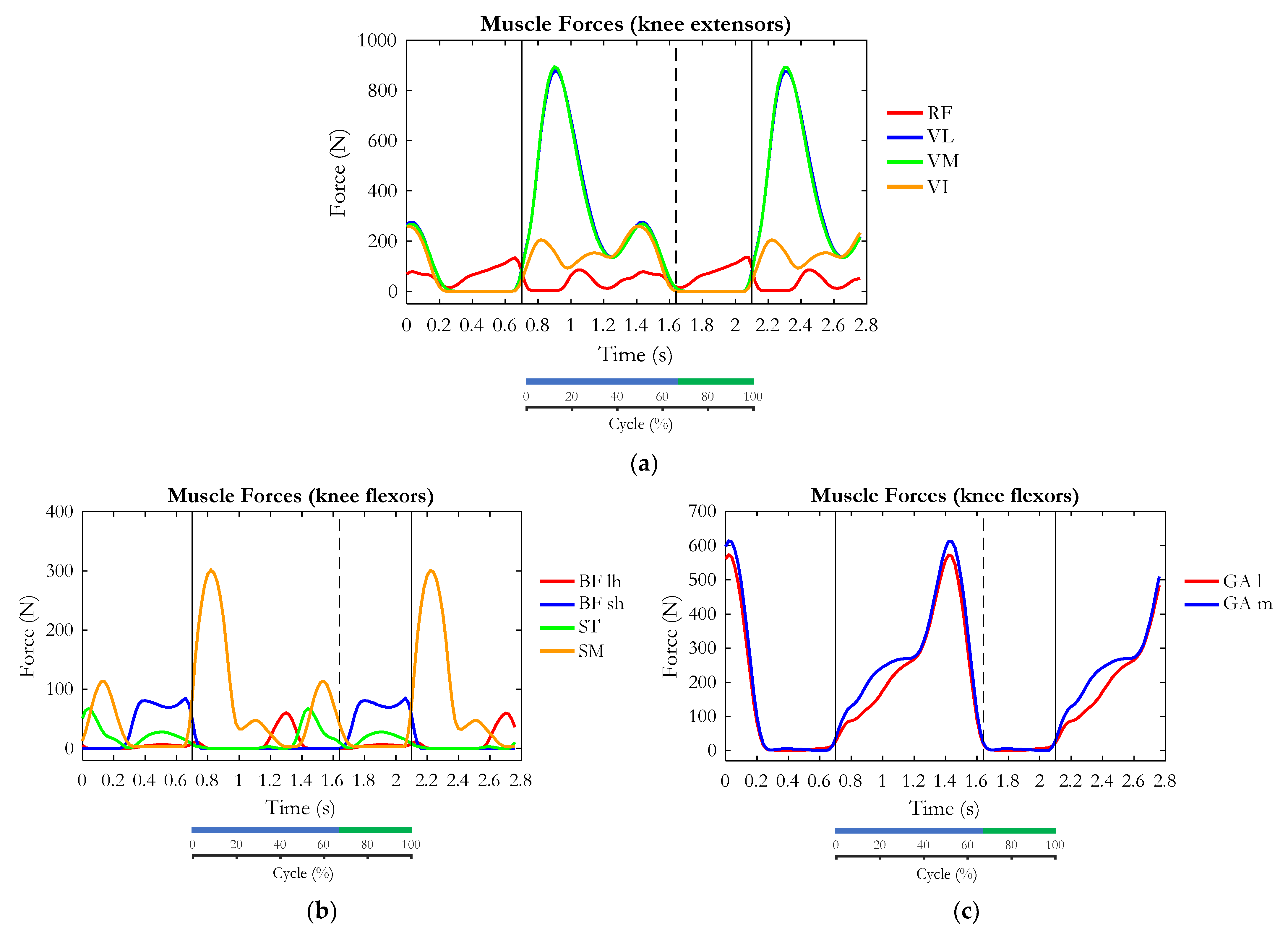
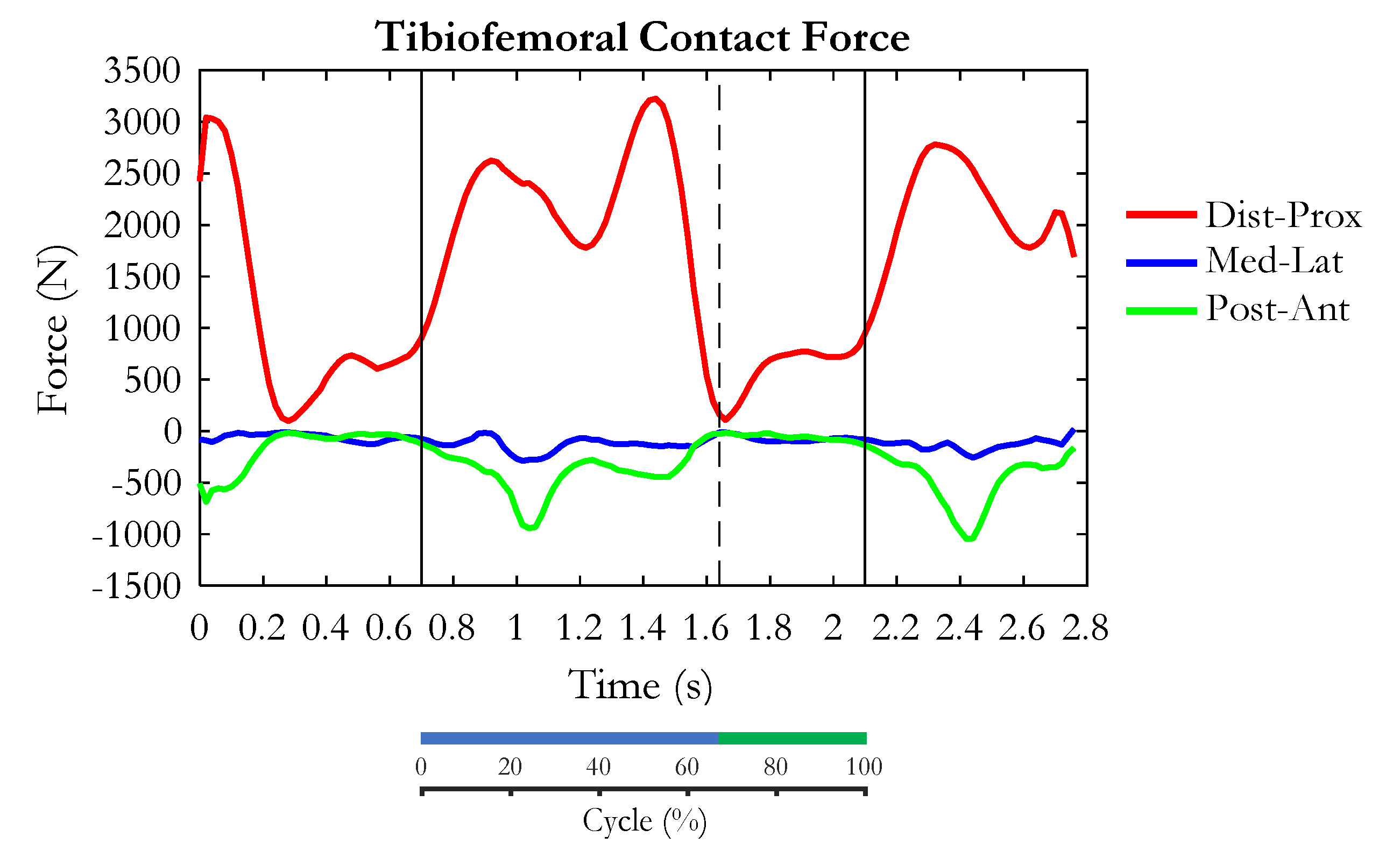
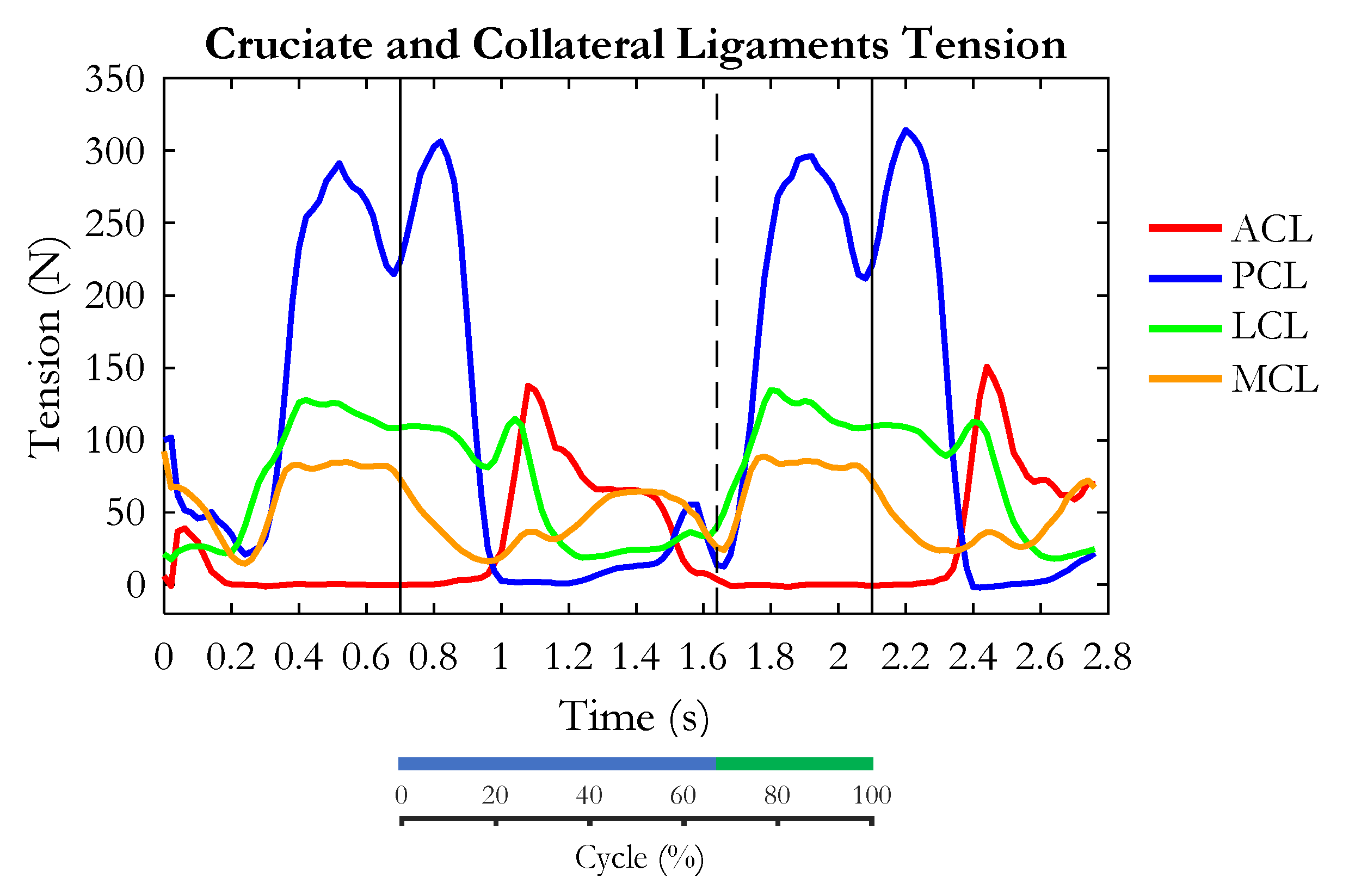
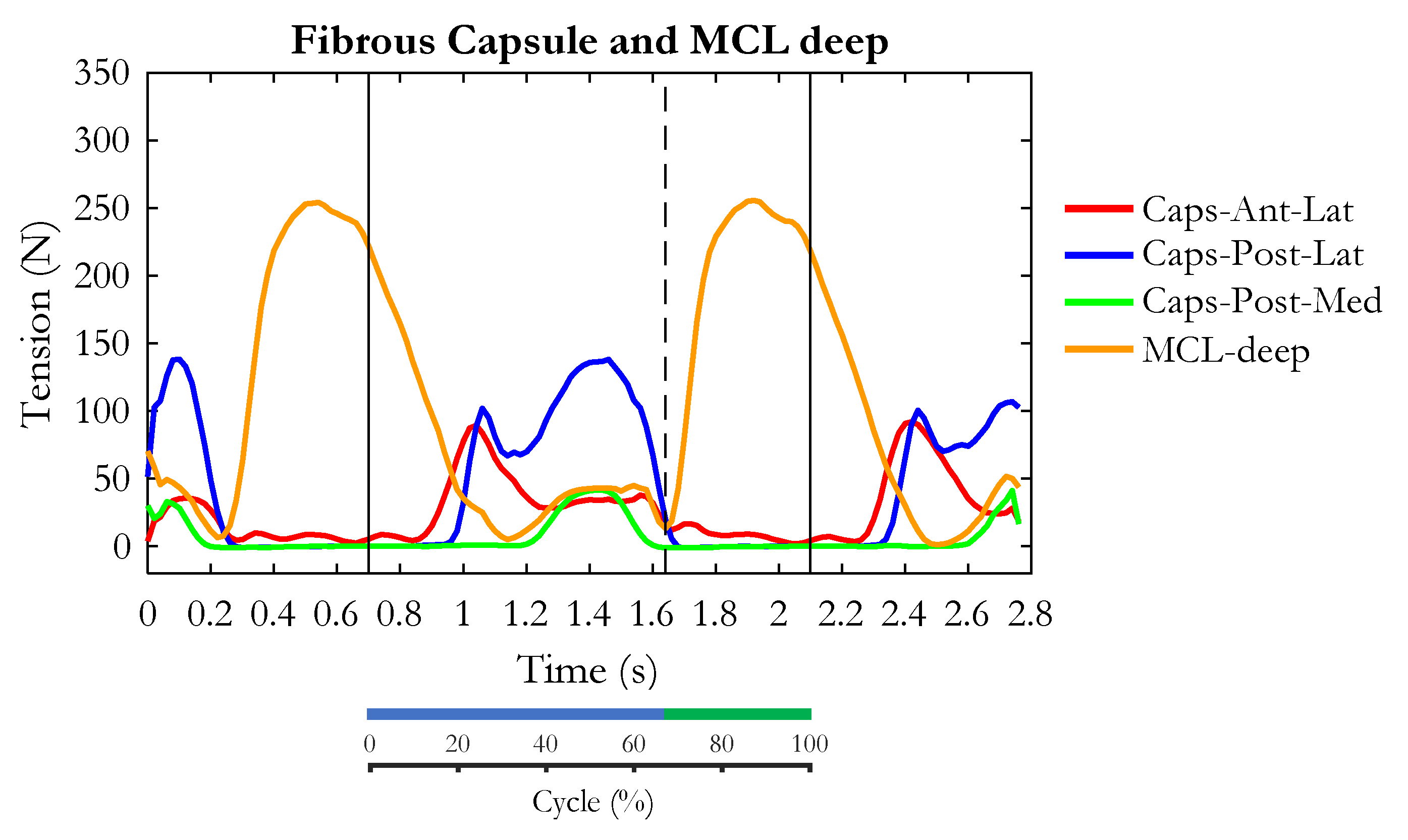
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boreham, C.A.G.; Wallace, W.F.M.; Nevill, A. Training Effects of Accumulated Daily Stair-Climbing Exercise in Previously Sedentary Young Women. Prev. Med. 2000, 30, 277–281. [Google Scholar] [CrossRef]
- Boreham, C.A.G. Training Effects of Short Bouts of Stair Climbing on Cardiorespiratory Fitness, Blood Lipids, and Homocysteine in Sedentary Young Women. Br. J. Sports Med. 2005, 39, 590–593. [Google Scholar] [CrossRef] [PubMed]
- Handsaker, J.C.; Brown, S.J.; Bowling, F.L.; Maganaris, C.N.; Boulton, A.J.M.; Reeves, N.D. Resistance Exercise Training Increases Lower Limb Speed of Strength Generation during Stair Ascent and Descent in People with Diabetic Peripheral Neuropathy. Diabet. Med. 2016, 33, 97–104. [Google Scholar] [CrossRef] [PubMed]
- Donath, L.; Faude, O.; Roth, R.; Zahner, L. Effects of Stair-Climbing on Balance, Gait, Strength, Resting Heart Rate, and Submaximal Endurance in Healthy Seniors: Stair-Climbing in Healthy Seniors. Scand. J. Med. Sci. Sports 2014, 24, e93–e101. [Google Scholar] [CrossRef] [PubMed]
- Zachazewski, J.E.; Riley, P.O.; Krebs, D.E. Biomechanical Analysis of Body Mass Transfer during Stair Ascent and Descent of Healthy Subjects. J. Rehabil. Res. Dev. 1993, 30, 412–422. [Google Scholar]
- Riener, R.; Rabuffetti, M.; Frigo, C. Stair Ascent and Descent at Different Inclinations. Gait Posture 2002, 15, 32–44. [Google Scholar] [CrossRef]
- Protopapadaki, A.; Drechsler, W.I.; Cramp, M.C.; Coutts, F.J.; Scott, O.M. Hip, Knee, Ankle Kinematics and Kinetics during Stair Ascent and Descent in Healthy Young Individuals. Clin. Biomech. 2007, 22, 203–210. [Google Scholar] [CrossRef]
- Novak, A.C.; Li, Q.; Yang, S.; Brouwer, B. Mechanical Energy Transfers across Lower Limb Segments during Stair Ascent and Descent in Young and Healthy Older Adults. Gait Posture 2011, 34, 384–390. [Google Scholar] [CrossRef]
- Nadeau, S.; McFadyen, B.J.; Malouin, F. Frontal and Sagittal Plane Analyses of the Stair Climbing Task in Healthy Adults Aged over 40 Years: What Are the Challenges Compared to Level Walking? Clin. Biomech. 2003, 18, 950–959. [Google Scholar] [CrossRef]
- Byrapogu, V.K.; Gale, T.; Hamlin, B.; Urish, K.L.; Anderst, W. Medial Unicompartmental Knee Arthroplasty Restores Native Knee Kinematics during Activities of Daily Living: A Pilot Study. Ann. Biomed. Eng. 2023, 51, 308–317. [Google Scholar] [CrossRef]
- Hamai, S.; Okazaki, K.; Shimoto, T.; Nakahara, H.; Higaki, H.; Iwamoto, Y. Continuous Sagittal Radiological Evaluation of Stair-Climbing in Cruciate-Retaining and Posterior-Stabilized Total Knee Arthroplasties Using Image-Matching Techniques. J. Arthroplast. 2015, 30, 864–869. [Google Scholar] [CrossRef]
- Hawker, G.A.; Bohm, E.; Dunbar, M.J.; Faris, P.; Jones, C.A.; Noseworthy, T.; Ravi, B.; Woodhouse, L.J.; Marshall, D.A. Patient Appropriateness for Total Knee Arthroplasty and Predicted Probability of a Good Outcome. RMD Open 2023, 9, e002808. [Google Scholar] [CrossRef]
- Lützner, J.; Beyer, F.; Lützner, C.; Riedel, R.; Tille, E. Ultracongruent Insert Design Is a Safe Alternative to Posterior Cruciate-Substituting Total Knee Arthroplasty: 5-Year Results of a Randomized Controlled Trial. Knee Surg. Sports Traumatol. Arthrosc. 2022, 30, 3000–3006. [Google Scholar] [CrossRef]
- Di Fabio, R.P.; Zampieri, C.; Tuite, P. Gaze Control and Foot Kinematics During Stair Climbing: Characteristics Leading to Fall Risk in Progressive Supranuclear Palsy. Phys. Ther. 2008, 88, 240–250. [Google Scholar] [CrossRef] [PubMed]
- Graci, V.; Rabuffetti, M.; Frigo, C.; Ferrarin, M. Is Lower Peripheral Information Weighted Differently as a Function of Step Number during Step Climbing? Gait Posture 2017, 52, 52–56. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.-J.; Chou, L.-S. Balance Control during Stair Negotiation in Older Adults. J. Biomech. 2007, 40, 2530–2536. [Google Scholar] [CrossRef] [PubMed]
- Reeves, N.D.; Spanjaard, M.; Mohagheghi, A.A.; Baltzopoulos, V.; Maganaris, C.N. The Demands of Stair Descent Relative to Maximum Capacities in Elderly and Young Adults. J. Electromyogr. Kinesiol. 2008, 18, 218–227. [Google Scholar] [CrossRef]
- Asay, J.L.; Mündermann, A.; Andriacchi, T.P. Adaptive Patterns of Movement during Stair Climbing in Patients with Knee Osteoarthritis: Adaptive patterns of movement. J. Orthop. Res. 2009, 27, 325–329. [Google Scholar] [CrossRef]
- Kaufman, K.R.; Hughes, C.; Morrey, B.F.; Morrey, M.; An, K.-N. Gait Characteristics of Patients with Knee Osteoarthritis. J. Biomech. 2001, 34, 907–915. [Google Scholar] [CrossRef]
- Taylor, S.J.G.; Walker, P.S.; Perry, J.S.; Cannon, S.R.; Woledge, R. The Forces in the Distal Femur and the Knee during Walking and Other Activities Measured by Telemetry. J. Arthroplast. 1998, 13, 428–437. [Google Scholar] [CrossRef]
- Shelburne, K.B.; Torry, M.R.; Pandy, M.G. Contributions of Muscles, Ligaments, and the Ground-Reaction Force to Tibiofemoral Joint Loading during Normal Gait. J. Orthop. Res. 2006, 24, 1983–1990. [Google Scholar] [CrossRef]
- Kutzner, I.; Heinlein, B.; Graichen, F.; Bender, A.; Rohlmann, A.; Halder, A.; Beier, A.; Bergmann, G. Loading of the Knee Joint during Activities of Daily Living Measured in vivo in Five Subjects. J. Biomech. 2010, 43, 2164–2173. [Google Scholar] [CrossRef]
- Walter, J.P.; Korkmaz, N.; Fregly, B.J.; Pandy, M.G. Contribution of Tibiofemoral Joint Contact to Net Loads at the Knee in Gait: Contribution of Tibiofemoral joint contact. J. Orthop. Res. 2015, 33, 1054–1060. [Google Scholar] [CrossRef] [PubMed]
- Lenhart, R.L.; Kaiser, J.; Smith, C.R.; Thelen, D.G. Prediction and Validation of Load-Dependent Behavior of the Tibiofemoral and Patellofemoral Joints during Movement. Ann. Biomed. Eng. 2015, 43, 2675–2685. [Google Scholar] [CrossRef] [PubMed]
- Bersini, S.; Sansone, V.; Frigo, C.A. A Dynamic Multibody Model of the Physiological Knee to Predict Internal Loads during Movement in Gravitational Field. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 571–579. [Google Scholar] [CrossRef]
- Taylor, W.R.; Heller, M.O.; Bergmann, G.; Duda, G.N. Tibio-Femoral Loading during Human Gait and Stair Climbing. J. Orthop. Res. 2004, 22, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Beynnon, B.D.; Fleming, B.C. Anterior Cruciate Ligament Strain in-vivo: A Review of Previous Work. J. Biomech. 1998, 31, 519–525. [Google Scholar] [CrossRef]
- Cerulli, G.; Benoit, D.L.; Lamontagne, M.; Caraffa, A.; Liti, A. In vivo Anterior Cruciate Ligament Strain Behaviour during a Rapid Deceleration Movement: Case Report. Knee Surg. Sports Traumatol. Arthrosc. 2003, 11, 307–311. [Google Scholar] [CrossRef]
- Fleming, B.C.; Beynnon, B.D.; Renstrom, P.A.; Johnson, R.J.; Nichols, C.E.; Peura, G.D.; Uh, B.S. The Strain Behavior of the Anterior Cruciate Ligament During Stair Climbing: An in vivo Study. Arthrosc. J. Arthrosc. Relat. Surg. 1999, 15, 185–191. [Google Scholar] [CrossRef]
- Frigo, C.A.; Donno, L. The Effects of External Loads and Muscle Forces on the Knee Joint Ligaments during Walking: A Musculoskeletal Model Study. Appl. Sci. 2021, 11, 2356. [Google Scholar] [CrossRef]
- Grood, E.S.; Suntay, W.J. A Joint Coordinate System for the Clinical Description of Three-Dimensional Motions: Application to the Knee. J. Biomech. Eng. 1983, 105, 136–144. [Google Scholar] [CrossRef]
- Donno, L.; Frigo, C.A. The Effects of Anterior Cruciate Ligament Sacrifice on the Behavior of the Knee Joint, Tested through the Use of a Musculoskeletal Model. Gait Posture 2022, 97, 1. [Google Scholar] [CrossRef]
- Donno, L.; Sansone, V.; Galluzzo, A.; Frigo, C.A. Walking in the Absence of Anterior Cruciate Ligament: The Role of the Quadriceps and Hamstrings. Appl. Sci. 2022, 12, 8667. [Google Scholar] [CrossRef]
- Blankevoort, L.; Huiskes, R.; De Lange, A. Recruitment of Knee Joint Ligaments. J. Biomech. Eng. 1991, 113, 94–103. [Google Scholar] [CrossRef]
- Rasmussen, J.; Damsgaard, M.; Voigt, M. Muscle Recruitment by the Min/Max Criterion—A Comparative Numerical Study. J. Biomech. 2001, 34, 409–415. [Google Scholar] [CrossRef]
- Andriacchi, T.P.; Andersson, G.B.; Fermier, R.W.; Stern, D.; Galante, J.O. A Study of Lower-Limb Mechanics during Stair-Climbing. J. Bone Jt. Surg. Am. 1980, 62, 749–757. [Google Scholar] [CrossRef]
- Gregor, R.J.; Cavanagh, P.R.; LaFortune, M. Knee Flexor Moments during Propulsion in Cycling—A Creative Solution to Lombard’s Paradox. J. Biomech. 1985, 18, 307–316. [Google Scholar] [CrossRef]
- Andrews, J.G. The Functional Roles of the Hamstrings and Quadriceps during Cycling: Lombard’s Paradox Revisited. J. Biomech. 1987, 20, 565–575. [Google Scholar] [CrossRef] [PubMed]
- Lombard, W.P.; Abbott, F.M. The mechanical effects produced by the contraction of individual muscles of the thigh of the frog. Am. J. Physiol.-Leg. Content 1907, 20, 1–60. [Google Scholar] [CrossRef]
- Frigo, C.; Pavan, E.E.; Brunner, R. A Dynamic Model of Quadriceps and Hamstrings Function. Gait Posture 2010, 31, 100–103. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frigo, C.A.; Grossi, M.; Donno, L. Loads on the Knee Joint Ligaments during Stair Climbing. Appl. Sci. 2023, 13, 7388. https://doi.org/10.3390/app13137388
Frigo CA, Grossi M, Donno L. Loads on the Knee Joint Ligaments during Stair Climbing. Applied Sciences. 2023; 13(13):7388. https://doi.org/10.3390/app13137388
Chicago/Turabian StyleFrigo, Carlo Albino, Maddalena Grossi, and Lucia Donno. 2023. "Loads on the Knee Joint Ligaments during Stair Climbing" Applied Sciences 13, no. 13: 7388. https://doi.org/10.3390/app13137388
APA StyleFrigo, C. A., Grossi, M., & Donno, L. (2023). Loads on the Knee Joint Ligaments during Stair Climbing. Applied Sciences, 13(13), 7388. https://doi.org/10.3390/app13137388








