Vibration Response Law of Aircraft Taxiing under Random Roughness Excitation
Abstract
:1. Introduction
2. Random Vibration Models
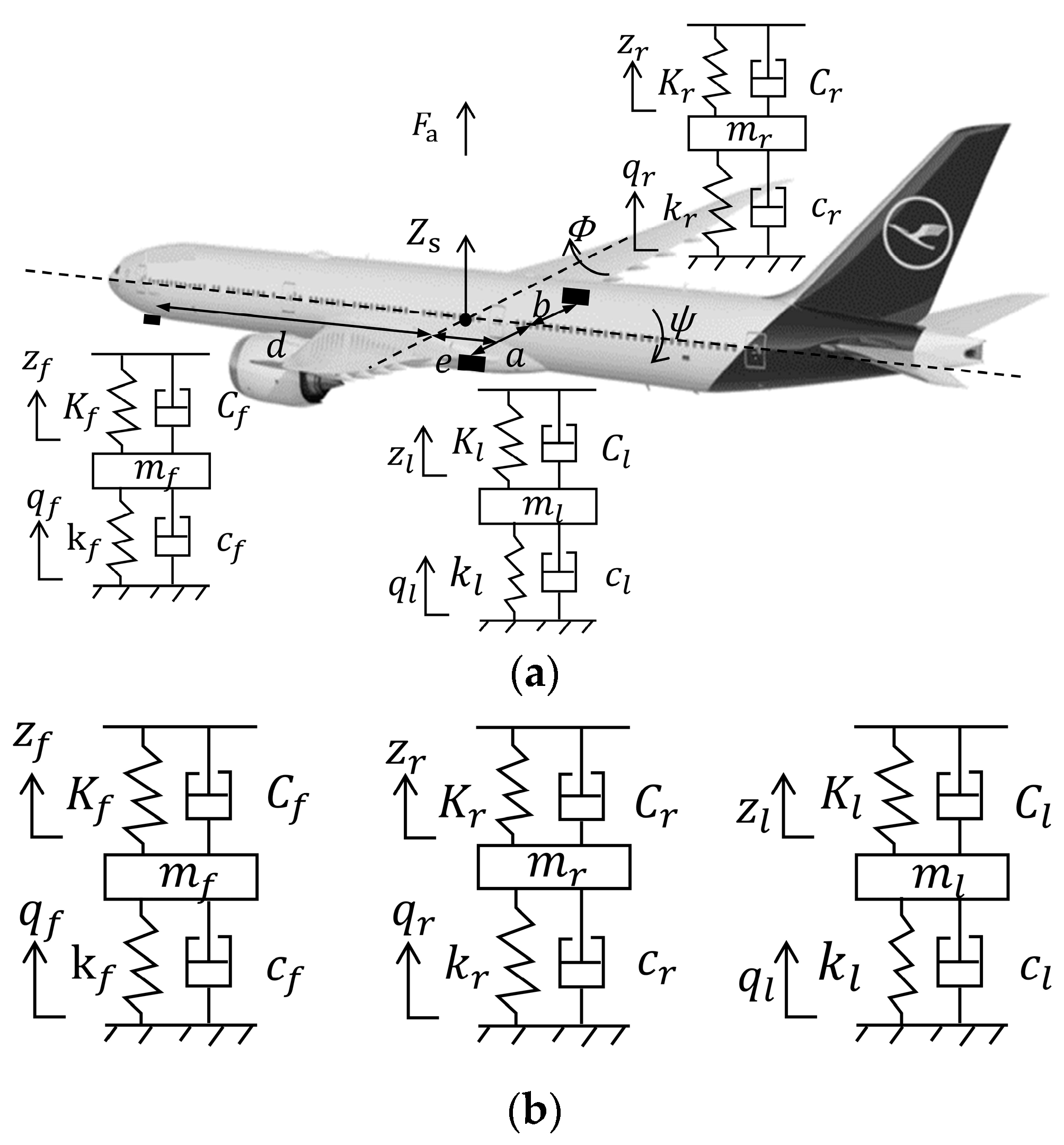
2.1. Aircraft Nonlinear Ground Dynamics Model
2.2. Statistical Linearization of the Nonlinear System
2.2.1. Nonlinear Function Expression
- (1)
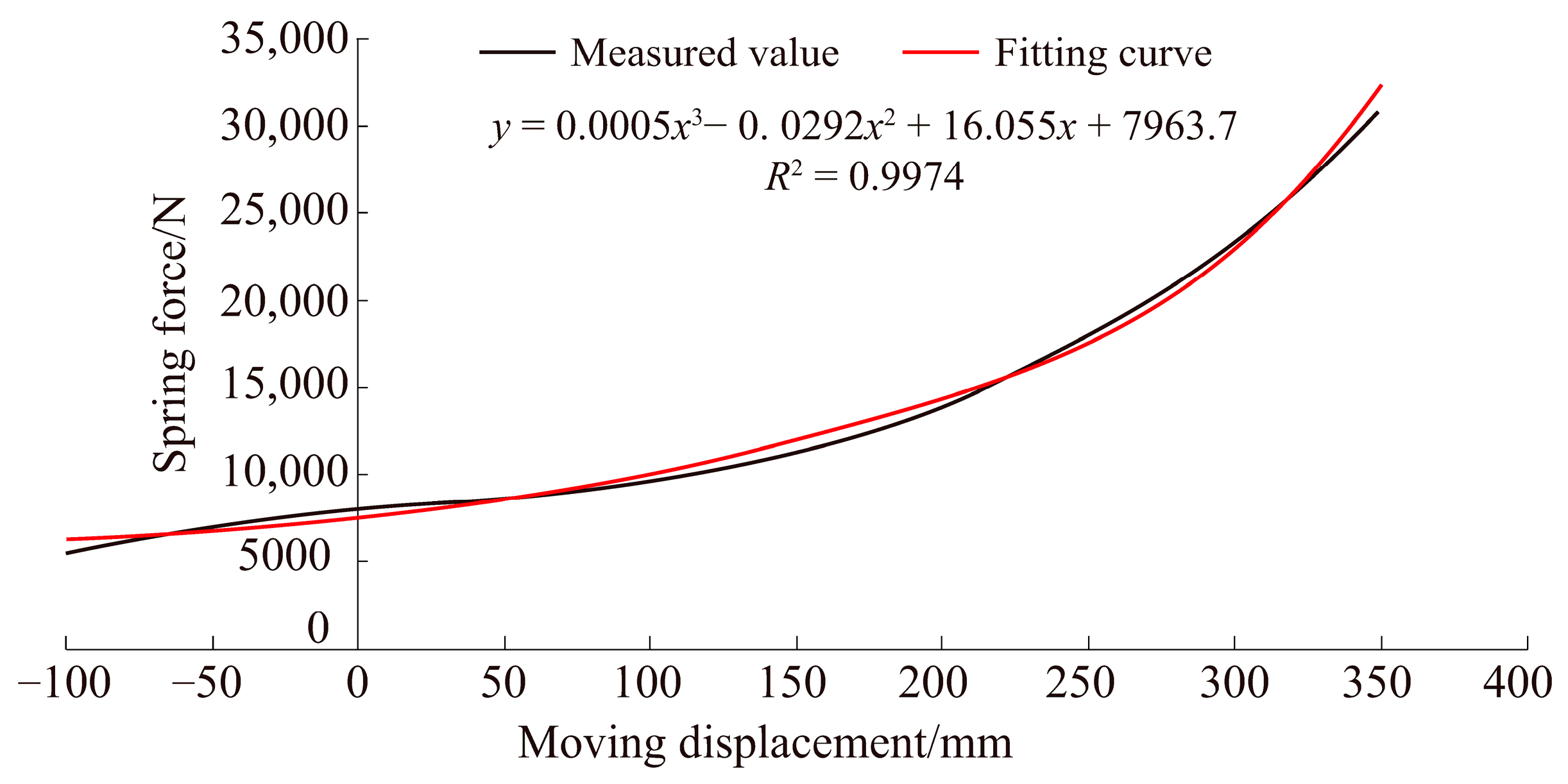
- Nonlinearity of landing gear elastic element
- (2)
- Nonlinearity of landing gear damping element
2.2.2. Calculation of Equivalent Stiffness and Equivalent Damping by Statistical Linearization
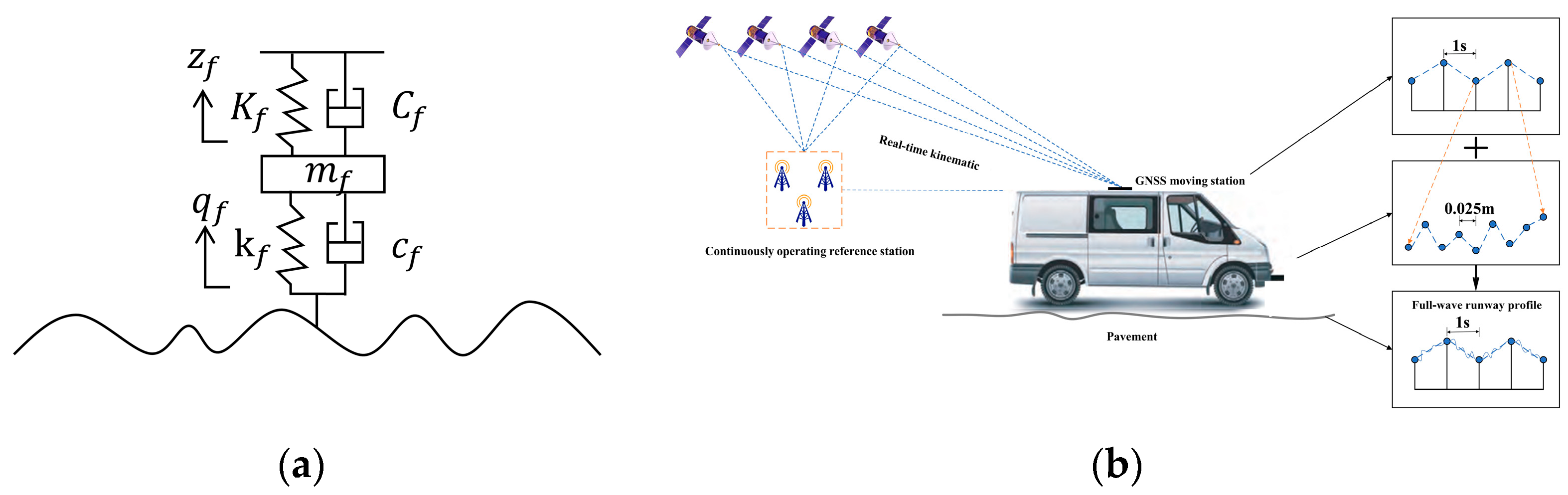
2.3. Pavement Roughness Models
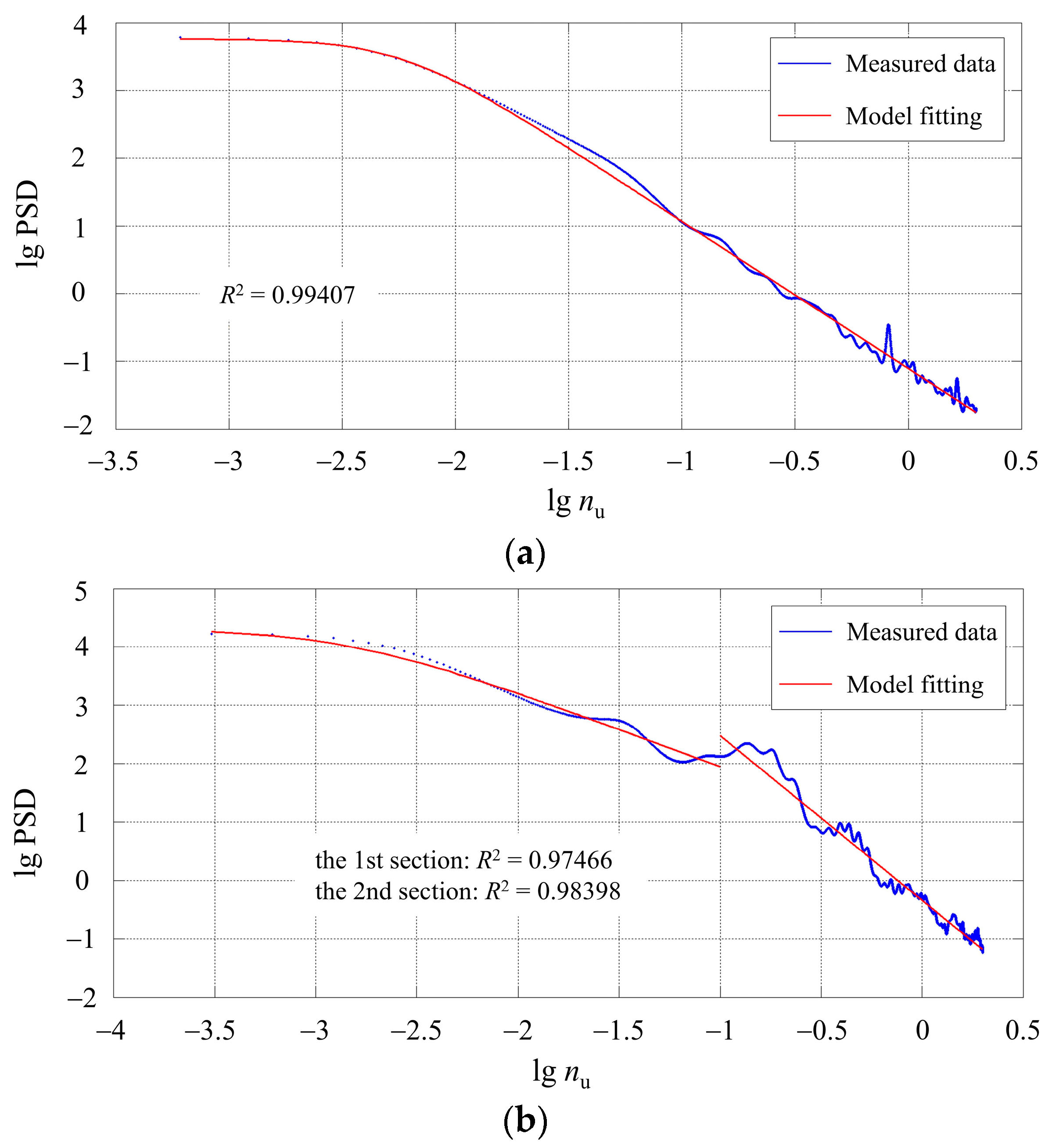
2.3.1. Asphalt Pavement Roughness Model
2.3.2. Cement Pavement Roughness Model
2.3.3. Pavement Roughness Excitation Input
3. Random Vibration Solution Method
3.1. Solution Method for Steady Random Vibration of Uniform Taxiing Aircraft
3.2. Solution Method for Non-Stationary Random Vibration of Takeoff and Landing Taxiing Aircraft
4. Application Scenarios
4.1. Aircraft Parameters
4.2. Pavement Roughness Parameters
5. Results and Discussion
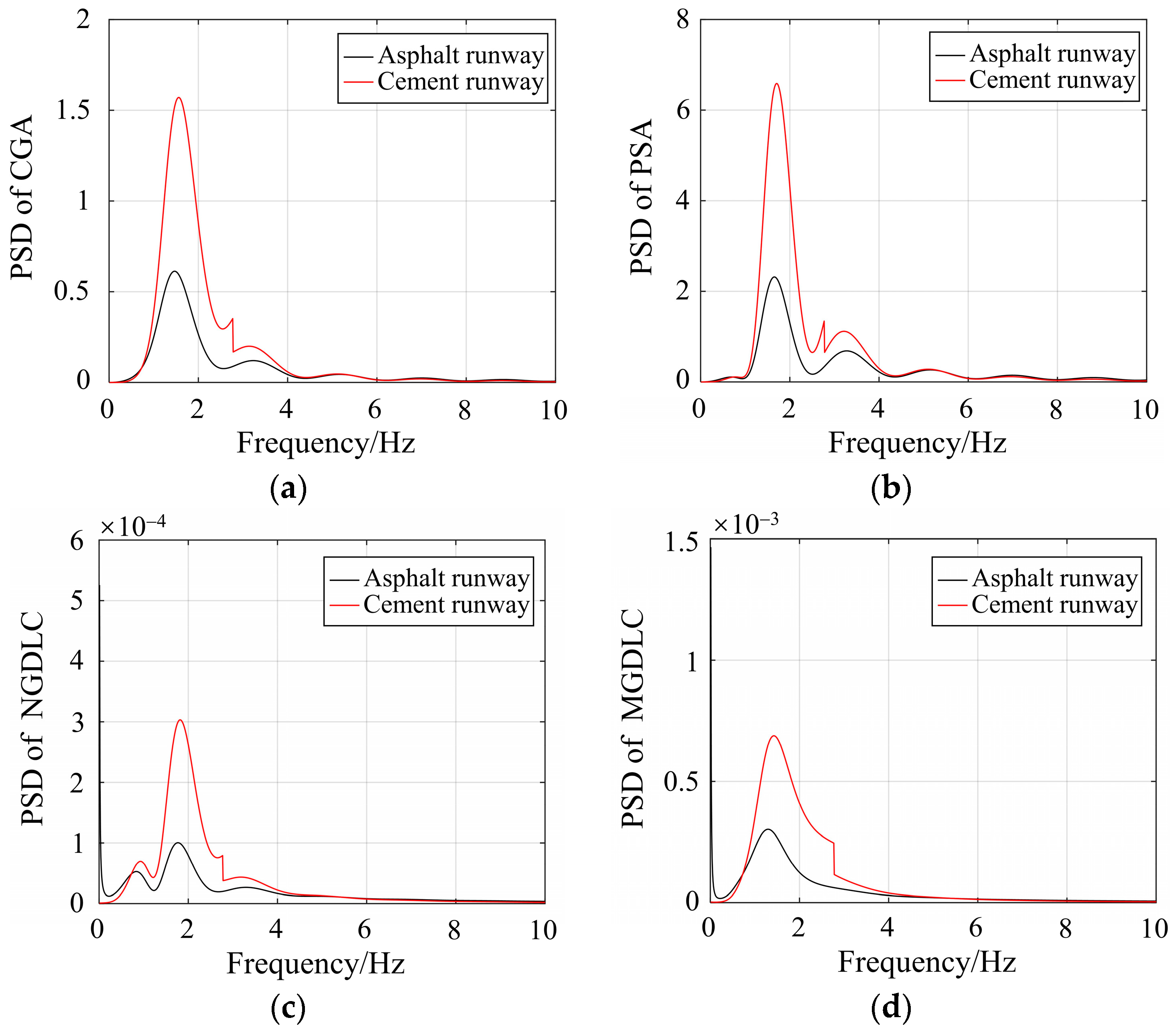
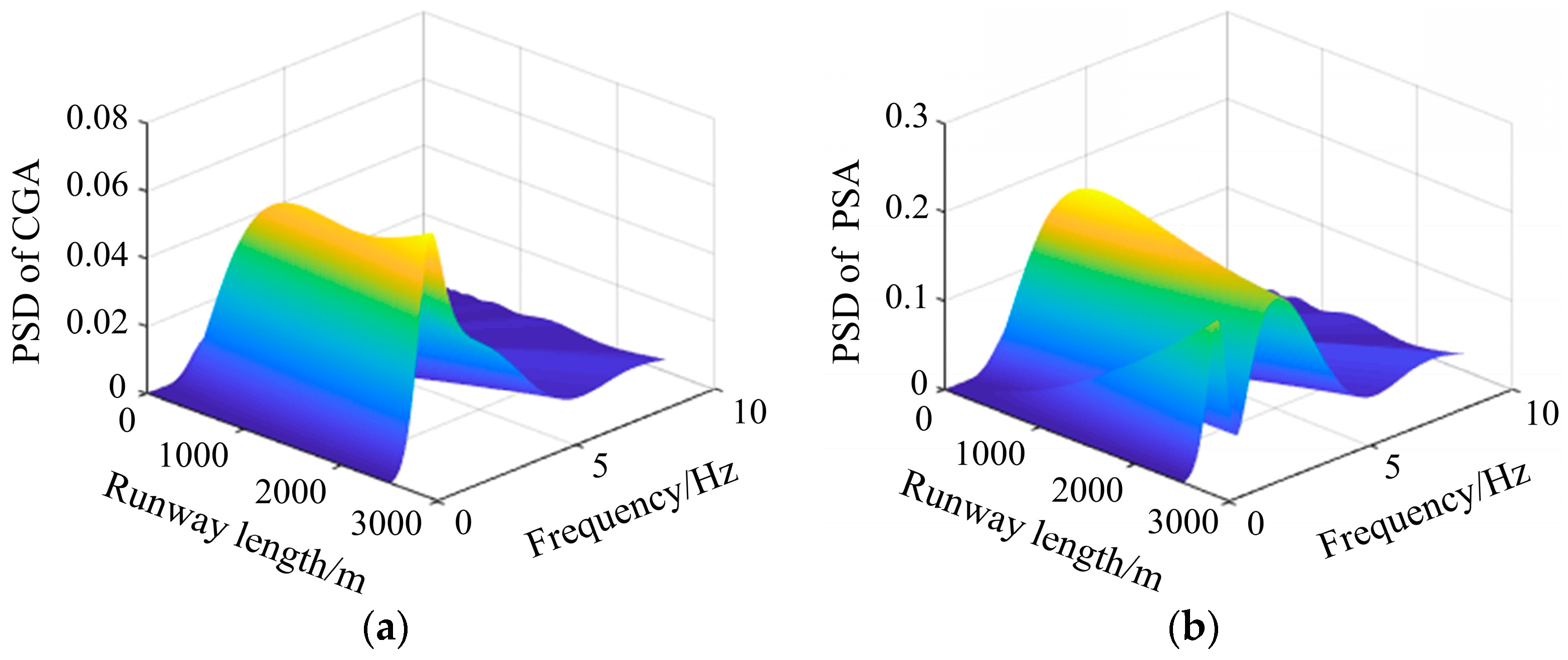
5.1. Vibration Response Analysis of Aircraft Taxiing under Different Pavement Types
5.2. Vibration Response Analysis of Aircraft Taxiing under Different Motion Attitudes
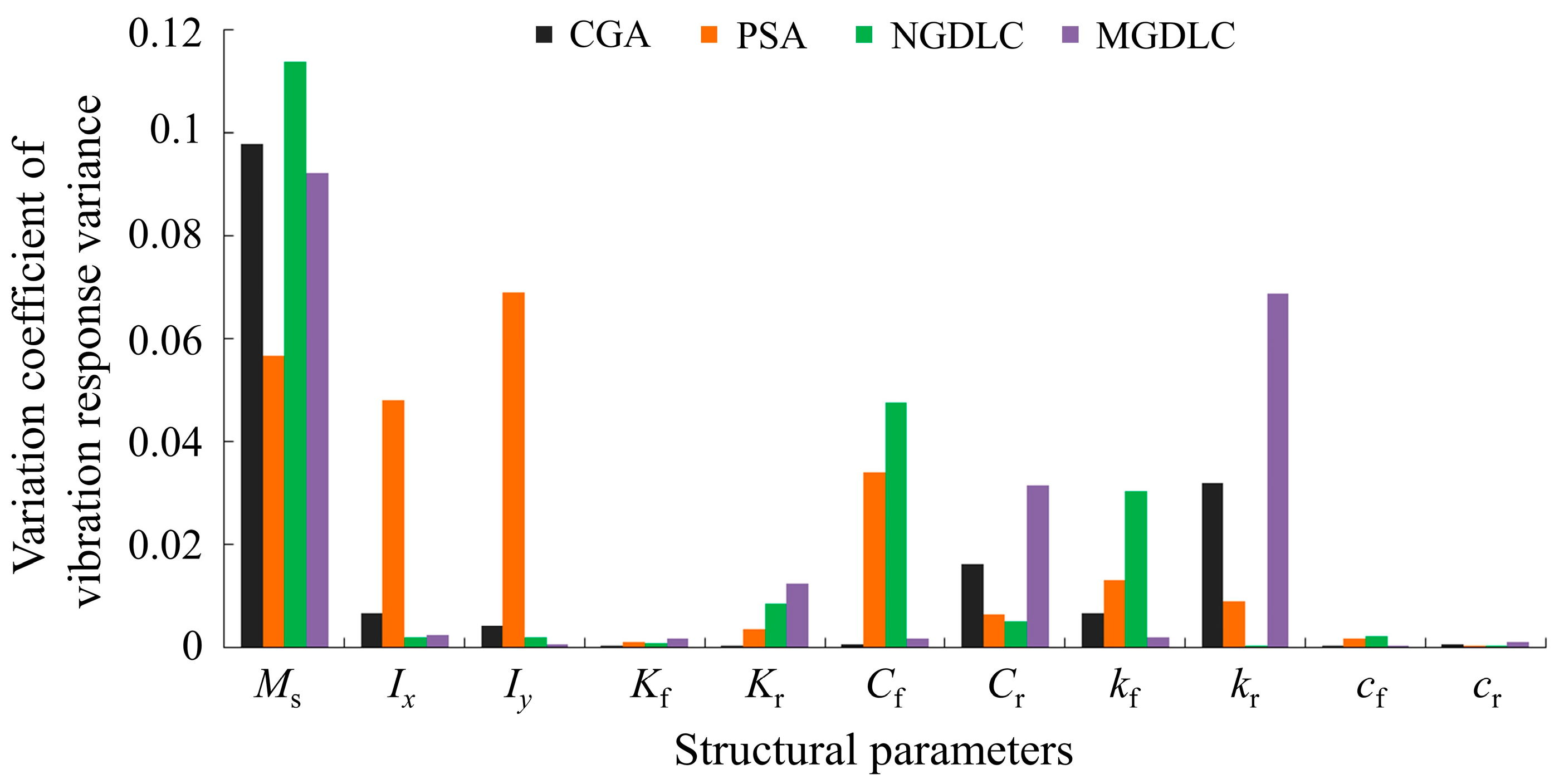
5.3. Vibration Response Analysis of Aircraft Taxiing under Stochastic Structural Parameters
6. Conclusions
- (1)
- The power spectra of asphalt pavement and cement pavement roughness are different. The corresponding pavement roughness models were developed in this paper and the measured data demonstrates that the fit is excellent, with R2 values greater than 0.95.
- (2)
- The pavement type has little influence on the PSD distribution of the aircraft vibration response. When the accuracy requirements are not high, the same pavement roughness model can be used for both cement and asphalt pavements.
- (3)
- The vibration response of the aircraft during landing is greater than that during takeoff under the same conditions. Managers should therefore pay more attention to the roughness of the landing runway compared to the takeoff runway.
- (4)
- The impact of stochastic structural parameters on the aircraft’s vibration response was analyzed using the Monte Carlo method. It was found that the randomness of the sprung mass has the greatest effect on the vibration response and can result in NGDLC reaching 0.113, followed by the tire stiffness and the aircraft’s rotational inertia.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Loprencipe, G.; Zoccali, P. Comparison of methods for evaluating airport pavement roughness. Int. J. Pavement Eng. 2019, 20, 782–791. [Google Scholar] [CrossRef]
- Andren, P. Power spectral density approximations of longitudinal road profiles. Int. J. Veh. Des. 2006, 40, 2–14. [Google Scholar] [CrossRef]
- Dodds, C.J.; Robson, J.D. The description of road surface roughness. J. Sound Vib. 1973, 31, 175–183. [Google Scholar] [CrossRef]
- Sussman, N.E. Statistical ground excitation models for high speed vehicle dynamic analysis. High Speed Ground Transp. J. 1974, 8, 145–154. [Google Scholar]
- Gillespie, T.D. Heavy Truck Ride; Society of Automotive Engineers: Warrendale, PA, USA, 1985. [Google Scholar]
- Marcondes, J.; Burgess, G.J.; Harichandran, R.; Snyder, M.B. Spectral analysis of highway pavement roughness. J. Transp. Eng. 1991, 117, 540–549. [Google Scholar] [CrossRef]
- Xu, D.M.; Mohamed, A.M.O.; Yong, R.N.; Caporuscio, F. Development of a criterion for road surface roughness based on power spectral density function. J. Terramech. 1992, 29, 477–486. [Google Scholar] [CrossRef]
- Houbolt, J.C. Runway roughness studies in the aeronautical field. Am. Soc. Civ. Eng. Trans. 1962, 127, 427–447. [Google Scholar] [CrossRef]
- Sivakumar, S.; Haran, A.P. Mathematical model and vibration analysis of aircraft with active landing gears. J. Vib. Control 2015, 21, 229–245. [Google Scholar] [CrossRef]
- Sivakumar, S.; Selvakumaran, T.; Sanjay, B. Investigation of random runway effect on landing of an aircraft with active landing gears using nonlinear mathematical model. J. Vibroengineering 2021, 23, 1785–1799. [Google Scholar] [CrossRef]
- Ling, D.S.; Sheng, W.J.; Huang, B. Influence of pavement unidirectional constraint on aircraft vibration response. J. Zhejiang Univ. Eng. Sci. 2021, 55, 1684–1693. [Google Scholar]
- Li, S.; Guo, J. Modeling and dynamic analysis of an aircraft–pavement coupled system. J. Vib. Eng. Technol. 2022, 1–13. [Google Scholar] [CrossRef]
- Ling, J.M.; Liu, S.F.; Yuan, J.; Lei, X.P. Comprehensive analysis of pavement roughness evaluation for airport and road with different roughness excitation. J. Tongji Univ. Nat. Sci. 2017, 45, 519–526. [Google Scholar]
- Durán, J.B.C.; Júnior, J.L.F. Airport pavement roughness evaluation based on cockpit and center of gravity vertical accelerations. Transportes 2020, 28, 147–159. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, J.H.; Zhang, X.M. Vibration response of rigid runway under aircraft-runway coupling. J. Vib. Shock 2021, 40, 64–72. [Google Scholar]
- Cheng, G.Y.; Hou, D.W.; Huang, X.D. Pavement roughness limit value standard based on aircraft vertical acceleration. J. Vib. Shock 2017, 36, 166–171. [Google Scholar]
- Shi, X.G.; Cai, L.C.; Wang, G.H.; Liang, L. A new aircraft taxiing model based on filtering white noise method. IEEE Access 2020, 8, 10070–10087. [Google Scholar] [CrossRef]
- Liu, S.F.; Tian, Y.; Liu, L.; Xiang, P.; Zhang, Z.K. Improvement of Boeing Bump method considering aircraft vibration superposition effect. Appl. Sci. 2021, 11, 2147. [Google Scholar] [CrossRef]
- Qian, J.S.; Pan, X.W.; Cen, Y.B.; Liu, D.L. Aircraft taxiing dynamic load induced by runway roughness. J. Vib. Shock 2022, 41, 176–184+269. [Google Scholar]
- Kirk, C.L.; Perry, P.J. Analysis of taxiing induced vibrations in aircraft by the power spectral density method. Aeronaut. J. 1971, 75, 182–194. [Google Scholar] [CrossRef]
- Tung, C.C. The effects of runway roughness on the dynamic response of airplanes. J. Sound Vib. 1967, 5, 164–172. [Google Scholar] [CrossRef]
- Nie, H.; Kortum, W. Analysis for aircraft taxiing at variable velocity on unevenness runway by the power spectral density method. Trans. Nanjing Univ. Aeronaut. Astronaut. 2000, 17, 64–70. [Google Scholar]
- Wang, C.Q. Dynamic response analysis of UAV’s landing gear structure subjected to random excitation. Comput. Simul. 2014, 31, 69–72+460. [Google Scholar]
- Liu, S.F.; Ling, J.M.; Tian, Y.; Hou, T.X.; Zhao, X.D. Random vibration analysis of a coupled aircraft/runway modeled system for runway evaluation. Sustainability 2022, 14, 2815. [Google Scholar] [CrossRef]
- Liu, S.F.; Tian, Y.; Yang, G.; Ling, J.M.; Li, P.L. Effect of space for runway roughness evaluation. Int. J. Pavement Eng. 2022, 1–11. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Surface Roughness Final Study Data Collection Report; Federal Aviation Administration: Washington, DC, USA, 2014.
- Qian, J.S.; Cen, Y.B.; Liu, D.L.; Li, J.S.; Liu, S.F. Measurement method of all-wave airport runway roughness. J. Traffic Transp. Eng. 2021, 21, 84–93. [Google Scholar]
- Lin, J.H.; Zhang, Y.H. Pseudo Excitation Method in Random Vibration; Science Press: Beijing, China, 2004. [Google Scholar]
- Lin, J.H.; Zhang, Y.H.; Zhao, Y. The pseudo-excitation method and its industrial applications in China and abroad. Appl. Math. Mech. 2017, 38, 1–31. [Google Scholar]
- Zhang, L.J.; He, H.; Wang, Y.S. Analysis on instantaneous spatial spectrum of vehicle response. J. Vib. Shock 2003, 22, 16–20. [Google Scholar]
- Lin, K.X.; Cen, G.P.; Li, L.; Liu, G. Simulation and analysis for airplanes performance of takeoff and landing. J. Air Force Eng. Univ. Nat. Sci. Ed. 2012, 13, 21–25. [Google Scholar]



| No. | International Air Transport Association (IATA) Code | Runway Type | Runway Length/m |
|---|---|---|---|
| 1 | HGH | cement | 3560 |
| 2 | DOY | 2/3 asphalt + 1/3 cement | 3600 |
| 3 | WUX | asphalt | 3180 |
| 4 | JGS | cement | 2590 |
| 5 | HYN | cement | 2490 |
| 6 | NGB | cement | 3160 |
| 7 | LCX | cement | 2390 |
| 8 | A military airport | cement | 2210 |
| 9 | A military airport | cement | 2280 |
| 10 | FOC | cement | 3580 |
| 11 | SWA | cement | 2480 |
| 12 | YNZ | cement | 2810 |
| 13 | LFQ | cement | 2710 |
| 14 | A military airport | cement | 2990 |
| 15 | A military airport | cement | 2470 |
| 16 | SHA (runway 1) | cement | 3290 |
| 17 | SHA (runway 2) | asphalt | 3290 |
| 18 | PVG (runway 1) | cement | 3410 |
| 19 | PVG (runway 2) | cement | 3770 |
| 20 | PVG (runway 3) | cement | 3390 |
| Parameter | Unit | Value | Description |
|---|---|---|---|
| Ms (Taxiing) | kg | 78,472 | sprung mass |
| Ms (Takeoff) | kg | 78,245 | sprung mass |
| Ms (Landing) | kg | 65,317 | sprung mass |
| mf | kg | 578 | unsprung mass of front landing gear |
| ml | kg | 1150 | unsprung mass of left rear landing gear |
| mr | kg | 1150 | unsprung mass of right rear landing gear |
| Kf | N/m | 58,027 | stiffness coefficient of front landing gear buffer |
| Kl | N/m | 996,531 | stiffness coefficient of left rear landing gear buffer |
| Kr | N/m | 996,531 | stiffness coefficient of right rear landing gear buffer |
| kf | N/m | 1,966,300 | stiffness coefficient of front landing gear tire |
| kl | N/m | 2,812,900 | stiffness coefficient of left rear landing gear tire |
| kr | N/m | 2,812,900 | stiffness coefficient of right rear landing gear tire |
| Cf | N·s/m | 131,500 | damping coefficient of front landing gear buffer |
| Cl | N·s/m | 572,500 | damping coefficient of left rear landing gear buffer |
| Cr | N·s/m | 572,500 | damping coefficient of right rear landing gear buffer |
| cf | N·s/m | 131,500 | damping coefficient of front landing gear tire |
| cl | N·s/m | 4066 | damping coefficient of left rear landing gear tire |
| cr | N·s/m | 4066 | damping coefficient of right rear landing gear tire |
| Ix | kg·m2 | 3,394,953 | rotational inertia of aircraft around x-axis |
| Iy | kg·m2 | 1,866,711 | rotational inertia of aircraft around y-axis |
| a | m | 2.86 | horizontal distance from left landing gear to y-axis |
| b | m | 2.86 | horizontal distance from right landing gear to y-axis |
| d | m | 14.6 | horizontal distance from front landing gear to x-axis |
| e | m | 1 | horizontal distances from rear landing gear to x-axis |
| Runways | C | w | |
|---|---|---|---|
| 2 runways in China | 0.0907~0.119 (0.1) | 0.00054~0.0014 (0.0009) | 2.199~2.285 (2.24) |
| 18 runways abroad | 0.0227~1.206 (0.1) | 0.00019~0.00178 (0.0005) | 2.042~3.162 (2.3) |
| Runways | C1 | w1 | |
| 18 runways in China | 0.0089–0.235 (0.025) | 0.00009–0.1503 (0.04) | 1.369–3.527 (2.4) |
| 19 runways abroad | 0.007–0.147 (0.025) | 0.0000152–0.0103 (0.005) | 1.21–3.22 (2.5) |
| Runways | C2 | w2 | |
| 18 runways in China | 0.049–0.597 (0.08) | 1.813–3.13 (2.5) | |
| 19 runways abroad | 0.029–0.308 (0.08) | 1.59–2.86 (2.2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, T.; Liu, S.; Ling, J.; Tian, Y.; Li, P.; Zhang, J. Vibration Response Law of Aircraft Taxiing under Random Roughness Excitation. Appl. Sci. 2023, 13, 7386. https://doi.org/10.3390/app13137386
Hou T, Liu S, Ling J, Tian Y, Li P, Zhang J. Vibration Response Law of Aircraft Taxiing under Random Roughness Excitation. Applied Sciences. 2023; 13(13):7386. https://doi.org/10.3390/app13137386
Chicago/Turabian StyleHou, Tianxin, Shifu Liu, Jianming Ling, Yu Tian, Peilin Li, and Jie Zhang. 2023. "Vibration Response Law of Aircraft Taxiing under Random Roughness Excitation" Applied Sciences 13, no. 13: 7386. https://doi.org/10.3390/app13137386
APA StyleHou, T., Liu, S., Ling, J., Tian, Y., Li, P., & Zhang, J. (2023). Vibration Response Law of Aircraft Taxiing under Random Roughness Excitation. Applied Sciences, 13(13), 7386. https://doi.org/10.3390/app13137386






