The Aerodynamic Interaction Effects between the Rotor and Fuselage on the Drag Performance of a Civil Helicopter in Forward Flight
Abstract
:1. Introduction
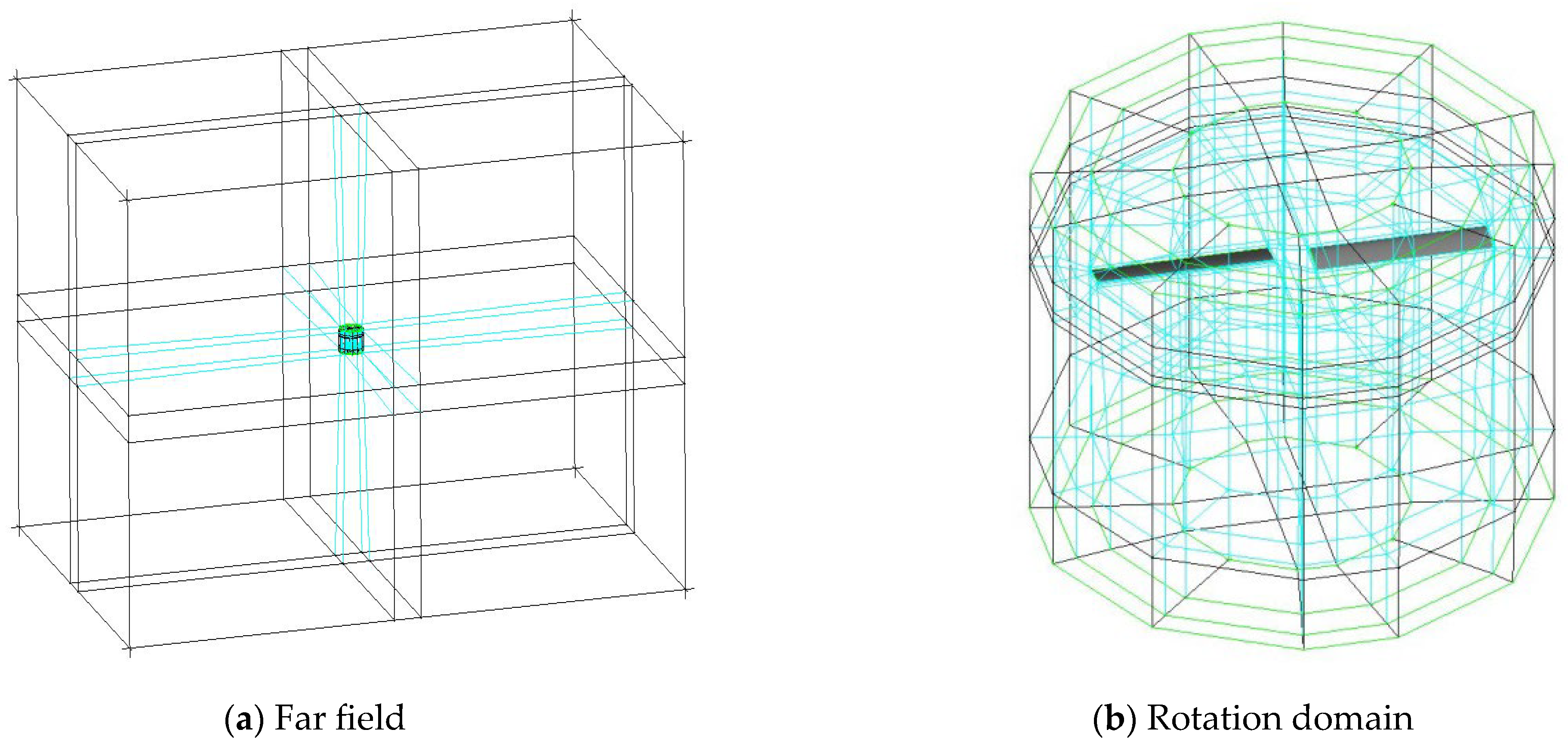
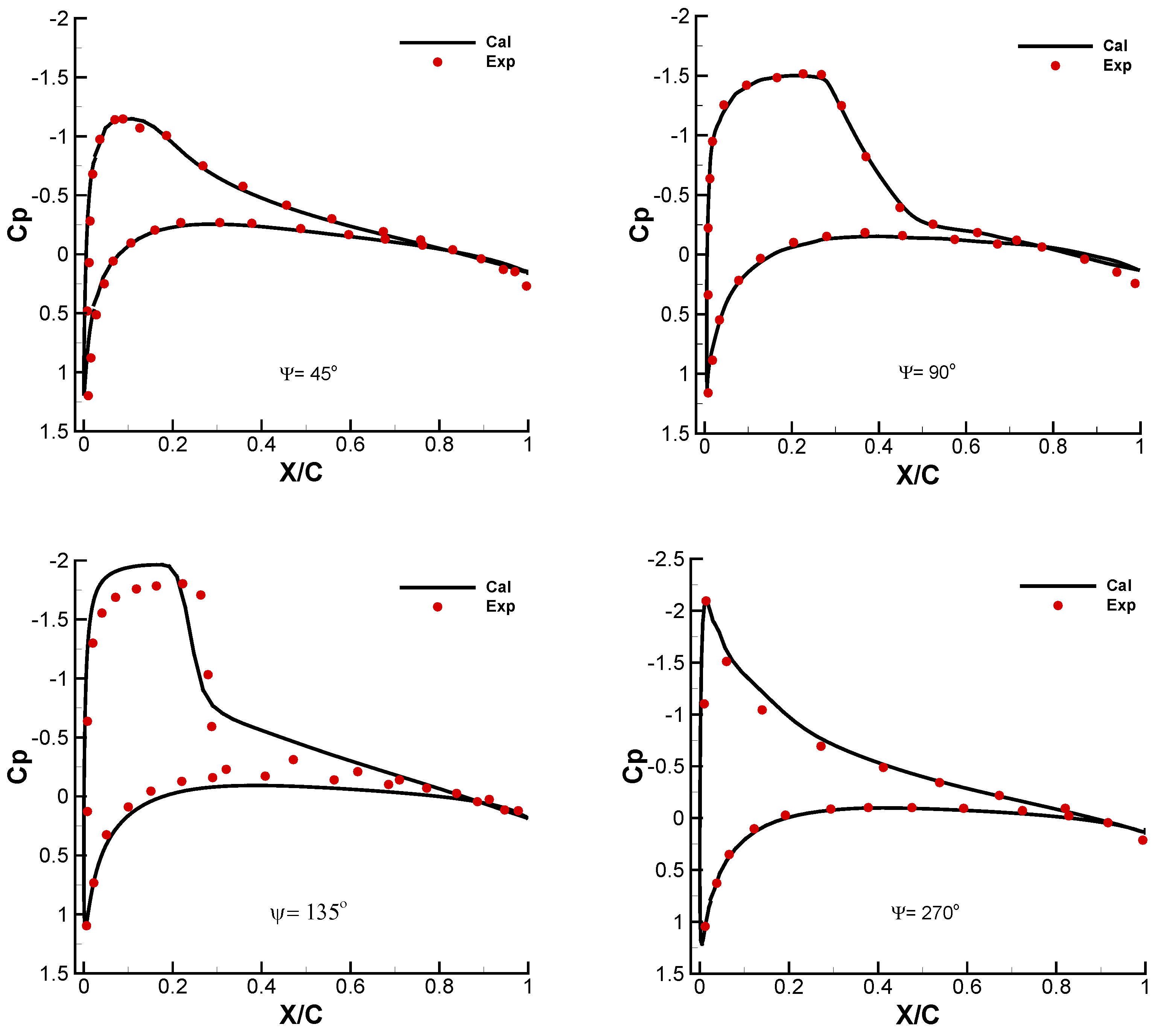
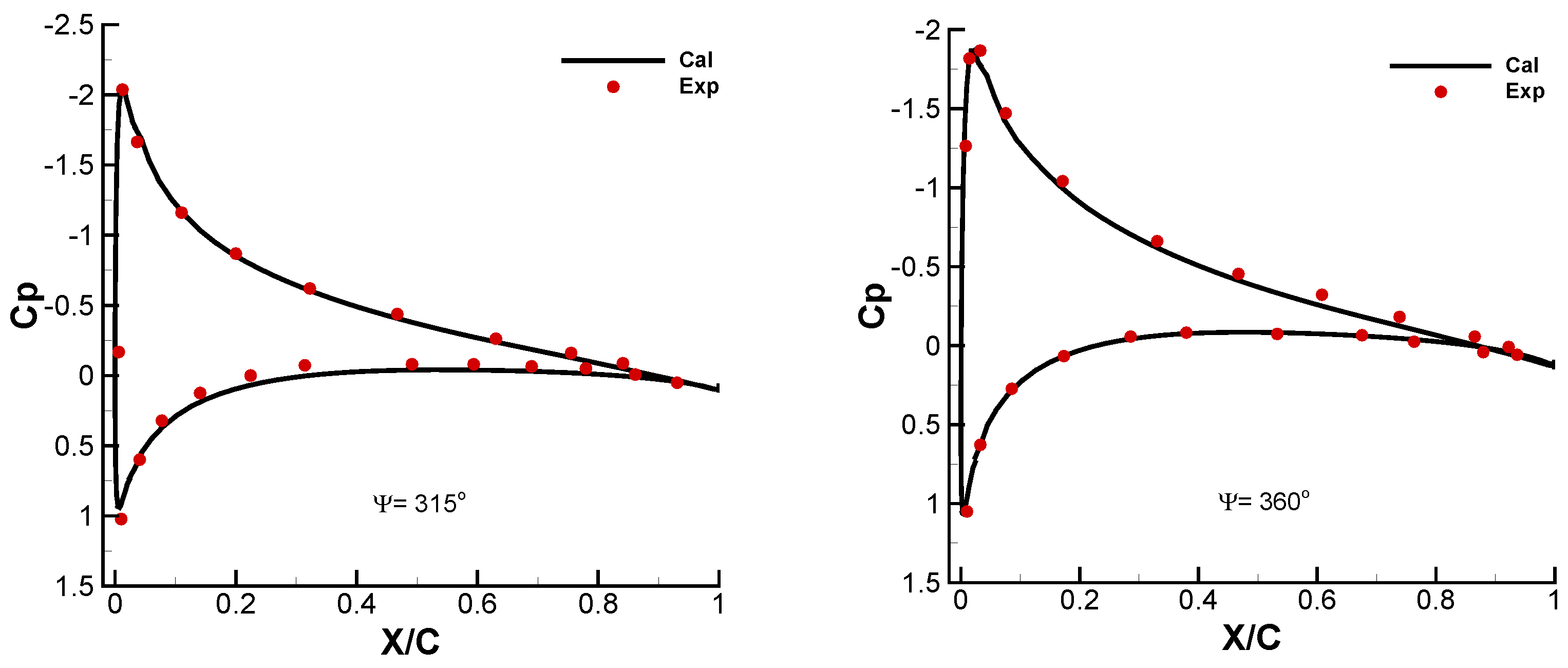
2. Methodology and Validation
3. Analysis of Main Rotor Rotating Effects
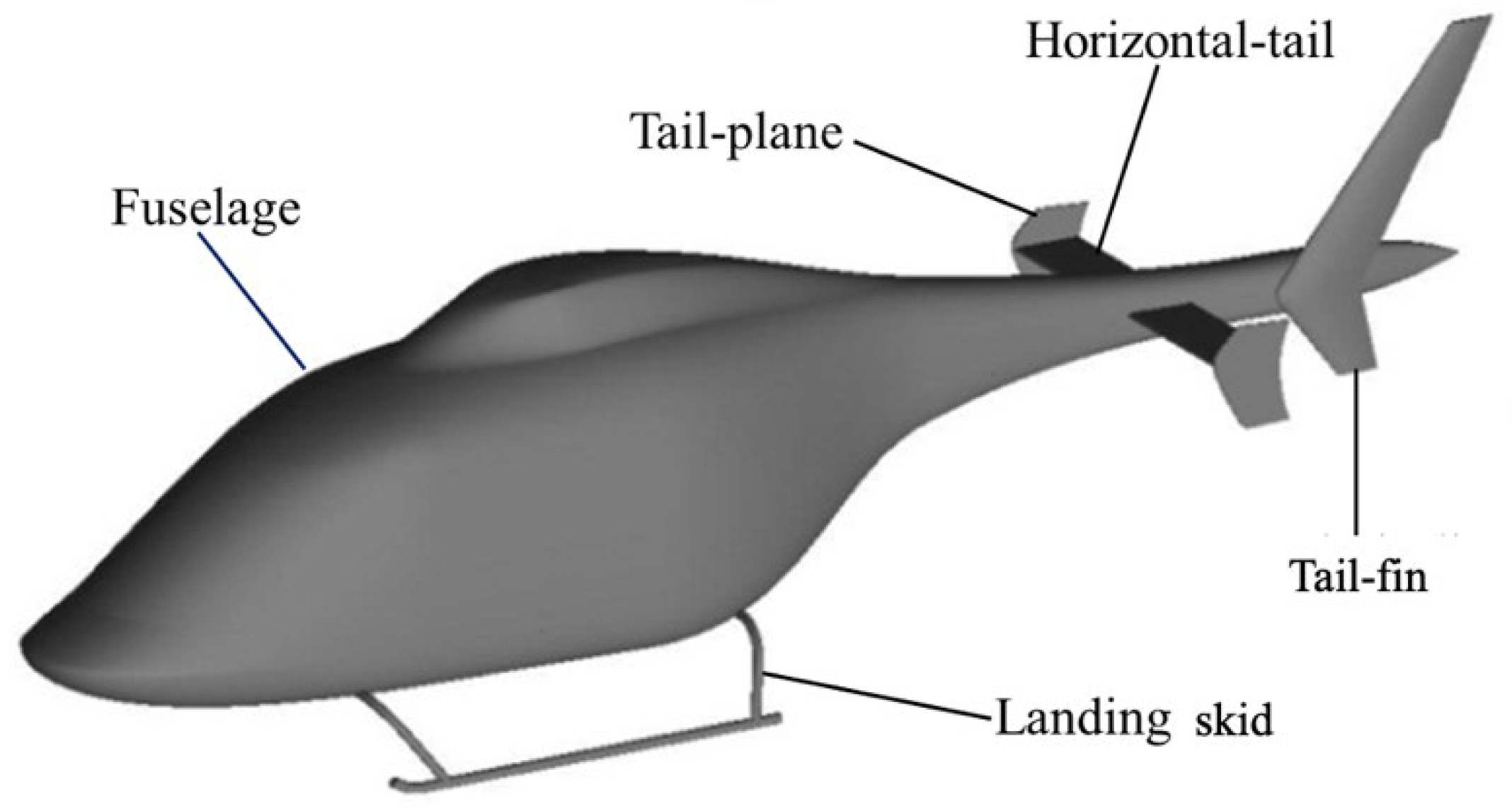
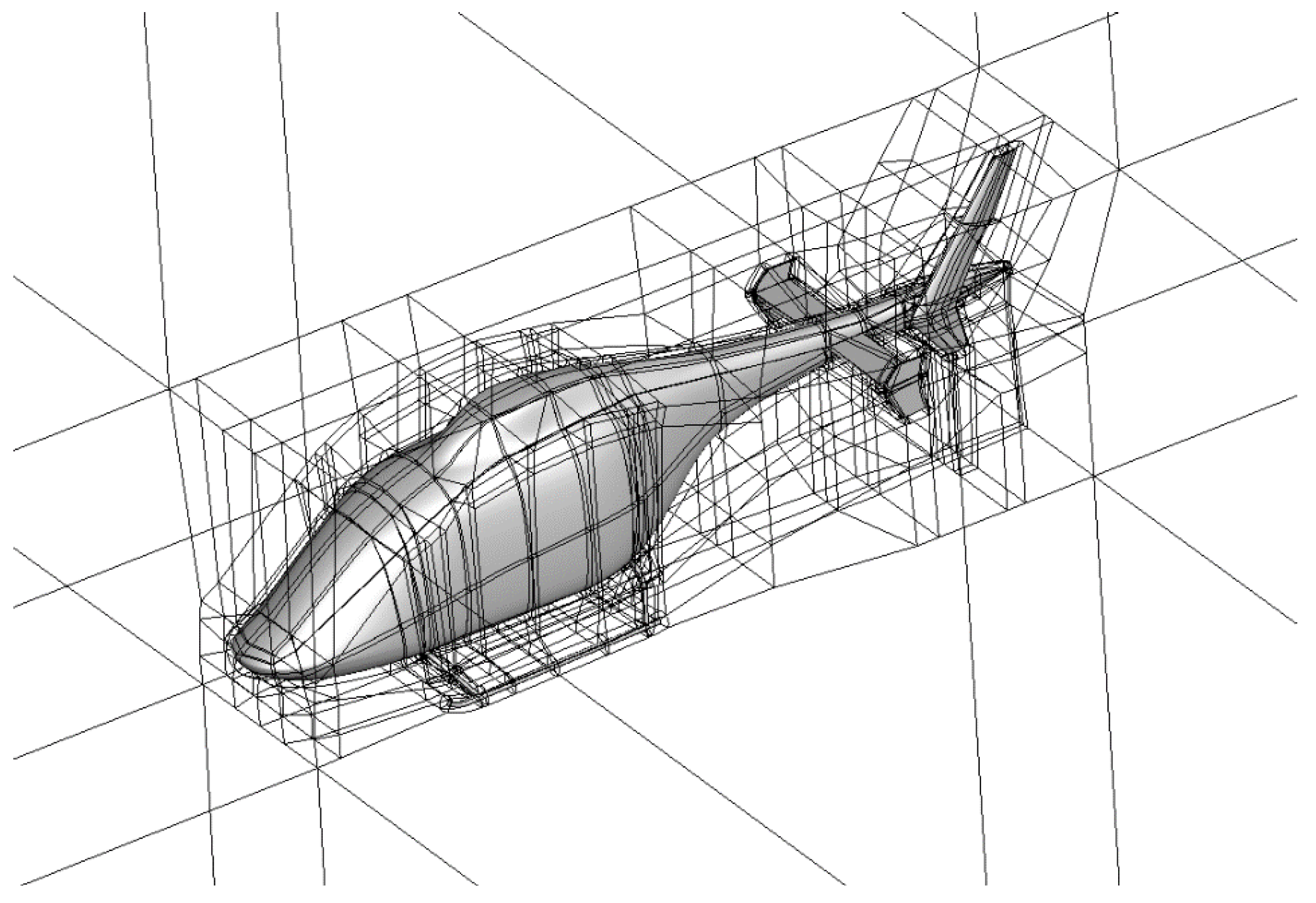
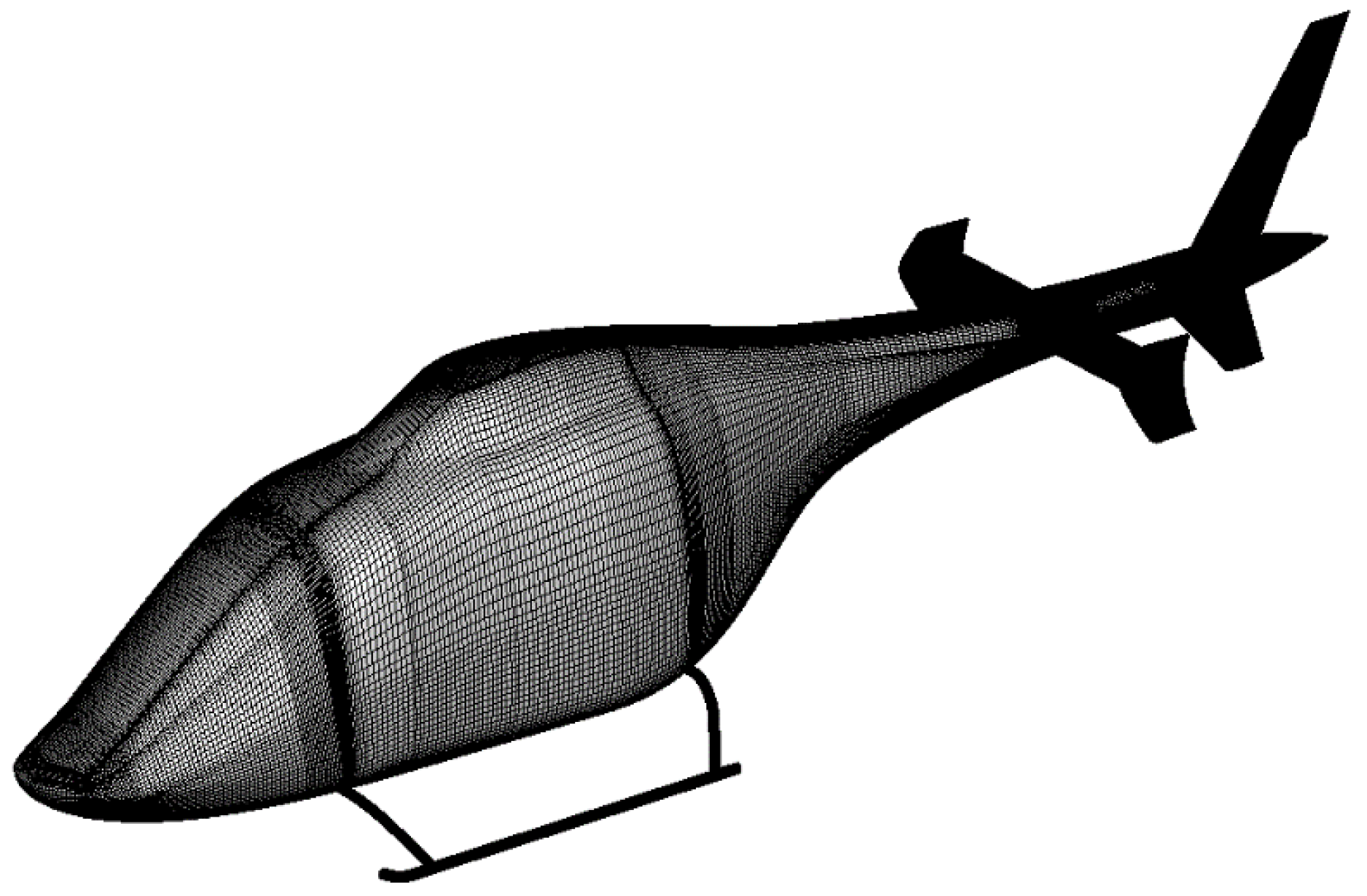
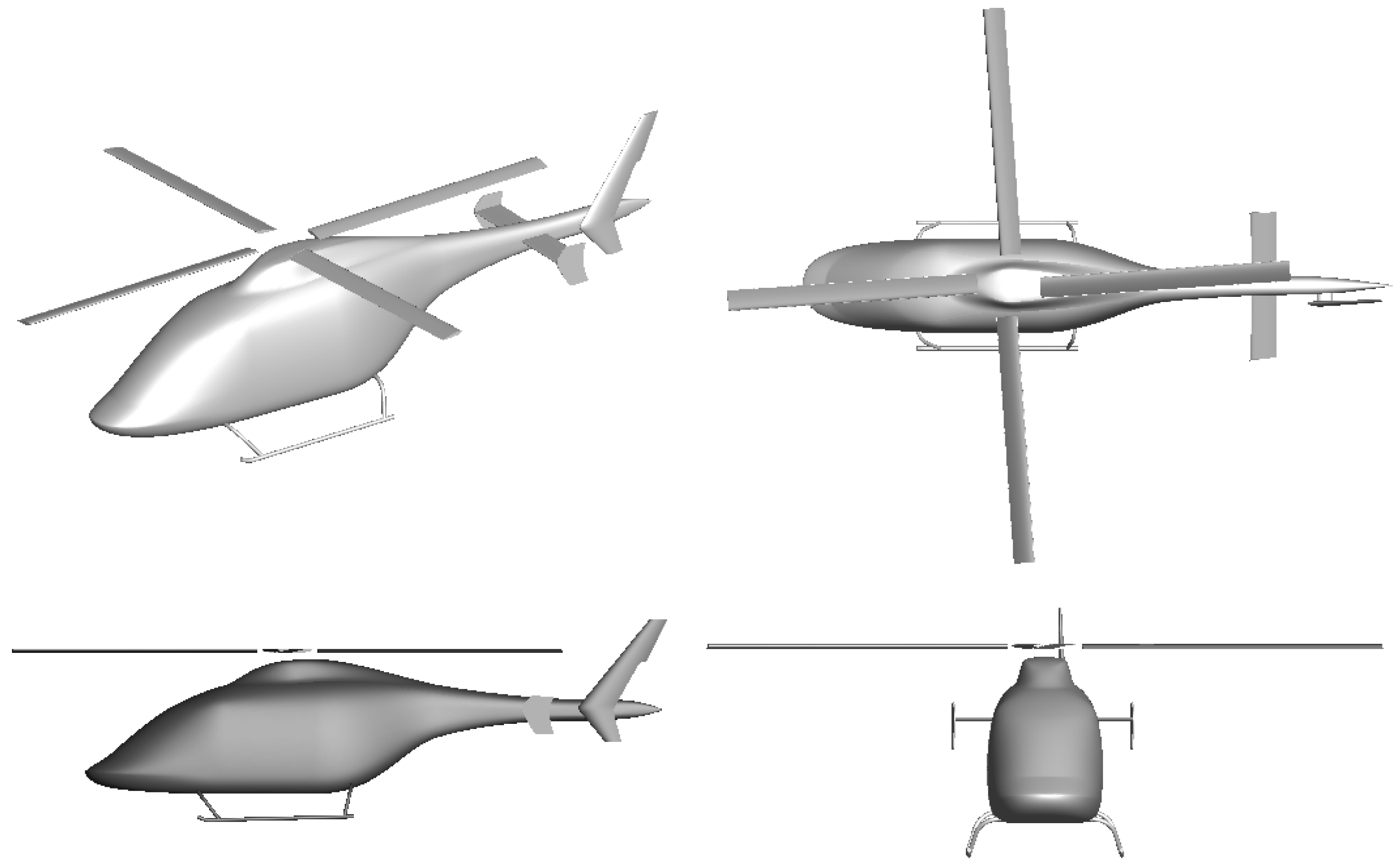
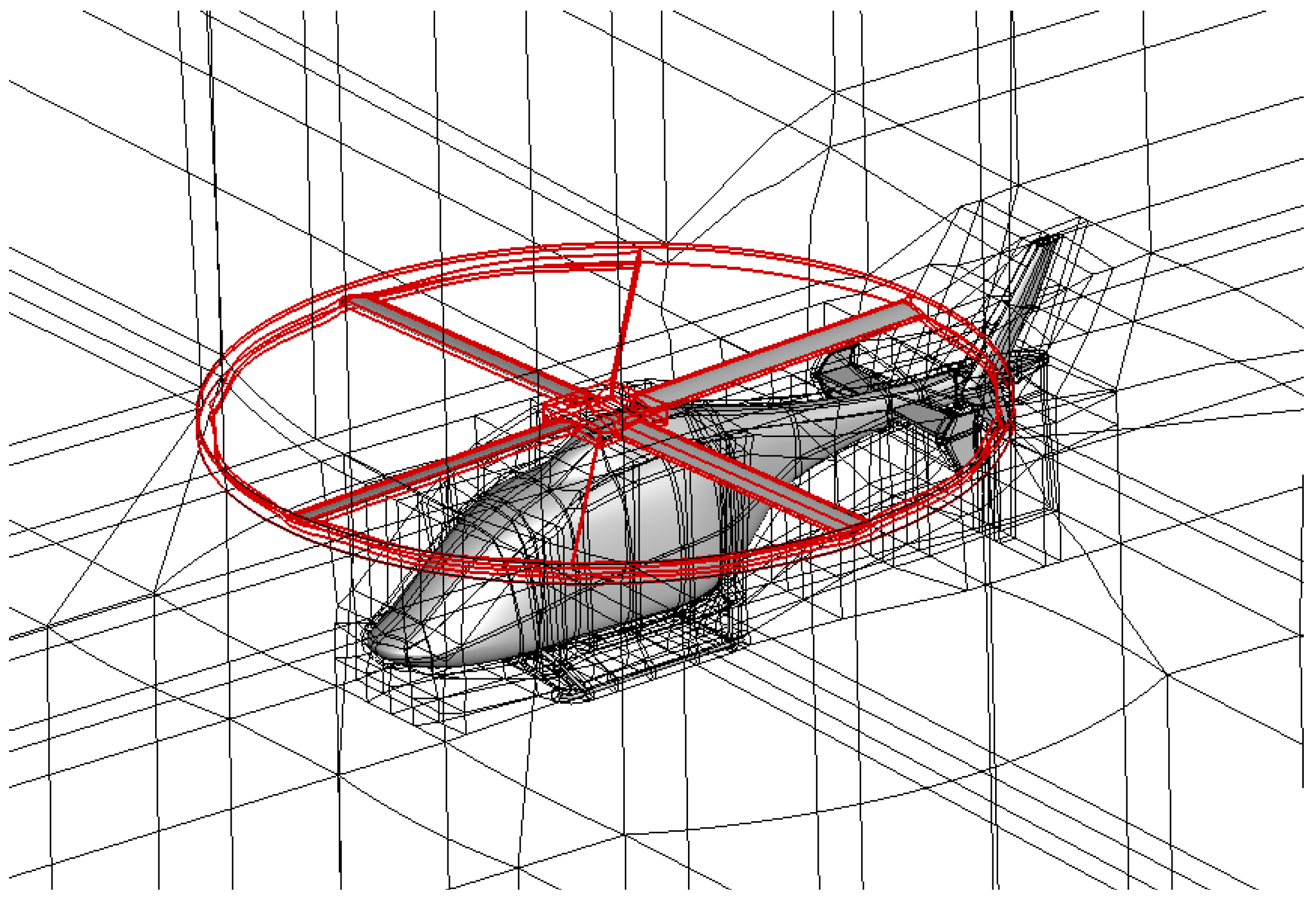
3.1. Configurations and Grid
3.2. Drag Performance
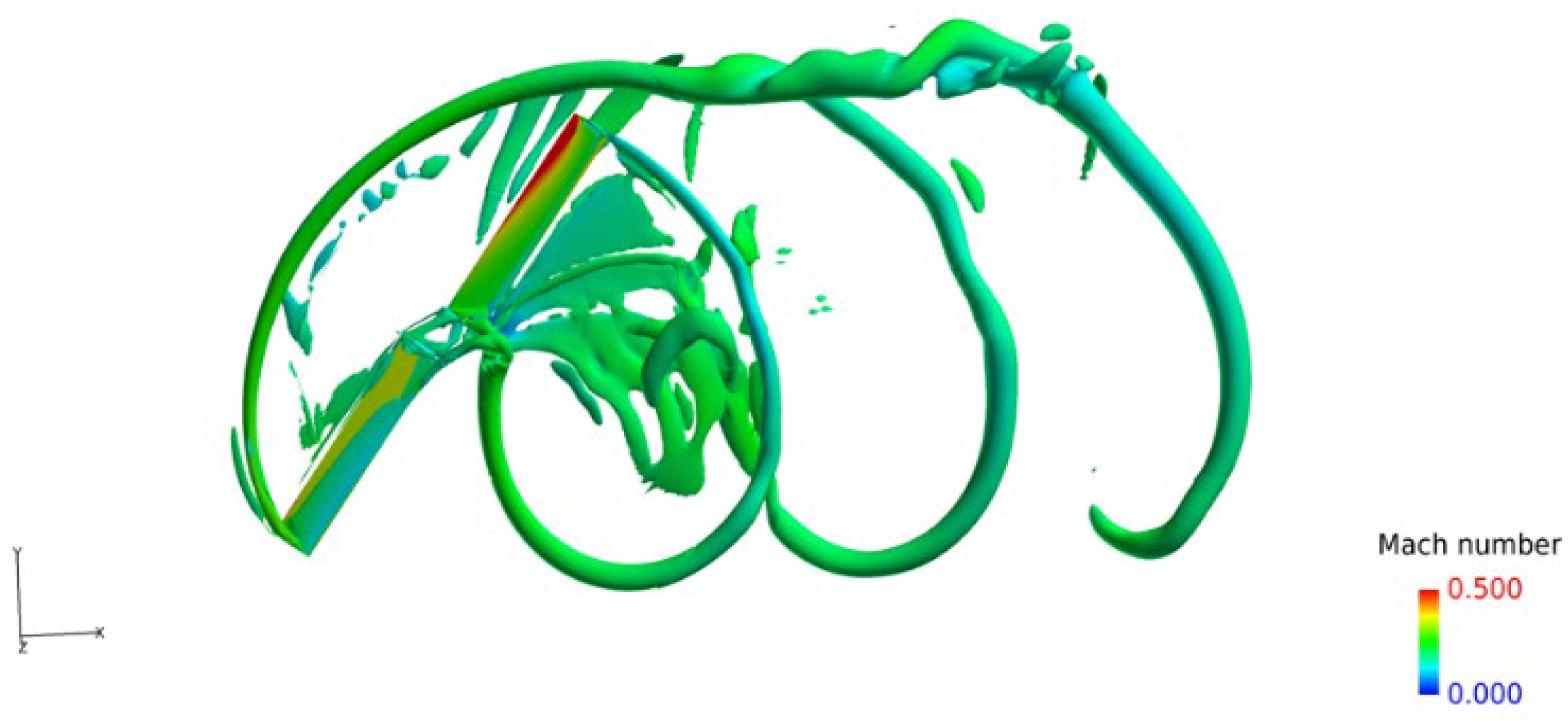
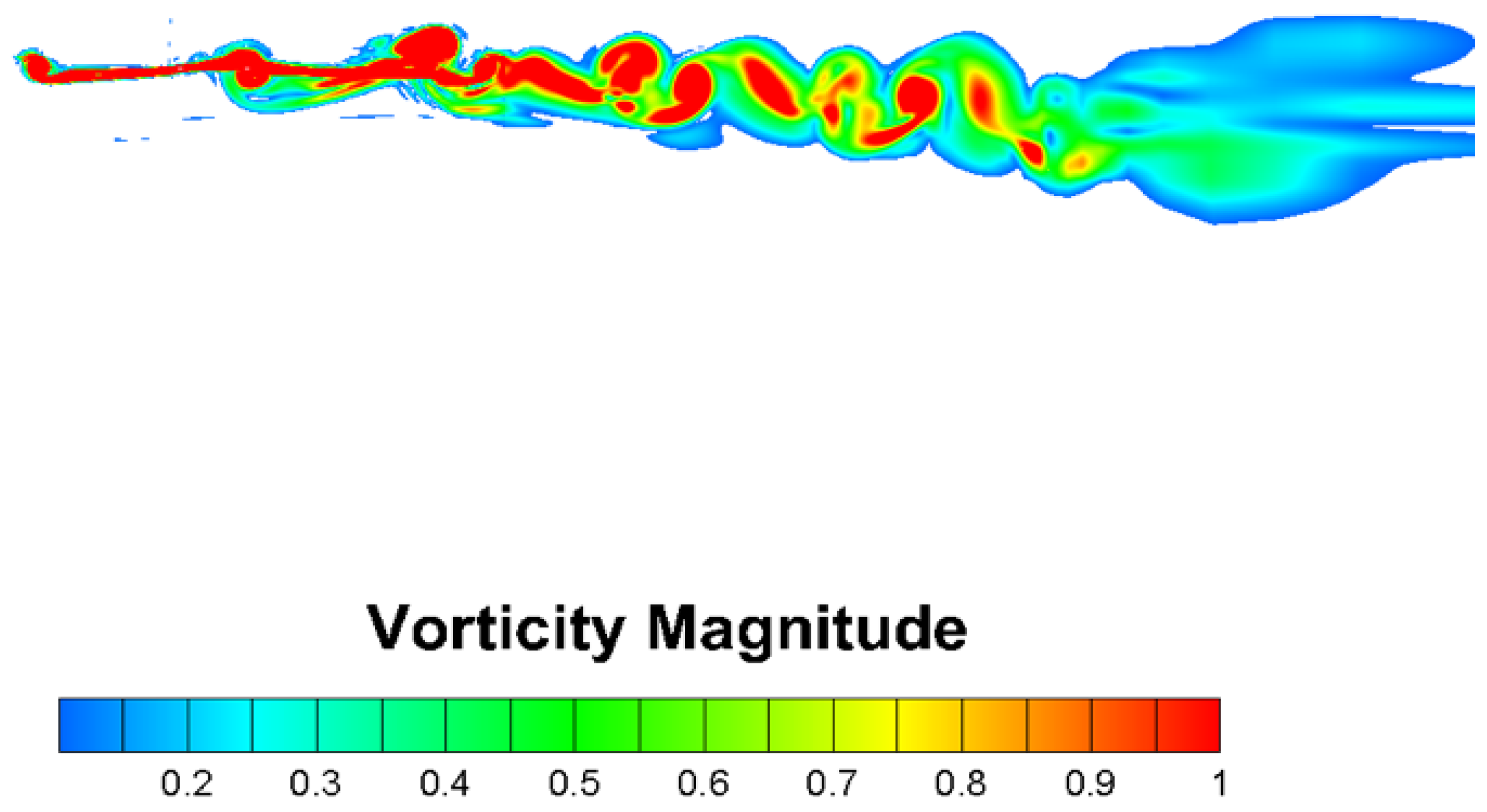
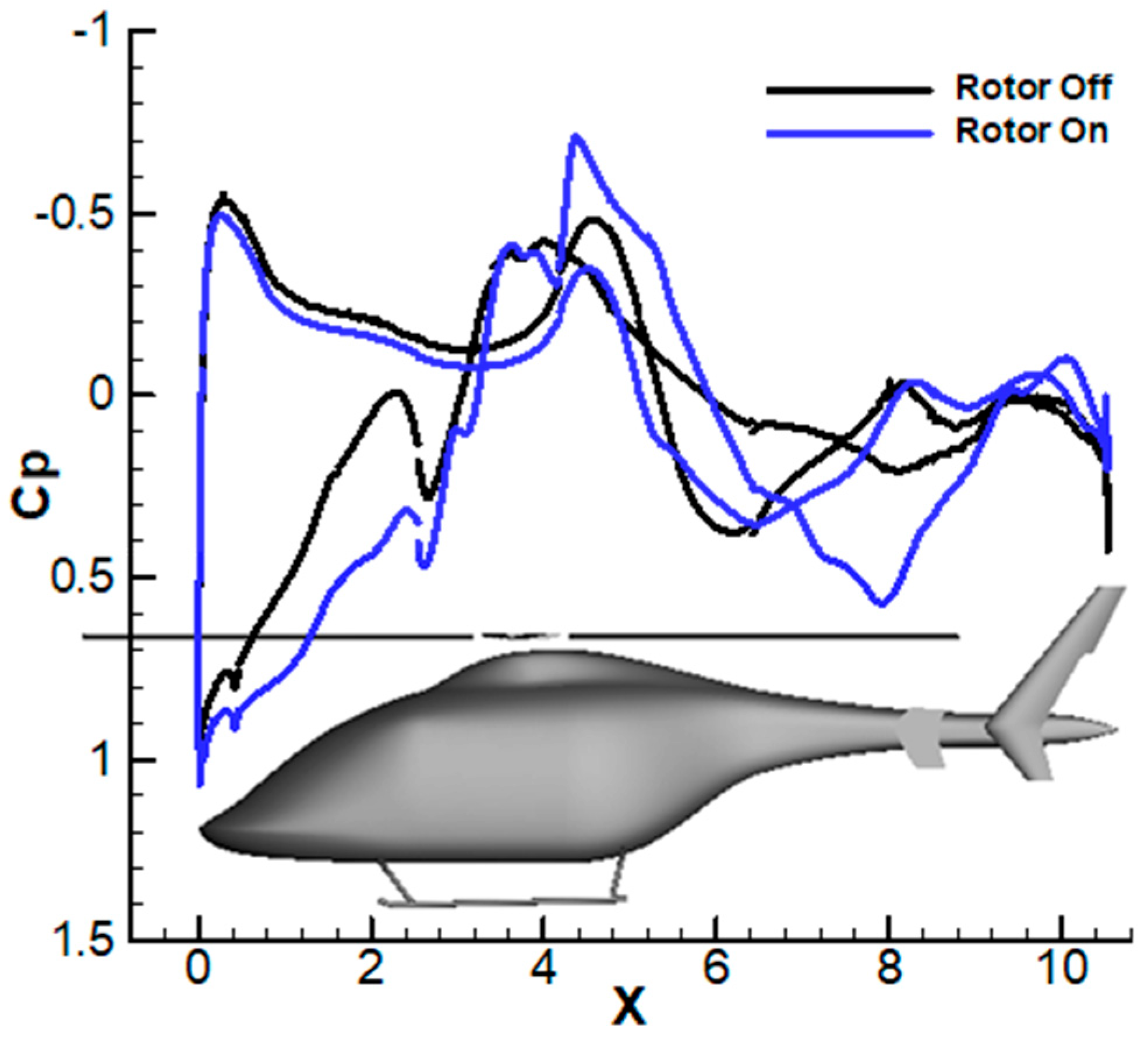
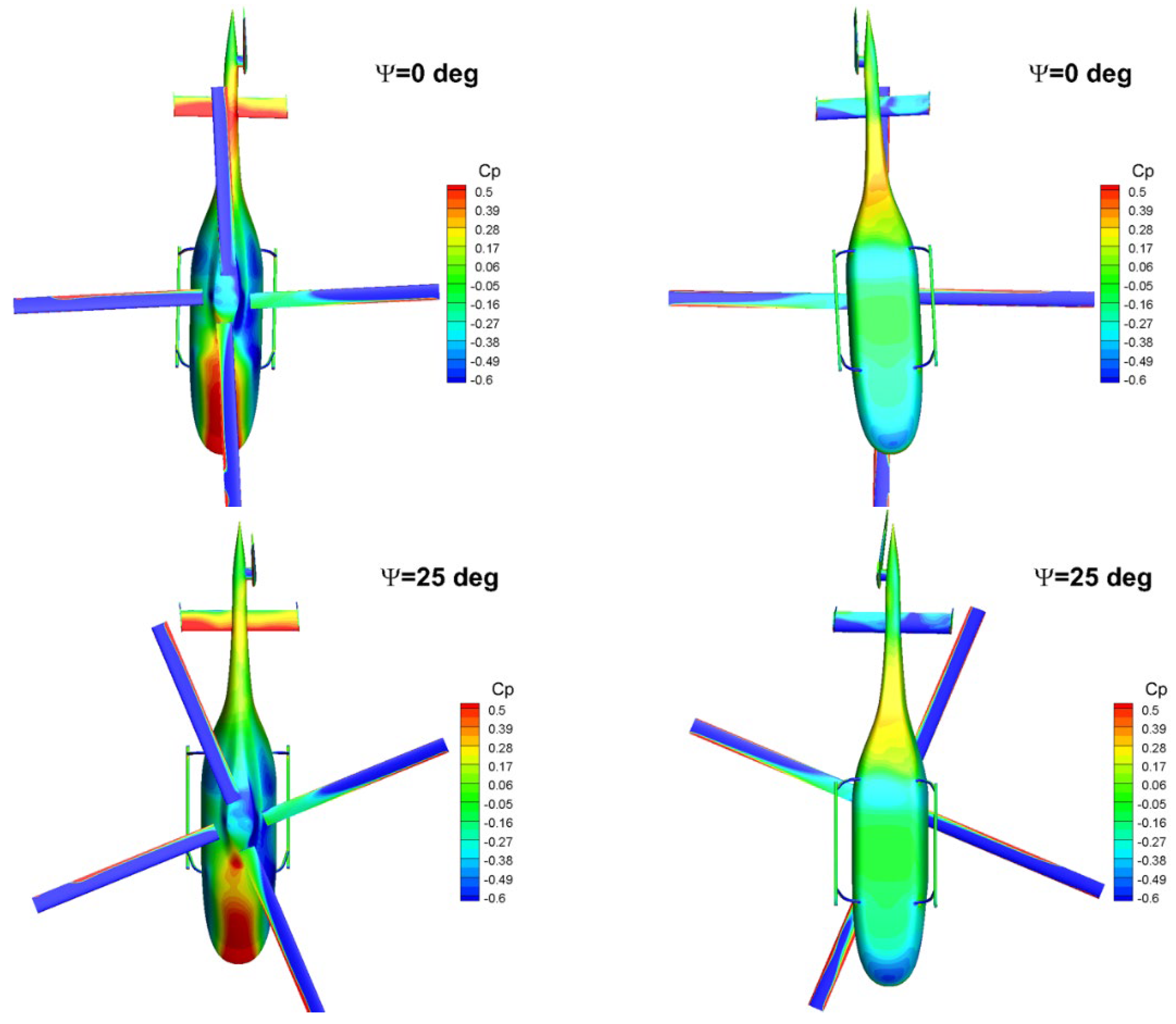
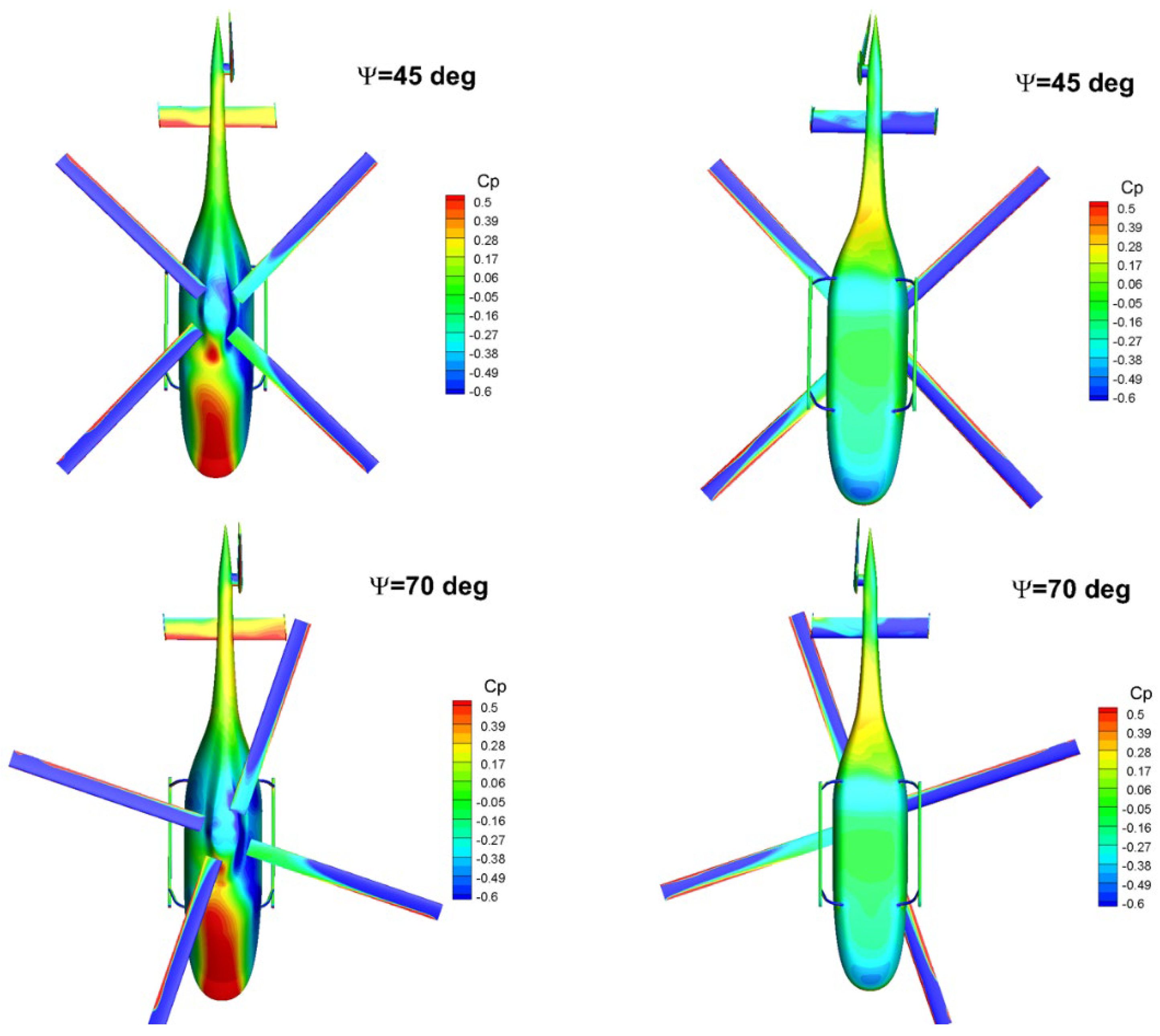
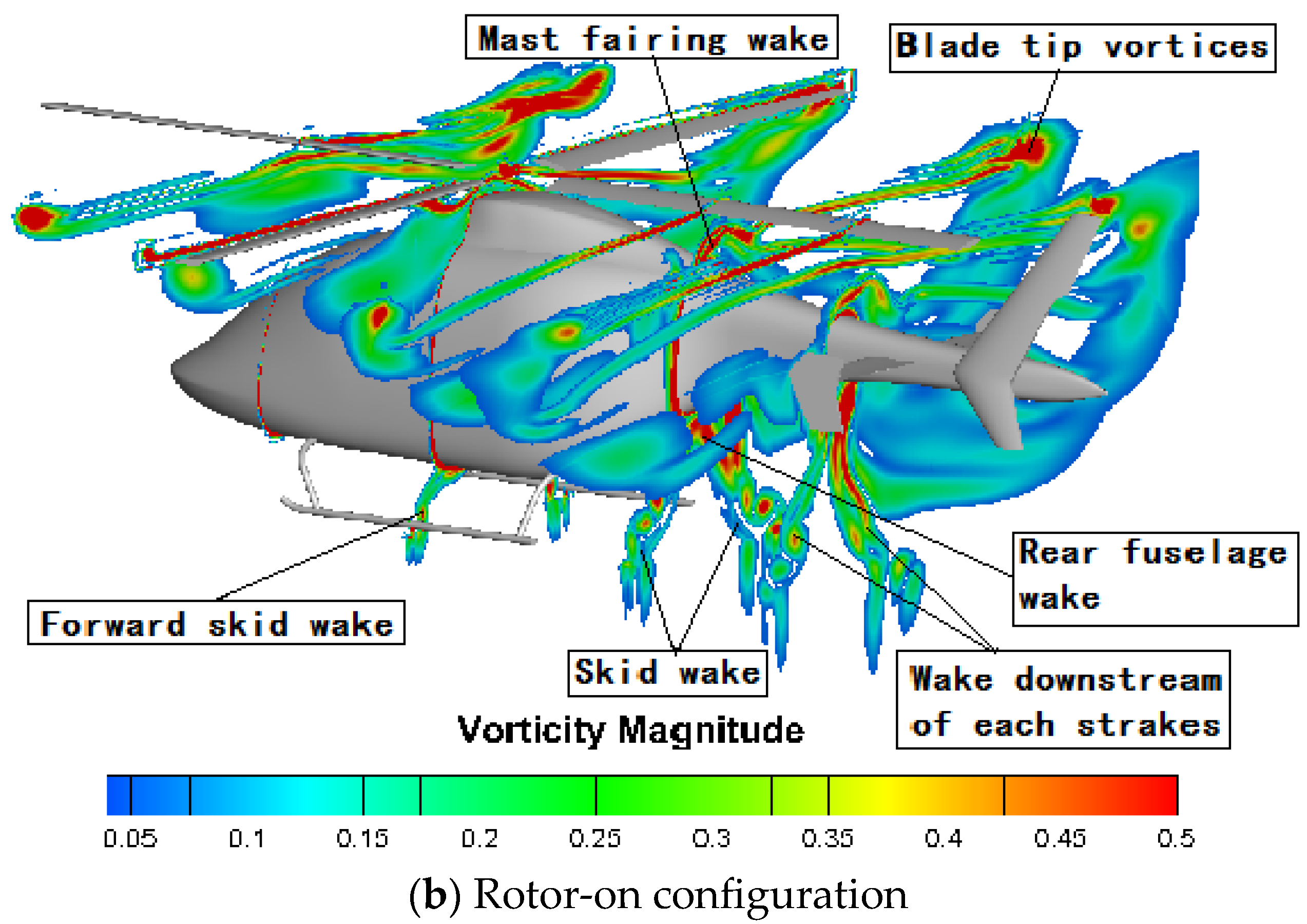
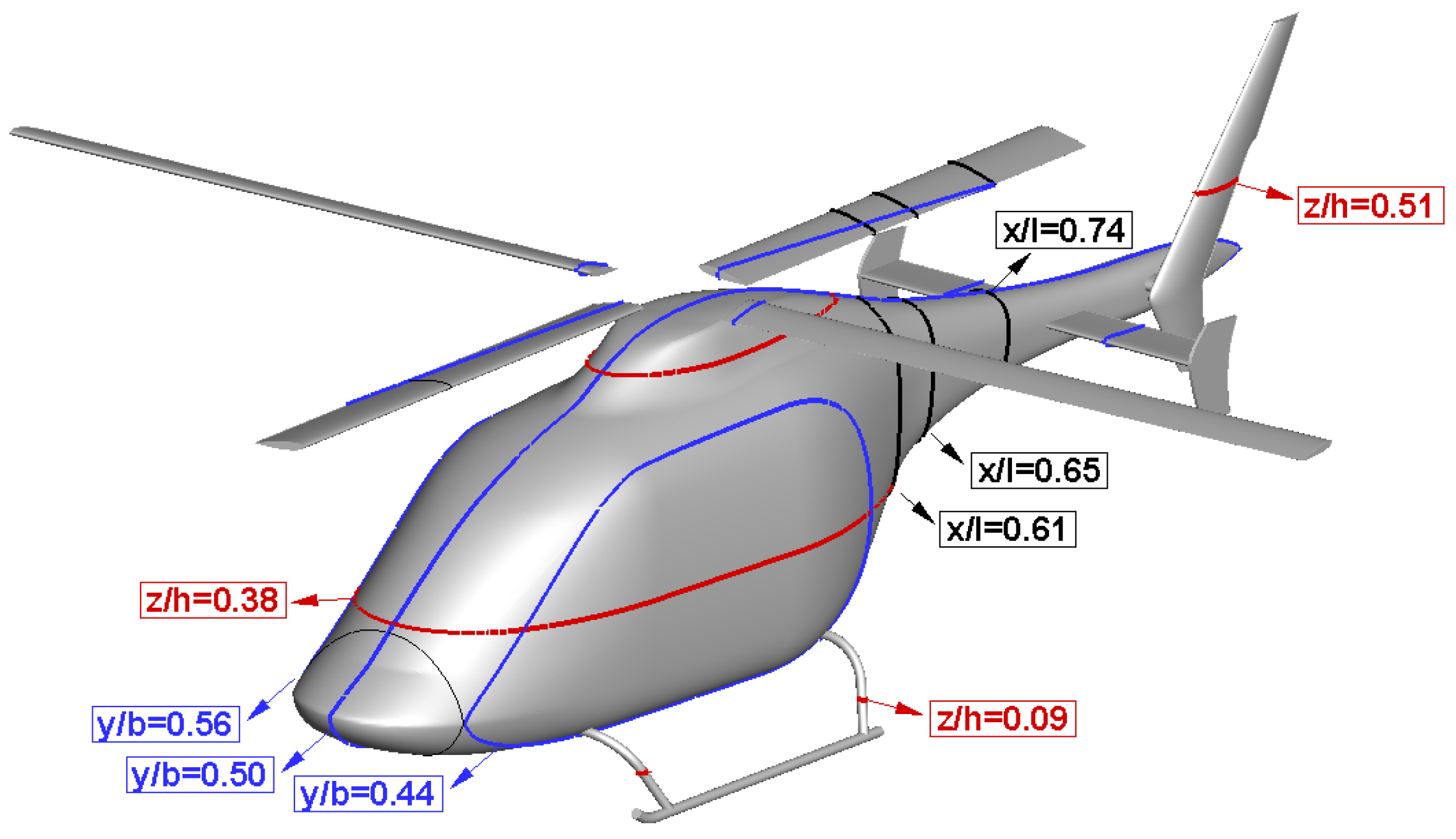
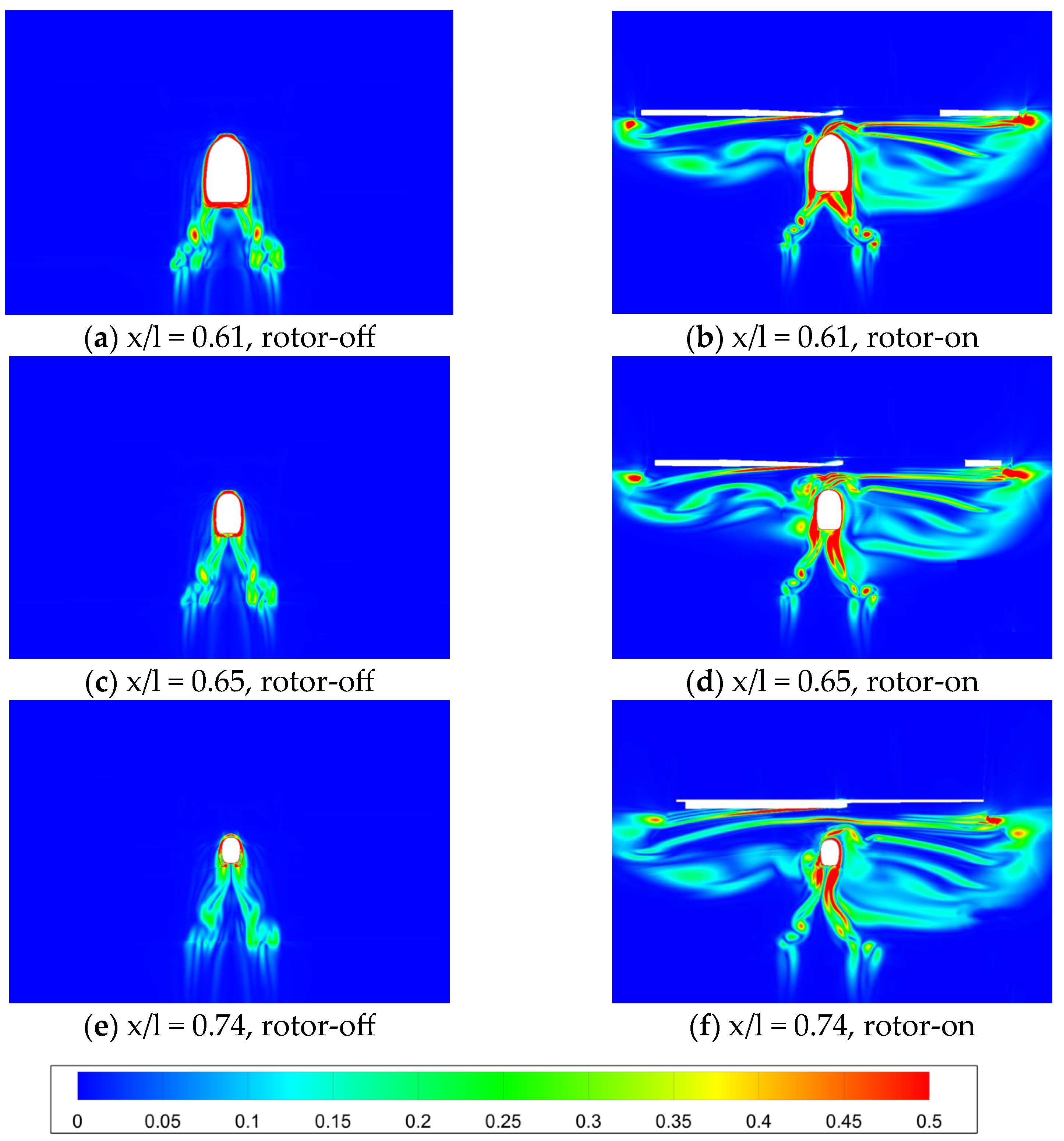
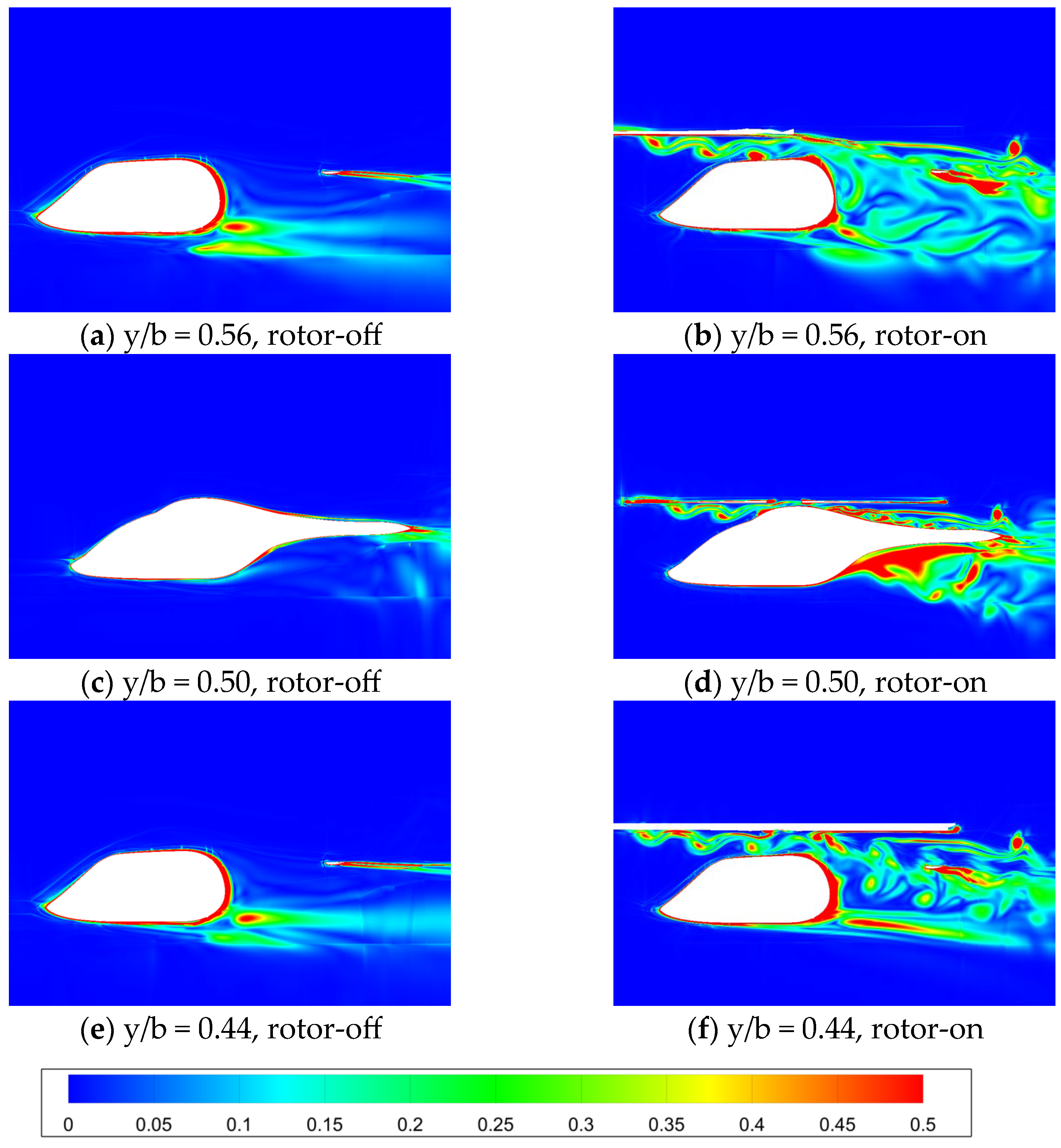
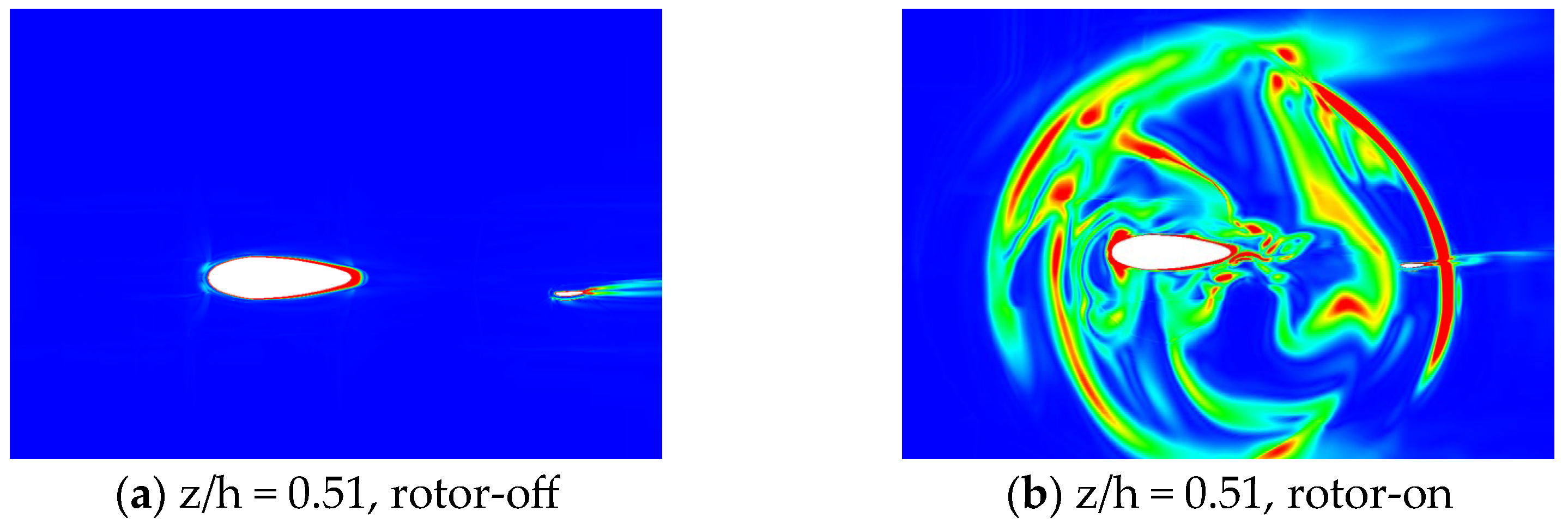
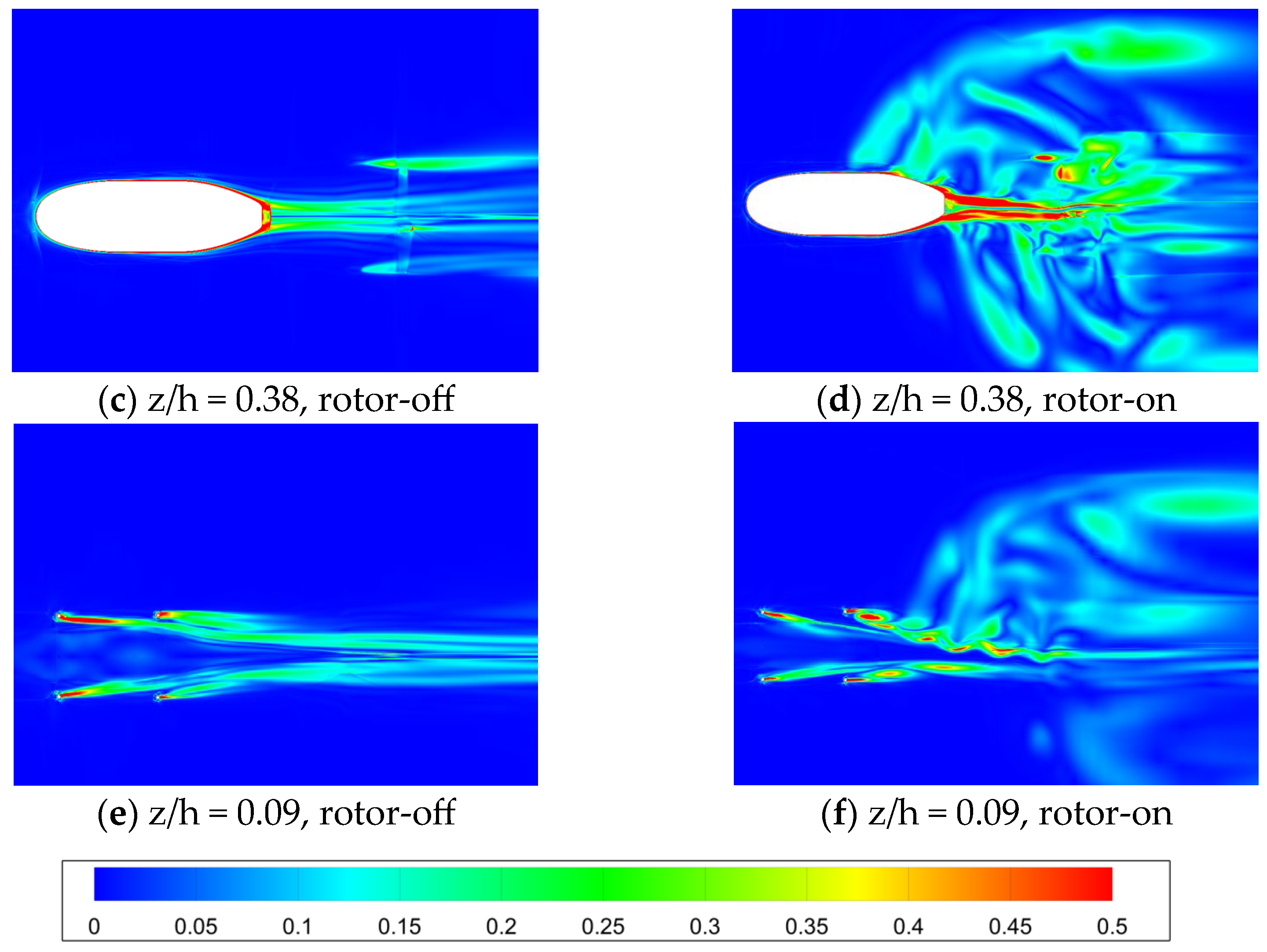
3.3. Flow Field
4. Conclusions
- (1)
- The comparison of the drag performance between the rotor-off and rotor-on configurations shows that the total drag increases by 57.9% while the drag of the fuselage and horizontal tail increases by 124.1%.
- (2)
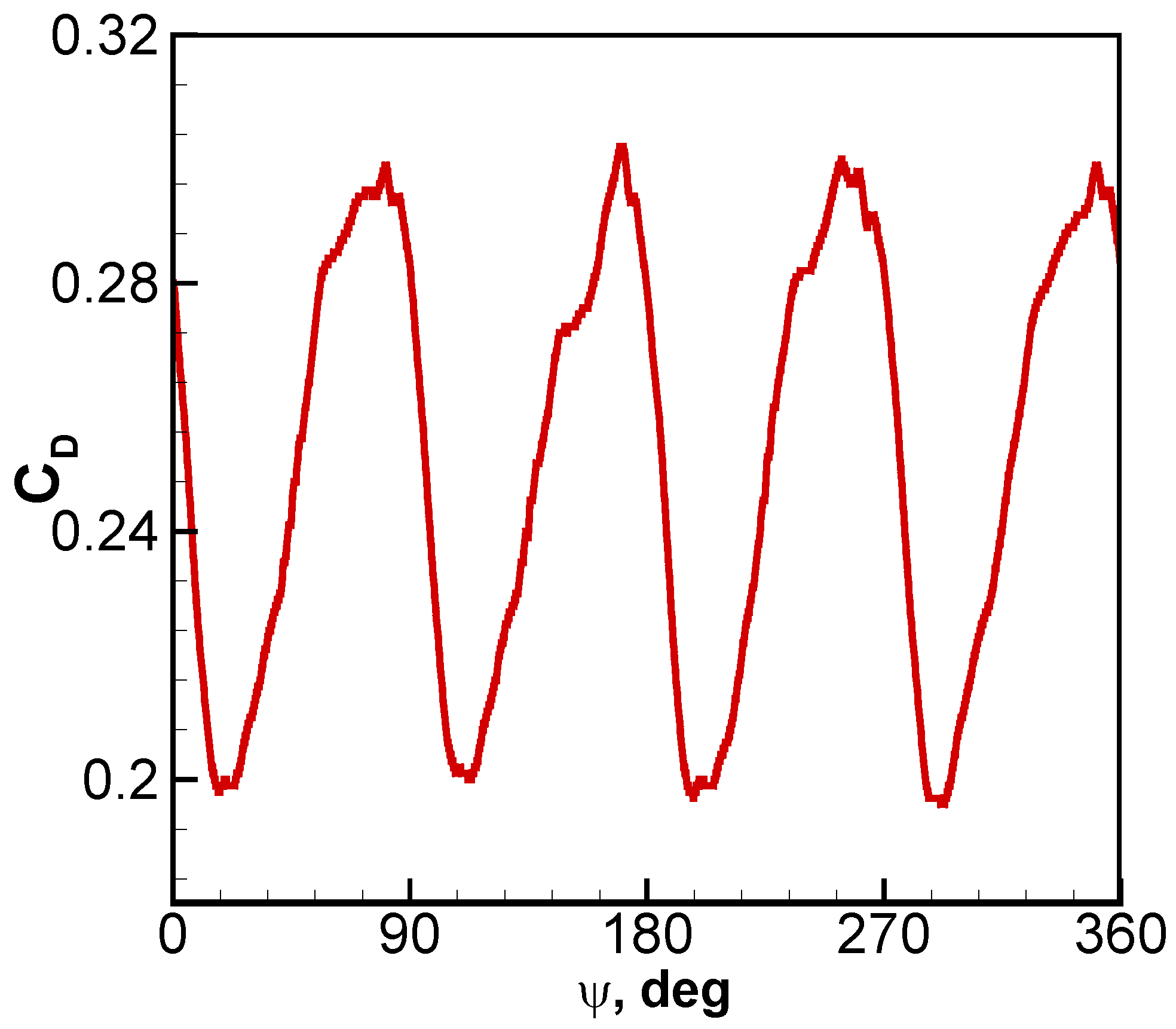
- The cycle of the drag fluctuation is observed in one full revolution of the rotor with a change in amplitude of ±20%. The change in the azimuth angle of the rotor mainly affects the drag performance of the fuselage and horizontal tail.
- (3)
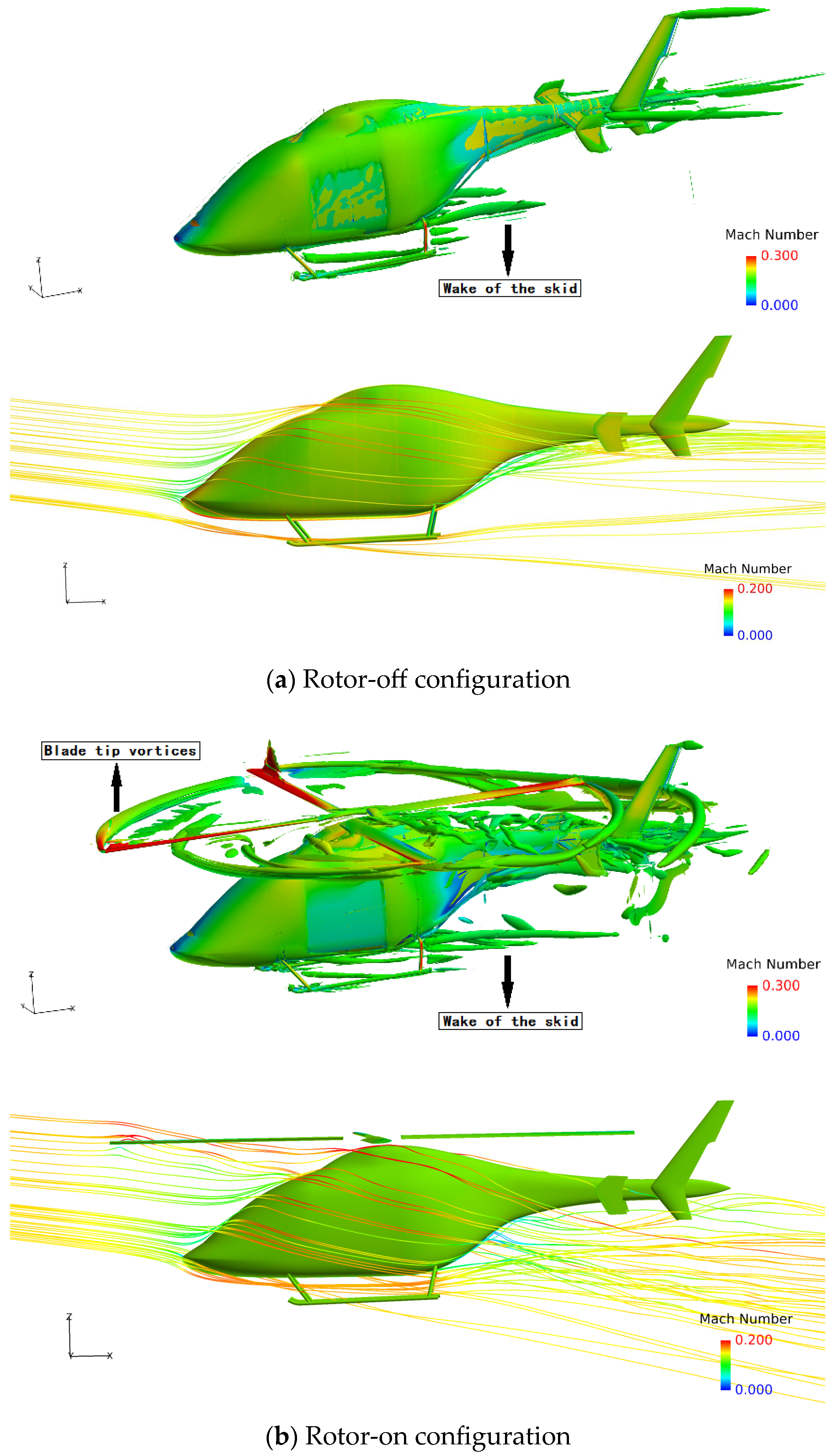
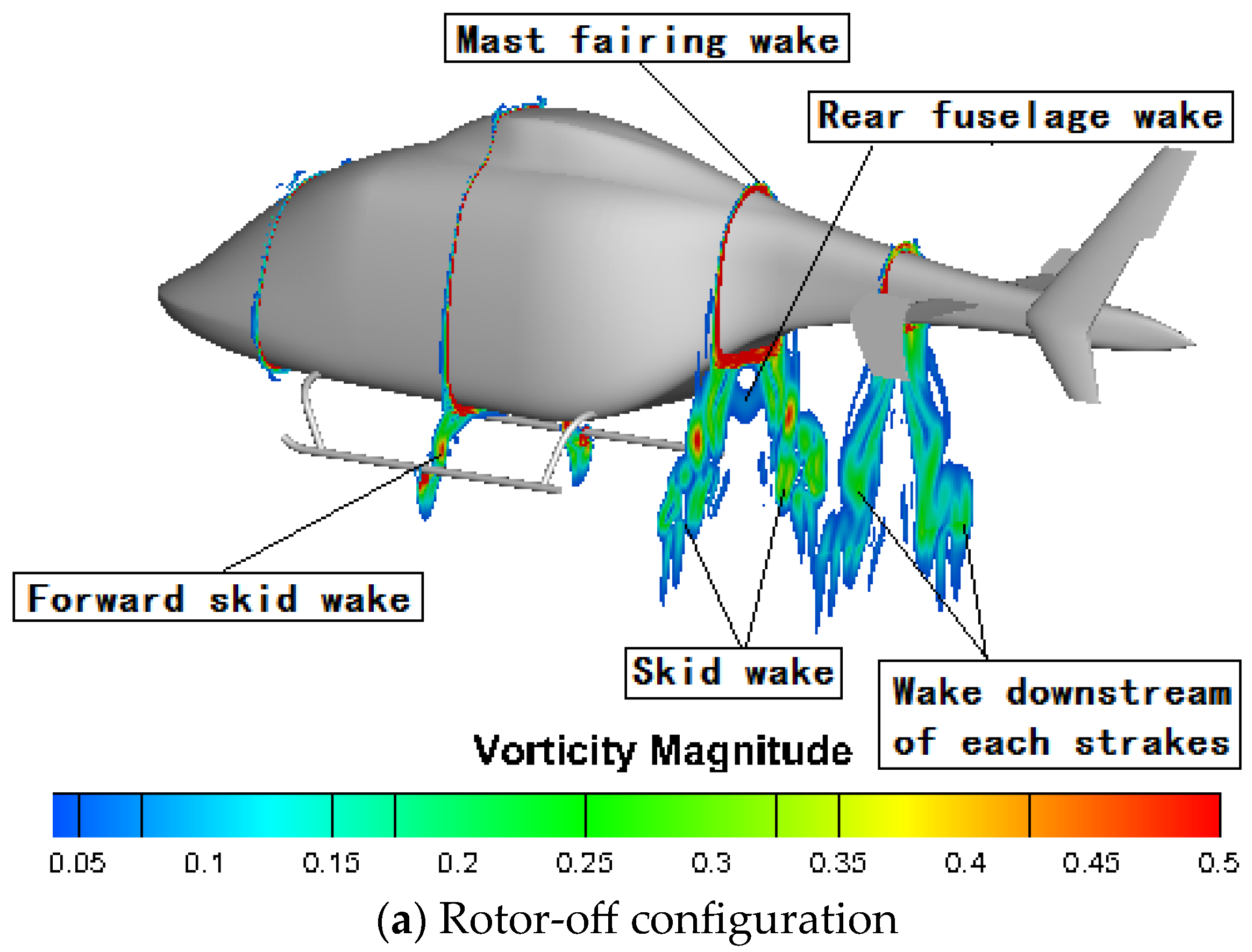
- The aerodynamic interaction effects between the rotor and fuselage on the drag performance are mainly reflected in the influence of the backward-developing rotor wake on the flow field of the rear part of the fuselage. Rotor rotation induces an additional afterbody vortices system.
- (4)
- The vorticity magnitude of the rotor-on configuration near the rear fuselage/tail boom increases significantly, suggesting that strong flow interactions occur between the rotor wake and the fuselage wake, forming a vortices system with a wide range. This vortices system causes a large reverse pressure gradient on the rear surface of the fuselage, which contributes to the increase in the pressure drag.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Conlisk, A.T. Modern helicopter rotor aerodynamics. Prog. Aerosp. Sci. 2001, 37, 419–476. [Google Scholar] [CrossRef]
- Stepanov, R.; Zherekhov, V.; Pakhov, V.; Mikhailov, S.; Garipov, A.; Yakubov, W.; Barakos, G.N. Experimental Study of Helicopter Fuselage Drag. J. Aircr. 2016, 53, 1343–1360. [Google Scholar] [CrossRef] [Green Version]
- Leishman, J.G.; Bi, N.-P. Aerodynamic Interactions between a Rotor and a Fuselage in Forward Flight. J. Am. Helicopter Soc. 1990, 35, 22–31. [Google Scholar] [CrossRef]
- Mavris, D.N.; Komerath, N.M.; McMahon, H.M. Prediction of Aerodynamic Rotor-fuselage Interactions in Forward Flight. J. Am. Helicopter Soc. 1989, 34, 37–46. [Google Scholar] [CrossRef]
- Zori, L.A.J.; Rajagopalan, R.G. Navier-Stokes Calculations of Rotor-fuselage Interaction in Forward Flight. J. Am. Helicopter Soc. 1995, 40, 57–67. [Google Scholar] [CrossRef]
- Batrakov, A.; Garipova, L.; Kusyumov, A.; Mikhailov, S.; Barakos, G. Computational Fluid Dynamics Modeling of Helicopter Fuselage Drag. J. Aircr. 2015, 52, 1634–1643. [Google Scholar] [CrossRef]
- Steijl, R.; Barakos, G.N. Computational Study of Helicopter Rotor-Fuselage Aerodynamic Interactions. AIAA J. 2009, 47, 2143–2157. [Google Scholar] [CrossRef]
- Steijl, R.; Barakos, G. CFD analysis of complete helicopter configurations—Lessons learnt from the GOAHEAD project. Aerosp. Sci. Technol. 2012, 19, 58–71. [Google Scholar] [CrossRef]
- Biava, M.; Vigevano, L. Simulation of a complete helicopter: A CFD approach to the study of interference effects. Aerosp. Sci. Technol. 2012, 19, 37–49. [Google Scholar] [CrossRef]
- Biava, M.; Khier, W.; Vigevano, L. CFD prediction of air flow past a full helicopter configuration. Aerosp. Sci. Technol. 2012, 19, 3–18. [Google Scholar] [CrossRef] [Green Version]
- Antoniadis, A.F.; Drikakis, D.; Zhong, B.; Barakos, G.; Steijl, R.; Biava, M.; Vigevano, L.; Brocklehurst, A.; Boelens, O.; Dietz, M.; et al. Assessment of CFD methods against experimental flow measurements for helicopter flows. Aerosp. Sci. Technol. 2012, 19, 86–100. [Google Scholar] [CrossRef]
- Quon, E.W.; Smith, M.J.; Whitehouse, G.R.; Wachspress, D. Unsteady Reynolds-averaged Navier-Stokes-based hybrid methodologies for rotor-fuselage interaction. J. Aircr. 2012, 49, 961–965. [Google Scholar] [CrossRef]
- Xu, H.Y.; Ye, Z.Y. Numerical simulation of rotor-fuselage aerodynamic interaction based on unstructured dynamic overset grids. Sci. China Technol. Sci. 2012, 55, 2798–2807. [Google Scholar] [CrossRef]
- Açıkgöz, M.B.; Aslan, A.R. Dynamic Mesh Analyses of Helicopter Rotor–Fuselage Flow Interaction in Forward Flight. J. Aerosp. Eng. 2016, 29, 04016050. [Google Scholar] [CrossRef]
- Petermann, J.; Jung, Y.S.; Baeder, J.; Rauleder, J.; Rauleder, J. Validation of Higher-Order Interactional Aerodynamics Simulations on Full Helicopter Configurations. J. Am. Helicopter Soc. 2019, 64, 1–13. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Jameson, A. Time dependent calculations using multigrid with applications to unsteady flows past airfoils and wings. In Proceedings of the 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–26 June 1991. [Google Scholar]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; p. 439. [Google Scholar]
- Shi, W.; Li, J.; Gao, H.; Zhang, H.; Yang, Z.; Jiang, Y. Numerical investigations on drag reduction of a civil light helicopter fuselage. Aerosp. Sci. Technol. 2020, 106, 106104. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, H.; Li, Y. Enhancing the Resolution of Blade Tip Vortices in Hover with High-Order WENO Scheme and Hybrid RANS–LES Methods. Aerospace 2023, 10, 262. [Google Scholar] [CrossRef]
- Caradonna, F.X.; Laub, G.H.; Tung, C. An Experimental Investigation of The Parallel Blade-Vortex Interaction; NASA-TM-19850005468; NASA Ames Research Center: Moffett Field, CA, USA, 1984. [Google Scholar]
- Strawn, R.C.; Caradonna, F.X.; Duque, E.P.N. 30 Years of Rotorcraft Computational Fluid Dynamics Research and Development. J. Am. Helicopter Soc. 2006, 51, 5–21. [Google Scholar] [CrossRef]
- Steijl, R.; Barakos, G. Sliding mesh algorithm for CFD analysis of helicopter rotor-fuselage aerodynamics. Int. J. Numer. Methods Fluids 2008, 58, 527–549. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. Studying Turbulence Using Numerical Simulation Databases, 2. Proceedings of the 1988 Summer Program, Stanford, CA, USA, December 1988. Available online: https://ntrs.nasa.gov/citations/19890015184 (accessed on 24 May 2023).



| Main rotor advanced ratio | 0.3 |
| Freestream Mach number | 0.188 |
| Main rotor tip Mach number | 0.628 |
| Reynolds number |
| Freestream Mach number | 0.16 |
| Reynolds number | 4.09 × 107 |
| Angle of attack | −8° |
| Main rotor advanced ratio (rotor-on configuration) | 0.2 |
| Main rotor tip Mach number (rotor-on configuration) | 0.8 |
| Component | Rotor-Off CD | Rotor-On CD | Δ |
|---|---|---|---|
| Fuselage | 0.079 | 0.177 | +124.1% |
| Horizontal tail | 0.024 | 0.038 | +58.3% |
| Left tail plane | 0.008 | 0.012 | +50.0% |
| Right tail plane | 0.010 | 0.006 | −40.0% |
| Landing skid | 0.038 | 0.022 | −42.1% |
| Vertical tail | 0.017 | 0.023 | +35.3% |
| Whole | 0.176 | 0.278 | +57.9% |
| Component | Fuselage | Horizontal Tail | Left Tail Plane | Right Tail Plane |
|---|---|---|---|---|
| Rotor-off | 0.079 | 0.024 | 0.008 | 0.010 |
| Ψ = 0° | 0.177 | 0.038 | 0.012 | 0.006 |
| Ψ = 25° | 0.104 | 0.033 | 0.011 | 0.006 |
| Ψ = 45° | 0.140 | 0.036 | 0.009 | 0.006 |
| Ψ = 70° | 0.185 | 0.041 | 0.011 | 0.006 |
| Component | Skid | Vertical Tail | Whole | Component |
| Rotor-off | 0.038 | 0.017 | 0.176 | Rotor-off |
| Ψ = 0° | 0.022 | 0.023 | 0.278 | Ψ = 0° |
| Ψ = 25° | 0.023 | 0.022 | 0.199 | Ψ = 25° |
| Ψ = 45° | 0.023 | 0.021 | 0.235 | Ψ = 45° |
| Ψ = 70° | 0.023 | 0.023 | 0.289 | Ψ = 70° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Zhang, H.; Li, Y. The Aerodynamic Interaction Effects between the Rotor and Fuselage on the Drag Performance of a Civil Helicopter in Forward Flight. Appl. Sci. 2023, 13, 7376. https://doi.org/10.3390/app13137376
Shi W, Zhang H, Li Y. The Aerodynamic Interaction Effects between the Rotor and Fuselage on the Drag Performance of a Civil Helicopter in Forward Flight. Applied Sciences. 2023; 13(13):7376. https://doi.org/10.3390/app13137376
Chicago/Turabian StyleShi, Wenbo, Heng Zhang, and Yuanxiang Li. 2023. "The Aerodynamic Interaction Effects between the Rotor and Fuselage on the Drag Performance of a Civil Helicopter in Forward Flight" Applied Sciences 13, no. 13: 7376. https://doi.org/10.3390/app13137376
APA StyleShi, W., Zhang, H., & Li, Y. (2023). The Aerodynamic Interaction Effects between the Rotor and Fuselage on the Drag Performance of a Civil Helicopter in Forward Flight. Applied Sciences, 13(13), 7376. https://doi.org/10.3390/app13137376





