Privacy-Preserving Federated Singular Value Decomposition

Abstract

Singular value decomposition (SVD) is a fundamental technique widely used in various applications, such as recommendation systems and principal component analyses. In recent years, the need for privacy-preserving computations has been increasing constantly, which concerns SVD as well. Federated SVD has emerged as a promising approach that enables collaborative SVD computation without sharing raw data. However, existing federated approaches still need improvements regarding privacy guarantees and utility preservation. This paper moves a step further towards these directions: we propose two enhanced federated SVD schemes focusing on utility and privacy, respectively. Using a recommendation system use-case with real-world data, we demonstrate that our schemes outperform the state-of-the-art federated SVD solution. Our utility-enhanced scheme (utilizing secure aggregation) improves the final utility and the convergence speed by more than 2.5 times compared with the existing state-of-the-art approach. In contrast, our privacy-enhancing scheme (utilizing differential privacy) provides more robust privacy protection while improving the same aspect by more than 25%.

1. Introduction

Advances in networking and hardware technology have led to the rapid proliferation of the Internet of Things (IoTs) and decentralized applications. These advancements, including fog computing and edge computing technologies, enable data processing and analysis to be performed at node devices, avoiding the need for data aggregation. This naturally brings benefits such as efficiency and privacy, but on the other hand, it forces data analysis tasks to be carried out in a distributed manner. To this end, federated learning (FL) has emerged as a promising solution in this context, allowing multiple parties to collaboratively train models without sharing raw data. Instead, only intermediate results are exchanged with an aggregator server, ensuring privacy preservation and decentralized data analysis [1].

With respect to machine learning tasks, research has shown that sensitive information can be leaked from the models [2,3,4,5]. For example, in [3], Shokri et al. demonstrated membership inference attacks against machine learning tasks. In such an attack, an attacker can determine whether a data sample has been used in the model training. This will violate privacy if the data sample is sensitive. Regardless of its privacy friendly status, FL suffers similar privacy issues, as demonstrated by Nasr, Shokri and Houmansadr [5]. This makes it necessary to incorporate additional privacy protection mechanisms into FL and to make it rigorously privacy-preserving.

To mitigate information leakages, FL can be aided with other privacy-enhancing technologies, such as secure aggregation (SA) [6] and differential privacy (DP) [7]. SA hides the individual contributions from the aggregator server in each intermediate step in a way that does not affect the trained model’s utility. In other words, the standalone updates are masked such that the masks cancel out during aggregation; therefore, the aggregated results remain intact. The masks could be seen as temporary noise; hence, the privacy protection does not extend to the aggregated data. In contrast, DP adds persistent noise to the model, i.e., it provides broader privacy protection but with an inevitable utility loss (due to the permanent noise). We differentiate between two DP settings depending on where the noise is injected. In local DP (LDP), the participants add noise to their updates, while in central DP (CDP), the server applies noise to the aggregate result. A comparison of LDP, CDP and SA is summarized in

Table 1. Comparing secure aggregation with local and central differential privacy.

Protects	The Individual Updates	The Aggregate
Secure Aggregation	✓	✗
Central DP	✗	✓
Local DP	✓	✓

. While there are many privacy protection mechanisms, incorporating them into FL is not a trivial task and remains as open challenges [1].

Among many data analysis methods, this paper focuses on singular value decomposition (SVD). Plainly, SVD factorizes a matrix into three new matrices. Originating from linear algebra, SVD has several interesting properties and conveys crucial insights about the underlying matrix. Hence, SVD has essential applications in data science, such as in recommendation systems [8,9], principal component analysis [10], latent semantic analysis [11], noise filtering [12,13], dimension reduction [14], clustering [15], matrix completion [16], etc. Existing federated SVD solutions fall into two categories: SVD over horizontally and vertically partitioned datasets [17]. In real-world applications, the former is much more common [18,19]; therefore, in this paper, we choose the horizontal setting and focus on the privacy protection challenges.

1.1. Related Work

The concept of privacy-preserving federated SVD has been studied in several works, which are briefly summarized below.

In the literature, many anonymization techniques have been proposed to enable privacy protection in federated machine learning and other tasks. Ref. [20] proposed substitute vectors and length-based frequent pattern tree (LFP-tree) to achieve the data anonymization. It focuses on what data can be published and how they can be published without associating subjects or identities. With the concept of data anonymization in mind, Ref. [21] proposed a strategy by decreasing the correlation between data and the identities. However, the utility of the data will be affected. And, Ref. [22] focused on high-dimensional dataset, which is divided into different subsets; then, each subset is generalized with a novel heuristic method based on local re-coding. While these works contain interesting techniques, they do not directly offer a solution for privacy-preserving federated SVD. A more detailed analysis can be found in [1].

Technically speaking, the algorithms utilized to compute SVD are mostly iterative, such as the power iteration method [23]. Recently, these algorithms were adopted to a distributed setting to solve large-scale problems [24,25]. While these works tackle important issues and advance the field, they all disregard privacy issues: we are only aware of two federated SVD solutions in the literature explicitly providing a privacy analysis [18,19]. Hartebrodt et al. [19] proposed a federated SVD algorithm with a star-like architecture for high-dimensional data such that the aggregator cannot access the complete eigenvector matrix of SVD results. Instead, each node device has access, but only to its shared part of the eigenvector matrix. In addition to the lack of a rigorous privacy analysis, its aim is different from most other federated SVD solutions where the aim is to jointly compute a global feature space. In contrast, Guo et al. [18] proposed a federated SVD algorithm based on the distributed power method, where both the server and all the participants learn the entire eigenvector matrix. Their solution incorporated additional privacy-preserving features, such as participant and aggregator server noise injection, but without a rigorous privacy analysis. We improve upon this solution by pointing out an error in its privacy analysis and by providing a tighter privacy protection with less utilized noise. Overall, these existing literature works do not provide a privacy-preserving federated SVD solution with a rigorous analysis in our setting.

1.2. Contribution and Organization

This work focuses on a setting similar to Guo et al. [18], i.e., when the server and all the participants are expected to learn the final eigenvector matrix. As our main contribution, we improve the FedPower algorithm [18] from two perspectives, i.e., both from the privacy and utility points of view. Our detailed contributions are summarized below.

• Firstly, we point out several inefficiencies and shortcomings of FedPower, such as the avoidable double noise injection steps and the unclear and confusing privacy guarantee.
• Secondly, we propose a utility enhanced solution, where the added noise is reduced due to the introduction of SA.
• Thirdly, we propose a privacy enhanced solution, which (in contrast to FedPower) satisfies DP.
• Finally, we empirically validate our proposed algorithms by measuring the privacy-utility trade-off using a real-world recommendation system use-case.

The rest of the paper is organized as follows. In Section 2, we list the fundamental definitions of the relevant techniques used throughout the paper. In Section 3, we recap the scheme proposed by Guo et al. [18], while in Section 4 and Section 5, we propose two improved schemes focusing on utility and privacy, respectively. In Section 6, we empirically compare the proposed schemes with the original work. Finally, in Section 7, we conclude the paper.

2. Preliminary

2.1. Singular Value Decomposition

Let $\mathbb{M}$ be a $s\times d$ matrix with assumption of $s\le d$. As shown in Figure 1, the full SVD of $\mathbb{M}$ is a factorization of the form $\mathbb{U}\Sigma {\mathbb{V}}^T$, where T means conjugate transpose. The left-singular vectors are $\mathbb{U}=[u_1,u_2,\cdots ,u_s]\in {\mathbb{R}}^{s\times s}$, the right-singular vectors are $\mathbb{V}=[v_1,v_2,\cdots ,v_d]\in {\mathbb{R}}^{d\times d}$, and the diagonal matrix with the singular values in decreasing order in its diagonal is $\Sigma =\mathsf{diag}\{{\sigma }_1,{\sigma }_1,\cdots ,{\sigma }_d\}\in {\mathbb{R}}^{s\times d}$. The partial or truncated SVD [26,27] is used to find the top k$(k\le d)$ singular vectors $\mathbb{U}=[u_1,u_2,\cdots ,u_k]$, $\mathbb{V}=[v_1,v_2,\cdots ,v_k]$ and singular values $\Sigma =\mathsf{diag}\{{\sigma }_1,{\sigma }_1,\cdots ,{\sigma }_k\}$.

If ${\mathbb{M}}^{\prime }=\frac{1}{s}{\mathbb{M}}^T\mathbb{M}\in {\mathbb{R}}^{d\times d}$, then the Power Method [23] could be used to compute the top k right singular vector of $\mathbb{M}$ and the top k eigenvectors of ${\mathbb{M}}^{\prime }$. It works by iterating $\mathbb{Y}={\mathbb{M}}^{\prime }\mathbb{Z}$ and $\mathbb{Z}=\mathsf{orth}\left(\mathbb{Y}\right)$, where both $\mathbb{Y}$ and $\mathbb{Z}$ are $d\times k$ matrices and $\mathsf{orth}(·)$ is the orthogonalization of the columns with QR factorization.

Moreover, if $\mathbb{M}$ is the composition of n matrices, then computation of the Power Method can be distributed. So, if ${\mathbb{M}}^T=[{\mathbb{M}}_1^T,{\mathbb{M}}_2^T,\cdots ,{\mathbb{M}}_n^T]\in {\mathbb{R}}^{s\times d}$ with $s={\sum }_{i=1}^n{s}_i$, where ${\mathbb{M}}_i\in {\mathbb{R}}^{s_i\times d}$ and ${\mathbb{M}}_i^{\prime }=\frac{1}{s_i}{\mathbb{M}}_i^T{\mathbb{M}}_i$, then Equation (1) holds. Thereby, $\mathbb{Y}$ can be written as $\mathbb{Y}={\sum }_{i=1}^n\frac{s_i}{s}{\mathbb{M}}_i^{\prime }\mathbb{Z}\in {\mathbb{R}}^{d\times k}$, which indicates that the Power Method can be processed in parallel by each data holder [18,28].

$${\mathbb{M}}^{\prime }=\frac{1}{s}{\mathbb{M}}^T\mathbb{M}=\sum _{i=1}^n\frac{1}{s}{\mathbb{M}}_i^T{\mathbb{M}}_i=\sum _{i=1}^n\frac{s_i}{s}{\mathbb{M}}_i^{\prime }=\sum _{i=1}^d{p}_i{\mathbb{M}}_i^{\prime }$$

(1)

2.2. Secure Aggregation

In simple terms, with SA, the original data of each node device are locally masked in a particular way and shared with the server, so when the masked data are aggregated on the server, the masks are canceled and offset. In contrast, the server does not know all individual node devices’ original unmasked intermediate results. In the FL literature, many solutions have widely used the SA protocol of Bonawitz et al. [29]. We recap this protocol in Appendix A and use it in Section 4 to benchmark our enhanced SVD solution.

2.3. Differential Privacy

Besides SA, DP is also exhaustively utilized in the FL literature. DP was introduced by Dwork et al. [30], which ensures that the addition, removal, or modification of a single data point does not substantially affect the outcome of the data-based analysis. One of the core strengths of DP comes from its properties, called composition and post-processing, which we also utilize in this paper. The former ensures that the output of two DP mechanisms still satisfies DP but with a parameter change. The latter ensures that a transformation of the results of a DP mechanism does not affect the corresponding privacy guarantees. Typically, DP is enforced by injecting calibrated noise (e.g., Laplacian or Gaussian) into the computation.

Definition 1 

($\epsilon ,\delta$)-Differential Privacy). A randomized mechanism $\mathcal{M}:\mathcal{X}\to \mathcal{R}$ with domain $\mathcal{X}$ and range $\mathcal{R}$ satisfies ε-differential privacy if for any two adjacent inputs $x,x^{\prime }\in \mathcal{X}$ and for any subset of output $S\subseteq \mathcal{R}$ it holds that

$$Pr(\mathcal{M}\left(x\right)\in S)\le e^{\epsilon }·Pr(\mathcal{M}\left(x^{\prime }\right)\in S)$$

(2)

The variable $\epsilon$ is called the privacy budget, which measures the privacy loss. It captures the trade-off between privacy and utility: the lower its value, the more noise is required to satisfy Equation (2), resulting in higher utility loss. Another widely used DP notion is approximate DP, where a small additive term $\delta$ is added to the right side of Equation (2). Typically, we are interested in values of $\delta$ that are smaller than the inverse of the database size. Although DP has been adopted to many domains [7] such as recommendation systems [31], we are not aware of any work besides [18] which adopts DP for SVD computation. Thus, as we later show a flaw in that work, we are the first to provide a distributed SVD computation with DP guarantees.

3. The FedPower Algorithm

Following Guo et al. [18], we assume there are n node devices, and each device i holds an independent dataset, an $s_i$-by-d matrix ${\mathbb{M}}_i$. Each row represents a record item, while the columns of each matrix correspond to the same feature space. Moreover, $\mathbb{M}$ denotes the composition of matrices ${\mathbb{M}}_i$ such that ${\mathbb{M}}^T=[{\mathbb{M}}_1^T,{\mathbb{M}}_2^T,\cdots ,{\mathbb{M}}_n^T]\in {\mathbb{R}}^{s\times d}$, with $s={\sum }_{i=1}^n{s}_i$. The solution proposed by Guo et al. [18] is presented in Algorithm 1 with the following parameters.

• T: the number of local computations performed by each node device.
• ${\mathcal{I}}_T^p$: the rounds where the node devices and the server communicate,
  i.e., ${\mathcal{I}}_T^p=\{0,p,2p,\cdots ,p⌊T/p⌋\}$.
• $(\epsilon ,\delta )$: the privacy budget.
• $(\sigma ,{\sigma }^{\prime })$: the variance of noises added by the clients and the server, respectively:

  $$\sigma =\frac{⌊T/p⌋}{\epsilon ·{min}_i\left(s_i\right)}\sqrt{2log\left(\frac{1.25⌊T/p⌋}{\delta }\right)}{\sigma }^{\prime }=\frac{⌊T/p⌋{max}_i\left(p_i\right)}{\epsilon ·{min}_i\left(s_i\right)}\sqrt{2log\left(\frac{1.25⌊T/p⌋}{\delta }\right)}$$

Algorithm 1 Full participation protocol of FedPower by Guo et al. [18].

Input:  Datasets ${\left\{{\mathbb{M}}_i\right\}}_{i=1}^n$, target rank k, iteration rank $r\ge k$, number of iteration T, synchronous set ${\mathcal{I}}_T^p$, and the variance of noises $(\sigma ,{\sigma }^{\prime })$ Output:  Approximated eigenspace ${\overline{\mathbb{Z}}}_T$ 1: initialise ${\mathbb{Z}}_0^{\left(i\right)}={\mathbb{Z}}_0\in {\mathbb{R}}^{d\times r}\sim \mathsf{N}{(0,1)}^{d\times r}$ 2: for $t=1$ to T do 3:    each node device i computes ${\mathbb{Y}}_t^{\left(i\right)}={\mathbb{M}}_i^{\prime }{\mathbb{Z}}_{t-1}^{\left(i\right)}$, where ${\mathbb{M}}_i^{\prime }=\frac{1}{s_i}{\mathbb{M}}_i^T{\mathbb{M}}_i$ 4:    if $t\in {\mathcal{I}}_T^p$ then 5:      each node device i computes ${\widehat{\mathbb{Y}}}_t^{\left(i\right)}={\mathbb{Y}}_t^{\left(i\right)}{\mathbb{D}}_t^{\left(i\right)}$ (orthogonal transformation) 6:      each node device i adds the Gaussian noise:      ${\mathbb{Y}}_t^{\prime \left(i\right)}={\widehat{\mathbb{Y}}}_t^{\left(i\right)}+{\mathbb{N}}^{\left(i\right)}\sim \mathsf{N}(0,||{\mathbb{Z}}_{t-1}^{\left(i\right)}{\left|\right|}_{max}^2{\sigma }^2{)}^{d\times r}$ 7:      each node device i sends ${\mathbb{Y}}_t^{\prime \left(i\right)}$ to the server 8:      the server performs perturbed aggregation with an extra Gaussian noise:      ${\mathbb{Y}}_t={\sum }_{i=1}^n\frac{s_i}{s}{\mathbb{Y}}_t^{\left(i\right)}+\mathbb{N}\sim \mathsf{N}(0,{max}_i\left|\right|{\mathbb{Z}}_{t-1}^{\left(i\right)}{\mathbb{D}}_t^{\left(i\right)}{\left|\right|}_{max}^2{\sigma }^{\prime 2}{)}^{d\times r}$ 9:      the server broadcasts ${\mathbb{Y}}_t$ to all node devices 10:      each node device i sets ${\mathbb{Y}}_t^{\left(i\right)}={\mathbb{Y}}_t$ 11:    end if 12:    each node device i performs orthgonalization: ${\mathbb{Z}}_t^{\left(i\right)}=\mathsf{orth}\left({\mathbb{Y}}_t^{\left(i\right)}\right)$ 13: end for 14: return approximated eigenspace $${\overline{\mathbb{Z}}}_T=\left\{\begin{array}{cc}\sum _{i=1}^n\frac{s_i}{s}{\mathbb{Z}}_T^{\left(i\right)}{\mathbb{D}}_{T+1}^{\left(i\right)}\hfill & \mathrm{if}T\notin {\mathcal{I}}_T^p\hfill \\ \sum _{i=1}^n\frac{s_i}{s}{\mathbb{Z}}_T^{\left(i\right)}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

In the proposed solution, each node device holds its raw data and processes the SVD locally, its eigenvectors are aggregated on the server by the orthogonal procrustes transformation (OPT) mechanism. The basic idea behind this is to find an orthogonal transformation matrix that maps one set onto another while preserving their relative characteristics. And, the aggregation result is sent back for further iterations. More details (e.g., the computation of ${\mathbb{D}}_t^{\left(i\right)}$) are given in [18].

4. Enhancing the Utility of FedPower

Adversary Model. Throughout this paper, we consider a semi-honest setup, i.e., where the clients and the server are honest but curious. This means that they follow the protocol truthfully, but in the meantime, they try to learn as much as possible about the dataset of other participants. We also assume that the server and the clients cannot collude, so the server cannot control node devices.

Utility Analysis of FedPower. It is not a surprise that adding Gaussian noise twice (i.e., the local and the central noise in Step 6 and 8 in Algorithm 1) severely affects the accuracy of the final result. A straightforward way to increase the utility is to eliminate some of this noise. As highlighted in Table 1, the local noise protects the individual clients from the server. Moreover, it also protects the aggregate from other clients and from external attackers. On the other hand, the central noise merely covers the aggregate. Hence, if the protection level against the server is sufficient against other clients and external attackers, the central noise becomes obsolete.

Moreover, all the locally added noise accumulates during aggregation, which also negatively affects the utility of the final result. Loosely speaking, as shown in Table 1, CDP combined with SA could provide the same protection as LDP. Consequently, by utilizing cryptographic techniques with a single local noise, we can hide the individual updates and protect the aggregate as well.

Utility Enhanced FedPower. We improve on FedPower [18] from two aspects: (1) we apply an SA protocol to hide the individual intermediate results of the node devices from the server, and (2) we use a secure multi-party computation (SMPC) protocol to enforce the CDP in an oblivious manner to the server. In SMPC, multiple parties can jointly compute a function over their private inputs without revealing those inputs to each other or to the server. More details of this topic can be found in the book [32]. We supplement the assumptions and the setup of Guo et al. [18] with a homomorphic encryption key pair generated by the server. The server holds the private key and shares the public key with all node devices. The remaining part of our solution is shown in Algorithm 2. To ease understanding, the pseudo code is simplified. The actual implementation is more optimized, e.g., the encrypted results are aggregated before decryption in Step 11, and in Step 7, the ciphertexts are re-randomized rather than generated from scratch. We describe all these tricks in Section 6.

By performing SA in Step 7, the server obtains the aggregated result with Gaussian noises from all node devices. With the simple SMPC procedure (Steps 8–12), the server receives all Gaussian noises apart from the one (i.e., node device j) is randomly selected (which is hidden from the node devices). Then, in Step 13, it removes them from the output of the SA protocol. Compared with FedPower [18], our intermediate aggregation result only contains a single instance of Gaussian noise from the randomly chosen node device instead of n. Consequently, via SA and SMPC, the proposed utility-enhancing protocol reduced the locally added noise n-fold and completely eliminated the central noise.

Computational Complexity. Regarding computational complexity, we compare the proposed scheme with the original solution in

Table 2. Complexity comparison between FedPower [18] and Algorithm 2.

		Addition	Multiplication	Noise	Encryption	Decryption	Secure
				Gen.			Agg.
[18]	Node	$T\times (k^2-k)+$	$T\times k^2$	$⌊T/p⌋\times$
		$⌊T/p⌋\times k^2$		$k^2$
	Server	$(⌊T/p⌋+1)\times$	$(⌊T/p⌋+1)\times d\times k^2$	$⌊T/p⌋\times$
		$k^2\times (d-1)+⌊T/p⌋$	$+⌊T/p⌋\times d+1$	$k^2$
Ours	Node	$T\times (k^2-k)+$	$T\times k^2+$	$⌊T/p⌋\times$			$⌊T/p⌋\times$
		$⌊T/p⌋\times k^2$	$⌊T/p⌋\times k^2$	$k^2$			$S{A}_e$
	Server	$⌊T/p⌋\times k^2\times d+$	$d\times (k^2+1)$		$⌊T/p⌋\times$	$⌊T/p⌋\times$	$⌊T/p⌋\times$
		$k^2\times (d-1)$			$k^2\times m$	$k^2\times m$	$S{A}_s$

. The major difference is that we have integrated SA to facilitate our new privacy protection strategy. Let $S{A}_e$ and $S{A}_s$ be the asymptotic computational complexities of SA on each node device and server side, respectively.

Although we have added more operations, as seen in Table 2, we have distributed some computations to individual node devices. Most importantly, we no longer add secondary server-side Gaussian noise to the final aggregation result and only retain the Gaussian noise from one node device.

Analysis. As we mentioned in our adversarial model, the semi-honest server cannot collude with any of the node devices, which are also semi-honest. Thus, the server cannot eliminate the remaining noise from the final result. In terms of the node device, since no one except the server is aware of the random index in Step 8, apart from its data, a node device only knows the aggregation result with the added noise, even if the retained noise comes from itself.

Algorithm 2 Utility-enhanced FedPower.

Input:  Datasets ${\left\{{\mathbb{M}}_i\right\}}_{i=1}^n$, target rank k, iteration rank r, number of iteration T, synchronous trigger p, the variance of noise $\sigma$, and key pair $(s{k}_{hm},p{k}_{hm})$ Output:  Approximated eigenspace ${\overline{\mathbb{Z}}}_T$ 1: initialise ${\mathbb{Z}}_0^{\left(i\right)}={\mathbb{Z}}_0\in {\mathbb{R}}^{d\times r}\sim \mathsf{N}{(0,1)}^{d\times r}$ with orthonormal columns and generate an $r\times r$ zero matrix $\mathbb{P}$ and another all-ones matrix ${\mathbb{P}}^{\prime }$ of the same size 2: for $t=1$ to T do 3:    each node device i computes ${\mathbb{Y}}_t^{\left(i\right)}={\mathbb{M}}_i^{\prime }{\mathbb{Z}}_{t-1}^{\left(i\right)}$, where ${\mathbb{M}}_i^{\prime }=\frac{1}{s_i}{\mathbb{M}}_i^T{\mathbb{M}}_i$ 4:    if $t\equiv 0\left(\mathrm{mod}p\right)$ then 5:      each node device i computes ${\widehat{\mathbb{Y}}}_t^{\left(i\right)}={\mathbb{Y}}_t^{\left(i\right)}{\mathbb{D}}_t^{\left(i\right)}$ (orthogonal transformation) 6:      each node device i adds Gaussian noise: ${\mathbb{Y}}_t^{\prime \left(i\right)}={\widehat{\mathbb{Y}}}_t^{\left(i\right)}+{\mathbb{N}}^{\left(i\right)}\sim \mathsf{N}{(0,\sigma )}^{d\times r}$ 7:      SA protocol is executed among the server and all node devices, with inputs ${\mathbb{Y}}_t^{\prime \left(i\right)}$ and output ${\mathbb{Y}}_t$ 8:      the server chooses one random index $j\in [1,n]$ and encrypts ${\mathbb{P}}^{\prime }$ and ${\mathbb{P}}^{\prime }$:      ${\mathbb{C}}^{\left(j\right)}={\mathsf{Enc}}_{p{k}_h}\left(\mathbb{P}\right)$ and ${\mathbb{C}}^{\left(j^{\prime }\right)}={\mathsf{Enc}}_{p{k}_h}\left({\mathbb{P}}^{\prime }\right)$ for $j^{\prime }\in [1,n]\setminus \left\{j\right\}$ 9:      the server sends value ${\mathbb{C}}^{\left(j\right)}$ and ${\mathbb{C}}^{\left(j^{\prime }\right)}$ to the appropriate node devices 10:      each node device i computes ${\mathbb{C}}^{\prime \left(i\right)}={\mathbb{N}}^{\left(i\right)}·{\mathbb{C}}_{\left(i\right)}$ which is      ${\mathsf{Enc}}_{p{k}_h}({\mathbb{N}}^{\left(i\right)}·{\mathbb{P}}^{\prime })$ if $i=j$ and ${\mathsf{Enc}}_{p{k}_h}({\mathbb{N}}^{\left(i\right)}·\mathbb{P})$ otherwise 11:      each node device i sends ${\mathbb{C}}^{\prime \left(i\right)}$ back to the server 12:      for all $i\in [1,n]\setminus \left\{j\right\}$, the server decrypts the receiving messages ${\mathbb{C}}^{\prime \left(i\right)}$ to obtain ${\mathbb{N}}^{\left(i\right)}\equiv {\mathbb{N}}^{\left(i\right)}·{\mathbb{P}}^{\prime }={\mathsf{Dec}}_{s{k}_h}\left({\mathbb{C}}^{\prime \left(i\right)}\right)$ 13:      the server updates aggregation result as ${\mathbb{Y}}_t^{″}={\mathbb{Y}}_t^{\prime }-{\sum }_{i\in [1,n]\setminus \left\{j\right\}}{\mathbb{N}}^{\left(i\right)}$ 14:      the server performs orthogonalization ${\mathbb{Z}}_t=\mathsf{orth}\left({\mathbb{Y}}_t^{″}\right)$ 15:      the server broadcasts ${\mathbb{Z}}_t$ to all node devices 16:      each node device i sets ${\mathbb{Z}}_t^{\left(i\right)}={\mathbb{Z}}_t$ 17:    else 18:      each node device i calculates the latest ${\mathbb{Z}}_t^{\left(i\right)}=\mathsf{orth}\left({\mathbb{Y}}_t^{\left(i\right)}\right)$ 19:    end if 20: end for 21: return approximated eigenspace $${\overline{\mathbb{Z}}}_T=\left\{\begin{array}{cc}\sum _{i=1}^n\frac{s_i}{s}{\mathbb{Z}}_T^{\left(i\right)}{\mathbb{D}}_{T+1}^{\left(i\right)}\hfill & \mathrm{if}T\notin {\mathcal{I}}_T^p\hfill \\ \sum _{i=1}^n\frac{s_i}{s}{\mathbb{Z}}_T^{\left(i\right)}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Compared with the original solution by Guo et al. [18], we have improved the utility of the aggregation result by keeping the added noise from one single node device. As a side effect, the complexity has grown due to the SA protocol. This is a trade-off between result accuracy and solution efficiency.

5. Differentially Private Federated SVD Solution

Privacy Analysis of FedPower. Algorithm 1 injects noise both at the local (Step 6) and the global (Step 8) levels. Consequently, the claimed privacy protection of Algorithm 1 is $(2\epsilon ,2\delta )$-DP, which originates from $(\epsilon ,\delta )$-LDP and $(\epsilon ,\delta )$-CDP [18]. Firstly, as we highlighted in Table 1, LDP and CDP provide different privacy protections; hence, merely combining them is inappropriate, so the claim must be more precise. Instead, Algorithm 1 seems to provide $(\epsilon ,\delta )$-DP for the clients from the server and stronger protection (due to the additional central noise) from other clients and external attackers.

Yet, this is still not entirely sound, as not all computations were included in the sensitivity calculation; hence, the noise scaling is incorrect. Indeed, the authors only considered the sensitivity of the multiplication with $\mathbb{Z}$ in Step 3 when determining the variance of the Gaussian noise in Step 6; however, the noise is only added after the multiplication with $\mathbb{D}$ in Step 5. Thus, the sensitivity of the orthogonalization is discarded.

Privacy-Enhanced FedPower. We improve on FedPower [18] from two aspects: (1) we incorporate clipping in the protocol to bound the sensitivity of the local operations performed by the clients and (2) we use SA with DP to obtain a strong privacy guarantee. For this reason, similar to FedPower [18], we assume that for all i the elements of ${\mathbb{M}}_i^{\prime }=\frac{1}{s_i}{\mathbb{M}}_i^T{\mathbb{M}}_i$ are bounded with $\widehat{m}$. In Algorithm 1, the computations the nodes undertake (besides noise injection at Step 6) are in Steps 3, 5 and 12, where the last two could be either discarded for the sensitivity computation or completely removed, as explained below.

• Step 12: Orthogonalization is intricate, so its sensitivity is not necessarily traceable. To tackle this, we propose applying the noise before, in which case it would not affect the privacy guarantee, as it would count as post-processing.
• Step 5: We remove this client-side operation from our privacy-enhanced solution, as it is not essential; only the convergence speed would be affected slightly.

The FedPower protocol with enhanced privacy is present in Algorithm 3, where besides the orthogonalization, clipping is also performed with $\widehat{z}$. The only client operation which must be considered for the sensitivity computation (i.e., before noise injection) is Step 3. We calculate its sensitivity in Theorem 1.

Theorem 1. 

If we assume $|m_{ij}^{\prime }|\le \widehat{m}$ for all $i,j\in [1,d]$, then the sensitivity (calculated via the Euclidean distance) of the client-side operations (i.e., Step 3 in Algorithm 3 is bounded by $2·\sqrt{r}·\widehat{m}·\widehat{z}$.

Proof. 

To make the proof easier to follow, we remove the subscript round counter from the notation. Let us define ${\mathbb{M}}^{\prime }$ and ${\tilde{\mathbb{M}}}^{\prime }$ such that they are equal except at position $1\le i,j\le d$. Now, multiply these with $\mathbb{Z}$ from the left results in $\mathbb{Y}$ and $\tilde{\mathbb{Y}}$, respectively, which are the same except in row i:

$$\begin{array}{c}[m_{i1}^{\prime }·z_{11}+\cdots \stackrel{abs(·)\le \widehat{m}·\widehat{z}}{\overbrace{+m_{ij}^{\prime }·z_{j1}+}}\cdots +m_{id}^{\prime }·z_{d1},\cdots ,m_{i1}^{\prime }·z_{1r}+\cdots \stackrel{abs(·)\le \widehat{m}·\widehat{z}}{\overbrace{+m_{ij}^{\prime }·z_{jr}+}}\cdots +m_{id}^{\prime }·z_{dr}]\mathrm{for}{\mathbb{Y}}^{\prime }\\ [m_{i1}^{\prime }·z_{11}+\cdots \underset{abs(·)\le \widehat{m}·\widehat{z}}{\underbrace{+{\tilde{m}}_{ij}^{\prime }·z_{j1}+}}\cdots +m_{id}^{\prime }·z_{d1},\cdots ,m_{i1}^{\prime }·z_{1r}+\cdots \underset{abs(·)\le \widehat{m}·\widehat{z}}{\underbrace{+{\tilde{m}}_{ij}^{\prime }·z_{jr}+}}\cdots +m_{id}^{\prime }·z_{dr}]\mathrm{for}{\tilde{\mathbb{Y}}}^{\prime }\end{array}$$

Hence, the Euclidean distance of $\mathbb{Y}$ and $\tilde{\mathbb{Y}}$ boils down to this row i:

$$dist(\mathbb{Y},\tilde{\mathbb{Y}})=\sqrt{\sum _{k=1}^d\sum _{l=1}^r{\left(y_{kl}-{\tilde{y}}_{kl}\right)}^2}=\sqrt{\sum _{l=1}^r{\left(y_{il}-{\tilde{y}}_{il}\right)}^2}=\sqrt{\sum _{l=1}^r{\left(m_{ij}^{\prime }·z_{jl}-{\tilde{m}}_{ij}^{\prime }·z_{jl}\right)}^2}$$

As a direct corollary of $abs(m·z)\le \widehat{m}·\widehat{z}$, we know that each of the r squared elements is bounded by $2·\widehat{m}·\widehat{z}$. Therefore, $dist(\mathbb{Y},\tilde{\mathbb{Y}})\le \sqrt{r·4·{\widehat{m}}^2·{\widehat{z}}^2}$.    □

It is known that adding Gaussian noise with ${\sigma }^2=\frac{2·s^{2}log(1.25/\delta )}{{\epsilon }^2}$ (where s is the sensitivity) results in $(\epsilon ,\delta )$-DP. As a corollary, we can state in Theorem 2 that a single round in Algorithm 3 is differentially private. An even tighter result was presented in [33]; we leave the exploration of this as future work. The best practice is to set $\delta$ as the inverse of the size of the underlying dataset, so there is a direct connection between the variance $\sigma$ and the privacy parameter $\epsilon$.

Theorem 2. 

If $T=1$, then Algorithm 3 provides $(\epsilon ,\delta )$-DP, where

$$ϵ=\frac{\sqrt{8·r·log(1.25/\delta )}·\widehat{m}·\widehat{z}}{\sigma }$$

Proof. 

Can be verified by combining the provided formula with the appropriate sensitivity.    □

Algorithm 3 Privacy-enhanced FedPower.

Input:  Datasets ${\left\{{\mathbb{M}}_i\right\}}_{i=1}^n$, target rank k, iteration rank r, number of iteration T, the clipping bound $\widehat{z}$, the variance of noise $\sigma$ Output:  Approximated eigenspace ${\overline{\mathbb{Z}}}_T$ 1: initialise ${\mathbb{Z}}_0^{\left(i\right)}={\mathbb{Z}}_0\in {\mathbb{R}}^{d\times r}\sim \mathsf{N}{(0,1)}^{d\times r}$ with orthonormal columns 2: for $t=1$ to T do 3:    each node device i computes ${\mathbb{Y}}_t^{\left(i\right)}={\mathbb{M}}_i^{\prime }{\mathbb{Z}}_{t-1}^{\left(i\right)}$, where ${\mathbb{M}}_i^{\prime }=\frac{1}{s_i}{\mathbb{M}}_i^T{\mathbb{M}}_i$ 4:    each node device i adds Gaussian noise: ${\mathbb{Y}}_t^{\prime \left(i\right)}={\mathbb{Y}}_t^{\left(i\right)}+{\mathbb{N}}^{\left(i\right)}\sim \mathsf{N}{(0,\sigma )}^{d\times r}$ 5:    if $t\equiv 0\left(\mathrm{mod}p\right)$ then 6:      SA protocol is executed among the server and all node devices, with inputs ${\mathbb{Y}}_t^{\prime \left(i\right)}$ and output ${\mathbb{Y}}_t$ 7:      the server performs orthogonalization and clipping ${\mathbb{Z}}_t=\mathsf{clip}(\mathsf{orth}\left({\mathbb{Y}}_t^{\prime }\right),\widehat{z})$ 8:      the server broadcasts ${\mathbb{Z}}_t$ to all node devices 9:      each node device i sets ${\mathbb{Z}}_t^{\left(i\right)}={\mathbb{Z}}_t$ 10:    else 11:      each node device i calculates the latest ${\mathbb{Z}}_t^{\left(i\right)}=\mathsf{clip}(\mathsf{orth}\left({\mathbb{Y}}_t^{\prime \left(i\right)}\right),\widehat{z})$ 12:    end if 13: end for 14: return approximated eigenspace $${\overline{\mathbb{Z}}}_T=\left\{\begin{array}{cc}\sum _{i=1}^n\frac{s_i}{s}{\mathbb{Z}}_T^{\left(i\right)}{\mathbb{D}}_{T+1}^{\left(i\right)}\hfill & \mathrm{if}T\notin {\mathcal{I}}_T^p\hfill \\ \sum _{i=1}^n\frac{s_i}{s}{\mathbb{Z}}_T^{\left(i\right)}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

One can easily extend this result for $T\ge 1$ with the composition property of DP: Algorithm 3 satisfies $(T·\epsilon ,T·\delta )$-DP. Besides this basic loose composition, one can obtain better results by utilizing more involved composition theorems such as in [34]. We leave this for future work.

Analysis. Similarly to Section 4, we protect the individual intermediate results with SA. On the other hand, it is equivalent to generate n Gaussian noise with variance $\sigma$ and select one, or to generate n Gaussian noise with variance $\frac{\sigma }{n}$ and sum them all up. Consequently, instead of relying on an SMPC protocol to eliminate most of the local noise, we could merely scale them down. combining SA with such a downsized local noise is, in fact, a common practice in FL: this is what distributed differential privacy (DDP) [35] does, i.e., DDP combined with SA provides LDP but with n times smaller noise, where n is the number of participants.

6. Empirical Comparison

In order to compare our proposed schemes with FedPower, we implement the schemes in Python [36]. As we only encrypt 0 and 1 in Section 4, we optimize the performance and take advantage of the utilized Paillier cryptosystem. More specifically, we re-randomize the corresponding ciphertexts to obtain new ciphertexts. In addition, we also exploit the homomorphic property, and instead of decrypting each value ($d\times r\times \left|numberofnodedevices\right|$ times), we first calculate the product of all the ciphertexts (elementary matrix multiplication) and then perform the decryption on a signal matrix. In this way, we obtain the sum of all Gaussian noises more efficiently. The decryption result is the sum of noise which will be canceled in Algorithm 2. Furthermore, we prepare the ${\mathbb{M}}_i^{\prime }=\frac{1}{s_i}{\mathbb{M}}_i^T{\mathbb{M}}_i$, ${\mathbb{Z}}_0^{\left(i\right)}$ and all keys of SA offline for each node device i.

Metric. We use Euclidean distance to represent the similarity of two $m\times n$ matrix $\mathbb{A}=\left(a_{ij}\right)$ and $\mathbb{B}=\left(b_{ij}\right)$, i.e., $dist(\mathbb{A},\mathbb{B})=\sqrt{{\sum }_{i=1}^m{\sum }_{j=1}^n{\left(a_{ij}-b_{ij}\right)}^2}$. Let $\mathbb{Z}$ denote the true eigenspace computed without any noise, let ${\mathbb{Z}}_g(\sigma ,{\sigma }^{\prime })$ denote the eigenspace generated with Algorithm 1, let ${\mathbb{Z}}_u\left(\sigma \right)$ denote the eigenspace generated with Algorithm 2, and let ${\mathbb{Z}}_p\left(\sigma \right)$ denote the eigenspace generated with Algorithm 3.

Setup. For our experiments, we used the well-known NETFLIX rating dataset [37], and we pre-process it similarly to [38] (instead of 10, we removed users and movies with less than 50 ratings). It consists of $96.310.835$ ratings corresponding to $17.711$ movies from $324.468$ users. We split them horizontally into 100 random blocks to simulate node devices. Moreover, we set the security parameter to 128; thus, we adopt 3072 bits for N in Paillier cryptosystem (this is equivalent to RSA-3072, which provides a 128-bit security level [39]). The number of iteration rank and top eigenvectors is set to $r=k=10$, and we keep the same synchronous trigger $p=4$ as [18]. To compare FedPower with our enhanced solutions, we set the noise size for these algorithms as $\sigma ={\sigma }^{\prime }=0.1$. Moreover, for Algorithm 3 we bounded ${\mathbb{M}}_i^{\prime }$ with $0.05$ and ${\mathbb{Z}}_t^{\left(i\right)}$ with $0.2$ for all possible i and t. Using Theorem 2, we can calculate that a single round corresponds to privacy budget $\epsilon =30.6$ with $\delta ={10}^{-5}$.

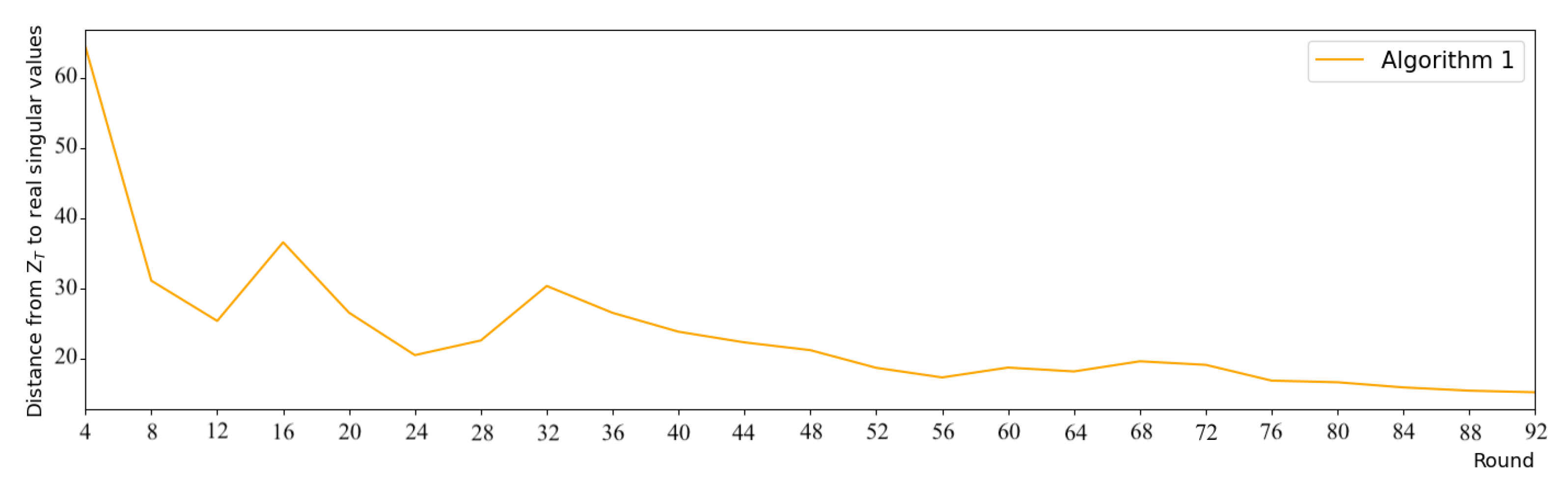
In order to determine the number of global rounds T, we set up a small experiment. We built a data matrix $\mathbb{M}$ of size $3000\times 100$ filled with integers in $[0,5]$, and randomly divided it for 100 node devices (each has at least 10 rows). We executed Algorithm 1 for 200 rounds and compared the distance between the aggregation result $\mathbb{Z}$ and the real singular values of $\mathbb{M}$. From the result in Figure 2, we can see that convergence occurs around the round 92, since the subsequent results vary only slightly ($<1\%$). Thus, we set $T=92$ for our experiments.

The experiment is implemented in a Docker container of 40-core Intel(R) Xeon(R) Silver 4210 CPU @ 2.20GHz and 755G RAM. We run our experiments 10-fold and take the average execution time.

Results. Firstly, we compare the efficiency of our enhanced schemes and the original algorithm. The computation times are presented in

Table 3. Runtime comparison of Algorithms 1–3 in milliseconds.

Name	Device		Computation Time		Running
		Aggr.	SMPC	Rest	Time 1
FedPower	Node	164	-	18,768	$2.698\times {10}^6$
	Server	37	-	127,449
Utility Enhanced	Node	15,829	$7.182\times {10}^5$	17,259	$9.203\times {10}^7$
	Server	20,647	$7.247\times {10}^5$	143,145
Privacy Enhanced	Node	15,742	-	17,291	$4.477\times {10}^6$
	Server	20,581	-	128,903

¹ Due to the large volume of memory required for matrix calculations, we had to access data by reading and writing local files, which caused the longer overall execution time.

. Compared with FedPower, the overall computation burden of the devices increased by a factor of $\times 39.68$ for the utility-enhanced solution in Section 4 and only $\times 1.74$ and the privacy-enhanced solution in Section 5. Concerning the server, the increase is $\times 6.97$ and $\times 1.17$, respectively.

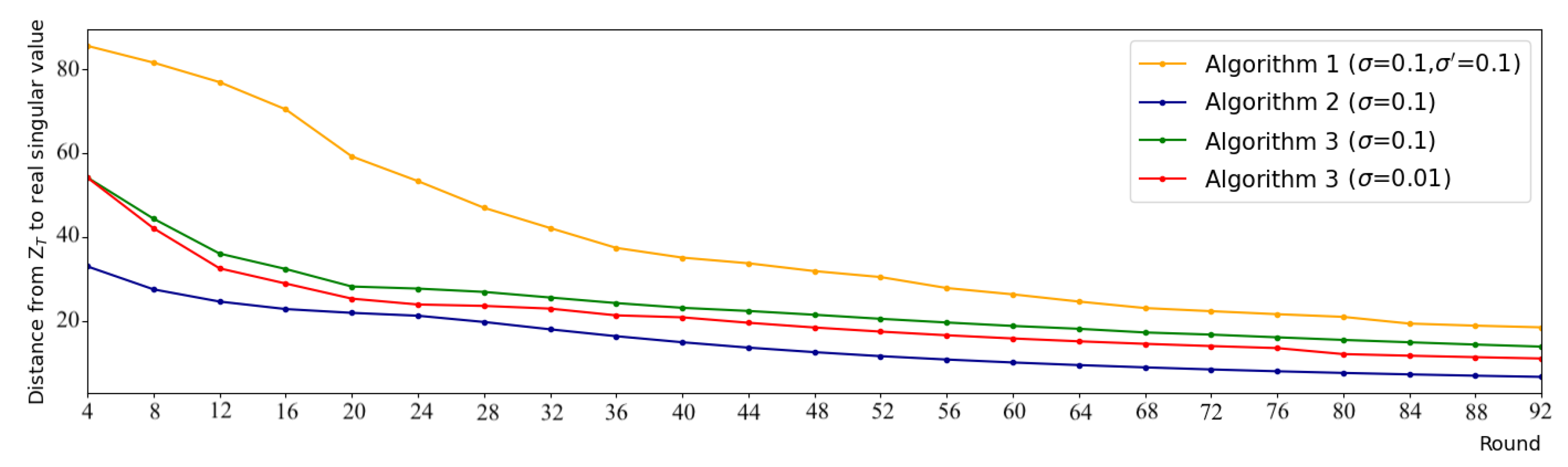
The rise in computational demand comes with benefits. Concerning Algorithm 2, significant progress is achieved in the utility while it offers a similar privacy guarantee as FedPower. Concerning Algorithm 3, the privacy guarantee is more robust, as it provides a formal DDP protection (while FedPower fails to satisfy DP). Moreover, it obtains a higher utility, which could make this solution preferable despite its computational appeal. We compare the distance between the results of each algorithm and the real eigenvalues, as shown in Figure 3, and the utility is improved (i.e., the distances are lower) with both Algorithms 2 and 3.

Our utility-enhanced solution significantly outperforms FedPower: after 92 rounds, the obtained error of our scheme is almost three times ($2.74\times$) smaller than that for FedPower. The final error of Algorithm 2 is $dist(\mathbb{Z},{\mathbb{Z}}_u\left(\sigma \right))=6.72$, while this value for Algorithm 1 is $dist(\mathbb{Z},{\mathbb{Z}}_g(\sigma ,{\sigma }^{\prime }))=18.42$. Note that this level of accuracy (∼18.5) was obtained using our method in the 32nd round, i.e., almost three times ($2.88\times$) faster. Hence, the superior convergence speed can compensate for most of the computational increase caused by SA and SMPC.

Let us shift our attention to our privacy-enhanced solution. In that case, we can see that besides more robust privacy protection, our solution offers better utility: Algorithms 1 and 3 obtains $dist(\mathbb{Z},{\mathbb{Z}}_g(\sigma ,{\sigma }^{\prime }))=18.42$ and $dist(\mathbb{Z},{\mathbb{Z}}_p\left(\sigma \right))=13.94$ RMSE values, respectively, i.e., we acquired a 24% error reduction. Our method (with actual DP guarantees) achieved the same level of accuracy ($\sim 18.5$) only after 65 rounds, which is a 29% convergence speed increase.

We also compare our two proposed schemes, in a way, that the size of the accumulated noises is equal. Besides the nature of noise injection (many small vs. one large), the only factor that differentiates the results is the clipping bounds. As expected, the error is $1.65\times$ larger with clipping, i.e., $dist(\mathbb{Z},{\mathbb{Z}}_p\left(\frac{\sigma }{10}\right))=11.11$ compared with $dist(\mathbb{Z},{\mathbb{Z}}_u\left(\sigma \right))=6.72$. Concerning the convergence speed, the utility enhanced solution is $1.7\times$ faster, reaching similar accuracy ($\sim 11$) in round 54. Note though that this result still vastly outperforms FedPower: the accuracy and the convergence speed are increased by 40% and 43%, respectively.

Finally, we study the effect of different levels of privacy protection on the accuracy of each algorithm. As we noticed in Figure 3, after the 60th round, the error ratios of the algorithms are reasonably stable, so for this experiment, we set $T=60$. Since the clipping rate $\widehat{z}$ and the noise variance $\sigma$ both contributed to the privacy parameter $\epsilon$ (as seen in Theorem 2), we varied each independently. Our results are presented in Figure 4. It is visible that the previously seen trends hold with other levels of privacy protection, making our proposed schemes favorable for a wide range of settings.

7. Conclusions

Motivated by Guo et al.’s distributed privacy-preserving SVD algorithm based on the federated power method [18], we have proposed two enhanced federated SVD schemes, focusing on utility and privacy, respectively. Both use secure aggregation to reduce the added noise, which reverts to the initial design intent and interest. Yet, the added cryptographic operations trade efficiency for superior performance ($\times 10$ better results) while providing either similar or superior privacy guarantee. Our work leaves several future research topics. One is to further investigate the computational complexity, particularly the secure aggregation, to achieve more efficient solutions. Another is to investigate the scalability of the proposed solutions, regarding larger datasets and different datasets in applications other than recommendation systems. In addition, scalability also concerns the number of node devices. Yet, another topic is to look further into the security assumptions. For example, the security assumptions can be weaker so that the server can be allowed to collude with one or more node devices.