Abstract
In recent times, there has been a significant focus on electromagnetic resonant shunt damping (ERSD) and quasi-zero-stiffness vibration isolators (QZS VI) as prominent solutions for vibration mitigation or energy harvesting. In this paper, an innovative retrofittable model is proposed for dual-functional energy harvesting and low-frequency vibration attenuation by combining the ERSD and two-stage quasi-zero-stiffness vibration isolator (TQZS VI). The viscous dissipative element between the TQZS VI upper and lower layers is implemented using an electromagnetic shunt transducer that is connected in parallel with a resonant RLC (resistor–inductor–capacitor) circuit. Firstly, the mathematical model of the electromagnetic resonant shunt series quasi-zero-stiffness isolator (ERS-TQZS VI) is developed. Then, the magnitude-frequency response equations of the ERS-TQZS VI system are approximately solved using the harmonic balance method (HBM) in combination with the pseudo-arc-length method (PLM). The analytical approach is validated using numerical simulations. Moreover, the force transmissibility and output power of the ERS-TQZS VI are defined, and detailed parametric analysis for energy harvesting and low-frequency vibration attenuation is performed to assess the critical design parameters that result in optimal performance of the ERS-TQZS VI. The results demonstrate that the ERS-TQZS VI exhibits a significant reduction in resonance peaks of low-frequency vibration while simultaneously enabling effective vibration energy harvesting.
1. Introduction
Vibration commonly occurs in various mechanical equipment and buildings. In recent years, research on vibration has developed in two directions—vibration control and vibration utilization—due to the two-sided nature of vibration. The development of better theoretical structural and device models is a crucial step towards vibration control [1,2] and vibration utilization [3,4].
High static and low dynamic stiffness QZS VI has received extensive attention as an effective means of attenuating low-frequency vibration [5,6,7]. The proper design of the QZS VI system enables the realization of targeted loading conditions with characteristics such as a small static deflection and a low natural frequency. QZS VI is typically achieved through the parallel integration of the positive stiffness mechanism (PSM) and the negative stiffness mechanism (NSM) [8]. Ibrahim [9] reviewed the development of nonlinear passive isolators and discussed the NSMs of QZS VI. The NSMs can be fulfilled by using passive, semi-active, or active mechanisms. The passive mechanisms mainly include mechanical springs [10,11,12], prebuckled beams [13,14], geometrically nonlinear structures [15,16,17], magnetic structures [18,19,20,21,22], bio-inspired structures [23,24,25], and composite structures [26,27,28]. Nevertheless, it is worth noting that many of the aforementioned NSMs are passive mechanisms, which means their stiffness cannot be adjusted. Passive isolators with unmodifiable stiffness typically lack the capability to effectively handle varying excitation frequencies. Although active control methods have been introduced to enhance the stability and isolation performance of the QZS VIs [29,30], it is crucial to take into account the potential drawbacks, such as the high costs associated with their implementation. Active or semi-active NSMs, as mentioned in references [31,32,33,34,35], offer improved adaptability to varying environmental conditions. By using high-precision sensors and actuators, it becomes possible to accurately control the NS characteristic. For magnetic NSM, the NS characteristic is achieved by employing carefully arranged magnets. These arrangements enable the non-contact force to exhibit the desired negative-stiffness behavior.
In vibrating systems, a damper is commonly employed as an energy dissipation device to suppress vibrations. Its primary function is to convert vibrational energy into other forms of energy. To utilize vibrational energy, the energy dissipated in the vibration-damping process can be converted into valuable electrical energy. Shunt dampers (SD) have emerged as a highly effective method for suppressing vibration and harvesting energy [36,37,38]. The SD demonstrate viscous damping effects, while the presence of an inductor and a resistor introduces electrical resonance, which can act as a vibration absorber. In 1979, Forward [39] was the pioneer in showcasing the application of passive circuit shunting to reduce narrow-band resonant mechanical responses. Subsequently, Hagood [40] provided analytical interpretation and experimental evidence to demonstrate that a piezoelectric shunt with an RL circuit can function as a TMD. Behrens [41] first proposed the concept of an electromagnetic shunt damper (ESD) equipped with an RC shunt circuit, which offers increased flexibility in adjusting damping force by altering the electrical resistance within the damper circuit. Furthermore, the vibrational energy initially dissipated by the damping element can be effectively transformed into electrical energy through the utilization of electromagnetic equipment. In pursuit of this objective, researchers have proposed the concept of electromagnetic-resonant-shunt-tuned mass dampers (ERS-TMD) [42] as well as electromagnetic-resonant-shunt-tuned mass dampers with inerters (ERS-TMDI) [43,44,45]. For further information on low-frequency vibration energy harvesting, a comprehensive review by Sun [46] provides additional insights and reports in this field.
Although there are many papers about vibration control or energy harvesting, studies focusing on the integration of both aspects are relatively scarce. The main contribution of this paper is to propose a novel retrofit model that combines dual functionality for energy harvesting and low-frequency vibration attenuation by integrating the ERSD and the TQZS VI. The nonlinear governing equations of the ERS-TQZS VI are approximately analytically solved using the HBM in combination with the PLM. Additionally, a comprehensive parametric study is performed to evaluate the performances of vibration attenuation and energy collection of the ERS-TQZS VI. This paper mainly studies the model structural design and theoretical analysis of the ERS-TQZS VI model. Furthermore, the analysis methodology proposed in this paper can also be used to design the ERS-TQZS VI established by other types of QZS structures.
The subsequent sections of this paper are structured as follows. In Section 2, the mathematical model of the ERS-TQZS VI and the analytical solution method are introduced. In Section 3, detailed numerical analysis of the ERS-TQZS VI and comparisons with TQZS VI and TL VI are presented. This includes the energy harvesting and low-frequency vibration control potential of the ERS-TQZS VI, the influence of the mechanical parameters, and the RLC circuit parameters. In Section 4, a concise discussion of the main results is provided. In Section 5, some conclusions are given.
2. Mathematical Modeling
Figure 1 illustrates the schematic diagram of the ERS-TQZS VI. The ERS-TQZS VI system comprises a primary mass suspended on an upper-stage QZS VI, which is connected to a secondary mass . The secondary mass is then grounded through the lower-stage QZS VI. The ERS-TQZS VI system is composed using two horizontal linear springs with stiffnesses and , along with two vertical linear springs with stiffness and . Additionally, two vertical linear dampers with damping coefficients and are incorporated. The subscripts 1 and 2 are used to denote the upper and lower stages, respectively. The horizontal springs have an initial length of , and when compressed in the horizontal position, they reach a static equilibrium position denoted by . Moreover, the viscous dissipative element between the upper-stage QZS VI and lower-stage QZS VI is supplied by an electromagnetic transducer of coil resistance and inductance . Figure 1 illustrates the schematic diagram of the ERSD equivalent circuit. The ERSD can take the form of either a linear or rotational mechanism with motion transmission and typically consists of a permanent magnet and a coil. When the ERS-TQZS VI is subjected to a harmonic force excitation , the relative motion between the mass and generates an induced voltage and an induced current proportional to the relative velocity.
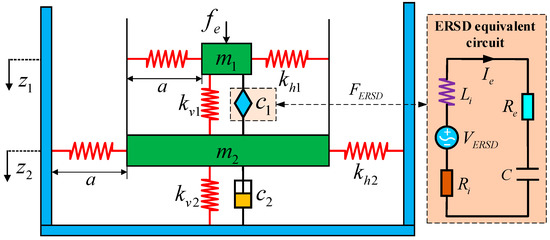
Figure 1.
Schematic diagram of the ERS-TQZS VI system.
The analytical model of the ERS-TQZS VI system mainly consists of two parts: three-spring QZS VI and ERSD. Among them, the analytical model of the three-spring QZS VI has been experimentally verified in our previous work [47]. In addition, the three-spring QZS VI and ERSD analytical models have also been separately studied in the following classic literature [41,42,48,49,50,51]. Considering the ERS-TQZS VI system being subjected to a harmonic force while positioned on a rigid base, the governing equation of the ERS-TQZS VI system at the static equilibrium position can be derived using Newton’s second law and Kirchhoff’s second law.
where and represent the displacements of the masses and , respectively, from the static equilibrium position. denotes the electromagnetic coupling coefficient, and represents the electromagnetic constant.
For small displacements of masses and , the spring forces in Equation (1) can be approximated using a Taylor series expansion around the respective static equilibrium positions. Consequently, Equation (1) can be simplified into two coupled Duffing equations:
where ; ; ; ; ; ; ; ; .
To obtain the dimensionless form of Equation (2), the following non-dimensional parameters are introduced:
where is the non-dimensional time; is the mass ratio; is the non-dimensional excitation force amplitude; is the frequency ratio; and are the non-dimensional resistances of the upper and lower linear system, respectively; is the non-dimensional current; is the non-dimensional resistance; is the non-dimensional capacitance; is the non-dimensional electromagnetic coupling coefficient; and is the non-dimensional electromagnetic constant.
By using these non-dimensional parameters, Equation (2) can be written in a non-dimensional form as
Since the magnitude–frequency curve of the nonlinear system always has turning points in the solution process, analytical solutions cannot be obtained. To obtain the solution for the governing equation of the ERS-TQZS VI system, Equation (3), we use the HBM in combination with the PLM [4,52]. It is the most efficient method for tracing out solution branches. The basic idea of the PLM is to regard the system excitation frequency as a new unknown variable, introduce the arc length of the amplitude–frequency curve of the system as an auxiliary parameter, and build an independent constraint equation using the normalized tangent vector of the amplitude–frequency curve.
The HBM is commonly employed alongside the assumption that the response amplitudes are dimensionless and follow a harmonic form. Therefore, we make the assumption that the solutions for the upper-layer mass, lower-layer mass, and ERSD current can be represented in the following forms:
or
It should be noted that Equation (4) only includes the first-order harmonics of cosine and sine terms. However, Equation (5) has first-order and third-order harmonics of cosine and sine terms.
In order to compare the approximation solutions of the first-order and third-order harmonics, we have used the amplitude–frequency response of the ERS-TQZS VI system . Figure 2 presents a comparison of the amplitude–frequency response curves for both the first-order and the third-order harmonics of the system solution. From Figure 2, we can observe that there is a slight difference between the two cases, which indicates that the first-order harmonic approximation of the ERS-TQZS VI system solution is basically consistent with the third-order approximate solution.
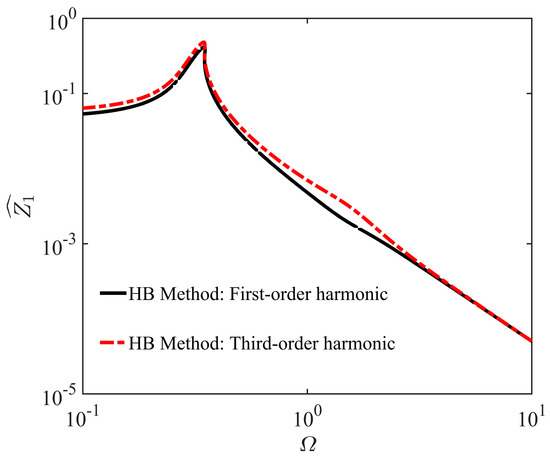
Figure 2.
Comparison between the first-order harmonic and third-order harmonic approximation of the amplitude–frequency response of the ERS-TQZS VI system (, , , , , , , ).
In this paper, we choose the approximate solution of the first-order harmonic. By substituting Equation (4) into Equation (3) and neglecting the high-order harmonic terms, the coefficients of and can be equated. This results in an amplitude–frequency response equation for the coefficients of displacements, which can be expressed as follows:
3. Results
In this section, the numerical calculations using the fourth-order Runge–Kutta algorithm are performed to validate the analytical solutions by the HBM in combination with the PLM. Then, the advantages of ERS-TQZS VI are presented in terms of energy harvesting and low-frequency vibration control. Finally, a comprehensive parametric analysis for low-frequency vibration attenuation and output power of the ERS-TQZS VI is demonstrated to assess the critical design parameters of the ERS-TQZS VI.
3.1. Validation of Analytical Solutions
To validate the accuracy of analytical solutions obtained using the HBM in combination with the PLM, the numerical calculation with the fourth-order Runge–Kutta algorithm is conducted, as shown in Figure 3. Comparisons between the analytical and numerical simulations are presented for two sets of parameters. The numerical solutions of the forward and backward frequency sweep are represented by cross and circle marks, respectively. In order to compare the analytical solutions with the numerical simulations, we utilize the amplitude–frequency response of the ERS-TQZS VI system . By observing Figure 3, it becomes evident that there is a good agreement between both methods, which validates the satisfactory accuracy of the HBM in combination with the PLM. Therefore, in the subsequent analysis of this paper, unless otherwise specified, we will use the approximate analytical method.
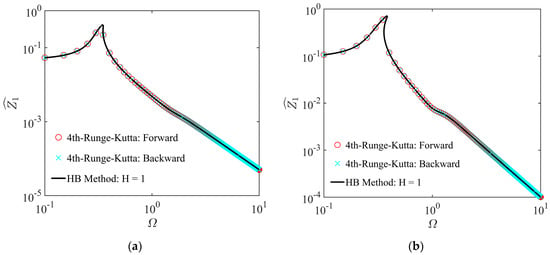
Figure 3.
Comparing the amplitude–frequency response of the ERS-TQZS VI system using analytical and numerical calculations for two sets of different parameters. (a) First set parameters (, , , , , , , ); (b) second set parameters (, , , , , , , ).
3.2. Performance Analysis of the ERS-TQZS VI
The accuracy of the analytical solution has been validated; the next step is to determine the advantages of the ERS-TQZS VI system over existing methods, i.e., TQZS VI and the two-stage linear vibration isolator (TL VI). For this, we compare the force transmissibility curve of the ERS-TQZS VI with the TQZS VI and the TL VI.
For a given frequency ratio , the amplitudes , , , , , and are determined by numerically solving a system of six nonlinear equations, as described in Equation (6). The transmitted force can be expressed as
Subsequently, utilizing the aforementioned equations, the force transmissibility of ERS-TQZS VI system can be derived as:
The comparison with TQZS VI and TL VI are shown in Figure 4a. The mechanical and electrical parameters of ERS-TQZS VI, TQZS VI and TL VI are , , , , , , , . Figure 4 reveals a notable reduction in the initial isolation frequency of the ERS-TQZS VI system of 55.0% (from 1.02 to 0.45) when compared to the TL VI system. These findings suggest that the ERS-TQZS VI successfully extends the frequency range for vibration attenuation towards lower frequencies, effectively mitigating the vibrations of such frequencies. Moreover, compared to the TL VI and TQZS VI systems, the resonance peak is reduced by 26.5% and 15.5%, respectively, which implies that the ERS-TQZS VI can considerably attenuate resonance peaks of low-frequency vibrations. Meanwhile, the resonance frequency is reduced by 7.2%, compared to that of the TQZS VI system. It should be noted that the ERSD component in TQZS VI provides better low-frequency vibration control than the conventional TQZS VI with viscous damping.
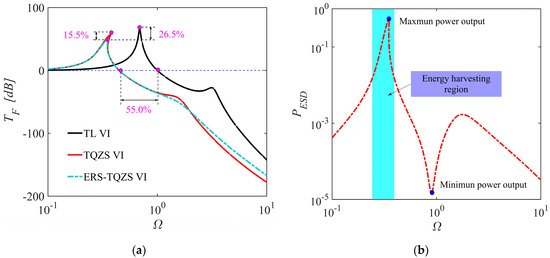
Figure 4.
The vibration attenuation and energy harvesting performance diagram of ERS-TQZS VI: (a) the force transmissibility curves of three types of two-stage isolation system (ERS-TQZS VI, TQZS VI, and TL VI); (b) output power curve of the ERS-TQZS VI.
Furthermore, the ERS-TQZS VI system can not only effectively attenuate low-frequency vibrations but can also harvest energy from such vibrations, as depicted in Figure 4b. We introduce the following output power expression to define the harvested energy of the ESD-TQZS VI as follows:
From Figure 4b, it can be observed that a notable disparity in output power exists between the resonant and anti-resonant frequencies. The significantly higher output power at the resonant frequency can be attributed to the considerably larger displacement amplitude response of the ERS-TQZS VI compared to the anti-resonant frequency. Moreover, in the energy harvesting range of the ERS-TQZS VI, the output power reaches the maximum value at the resonant frequency. The findings suggest that the ERS-TQZS VI system can not only effectively suppress resonance peaks of low-frequency vibration but can also convert vibrational energy into electrical energy. Furthermore, the ERS-TQZS VI system exhibits the ability to harvest vibrational energy within a broad frequency range. More importantly, we emphasize that the main purpose of the ERS-TQZS VI system is to suppress low-frequency vibration while simultaneously maximizing vibrational energy harvesting by optimizing the ERS-TQZS VI to balance between these two functions.
3.3. Parametric Study
Figure 5 illustrates the impact of the mass ratio on both the vibration attenuation and energy harvesting performances of the ERS-TQZS VI system. From Figure 5a, it can be observed that the resonance frequency of the system decreases by 17.9%. Meanwhile, the resonance peak decreases by 17.1% as the mass ratio increases from 0.2 to 1.0. These findings suggest that a higher mass ratio contributes to improved performance in attenuating low-frequency vibrations. Consequently, it is advisable to select a larger mass ratio within the practical limitation of the ERS-TQZS VI system to optimize its performance. For energy harvesting performance, Figure 5b demonstrates that the maximum output power of the system decreases by 86.1% with a mass ratio increase from 0.2 to 1.0. Therefore, the energy harvesting performance of the ESD-TQZS VI system decreases as the mass ratio increases. However, it is important to note that the resonant frequency at which the maximum output power occurs decreases as the frequency ratio increases.
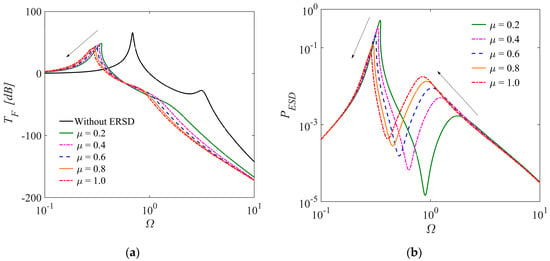
Figure 5.
The force transmissibility and output power curves of ERS-TQZS VI system under different mass ratio (, , , , , , ): (a) the force transmissibility; (b) the output power.
Figure 5 illustrates the impact of the mass ratio on both the vibration attenuation and energy harvesting performances of the ERS-TQZS VI system.
Figure 6 illustrates force transmissibility and output power curves under different damping ratios . We can observe from Figure 6a that the resonance peak decreases by 24.2% and that the resonance frequency decreases by 7.9% with a damping ratio increase from 0.01 to 0.1. The results indicate that a higher contributes to improved performance in attenuating low-frequency vibrations. From the perspective of energy harvesting, we can observe that the maximum output power at the resonant frequency decreases by 76.6% as increases from 0.01 to 0.1. Moreover, the influence of on the frequency range of energy harvesting can be considered negligible.
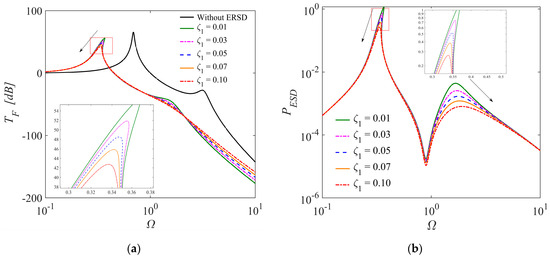
Figure 6.
The force transmissibility and output power curves of ERS-TQZS VI system under different damping ratio (, , , , , , , ): (a) the force transmissibility; (b) the output power.
Figure 7 shows the force transmissibility and output power curves of the ERS-TQZS VI system under different excitation amplitudes and also provides a comparison to the linearized system without ERSD. From Figure 7a, we can observe that the excitation amplitude has nearly no effect on the resonance peak of the ERS-TQZS VI system. However, the resonance frequency increases by 23.7% as increases from 0.001 to 0.01, leading to a degradation in the performance of low-frequency vibration attenuation. Conversely, from an energy harvesting standpoint, Figure 7b demonstrates a substantial increase in the maximum output power at the resonant frequency with the increases in from 0.001 to 0.01.
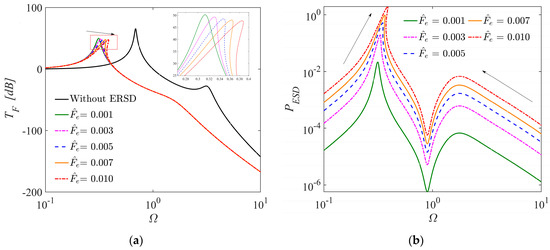
Figure 7.
The force transmissibility and output power curves of ERS-TQZS VI system under different excitation amplitude (, , , , , , ): (a) the force transmissibility; (b) the output power.
Figure 8 illustrates the influence of the shunt resistor on both the vibration attenuation and energy harvesting performances of the ERS-TQZS VI system. From Figure 8a, we can observe that the resonance frequency of the ERS-TQZS VI system increases by 15.1%. Meanwhile, the resonance peak increases by 32.8% as the shunt resistor increases from 1.0 to 18.0. The results indicate that a smaller shunt resistor is advantageous for a better performance of low-frequency vibration attenuation. Therefore, as small of a shunt resistor as possible should be selected under the practical limitation of the ERS-TQZS VI. For energy harvesting performance, we can observe from Figure 8b that the resonant frequency at the maximum output power increases by 15.3% with the shunt resistor’s increase. However, the shunt resistor nearly has no influence on the resonance peak of the ERS-TQZS VI system.
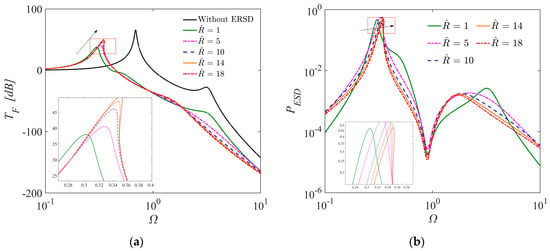
Figure 8.
The force transmissibility and output power curves of ERS-TQZS VI system under different shunt resistor (, , , , , , ): (a) the force transmissibility; (b) the output power.
Figure 9 illustrates the influence of the shunt capacitor on both the vibration attenuation and energy harvesting the performances of the ERS-TQZS VI system. From Figure 9, we can observe that the force transmissibility and output power curves of the ERS-TQZS VI system remain almost unchanged with the increase in shunt capacitance. Hence, the impact of the shunt capacitor on the performance of energy harvesting and vibration attenuation can be neglected.
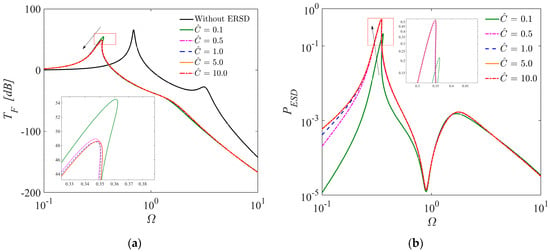
Figure 9.
The force transmissibility and output power curves of ERS-TQZS VI system under different shunt capacitor (, , , , , , ): (a) the force transmissibility; (b) the output power.
4. Discussion
The combination of analytical and numerical calculations, coupled with the parameter analysis, offers valuable insights into the performance of the ERS-TQZS VI. Our observations reveal that the ERS-TQZS VI configuration surpasses existing alternatives, such as the conventional TL VI and the TQZS VI, particularly in terms of its superior capability for attenuating low-frequency vibration. The results indicate that the ERS-TQZS VI can considerably attenuate resonance peaks of low-frequency vibration. Furthermore, the parameter study revealed that decreasing the shunt resistors improves low-frequency vibration attenuation while also maintaining the maximum energy harvested for a given excitation force. Additionally, the maximum output power at the resonant frequency exhibits a notable increase with higher excitation amplitude. These findings underscore the importance of maintaining optimal values for the remaining parameters, as deviating from these values can negatively impact the overall performance of the ERS-TQZS VI system.
5. Conclusions
This study introduces a novel ERS-TQZS VI system that offers dual functionalities of low-frequency vibration control and energy harvesting. The magnitude–frequency response equations of the ERS-TQZS VI system are solved analytically by employing the HBM in combination with the PLM. Then, numerical simulations are performed using the fourth-order Runge–Kutta method to verify the mathematical model of the ERS-TQZS VI system and analytical method. Finally, the effect of the ERS-TQZS VI system mechanical and electrical parameters on vibration attenuation and energy harvesting performance is analyzed. Some conclusions can be given as follows:
- (a)
- The ERS-TQZS VI can effectively attenuate low-frequency vibration while concurrently harvesting energy from these vibrations.
- (b)
- The mass ratio and excitation amplitude of ESD-TQZS VI have an opposite influence on both low-frequency vibration control and energy harvesting performance, while a higher damping ratio can effectively attenuate resonance peak but has minimal effect on energy harvesting.
- (c)
- The shunt resistance of the ESD-TQZS VI system should not be too large. Higher shunt resistance is not conducive to attenuating resonance peaks and will also narrow the vibration isolation frequency range. However, the shunt capacitor has a negligible impact on both low-frequency vibration attenuation and energy harvesting.
The optimization and global characteristics analysis of the ERS-TQZS VI system are left as future directions. Future research will focus on developing a robust optimization methodology to enhance the current solution for the ERS-TQZS VI system. Finally, the results will be experimentally validated.
Author Contributions
Conceptualization, methodology, investigation, writing—original draft, writing—review and editing, funding acquisition, Q.Y.; conceptualization, methodology, formal analysis, investigation, writing—original draft, writing—review and editing., Z.M.; resources, supervision, funding acquisition, validation, R.Z.; resources, supervision, project administration, H.P.L.; formal analysis, validation, K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (51579242/51839005/52201389, the funders are Yang Qingchao, Zhou Ruiping, and Chai Kai), the Natural Science Foundation of Hubei Province, China (2018CFB182/2022CFB405, the funder is Yang Qingchao), and the China Scholarship Council (202206950004, the funder is Ma Zhaozhao).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Q.; Zhou, J.; Wang, K.; Lin, Q.; Xu, D.; Wen, G. A compact quasi-zero-stiffness device for vibration suppression and energy harvesting. Int. J. Mech. Sci. 2023, 250, 108284. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Zhao, L.; Ding, H.; Chen, L. A dual-functional metamaterial for integrated vibration isolation and energy harvesting. J. Sound Vibr. 2021, 509, 116251. [Google Scholar] [CrossRef]
- Wang, T. Pendulum-based vibration energy harvesting: Mechanisms, transducer integration, and applications. Energy Conv. Manag. 2023, 276, 116469. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Wang, K.; Gao, J.; Lin, Q.; Chang, Y.; Wen, G. Dual-function quasi-zero-stiffness dynamic vibration absorber: Low-frequency vibration mitigation and energy harvesting. Appl. Math. Model. 2023, 116, 636–654. [Google Scholar] [CrossRef]
- Zeng, R.; Yin, S.; Wen, G.; Zhou, J. A non-smooth quasi-zero-stiffness isolator with displacement constraints. Int. J. Mech. Sci. 2022, 225, 107351. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C. An origami inspired quasi-zero stiffness vibration isolator using a novel truss-spring based stack Miura-ori structure. Mech. Syst. Signal Proc. 2022, 165, 108383. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Wang, K.; Xu, D.; Wen, G. Design and experimental study of a compact quasi-zero-stiffness isolator using wave springs. Sci. China-Technol. Sci. 2021, 64, 2255–2271. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, D.; Bishop, S. A torsion quasi-zero stiffness vibration isolator. J. Sound Vib. 2015, 338, 121–133. [Google Scholar] [CrossRef]
- Ibrahim, R. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Ye, K.; Luo, Q. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. Int. J. Mech. Sci. 2021, 192, 106093. [Google Scholar] [CrossRef]
- Liu, C.; Yu, K. Design and experimental study of a quasi-zero-stiffness vibration isolator incorporating transverse groove springs. Arch. Civ. Mech. Eng. 2020, 20, 67. [Google Scholar] [CrossRef]
- Wen, G.; He, J.; Liu, J.; Lin, Y. Design, analysis and semi-active control of a quasi-zero stiffness vibration isolation system with six oblique springs. Nonlinear Dyn. 2021, 106, 309–321. [Google Scholar] [CrossRef]
- Liu, X.; Huang, X.; Hua, H. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. J. Sound Vib. 2013, 332, 3359–3376. [Google Scholar] [CrossRef]
- Huang, X.; Liu, X.; Sun, J.; Zhang, Z.; Hua, H. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: A theoretical and experimental study. J. Sound Vib. 2014, 333, 1132–1148. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Xu, D. Sensitivity analysis of parametric errors on the performance of a torsion quasi-zero-stiffness vibration isolator. Int. J. Mech. Sci. 2017, 134, 336–346. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C.; Brown, T. Design of a quasi-zero stiffness isolation system for supporting different loads. J. Sound Vib. 2020, 471, 115198. [Google Scholar] [CrossRef]
- Gatti, G. An adjustable device to adaptively realise diverse nonlinear force-displacement characteristics. Mech. Syst. Signal Process. 2022, 180, 109379. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, X.; Luo, Y.; Zhang, Y.; Xie, S. Analytical study of the low frequency multi-direction isolator with high-static-low-dynamic stiffness struts and spatial pendulum. Mech. Syst. Signal Process. 2018, 110, 521–539. [Google Scholar] [CrossRef]
- Wang, S.; Xin, W.; Ning, Y.; Li, B.; Hu, Y. Design, experiment, and improvement of a quasi-zero-stiffness vibration isolation system. Appl. Sci. 2020, 10, 2273. [Google Scholar] [CrossRef]
- Sun, Y.; Meng, K.; Yuan, S.; Zhao, J.; Xie, R.; Yang, Y.; Pu, H. Modeling electromagnetic force and axial-stiffness for an electromagnetic negative-stiffness spring toward vibration isolation. IEEE Trans. Magn. 2019, 55, 8000410. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, Y.; Zhao, J.; Meng, K.; Wang, M.; Pu, H.; Xie, S. A tunable quasi-zero stiffness isolator based on a linear electromagnetic spring. J. Sound Vib. 2020, 482, 115449. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Zhang, L.; Zheng, W.; Wang, K.; Wu, C. A bistable vibration isolator with nonlinear electromagnetic shunt damping. Mech. Syst. Signal Process. 2020, 136, 106504. [Google Scholar] [CrossRef]
- Dai, H.; Jing, X.; Wang, Y.; Yue, X.; Yuan, J. Post-capture vibration suppression of spacecraft via a bio-inspired isolation system. Mech. Syst. Signal Process. 2018, 105, 214–240. [Google Scholar] [CrossRef]
- Gatti, G. Optimizing elastic potential energy via geometric nonlinear stiffness. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 106035. [Google Scholar] [CrossRef]
- Yan, G.; Wang, S.; Zou, H.; Zhao, L.; Gao, Q.; Zhang, W. Bio-inspired polygonal skeleton structure for vibration isolation: Design, modelling, and experiment. Sci. China-Technol. Sci. 2020, 63, 2617–2630. [Google Scholar] [CrossRef]
- Lakes, R.S. Extreme damping in compliant composites with a negative-stiffness phase. Philos. Mag. Lett. 2001, 81, 95–100. [Google Scholar] [CrossRef]
- Virk, K.; Monti, A.; Trehard, T.; Marsh, M.; Hazra, K.; Boba, K.; Farrow, I.R. SILICOMB PEEK Kirigami cellular structures: Mechanical response and energy dissipation through zero and negative stiffness. Smart Mater. Struct. 2013, 22, 084014. [Google Scholar] [CrossRef]
- Fan, H.; Yang, L.; Tian, Y.; Wang, Z. Design of metastructures with quasi-zero dynamic stiffness for vibration isolation. Compos. Struct. 2020, 243, 112244. [Google Scholar] [CrossRef]
- Ahn, K.K. Active pneumatic vibration isolation system using negative stiffness structures for a vehicle seat. J. Sound Vib. 2014, 333, 1245–1268. [Google Scholar] [CrossRef]
- Pu, H.; Yuan, S.; Peng, Y.; Meng, K.; Zhao, J.; Xie, R.; Chen, X. Multi-layer electromagnetic spring with tunable negative stiffness for semi-active vibration isolation. Mech. Syst. Signal Process. 2019, 121, 942–960. [Google Scholar] [CrossRef]
- Palomares, E.; Nieto, A.J.; Morales, A.L.; Chicharro, J.M.; Pintado, P. Numerical and experimental analysis of a vibration isolator equipped with a negative stiffness system. J. Sound Vib. 2018, 414, 31–42. [Google Scholar] [CrossRef]
- Kim, M.H.; Kim, H.Y.; Kim, H.C.; Ahn, D.; Gweon, D.G. Design and control of a 6-DOF active vibration isolation system using a Halbach magnet array. IEEE-ASME Trans. Mechatron. 2016, 21, 2185–2196. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Ouyang, H.; Cheng, L.; Xu, D. A semi-active metamaterial beam with electromagnetic quasi-zero-stiffness resonators for ultralow-frequency band gap tuning. Int. J. Mech. Sci. 2020, 176, 105548. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, J.; Zhao, J.; Bian, X.; Zou, L. Improving low frequency isolation performance of optical platforms using electromagnetic active-negative-stiffness method. Appl. Sci. 2020, 10, 7342. [Google Scholar] [CrossRef]
- Liu, S.; Feng, L.; Zhao, D.; Shi, X.; Zhang, Y.; Jiang, J.; Chen, L. A real-time controllable electromagnetic vibration isolator based on magnetorheological elastomer with quasi-zero stiffness characteristic. Smart Mater. Struct. 2019, 28, 085037. [Google Scholar] [CrossRef]
- Yigit, U.; Cigeroglu, E.; Budak, E. Chatter reduction in boring process by using piezoelectric shunt damping with experimental verification. Mech. Syst. Signal Proc. 2017, 94, 312–321. [Google Scholar] [CrossRef]
- Ma, H.; Yan, B. Nonlinear damping and mass effects of electromagnetic shunt damping for enhanced nonlinear vibration isolation. Mech. Syst. Signal Proc. 2021, 146, 107010. [Google Scholar] [CrossRef]
- Sun, R.; Wong, W.; Cheng, L. Bi-objective optimal design of an electromagnetic shunt damper for energy harvesting and vibration control. Mech. Syst. Signal Proc. 2023, 182, 109571. [Google Scholar] [CrossRef]
- Forward, R.L. Electronic damping of vibrations in optical structures. Appl. Opt. 1979, 18, 690–697. [Google Scholar] [CrossRef]
- Hagood, N.; Von Flotow, A. Damping of structural vibrations with piezoelectric materials and passive electrical networks. J. Sound Vib. 1991, 146, 243–268. [Google Scholar] [CrossRef]
- Behrens, S.; Fleming, A.; Moheimani, S. Electromagnetic shunt damping. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume 2, pp. 1145–1150. [Google Scholar] [CrossRef]
- Zuo, L.; Cui, W. Dual-functional energy-harvesting and vibration control: Electromagnetic resonant shunt series tuned mass dampers. J. Vib. Acoust.-Trans. ASME 2013, 135, 051018. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Luo, Y.; Wang, X.; Zuo, L. Seismic control of a SDOF structure through electromagnetic resonant shunt tuned mass-damper-inerter and the exact H2 optimal solutions. J. Vibroeng. 2017, 19, 2063–2079. [Google Scholar] [CrossRef]
- Luo, Y.; Sun, H.; Wang, X.; Zuo, L.; Chen, N. Wind induced vibration control and energy harvesting of electromagnetic resonant shunt tuned mass-damper-inerter for building structures. Shock Vib. 2017, 2017, 4180134. [Google Scholar] [CrossRef]
- Kakou, P.; Barry, O. Simultaneous vibration reduction and energy harvesting of a nonlinear oscillator using a nonlinear electromagnetic vibration absorber-inerter. Mech. Syst. Signal Proc. 2021, 156, 107607. [Google Scholar] [CrossRef]
- Sun, R.; Zhou, S.; Cheng, L. Ultra-low frequency vibration energy harvesting: Mechanisms, enhancement techniques, and scaling laws. Energy Conv. Manag. 2023, 276, 116585. [Google Scholar] [CrossRef]
- Yang, Q.; Lou, J.; Zhu, S.; Liu, S. Force transmissibility of quasi-zero-stiffness system and experimental investigation. J. Naval Eng. Univ. 2014, 26, 19–23. Available online: http://www.cqvip.com/qk/91072x/201403/50169319.html (accessed on 10 May 2023).
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Lu, Z.; Yang, T.; Brennan, M.J.; Li, X.; Liu, Z. On the performance of a two-stage vibration isolation system which has geometrically nonlinear stiffness. J. Vib. Acoust.-Trans. ASME 2014, 136, 064501. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Neild, S.A.; Jiang, J.Z. Comparison of the dynamic performance of nonlinear one and two degree-of-freedom vibration isolators with quasi-zero stiffness. Nonlinear Dyn. 2017, 88, 635–654. [Google Scholar] [CrossRef]
- Kremer, D.; Liu, K. A nonlinear energy sink with an energy harvester: Transient responses. J. Sound Vib. 2014, 333, 4859–4880. [Google Scholar] [CrossRef]
- Renson, L.; Kerschen, G.; Cochelin, B. Numerical computation of nonlinear normal modes in mechanical engineering. J. Sound Vib. 2016, 364, 177–206. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).