An Unsupervised Image Denoising Method Using a Nonconvex Low-Rank Model with TV Regularization
Abstract
1. Introduction
- 1.
- We design an unsupervised image denoising method based on nonconvex -norm and RPCA. To the best of our knowledge, this should be the first application of the nonconvex -norm to image denoising. The use of the -norm avoids the problem of overpunishing large singular values by the nuclear norm and provides a high robustness and rank approximation. Combined with the associated solution algorithm, the overall model is highly efficient and converges fast, which facilitates the overall denoising model in quickly discarding matrix elements with large approximation errors and providing a high estimation accuracy.
- 2.
- The denoising effect is facilitated by combining the -norm and a TV norm regularization. The -norm can effectively enhance the sparsity of the noise, while the TV norm can exploit the sparsity of the image in the gradient domain to further enhance the smoothness of the image while preserving the edge information of the denoised image.
- 3.
- Our method does not require any labeled images for training, and its unsupervised denoising principle makes it easy to generalize to different scenarios for application. Extensive experiments show that the proposed method can preserve the image’s edge structure information, preserve important features of the image, and maintain excellent visual effects in brightness smoothing under different scenes and different levels of noise.
2. Related Work
2.1. Image Denoising Literature Review
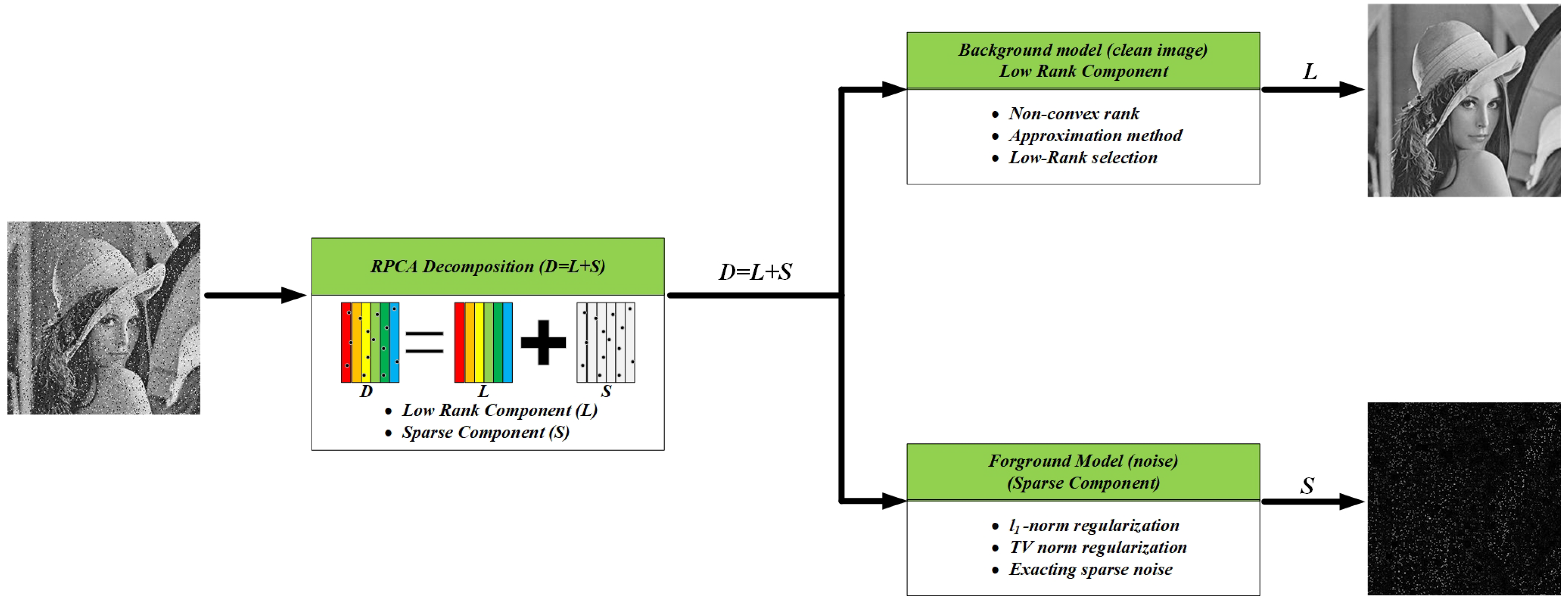
2.2. Robust Principal Component Analysis (RPCA)
2.3. Nonconvex -Norm
2.4. TV Norm
2.5. -Norm
3. Proposed Method
| Algorithm 1 Solving (7) by ADMM |
Input: Observed data and Initialization: compute and , , , , While and inneriter do
Output:, . |
3.1. Updating L
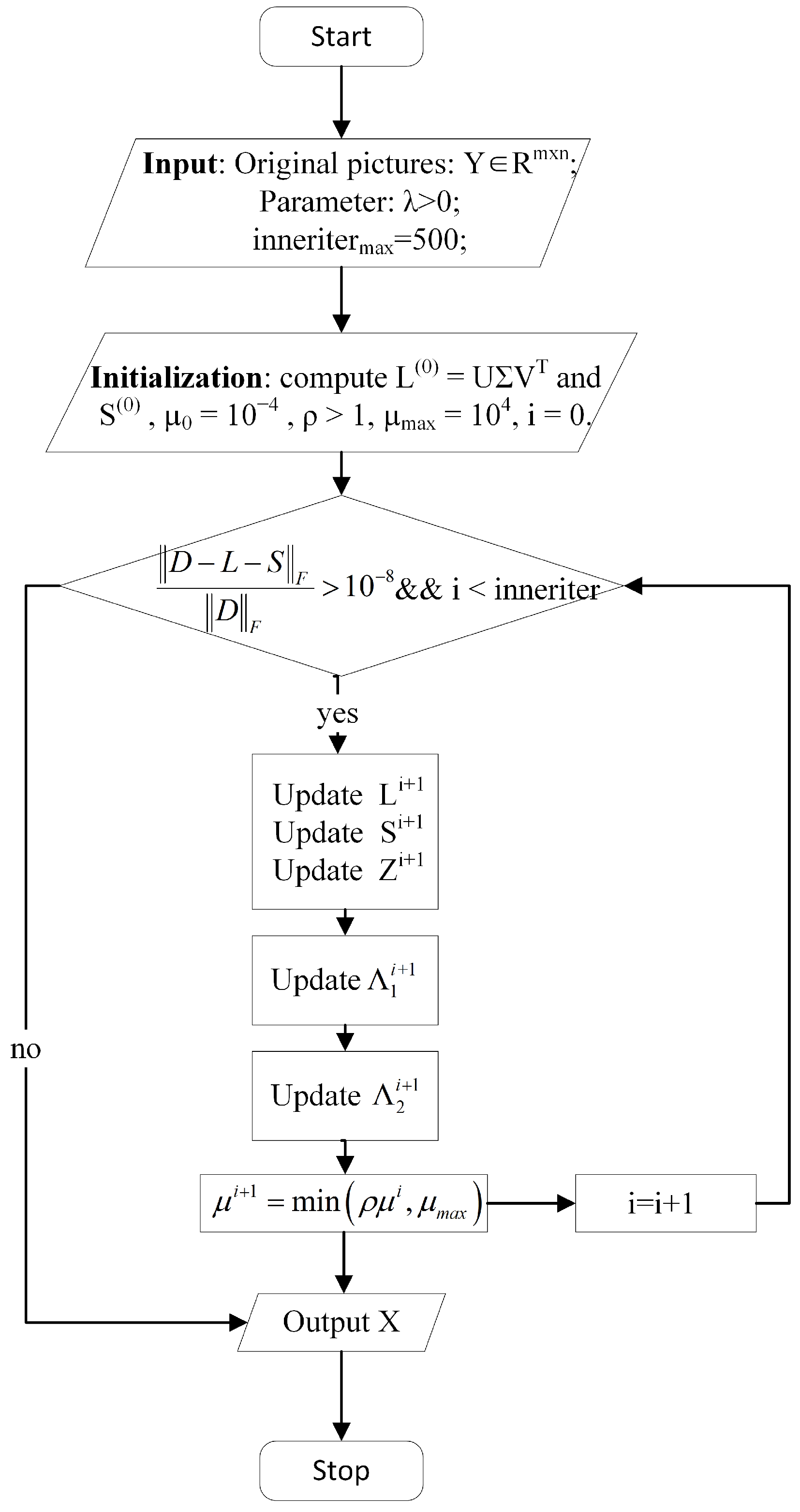
3.2. Updating S
3.3. Updating Z
3.4. Updating and
4. Experimental Results and Analysis
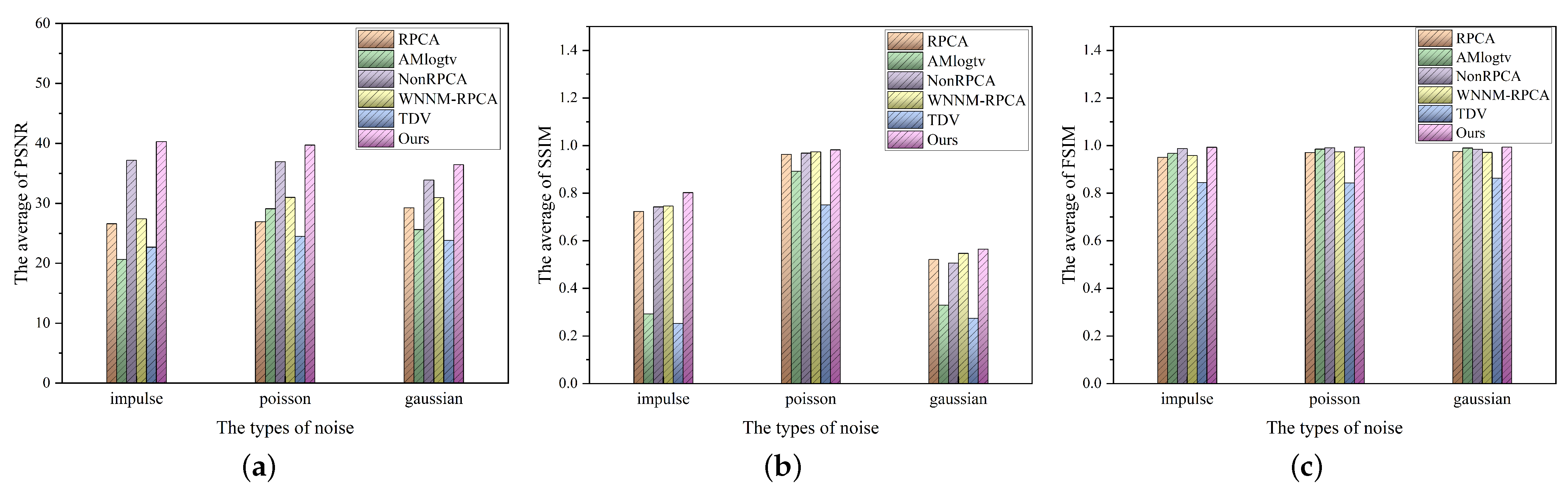
4.1. Natural Image Denoising


4.2. Medical Image Denoising

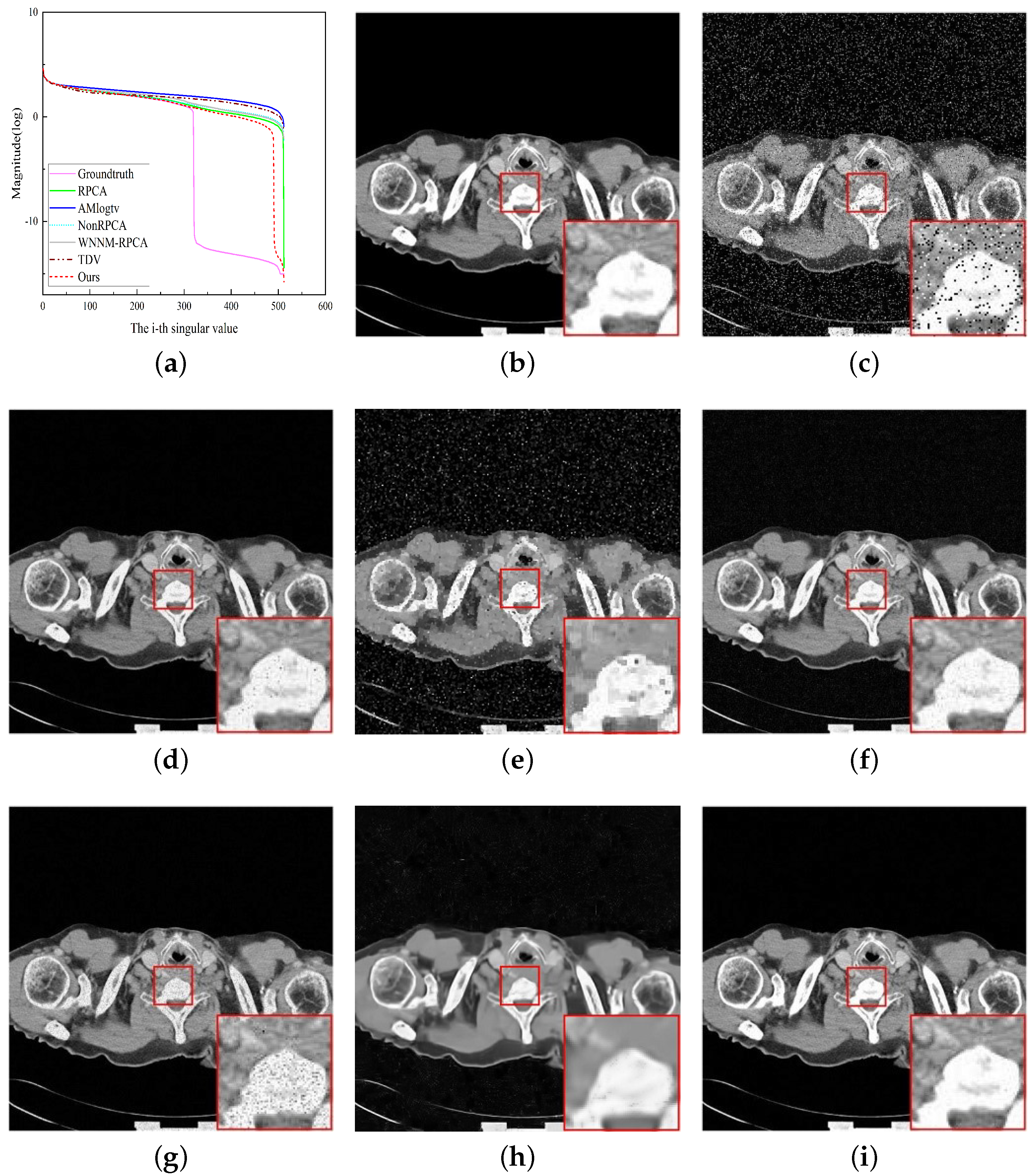


| Noise Type | Images | RPCA | AMlogtv | NonRPCA | WNNM−RPCA | TDV | Ours |
|---|---|---|---|---|---|---|---|
| Impulse noise | 1 | 34.1086 | 20.8109 | 39.3910 | 30.0661 | 22.6606 | 43.9398 |
| 2 | 29.7339 | 20.7488 | 39.8981 | 28.6808 | 22.5140 | 42.6776 | |
| 3 | 27.5287 | 20.7872 | 36.5463 | 29.3167 | 22.3062 | 40.9121 | |
| 4 | 34.5260 | 20.7857 | 41.9476 | 31.1892 | 22.3296 | 43.9249 | |
| 5 | 22.7421 | 20.6817 | 36.5971 | 26.6155 | 22.6972 | 39.0744 | |
| 6 | 21.6578 | 20.5327 | 36.2646 | 24.5502 | 23.0144 | 38.7777 | |
| 7 | 21.5732 | 20.4626 | 33.8149 | 25.8391 | 23.0563 | 36.7197 | |
| 8 | 20.8001 | 20.3707 | 32.7776 | 22.9537 | 22.9246 | 36.3267 | |
| Average | 26.5838 | 20.6475 | 37.1546 | 27.4014 | 22.6878 | 40.2941 | |
| Poisson noise | 1 | 25.3796 | 29.2750 | 37.8533 | 30.4089 | 23.4745 | 40.7487 |
| 2 | 25.9954 | 29.2576 | 37.7551 | 31.2219 | 23.5091 | 41.3824 | |
| 3 | 32.0855 | 29.0463 | 40.0718 | 40.0718 | 23.8365 | 42.0702 | |
| 4 | 27.2295 | 29.0262 | 39.0888 | 32.7282 | 24.2402 | 40.3903 | |
| 5 | 24.7137 | 29.2884 | 35.0703 | 27.0225 | 23.7425 | 38.5899 | |
| 6 | 25.3914 | 29.0887 | 36.5243 | 27.4036 | 22.3025 | 40.6466 | |
| 7 | 28.2686 | 28.8807 | 29.3977 | 31.1992 | 27.3887 | 37.9662 | |
| 8 | 26.2732 | 28.8691 | 33.4158 | 28.9564 | 27.4388 | 35.8507 | |
| Average | 26.9171 | 29.0915 | 36.9186 | 30.9760 | 24.4916 | 39.7056 | |
| Gaussian noise | 1 | 29.0228 | 25.7441 | 34.9713 | 32.3936 | 23.5661 | 37.0809 |
| 2 | 29.0297 | 25.7769 | 33.8007 | 33.1549 | 23.5022 | 37.4827 | |
| 3 | 33.8497 | 25.6839 | 34.8873 | 35.2871 | 23.2967 | 37.9355 | |
| 4 | 30.3547 | 25.6564 | 33.3377 | 31.6763 | 23.4633 | 35.8458 | |
| 5 | 27.5425 | 25.7290 | 34.7948 | 30.7608 | 23.7899 | 36.1815 | |
| 6 | 27.9469 | 25.5031 | 32.8209 | 28.5334 | 24.3505 | 35.7714 | |
| 7 | 26.7573 | 25.4181 | 32.1886 | 27.2011 | 24.4782 | 34.9603 | |
| 8 | 29.3714 | 25.3123 | 34.1811 | 28.4058 | 24.1735 | 36.1523 | |
| Average | 29.2344 | 25.6030 | 33.8728 | 30.9266 | 23.8275 | 36.4263 |
| Noise Type | Images | RPCA | AMlogtv | NonRPCA | WNNM−RPCA | TDV | Ours |
|---|---|---|---|---|---|---|---|
| Impulse noise | 1 | 0.8401 | 0.2979 | 0.7965 | 0.7915 | 0.2491 | 0.8709 |
| 2 | 0.7893 | 0.3024 | 0.7830 | 0.7847 | 0.2533 | 0.8524 | |
| 3 | 0.7605 | 0.3158 | 0.7402 | 0.7937 | 0.2670 | 0.8437 | |
| 4 | 0.8474 | 0.3109 | 0.8179 | 0.7987 | 0.2618 | 0.8750 | |
| 5 | 0.6546 | 0.2922 | 0.7103 | 0.7359 | 0.2513 | 0.7766 | |
| 6 | 0.6337 | 0.2741 | 0.6918 | 0.7015 | 0.2475 | 0.7741 | |
| 7 | 0.6276 | 0.2690 | 0.7090 | 0.7140 | 0.2481 | 0.7159 | |
| 8 | 0.6285 | 0.2732 | 0.6860 | 0.6430 | 0.2437 | 0.7080 | |
| Average | 0.7227 | 0.2919 | 0.7418 | 0.7453 | 0.2527 | 0.8020 | |
| Poisson noise | 1 | 0.9589 | 0.8826 | 0.9740 | 0.9766 | 0.6923 | 0.9883 |
| 2 | 0.9620 | 0.8792 | 0.9732 | 0.9776 | 0.6897 | 0.9895 | |
| 3 | 0.9816 | 0.8739 | 0.9847 | 0.9840 | 0.7149 | 0.9903 | |
| 4 | 0.9654 | 0.8779 | 0.9794 | 0.9774 | 0.7430 | 0.9840 | |
| 5 | 0.9479 | 0.8940 | 0.9539 | 0.9610 | 0.7055 | 0.9791 | |
| 6 | 0.9573 | 0.9022 | 0.9628 | 0.9664 | 0.6900 | 0.9821 | |
| 7 | 0.9682 | 0.9070 | 0.9658 | 0.9734 | 0.8766 | 0.9745 | |
| 8 | 0.9600 | 0.9160 | 0.9509 | 0.9645 | 0.8944 | 0.9694 | |
| Average | 0.9626 | 0.8916 | 0.9680 | 0.9726 | 0.7508 | 0.9821 | |
| Gaussian noise | 1 | 0.5095 | 0.3330 | 0.5307 | 0.5627 | 0.2681 | 0.5862 |
| 2 | 0.5185 | 0.3425 | 0.5144 | 0.5737 | 0.2739 | 0.5981 | |
| 3 | 0.6098 | 0.3639 | 0.5844 | 0.5988 | 0.2879 | 0.6233 | |
| 4 | 0.5725 | 0.3535 | 0.5310 | 0.5790 | 0.2866 | 0.5832 | |
| 5 | 0.5293 | 0.3287 | 0.5352 | 0.5428 | 0.2726 | 0.5680 | |
| 6 | 0.4550 | 0.3071 | 0.4537 | 0.5142 | 0.2696 | 0.5432 | |
| 7 | 0.4861 | 0.3042 | 0.4412 | 0.5022 | 0.2716 | 0.5115 | |
| 8 | 0.4883 | 0.2991 | 0.4628 | 0.5005 | 0.2657 | 0.5224 | |
| Average | 0.5211 | 0.3290 | 0.5067 | 0.5467 | 0.2745 | 0.5669 |
| Noise Type | Images | RPCA | AMlogtv | NonRPCA | WNNM−RPCA | TDV | Ours |
|---|---|---|---|---|---|---|---|
| Impulse noise | 1 | 0.9904 | 0.9630 | 0.9924 | 0.9761 | 0.8230 | 0.9968 |
| 2 | 0.9761 | 0.9656 | 0.9928 | 0.9675 | 0.8219 | 0.9956 | |
| 3 | 0.9645 | 0.9709 | 0.9880 | 0.9662 | 0.8086 | 0.9938 | |
| 4 | 0.9907 | 0.9657 | 0.9952 | 0.9759 | 0.8328 | 0.9759 | |
| 5 | 0.9392 | 0.9652 | 0.9850 | 0.9602 | 0.8573 | 0.9912 | |
| 6 | 0.9243 | 0.9651 | 0.9827 | 0.9441 | 0.8681 | 0.9909 | |
| 7 | 0.9159 | 0.9665 | 0.9816 | 0.9501 | 0.8771 | 0.9870 | |
| 8 | 0.9057 | 0.9732 | 0.9831 | 0.9226 | 0.8658 | 0.9879 | |
| Average | 0.9508 | 0.9669 | 0.9876 | 0.9578 | 0.8443 | 0.9925 | |
| Poisson noise | 1 | 0.9619 | 0.9900 | 0.9919 | 0.9769 | 0.8163 | 0.9954 |
| 2 | 0.9656 | 0.9870 | 0.9918 | 0.9786 | 0.8187 | 0.9956 | |
| 3 | 0.9917 | 0.9775 | 0.9938 | 0.9928 | 0.8221 | 0.9957 | |
| 4 | 0.9756 | 0.9673 | 0.9939 | 0.9834 | 0.8533 | 0.9945 | |
| 5 | 0.9490 | 0.9921 | 0.9899 | 0.9504 | 0.8443 | 0.9944 | |
| 6 | 0.9570 | 0.9880 | 0.9905 | 0.9577 | 0.7483 | 0.9943 | |
| 7 | 0.9846 | 0.9902 | 0.9898 | 0.9771 | 0.9213 | 0.9917 | |
| 8 | 0.9782 | 0.9885 | 0.9844 | 0.9687 | 0.9231 | 0.9894 | |
| Average | 0.9704 | 0.9851 | 0.9907 | 0.9732 | 0.8434 | 0.9938 | |
| Gaussian noise | 1 | 0.9749 | 0.9944 | 0.9907 | 0.9907 | 0.8388 | 0.9949 |
| 2 | 0.9752 | 0.9961 | 0.9882 | 0.9821 | 0.8374 | 0.9965 | |
| 3 | 0.9916 | 0.9968 | 0.9867 | 0.9890 | 0.8248 | 0.9980 | |
| 4 | 0.9821 | 0.9770 | 0.9823 | 0.9760 | 0.8547 | 0.9960 | |
| 5 | 0.9640 | 0.9902 | 0.9840 | 0.9701 | 0.8755 | 0.9909 | |
| 6 | 0.9698 | 0.9873 | 0.9782 | 0.9601 | 0.8884 | 0.9890 | |
| 7 | 0.9603 | 0.9848 | 0.9756 | 0.9478 | 0.8935 | 0.9853 | |
| 8 | 0.9791 | 0.9915 | 0.9893 | 0.9625 | 0.8858 | 0.9926 | |
| Average | 0.9746 | 0.9897 | 0.9844 | 0.9709 | 0.8623 | 0.9929 |
4.3. Face Denoising with Illumination Variation
4.4. Implementation Computational Cost



5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RPCA | Robust principal component analysis |
| TV | Total variational regularization |
| AWRR | Adaptive weighted rank reduction |
| SJSCCA | Structured joint sparse canonical correlation analysis |
| SR | Sparse representation |
| LMMSE | Linear minimum mean-squared error estimator |
| CT | Computed tomography |
| PSNR | Peak signal-to-noise ratio |
| SSIM | Structure similarity index measure |
| FSIM | Feature similarity index measure |
References
- Diwakar, M.; Singh, P. CT image denoising using multivariate model and its method noise thresholding in non-subsampled shearlet domain. Biomed. Signal Process. Control 2021, 57, 101754. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, F.; Fan, H.; Zhang, C. Brief review of image denoising techniques. Vis. Comput. Ind. Biomed. Art 2019, 2, 7. [Google Scholar] [CrossRef] [PubMed]
- Pradeep, S.; Nirmaladevi, P. A review on speckle noise reduction techniques in ultrasound medical images based on spatial domain, transform domain and CNN methods. In IOP Conference Series: Materials Science and Engineering; IOP Conference: Erode, India, 2021; p. 012116. [Google Scholar]
- Rakshit, S.; Ghosh, A.; Shankar, B.U. Fast mean filtering technique (FMFT). Pattern Recognit. 2007, 40, 890–897. [Google Scholar] [CrossRef]
- Justusson, B.I. Median filtering: Statistical properties. In Two-Dimensional Digital Signal Prcessing II: Transforms and Median Filters; Springer: Berlin/Heidelberg, Germany, 2006; pp. 161–196. [Google Scholar]
- Chen, J.; Benesty, J.; Huang, Y.; Doclo, S. New insights into the noise reduction Wiener filter. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 1218–1234. [Google Scholar] [CrossRef]
- Özen Acarbay, E.; Özkurt, N. Performance analysis of the speech enhancement application with wavelet transform domain adaptive filters. Int. J. Speech Technol. 2023, 26, 245–258. [Google Scholar] [CrossRef]
- Grotevent, M.J.; Yakunin, S.; Bachmann, D.; Romero, C.; Vázquez de Aldana, J.R.; Madi, M.; Calame, M.; Kovalenko, M.V.; Shorubalko, I. Integrated photodetectors for compact Fourier-transform waveguide spectrometers. Nat. Photon. 2023, 17, 59–64. [Google Scholar] [CrossRef]
- Scribano, C.; Franchini, G.; Prato, M.; Bertogna, M. DCT-Former: Efficient Self-Attention with Discrete Cosine Transform. J. Sci. Comput. 2023, 94, 67. [Google Scholar] [CrossRef]
- Scribano, C.; Zheng, M.; Prato, M.; Zuo, W.; Zhang, B.; Zhang, Y.; Zhang, D. Multi-stage image denoising with the wavelet transform. Pattern Recognit. 2023, 134, 109050. [Google Scholar]
- Farmani, B.; Pal, Y.; Pedersen, M. Motion sensor noise attenuation using deep learning. First Break 2023, 41, 45–51. [Google Scholar] [CrossRef]
- Wang, S.; Nie, F.; Wang, Z.; Wang, R.; Li, X. Robust Principal Component Analysis via Joint Reconstruction and Projection. IEEE Trans. Neural Netw. Learn. Syst. 2022. early access. [Google Scholar] [CrossRef]
- Pokala, P.K.; Hemadri, R.V.; Seelamantula, C.S. Iteratively reweighted minimax-concave penalty minimization for accurate low-rank plus sparse matrix decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 8992–9010. [Google Scholar] [CrossRef]
- Bayati, F.; Trad, D. 3-D Data Interpolation and Denoising by an Adaptive Weighting Rank-Reduction Method Using Multichannel Singular Spectrum Analysis Algorithm. Sensors 2023, 23, 577. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, D.; Hou, W.S. Weighted Schatten p-norm minimization for impulse noise removal with TV regularization and its application to medical images. Biomed. Signal Process. Control 2021, 66, 102123. [Google Scholar] [CrossRef]
- Xiu, X.; Yang, Y.; Kong, L. Laplacian regularized robust principal component analysis for process monitoring. J. Process Control 2020, 92, 212–219. [Google Scholar] [CrossRef]
- Xiu, X.; Yang, Y.; Kong, L. Data-driven process monitoring using structured joint sparse canonical correlation analysis. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 361–365. [Google Scholar] [CrossRef]
- Javed, S.; Mahmood, A.; Al-Maadeed, S. Moving object detection in complex scene using spatiotemporal structured-sparse RPCA. IEEE Trans. Image Process. 2018, 28, 1007–1022. [Google Scholar] [CrossRef]
- Liu, J.; Xiu, X.; Jiang, X. MManifold constrained joint sparse learning via non-convex regularization. Neurocomputing 2021, 458, 112–126. [Google Scholar] [CrossRef]
- Zhong, X.; Xu, L.; Li, Y. A nonconvex relaxation approach for rank minimization problems. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; AAAI: Palo Alto, CA, USA, 2015. [Google Scholar]
- Peng, Y.; Suo, J.; Dai, Q.; Xu, W. Reweighted low-rank matrix recovery and its application in image restoration. IEEE Trans. Cybern. 2014, 44, 2418–2430. [Google Scholar] [CrossRef]
- Dong, J.; Xue, Z.; Guan, J.; Han, Z.F.; Wang, W. Low rank matrix completion using truncated nuclear norm and sparse regularizer. Signal Process. Image Commun. 2018, 68, 76–87. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Luo, X. Large-scale affine matrix rank minimization with a novel nonconvex regularizer. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4661–4675. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Z.; Li, J. ovel RPCA with nonconvex logarithm and truncated fraction norms for moving object detection. Digit. Signal Process. 2023, 133, 103892. [Google Scholar] [CrossRef]
- Sun, Q.; Xiang, S.; Ye, J. Robust principal component analysis via capped norms. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; ACM: New York, NY, USA, 2013. [Google Scholar]
- Xiang, S.; Tong, X.; Ye, J. Efficient sparse group feature selection via nonconvex optimization. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 11–19 June 2013; PMLR: Atlanta, GA, USA, 2013. [Google Scholar]
- Lv, T.; Pan, Z.; Wei, W. Iterative deep neural networks based on proximal gradient descent for image restoration. PLoS ONE 2022, 17, e0276373. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Park, D. Element-wise adaptive thresholds for learned iterative shrinkage thresholding algorithms. IEEE Access 2020, 8, 45874–45886. [Google Scholar] [CrossRef]
- Jia, X.; Kanzow, C.; Mehlitz, P.; Wachsmuth, G. An augmented Lagrangian method for optimization problems with structured geometric constraints. Math. Program. 2022, 199, 1–51. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Threshold selection for wavelet shrinkage of noisy data. In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Baltimore, MD, USA, 3–6 November 1994; IEEE: Baltimore, MD, USA, 1994. [Google Scholar]
- Huang, G.; Bai, M.; Zhao, Q. Erratic noise suppression using iterative structure-oriented space-varying median filtering with sparsity constraint. Geophys. Prospect. 2021, 69, 101–121. [Google Scholar] [CrossRef]
- Saito, Y.; Miyata, T. Recovering Texture with a Denoising-Process-Aware LMMSE Filter. Signals 2021, 2, 286–303. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Liao, W.; Lamoureux, M.P. Antileakage least-squares spectral analysis for seismic data regularization and random noise attenuation. Geophysics 2018, 83, V157–V170. [Google Scholar] [CrossRef]
- Chen, Z.; Zeng, Z.; Shen, H.; Zheng, X.; Dai, P.; Ouyang, P. DN-GAN: Denoising generative adversarial networks for speckle noise reduction in optical coherence tomography images. Biomed. Signal Process. Control 2020, 55, 101632. [Google Scholar] [CrossRef]
- Valsesia, D.; Fracastoro, G.; Magli, E. Deep graph-convolutional image denoising. IEEE Trans. Image Process. 2020, 29, 8226–8237. [Google Scholar] [CrossRef]
- Wang, S.; Xia, K.; Wang, L. Improved RPCA method via non-convex regularisation for image denoising. IET Signal Process. 2020, 14, 269–277. [Google Scholar] [CrossRef]
- Peng, C.; Liu, Y.; Kang, K. Hyperspectral Image Denoising Using Nonconvex Local Low-Rank and Sparse Separation With Spatial-Spectral Total Variation Regularization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5538617. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Li, J. Nonlocal weighted robust principal component analysis for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1745–1756. [Google Scholar] [CrossRef]
- Mahdaoui, A.E.; Ouahabi, A.; Moulay, M.S. Image denoising using a compressive sensing approach based on regularization constraints. Sensors 2022, 22, 2199. [Google Scholar] [CrossRef]
- Qi, G.; Hu, G.; Mazur, N. A novel multi-modality image simultaneous denoising and fusion method based on sparse representation. Computers 2021, 10, 129. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. Adv. Neural Inf. Process. Syst. 2009, 22, 1–9. [Google Scholar]
- Kang, Z.; Peng, C.; Cheng, Q. Robust PCA via nonconvex rank approximation. In Proceedings of the 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; IEEE: Orlando, FL, USA, 2015. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y. Robust principal component analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, G.; Zhu, Z. Alternating direction method of multipliers for nonconvex log total variation image restoration. Appl. Math. Model. 2023, 114, 338–359. [Google Scholar] [CrossRef]
- Gu, S.; Xie, Q.; Meng, D.; Zuo, W.; Feng, X. Weighted nuclear norm minimization and its applications to low level vision. Int. J. Comput. Vis. 2017, 121, 183–208. [Google Scholar] [CrossRef]
- Parisotto, S.; Lellmann, J.; Masnou, S. Higher-order total directional variation: Imaging applications. SIAM J. Imaging Sci. 2020, 13, 2063–2104. [Google Scholar] [CrossRef]
- Singhadia, A.; Pati, P.S.; Singhal, C. Efficient HEVC encoding to meet bitrate and PSNR requirements using parametric modeling. Circuits Syst. Signal Process. 2022, 41, 4479–4511. [Google Scholar] [CrossRef]
- Bakurov, I.; Buzzelli, M.; Schettini, R. Structural similarity index (SSIM) revisited: A data-driven approach. Expert Syst. Appl. 2022, 189, 116087. [Google Scholar] [CrossRef]
- Sara, U.; Akter, M.; Uddin, M.S. Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef]
- Pan, J.; Li, R.; Liu, H. Highlight removal for endoscopic images based on accelerated adaptive non-convex RPCA decomposition. Comput. Methods Programs Biomed. 2023, 228, 107240. [Google Scholar] [CrossRef]



| Noise Type | Images | RPCA | AMlogtv | NonRPCA | WNNM−RPCA | TDV | Ours |
|---|---|---|---|---|---|---|---|
| Impulse noise | Butterfly | 32.5246 | 20.8745 | 33.8365 | 30.9500 | 18.4085 | 41.6482 |
| House | 32.5501 | 24.5450 | 35.0507 | 31.1299 | 24.3206 | 41.7090 | |
| Peppers | 30.9569 | 22.1821 | 31.9384 | 26.9935 | 21.8727 | 34.1587 | |
| Lena | 33.1704 | 22.6855 | 34.8620 | 30.4863 | 22.0347 | 41.1695 | |
| Room | 33.3740 | 22.9321 | 35.3441 | 33.8834 | 21.4471 | 41.4602 | |
| Bird | 30.4850 | 21.6382 | 30.4429 | 28.0903 | 20.8948 | 33.2591 | |
| Camera | 30.8366 | 21.7976 | 30.7196 | 30.9059 | 21.2003 | 33.4341 | |
| Starfish | 30.2611 | 21.9611 | 32.7050 | 31.8355 | 20.7648 | 33.7062 | |
| Average | 31.7698 | 22.3270 | 33.1124 | 30.5343 | 21.3679 | 37.5681 | |
| Poisson noise | Butterfly | 33.1761 | 25.2643 | 37.8854 | 37.5122 | 19.3446 | 41.8914 |
| House | 33.1059 | 30.1854 | 35.1456 | 34.7763 | 25.9563 | 37.3046 | |
| Peppers | 31.8290 | 25.5136 | 32.0457 | 31.9485 | 23.3223 | 33.0805 | |
| Lena | 34.3953 | 26.2260 | 35.4915 | 35.3024 | 23.0865 | 37.6541 | |
| Room | 35.2429 | 25.7317 | 35.5204 | 35.2885 | 22.2211 | 37.6050 | |
| Bird | 31.0893 | 26.0181 | 31.4407 | 31.3215 | 21.9071 | 34.0229 | |
| Camera | 30.6940 | 25.4728 | 32.7069 | 32.5430 | 22.0588 | 33.8362 | |
| Starfish | 27.1146 | 25.6538 | 28.4586 | 28.8304 | 20.8408 | 29.3038 | |
| Average | 32.0808 | 26.2582 | 33.5868 | 33.4403 | 22.3421 | 35.5873 | |
| Gaussian noise | Butterfly | 33.2683 | 23.6624 | 37.4013 | 38.9586 | 20.4690 | 42.1629 |
| House | 33.1171 | 28.5725 | 37.9599 | 38.4267 | 25.7665 | 42.1794 | |
| Peppers | 31.0499 | 24.5416 | 33.4540 | 34.0774 | 23.0379 | 34.6498 | |
| Lena | 33.6107 | 25.2392 | 37.5569 | 38.8699 | 23.0261 | 42.3696 | |
| Room | 33.6502 | 25.0528 | 37.4442 | 37.9283 | 22.0668 | 42.1284 | |
| Bird | 30.6875 | 24.7570 | 32.3656 | 33.0949 | 21.7068 | 33.6199 | |
| Camera | 30.7358 | 24.6608 | 32.5424 | 32.5958 | 21.9053 | 33.6987 | |
| Starfish | 30.7621 | 24.6617 | 32.8105 | 33.5210 | 20.7648 | 34.0942 | |
| Average | 32.1102 | 25.1435 | 35.1919 | 35.9340 | 22.3429 | 38.1129 |
| Noise Type | Images | RPCA | AMlogtv | NonRPCA | WNNM−RPCA | TDV | Ours |
|---|---|---|---|---|---|---|---|
| Impulse noise | Butterfly | 0.9635 | 0.6670 | 0.9318 | 0.7651 | 0.6336 | 0.9863 |
| House | 0.9455 | 0.6096 | 0.8849 | 0.6157 | 0.7367 | 0.9735 | |
| Peppers | 0.9025 | 0.5965 | 0.8651 | 0.6368 | 0.6742 | 0.9220 | |
| Lena | 0.9514 | 0.5835 | 0.9172 | 0.6705 | 0.6469 | 0.9783 | |
| Room | 0.9694 | 0.5389 | 0.9442 | 0.7807 | 0.4661 | 0.9859 | |
| Bird | 0.9086 | 0.5658 | 0.8395 | 0.6933 | 0.6691 | 0.9280 | |
| Camera | 0.8935 | 0.5237 | 0.8128 | 0.7930 | 0.6357 | 0.9174 | |
| Starfish | 0.9226 | 0.5696 | 0.9301 | 0.8667 | 0.5382 | 0.9403 | |
| Average | 0.9321 | 0.5818 | 0.8907 | 0.7277 | 0.6251 | 0.9539 | |
| Poisson noise | Butterfly | 0.9559 | 0.8563 | 0.9652 | 0.9600 | 0.6689 | 0.9902 |
| House | 0.9255 | 0.8427 | 0.9220 | 0.9104 | 0.7622 | 0.9764 | |
| Peppers | 0.8913 | 0.8196 | 0.8981 | 0.8910 | 0.7094 | 0.9310 | |
| Lena | 0.9366 | 0.7906 | 0.9482 | 0.9420 | 0.6774 | 0.9857 | |
| Room | 0.9578 | 0.6895 | 0.9646 | 0.9597 | 0.4969 | 0.9905 | |
| Bird | 0.8936 | 0.8164 | 0.8997 | 0.8920 | 0.7045 | 0.9410 | |
| Camera | 0.8784 | 0.7814 | 0.8803 | 0.8731 | 0.6741 | 0.9241 | |
| Starfish | 0.9119 | 0.7654 | 0.9086 | 0.9155 | 0.5388 | 0.9324 | |
| Average | 0.9188 | 0.7952 | 0.9233 | 0.6540 | 0.9180 | 0.9589 | |
| Gaussian noise | Butterfly | 0.9581 | 0.8154 | 0.9589 | 0.9684 | 0.7226 | 0.9848 |
| House | 0.9339 | 0.8100 | 0.9256 | 0.9316 | 0.7593 | 0.9706 | |
| Peppers | 0.8933 | 0.7645 | 0.8948 | 0.9107 | 0.7017 | 0.9258 | |
| Lena | 0.9416 | 0.7445 | 0.9437 | 0.9539 | 0.6737 | 0.9795 | |
| Room | 0.9598 | 0.6556 | 0.9618 | 0.9476 | 0.4881 | 0.9851 | |
| Bird | 0.8912 | 0.7688 | 0.8906 | 0.9125 | 0.6947 | 0.9306 | |
| Camera | 0.8812 | 0.7513 | 0.8744 | 0.8705 | 0.6626 | 0.9168 | |
| Starfish | 0.9175 | 0.7217 | 0.9198 | 0.9321 | 0.5382 | 0.9421 | |
| Average | 0.9220 | 0.7539 | 0.9212 | 0.9284 | 0.6551 | 0.9544 |
| Noise Type | Images | RPCA | AMlogtv | NonRPCA | WNNM−RPCA | TDV | Ours |
|---|---|---|---|---|---|---|---|
| Impulse noise | Butterfly | 0.9802 | 0.9860 | 0.9592 | 0.9015 | 0.7521 | 0.9911 |
| House | 0.9751 | 0.9725 | 0.9519 | 0.8593 | 0.7616 | 0.9880 | |
| Peppers | 0.9551 | 0.9436 | 0.9374 | 0.8510 | 0.7726 | 0.9647 | |
| Lena | 0.9768 | 0.9737 | 0.9596 | 0.8735 | 0.7423 | 0.9888 | |
| Room | 0.9827 | 0.9717 | 0.9720 | 0.9307 | 0.5929 | 0.9925 | |
| Bird | 0.9588 | 0.9526 | 0.9333 | 0.8878 | 0.7480 | 0.9666 | |
| Camera | 0.9530 | 0.9579 | 0.9148 | 0.9165 | 0.7002 | 0.9594 | |
| Starfish | 0.9558 | 0.9583 | 0.9638 | 0.9452 | 0.7004 | 0.9676 | |
| Average | 0.9671 | 0.9645 | 0.9490 | 0.8956 | 0.7212 | 0.9773 | |
| Poisson noise | Butterfly | 0.9755 | 0.9848 | 0.9804 | 0.9792 | 0.7675 | 0.9942 |
| House | 0.9667 | 0.9774 | 0.9655 | 0.9611 | 0.7848 | 0.9883 | |
| Peppers | 0.9495 | 0.9415 | 0.9538 | 0.9513 | 0.7925 | 0.9697 | |
| Lena | 0.9694 | 0.9843 | 0.9746 | 0.9718 | 0.7626 | 0.9929 | |
| Room | 0.9782 | 0.9746 | 0.9824 | 0.9806 | 0.6177 | 0.9950 | |
| Bird | 0.9547 | 0.9661 | 0.9576 | 0.9542 | 0.7619 | 0.9709 | |
| Camera | 0.9496 | 0.9578 | 0.9502 | 0.9472 | 0.7118 | 0.9641 | |
| Starfish | 0.9561 | 0.9682 | 0.9541 | 0.9582 | 0.7005 | 0.9690 | |
| Average | 0.9624 | 0.9693 | 0.9648 | 0.9630 | 0.7374 | 0.9805 | |
| Gaussian noise | Butterfly | 0.9744 | 0.9835 | 0.9762 | 0.9807 | 0.8007 | 0.9900 |
| House | 0.9690 | 0.9813 | 0.9664 | 0.9696 | 0.7821 | 0.9865 | |
| Peppers | 0.9499 | 0.9590 | 0.9521 | 0.9586 | 0.7899 | 0.9663 | |
| Lena | 0.9698 | 0.9847 | 0.9712 | 0.9766 | 0.7617 | 0.9890 | |
| Room | 0.9788 | 0.9762 | 0.9800 | 0.9765 | 0.6106 | 0.9919 | |
| Bird | 0.9527 | 0.9558 | 0.9523 | 0.9599 | 0.7583 | 0.9666 | |
| Camera | 0.9452 | 0.9488 | 0.9429 | 0.9419 | 0.7083 | 0.9596 | |
| Starfish | 0.9555 | 0.9592 | 0.9573 | 0.9633 | 0.7004 | 0.9687 | |
| Average | 0.9619 | 0.9685 | 0.9623 | 0.9658 | 0.7390 | 0.9773 |
| Methods | Processing time |
|---|---|
| RPCA | 2.1188 |
| AMlogtv | 1.5780 |
| NonRPCA | 3.6567 |
| WNNM-RPCA | 2.3520 |
| TDV | 3.5570 |
| Ours | 3.4204 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Xiang, Q.; Zhao, D.; Sun, L. An Unsupervised Image Denoising Method Using a Nonconvex Low-Rank Model with TV Regularization. Appl. Sci. 2023, 13, 7184. https://doi.org/10.3390/app13127184
Chen T, Xiang Q, Zhao D, Sun L. An Unsupervised Image Denoising Method Using a Nonconvex Low-Rank Model with TV Regularization. Applied Sciences. 2023; 13(12):7184. https://doi.org/10.3390/app13127184
Chicago/Turabian StyleChen, Tianfei, Qinghua Xiang, Dongliang Zhao, and Lijun Sun. 2023. "An Unsupervised Image Denoising Method Using a Nonconvex Low-Rank Model with TV Regularization" Applied Sciences 13, no. 12: 7184. https://doi.org/10.3390/app13127184
APA StyleChen, T., Xiang, Q., Zhao, D., & Sun, L. (2023). An Unsupervised Image Denoising Method Using a Nonconvex Low-Rank Model with TV Regularization. Applied Sciences, 13(12), 7184. https://doi.org/10.3390/app13127184





