Abstract
With the rapid development of wireless communication technologies, free-space optical (FSO) communication has gained much attention in recent years. The FSO technology, which is usually used for communication in terrestrial environments, is expanding its regime to communication in maritime environments. In this study, we analyze the ergodic capacity of FSO communication between mobile platforms in maritime environments under foggy conditions, pathloss, and pointing error. More specifically, based on the moment expressions, we derive the closed-form expression of asymptotic ergodic capacity using conventional detection techniques (i.e., heterodyne and intensity modulation/direct detection). The derived analytical results are cross-verified with simulation results via Monte Carlo simulations. The results show that the combined effects of fog with pathloss and pointing error degrade the FSO performance and that it is important to apply the appropriate detection technique according to the communication environment.
1. Introduction
Owing to its many attractive advantages [1,2,3], considerable research has already been carried out to apply free-space optical (FSO) communication to terrestrial environments. Recently, research has been conducted with the objective of applying FSO communication to maritime environments [4,5]. However, in the system design of FSO communication for application in maritime environments, various impairments must be considered. First, the performance of FSO links is affected by various weather conditions; among these, fog is considered one of the most serious limiting factors because, in the worst case, a high attenuation of up to 480 dB/km can reduce visibility to several meters [3]. Most of the work carried out in modeling foggy channels over the past decade has assumed that the channel is deterministic [6]. However, a recent study has demonstrated that the fog attenuation effect follows a random behavior following the Gamma distribution [7].
Another possible impairment is the motion of mobile platforms. Unlike the conventional FSO case in terrestrial environments, platforms in maritime environments float over water. Therefore, in maritime environments, mobile platforms should be considered, and communication on mobile platforms leads to degradation factors such as pathloss and pointing error. Pathloss occurs according to a change in the distance between the transmitter (Tx) and receiver (Rx) and can be expressed as visibility that can be measured directly in the atmosphere [8]. With regard to pointing error issues, the rolling, pitching, and yawing motions of the mobile platform in maritime environments lead to pointing error that does not typically arise in FSO communication between fixed platforms [2] and this can lead to considerable performance degradation.
Studies have been conducted on the factors that degrade the performance of FSO communication systems [1,3,9,10,11,12]. In [3], various metrics such as signal-to-noise ratio (SNR), channel capacity, and bit error rate (BER) were used to study the performance under different types of fog conditions. Moreover, in [9,10], the performance analysis considering the combined effects of both atmospheric turbulence and pointing error was conducted using composite statistics (i.e., probability density functions (PDF)). In [9], based on the Beckmann distribution, the generalized pointing error model was studied, and the general asymptotic channel capacity expression was derived under complex impairments caused by both turbulence and generalized pointing error. In [10], the statistical analysis of the channel model considering both weak atmospheric turbulence and pointing error was performed. In [1,11,12], considering the pathloss to be deterministic with propagation length, a performance analysis was undertaken that considered the combined effects of pathloss, atmospheric turbulence, and pointing error based on the composite PDF. In [1], the ergodic capacity performance of widely used detection techniques (i.e., heterodyne detection (HD) and intensity modulation/direct detection (IM/DD)) with nonzero boresight pointing errors under the Lognormal, Rician-lognormal, and Malaga turbulence models was studied. In [11], the authors assumed the pointing error model following the Rician distribution and analyzed the error rate with IM/DD over the Lognormal/Gamma–Gamma fading channels. In [12], BER performance over a strong turbulence channel with the pointing error model of the Rayleigh distribution was investigated.
There are existing research results of some performance analyses that consider three factors: fog, pathloss, and pointing error in terrestrial or maritime environments. However, there were no results analyzing ergodic capacity, which is one of the important performance indicators, while considering the combined effects of all three factors based on the most commonly applied HD or IM/DD-based detection techniques. Therefore, in this context, the performance analysis of asymptotic ergodic capacity is considered based on the above-mentioned three factors in maritime environments based on mobile platforms. We statistically analyze ergodic capacity performance based on our system and channel models. Subsequently, using the moment expressions, we derive the closed-form expression of asymptotic ergodic capacity with both HD and IM/DD.
2. System and Channel Models
As shown in Figure 1, in the FSO communication in maritime environments, both Tx and Rx have the characteristic of being mobile platforms. Because of these characteristics, the pointing error that continues to occur even after beam alignment, especially the effects of jitter, is the major factor affecting performance. As the distance between these mobile platforms is not fixed, its impact is also a major factor affecting performance. Furthermore, in the typical case of applying FSO communication in terrestrial environments, the main consideration is the horizontal link between fixed platforms or the vertical link between fixed mobile platforms, which has been extensively studied recently, whereas, in maritime environments, the horizontal link between mobile platforms is the main consideration. Furthermore, as the occurrence of fog is higher than in terrestrial environments owing to the nature of the ocean, fog acts as the major factor in performance degradation compared to terrestrial environments. Based on these considerations, we assume that the irradiance can be modeled as , where , , and denote the pathloss, foggy channel, and pointing error, respectively, and are random variables discussed below [8], and is deterministic.
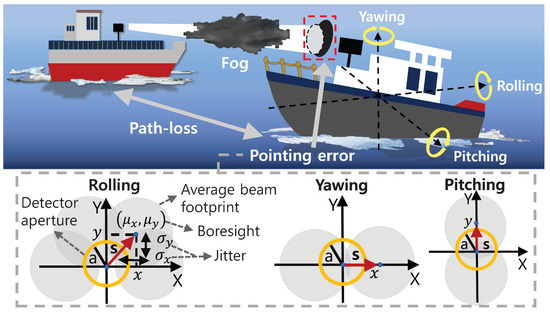
Figure 1.
System and channel models of FSO communication between mobile platforms in maritime environments.
2.1. Foggy Channel
When considering the mobile platform-based fog effect in terrestrial environments, it is difficult to directly apply the foggy channel characteristics studied in [7] because the channel model is based on the form of the vertical or horizontal link. However, as the mobile platform considered in maritime environments has a model in the form of the horizontal link, the statistical characteristics of the foggy channel in [7] can be directly applied. Therefore, in this study, we assume that the random foggy channel follows the Gamma distribution by applying the statistical model of the foggy channel given in [7], and that it has isotropic properties. Based on the relation between the link length and the related signal attenuation (i.e., the Beer–Lambert law) in [7], the state of the foggy channel is given as
where l and represent the length of the propagation link (km) and the related signal attenuation random variable (dB/km), respectively. Based on [7], the PDF of can be written as
where , , is a continuous scale parameter, and is the Gamma function for , which is a continuous shape parameter that defines four types of fog (dense, thick, moderate, and light) according to the visible range in meters (V) [6]. The corresponding values of k and are listed in Table 1.

Table 1.
Parameter values for different types of fog.
2.2. Pathloss
Based on [13], pathloss can be assumed as
where represents the attenuation coefficient. In order to model the attenuation caused by fog, the Kim model is used to predict the attenuation coefficient [14,15]:
where is the wavelength, is the visibility, and q represents the size distribution of the scattering particles.
2.3. Pointing Error
In maritime environments, both Tx and Rx are mobile platforms; therefore, the performance is mainly affected by the pointing error, especially the jitter that continues to occur even after beam alignment. In particular, as shown in Figure 1, the movements of the mobile platform in maritime environments cause pointing errors that can be classified as rolling, yawing, and pitching. Rolling is a movement wherein the left and right sides of the mobile platform swing up and down, respectively, and yawing is a movement wherein the mobile platform swings left and right around the keel point. Pitching is a movement in which the front and rear of the mobile platform swing up and down, respectively. Yawing and pitching cause displacement only in the x or y axes, whereas rolling causes displacement in both the x and y axes. Therefore, the effect of yawing and pitching can be modeled with the single-sided pointing error model, whereas the effect of rolling can be modeled with the double-sided pointing error model [16]. In general, the mobile platform in maritime environments is affected by more than two of the three main factors mentioned above: the pointing error can be modeled using a double-sided error model [16].
Based on [2,16], we assume that the beamwidth of a Gaussian beam is and the aperture radius is a. Then, at distance l, we can approximate the fraction of the collected power as
where, as shown in Figure 1, s is the radial displacement between the centers of the beam and the detector, is the fraction of the collected power at when the ratio between the beamwidth and aperture radius is , and is the equivalent beamwidth, where is the error function. When , the approximation expression of is valid, which is also valid for typical FSO communication systems [2]. Pointing error models can be classified according to boresight and jitter. In this study, the effect of jitter that continues to occur even after beam alignment is considered; in particular, a simple situation in which jitter occurs equally is considered (i.e., zero boresight and identical jitters). Therefore, we assume that our pointing error model follows a Rayleigh distribution [8] and the corresponding PDF of can be expressed as
where is the ratio of the equivalent beam radius at the receiver to the standard deviation of the pointing error displacement at the receiver.
3. Performance Analysis: Ergodic Capacity
Based on [17], we can express the ergodic capacity as
where is the instantaneous SNR and r is for HD and for IM/DD detection techniques commonly used in wireless optical communication systems. The average electrical SNR can be expressed as
Since is deterministic and and are independent random variables, the power of expectation of can be obtained as . With and , derived in the Appendix A, Appendix B, Appendix C, Appendix D, the resulting average electrical SNR can be written as
For , it can be assumed that the pointing error is negligible. Therefore, this can be simplified as
In our case, it is impossible or extremely difficult to obtain the ergodic capacity in a closed-form expression. Therefore, the ergodic capacity can be analyzed using the moment expressions in the following section. Based on [17], asymptotic ergodic capacity can be written as
where, with the definition of the average electrical SNR, the nth moment of in (11) can be obtained using irradiance as [9]
Subsequently, by applying the quotient rule for differentiation, the derivative of (12) can be obtained as given in (13). As a result, after some manipulation, we can obtain asymptotic ergodic capacity in a closed-form expression, as given in (14).
where, as derived in the Appendix A, Appendix B, Appendix C and Appendix D,
| Power of expectation | ||
| nth moment | ||
| Derivative of power of expectation | ||
| Derivative of nth moment |
For , the power of the expectation of and the nth moment of changes as , , respectively. Therefore, (14) can be rewritten as
4. Numerical Results
In this section, selected results for the ergodic capacity of FSO communication between mobile platforms under varying fog types, pathloss, and pointing errors in maritime environments are presented. To validate our analytical results, the Monte Carlo simulation results were used. In the following figures, the markers and lines represent the asymptotic and simulation results, respectively.
In each figure, the parameters (i.e., , a, , and l) and their corresponding values listed in Table 2 are considered unless otherwise noted. Figure 2, Figure 3 and Figure 4 are under both the HD and IM/DD techniques at , 1 km, and km, respectively. In all figures, the analytical results perfectly match the simulation results. In addition, as increases, the asymptotic results approach exact results. Even if the results do not match perfectly, they are useful as upper bounds. However, in some results (i.e., dense fog type, high pointing error, or a bad case), we can observe a large difference in ergodic capacity between the asymptotic results and the exact results at a low SNR. Here, the bad case considers both the dense fog type and high pointing error. Typical FSO communication systems operate over a wide range, especially in the high SNR range, compared to RF-based systems [18]. Therefore, the high SNR regime has a more important meaning, so we should focus on convergence to the exact results at a high SNR. Figure 2 shows the impact of varying fog types (i.e., dense, light) on the ergodic capacity with fixed values of pathloss (i.e., in dense, in light) and pointing error (i.e., ). Expectedly, as fog density increased, ergodic capacity performance decreased.

Table 2.
Parameter settings in results.
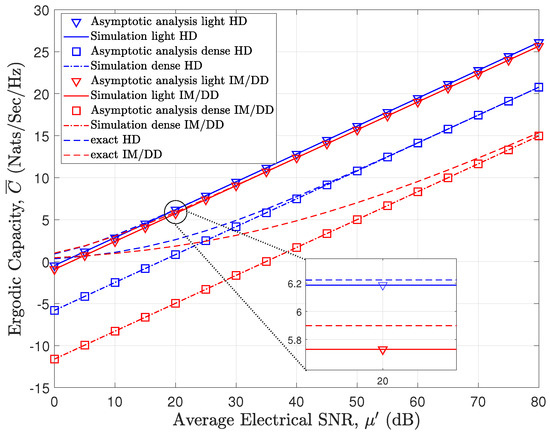
Figure 2.
Ergodic capacity results for varying fog types under both HD and IM/DD techniques with km.
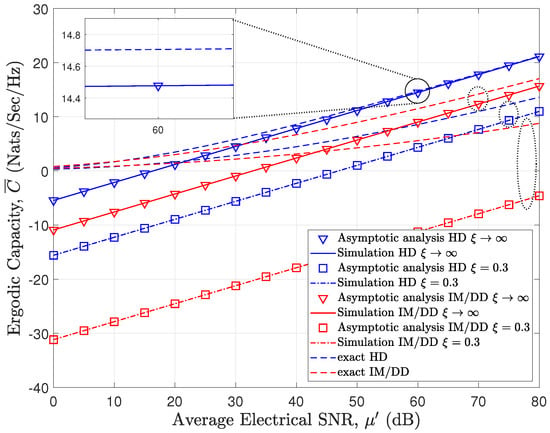
Figure 3.
Ergodic capacity results for varying pointing errors under both HD and IM/DD techniques with km.
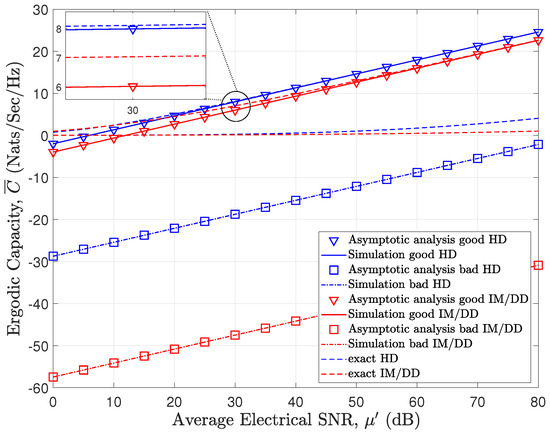
Figure 4.
Ergodic capacity results for combined effects of foggy channel with pathloss and pointing error under both HD and IM/DD techniques with km.
Figure 3 shows the impact of varying pointing errors (i.e., ) on the ergodic capacity with fixed values of pathloss (i.e., ) and moderate fog type (i.e., and ). Expectedly, the more severe the impact of the pointing error, the worse the performance (i.e., the lower , the lower the ergodic capacity performance).
Figure 4 presents the impact of the bad case and the good case of the combined foggy channel and pointing error with fixed pathloss value on the ergodic capacity performance. The bad case considers both the dense fog type and high pointing error (i.e., , , and ) with , but the good case considers both the light fog type and no pointing error (i.e., , , and ) with . Expectedly, the good case results in a better ergodic capacity performance than the bad case.
As the pathloss is the value determined by the visibility related to fog, the effect of varying the pathloss is not seen separately in the graph. As seen in all figures, the HD technique provides better ergodic capacity performance than the IM/DD technique. This is because the HD technique applies two-dimensional modulation in terms of phase and amplitude, whereas the IM/DD technique is limited to one dimension in terms of intensity; therefore, the IM/DD technique requires a higher SNR than the HD technique to achieve the same rate performance [19]. In good communication environments (i.e., light fog type, no pointing error, or good case), the difference in ergodic capacity performance between the HD and IM/DD techniques is small, whereas in bad communication environments (i.e., dense fog type, high pointing error, or bad case), the difference in ergodic capacity performance between the HD and IM/DD techniques is large. Therefore, owing to the characteristics of the HD and IM/DD techniques [19], applying the IM/DD technique in normal environments is more appropriate. When communication environments deteriorate, it is more appropriate to apply the HD technique to achieve a high system capacity performance. Note that we can consider ergodic capacity (in bits/sec/Hz, which is the universal unit), by multiplying in our derived results.
5. Conclusions
In this study, we analyzed the performance of the ergodic capacity of FSO communication between mobile platforms, particularly under foggy channel, pathloss, and pointing error conditions in maritime environments. In particular, among the pointing errors, jitter was considered. In the case of foggy conditions, the beam is diffused by scattering while passing through the foggy channel [20]. Moreover, even if the maritime FSO communication system was initially aligned without boresight error by various tracking methods, this boresight error may still occur due to various factors (e.g., thermal expansion of the ship, maritime environmental factors, etc.). In this case, the performance will vary greatly due to the complex effects of the beam spread by foggy conditions and jitter.
More specifically, looking at the result of zero boresight error in Figure 5, it can be seen that the performance is better when there is no jitter. This is because jitter makes the transmitted beam from the transmitter more likely to deviate from the receiver’s photodetector (PD) [21]. On the other hand, when the boresight error is not zero, and there is a jitter, the diffused beam due to fog is more likely to be affected by the jitter, which can lead to an increase in the probability of detecting the beam in the photodetector (PD). As a result, there may be cases where the performance of the system is improved compared to the case without jitter. This can happen because the combined effects of jitter and diffuse beams can increase the detection probability at the PD, which can compensate for the reduced signal detection probability due to boresight errors. However, this improvement is not always guaranteed and depends on various factors such as the amount of jitter, the size of the beam, and the characteristics of the fog. On the other hand, when (i.e., when the beam deviates relatively less from the center of the PD), it can be seen that the performance is reversed when the SNR increases in the above environments. This is because beam spread is relatively reduced with an increase in SNR, and as a result, the complex effects caused by beam spread and jitter which have a positive effect on performance are reduced. Through these results, it can be confirmed that the effect of jitter on performance is relatively important in foggy conditions, so the effect of jitter is mainly considered in this paper.
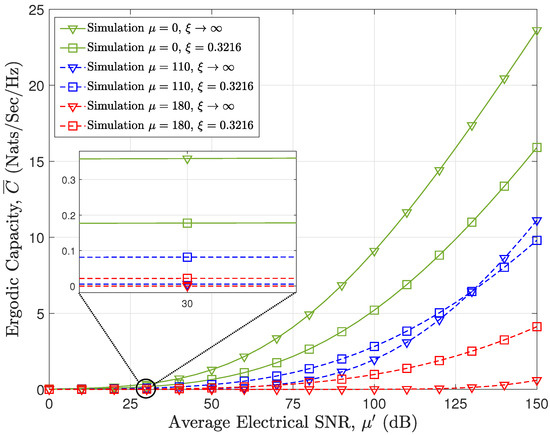
Figure 5.
Ergodic capacity results for varying both boresight (i.e., ) and jitter (i.e., ) with dense fog and under HD technique with km.
Based on the moment expressions, we derived the closed-form expression of asymptotic ergodic capacity for both conventional detection techniques (i.e., HD and IM/DD techniques). Subsequently, our derived analytical results were cross-verified with the simulation results via Monte Carlo simulations. Based on some selected results, we can confirm that the combined effects of the foggy channel with pathloss and pointing error degrade FSO performance, especially under dense fog type and high pointing error conditions. In addition, the results show the numerical difference between HD and IM/DD techniques and can thus help determine the appropriate detection technique.
Author Contributions
Validation, D.D.H.; Formal analysis, J.E.H.; Investigation, S.S.N.; Supervision, M.-S.A.; Funding acquisition, C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Research Foundation of Korea (NRF) grant funded by the Korean government (NRF-2021R1F1A1047271) and by the Gachon University research fund of 2021 (GCU-202110170001) and in part by IITP grant funded by the Korean government (MSIT, MOIS, MOLIT, MOTIE) (No. 2020-0-00061).
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Funding statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| Notation | Definition |
| FSO | Free-space optical |
| Tx | Transmitter |
| Rx | Receiver |
| SNR | Signal-to-noise ratio |
| BER | Bit error rate |
| Probability density function | |
| HD | Heterodyne detection |
| IM/DD | Intensity modulation/direct detection |
| PD | Photo-detector |
| Parameters | Definition |
| pathloss | |
| foggy channel | |
| pointing error | |
| l | the length of the propagation link (km) |
| signal attenuation random variable (dB/km) | |
| continuous scale parameter | |
| Gamma function | |
| k | continuous shape parameter of fog |
| V | visibility |
| wavelength | |
| q | size distribution of the scattering particles |
| beamwidth of a Gaussian beam | |
| a | aperture radius |
| s | the radial displacement between the centers of the beam and the detector |
| fraction of the collected power at | |
| v | ratio between the beamewidth and aperture radius |
| the equivalent beamwidth | |
| error function | |
| raio of the equivalent beam radius at the receiver | |
| standard deviation of the pointing error displacement at the receiver | |
| ergodic capacity | |
| instantaneous SNR | |
| average electrical SNR |
Appendix A. Derivative of Expectation of Ia
The power of expectation of is given as
Subsequently, utilizing ([23], Eq. (01.02.20.0003.01)), the first derivative of (A3) can be expressed as
Appendix B. Derivative of Expectation of Ip
The power of expectation of is given as
Subsequently, utilizing ([23], Eq. (01.02.20.0003.01)), the first derivative of (A7) can be expressed as
Appendix C. Derivative of the Moments of Ia
The nth moment of is given by
Subsequently, utilizing ([23], Eq. (01.02.20.0001.01)), the first derivative of the moment given in (A11) can be expressed as
References
- Ansari, I.S.; Alouini, M.S.; Cheng, J. Ergodic Capacity Analysis of Free-Space Optical Links With Nonzero Boresight Pointing Errors. IEEE Trans. Wirel. Commun. 2015, 14, 4248–4264. [Google Scholar] [CrossRef]
- Jung, K.J.; Nam, S.S.; Alouini, M.S.; Ko, Y.C. Unified Finite Series Approximation of FSO Performance Over Strong Turbulence Combined With Various Pointing Error Conditions. IEEE Trans. Commun. 2020, 68, 6413–6425. [Google Scholar] [CrossRef]
- Esmail, M.A.; Fathallah, H.; Alouini, M.S. Analysis of fog effects on terrestrial Free Space optical communication links. In Proceedings of the 2016 IEEE International Conference on Communications Workshops (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 151–156. [Google Scholar]
- Trichili, A.; Cox, M.A.; Ooi, B.S.; Alouini, M.S. Roadmap to free space optics. J. Opt. Soc. Am. B 2020, 37, A184–A201. [Google Scholar] [CrossRef]
- Alqurashi, F.S.; Trichili, A.; Saeed, N.; Ooi, B.S.; Alouini, M.S. Maritime Communications: A Survey on Enabling Technologies, Opportunities, and Challenges. IEEE Internet Things J. 2023, 10, 3525–3547. [Google Scholar] [CrossRef]
- Esmail, M.A.; Fathallah, H.; Alouini, M.S. Outage Probability Analysis of FSO Links Over Foggy Channel. IEEE Photon. J. 2017, 9, 7902312. [Google Scholar] [CrossRef]
- Esmail, M.A.; Fathallah, H.; Alouini, M.S. Channel modeling and performance evaluation of FSO communication systems in fog. In Proceedings of the 2016 23rd International Conference on Telecommunications (ICT), Thessaloniki, Greece, 16–18 May 2016; pp. 1–5. [Google Scholar]
- Farid, A.A.; Hranilovic, S. Outage Capacity Optimization for Free-Space Optical Links With Pointing Errors. J. Lightwave Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- AlQuwaiee, H.; Yang, H.C.; Alouini, M.S. On the Asymptotic Capacity of Dual-Aperture FSO Systems With Generalized Pointing Error Model. IEEE Trans. Wirel. Commun. 2016, 15, 6502–6512. [Google Scholar] [CrossRef]
- Jung, K.J.; Nam, S.S.; Alouini, M.S.; Ko, Y.C. Unified Statistical Channel Model of Ship (or Shore)-to-Ship FSO Communications with Pointing Errors. In Proceedings of the 2019 IEEE Conference on Standards for Communications and Networking (CSCN), Granada, Spain, 28–30 October 2019; pp. 1–4. [Google Scholar]
- Yang, F.; Cheng, J.; Tsiftsis, T.A. Free-Space Optical Communication with Nonzero Boresight Pointing Errors. IEEE Trans. Commun. 2014, 62, 713–725. [Google Scholar] [CrossRef]
- Cao, L.L.; Sheng, M.; Feng, M.; Xie, X.X. BER performance of free-space optical communication in strong turbulence with pointing errors. In Proceedings of the 2012 International Conference on Wireless Communications and Signal Processing (WCSP), Huangshan, China, 25–27 October 2012; pp. 1–5. [Google Scholar]
- Al Naboulsi, M.C.; Sizun, H.; de Fornel, F. Fog attenuation prediction for optical and infrared waves. Opt. Eng. 2004, 43, 319–329. [Google Scholar] [CrossRef]
- Kappala, V.K.; Pradhan, J.; Sahu, M.; Turuk, A.K.; Das, S.K. Performance Analysis of FSO for Different Modulation Techniques under Atmospheric Turbulence with Pointing Errors. In Proceedings of the 2021 2nd International Conference on Range Technology (ICORT), Chandipur, Balasore, India, 5–6 August 2021; pp. 1–5. [Google Scholar]
- Singh, H.; Chechi, D.P. Performance Evaluation of Free Space Optical (FSO) Communication Link: Effects of Rain, Snow and Fog. In Proceedings of the 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; pp. 387–390. [Google Scholar]
- Jung, K.J.; Nam, S.S.; Shin, J.; Ko, Y.C. Unified statistical performance of FSO link due to the combined effect of weak turbulence and generalized pointing error with HD and IM/DD. IEEE J. Commun. Netw. 2020, 22, 476–483. [Google Scholar] [CrossRef]
- Yilmaz, F.; Alouini, M.S. A novel ergodic capacity analysis of diversity combining and multihop transmission systems over generalized composite fading channels. In Proceedings of the 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 4605–4610. [Google Scholar]
- Nam, S.S.; Alouini, M.S.; Zhang, L.; Ko, Y.C. Threshold-Based Multiple Optical Signal Selection Scheme for Free-Space Optical Wavelength Division Multiplexing Systems. J. Opt. Commun. Netw. 2017, 9, 1085–1096. [Google Scholar] [CrossRef]
- Chaaban, A.; Alouini, M.S. Optical intensity modulation direct detection versus heterodyne detection: A high-SNR capacity comparison. In Proceedings of the 2015 5th International Conference on Communications and Networking (COMNET), Tunis, Tunisia, 4–7 November 2015; pp. 1–5. [Google Scholar]
- Anbarasi, K.; Hemanth, C.; Sangeetha, R.G. A review on channel models in free space optical communication systems. Opt. Laser Technol. 2017, 97, 161–171. [Google Scholar] [CrossRef]
- Najafi, M.; Ajam, H.; Jamali, V.; Diamantoulakis, P.D.; Karagiannidis, G.K.; Schober, R. Statistical modeling of the FSO fronthaul channel for UAV-based communications. IEEE Trans. Commun. 2020, 68, 3720–3736. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic: New York, NY, USA, 2007. [Google Scholar]
- Wolfram, I. Research, Mathematica Edition: Version 8.0; Wolfram Research, Inc.: Champaign, IL, USA, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).