Abstract
We present a mode−locked GaSb−based optically pumped semiconductor disk laser operating at 2 µm based on the self−mode−locked mechanism. Using the delay differential equation model, we discuss the influence of cavity length on the stability of self−mode−locking and design a Z−shaped long cavity for self−mode−locking. Employing an aperture and an F−P etalon in the cavity length of ~365 mm, we obtain stable self−mode−locking at a center wavelength of 2034.5 nm, with a pulse duration of 255.48 ps and average output power of 173 mW at a repetition rate of 404 MHz.
1. Introduction
Optical pumped semiconductor disk lasers (SDLs), also known as vertical−external−cavity surface−emitting lasers (VECSELs), are versatile lasers in applications requiring both high power and good beam quality at a variety of wavelengths [1,2,3,4]. Gallium−antmonide (GaSb) material systems can be used to fabricate SDLs that operate at wavelengths of 2~4 μm [5,6,7,8]. High−pulse−energy lasers with a short pulse at the mid−infrared wavelength region have particularly important applications for time−resolved molecular spectroscopy, remote sensing, infrared countermeasures, medical, and optical free−space communications [9,10,11,12,13]. At present, the methods of generating short pulses at mid-infrared wavelengths [14] mainly include Kerr−lens mode−locking (KML), nonlinear polarization rotation (NPR), and intracavity semiconductor saturable absorption mirror (SESAM). GaSb−based materials are more used as SESAMs with ~2 μm wavelength in applications [15,16,17,18]. Studies on mode−locking of GaSb−based disk lasers are relatively sparse [19,20,21]. The main challenge to achieving mode−locking operation in the GaSb−based SDLs is the high quality and reliable epitaxial growth of GaSb−based SDLs and SESAMs wafers. More details of the passively mode−locked GaSb−based SDLs with SESAM can be found in Table 1. Obviously, the lower performance index means that there is still a great possibility of progress in the research of this field.

Table 1.
Passively mode−locked GaSb−based SDLs with SESAM at 2 μm wavelength. τp is the pulse duration. f0 is the pulse repetition rate. λ0 is the center wavelength of the laser. Pout is the average output power.
One intriguing phenomenon that has been observed in near−infrared GaAs−based SDLs is so−called self−mode−locking (SML) [22,23,24,25,26], which forms a stable mode−locked pulse laser output without an intracavity SESAM. The origin of self−mode−locking is conjectured to result from the nonlinear Kerr lens effect from the semiconductor epitaxial structure itself [22]. In this way, the SML SDLs can more easily realize mode−locked pulse operation with simplified system design and broader spectrum coverage. The physical mechanism of SML was described as Kerr lens mode−locking has been widely studied in semiconductor materials such as GaAs and InP [27,28,29,30,31], and soli−state crystal lasers such as Ti: Sapphire [32,33,34,35]. The strong self−focusing of the laser beam combined with either a hard aperture or a soft aperture in Kerr medium is employed to produce a self−amplitude modulation [36]. In addition to mode−locked lasers, devices developed based on this mechanism also include wavelength/frequency division multiplexing [37,38,39], optical frequency comb [40,41,42,43], supercontinuum generation [44,45,46], and so on. However, there are currently no relevant reports on the Kerr effect in GaSb−based gain materials, nor have there been corresponding reports on self−mode−locked GaSb−based lasers.
Inspired by the self−mode−locking effect observed in GaAs−based SDLs [22,23], this paper validated and implemented continuous−wave (CW) mode−locked GaSb−based SDLs employing self−mode−locking. Based on the pulse dynamics simulated by delay differential equations (DDE), we designed a Z−shaped cavity with a long cavity length for SML GaSb−based SDLs. Then, we systematically measured the pulse characteristics of the SML GaSb−based SDLs.
2. Experiment Design and Setup
Self−mode−locked pulses of SDLs are realized by the nonlinear Kerr lens effect of the pump spot, and it has been demonstrated that the nonlinear refractive index n2 is large enough to cause perturbations of the cavity beam profile [47,48,49]. The Kerr lens effect has been explored both experimentally and theoretically in solid−state crystal lasers. In most cases, Haus master equations can explain the pulse dynamics [50]. However, it cannot describe mode−locking in semiconductor lasers satisfactorily because it is based on small changes of gain and losses in laser pulse shape within one round trip. Instead, the delay differential equation (DDE) model is widely used to describe the pulse dynamics in semiconductor lasers [51,52,53].
According to Refs [25,26], the DDE equations can be expressed as:
where A is the laser field amplitude. g and q are saturable gain and loss. γ is the corresponding bandwidth of the spectral filtering element. The gain bandwidth of quantum wells (QWs) is usually about 10 nm, so here we set γ as 200. κ is the linear nonresonant attenuation factor per round−trip pass; in SDLs, κ can be expressed as κ = √(R1R2). Based on our experimental conditions, the reflectivity of the two end mirrors of the cavity R1 = 99.9%, R2 = 95%, and the value of κ is 0.9742. αg and αq are the linewidth enhancement (self−phase modulation) factors; for simplicity, we restrict our numerical analysis to the case in αg = αq = 0. g0 and q0 are the small−signal gain and loss, and also the initial value of g and q. γg and γq are the carrier density relaxation rates in the gain and absorbing sections; here, we set the relaxation time γg−1 and recovery time γq−1 as 10 ns and 10 ps, respectively. s is the ratio of saturation energy of gain and absorber. Referring to the value in Refs. [26,52], we set s as 25. The delay parameter τr is the cavity round trip time. All the time in the calculation was normalized. The traditional way to obtain higher single pulse energy is to reduce the pulse repetition rate and compress the pulse width. The pulse repetition rate is inversely proportional to the cavity length. A longer cavity length means a larger τr, which may have a negative impact on the mode−locked pulse. In the DDE model, the threshold condition can be expressed as g = q − ln(κ). By selecting a pair of q0 = 1.0 and g0 = 2.0, which are low power levels slightly higher than the threshold value, to achieve mode−locked resonance, we can calculate the time−dependent variation trend of A, g, and q under different cavity lengths. Figure 1 and Table 2 show the calculation results when the cavity length was set as 200 mm, 400 mm, 600 mm, and 800 mm, respectively.
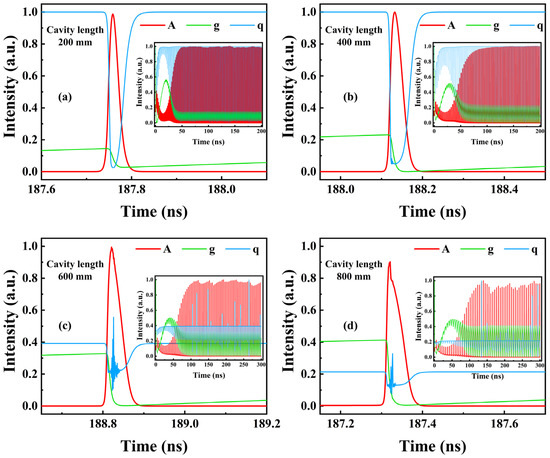
Figure 1.
Simulated pulse train of the SML SDLs with q0 = 1.0 and g0 = 2.0 under different cavity lengths.

Table 2.
Parameters used in the calculation.
As shown in Figure 1, the relative value of loss caused by saturated absorption will decrease with the increase of cavity length and the cavity round−trip time. An unstable jitter occurs after the loss drops to the bottom in a single pulse cycle of the long cavity length. This phenomenon began to appear when the cavity length was 400 mm, but it did not significantly affect the pulse waveform. When the cavity length is extended to 600 mm and 800 mm, a single pulse will be irregularly broadened and the pulse waveform will become irregular too. This instability may be due to the long cavity length increasing the round−trip time τr and approaching the gain relaxation time, and the long cavity length will also increase the loss of the resonator. If we want to offset the loss fluctuation caused by this cavity length, we can only increase g0 by increasing the pump power continuously. However, it is difficult to achieve SDLs in the GaSb which have an obvious upper heat dissipation limit [8]. Therefore, we believe that it is more reliable to select a cavity length of less than 400 mm for verification of self−mode−locking in GaSb−based SDLs.
A Te−doped 2″ (001) GaSb wafer was grown in a VECCO Gen−II solid source molecular beam epitaxy system at ~430 °C for the SDLs chip structure. First, a buffer layer of GaSb was grown on the substrate. A Distributed Bragg Reflector (DBR) comprising 21.5 pairs of GaSb/AlAs0.08Sb0.92 quarter wavelength layers follows. The DBR has a broadband reflectance of ~99.9%, centered at a wavelength of 2 μm. The active regions were grown directly on top of DBRs with resonant periodic gains (RPG) and symmetric structures. Ten In0.2Ga0.8Sb QWs with a thickness of ~10 nm, arranged in five groups of two QWs each, make up the active region. The QWs are separated by 20 nm thick layers of GaSb and equally enclosed by λ/2 GaSb barrier layers. In comparison with Al0.3Ga0.7As0.02Sb0.98, the GaSb barrier layer can provide relatively high thermal conductivity. In addition, the pump source with a wavelength of 1470 nm can be used to reduce quantum defects, therefore reducing heat generation and improving laser performance. An Al0.8Ga0.2As0.03Sb0.97 confinement layer was grown on top of the gain region to prevent carrier nonradiative recombination. The surface was protected from oxidation with a thin GaSb cap layer. We cleaved the chip into 3 × 3 mm2 pieces, which were then liquid−capillary−bonded [54] to an uncoated 400 μm thick 6H−SiC intracavity heat spreader of 5 × 5 mm2 dimensions. The SDLs chip package was then mounted on a copper heat sink cooled by Peltier elements. The heat sink temperature was controlled at 10 ± 1 °C.
The gain chip was set up in a Z−shaped laser resonator, as shown in Figure 2a. The cavity was formed by the DBR, curved high−reflectivity mirror M1 with a radius of curvature r = 200 mm, plane high−reflectivity mirror M2, and output coupler M3 with a reflectivity R = 95% at 2 μm wavelength. The pump laser we used was a DILAS M1F4S22 with an emission wavelength of 1470 nm. The 400 μm core diameter fiber−coupled pump beam was focused into a spot on the SDLs chip with a diameter of ~400 μm. The incident angle of the pump beam was ~30°. The reflectivity of the incident pump laser was measured to be 48 ± 2% on the SiC–air interface. To make the transmission mode in the cavity close to circular, the folding angle of the Z−shaped cavity should be as small as possible. While ensuring that the resonator is in a steady state, it is also necessary to consider that the spatial positions between mirrors cannot conflict with each other. Here, we set L1 to 110 mm, which is slightly larger than half of the radius curvature of M1. Additionally, the length of L2 was set as 75 mm. For spectral control, an F−P etalon was inserted into the cavity. Based on the configuration of the resonator, we used the transmission matrix to calculate the fundamental transverse mode size in the cavity, as shown in Figure 2c. For the F−P etalon, any position after M2 can be set because the size change of the transmission mode is very small. Here, we set L3 to 70 mm. The mode size on the chip surface was an ellipse close to a circle, with the major axis ωy = 252 μm and the minor axis ωx = 243 μm. The design of this Z−shaped cavity allows us to change the cavity length only by lengthening the L4 arm without moving other components. At this condition, the pump spot diameter was larger than the mode. Therefore, we introduced a variable aperture at the L4 arm to suppress the resonance of higher−order transverse modes [55,56] and assist the self−mode−locking process to initiate. The aperture will not be adjusted to smaller than the size of the fundamental mode, so the mode−locking essentially operates in the soft aperture mode [24,57]. Based on the simulation results in the previous section, we set two groups of experiments as controls. One was a relatively stable cavity with a cavity length of less than 400 mm (L4 = 110 mm and the total length was ~365 mm, as shown in Figure 3), and the other one was a relatively unstable cavity with a cavity length of more than 800 mm (L4 = 645 mm and the total length was ~900 mm). The laser output through the plane output−coupling mirror M3 will incident in a wedged plane beamsplitter with AR coating at 2 μm, as shown in Figure 2a. About 99% of the laser transmission incident into the optical power meter kits. Two beams of weak reflected laser with different angles were used: one beam was coupled into the optical spectrum analyzers, and the other beam incident into the high−speed photodetector connected to the digital oscilloscope.

Figure 2.
(a) Schematic diagram of the Z−shaped self−mode−locked optically pumped GaSb SDLs. (b) Photograph of the self−mode−locked optically pumped GaSb SDLs experiment setup with a Z−shaped cavity. (c) The calculated fundamental transverse mode of the resonator configuration.

Figure 3.
Output pulse train with (a) 365 mm cavity length, 404 MHz repetition rate, (b) 900 mm cavity length, and 166 MHz repetition rate. Insets: the pulse train in a 1 μs time segment. The simulated pulse train of the SML SDLs with a cavity length of (c) 365 mm, (d) 900 mm.
3. Results and Discussion
First, to measure the temporal characteristics of the self−mode−locked pulses, a high−speed 2 µm InGaAs photodetector (EOT, ET−5000, 12.5 GHz, Walnut, CA, USA) combined with a 59 GHz digital storage oscilloscope (Tektronix, DPO75902SX, Beaverton, OR, USA) was used. Figure 3a,b show the typical time trace of our SML GaSb−based SDLs measured at the cavity length of ~365 mm and ~900 mm, respectively. Their average output power is 168 mW. The pulse separation of ~2.47 ns and ~6.03 ns corresponds right to the round−trip time of their cavity length. The pulse train with ~404 MHz and ~166 MHz repetition rate can be calculated. A representative 1 μs long−span pulse train is shown in the insertion of Figure 3a,b. The intensity fluctuation of the mode−locked pulses in Figure 3a is obviously more stable than in Figure 3b. This experimental result is consistent with our previous prediction of the cavity length. Based on the DDE model, we also calculated the pulse train with a 365 mm and a 900 mm cavity length. As shown in Figure 3c,d, the measured pulse repetition frequency is consistent with the calculated result. The smaller error within tolerance may be due to the error in device installation and adjustment. Subsequent experiment results were measured under a relatively stable cavity length of ~365 mm.
The mode−locked pulse duration was also directly measured by the high−speed photodetector and oscilloscope. The pulse duration was ~255.48 ps with a near−Lorentz shape, as shown in Figure 4a. The experimentally measured pulse duration was much larger than our simulation results because we did not consider the nonlinear effects, such as group delay dispersion, in our calculations. A strong nonlinear has been observed in GaSb−based SESAMs which have a similar multi−QW epitaxial structure to GaSb SDLs [58]. Positive intracavity roundtrip group delay dispersion of 2030 nm GaSb SDLs is on the order of 1000 fs2, which has an intense negative impact on the pulse duration and the laser performance [21]. Considering the nonlinear effects introduced by quartz F−P etalon, SiC heat spreader, and GaSb gain chip, it is difficult to accurately simulate the pulse duration of SML GaSb SDLs. The spectral filtering element in the resonant cavity also affects the pulse duration. Further study is required to analyze these in more detail.
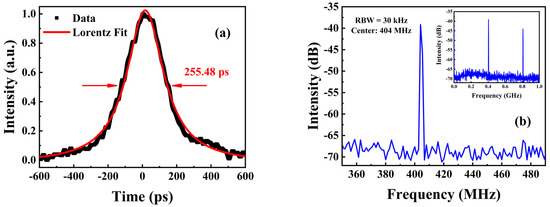
Figure 4.
(a) The pulse duration of a single pulse is directly measured by the high−speed photodetector and oscilloscope. (b) The radio−frequency spectrum of the output pulse train. Resolution bandwidth 30 kHz. Inset, wide−scan RF spectrum.
The radio frequency (RF) spectrum was measured by a mixed−domain oscilloscope with 1 GHz bandwidth (Tektronix, MPO3104, Beaverton, OR, USA). At the repetition rate of ~404 MHz, the RF spectrum shows a clean peak without side peaks, as shown in Figure 4b. This reveals the GaSb SDLs operating in a stable SML mode and a near−fundamental transverse mode. As shown in the insert of Figure 4b, the 1 GHz wide−span RF spectrum measurement indicated the single−pulse operation of the mode−locked GaSb SDLs.
The laser output power characteristics were measured with a power meter (Thorlabs, S425C−L, PM100D, Newton, NJ, USA). Without the aperture and the F−P etalon, the laser operated in CW mode could reach 560 mW with the incident pump power of 10.7 W, as shown in Figure 5a. This value is lower than our previous work [59], mainly because we used a longer cavity and an output coupling mirror with higher transmittance. The laser spectra were measured using a Fourier transform optical spectrum analyzer (Thorlabs, OSA207C, Newton, NJ, USA), as shown in the insert of Figure 5. Without other components in the cavity, the uncoated SiC heat spreader on the chip surface acted as an F−P etalon. The emission spectra have multiple equally spaced peaks simultaneously, which is not conducive to realizing the mode−locking. Self−mode−locking of the GaSb−based SDLs was accomplished by inserting an aperture and an F−P etalon in the cavity. The output power of the SML GaSb SDLs is shown in Figure 5b. The additional etalon filters the spectrum into a single peak with a width of 1.1 nm. At a low output power of ~42 mW, the laser switched immediately to self−mode−locked operation. With the increase of pump power, the emitting wavelength switched from 2031.8 nm to 2034.5 nm, as shown in the insert of Figure 5b. The maximum average output power achieved for the SML GaSb SDLs amounted to 173 mW at an incident pump power of 11.2 W.
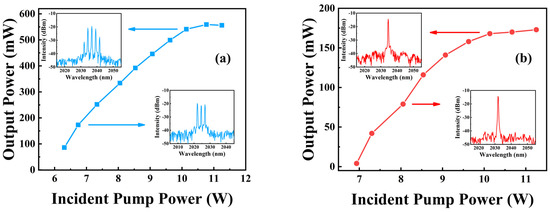
Figure 5.
Output power versus incident pump power of GaSb SDLs operating in (a) CW mode, and (b) self−mode−locking mode. Insets, the lasing spectra for different points.
4. Conclusions
In conclusion, we have presented analytical considerations of self−mode−locking semiconductor disk laser operation in different cavity lengths configuration by the DDE model. For self−mode−locking, the cavity length cannot be increased unboundedly for a low repetition rate. It needs to be configured according to the gain, loss, and thermal limits of the actual device. Furthermore, we demonstrated the self−mode−locked operation of GaSb−based SDLs based on an optimized long cavity length of ~365 mm and obtained stable self−mode−locking at a center wavelength of 2034.5 nm. During mode−locked operation, the pulse duration of GaSb−based SDLs was 255.48 ps with a repetition rate of 404 MHz. The maximum average output power was 173 mW. Further optimization of the epitaxial structure of the SML GaSb−based SDLs and compensation of the intracavity nonlinear dispersions are expected to generate shorter pulses and higher single−pulse energy.
Author Contributions
Conceptualization, J.F.; methodology, J.F., J.S. and X.Z.; software, J.F. and B.M.; validation, J.F.; formal analysis, J.F., B.M. and X.Z.; investigation, J.F. and J.S.; resources, J.S. and Y.Z.; data curation, J.F. and B.M.; writing—original draft preparation, J.F.; writing—review and editing, B.M. and C.T.; visualization, J.F.; supervision, C.T.; project administration, Y.Z. and C.T.; funding acquisition, C.T., Z.N. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. 61790584, 62025506, 62174159, 62061136010), Key R&D Program of Shanxi Province (grant number 202102030201004), and the K.C. Wong Education Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kuznetsov, M.; Hakimi, F.; Sprague, R.; Mooradian, A. Design and characteristics of high−power(>0.5W CW) diode pumped vertical external cavity surface emitting semiconductor lasers with circular TEM00 beams. IEEE J. Sel. Top. Quantum Electron. 1999, 5, 561–573. [Google Scholar] [CrossRef]
- Guina, M.; Rantamaki, A.; Harkonen, A. Optically pumped VECSELs: Review of technology and progress. J. Phys. D Appl. Phys. 2017, 50, 383001. [Google Scholar] [CrossRef]
- Tilma, B.W.; Mangold, M.; Zaugg, C.A.; Link, S.M.; Waldburger, D.; Klenner, A.; Mayer, A.S.; Gini, E.; Golling, M.; Keller, U. Recent advances in ultrafast semiconductor disk lasers. Light Sci. Appl. 2015, 4, e310. [Google Scholar] [CrossRef]
- Calvez, S.; Hastie, J.E.; Guina, M.; Okhotnikov, O.G.; Dawson, M.D. Semiconductor disk lasers for the generation of visible and ultraviolet radiation. Laser Photonics Rev. 2009, 3, 407–434. [Google Scholar] [CrossRef]
- Schulz, N.; Hopkins, J.M.; Rattunde, M.; Burns, D.; Wagner, J. High−brightness long−wavelength semiconductor disk lasers. Laser Photonics Rev. 2008, 2, 160–181. [Google Scholar] [CrossRef]
- Holl, P.; Rattunde, M.; Adler, S.; Bächle, A.; Diwo−Emmer, E.; Aidam, R.; Wagner, J. GaSb−based 2.0 μm SDL with 17 W output power at 20 °C. Electron. Lett. 2016, 52, 1794–1795. [Google Scholar] [CrossRef]
- Shu, S.; Hou, G.; Feng, J.; Wang, L.; Tian, S.; Tong, C.; Wang, L. Progress of optically pumped GaSb based semiconductor disk laser. Opto−Electron. Adv. 2018, 1, 170003. [Google Scholar] [CrossRef]
- Holl, P.; Rattunde, M.; Adler, S.; Kaspar, S.; Bronner, W.; Bachle, A.; Aidam, R.; Wagner, J. Recent Advances in Power Scaling of GaSb−Based Semiconductor Disk Lasers. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 324–335. [Google Scholar] [CrossRef]
- Gaafar, M.A.; Rahimi−Iman, A.; Fedorova, K.A.; Stolz, W.; Rafailov, E.U.; Koch, M. Mode−locked semiconductor disk lasers. Adv. Opt. Photonics 2016, 8, 370–400. [Google Scholar] [CrossRef]
- Price, J.H.V.; Monro, T.M.; Ebendorff−Heidepriem, H.; Poletti, F.; Horak, P.; Finazzi, V.; Leong, J.Y.Y.; Petropoulos, P.; Flanagan, J.C.; Brambilla, G.; et al. Mid−IR Supercontinuum Generation From Nonsilica Microstructured Optical Fibers. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 738–749. [Google Scholar] [CrossRef]
- Targ, R.; Steakley, B.C.; Hawley, J.G.; Ames, L.L.; Forney, P.; Swanson, D.; Stone, R.; Otto, R.G.; Zarifis, V.; Brockman, P.; et al. Coherent lidar airborne wind sensor II: Flight−test results at 2 and 10 μm. Appl. Opt. 1996, 35, 7117–7127. [Google Scholar] [CrossRef]
- Ebrahim−Zadeh, M.; Helmy, A.S.; Leo, G.; Schunemann, P.G. Mid−infrared coherent sources and applications: Introduction. J. Opt. Soc. Am. B 2021, 38, MIC1. [Google Scholar] [CrossRef]
- Gattass, R.R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- Ma, J.; Qin, Z.; Xie, G.; Qian, L.; Tang, D. Review of mid−infrared mode−locked laser sources in the 2.0 μm–3.5 μm spectral region. Appl. Phys. Rev. 2019, 6, 021317. [Google Scholar] [CrossRef]
- Yang, K.; Heinecke, D.; Paajaste, J.; Kolbl, C.; Dekorsy, T.; Suomalainen, S.; Guina, M. Mode−locking of 2 µm Tm,Ho:YAG laser with GaInAs and GaSb−based SESAMs. Opt. Express 2013, 21, 4311–4318. [Google Scholar] [CrossRef]
- Gluth, A.; Wang, Y.; Petrov, V.; Paajaste, J.; Suomalainen, S.; Harkonen, A.; Guina, M.; Steinmeyer, G.; Mateos, X.; Veronesi, S.; et al. GaSb−based SESAM mode−locked Tm:YAG ceramic laser at 2 µm. Opt. Express 2015, 23, 1361–1369. [Google Scholar] [CrossRef]
- Gaponenko, M.; Wittwer, V.J.; Harkonen, A.; Suomalainen, S.; Kuleshov, N.; Guina, M.; Sudmeyer, T. Diode−pumped Tm:KY(WO(4))(2) laser passively modelocked with a GaSb−SESAM. Opt. Express 2017, 25, 25760–25766. [Google Scholar] [CrossRef]
- Tomilov, S.; Wang, Y.; Hoffmann, M.; Heidrich, J.; Golling, M.; Keller, U.; Saraceno, C.J. 50−W average power Ho:YAG SESAM−modelocked thin−disk oscillator at 2.1 µm. Opt. Express 2022, 30, 27662–27673. [Google Scholar] [CrossRef]
- Harkonen, A.; Paajaste, J.; Suomalainen, S.; Alanko, J.P.; Grebing, C.; Koskinen, R.; Steinmeyer, G.; Guina, M. Picosecond passively mode−locked GaSb−based semiconductor disk laser operating at 2 um. Opt. Lett. 2010, 35, 4090–4092. [Google Scholar] [CrossRef]
- Härkönen, A.; Grebing, C.; Paajaste, J.; Koskinen, R.; Alanko, J.P.; Suomalainen, S.; Steinmeyer, G.; Guina, M. Modelocked GaSb disk laser producing 384 fs pulses at 2 µm wavelength. Electron. Lett. 2011, 47, 454–456. [Google Scholar] [CrossRef]
- Heidrich, J.; Gaulke, M.; Golling, M.; Alaydin, B.O.; Barh, A.; Keller, U. 324−fs Pulses From a SESAM Modelocked Backside−Cooled 2−μm VECSEL. IEEE Photonics Technol. Lett. 2022, 34, 337–340. [Google Scholar] [CrossRef]
- Kornaszewski, L.; Maker, G.; Malcolm, G.P.A.; Butkus, M.; Rafailov, E.U.; Hamilton, C.J. SESAM−free mode−locked semiconductor disk laser. Laser Photonics Rev. 2012, 6, L20–L23. [Google Scholar] [CrossRef]
- Gaafar, M.; Richter, P.; Keskin, H.; Möller, C.; Wichmann, M.; Stolz, W.; Rahimi−Iman, A.; Koch, M. Self−mode−locking semiconductor disk laser. Opt. Express 2014, 22, 28390–28399. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, A.R.; Wang, Y.; Ghasemkhani, M.; Seletskiy, D.V.; Cederberg, J.G.; Sheik−Bahae, M. Exploring ultrafast negative Kerr effect for mode−locking vertical external−cavity surface−emitting lasers. Opt. Express 2013, 21, 28801–28808. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Zhu, R.; Wang, T.; Wu, Y.; Tong, C.; Wang, L.; Song, Y. Dynamics Simulation and Experimental Investigation of Q−Switching in a Self−Mode−Locked Semiconductor Disk Laser. IEEE Photonics J. 2022, 14, 1–8. [Google Scholar] [CrossRef]
- Wang, T.; Zhu, R.; Tong, C.; Liu, Y.; Zhang, P. Dynamics Simulation of Self−Mode−Locking in a Semiconductor Disk Laser Using Delay Differential Equations. Photonics 2022, 9, 859. [Google Scholar] [CrossRef]
- Merghem, K.; Akrout, A.; Martinez, A.; Moreau, G.; Tourrenc, J.P.; Lelarge, F.; Van Dijk, F.; Duan, G.H.; Aubin, G.; Ramdane, A. Short pulse generation using a passively mode locked single InGaAsP/InP quantum well laser. Opt. Express 2008, 16, 10675–10683. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wei, W.Q.; Feng, Q.; Wang, T.; Zhang, J.J. InAs/GaAs quantum dot single−section mode−locked lasers on Si (001) with optical self−injection feedback. Opt. Express 2021, 29, 674–683. [Google Scholar] [CrossRef]
- Khan, M.Z.M.; Ng, T.K.; Ooi, B.S. Self−assembled InAs/InP quantum dots and quantum dashes: Material structures and devices. Prog. Quant. Electron. 2014, 38, 237–313. [Google Scholar] [CrossRef]
- Yadav, A.; Chichkov, N.B.; Avrutin, E.A.; Gorodetsky, A.; Rafailov, E.U. Edge emitting mode−locked quantum dot lasers. Prog. Quant. Electron. 2023, 87, 100451. [Google Scholar] [CrossRef]
- Keller, U.; Tropper, A.C. Passively modelocked surface−emitting semiconductor lasers. Phys. Rep. 2006, 429, 67–120. [Google Scholar] [CrossRef]
- Keller, U.; ’tHooft, G.W.; Knox, W.H.; Cunningham, J.E. Femtosecond pulses from a continuously self−starting passively mode−locked Ti:sapphire laser. Opt. Lett. 1991, 16, 1022–1024. [Google Scholar] [CrossRef]
- Salin, F.; Squier, J.; Piché, M. Mode locking of Ti:Al2O3 lasers and self−focusing: A Gaussian approximation. Opt. Lett. 1991, 16, 1674–1676. [Google Scholar] [CrossRef]
- Herrmann, J. Theory of Kerr−lens mode locking: Role of self−focusing and radially varying gain. J. Opt. Soc. Am. B 1994, 11, 498–512. [Google Scholar] [CrossRef]
- Yefet, S.; Pe’er, A. A Review of Cavity Design for Kerr Lens Mode−Locked Solid−State Lasers. Appl. Sci. 2013, 3, 694–724. [Google Scholar] [CrossRef]
- Keller, U.; Weingarten, K.J.; Kartner, F.X.; Kopf, D.; Braun, B.; Jung, I.D.; Fluck, R.; Honninger, C.; Matuschek, N.; Au, J.A.d. Semiconductor saturable absorber mirrors (SESAM’s) for femtosecond to nanosecond pulse generation in solid−state lasers. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 435–453. [Google Scholar] [CrossRef]
- Pankratova, M.; Vasylchenkova, A.; Derevyanko, S.A.; Chichkov, N.B.; Prilepsky, J.E. Signal−Noise Interaction in Optical−Fiber Communication Systems Employing Nonlinear Frequency−Division Multiplexing. Phys. Rev. Appl. 2020, 13, 054021. [Google Scholar] [CrossRef]
- Calò, C.; Vujicic, V.; Watts, R.; Browning, C.; Merghem, K.; Panapakkam, V.; Lelarge, F.; Martinez, A.; Benkelfat, B.E.; Ramdane, A.; et al. Single−section quantum well mode−locked laser for 400 Gb/s SSB−OFDM transmission. Opt. Express 2015, 23, 26442–26449. [Google Scholar] [CrossRef]
- Khan, M.Z.M. Towards InAs/InP Quantum−Dash Laser−Based Ultra−High Capacity Heterogeneous Optical Networks: A Review. IEEE Access 2022, 10, 9960–9988. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef]
- Columbo, L.; Piccardo, M.; Prati, F.; Lugiato, L.A.; Brambilla, M.; Gatti, A.; Silvestri, C.; Gioannini, M.; Opačak, N.; Schwarz, B.; et al. Unifying Frequency Combs in Active and Passive Cavities: Temporal Solitons in Externally Driven Ring Lasers. Phys. Rev. Lett. 2021, 126, 173903. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Chen, J.; Huang, J.; Wang, Z.; Zhang, J.; Wang, T. Advances of semiconductor mode−locked laser for optical frequency comb generation. Natl. Sci. Open 2022, 1, 20220026. [Google Scholar] [CrossRef]
- Chen, J.J.; Wei, W.Q.; Qin, J.L.; Yang, B.; Huang, J.Z.; Wang, Z.H.; Wang, T.; Yu, C.Y.; Zhang, J.J. Multi−wavelength injection locked semiconductor comb laser. Photon. Res. 2022, 10, 1840–1847. [Google Scholar] [CrossRef]
- Rutkauskas, M.; Srivastava, A.; Reid, D.T. Supercontinuum generation in orientation−patterned gallium phosphide. Optica 2020, 7, 172–175. [Google Scholar] [CrossRef]
- Kolesik, M.; Katona, G.; Moloney, J.V.; Wright, E.M. Theory and simulation of supercontinuum generation in transparent bulk media. Appl. Phys. B 2003, 77, 185–195. [Google Scholar] [CrossRef]
- Silva, F.; Austin, D.R.; Thai, A.; Baudisch, M.; Hemmer, M.; Faccio, D.; Couairon, A.; Biegert, J. Multi−octave supercontinuum generation from mid−infrared filamentation in a bulk crystal. Nat. Commun. 2012, 3, 807. [Google Scholar] [CrossRef]
- Quarterman, A.H.; Tyrk, M.A.; Wilcox, K.G. Z−scan measurements of the nonlinear refractive index of a pumped semiconductor disk laser gain medium. Appl. Phys. Lett. 2015, 106, 011105. [Google Scholar] [CrossRef]
- Shaw, E.A.; Quarterman, A.H.; Turnbull, A.P.; Sverre, T.C.; Head, C.R.; Tropper, A.C.; Wilcox, K.G. Nonlinear Lensing in an Unpumped Antiresonant Semiconductor Disk Laser Gain Structure. IEEE Photonics Technol. Lett. 2016, 28, 1395–1398. [Google Scholar] [CrossRef]
- Quarterman, A.H.; Mirkhanov, S.; Smyth, C.J.C.; Wilcox, K.G. Measurements of nonlinear lensing in a semiconductor disk laser gain sample under optical pumping and using a resonant femtosecond probe laser. Appl. Phys. Lett. 2016, 109, 121113. [Google Scholar] [CrossRef]
- Haus, H.A. Mode−locking of lasers. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1173–1185. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Turaev, D.; Kozyreff, G. Delay differential equations for mode−locked semiconductor lasers. Opt. Lett. 2004, 29, 1221–1223. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Turaev, D. Model for passive mode locking in semiconductor lasers. Phys. Rev. A 2005, 72, 033808. [Google Scholar] [CrossRef]
- Schelte, C.; Javaloyes, J.; Gurevich, S.V. Dynamics of temporally localized states in passively mode−locked semiconductor lasers. Phys. Rev. A 2018, 97, 053820. [Google Scholar] [CrossRef]
- Liau, Z.L. Semiconductor wafer bonding via liquid capillarity. Appl. Phys. Lett. 2000, 77, 651–653. [Google Scholar] [CrossRef]
- Tsou, C.H.; Liang, H.C.; Wen, C.P.; Su, K.W.; Huang, K.F.; Chen, Y.F. Exploring the influence of high order transverse modes on the temporal dynamics in an optically pumped mode−locked semiconductor disk laser. Opt. Express 2015, 23, 16339–16347. [Google Scholar] [CrossRef]
- Liang, H.C.; Tsou, C.H.; Lee, Y.C.; Huang, K.F.; Chen, Y.F. Observation of self−mode−locking assisted by high−order transverse modes in optically pumped semiconductor lasers. Laser Phys. Lett. 2014, 11, 105803. [Google Scholar] [CrossRef]
- Gaafar, M.; Möller, C.; Wichmann, M.; Heinen, B.; Kunert, B.; Rahimi Iman, A.; Stolz, W.; Koch, M. Harmonic self−mode−locking of optically pumped semiconductor disc laser. Electron. Lett. 2014, 50, 542–543. [Google Scholar] [CrossRef]
- Koskinen, R.; Suomalainen, S.; Paajaste, J.; Kivistö, S.; Guina, M.; Okhotnikov, O.; Pessa, M. Highly nonlinear GaSb−based saturable absorber mirrors. Proc. SPIE 2009, 7354, 73540G. [Google Scholar] [CrossRef]
- Shang, J.; Feng, J.; Yang, C.; Xie, S.; Zhang, Y.; Tong, C.; Zhang, Y.; Niu, Z. High quality 2−μm GaSb−based optically pumped semiconductor disk laser grown by molecular beam epitaxy*. Chin. Phys. B 2019, 28, 034202. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).