3.1. Tightening Scheme Design Based on the Elastic Interaction Coefficient Method
When a bolt is tightened, the alternating load between the bolt that is tightened later and the bolt that was tightened first is called the elastic interaction. Due to this elastic interaction, different tightening sequences will have different effects on the tightened parts in the process of tightening. In selecting a tightening sequence, the goal is to obtain a uniform final load under the same initial load conditions. The elastic interaction coefficient method (EICM) is used as a benchmark to optimize the bolt tightening sequence of aviation components. The EICM is based on an assumed linear relationship between the load variation of the tightened bolt and the final preload. This relationship can be expressed using an elastic interaction coefficient matrix. Different tightening sequences will result in different elastic interaction matrices. A detailed explanation and solution method for elastic interaction matrix A can be obtained by referring to the literature [
15] and this will not be repeated in this paper.
Based on the EICM method, the relationship between the initial load and the final load of bolts in different sequences is as follows:
where
is the final load,
is the initial load, and
is the elastic interaction matrix. In a system composed of n bolts, Formula (
1) can be expressed as:
where
is the final load of bolt k and
is the initial load of bolt k. Taking the final load of bolt 1 as an example, according to Formula (
2), the final load of bolt 1 can be expressed as:
According to Formula (
3), the final load of any bolt can be calculated under given conditions.
When two bolts are tightened on the aviation component diagonally and at the same time, Formula (
2) can be expressed as follows:
When two bolts are tightened the aviation component apart simultaneously, Formula (
2) can be expressed as follows:
By contrasting Formulas (
2), (
4) and (
5), it can be found that when two bolts are used to tighten the aviation component at the same time, the 0 values in the corresponding elastic interaction coefficient matrix increase, and this means that the effect of elastic interaction during the aviation component tightening process is reduced. The correctness of the scheme is verified in theory.
In matrix A, a bolt that has been tightened has no effect on the bolt that is subsequently tightened. So its coefficient in the matrix is zero. Usually the elastic interaction coefficient in the matrix is negative because the change of load is usually a loss. Under the condition that the tightening sequence is known, the elastic interaction coefficient matrix A can be obtained. When the matrix A is known, the initial load can be solved according to Formula (
6).
3.2. Verification of the Tightening Scheme Based on a Finite Element Simulation Method
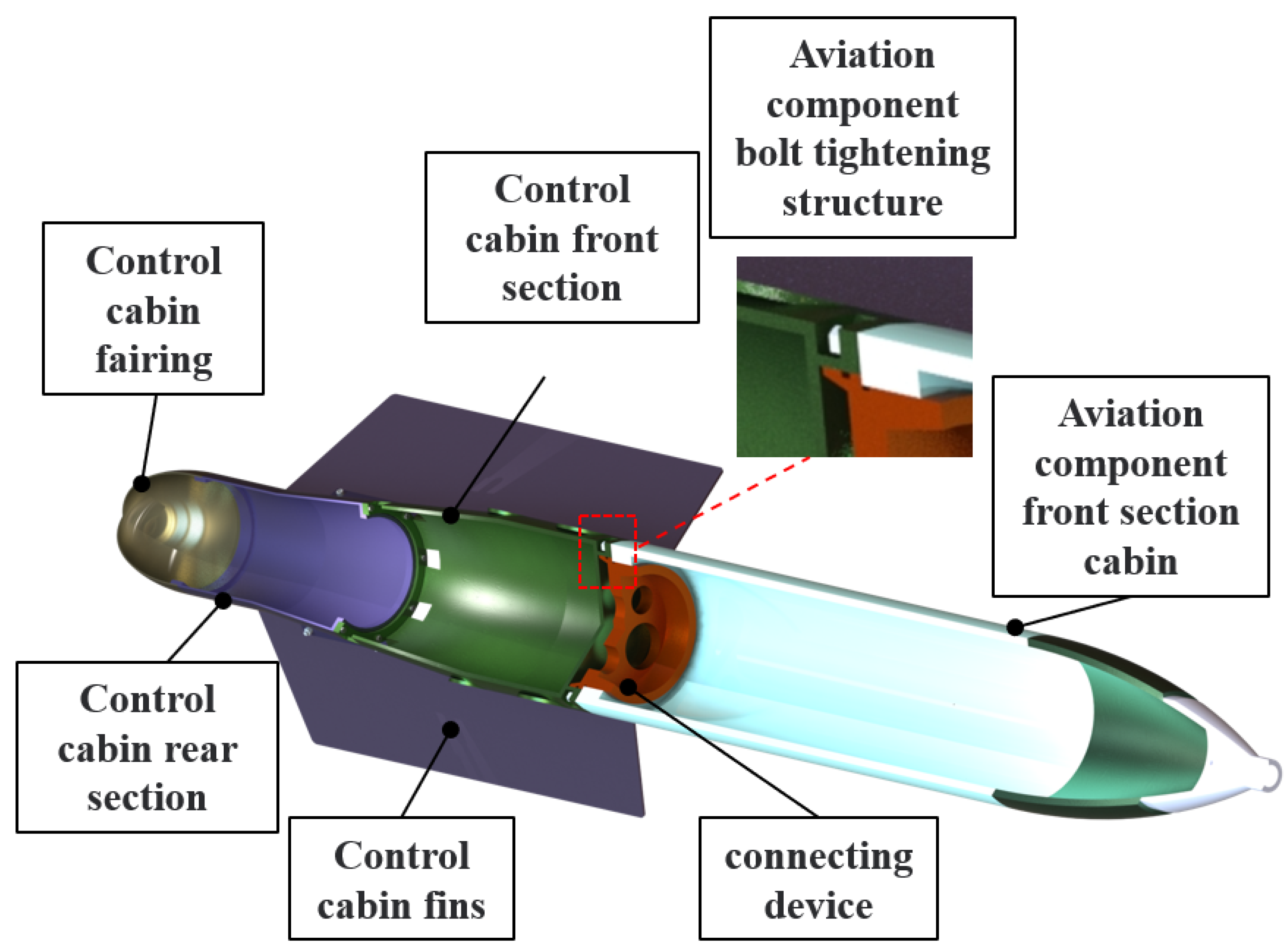
As the aviation component cannot be seamlessly docked during the docking process, there will be a gap between the control cabin front section and the aviation component front section cabin, as shown in
Figure 4. During the process of aviation component bolt tightening, the gap between the control cabin and the aviation component front section cabin will affect the tightening process. Therefore, in the process of bolt tightening and subsequent analysis, the gap between the control cabin front section and the aviation component front section cabin is considered. As described in
Section 2, the gap value is known in the process of building the finite element model and subsequent surrogate model of the aviation component bolt tightening.
A finite element simulation model of the aviation component bolt tightening was constructed with Ansys Workbench. The aviation component material and bolt material were all high strength steel, its Young’s modulus was 209 GPa at room temperature, and the Poisson’s ratio was 0.29. In order to improve the accuracy of the calculation, the mesh on the contact surface was subdivided. Due to of the irregular shape of the aviation component, the main volume of the aviation component was divided into different volumes to apply the hex dominant meshing method. The mesh cell size was set to 4 mm. The grid of the bolt and the screwed surface was refined, and the grid of the fixed support (bottom surface) was roughened. The grid was generated following the above method, the aviation component generated 683,712 nodes and 341,801 cells, as shown in
Figure 5.
In the connection setting of the finite element simulation model, the contact type between the bolts and the aviation component front section cabin was set as“non-separation”. The contact type between the screw and the bolt hole was set as“frictional” contact, and the contact type between the control cabin front section and the aviation component front section cabin was set as“frictional” contact; the friction coefficient was 0.2 (0.2 is the friction coefficient between a rigid body and another rigid body). The Lagrange algorithm was used as the contact formula in advanced settings to improve the calculation accuracy. In order to improve the convergence of calculation, the contact behavior mode was set to symmetrical contact. The small sliding algorithm was used to improve the convergence rate.
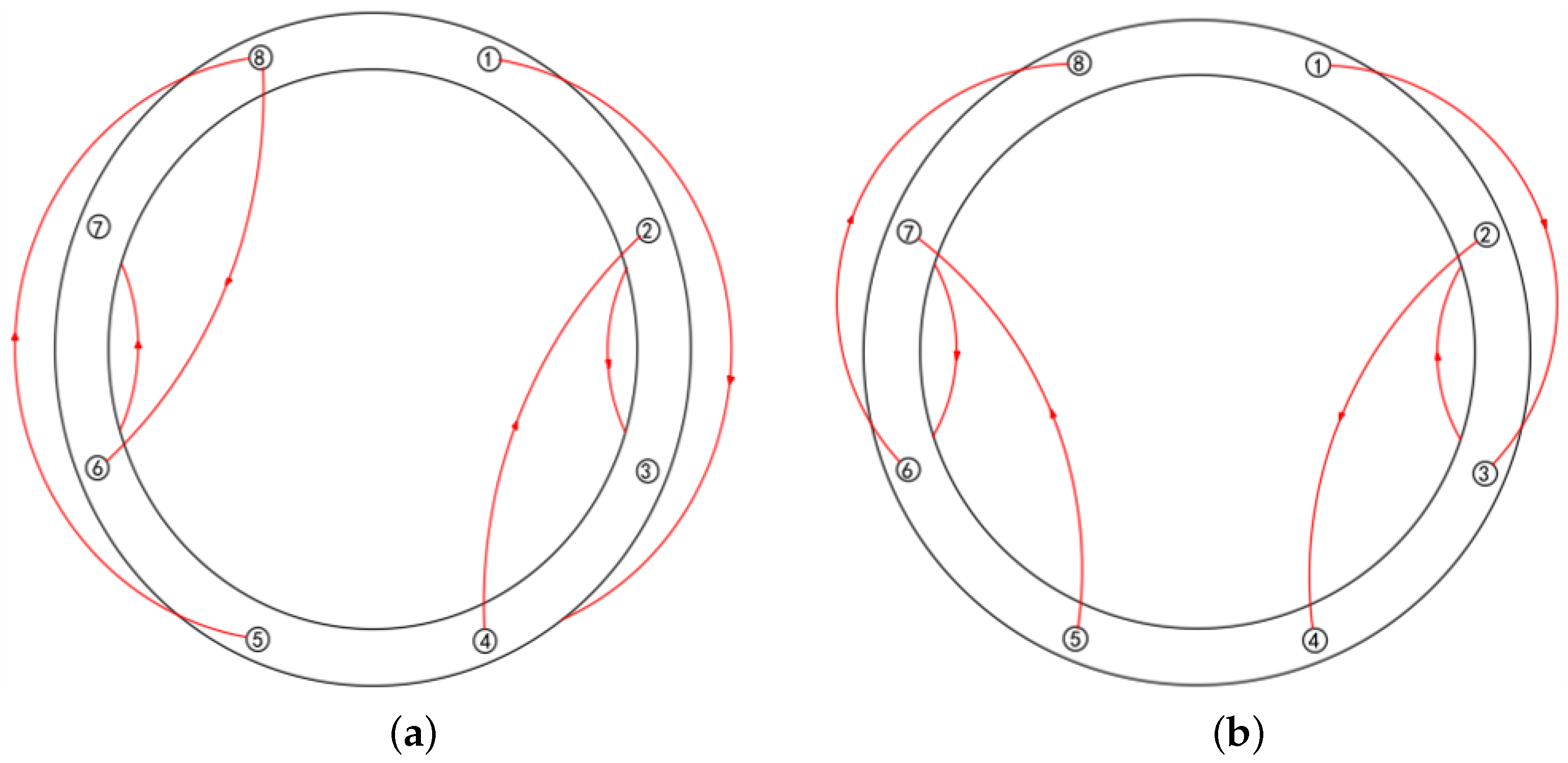
In the case of considering the gap between the control cabin front section and the aviation component front section cabin, tightening the bolts with a small gap first made the bolt tightening face corresponding to the large gap tilt upward. The result was that there was a bigger gap between the control cabin front section and the aviation component front section cabin. This larger gap and the larger deformation of the aviation component would make the bolt tightening more difficult and produce an uneven residual preload of the bolts. Therefore, the bolts located at the larger gap should be tightened first. The bolt at the largest tightening gap was marked as bolt 1. The number of bolts that needed to be tightened between the control cabin front section and the aviation component front section cabin was only eight, and the eight bolts were symmetrically and evenly distributed. After tightening bolt 1, tightening bolt 8 or bolt 2 would have the same effect. Therefore, the following simulation sequence was set in this paper: single-bolt sequence tightening: 1→2→3→4→5→6→7→8; single-bolt interval tightening: 1→3→5→7→2→4→6→8; single bolt interval two-bolt tightening: 1→4→7→2→5→8→3→6; single-bolt diagonal tightening: 1→5→2→6→3→7→4→8.
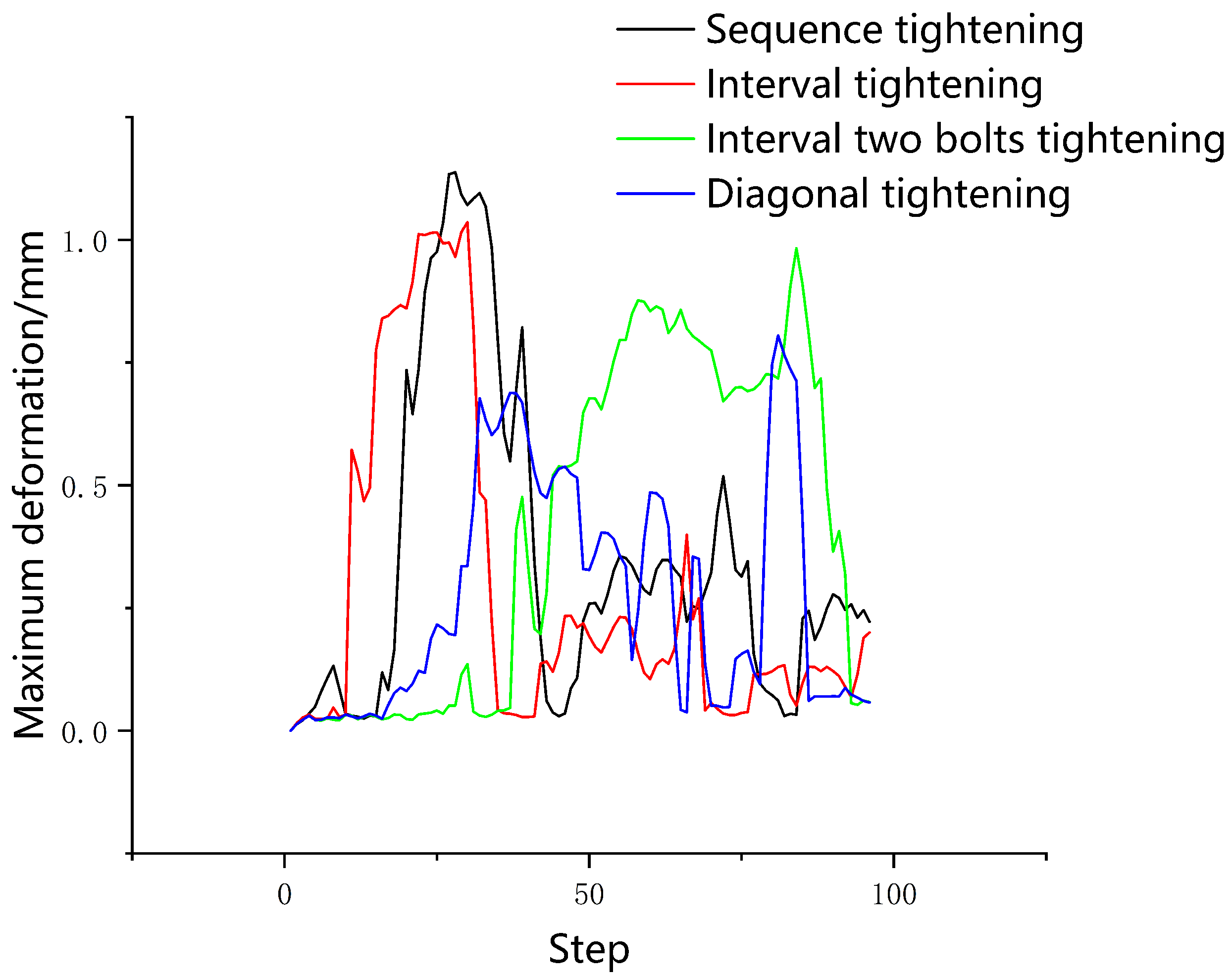
The preload was set to 72 KN and the time step was used to control the bolt tightening sequence. In order to ensure the accuracy of the simulation results without mutation, a total of 96 steps were set. With 96 load steps, every 8 load steps, the bolt stress value reached 72 KN. At step 96, the preload of all bolts was 72 KN. The maximum gap between the aviation component front section cabin and the control cabin was 0.1 mm, and the axis inclination angle was 0.2°. The maximum deformation curve of the aviation component is shown in
Figure 6.
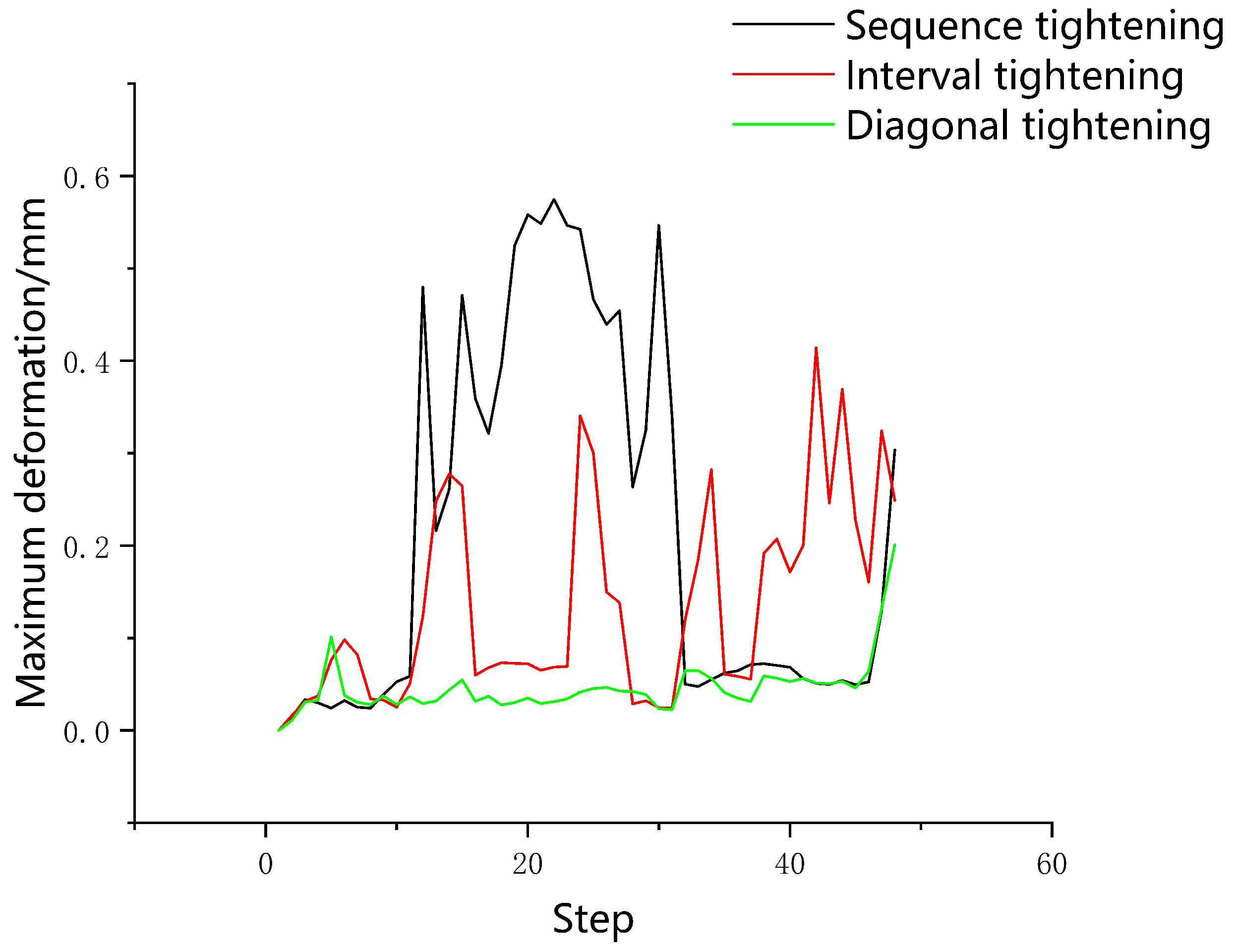
It can be seen from
Figure 6 that the maximum deformation of the aviation component corresponding to sequence tightening and interval tightening exceeded 1 mm. Among the four tightening sequences, the deformation of the aviation component caused by sequence tightening was the largest. The deformation of the aviation component caused by interval two-bolt tightening was close to 1 mm, and the deformation caused by diagonal tightening was the smallest, at about 0.8 mm. Using the above four methods to tighten the aviation component, the maximum deformation reached the peak value many times, and the damage was serious.
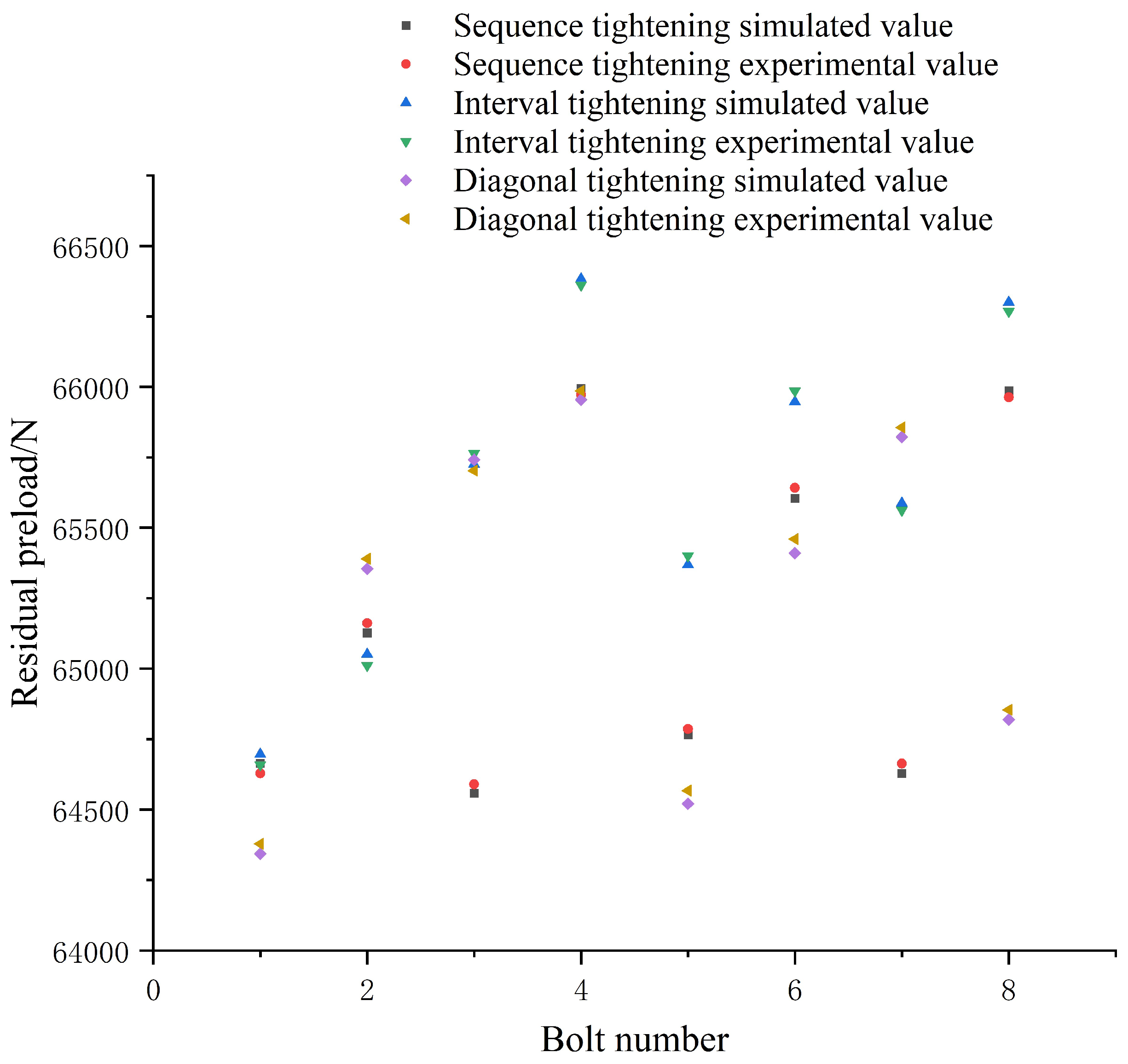
In addition to observing the maximum deformation of the aviation component, the magnitude and uniformity of the residual preload of bolts were also taken as evaluation parameters. We compared the tightening sequences as good or bad based on these two characteristics. In addition to using finite element simulation to measure the bolts’ residual preload, an ultrasonic measuring instrument was used to measure the residual preload of the bolts. The name of the measuring equipment was an electromagnetic ultrasonic double-wave bolt stress instrument, and the equipment model is ST100, as shown in
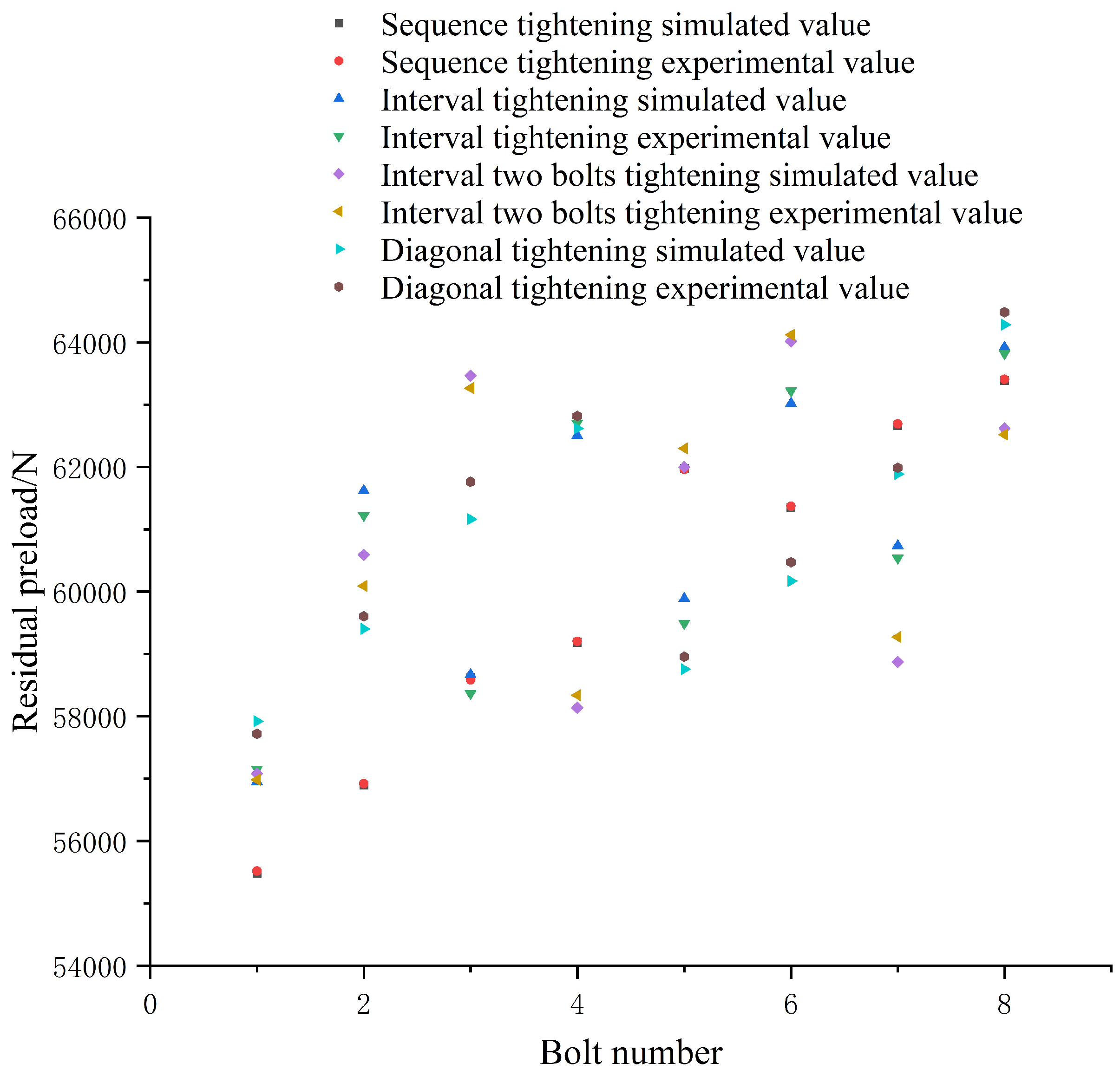
Figure 7. As the temperature affects the speed of the ultrasound, the experiment temperature remained unchanged. The accuracy of the instrument is less than ±3%, which ensured the precision of the experiment. An ultrasonic generator was installed at the bolt end, to measure the time delta between the transmitting and receiving signals of the ultrasonic equipment under the conditions of unscrewed and screwed bolts. The deformation of the bolt during the tightening process was calculated. By multiplying the deformation by the cross-sectional area of the bolt, the elastic modulus of the bolt material, and then dividing by the clamping length of the bolt, the preload of the bolt could be obtained. The residual preload of the bolts in the above four sequences was measured with an ultrasonic measuring instrument and compared with the simulation value under the condition of a 0.1 mm gap. The results are shown in
Figure 8.
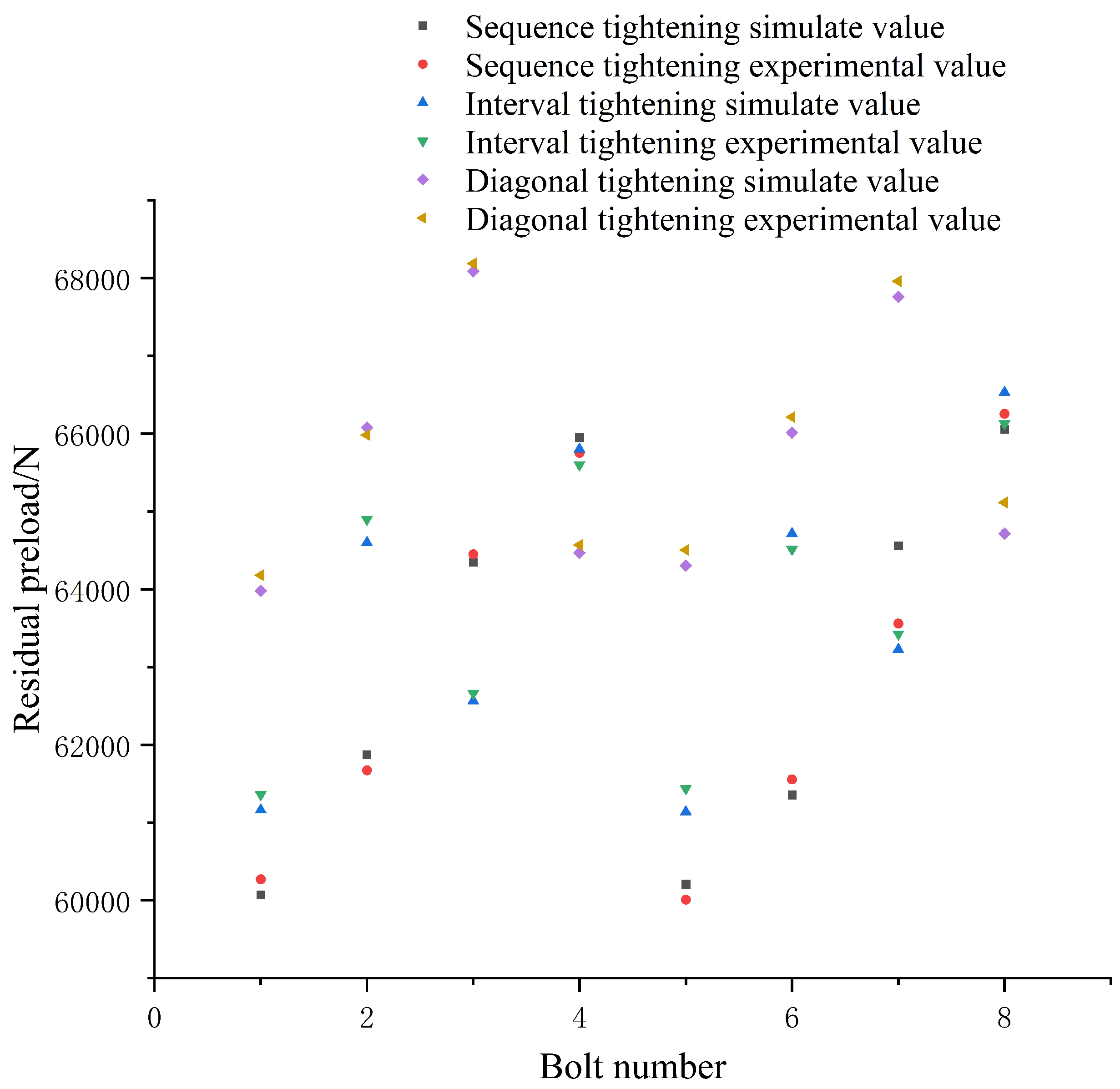
It can be seen from
Figure 8 that the maximum error between the simulation value and the experimental value of the four sequences was less than 45.0, which accounted for 0.75% of the simulation value. This verified the correctness of the simulation results. The average values of the four tightening methods’ residual preload were 59,946 N, 60,915.1 N, 60,847.9 N, and 60,775.5 N, respectively. When we used the interval tightening sequence to tighten the aviation component, the average residual preload value of the aviation component was the largest. The variance was used to judge the average degree of residual preload. The residual preload variance of the sequence tightening was 949.474, which is the lowest average. The residual preload variance of interval tightening was 780.079 and the residual preload variance of interval two-bolt tightening was 862.461. The corresponding variance of the diagonal tightening was 707.967, which was the most uniform. It can be seen that the average degree of unevenness of the diagonal tightening was still large, so the tightening sequence needed to be optimized.According to the optimization scheme proposed above, the optimization was carried out by tightening two bolts simultaneously.
The new method was to use two bolts to tighten the aviation component at the same time, and two diagonal bolts were chosen as a group. The preload was still set to 72 KN, and 48 steps were set. The following simulation sequences were constructed: two-bolt sequence tightening: 1,5→2,6→3,7→4,8; two-bolt interval tightening: 1,5→3,7→2,6→4,8; two-bolt diagonal tightening: 1,5→4,8→2,6→3,7. The maximum deformation of the aviation component in the above three sequences is shown in
Figure 9.
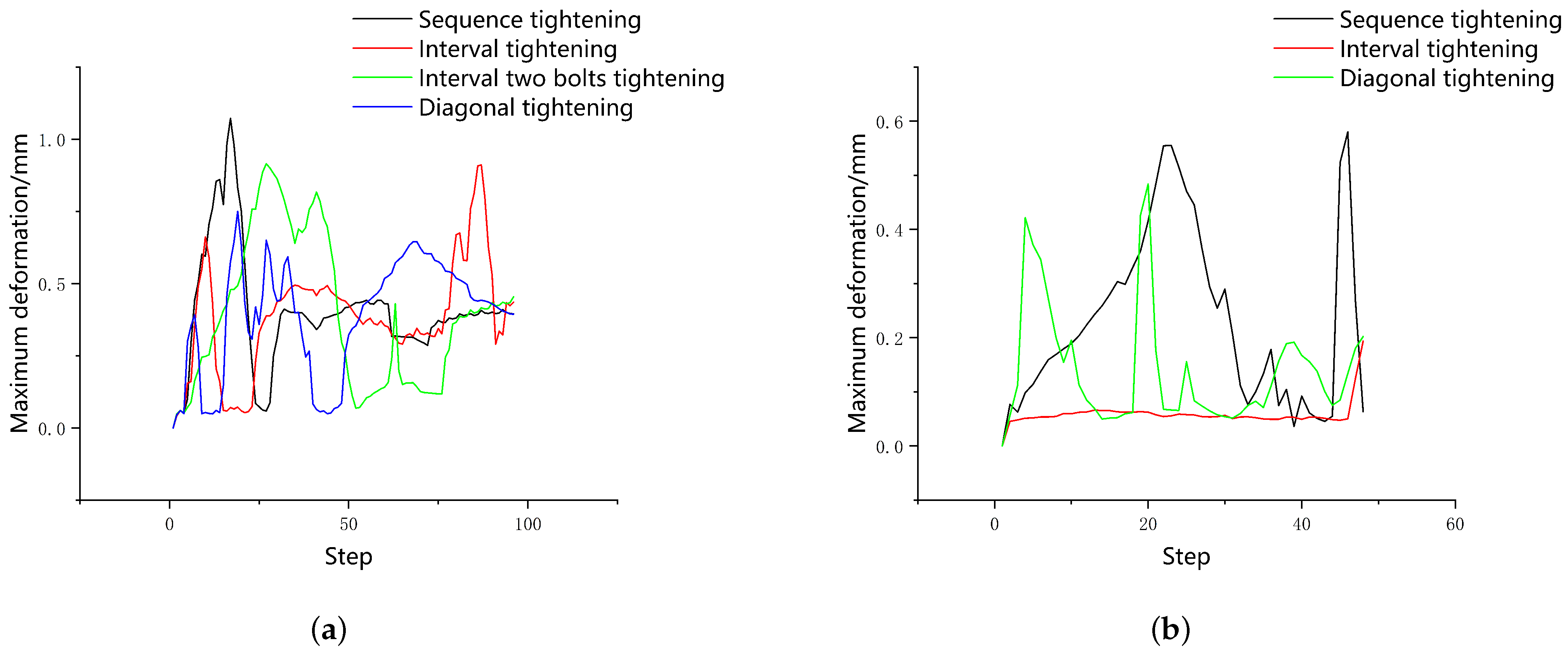
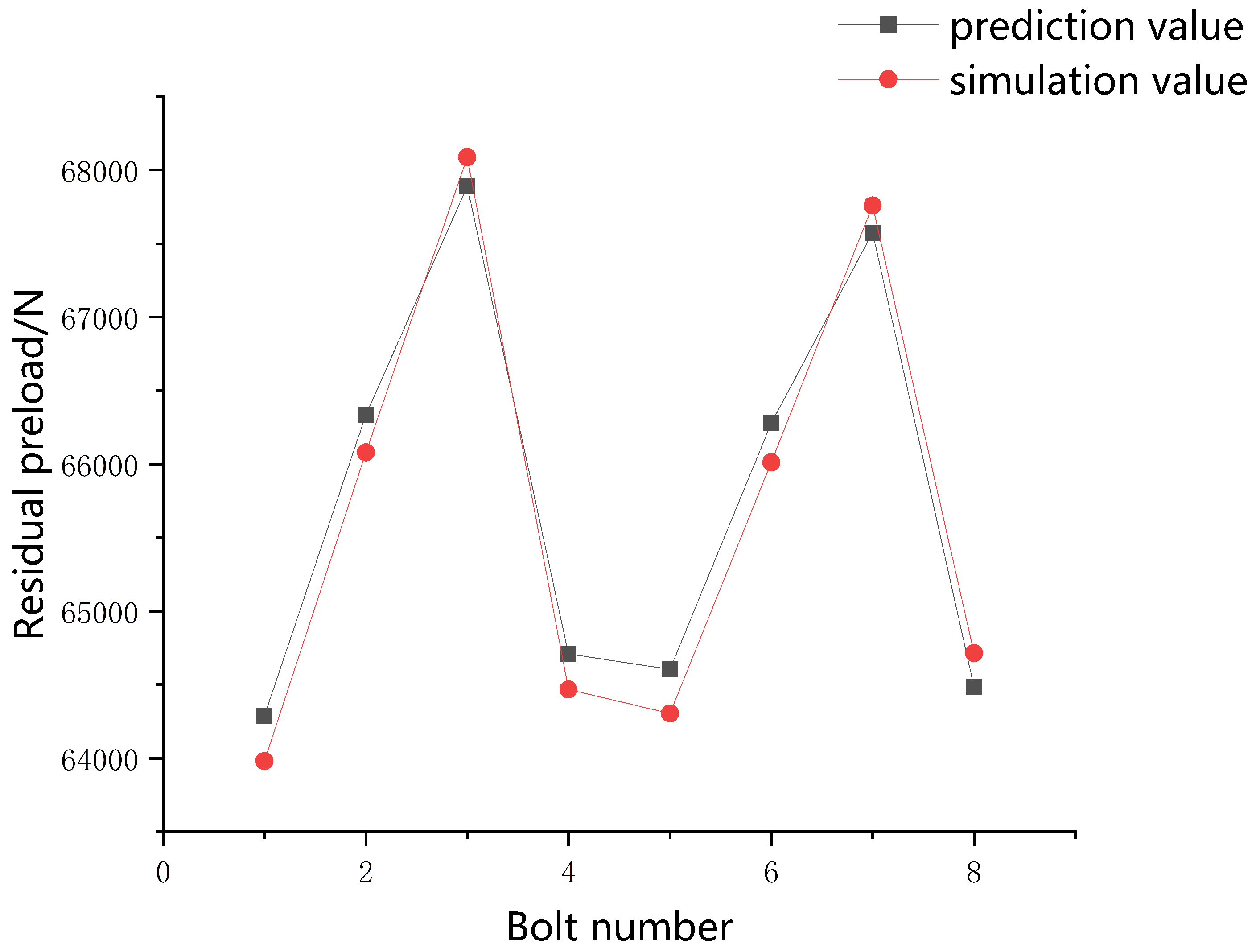
It can be seen from
Figure 9 that the deformation caused by the two-bolt sequence tightening was close to 0.6 mm. The maximum deformation caused by two-bolt interval tightening exceeded 0.4 mm, and the deformation reached the peak value many times during the tightening process. The deformation caused by the two-bolt diagonal tightening was about 0.2 mm, and the deformation curve was smooth, with no sudden changes during the tightening process. The simulation and experimental values of the residual preload of the bolts are shown in
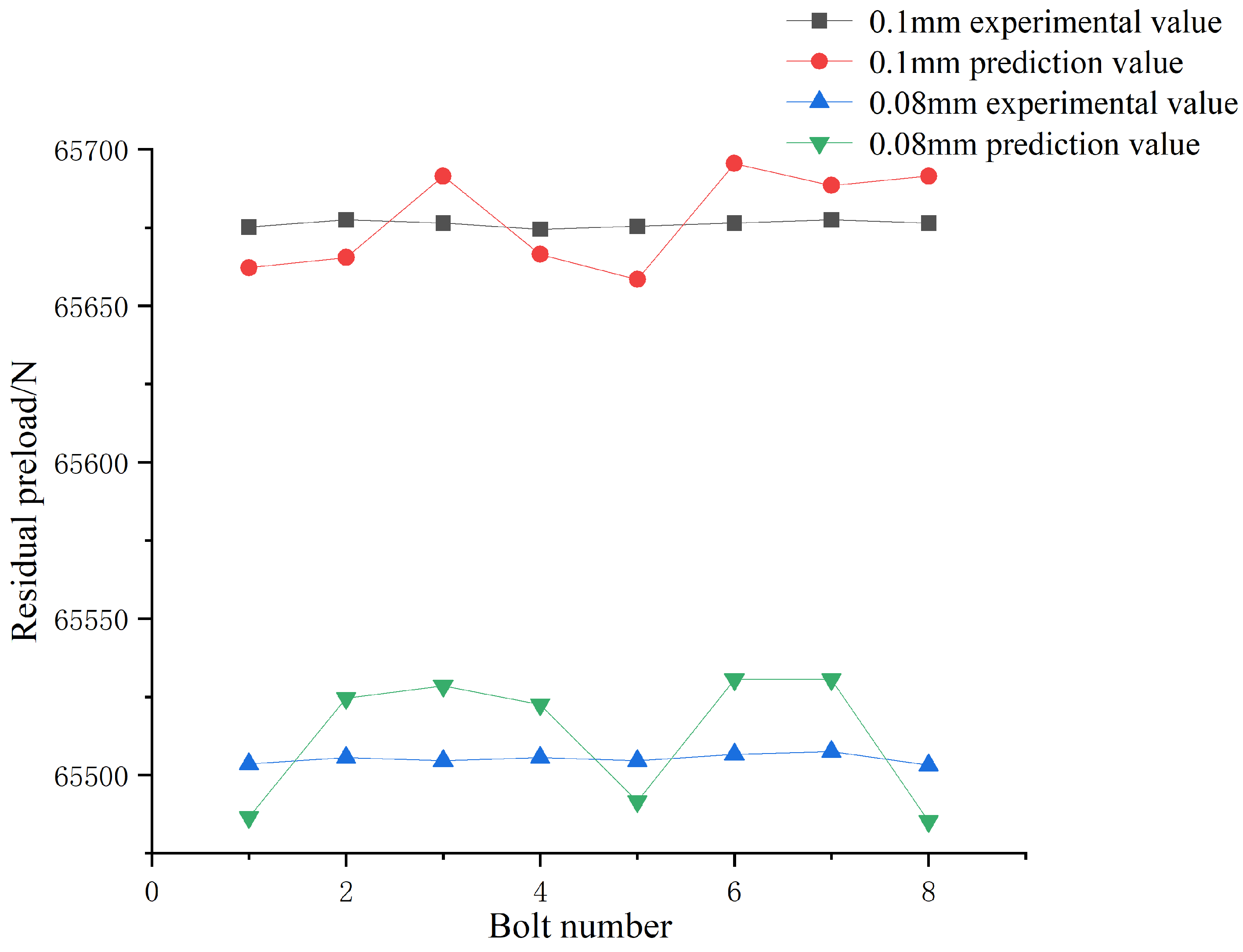
Figure 10.
It can be seen from
Figure 10 that the average value of the residual preload and uniformity of two-bolt tightening were improved compared with single-bolt tightening. The average values of the residual preload of the three sequences were 63,053 N, 63,716 N, and 65,676 N, respectively. The two-bolt diagonal tightening had the highest degree of uniformity, its variance was 478.2. In addition, the average value of two-bolt diagonal tightening of the aviation component was the highest. By comparing all the above sequences, it can be concluded that when the maximum gap was 0.1 mm and the axis inclination angle was 0.2°, two-bolt diagonal tightening was the best tightening sequence for the aviation component.
When the maximum gap between the front section cabin and the control cabin was 0.08 mm, and the axis inclination angle was 0.15°, the maximum deformation curve of the aviation component was as shown in
Figure 11.
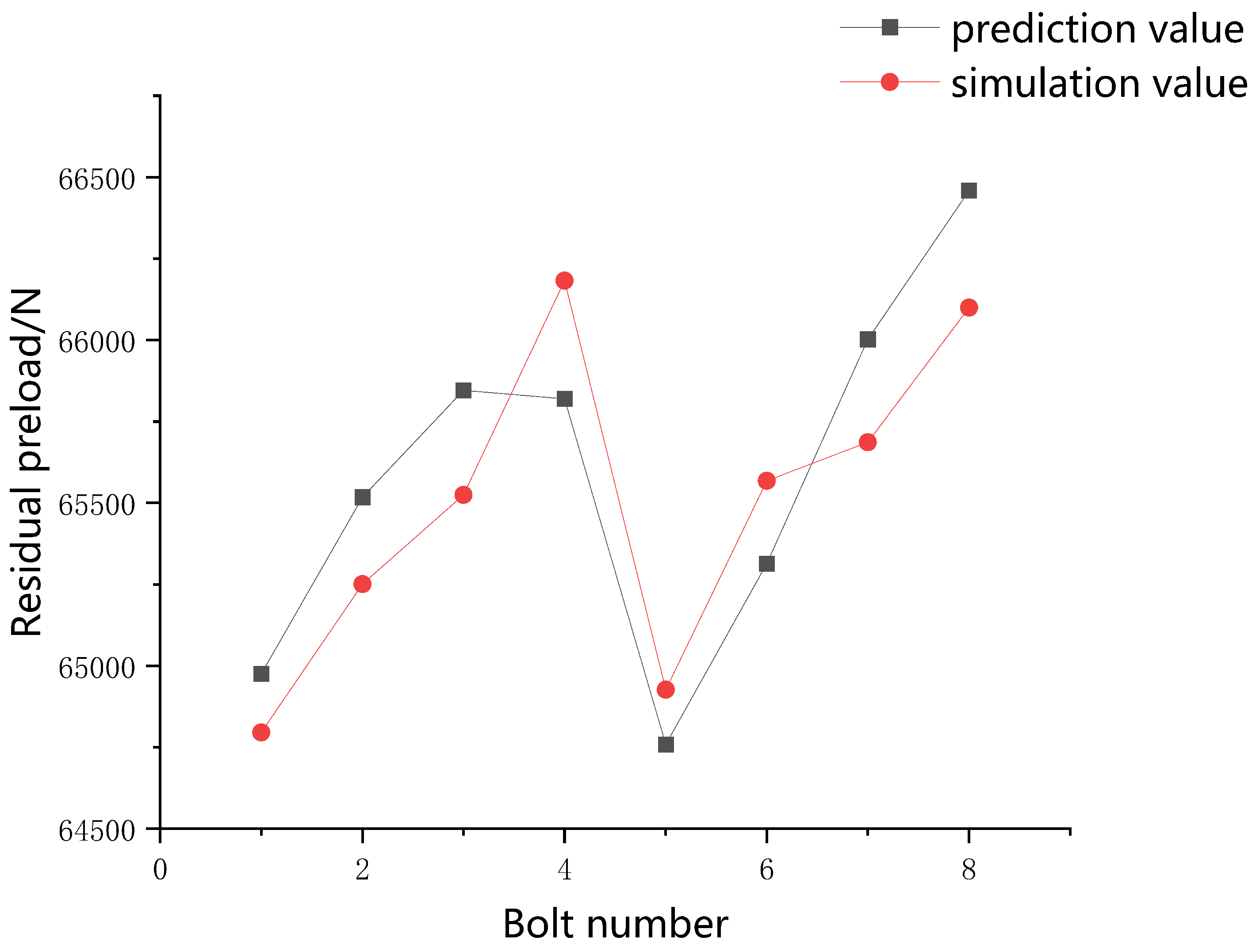
It can be seen from
Figure 11 that the maximum deformation of two-bolt tightening was generally lower than that of single-bolt tightening, which verified the correctness of the sequence selection. In the three sequences of two-bolt tightening at the same time, the maximum deformation caused by the two-bolt interval tightening was the smallest, and the deformation curve was the smoothest. The simulation value and experimental value of the residual preload corresponding to the above tightening method are shown in the following
Figure 12 and
Figure 13:
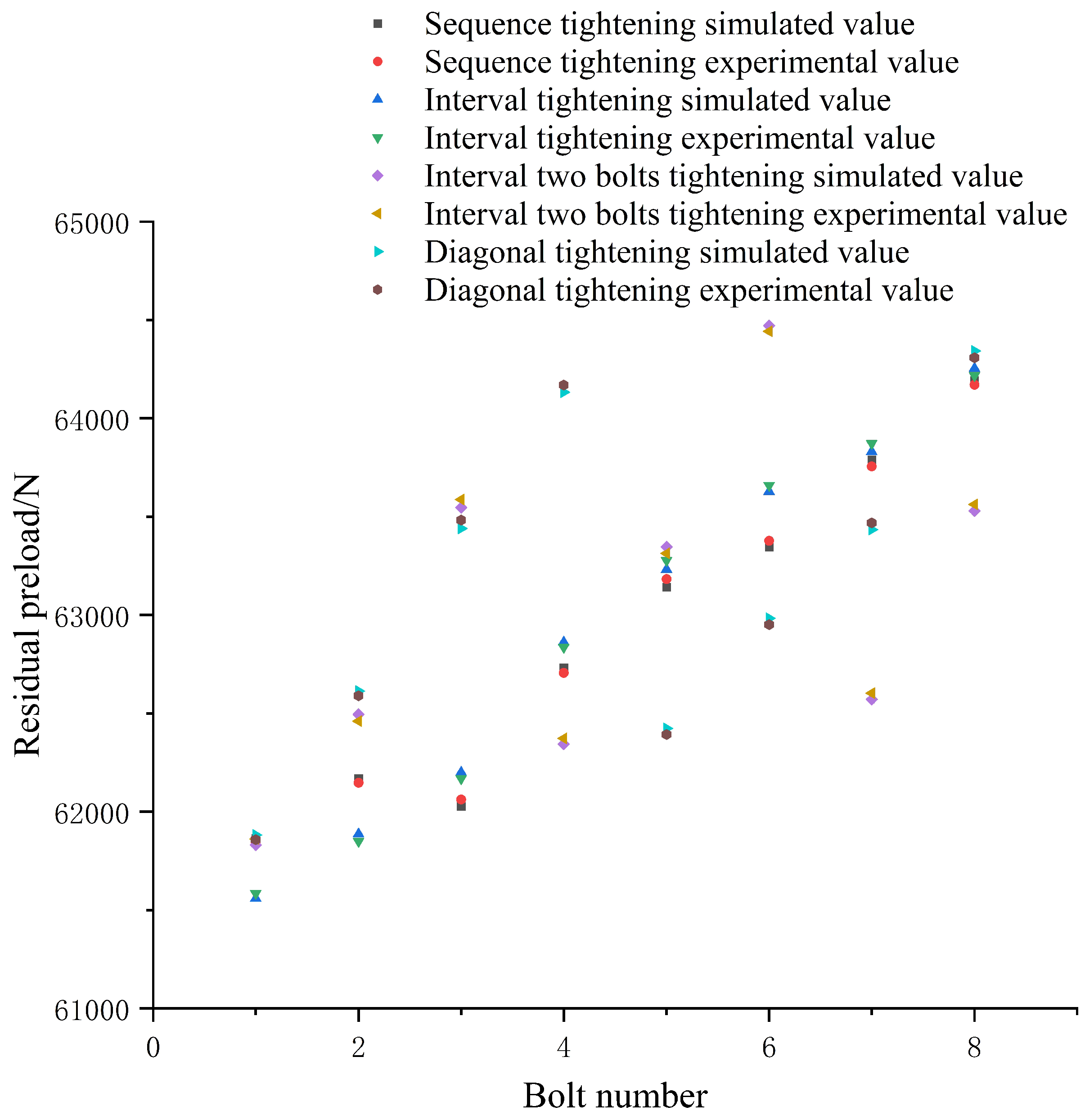
The mean values of the residual preload of the four single-bolt tightening sequences were 62,884.9 N, 62,956.1 N, 62,966.6 N, and 63,006.3 N, respectively. The mean values of the residual preload of the three kinds of two-bolt tightening sequence were 65,090.9 N, 65,504.6 N, and 65,208.1 N, respectively. The average value of the residual preload was the highest when two bolts were tightened at an interval simultaneously. The corresponding variance was 450.3, which was the smallest of all the tightening sequences. Therefore, when the gap value was 0.8 mm and the axis inclination angle was 0.15°, the two-bolt tightening interval at the same time was the best sequence. The two optimal tightening sequences of the aviation component are shown in
Figure 14. It can be concluded that the optimal tightening sequence for the aviation component was different under different conditions.