A Jacobian-Free Newton–Krylov Method to Solve Tumor Growth Problems with Effective Preconditioning Strategies
Abstract
1. Introduction
2. Governing Equations
3. Numerical Algorithm
3.1. The Backward Euler (BE) Method
3.2. The Crank–Nicolson (CN) Method
3.3. The Jacobian-Free Newton–Krylov Method
- Step-1:
- Given , solve for z (e.g., )
- Step-2:
- Perform ,
3.4. The Physics-Based Preconditioners
3.4.1. Based on the Backward Euler Method
3.4.2. Based on the Crank–Nicolson Method
4. Results
4.1. 1D Case
4.1.1. Convergence Analysis
4.1.2. Performance Study of the Preconditioners
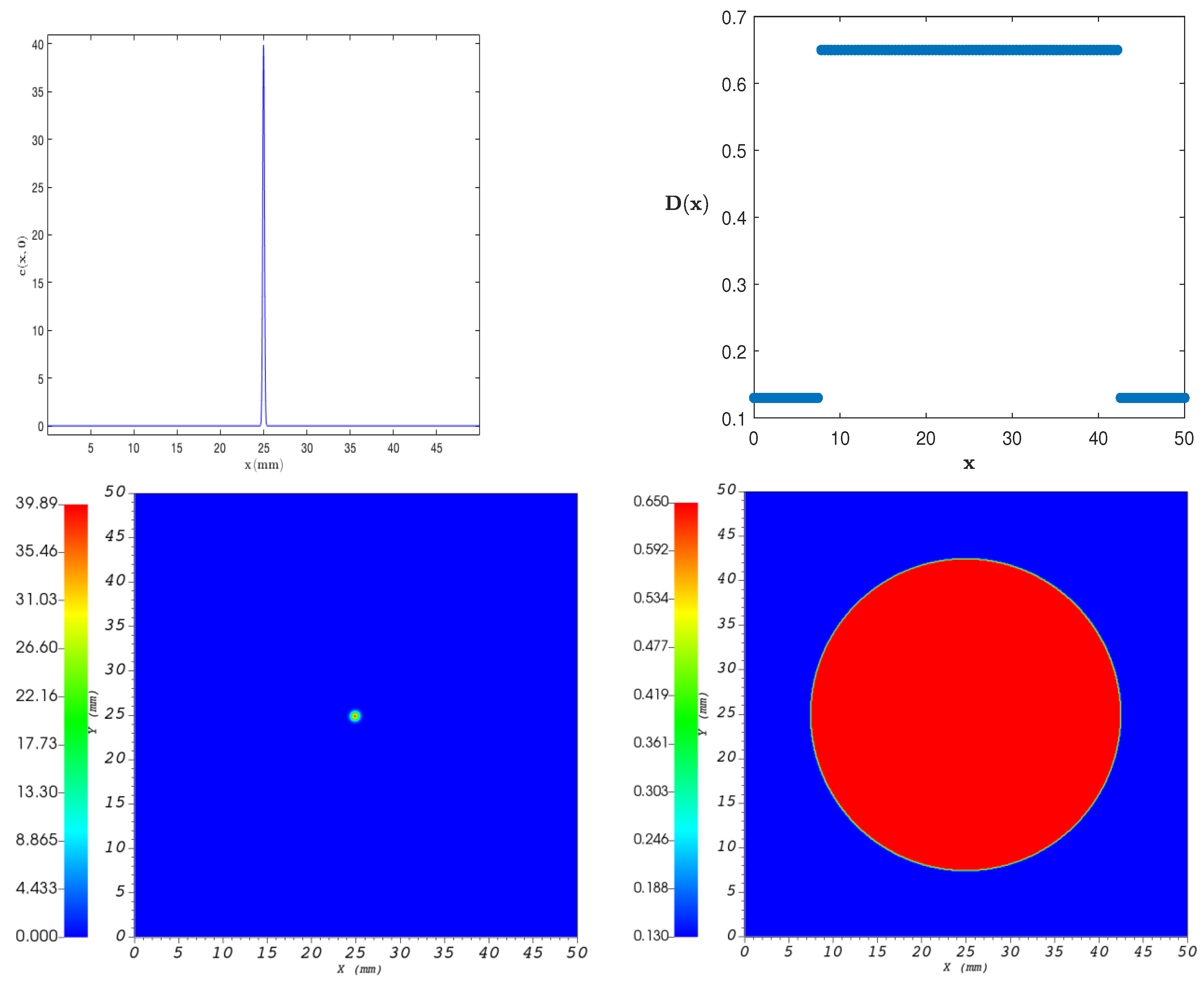
4.2. Two-Dimensional Case
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Stability Analysis
Appendix A.2. Accuracy Analysis
References
- Martirosyan, N.L.; Rutter, E.M.; Ramey, W.L.; Kostelich, E.J.; Kuang, Y.; Preul, M.C. Mathematically modeling the biological properties of gliomas: A review. Math. Biosci. Eng. 2015, 12, 879–905. [Google Scholar] [CrossRef] [PubMed]
- Alfonso, J.C.L.; Talkenberger, K.; Seifert, M.; Klink, B.; Hawkins-Daarud, A.; Swanson, K.R.; Hatzikirou, H.; Deutsch, A. The biology and mathematical modelling of glioma invasion: A review. J. R. Soc. Interface 2017, 14, 20170490. [Google Scholar] [CrossRef] [PubMed]
- Anvari, S.; Nambiar, S.; Pang, J.; Maftoon, N. Computational Models and Simulations of Cancer Metastasis. Arch. Comput. Methods Eng. 2021, 28, 4837–4859. [Google Scholar] [CrossRef]
- Hormuth, D.A.; Phillips, C.; Wu, C.; Lima, E.A.B.F.; Lorenzo, G.; Jha, P.K.; Jarrett, A.M.; Oden, J.T.; Yankeelov, T.E. Biologically-Based Mathematical Modeling of Tumor Vasculature and Angiogenesis via Time-Resolved Imaging Data. Cancers 2021, 13, 3008. [Google Scholar] [CrossRef]
- Tunc, B.; Hormuth, D.; Biros, G.; Yankeelov, T. Modeling of Glioma Growth with Mass Effect by Longitudinal Magnetic Resonance Imaging. IEEE Trans. Biomed. Eng. 2021, 68, 3713–3724. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Lee, E.; Li, G. Numerical solutions of the reaction-diffusion equation: An integral equation method using the variational iteration method. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 265–271. [Google Scholar] [CrossRef]
- de la Cruz, R.; Guerrero, P.; Calvo, J.; Alarcón, T. Coarse-graining and hybrid methods for efficient simulation of stochastic multi-scale models of tumour growth. J. Comput. Phys. 2017, 350, 974–991. [Google Scholar] [CrossRef] [PubMed]
- Adenis, L.; Plaszczynski, S.; Grammaticos, B.; Pallud, J.; Badoual, M. The Effect of Radiotherapy on Diffuse Low-Grade Gliomas Evolution: Confronting Theory with Clinical Data. J. Pers. Med. 2021, 11, 818. [Google Scholar] [CrossRef]
- Mach, J.; Benes, M.; Strachota, P. Nonlinear Galerkin finite element method applied to the system of reaction—Diffusion equations in one space dimension. Comput. Math. Appl. 2017, 73, 2053–2065. [Google Scholar] [CrossRef]
- de Montigny, J.; Iosif, A.; Breitwieser, L.; Manca, M.; Bauer, R.; Vavourakis, V. An in silico hybrid continuum-/agent-based procedure to modelling cancer development: Interrogating the interplay amongst glioma invasion, vascularity and necrosis. Methods 2021, 185, 94–104, Methods on simulation in biomedicine,. [Google Scholar] [CrossRef] [PubMed]
- Engwer, C.; Wenske, M. Estimating the extent of glioblastoma invasion. J. Math. Biol. 2021, 82. [Google Scholar] [CrossRef] [PubMed]
- Kapoor, M.; Joshi, V. Numerical approximation of 1D and 2D reaction diffusion system with modified cubic UAH tension B-spline DQM. J. Math. Comput. Sci. 2021, 11, 1650–1667. [Google Scholar]
- Jaroudi, R.; Baravdish, G.; Johansson, B.T.; Astrom, F. Numerical reconstruction of brain tumours. Inverse Probl. Sci. Eng. 2019, 27, 278–298. [Google Scholar] [CrossRef]
- Amereh, M.; Edwards, R.; Akbari, M.; Nadler, B. In-Silico Modeling of Tumor Spheroid Formation and Growth. Micromachines 2021, 12, 749. [Google Scholar] [CrossRef] [PubMed]
- Lipková, J.; Angelikopoulos, P.; Wu, S.; Alberts, E.; Wiestler, B.; Diehl, C.; Preibisch, C.; Pyka, T.; Combs, S.; Hadjidoukas, P.; et al. Personalized Radiotherapy Design for Glioblastoma: Integrating Mathematical Tumor Models, Multimodal Scans, and Bayesian Inference. IEEE Trans. Med. Imaging 2019, 38, 1875–1884. [Google Scholar] [CrossRef]
- Dehghan, M.; Narimani, N. An element-free Galerkin meshless method for simulating the behavior of cancer cell invasion of surrounding tissue. Appl. Math. Model. 2018, 59, 500–513. [Google Scholar] [CrossRef]
- Dehghan, M.; Narimani, N. Radial basis function-generated finite difference scheme for simulating the brain cancer growth model under radiotherapy in various types of computational domains. Comput. Methods Programs Biomed. 2020, 195, 105641. [Google Scholar] [CrossRef] [PubMed]
- Gaw, N.; Hawkins-Daarud, A.; Hu, L.S.; Yoon, H.; Wang, L.; Xu, Y.; Jackson, P.R.; Singleton, K.W.; Baxter, L.C.; Eschbacher, J.; et al. Integration of machine learning and mechanistic models accurately predicts variation in cell density of glioblastoma using multiparametric MRI. Sci. Rep. 2019, 9, 10063. [Google Scholar] [CrossRef] [PubMed]
- Ozugurlu, E. A note on the numerical approach for the reaction–diffusion problem to model the density of the tumor growth dynamics. Comput. Math. Appl. 2015, 69, 1504–1517. [Google Scholar]
- Knoll, D.A.; Keyes, D.E. Jacobian-Free Newton Krylov Methods: A survey of approaches and applications. J. Comput. Phys. 2004, 193, 357–397. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Zhang, H.; Guo, J.; Lu, J.; Li, F.; Xu, Y. The comparison between nonlinear and linear preconditioning JFNK method for transient neutronic/thermal-hydraulics coupling problem. Ann. Nucl. Energy 2019, 132, 357–368. [Google Scholar] [CrossRef]
- Hossain, M.A.; Alam, J.M. Assessment of a symmetry preserving JFNK method for atmospheric convection. Comput. Phys. Commun. 2021, 269, 108113. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, J.; Lu, J.; Li, F.; Xu, Y.; Downar, T. An assessment of coupling algorithms in HTR simulator TINTE. Nucl. Sci. Eng. 2018, 190, 287–309. [Google Scholar] [CrossRef]
- Axelsson, O.; Blaheta, R.; Byczanski, P.; Karátson, J.; Ahmad, B. Preconditioners for regularized saddle point problems with an application for heterogeneous Darcy flow problems. J. Comput. Appl. Math. 2015, 280, 141–157. [Google Scholar] [CrossRef]
- Park, H.; Gaston, D.; Kadioglu, S.; Knoll, D. Tightly Coupled Multiphysics Simulations For Pebble Bed Reactors. In American Nuclear Society 2009 International Conference on Advances in Mathematics, Computational Methods and Reactor Physics; Springs: Saratoga, NY, USA, 2009; pp. 3–7. [Google Scholar]
- Wang, B.; Feng, Z.; Chen, Y.; Zhang, D.; Wu, Z.; Li, J.; Li, M.; Ma, R.; Li, C. Optimization and Improvement of Sodium Heated Once-through Steam Generator Transient Analysis Code Based on the JFNK Algorithm. Energies 2023, 16, 482. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, S.; Prelim Verif, C.Y. Incompressible Navier–Stokes Equations Solved Newton Method. Int. J. Adv. Nucl. React. Desing Tech. 2020, 2, 69–85. [Google Scholar] [CrossRef]
- Ascher, U.M.; Greif, C. A First Course in Numerical Methods; SIAM: Philadelphia, PA, USA, 2011. [Google Scholar]
- Kelley, C.T. Iterative Methods for Solving Linear and Nonlinear Equations; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Kadioglu, S.Y.; Knoll, D.A. A Jacobian-Free Newton Krylov Implicit-Explicit Time Integration Method for Incompressible Flow Problems. Commun. Comput. Phys. 2013, 13, 1408–1431. [Google Scholar] [CrossRef]
- Kadioglu, S.Y.; Knoll, D.A. A Fully Second Order Implicit/Explicit Time Integration Technique for Hydrodynamics Plus Nonlinear Heat Conduction Problems. J. Comput. Phys. 2010, 229, 3237–3249. [Google Scholar] [CrossRef]
- Kadioglu, S.Y.; Knoll, D.A.; Lowrie, R.B.; Rauenzahn, R.M. A Second Order Self-Consistent IMEX Method for Radiation Hydrodynamics. J. Comput. Phys. 2010, 229, 8313–8332. [Google Scholar] [CrossRef]
- Kadioglu, S. A Second-Order IMEX Method for Multi-Phase Flow Problems. Int. J. Comput. Methods 2017, 14, 1750056. [Google Scholar] [CrossRef]
- Kadioglu, S.Y. Analysis of the Self-Consistent IMEX Method for Tightly Coupled Non-linear Systems. J. Comp. Appl. Math. 2017, 322, 148–160. [Google Scholar] [CrossRef]
- Everett, R.; BFlores, K.; Henscheid, N.; Lagergren, J.; Larripa, K.; Li, D.; TNardini, J.; TTNguyen, P.; Bruce Pitman, E.; MRutter, E. A Tutorial Review of Mathematical Techniques for Quantifying Tumor Heterogeneity. Math. Biosci. Eng. 2020, 17, 3660–3709. [Google Scholar] [CrossRef] [PubMed]
- Murray, J. Mathematical Biology II: Spatial Models and Biomedical Applications; Springer: New York, NY, USA, 2003. [Google Scholar]
- Swanson, K.; Harpold, H.; Peacock, D.; Rockne, R.; Pennington, C.; Kilbride, L.; Grant, R.; Wardlaw, J.; Alvord, E.A., Jr. Velocity of radial expansion of contrast-enhancing gliomas and the effectiveness of radiotherapy in individual patients: A proof of principle. Clin. Oncol. 2008, 20, 301–308. [Google Scholar] [CrossRef] [PubMed]
- Shim, E.; Kwon, Y.G.; Ko, H.J. Computational Analysis of Tumor Angiogenesis Patterns Using a Two-dimensional Model. Yonsei Med. J. 2005, 46, 275–283. [Google Scholar] [CrossRef]
- Dembo, R.S.; Eisenstat, S.C.; Steihaug, T. Inexact Newton methods. SIAM J. Num. Anal. 1982, 19, 400–408. [Google Scholar] [CrossRef]
- Kelley, C.T. Solving Nonlinear Equations with Newton’s Method; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Brown, P.; Saad, Y. Hybrid Krylov Methods for Nonlinear Systems of Equations. SIAM J. Sci. Stat. Comput. 1990, 11, 450–481. [Google Scholar] [CrossRef]
- Briggs, W.L. A Multigrid Tutorial; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Zemkov, E.P.; Loskutov, A. Exact analytical solutions for nonlinear waves in the inhomogeneous Fisher-Kolmogorov equation. Eur. Phys. J. B 2011, 79, 79–84. [Google Scholar] [CrossRef]
- Thomas, J. Numerical Partial Differential Equations I (Finite Difference Methods); Texts in Applied Mathematics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Strikwerda, J.C. Finite Difference Schemes Partial Differential Equations; Wadsworth & Brooks/Cole, Advance Books & Software: Pacific Grove, CA, USA, 1989. [Google Scholar]
- Thomas, J. Numerical Partial Differential Equations II (Conservation Laws and Elliptic Equations); Texts in Applied Mathematics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Leveque, R.J. Finite Volume Methods for Hyperbolic Problems; Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Mishra, S.; Svard, M. On stability of numerical schemes via frozen coefficients and the magnetic induction equation. BIT Numer. Math. 2010, 50, 85–108. [Google Scholar] [CrossRef]
- Appadu, A.R.; Lubuma, J.; Mphephu, N. Computational Study of three numerical methods for some linear and nonlinear advection-diffusion-reaction problems. Prog. Comput. Fluid Dyn. 2017, 17, 114–129. [Google Scholar] [CrossRef]
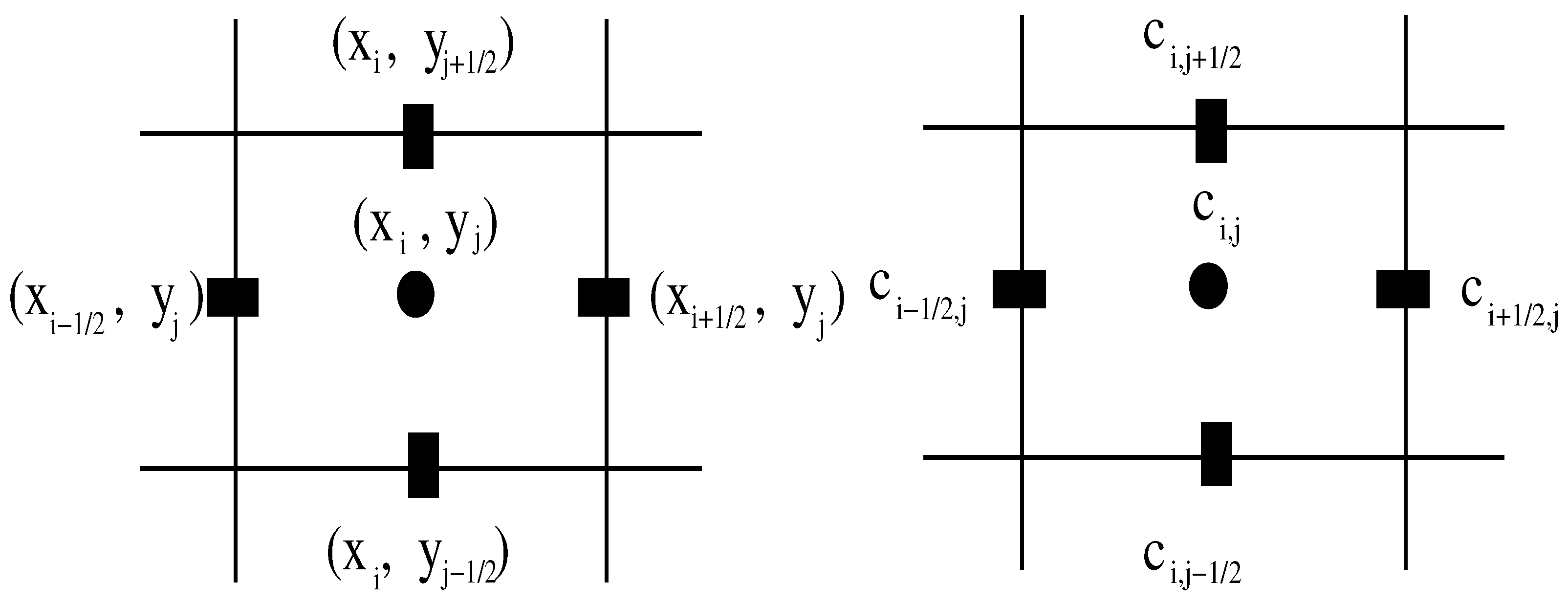



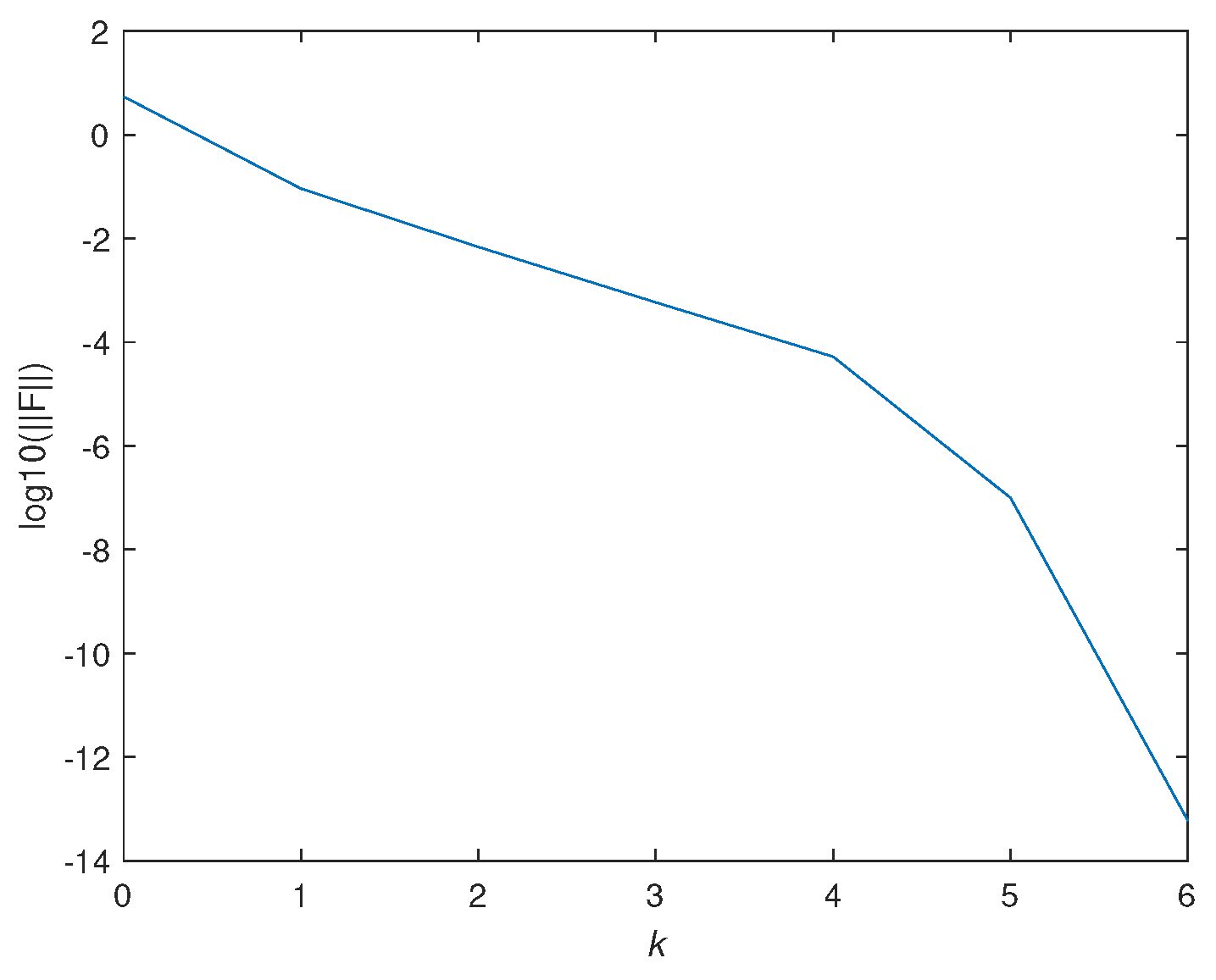


| Time Convergence Analysis with in Columns 1, 3, 5 | |||||
|---|---|---|---|---|---|
| Conv. Rate ( in (25)) | Conv. Rate ( in (25)) | Conv. Rate ( in (25)) | |||
| 2.0000 | 2.0004 | 2.0005 | |||
| 2.0000 | 2.0001 | 2.0001 | |||
| 2.0029 | 1.9985 | 1.9973 | |||
| 1.9980 | 1.9992 | 1.9998 | |||
| 1.9711 | 2.0105 | 2.0172 | |||
| 1.9506 | 2.0359 | 2.0687 | |||
| 1.9014 | 2.0615 | 2.1685 | |||
| Time Convergence Analysis with in Columns 1, 3, 5 | |||||
|---|---|---|---|---|---|
| Conv. Rate ( in (25)) | Conv. Rate ( in (25)) | Conv. Rate ( in (25)) | |||
| 0.9969 | 0.9984 | 0.9996 | |||
| 0.9983 | 0.9989 | 0.9989 | |||
| 0.9991 | 0.9993 | 0.9991 | |||
| 0.9995 | 0.9996 | 0.9995 | |||
| 0.9998 | 0.9998 | 0.9997 | |||
| 0.9999 | 0.9999 | 0.9998 | |||
| 0.9999 | 0.9999 | 0.9999 | |||
| Spatial Convergence Analysis with in Columns 1, 3, 5 | |||||
|---|---|---|---|---|---|
| Conv. Rate | Conv. Rate | Conv. Rate | |||
| 1.9975 | 1.9987 | 1.9224 | |||
| 2.0006 | 1.9985 | 1.9972 | |||
| 2.0001 | 1.9999 | 1.9994 | |||
| 2.0002 | 1.9950 | 1.9847 | |||
| 2.0015 | 2.0064 | 2.0220 | |||
| 1.9639 | 2.0005 | 2.0647 | |||
| 1.9678 | 2.0402 | 2.2178 | |||
| Time Convergence Analysis with in Columns 1, 3, 5 | |||||
|---|---|---|---|---|---|
| Conv. Rate | Conv. Rate | Conv. Rate | |||
| 2.0007 | 2.0008 | 2.0001 | |||
| 2.0003 | 2.0002 | 2.0000 | |||
| 2.0057 | 2.0026 | 2.0030 | |||
| 2.0087 | 2.0071 | 2.0079 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadioglu, S.Y.; Ozugurlu, E. A Jacobian-Free Newton–Krylov Method to Solve Tumor Growth Problems with Effective Preconditioning Strategies. Appl. Sci. 2023, 13, 6579. https://doi.org/10.3390/app13116579
Kadioglu SY, Ozugurlu E. A Jacobian-Free Newton–Krylov Method to Solve Tumor Growth Problems with Effective Preconditioning Strategies. Applied Sciences. 2023; 13(11):6579. https://doi.org/10.3390/app13116579
Chicago/Turabian StyleKadioglu, Samet Y., and Ersin Ozugurlu. 2023. "A Jacobian-Free Newton–Krylov Method to Solve Tumor Growth Problems with Effective Preconditioning Strategies" Applied Sciences 13, no. 11: 6579. https://doi.org/10.3390/app13116579
APA StyleKadioglu, S. Y., & Ozugurlu, E. (2023). A Jacobian-Free Newton–Krylov Method to Solve Tumor Growth Problems with Effective Preconditioning Strategies. Applied Sciences, 13(11), 6579. https://doi.org/10.3390/app13116579




