Multi-Domain Substructure Synthesis with Normalized Interpolation Technique for Non-Matching Interfaces
Abstract
1. Introduction
2. Concept of Impulse-Based Substructuring Method
3. Assembly of Substructure with Non-Matching Interfaces
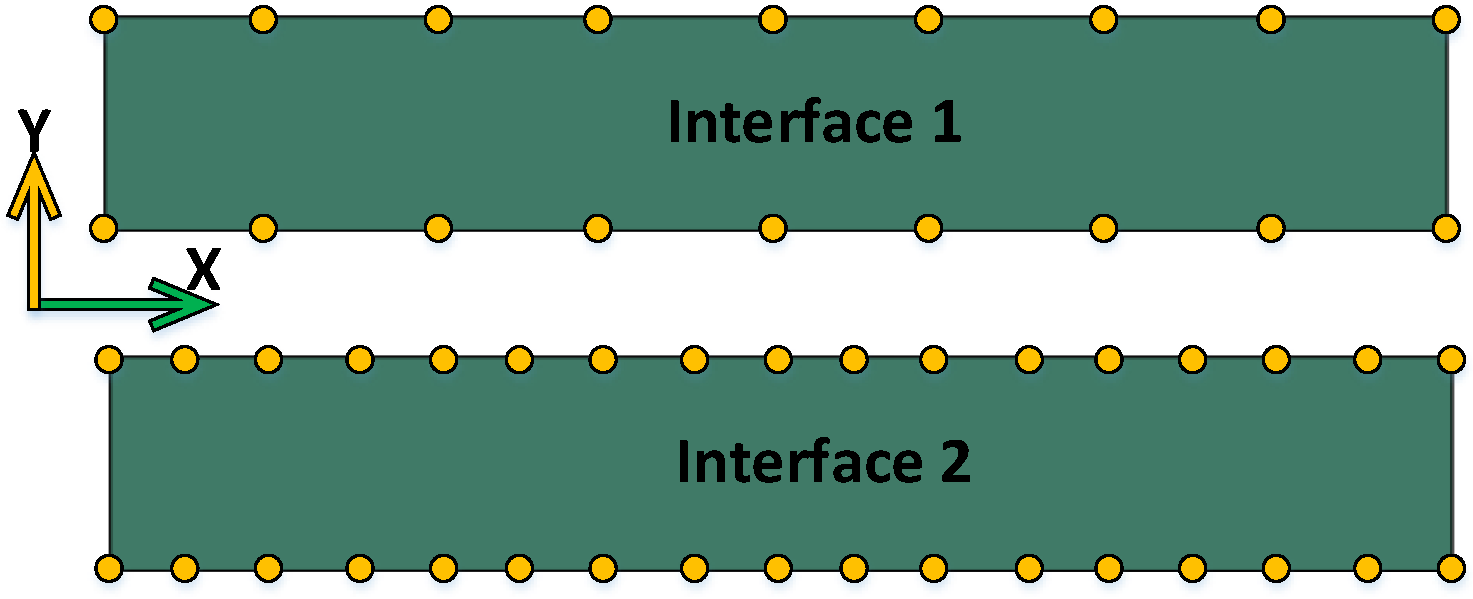
3.1. Assembly of Impulse-Based Substructures with Non-Matching Interfaces
3.2. Assembly of IBS and Finite Element Substructures with Non-Matching Interfaces
3.3. Assembly of IBS and Modal Substructures with Non-Matching Interfaces
4. Basic Interpolation Rule and Interpolation Functions
4.1. Basic Interpolation Rule and Interpolation Functions
4.2. Moving Kriging and Moving Least Squares Interpolation Methods
5. Numerical Examples
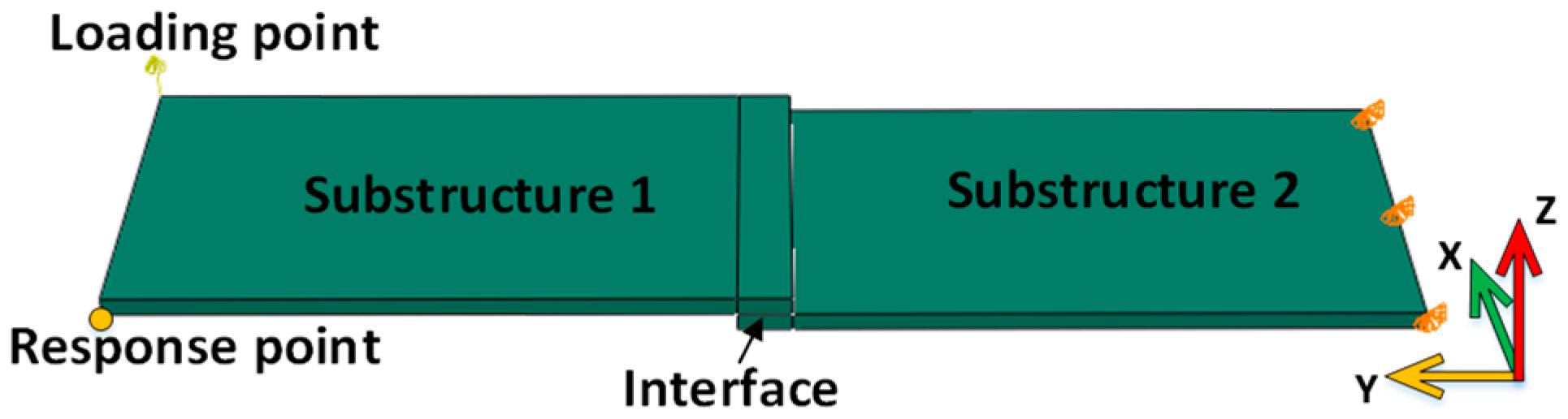
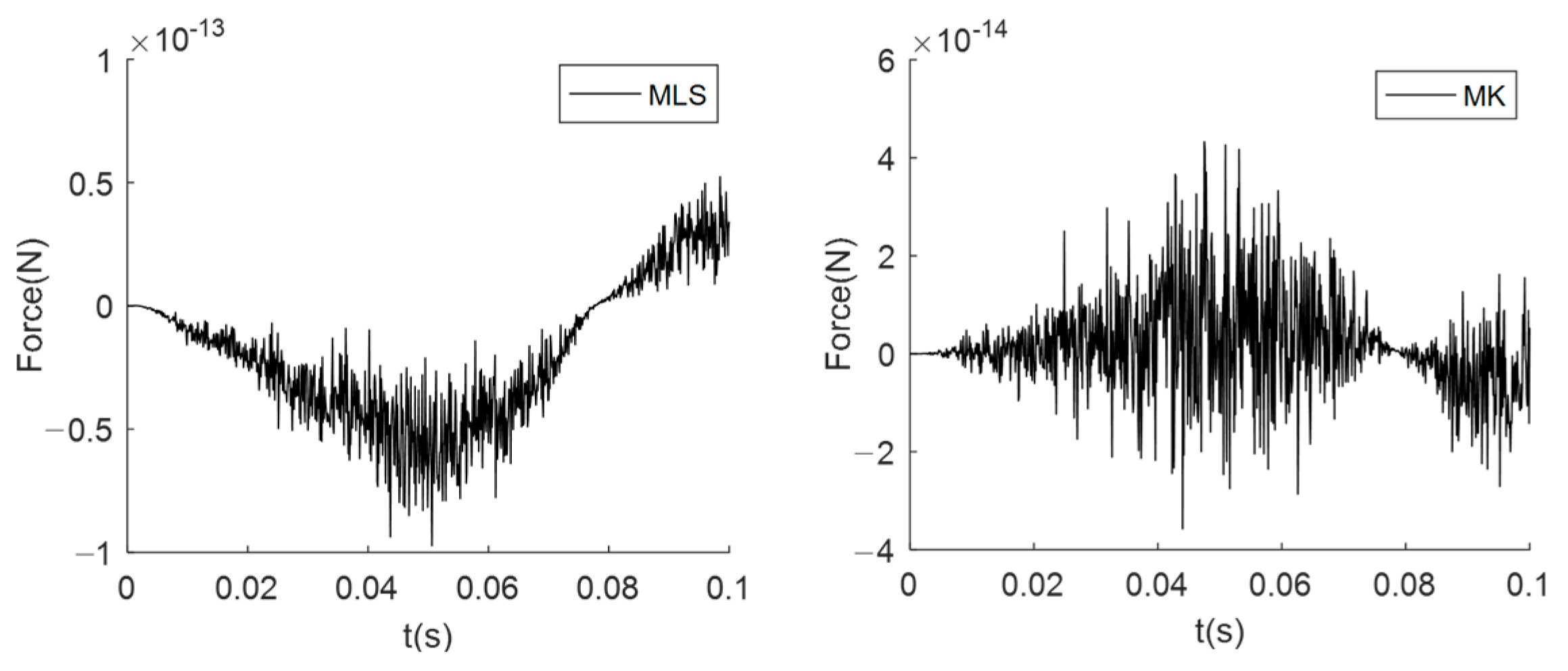
5.1. Solid Plate Numerical Example
5.2. Application to Lunar Lander with a Rover
6. Conclusions
- (1)
- A method for assembling multi-domain substructures with non-matching interfaces is proposed in this paper. It is an extension of the available IBS techniques and makes the IBS method more practical for coupling multi-domain substructures. Like the original IBS, this method can deal with complex dynamics efficiently.
- (2)
- The basic rule of generating the interpolation functions is discussed, and by achieving the normalization condition, force equilibrium and energy conservation can be conveniently satisfied. Compared with the approach of constructing transition elements, it is unnecessary to implement a complicated element construction process; only the distribution of support nodes and the coefficients are needed, and a different model can be used for interpolation functions when it satisfies the normalization condition.
- (3)
- The advantageous performance of this method in dynamic prediction is validated by two numerical examples: one is the dynamic simulation of the landing process of a lunar lander. With high accuracy, the time-consuming simulation of the landing process is drastically reduced by the employment of the proposed method.
- (4)
- Not all mesh grid points on interfaces are needed, and the support nodes can be selected properly considering the features of the interfaces and the engineering accuracy requirements. A more rigorous study about the support node selection considering their precise influence will be further studied as an alternative reduction of the interfaces.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hurty, W.C. Vibrations of structural systems by component mode synthesis. J. Eng. Mech. Div. 1960, 86, 51–70. [Google Scholar] [CrossRef]
- Craig, R.R., Jr. Coupling of substructures for dynamic analyses: An overview. In Proceedings of the 41st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, GA, USA, 3–6 April 2000; AIAA Paper 2000-1573. The University of Texas: Austin, TX, USA, 2000. [Google Scholar]
- Jetmundsen, B.; Bielawa, R.L.; Flannelly, W.G. Generalized frequency domain substructure synthesis. J. Am. Helicopter Soc. 1988, 33, 55–64. [Google Scholar] [CrossRef]
- Rixen, D.J.; van der Valk, P.L.C. An Impulse Based Substructuring approach for impact analysis and load case simulations. J. Sound Vib. 2013, 332, 7174–7190. [Google Scholar] [CrossRef]
- De Klerk, D.; Rixen, D.J.; Voormeeren, S.N. General framework for dynamic substructuring: History, review, and classification of techniques. AIAA J. 2008, 46, 1169–1181. [Google Scholar] [CrossRef]
- Rixen, D.; Haghighat, N. Truncating the Impulse Responses of Substructures to Speed Up the Impulse-Based Substructuring. In Proceedings of the 30th International Modal Analysis Conference, Jacksonville, FL, USA, 1–4 February 2012; Springer: New York, NY, USA, 2012; Volume 2, pp. 137–148. [Google Scholar] [CrossRef]
- Gordis, J.H. Integral equation formulation for transient structural synthesis. AIAA J. 1995, 33, 320–324. [Google Scholar] [CrossRef]
- Rixen, D.J. Substructuring Using Impulse Response Functions for Impact Analysis. In Proceedings of the 28th International Modal Analysis Conference, Jacksonville, FL, USA, 1–4 February 2010; Springer: New York, NY, USA, 2010; Volume 3, pp. 637–646. [Google Scholar]
- Rixen, D.J. A Substructuring Technique Based on Measured and Computed Impulse Response Functions of Components. In Proceedings of the Isma2010—International Conference on Noise and Vibration Engineering, KU Leuven, Leuven, Belgium, 20–22 September 2010; pp. 1939–1954. [Google Scholar]
- Van der Seijs, M.V.; Rixen, D.J. Efficient impulse based substructuring using truncated impulse response functions and mode superposition. In Proceedings of the International Conference on Noise and Vibration Engineering, KU Leuven, Leuven, Belgium, 14–15 September 2012; pp. 3487–3499. [Google Scholar]
- Van der Valk, P.L.C.; Rixen, D.J. An Effective Method for Assembling Impulse Response Functions to Linear and Non-Linear Finite Element Models. In Proceedings of the 30th International Modal Analysis Conference, Jacksonville, FL, USA, 1–4 February 2012; Springer: New York, NY, USA, 2012; Volume 2, pp. 123–135. [Google Scholar]
- Van der Valk, P.L.C.; Rixen, D.J. An Impulse Based Substructuring method for coupling impulse response functions and finite element models. Comput. Methods Appl. Mech. Eng. 2014, 275, 113–137. [Google Scholar] [CrossRef]
- Dong, W.-L.; Liu, L.; Zhou, S.-D.; Chen, S.-L. Substructure Synthesis in Time Domain with Rigid-Elastic Hybrid Joints. AIAA J. 2015, 53, 504–509. [Google Scholar] [CrossRef]
- Zhou, S.-D.; Liu, L.; Dong, W.-L. Time-Domain Substructure Synthesis with Hybrid Rigid and Nonlinear-Elastic Joints. AIAA J. 2016, 54, 2545–2551. [Google Scholar] [CrossRef]
- Chen, S.; Liu, L.; Zhou, S.; Chen, Z.; Yue, Z. Multi-domain substructures synthesis with general joints for the dynamics of large structures. AIP Adv. 2017, 7, 105007. [Google Scholar] [CrossRef]
- Aminpour, M.; Ransom, J.; McCleary, S. Coupled analysis of independently modeled finite element subdomains. In Proceedings of the 33rd Structures, Structural Dynamics and Materials Conference, Dallas, TX, USA, 13–15 April 1992; pp. 109–120. [Google Scholar] [CrossRef]
- Aminpour, M.; Pageau, S.; Shin, Y. Improved interface modeling technology. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, Anaheim, CA, USA, 11–14 June 2001; p. 1548. [Google Scholar] [CrossRef]
- Ransom, J.; McCleary, S.; Aminpour, M. A New Interface Element for Connecting Independently Modeled Substructures. In Proceedings of the 34th Structures, Structural Dynamics and Materials Conference, La Jolla, CA, USA, 19–22 April 1993; p. 1503. [Google Scholar]
- Park, K.C.; Felippa, C.A. A variational principle for the formulation of partitioned structural systems. Int. J. Numer. Methods Eng. 2000, 47, 395–418. [Google Scholar] [CrossRef]
- Bfer, G. An Isoparametric Joint Interface Element for Finite-Element Analysis. Int. J. Numer. Methods Eng. 1985, 21, 585–600. [Google Scholar] [CrossRef]
- Gens, A.; Carol, I.; Alonso, E.E. An interface element formulation for the analysis of soil-reinforcement interaction. Comput. Geotech. 1989, 7, 133–151. [Google Scholar] [CrossRef]
- Dávila, C.G. Solid-To-Shell Transition-Elements for the Computation of Interlaminar Stresses. Comput. Syst. Eng. 1994, 5, 193–202. [Google Scholar] [CrossRef]
- Kim, H.G. Interface element method (IEM) for a partitioned system with non-matching interfaces. Comput. Methods Appl. Mech. Eng. 2002, 191, 3165–3194. [Google Scholar] [CrossRef]
- Cho, Y.-S.; Jun, S.; Im, S.; Kim, H.-G. An improved interface element with variable nodes for non-matching finite element meshes. Comput. Methods Appl. Mech. Eng. 2005, 194, 3022–3046. [Google Scholar] [CrossRef]
- Cho, J.Y.; An, J.; Jee, Y.B. Displacement Welding Technique for Coupled Analysis of Independently Modeled Finite Element Substructures. In Proceedings of the 44th AIAA/ASME/ASCE/AHS Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003; p. 1677. [Google Scholar] [CrossRef]
- De Boer, A.; van Zuijlen, A.; Bijl, H. Review of coupling methods for non-matching meshes. Comput. Methods Appl. Mech. Eng. 2007, 196, 1515–1525. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T.W. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Dai, K.Y.; Liu, G.R.; Lim, K.M.; Gu, Y.T. Comparison between the radial point interpolation and the Kriging interpolation used in meshfree methods. Comput. Mech. 2003, 32, 60–70. [Google Scholar] [CrossRef]
- Chassaing, J.-C.; Nogueira, X.; Khelladi, S. Moving Kriging reconstruction for high-order finite volume computation of compressible flows. Comput. Methods Appl. Mech. Eng. 2013, 253, 463–478. [Google Scholar] [CrossRef]
- Gu, L. Moving kriging interpolation and element-free Galerkin method. Int. J. Numer. Methods Eng. 2003, 56, 1–11. [Google Scholar] [CrossRef]
- Pian, T.H.H.; Tong, P. Basis of finite element methods for solid continua. Int. J. Numer. Methods Eng. 1969, 1, 3–28. [Google Scholar] [CrossRef]
- Belytschko, T.; Organ, D.; Krongauz, Y. A coupled finite element-element-free Galerkin method. Comput. Mech. 1995, 3, 186–195. [Google Scholar] [CrossRef]


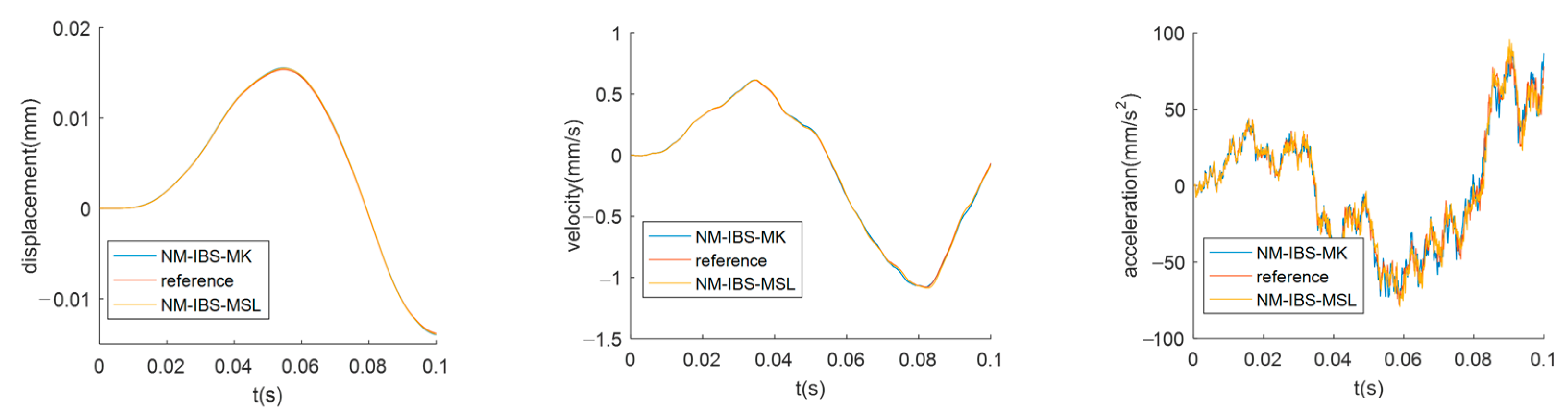





| R2 | RAAE | |||
|---|---|---|---|---|
| NMI-IBS-MK | NMI-IBS-MSL | NMI-IBS-MK | NMI-IBS-MSL | |
| Displacement | 0.99987 | 0.99986 | 0.00984 | 0.00875 |
| Velocity | 0.99961 | 0.99972 | 0.01283 | 0.00932 |
| Acceleration | 0.97904 | 0.98493 | 0.10491 | 0.08743 |
| 60 | 85 | 100 | 200 | 300 | 400 | 500 | 600 | |
|---|---|---|---|---|---|---|---|---|
| NMI-IBS-MK | 0.96423 | 0.97903 | 0.97313 | 0.98650 | 0.98296 | 0.97836 | 0.98239 | — |
| NMI-IBS-MSL | — | 0.98491 | 0.98317 | 0.97977 | 0.95931 | 0.92501 | 0.90041 | 0.88771 |
| 0.25 | 0.5 | 1 | 2 | 4 | |
|---|---|---|---|---|---|
| NMI-IBS-MK | 0.96434 | 0.96685 | 0.97903 | 0.98816 | 0.91627 |
| NMI-IBS-MSL | 0.98576 | 0.98563 | 0.98491 | 0.98494 | 0.98646 |
| R2 | RAAE | |||
|---|---|---|---|---|
| NMI-IBS | NMI-IBS-FEM | NMI-IBS | NMI-IBS-FEM | |
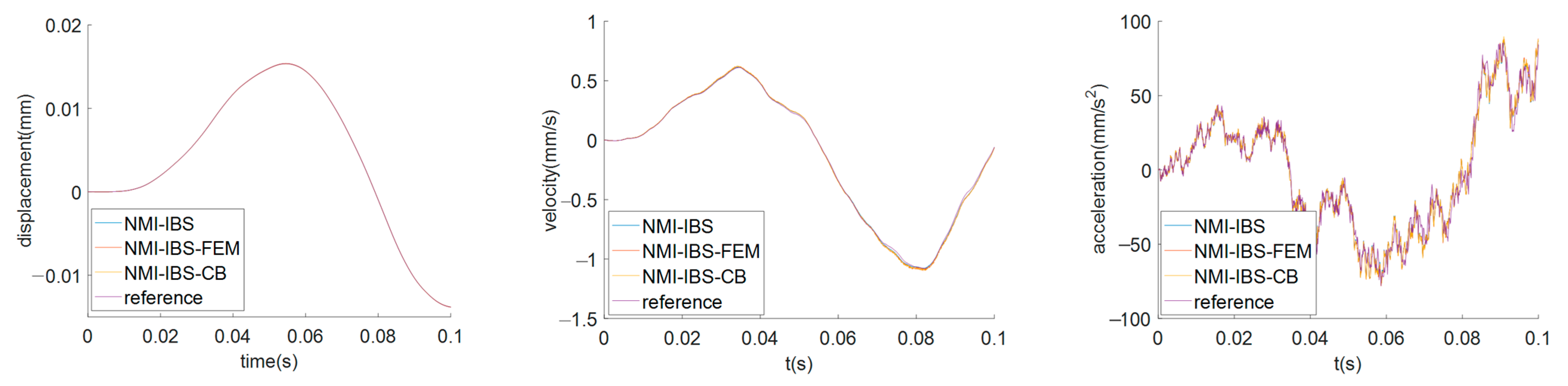
| Displacement | 0.99984 | 0.99971 | 0.00942 | 0.01367 |
| Velocity | 0.99963 | 0.99955 | 0.01121 | 0.01567 |
| Acceleration | 0.97822 | 0.97885 | 0.10453 | 0.10514 |
| Response Point 1 | Response Point 2 | |||||
|---|---|---|---|---|---|---|
| NMI-IBS | NMI-IBS-FEM | NMI-IBS-CB | NMI-IBS | NMI-IBS-FEM | NMI-IBS-CB | |
| Displacement | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| Velocity | 0.99978 | 0.99986 | 0.99985 | 0.99988 | 0.99893 | 0.99887 |
| Acceleration | 0.90056 | 0.89039 | 0.89039 | 0.99466 | 0.94777 | 0.94774 |
| NMI-IBS | NMI-IBS-FEM | NMI-IBS-CB | Full Newmark-β | |
|---|---|---|---|---|
| CPU time | 38.63 s | 173.96 s | 158.87 | 2685 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Liu, L.; Chen, S. Multi-Domain Substructure Synthesis with Normalized Interpolation Technique for Non-Matching Interfaces. Appl. Sci. 2023, 13, 6525. https://doi.org/10.3390/app13116525
Chen Z, Liu L, Chen S. Multi-Domain Substructure Synthesis with Normalized Interpolation Technique for Non-Matching Interfaces. Applied Sciences. 2023; 13(11):6525. https://doi.org/10.3390/app13116525
Chicago/Turabian StyleChen, Zhaoyue, Li Liu, and Shulin Chen. 2023. "Multi-Domain Substructure Synthesis with Normalized Interpolation Technique for Non-Matching Interfaces" Applied Sciences 13, no. 11: 6525. https://doi.org/10.3390/app13116525
APA StyleChen, Z., Liu, L., & Chen, S. (2023). Multi-Domain Substructure Synthesis with Normalized Interpolation Technique for Non-Matching Interfaces. Applied Sciences, 13(11), 6525. https://doi.org/10.3390/app13116525






