State-of-Charge Prediction Model for Ni-Cd Batteries Considering Temperature and Noise

Abstract

The accurate prediction of the state of charge (SOC) of Ni-Cd batteries is critical for developing battery management systems for high-speed trains. To address the challenges of the large floating charge voltage of Ni-Cd batteries and the vulnerability of a battery’s SOC to environmental factors such as temperature, this paper proposes an adaptive adjustment mechanism-based particle swarm optimization (APSO) generalized regression neural network (GRNN) model. The proposed model introduces the concept of the particle aggregation degree to quantify the convergence of the particle swarm optimization (PSO) algorithm. Furthermore, the speed weight of the particle swarm is adaptively adjusted using a comprehensive loss function to optimize the parameters of the GRNN model. To validate the proposed method, simulation experiments are conducted under test conditions using Ni-Cd batteries, and the prediction accuracies of various algorithms are compared. The experimental results demonstrate that the APSO-GRNN model significantly reduces the model’s prediction error. In addition, under the influence of different temperatures and noises, this method demonstrates strong robustness and high practical application value by accurately predicting the SOC, even with limited data samples.

1. Introduction

Railway transportation is one of the most critical modes of transportation in China, and high-speed electric multiple units (EMUs) have become a popular choice due to their high carrying efficiency. However, the existing equipment associated with high-speed EMUs in China is not flawless. The Ni-Cd battery management system in the vehicle cannot predict the state of charge (SOC) of the battery [1]. The SOC of the battery can directly reflect its sustainable power supply capacity and is essential for battery energy management [2]. To address this issue and alleviate “range anxiety”, it is imperative to develop an accurate SOC prediction model [3]. Such a model would aid in formulating an appropriate battery energy management strategy, extending the battery’s service life, and ensuring its safe operation [4]. As the SOC of the battery cannot be directly measured, it can only be indirectly estimated by parameters such as the voltage and current [5,6]. Additionally, the battery SOC is affected by temperature and aging, making precise estimation a challenging task [7,8]. For Ni-Cd batteries, which have a large capacity and extended discharge cycle [9,10], establishing an SOC prediction model is even more complex compared to lithium batteries.

Establishing an accurate state-of-charge (SOC) prediction model is a research focus worldwide. Several methods have been proposed in the literature to address this issue. For instance, Zhang et al. [11] proposed an adaptive adjustment mechanism for an unscented Kalman filter algorithm to predict the SOC based on stochastic difference equations of the battery model. However, since numerical methods were used to solve the system state equation, calculation errors increased over time and failed to respond to abrupt changes in the SOC. Chen et al. [12] used gray theory for parameter analysis and behavior prediction during battery charging and discharging and proposed a piecewise gray model based on extensive battery aging data to enhance SOC prediction accuracy. Yan et al. [13] developed an extended Kalman filter based on Lebesgue sampling to estimate the SOC, which can reduce computational complexity and cost. Wang et al. [14] used particle swarm optimization to predict the SOC of supercapacitors but the prediction range was limited. Neural networks have been increasingly used due to their strong nonlinear processing and adaptive learning abilities. For example, Hong et al. [15] used multiple linear regression to optimize a long short-term memory (LSTM) network for the dual control of SOC prediction accuracy and range. Mao et al. [16] optimized a backpropagation neural network (BPNN) using a flight strategy and particle swarm optimization to minimize prediction errors. Zhao et al. [17] used a recurrent neural network (RNN) as the prediction model and a convolutional neural network (CNN) to extract relevant features from battery data, enhancing the model’s generalization ability. The estimation algorithm for the SOC based on recurrent neural networks offers high prediction accuracy. However, it has a complex model structure and long training time, particularly for nickel-cadmium batteries, as in the case of LSTM [18]. A feedforward neural network, known for its simple structure and suitability for online systems due to its limited data requirements, is another option [19]. However, its prediction accuracy is dependent on the initial parameter settings [20,21], as in the case of a GRNN. It is feasible to optimize its parameters using an optimization algorithm to make the feedforward neural network suitable for adaptive adjustment. Given its simple structure, fewer parameters, strong nonlinear mapping ability, and fast learning speed, a GRNN is ideal for predicting small sample data and can handle unstable data [22,23]. However, the prediction results obtained using the GRNN model are highly susceptible to the initial parameters. Manual parameter adjustment proves challenging in attaining the optimal model parameters, hindering its adaptability to varying battery working conditions. Furthermore, the prediction outcomes are vulnerable to noise interference and ambient temperature fluctuations. To address these limitations, we propose an adaptive particle swarm optimization APSO-GRNN prediction model.

The APSO-GRNN model employs the particle swarm algorithm to optimize the parameters of the GRNN model. It incorporates a scoring function to evaluate the prediction effectiveness of each neuron within the model. Additionally, it dynamically adjusts the weight of the particle swarm’s velocity based on the prediction results. This adaptive adjustment allows the model to prioritize training data that exert a more significant influence on the current SOC prediction, thereby mitigating the impact of battery rebound voltage on the model’s prediction outcomes under various working conditions [24]. Furthermore, it enhances the model’s resilience to diverse ambient temperatures.

To assess the robustness and anti-interference capability of the APSO-GRNN model, experiments are conducted considering two factors: noise and temperature. A comparative analysis is performed, where APSO-GRNN is compared with SVR, XGBoost, and GRNN to elucidate the advantages of APSO-GRNN over other prevalent regression algorithms. Ultimately, the efficacy of the APSO-GRNN model is confirmed based on the experimental findings.

2. Optimal Feature Selection

The selection of input features can significantly impact a model’s training time and prediction accuracy. Thus, choosing the appropriate input features to optimize the algorithm is crucial. In this study, we utilize a random forest (RF) algorithm to improve the electrical characteristics of batteries during discharge.

RF consists of different decision trees [25], where each tree selects a feature as the splitting feature for a node. The importance of each feature on the prediction accuracy can be estimated by the out-of-bag error rate [26,27]. In particular, we employ random forest to predict the state of charge (SOC) and select the following features as candidates: voltage, current, temperature, voltage change rate (dV/dt), and current change rate (dI/dt). These features are used to construct the feature matrix, $F=[f_1,f_2,\dots ,f_N]$. The feature $f_i$ scoring function is shown in Equation (1):

$$F_s=\frac{e_T}{e_i}$$

(1)

where $e_i$ is the out-of-bag error after random rearrangement of the feature $f_i$, and $e_T$ is the sampling error in the decision tree T. Figure 1 displays the results, which show that the voltage, current, and ambient temperature are influential factors for predicting the SOC. In contrast, for predicting the rates of dV/dt and dI/dt, only factors of 0.765 and 0.382, respectively, are influential. Although these influencing factors are small, the data acquisition system can directly obtain the battery’s working voltage, current, and temperature in practical applications. These electrical characteristics are chosen as input features for the model.

3. APSO-GRNN Algorithm

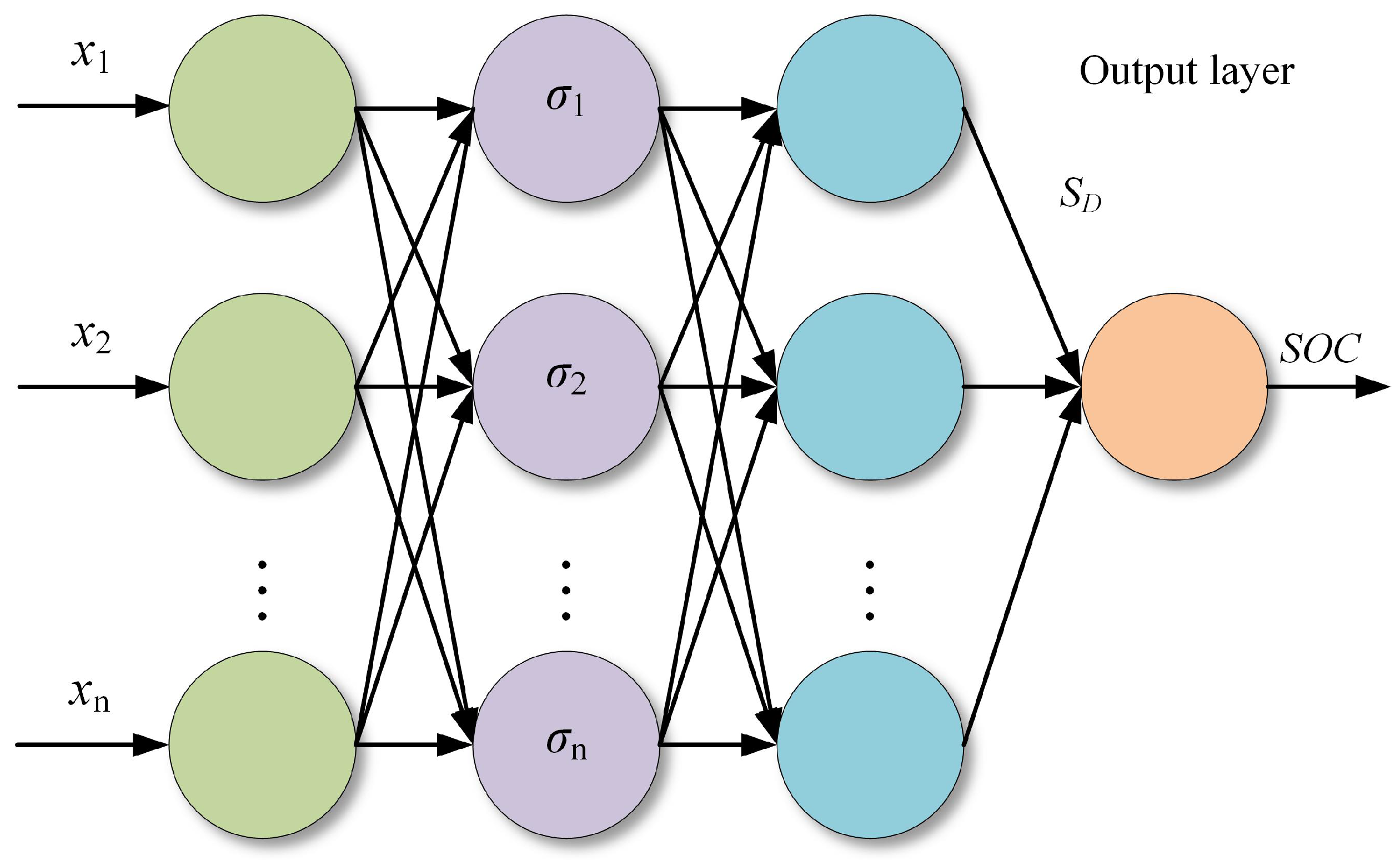
3.1. The GRNN Model

A GRNN is a type of feedforward network that exhibits superior nonlinear mapping capability and faster learning speed than the radial basis network. Additionally, it can achieve better prediction performance in scenarios with limited data volume and high data noise. As a result, a GRNN is commonly utilized in regression analysis. The network architecture of a GRNN includes four layers: the input layer, mode layer, summation layer, and output layer. A detailed explanation of each layer is presented below:

• Input layer
  The number of neurons in the input layer is equal to the vector dimension of the sample dataset, and each neuron in the input layer is equivalent to an identical function, which directly passes the input variable to the pattern layer.
• Pattern layer
  The pattern layer is fully connected and the number of neurons is set to the total number of training samples n. Each neuron corresponds to a different training sample. The value of the Gassu function for any training sample $tr{x}_i$ and test sample $te{x}_j$ is shown in Equation (2).

  $$Gauss(te{x}_i-tr{x}_j)=e^{-\frac{∥te{x}_i-tr{x}_j∥}{2{\sigma }^2}}$$

  (2)

  where $\sigma$ is the model smoothing factor.
• Summation layer
  The number of neurons in the summation layer is one more than the sample dimension. The summation layer has two outputs: the first neuron output is the summation of the pattern layer outputs. For any summation layer neuron with inputs $\{g_1,g_2,g_3,\dots ,g_i\}$, the transfer function for the first summation layer neuron is as follows:

  $$S_D=\sum _{i=1}^m{g}_i$$

  (3)
  The remaining neuron outputs are the weighted sum of the pattern layer outputs, with a transfer function as follows:

  $$S_{Nj}=\sum _{i=1}^m{k}_j{g}_i$$

  (4)

  where $k_j$ is the corresponding eigenvalue of any training sample.
• Output layer
  The number of neurons in the output layer is equal to the output vector dimension of the training samples, and the output is a vector consisting of the quotient of each $S_{N}j$ and $S_D$. The transfer function is shown in Equation (5), and the structure of the GRNN is shown in Figure 2.

  $$y_i=\frac{S_{Nj}}{S_D}$$

  (5)

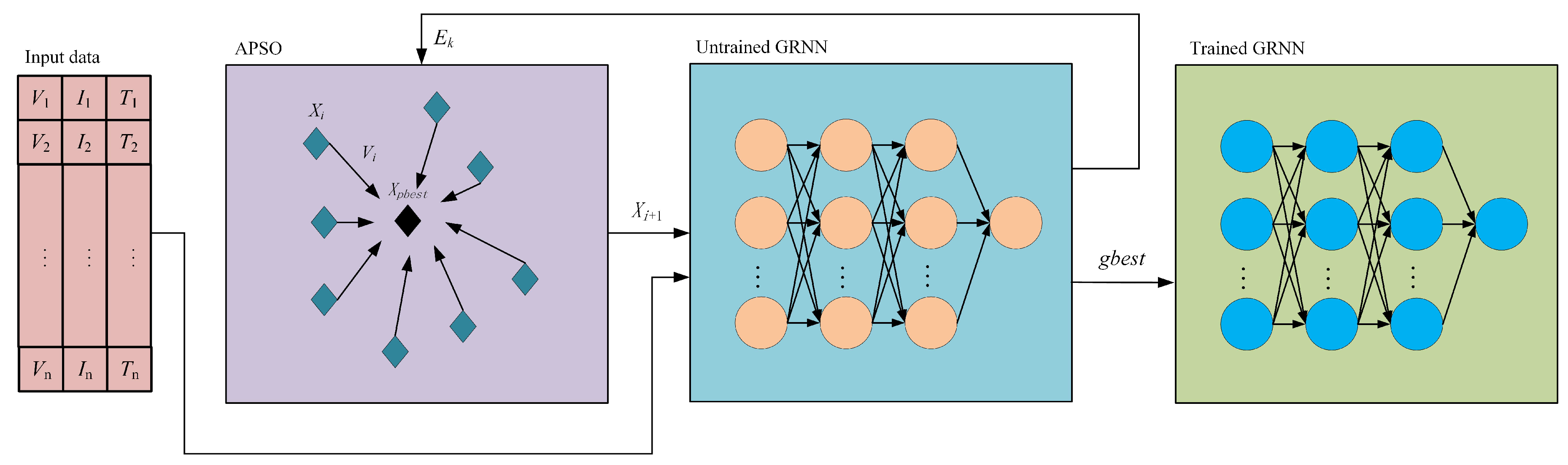
3.2. Optimization Process of APSO Algorithm

According to the model’s prediction error, APSO automatically adjusts the velocity weight of the particles to control the convergence speed and improve the model’s prediction accuracy. Assuming that the number of particles is n, the particle search space dimension is M and the basic particle swarm algorithm formula is

$$v_i^{k+1}=w{v}_i^k+c_1{r}_1(p_i^k-x_i^k)+c_2{r}_2(g_M^k-x_i^k)$$

(6)

$$x_i^{k+1}=x_i^k+v_i^{k+1}$$

(7)

$$\left\{\begin{array}{cc}-v_{max}& v_i^{k+1}<-v_{max}\\ v_{max}& v_i^{k+1}<-v_{max}\end{array}\right.$$

(8)

where k is the number of iterations, $x_i$ is the position vector of the particle, the corresponding velocity vector is $v_i$, $p_i$ is the historical optimal value of the particle, $g_M$ is the group optimal value in the current particle population, $c_1$ and $c_2$ are the learning factors, $c_1>0$, $c_1>0$, $r_1$, $r_2$ are random numbers in the range of [0, 1], and $v_{max}$ is the maximum velocity limit for the particle.

The weight parameter, denoted as w, is a critical component in particle swarm optimization. When the speed weight increases, the global optimization ability of the particle swarm improves while the local optimization ability decreases, and vice versa. Static weight parameters are insufficient to meet the requirements for convergence speed and global optimization simultaneously. Additionally, the number of neurons in the output layer of the GRNN is determined by the number of samples in the prediction set. However, due to the long discharge time of Ni-Cd batteries, the voltage drop gradient changes significantly at different times, resulting in decreased prediction accuracy. Moreover, the historical data of input samples exert various influences on the current SOC prediction results, and using a uniform weight in the summation layer further increases the error. To address these issues, the speed weight of particles requires adjustment. Specifically, we define the prediction model as $f\left(x\right)$ and the loss function as

$$E_k=\left|f(x,\sigma )-y_k\right|$$

(9)

where $y_k$ is the true value of the training set. To measure the magnitude of the error in the output of individual pattern layer neurons relative to the global one, a conditioning scoring function is introduced:

$$h_k=\frac{E_k-min\left(E_k\right)}{max\left(E_k\right)-min\left(E_k\right)}$$

(10)

The matrix $E_k$ represents the errors of the kth iteration output. The scoring function measures the magnitude of the prediction error relative to the overall prediction error. To obtain the score matrix h, the scores of n neurons are calculated and organized as $h_k={[h_{k1},h_{k2},\dots ,h_{kn}]}^T$. Although the scoring function indicates the size of the prediction error relative to the overall prediction error, larger values of $h_k$ correspond to worse prediction performance of the particle and thus require a higher weight. However, when the overall prediction error of the particle swarm is large, some particles may account for only a small fraction of it, which diminishes the global search ability of the swarm. Therefore, the bias vector B needs to be added to ensure the strong global optimization ability of the particle swarm in the early stages of iteration:

$$B=\frac{2}{T}ln\frac{E_k}{E_{target}}$$

(11)

T represents the number of iterations and $E_{target}$ is the error threshold the particle swarm should reach to stop the iteration. The bias vector decreases as the error decreases, enhancing the particle swarm’s global search ability in the early stages.

Although the scoring function can adjust the weight based on the error, it cannot evaluate the convergence of the particle swarm optimization algorithm. There may be a large prediction error but the algorithm has converged. Therefore, the polymerization degree is introduced to further optimize particle performance. This degree is defined as follows:

$$d=\frac{E_{gbest}}{E_{mbest}}$$

(12)

$E_{gbest}$ is the prediction error of the global optimal particle, $E_{mbest}$ is the average optimal fitness of all particles in the current era, and $0<d\le 1$. The degree of polymerization indicates the degree of aggregation of the particle swarm. The larger the value of d, the more concentrated the particles. When $d=1$, the particles converge at one point, indicating complete algorithmic convergence. If the particles are concentrated, the particle weight increases to enhance global optimization ability, whereas if they are dispersed, the particle weight is reduced to promote local search. The weight parameter expression is

$$w=B+{\beta }_1{h}_k+{\beta }_{2}d$$

(13)

The weight of fractional control is denoted by ${\beta }_1$ and the weight of aggregation control is denoted by ${\beta }_2$. The scoring function and the aggregation degree quantify the particle swarm’s individual error and convergence degree, respectively, and control the particles’ inertia weight w. This approach balances the particle swarm’s global and local search performance, and the scoring function determines the particles’ evolution direction. As a result, the model prioritizes data that have a more significant impact on the SOC at the current time, thereby improving the accuracy of SOC prediction.

3.3. Prediction Process of Battery SOC Based on APSO-GRNN Model

Although a GRNN is suitable for regression analysis, it is easily affected by the initial parameter matrix. To overcome this limitation, the APSO algorithm proposed in this paper has faster convergence and better global optimization ability than ordinary PSO. Optimizing the GRNN’s parameters using APSO can compensate for the GRNN’s defects. The GRNN model uses the battery terminal voltage V, output current I, and temperature T as input values, and the GRNN prediction model is used as the evaluation function $f\left(x\right)$. The specific steps in this approach are as follows:

• Initialize the particle swarm algorithm parameters. The initial particle population size is m × n, where m is the number of particle vectors, n is the number of neurons in the summation layer, and the number of iterations is T. The smoothing factor of each neuron in the summation layer is taken as the position attribute of the particle $x_i$, and the particle position parameters and matrix parameters are randomly initialized.

  $$x=\left[\begin{array}{ccc}{\sigma }_{11}& ...& {\sigma }_{1n}\\ ⋮& ⋮& ⋮\\ {\sigma }_{m1}& \cdots & {\sigma }_{mn}\end{array}\right]v=\left[\begin{array}{ccc}{v}_{11}& ....& v_{1n}\\ ⋮& ⋮& ⋮\\ v_{m1}& ...& v_{mn}\end{array}\right]$$

  (14)
• Assuming that the GRNN model is a fitness calculation model, the error matrix of the particle swarm is calculated using Equations (9) and (13) as e, and the error vector of a single particle is $E_i$.

  $$e=\left[\begin{array}{ccc}{E}_{11}& \cdots & E_{1n}\\ ⋮& \cdots & ⋮\\ E_{m1}& \cdots & E_{mn}\end{array}\right]E_i=\left[\begin{array}{c}{E}_{i1}\\ ⋮\\ E_{in}\end{array}\right]$$

  (15)
• The local optimal value $p_i$ and each particle’s global optimal value $g_M$ are updated according to the error matrix. The particle swarm velocity weight matrix w is modified using Equation (13), and the particle swarm position vector and velocity vector are updated using Equations (7) and (8).
• Repeat Steps 2 and 3 until the error of the global optimal particle is less than the target error $E_{target}$ or the maximum number of iterations $T_{max}$ and then end the iteration. The algorithm’s structure is shown in Figure 3.

4. Analysis of SOC Prediction Results of Ni-Cd Battery Using APSO-GRNN

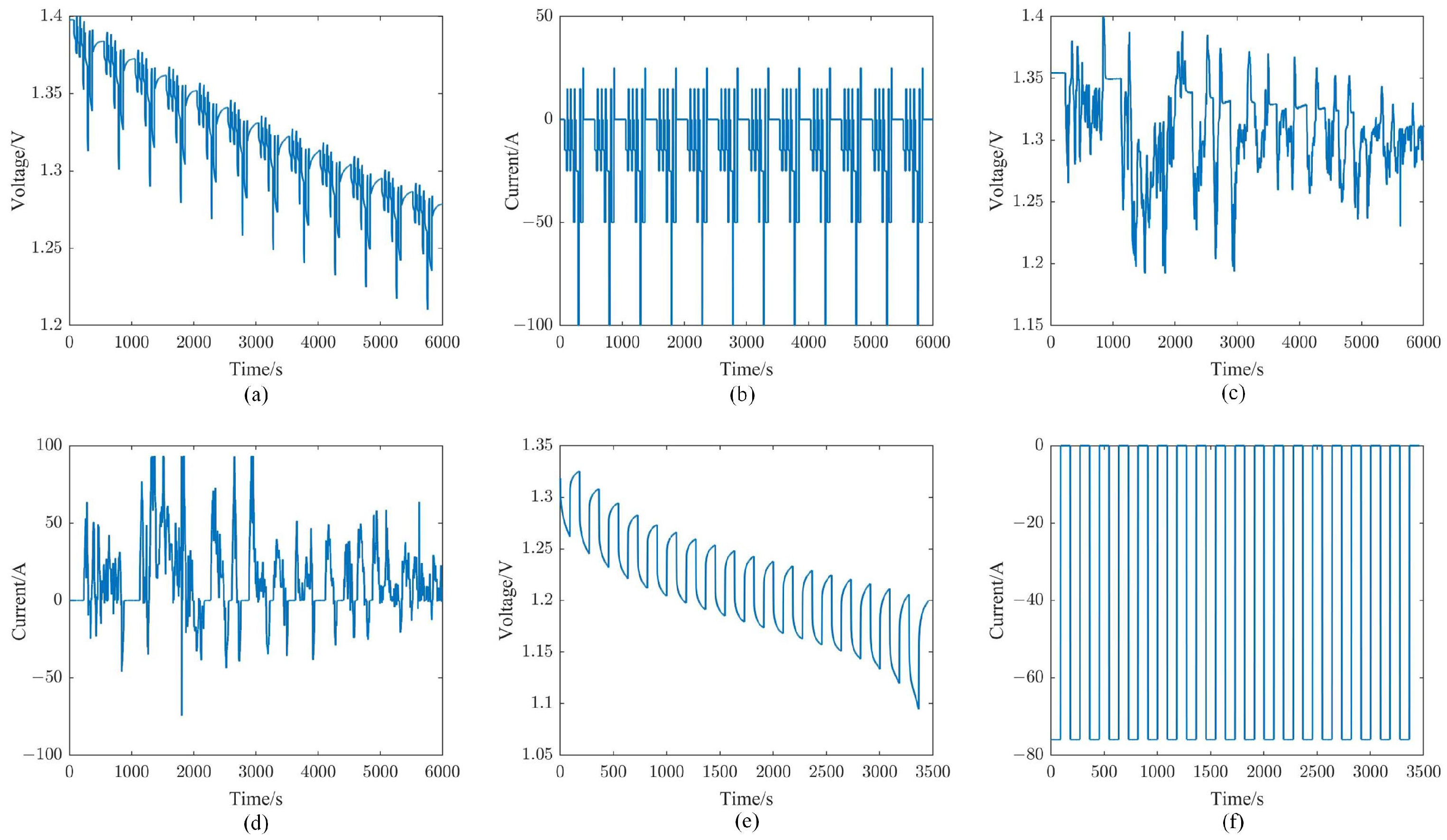
4.1. Test Platform and Experimental Method

A Ni-Cd battery installed on a 380A high-speed locomotive was used as the test object, and

Table 1. Detailed battery parameters.

Item	Parameter
Nominal capacity	190 Ah
Initial weight	6.1 kg
Initial voltage	1.35 V
Resistance	$1.35\mathsf{\Omega }$
Initial density	1.23 g/cm${}^3$

shows the detailed battery parameters. The nickel-cadmium battery was tested in a constant-temperature test chamber using the BTS-3000n power battery detection cabinet as the charging and discharging experimental platform. The charging and discharging voltage and current were adjusted to meet the experimental conditions and the acquisition module was used to measure them. The voltage measurement accuracy was ±0.1 mV, the current measurement accuracy was ±0.01 mA, and the battery discharge capacity was calculated accordingly. Multiple batteries were subjected to repeated experiments to verify the validity of the experimental data. The voltage, current, and other electrical data were transmitted to the host computer and stored in the database. Figure 4 shows the experimental platform used in the study.

The working condition method is widely considered the most scientific battery testing method. It involves splitting, cutting, simplifying, and statistically analyzing the power distribution of the battery to obtain a dataset that can be conveniently tested using charging and discharging equipment. This method can simulate the actual use of the battery and is suitable for evaluating the effectiveness of battery SOC prediction models.

In this study, we employed three different battery test conditions, a dynamic stress test (DST), a federal urban driving schedule (FUDS), and cyclic pulse conditions, to charge and discharge the battery. The DST and FUDS testing procedures outlined in the battery test manual are widely used and enable the formulation of battery charge and discharge strategies based on actual battery usage. Consequently, they comprehensively reflect feature vectors in battery usage and are suitable for training and testing SOC prediction models. Meanwhile, the pulse-discharge conditions reflect the electrical characteristics of the battery at different temperatures. A power battery cabinet was used to simulate these three test conditions, and the resulting data, including the discharge voltage, current, and temperature, were collected and used as the training data for the prediction model. The experimental steps are outlined in

Table 2. Experimental procedure for a battery.

Test Type	Experimental Process
DST	Step 1: The battery is discharged to the cutoff voltage (1 V) at a constant current rate of 0.5 C and a set temperature of 20 °C. Step 2: Static battery for one hour. Step 3: The battery is charged to the cutoff voltage (1.52 V) at a rate of 1 C and then charged to the cutoff current (20 A) at a constant voltage. Step 4: The charge-discharge cycle is set to 6 min and the charge-discharge experiment is carried out according to the DST power meter.
FUDS	Step 1: The battery is discharged to the cutoff voltage (1 V) at a constant current rate of 0.5 C and a set temperature of 20 °C. Step 2: Static battery for one hour. Step 3: The battery is charged to the cutoff voltage (1.52 V) at a rate of 1 C and then charged to the cutoff current (20 A) at a constant voltage. Step 4: Discharge under FUDS conditions.
Cyclic Pulse	Step 1: The battery is discharged to the cutoff voltage (1 V) at a constant current rate of 0.5 C and set temperature. Step 2: Static battery for one hour. Step 3: The battery is charged to the cutoff voltage (1.52 V) at a rate of 1 C and then charged to the cutoff current (8.5 A) at a constant voltage. Step 4: The discharge cycle is set to 15 min and the pulse-discharge experiment is carried out.

.

The experiments were carried out in a constant temperature test chamber at 20 °C for the DST and FUDS and at 0 °C, 10 °C, 30 °C, and 40 °C for the pulse-discharge experiments. The sampling period T was set to 1 s. Before the experiments, the discharge parameters such as the voltage, current, and power were loaded into the battery test cabinet. The changes in the battery voltage and current under these three working conditions are depicted in Figure 5.

Figure 5b,d illustrate the current under the DST and FUDS working conditions, respectively. These conditions involve three distinct states: discharging, standing, and charging. They provide a comprehensive description of the actual working state of the battery and can be used as training data for the model. Figure 5e,f demonstrate that transitioning from resting to discharging induced a noticeable voltage rebound. Therefore, the model must possess the ability to focus on correlated data, prioritizing the historical data that are most relevant to the test point. This correlation-focused ability enhances the accuracy of the model’s predictions.

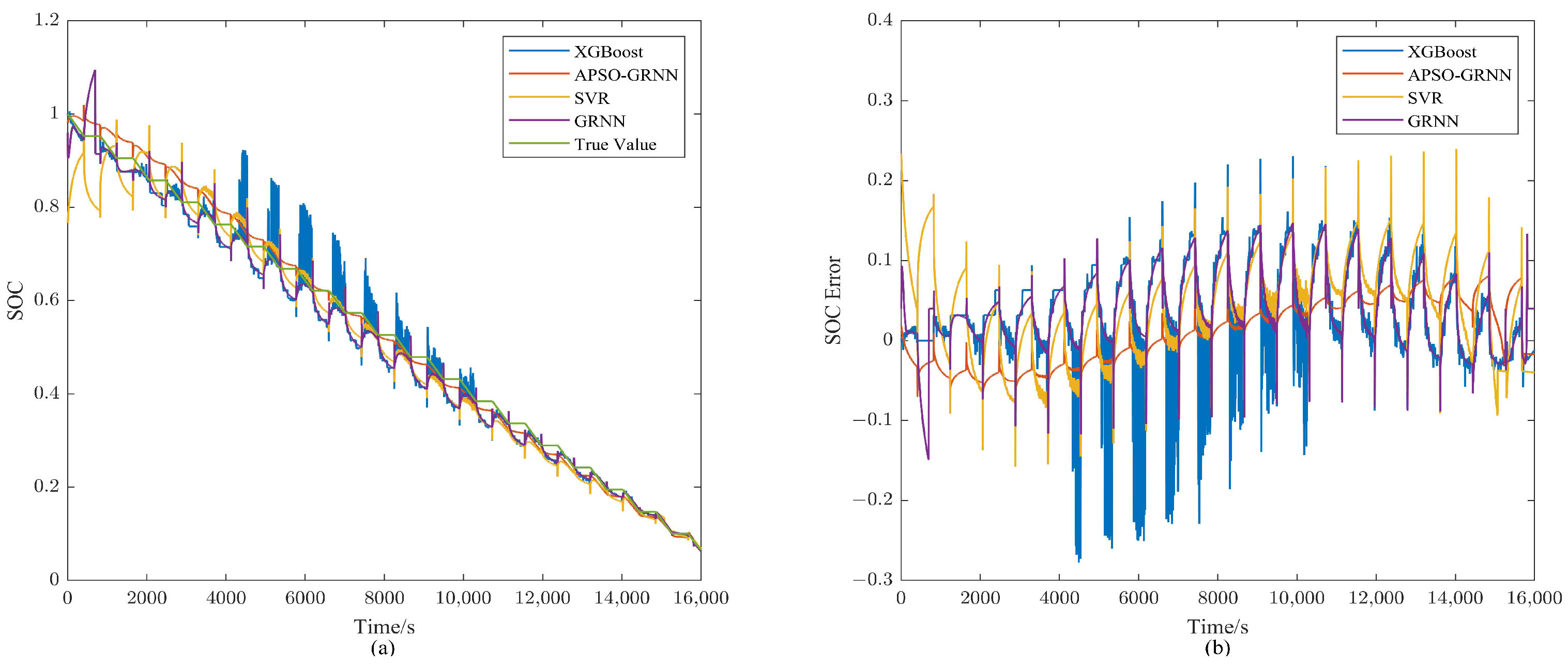
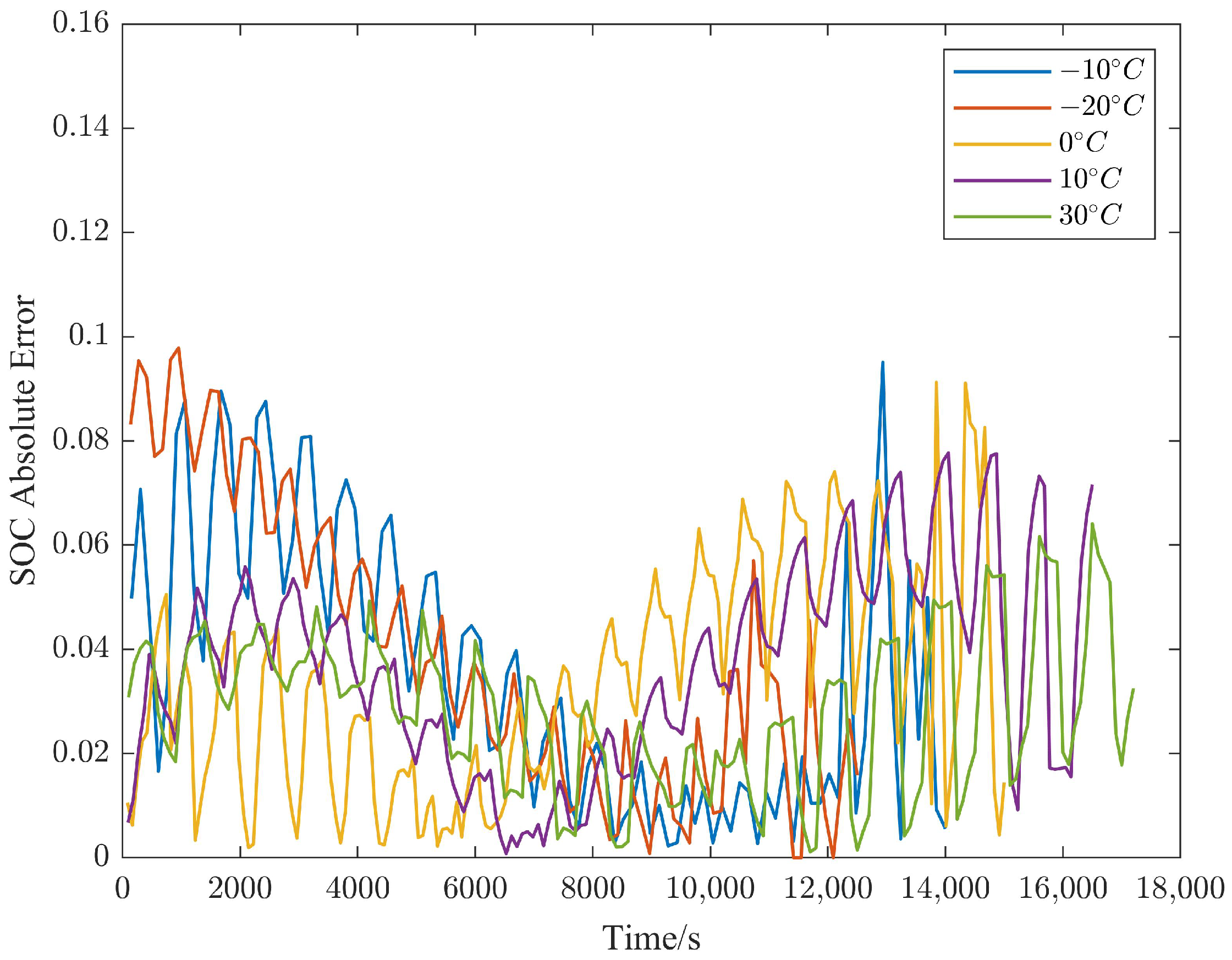
4.2. SOC Prediction Algorithm Results and Discussion

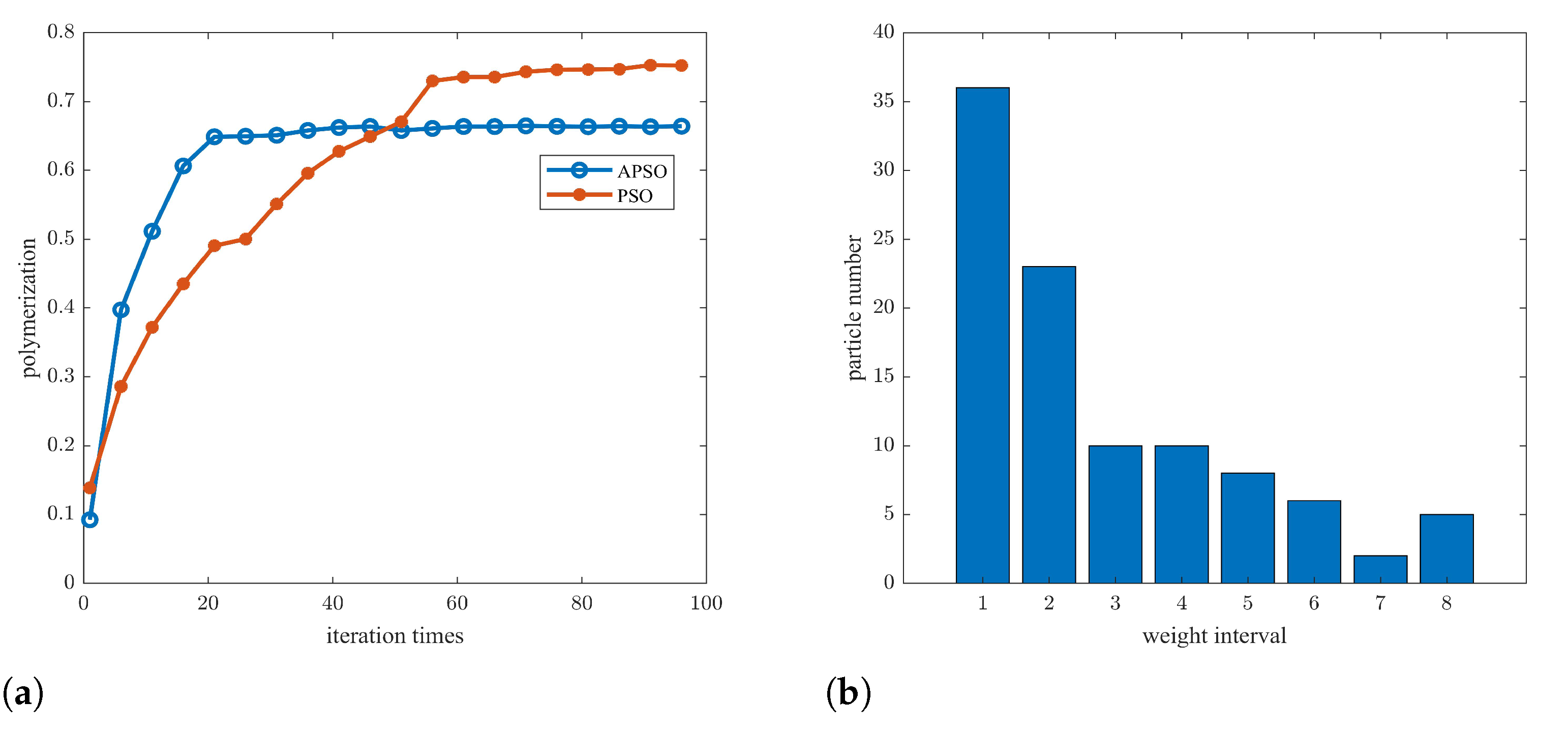
4.2.1. APSO-GRNN Model Training Results

The estimation of Ni-Cd battery SOC values is expected to have errors. Therefore, error assessment is an essential aspect of analyzing the accuracy of prediction algorithms [28,29]. Using only one form of error calculation is insufficient to assess the overall accuracy of the model. Thus, multiple forms of error calculation, such as the mean absolute error ($\delta$), root mean square error (${\delta }_{RMSE}$), and Pearson correlation (${\delta }_p$), are commonly used to comprehensively assess the accuracy of a model [30,31].

$$\delta =\frac{1}{N}\sum _{i=1}^N\left|\frac{y_i-y_i^{*}}{y_i}\right|$$

(16)

$${\delta }_{RMSE}=\sqrt{\frac{1}{N}\sum _{i=1}^N{(y_i-y_i^{*})}^2}$$

(17)

$${\delta }_p=\frac{{\sum }_{i=1}^N(y_i-\overline{y_i})(y_i^{*}-\overline{y_i^{*}})}{\sqrt{{\sum }_{i=1}^N(y_i-\overline{y_i})}\sqrt{{\sum }_{i=1}^N(y_i^{*}-\overline{y_i^{*}})}}$$

(18)

To verify the accuracy and advantages of the model proposed in this paper, three common regression prediction models were selected for comparison with the APSO-GRNN: the support vector regression algorithm (SVR), unoptimized generalized neural network (GRNN), and extreme gradient boosting algorithm (XGBoost). The parameters of each model are shown in

Table 3. Initial parameters of the model.

Model	Parameter
SVR	Kernel function: radial basis; Penalty factor: 2.5
XGBoost	Number of decision trees: 200; Learning rate: 0.05; Depth of a single tree: 6
GRNN	Smoothing factor: 0.2; Number of neurons: 100
APSO-GRNN	Initial particle position: random numbers ranging from 0.01 to 0.5; Initial velocity weight: 1; Learning factor: 2

:

The training process for estimating Ni-Cd battery SOC values began with the FUDS data, with a 7:3 ratio used to divide the data into training and verification sets. Cross-validation was used to enhance the efficiency of data utilization. The proposed model was used as the pre-training model, and the training continued based on the pulse-discharge experimental data acquired at 40 °C. The use of pre-trained models can enhance the robustness of the algorithm. Finally, the model was evaluated using a noisy DST dataset and cyclic pulse dataset at different temperatures.

The FUDS adopted a discharge strategy that accounted for the actual power change of the battery, resulting in significant differences in voltage and current distribution compared to the pulse-discharge experiments. Using these data to train the model can enhance the robustness of the model. The APSO-GRNN model demonstrated better stability and prediction accuracy than the other three models under the FUDS conditions, with more minor prediction errors and fluctuations, as shown in Figure 6a. The APSO-GRNN model maintained high prediction accuracy even under conditions where there were significant differences in the voltage and current distribution. Moreover, Figure 6b shows that the correlation between the APSO-GRNN model’s predicted results and the actual values was more robust than that of the other three models. Combined with Figure 5e, it can be seen that the APSO-GRNN model can reduce the impact of voltage rebound on battery SOC prediction and improve prediction accuracy. The degree of polymerization indicates the degree of particle aggregation and its stabilization indicates algorithm convergence.

The degree of polymerization represented the degree of aggregation of the particles, and as the degree of polymerization no longer changed, this indicated the algorithm’s convergence. Figure 7a shows that APSO converged faster than PSO, with a final particle aggregation degree of 0.66, which was lower than that of PSO at 0.78. These results support the conclusion that APSO has a stronger local search ability compared to PSO. Figure 7b also shows that the APSO-GRNN model can enhance particle diversity compared to the unoptimized GRNN model, making it less likely to fall into local optima and improving the comprehensive search for optimal values.

4.2.2. Model Robustness Test Results for Noise

To further verify the superiority of the APSO-GRNN model, Gaussian white noise was introduced into the original DST working condition data, and the processed data were used as input in the trained model for prediction. The prediction results are shown in Figure 8a,b. After adding Gaussian white noise, each model’s error and mean square error increased. To further observe the prediction errors of the three prediction algorithm models, the average relative error, root mean square error, and Pearson correlation of the three average models were calculated, and the data are shown in

Table 4. Prediction errors of noisy data.

	$\mathit{\delta }$	${\mathit{\delta }}_{\mathbf{RMSE}}$	${\mathit{\delta }}_{\mathit{p}}$
SVR	4.58	0.0237	0.9597
XGBoost	3.59	0.0184	0.9656
GRNN	3.86	0.0189	0.9534
APSO-GRNN	1.70	0.0107	0.9789

.

Table 4 shows that the model developed in this study produced better prediction results on the noisy DST dataset than the other three models. The mean absolute error of the state-of-charge (SOC) prediction was less than that of the GRNN, XGBoost, and SVR models by 57.25%, 58.12%, and 63.97%, respectively. Moreover, the correlation coefficient of the predicted values was more robust compared to the other three models. Additionally, Figure 8 shows that the variation in the relative error of the model developed in this study was smaller compared to the GRNN and XGBoost models. The SVR model exhibited overfitting due to the limited amount of data used, leading to a significant increase in the error on the training set. The decision tree in the XGBoost model was susceptible to interference effects, resulting in a significant variation in the prediction error. The unoptimized GRNN model had the same neuron weight as the model layer, leading to a more significant influence of historical time data on the current time node, especially toward the end of the discharge process. The adaptive particle swarm optimization algorithm used in the model developed in this study adjusted the velocity weight of the particle swarm to converge the neuron weights to the corresponding optimal value. This allowed the model to prioritize the historical data that had a more significant impact on the current moment, thereby improving the prediction accuracy and anti-interference ability of the model, reducing the variation in the prediction error, and accelerating convergence.

4.2.3. Model Robustness Test Results for Temperature

The temperature greatly influenced the available capacity and discharge time of the battery [32]. To study the prediction effect of the model at different temperatures, pulse-discharge experiments of the battery at different temperatures were carried out. The experimental results are shown in Figure 9.

The results in Figure 9 indicate that an increase in temperature led to an increase in both the available capacity and discharge time of the battery, whereas a decrease in the temperature resulted in a lower available capacity and shorter discharge time. Thus, temperature is a critical parameter in the SOC prediction model. Since the model training set only included battery discharge data at 20 °C and 40 °C, this study used 10 °C pulse-discharge data to verify the advantages of the APSO-GRNN model over the other models in terms of prediction accuracy and robustness. Figure 10a,b display the experimental outcomes, and the data are presented in

Table 5. Pulse data prediction error.

	$\mathit{\delta }$	${\mathit{\delta }}_{\mathbf{RMSE}}$	${\mathit{\delta }}_{\mathit{p}}$
SVR	6.86	0.0378	0.9421
XGBoost	5.09	0.0326	0.9561
GRNN	7.11	0.0418	0.9452
APSO-GRNN	2.56	0.0176	0.9746

.

An implicit relationship between the battery discharge data at different temperatures can be established by introducing a pre-training method. The experimental results demonstrated that the prediction errors of the SVR, XGBoost, and GRNN models increased significantly and fluctuated considerably when experiments were conducted at different temperatures, especially in the early and late stages of discharge, where different temperatures led to a substantial variation in the voltage distribution, thereby amplifying the prediction errors. The APSO-GRNN model fine-tuned the model based on the previous training results using the pre-training model and adaptive adjustment mechanism, acquiring a mapping of the implicit relationship between the different temperatures, which improved the model’s robustness. Although the prediction error of the APSO-GRNN model also increased, the error fluctuated considerably only in the early stage of discharge, as seen in Figure 10b. As the battery SOC decreased, the voltage distribution difference gradually decreased, thereby reducing the prediction error of the APSO-GRNN model.

Figure 9 shows a clear degradation in the battery capacity when operating below 0 °C, accompanied by a voltage distribution that significantly deviated from the discharge data observed at room temperature. To investigate the prediction accuracy of the model at different temperatures, prediction experiments were conducted at different temperature nodes. The corresponding experimental outcomes are presented in Figure 11.

The results presented in Figure 11 indicate that the model exhibited its highest prediction accuracy at approximately 30 °C, yielding an average relative error of 2.51%. Conversely, the lowest prediction accuracy was observed at −20 °C, with an average relative error of 4.11%. As the temperature decreased, both the battery’s discharge capacity and the magnitude of the prediction error increased. Notably, the prediction error in the early stage was large, and the stability of the model decreased. This phenomenon can be attributed to the reduced available capacity of the battery and the substantial voltage rebound experienced under low ambient temperatures. When the battery was discharged rapidly, its terminal voltage declined sharply. Compared to normal temperature conditions, the rate of the voltage decline exhibited a significant increase, which resulted in a substantial disparity in the voltage distribution, leading to a drop in the accuracy of the model predictions.

5. Conclusions

• The advantages and disadvantages of SOC prediction models proposed in the literature were analyzed, and a GRNN model with adaptive adjustment was proposed based on the characteristics of nickel-cadmium batteries. This contribution enriches the research methods for the SOC prediction of nickel-cadmium batteries and provides a new theoretical reference for developing energy management strategies for train battery packs.
• A comparison of the prediction results of the APSO-GRNN and GRNN models showed that APSO can enhance the diversity of mode-layer smoothing factors and improve the accuracy of SOC prediction. It was demonstrated that APSO can filter the time series and adjust the size of each neuron smoothing factor based on the correlation of the time series. Thus, the model prioritizes historical data that has a more significant impact on the current moment.
• Two experimental scenarios were designed to verify the robustness of the APSO-GRNN model against noise interference and temperature changes. The prediction results were compared with those of the GRNN, SVR, and XGBoost models. The experimental results demonstrated that the APSO-GRNN model can maintain a high prediction accuracy, even under changing experimental conditions, temperatures, and noise interference.
• The APSO-GRNN model is suitable for the online prediction of the SOC of nickel-cadmium batteries due to its reduced number of parameters, shorter training time, and stronger real-time performance. It can be deployed in an onboard battery management system (BMS) to provide a theoretical basis for battery energy management strategies. In future research, we plan to broaden the scope of this study by incorporating real-world applications of train Ni-Cd batteries.