Development of Pitch Cycle-Based Iterative Learning Contour Control for Thread Milling Operations in CNC Machine Tools

Abstract

The helical contour motion accuracy of feed drive axes is important for thread milling operations in computer numerical control (CNC) machine tools. However, the motion dynamics and external disturbances significantly affect the contour motion results, while the feed drive axes perform helical motions in thread milling operations. Although existing iterative learning contour control (ILCC) methods can improve contour motion accuracy, the problems of data recording and processing on memory usage and computational burden in control systems, wasted materials, and increased costs in thread manufacturing still limit the practical applications of ILCC. Therefore, considering the similar motion dynamics and external disturbances of the feed drive axes during the pitch cycle motions of a helical path, this study developed a pitch cycle-based iterative learning contour control (PCB-ILCC) method to address the control system and thread manufacturing problems caused by the use of ILCC. For PCB-ILCC, this study adopted contour error vector estimation by referring to the interpolated positions on the pitch cycle of the helical path to simplify the computational complexity and designed the ILCC using the cycle learning method to easily implement the ILCC structure. Thus, this study developed a permanent magnet synchronous motor (PMSM) driving control utilizing the robust control method to mitigate the problems of motion dynamics and external disturbances on the feed drive axes. Thread milling experiments performed on a five-axis CNC machining center demonstrated the feasibility of the PCB-ILCC and validated that it can significantly improve the helical contour motion accuracy of the feed drive axes and achieve an 80% contour error reduction rate in comparison with the proportional–proportional–integral control, which is extensively used in commercialized PMSM drivers and CNC controllers.

1. Introduction

A thread milling operation is a machining process in which the feed drive axes of a machine tool simultaneously move a thread milling tool along a helical path to perform a cutting operation. Therefore, the helical contour motion accuracy of feed drive axes while performing thread milling operations becomes crucial. In recent decades, owing to the importance of the contour motion accuracy of computer numerical control (CNC) machine tools, many contour control designs have been proposed to improve the contour motions of feed drive axes. Liu et al. [1] proposed a velocity-based contour control method that used a B-spline-based wavelet neural network to approximate unknown dynamics and used neural network identification to design a robust control to improve the contour motion of dual-linear-motor-driven gantry stages. Chen et al. [2] transformed the desired contour path and tool orientation in the workpiece coordinate frame to a five-dimensional hypercurve in a machine coordinate frame and then adopted the equivalent error method to design a contouring controller to reduce the errors of the contour path and tool orientation. Zhao et al. [3] compensated weighted contour error components to velocity commands in the robotic task space of a six-degrees-of-freedom robot arm. They proposed a component-based contour control mechanism that can improve the contour motion accuracy of the robot arm performing machining tasks. Liu et al. [4] integrated generalized predictive control and feedback correction algorithms to develop a real-time contour error control design for five-axis machine tools. Bo et al. [5] improved the conventional cross-coupled control design to increase the contour accuracy of biaxial motion control systems. Li et al. [6] adopted a neural memory network to develop a contour error estimation and compensation method for CNC systems. Song et al. [7] designed a five-axis cross-coupling control method in joint space to simultaneously reduce task-space and joint-space contour errors. Wang et al. [8] referred to the calculations of distance and contour errors and adopted the trajectory compensation method with gain adjustment to modify the reference trajectory for improving the contour control performance of motion control systems. Zhang et al. [9] considered the input and output data of a two-dimensional linear motor system while performing reciprocating motions and then proposed a model-free adaptive control algorithm that can improve the contour motion accuracy of the linear motor system. Kuang et al. [10] proposed a discrete-time fractional-order sliding-mode contour error control design based on fractional-order sliding surface stability analysis and linear matrix inequality. Ma et al. [11] proposed an equivalent-plane cross-coupling control design to apply the developed biaxial cross-coupling control to three-axis contour error control. Shi and Lou [12] transformed a three-dimensional contour coordinate frame into a two-dimensional contour coordinate frame represented by radial and angular axes and then adopted the computed-torque control and proportional-derivative control to design a motion controller. Wang et al. [13] proposed a contour error control design based on the generalized extended state observer and model predictive control to reduce the contour errors of networked multi-axis motion systems caused by network-induced delays. Many contour control designs that can effectively improve the contour motion accuracy of the feed drive axis have been proposed; however, most of them focus on improving contour motion properties, but the adverse influence of external disturbances on the feed drive axes has yet to be carefully discussed. Particularly, the cutting force in the thread milling operations affects the contour motion accuracy of feed drive axes while performing a helical path. Disturbance estimation and friction compensation can effectively suppress the influence of external disturbances but cannot mitigate the motion perturbation induced by model uncertainty and external disturbance variation.

For repeatedly performed positional command paths, if repeated external disturbances influence the motion of a feed drive axis, iterative learning control can effectively suppress the influence of external disturbances and provide better positional motion results to the feed drive axis. Therefore, iterative learning control was applied to design iterative learning contour control (ILCC) to improve the contour motion accuracy of feed drive axes. Li et al. [14] adopted a hidden Markov model to spatially map the command path and actual trajectory, and proposed a hybrid evaluation function to estimate the contour error of the tool position and orientation. Furthermore, they used spatial iterative learning control to compensate for the contour errors and generate numerical control commands to improve the contour accuracy of five-axis CNC machine tools. Wang et al. [15] transformed the planar motion in a Cartesian coordinate frame into a polar coordinate frame, defined the polar-radius error, and designed a real-time iterative compensation method to reduce the polar-radius error-equivalent contour error for planar motion control systems. Based on a third-order contour error prediction model, Wang et al. [16] proposed an online iterative trajectory pre-compensation control design to improve the contour motion performance of multi-axis motion systems. Considering that motion control systems are usually influenced by factors such as model parameter variations, external disturbance, and non-linear friction, Yuan and Zhao [17] adopted the asymmetric Gaussian-like function to design an adaptive learning law and then suggested contour error control using the iterative learning method. Xu et al. [18] considered the properties of motion trajectory and time-varying random disturbance to design a time-varying weighting matrix and then proposed a norm-optimal cross-coupling iterative learning control using a time-varying control method. Li et al. [19] transformed the dynamic model of the motion control system from time domain to space domain and then proposed the spatial iterative learning control. Xu et al. [20] proposed a double-iterative learning and cross-coupling control design to improve the individual axis and contour tracking performance of biaxial motion systems. Hendrawan et al. [21] proposed an ILCC design that modified numerical control programs by an iterative approach to improve the contour motion performance of the feed drive axes of a CNC machine tool. Hendrawan et al. [22] referred to contour errors and proposed an embedded ILCC that can diminish the contour errors of a CNC machine tool during feed drive motions by iteratively modifying the reference trajectory of each feed drive axis. Due to the complexity of contour error models and the requirement of a large amount of collected data and processing time while using the offline iterative learning control, Dao and Chen [23] developed an online iterative learning control that referred to equivalent contour errors as the control target. Ling et al. [24] adopted the concept of position domain control and then designed the cross-coupled iterative learning control to improve the synchronization and performance of non-linear contour tracking motions. Simba et al. [25] integrated the proportional-derivative control and disturbance observer to develop an ILCC that can simultaneously improve contour motion accuracy and degrade the influence of external disturbance on the feed drive axes of a CNC machine tool. Based on the Newton extremum-seeking algorithm, Wang et al. [26] proposed an ILCC design to project contour errors to each motion axis and then adjust the axial position reference commands using an iterative learning approach. Although the ILCC can effectively reduce the contour errors of feed drive axes while performing repeated positional command paths, the motion control design of each feed drive axis must mitigate the adverse influence of model uncertainty and external disturbance variation. In addition, feed drive axes must have similar motion dynamics and external disturbance properties to match multi-axis motions and increase contour accuracy. Moreover, an ILCC that combines contour error estimation and iterative learning control must have an easy-to-implement control structure and must not excessively increase the computational burden of motion control systems to facilitate the realization of ILCC in industrial applications.

During thread milling operations, the three feed drive axes of a CNC machine tool perform synchronous motions along a helical path so that the thread milling tool can move along the helical path for thread cutting. Therefore, the cutting force in milling operations and the motion dynamics and friction disturbance of each feed drive axis affect the contour motion accuracy of feed drive axes while performing helical paths. Existing ILCC methods can improve the contour motion accuracy of feed drive axes; however, motion control systems were required to record and process a large amount of collected data, requiring longer data processing and computing time that usually increases the computational burden. In addition, before the convergence of the applied iterative learning processes, the existing ILCC could produce a few defective products due to the low contour control accuracy, which waste materials and increase manufacturing costs. A helical path consists of multiple pitch cycles, and, thus, feed drive axes perform repeated synchronous motions in pitch cycles. Moreover, during the motions of pitch cycles in a thread milling operation, feed drive axes possess the same motion dynamics and influence of the cutting force and friction disturbance. Therefore, this study developed a pitch cycle-based ILCC (PCB-ILCC) to address the control system and thread manufacturing problems caused by applying the ILCC to thread milling operations. The PCB-ILCC applied the ILCC to pitch cycles so that the contour error produced by feed drive axes while performing synchronous motions in the previous pitch cycle can be used to compute and modify the positional commands of synchronous motions in the current pitch cycle. Thus, the PCB-ILCC, pitch by pitch, gradually improves the contour motion accuracy of feed drive axes while performing helical paths. To achieve the design goal, the PCB-ILCC must integrate with the contour error vector (CEV) estimation method without excessive computational burden, the ILCC design with a simple and easy-to-implement structure, and the driving control design of the feed drive axis with robust motion properties. Therefore, this study estimated the CEV by referring to the interpolated positions on the helical cycle and the response positions on the response cycle produced by the feed drive axes. The ILCC design with the previous cycle learning method was modified and applied to generate a command cycle for the feed drive axes. This study also considered the dynamic characteristics of the feed drive axis actuated by a permanent magnet synchronous motor (PMSM) and applied the robust control with friction and dynamic compensations to design a PMSM driving control so that the feed drive axes can have robust motion performance.

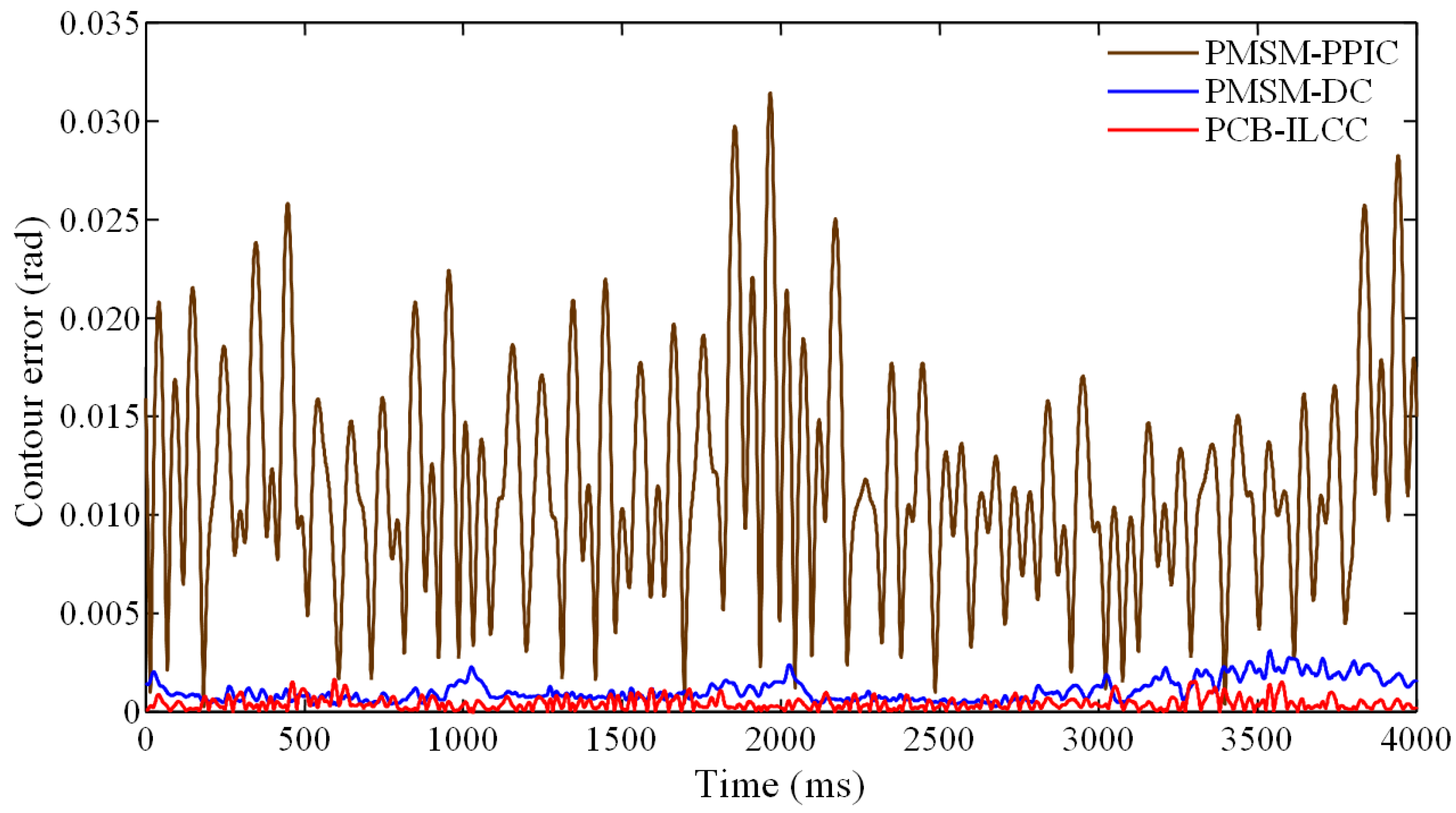
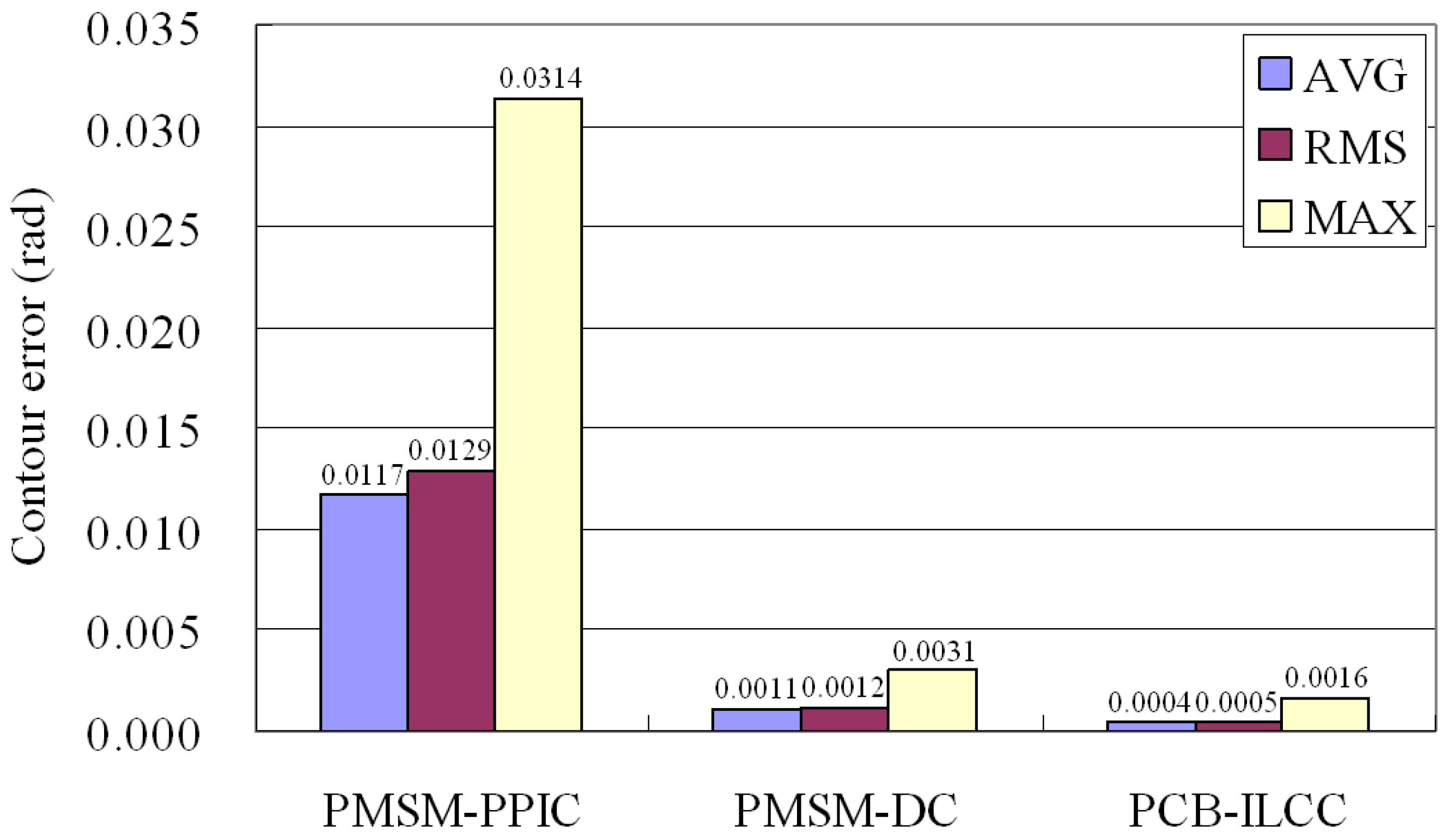
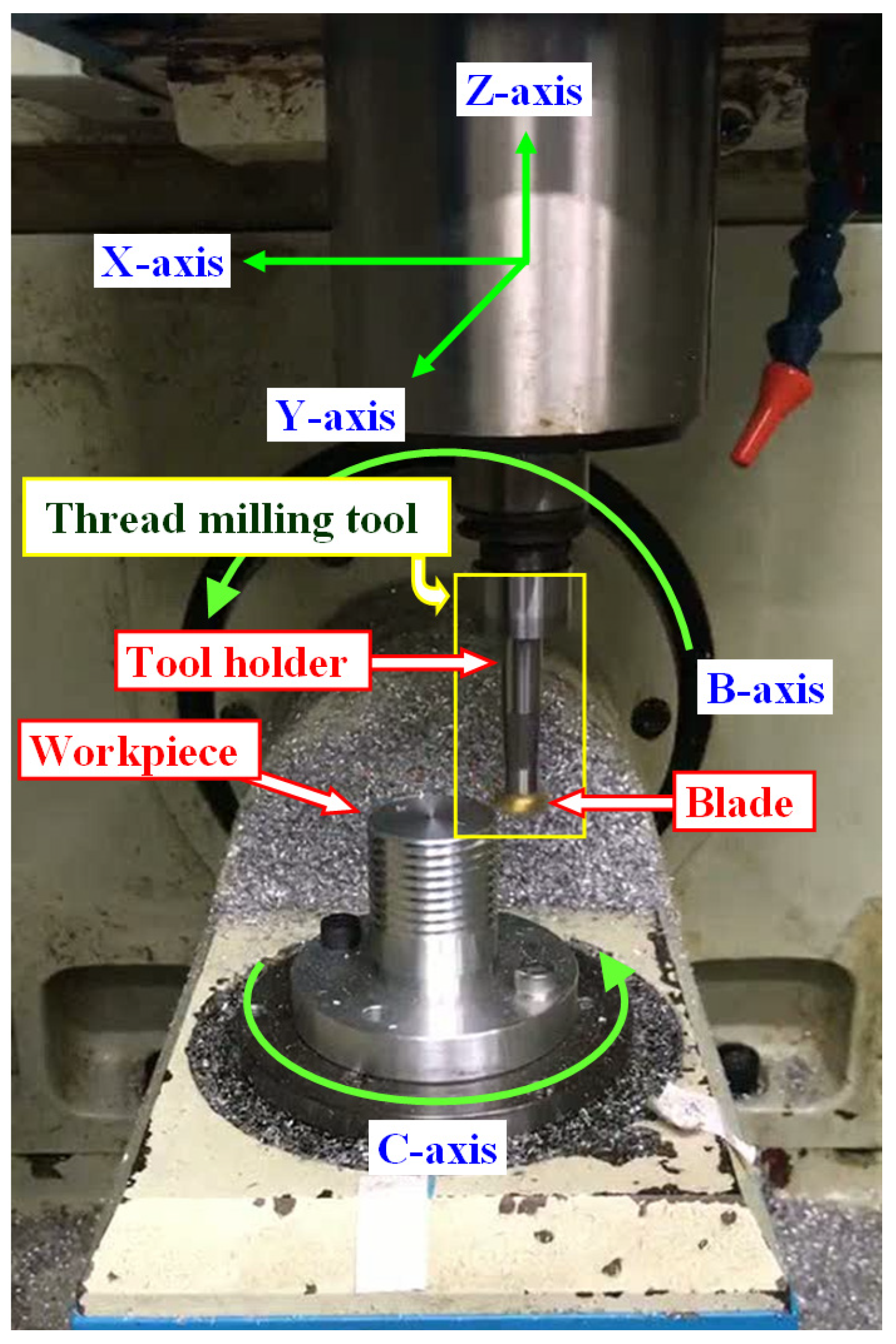
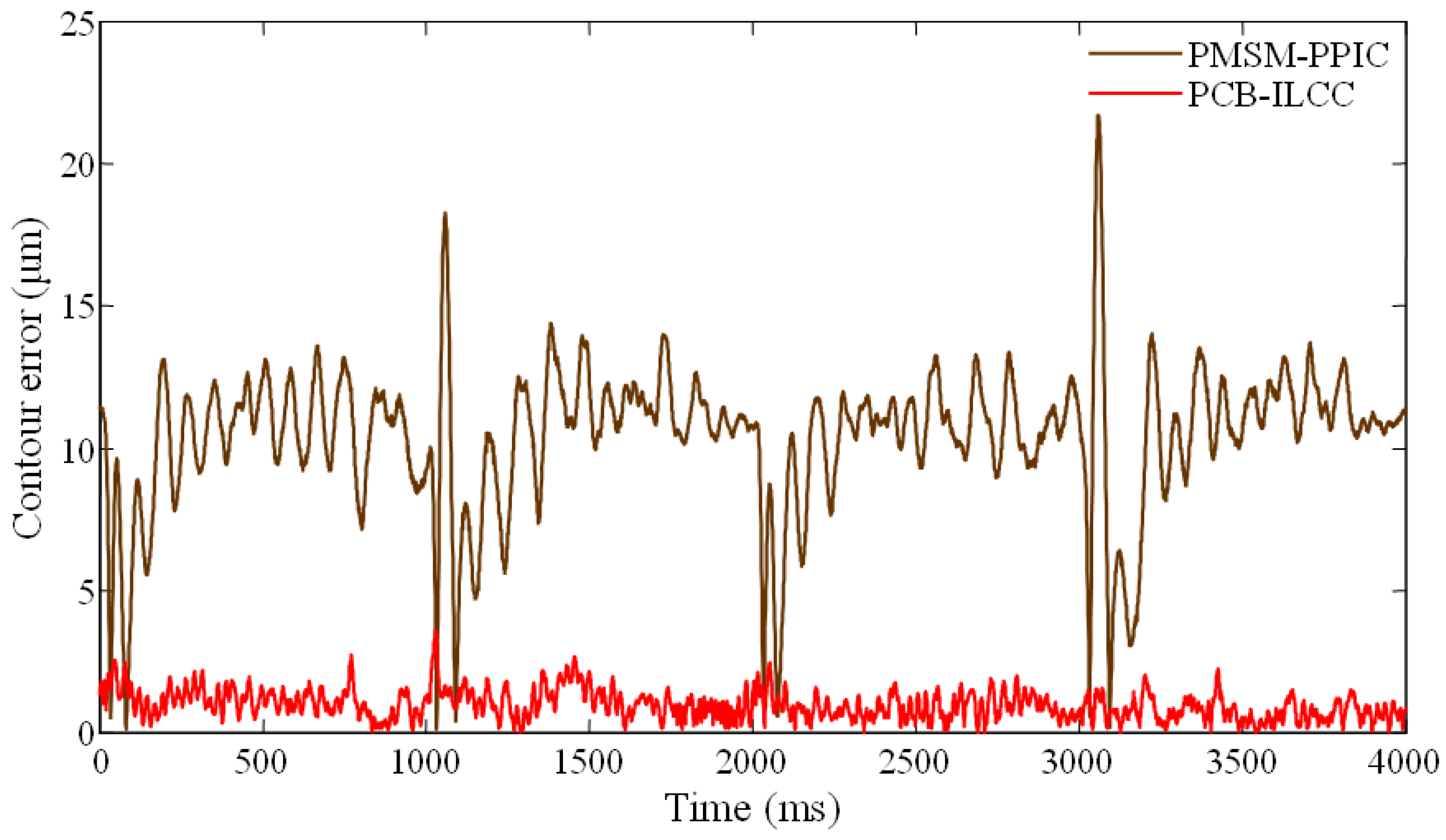
To evaluate and validate the feasibility and performance of the PCB-ILCC design, this study performed a PMSM motion control experiment on a PMSM testbench and a machine tool thread milling experiment on a five-axis CNC machining center. The results of this experiment showed that in comparison to the proportional–proportional–integral control extensively used in commercialized PMSM driving control, the rate of reduction achieved by the PCB-ILCC is significant. The reduction rates of the average, root-mean-square, and maximum contour errors achieved were 96.27%, 95.92%, and 94.76%, respectively. The machine tool thread milling experiment results indicated that the PCB-ILCC could provide good helical contour accuracy even though the feed drive axes suffered the adverse influence of the friction disturbance and cutting force. The reduction rates of the average, root-mean-square, and maximum contour errors achieved 90.56%, 89.68%, and 83.35%, respectively. Therefore, the experimental results validated that the PCB-ILCC can effectively mitigate the adverse influence of the friction disturbance and cutting force to significantly improve the contour accuracy of the feed drive axes while performing the helical path in thread milling operations.

This paper is organized as follows. Section 2 describes the design of the PCB-ILCC and the difference between the PCB-ILCC and conventional ILCC designs. Section 3 presents the CEV estimation method and the ILCC design with previous cycle learning. Section 4 presents the PMSM driving control design for the feed drive axes with robust motion performance. Section 5 presents the experimental results performed on a PMSM testbench and a five-axis CNC machining center to demonstrate the feasibility and performance of the PCB-ILCC developed in this study. Section 6 concludes this paper.

2. Design of PCB-ILCC

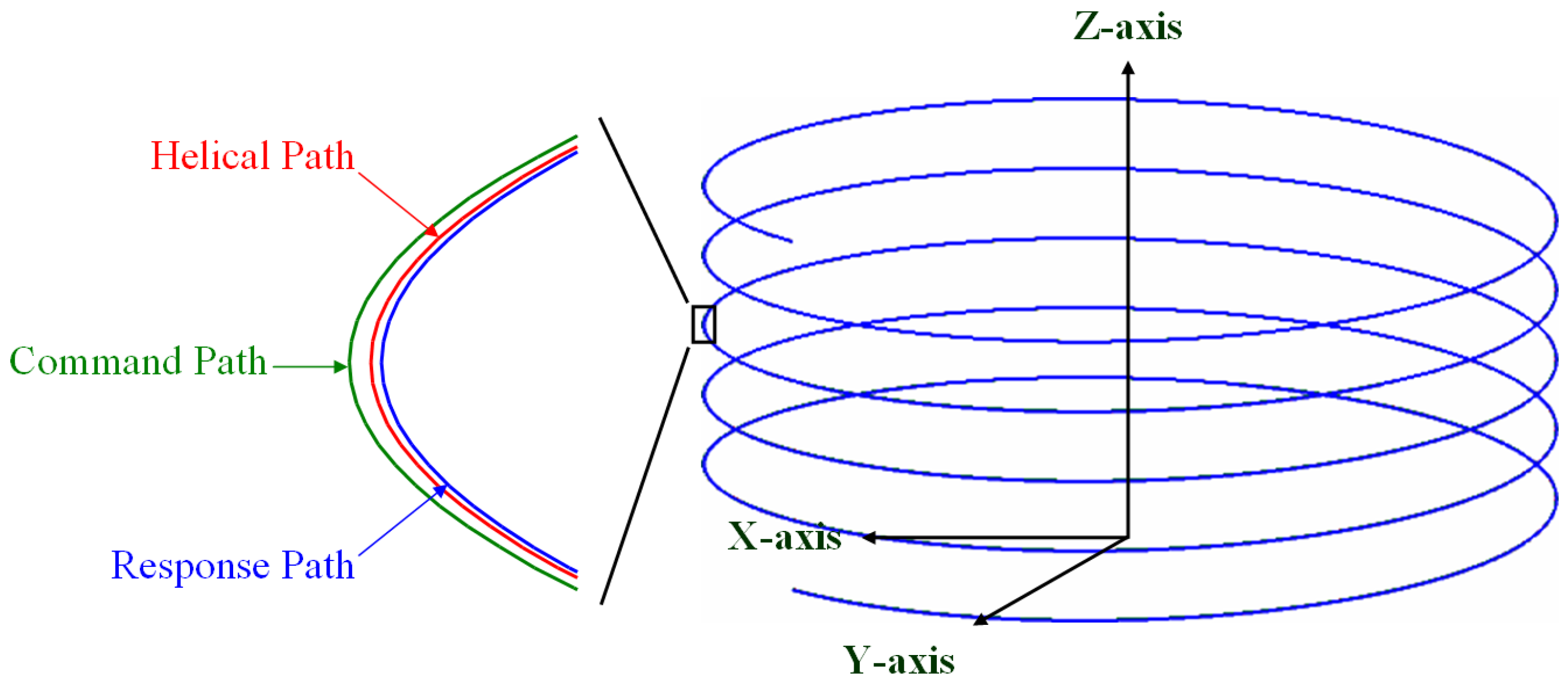
Three paths are considered in thread milling operations, including the helical, command, and response paths, as shown in Figure 1. Here, the helical path denotes the path formed by the thread contour to be machined, the command path represents the path referenced by the feed drive axes, and the response path denotes the path produced by the feed drive axes. For thread milling operations, the feed drive axes perform synchronous motions for the given command path so that a thread milling tool can move along the response path for thread cutting. Conventionally, the command path is given as the helical path, and the feed drive axes are controlled so that the response path can accurately follow the command to make the thread milling tool perform precise helical motions. However, due to the external disturbances and motion dynamics of feed drive axes, the response path is generally different from the command path; thus, the accuracy of helical motions is limited.

Applying conventional ILCC methods, as shown in Figure 2, the command path can be iteratively modified to reduce the contour error between the helical and response paths. Here, ${\mathrm{P}}_k$ and ${\mathrm{R}}_k$ denote the command and response paths at the $\left(k\right)$th iteration, respectively. The helical path $\mathrm{H}$ and response path ${\mathrm{R}}_k$ were used to calculate the contour error ${\mathsf{\epsilon }}_k$ at the $\left(k\right)$th iteration. Then, the contour error ${\mathsf{\epsilon }}_k$ was recorded in memories for further use in the next iteration. ${\mathrm{P}}_{k-1}$, that has been recorded in memories, denotes the command path at the $\left(k-1\right)$th iteration. The recorded contour error ${\mathsf{\epsilon }}_{k-1}$ and command path ${\mathrm{P}}_{k-1}$ were adopted by an iterative learning contour controller to modify the command path ${\mathrm{P}}_k$. The command path ${\mathrm{P}}_k$ was referenced by the feed drive axes to produce the response path ${\mathrm{R}}_k$, and was recorded in memories for further use in the next iteration. Although conventional ILCC methods can improve the accuracy of helical motions, ILCC methods usually require huge memories to record a large amount of collected data and take longer data processing and computing time. Therefore, ILCC methods are usually difficult to implement on compact controllers with a limited number of memories and computation speed. Furthermore, ILCC methods could produce a few defective products before achieving convergence, increasing manufacturing costs.

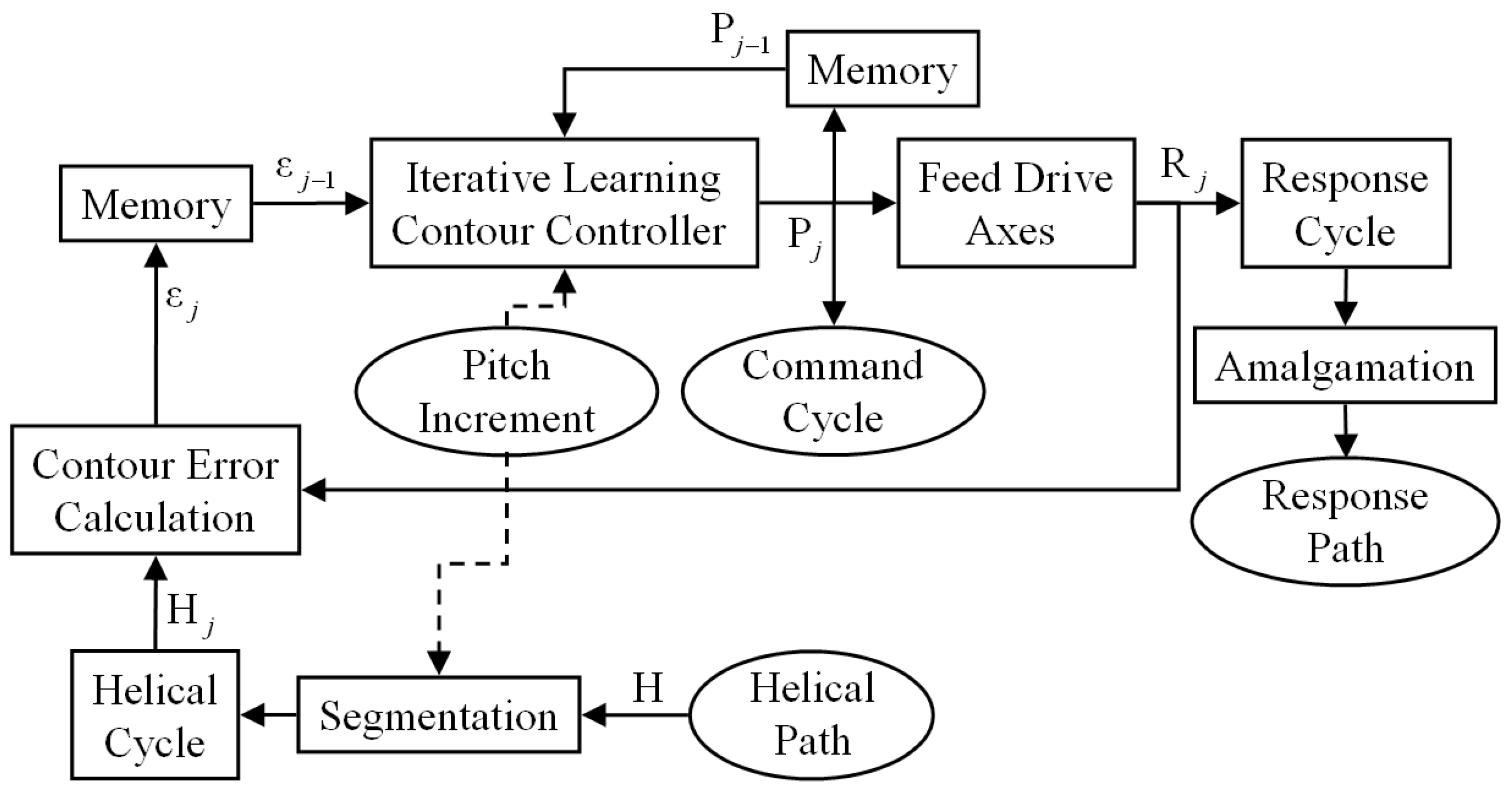
Since a helical path is composed of multiple pitch cycles, and feed drive axes generally possess similar external disturbances and motion dynamics during pitch cycle motions, the PCB-ILCC developed in this study applies the ILCC to the pitch cycles so that the contour error of the previous pitch cycle ${\mathsf{\epsilon }}_{j-1}$ can be considered with the previous command cycle ${\mathrm{P}}_{j-1}$ to modify the current command cycle ${\mathrm{P}}_j$ through the iterative learning contour controller, as shown in Figure 3. Compared with the conventional ILCC structure shown in Figure 2, the helical path $\mathrm{H}$ must be segmented to obtain the helical cycle ${\mathrm{H}}_j$ and the response path is naturally amalgamated by the response cycle ${\mathrm{R}}_j$ through the motions of the feed drive axes. In addition, the operation of the pitch increment is required in the segmentation process and iterative learning contour controller to make the thread milling operation move from the current pitch cycle to the next pitch cycle. The contour error of the $\left(j\right)$th pitch cycle ${\mathsf{\epsilon }}_j$ was calculated by referring to the $\left(j\right)$th helical cycle ${\mathrm{H}}_j$ and the $\left(j\right)$th response cycle ${\mathrm{R}}_j$. Both the contour error ${\mathsf{\epsilon }}_j$ and command cycle ${\mathrm{P}}_j$ were recorded in different memories for the modification of the next command cycle. Therefore, the PCB-ILCC can gradually improve the accuracy of helical motions pitch by pitch and mitigate the problems of applying conventional ILCC methods to thread milling operations. Nevertheless, as indicated by Figure 3, some issues must be carefully considered in this study when applying the PCB-ILCC in practice, including the estimation of the CEV (adopted in the contour error calculation to approximately calculate the contour error of each pitch cycle), the design of the ILCC (adopted in the iterative learning contour controller to gradually reduce the contour errors of the pitch cycles), and the design of the PMSM driving control (adopted in the feed drive axes to actuate the feed drive axes with a stable and improved motion performance).

3. CEV Estimation and ILCC Design

The CEV is the shortest distance vector between the response position (on the response path) and the helical path; thus, the precise calculation of the CEV is generally difficult and time-consuming. Although many CEV estimation methods have been proposed in recent decades, the accuracy, complexity, and calculation time of the estimated CEV must be carefully considered in the PCB-ILCC design. Therefore, this study used the interpolated positions on a helical path to estimate the CEV [27]. As shown in Figure 4, $R$ denotes the response position on the response path; $H_i$ and $H_{i-1}$ denote the interpolated positions that are the positions on the helical path and close to the response position $R$; $H_c$ denotes the position on the $\overrightarrow{H_{i-1}{H}_i}$ vector, and the $\overrightarrow{R{H}_c}$ vector is perpendicular to the $\overrightarrow{H_{i-1}{H}_i}$ vector so that the $\overrightarrow{R{H}_c}$ vector can be obtained as the estimated CEV $\epsilon$ (i.e., $\epsilon =\overrightarrow{R{H}_c}$). Here, $\epsilon ={\left[\begin{array}{ccc}{\epsilon }_x& {\epsilon }_y& {\epsilon }_z\end{array}\right]}^T$, where ${\epsilon }_x$, ${\epsilon }_y$, and ${\epsilon }_z$ are the axial components of the estimated CEV $\epsilon$ on the X-axis, Y-axis, and Z-axis, respectively.

Let $d_{i-1}$ and $d_i$, respectively, denote the distance from $R$ to $H_{i-1}$ and $H_i$, and let $D_{i-1}$ and $D_i$, respectively, denote the distance from $H_c$ to $H_{i-1}$ and $H_i$. Referring to the geometric relationship shown in Figure 4, the distance relations can be obtained as Equations (1) and (2):

$${\left(d_{i-1}\right)}^2-{\left(D_{i-1}\right)}^2={\left(d_i\right)}^2-{\left(D_i\right)}^2$$

(1)

$$D_{i-1}+D_i=‖H_i-H_{i-1}‖$$

(2)

Here, $D_{i-1}$ and $H_c$ can be, respectively, calculated by Equations (3) and (4):

$$D_{i-1}=\frac{\left({\left(d_{i-1}\right)}^2-{\left(d_i\right)}^2\right)+{‖H_i-H_{i-1}‖}^2}{2‖H_i-H_{i-1}‖}$$

(3)

$$H_c=H_{i-1}+\frac{\left(H_i-H_{i-1}\right)}{‖H_i-H_{i-1}‖}{D}_{i-1}$$

(4)

Therefore, the estimated CEV $\epsilon$ can be obtained as:

$$\epsilon =\overrightarrow{R{H}_c}=H_c-R=\left(H_{i-1}-R\right)+\frac{\left(H_i-H_{i-1}\right)}{‖H_i-H_{i-1}‖}{D}_{i-1}$$

(5)

Because the helical path is adopted in thread milling operations, the estimated CEV $\epsilon$ can provide a good approximation to the actual CEV when the helical path has a large helical radius, and the thread milling tool moves with a low feed rate. While the response position $R$ moves on the response path $\mathrm{R}$, the contour error $\mathsf{\epsilon }$ can be obtained by collecting the estimated CEV $\epsilon$ with the given helical path $\mathrm{H}$, as shown in Figure 2 for the conventional ILCC methods; therefore, for the simplified expression, Equation (6) is used to represent the calculation of the contour error $\mathsf{\epsilon }$:

$$\mathsf{\epsilon }=ctrerr \left(\mathrm{H}-\mathrm{R}\right)$$

(6)

where $ctrerr \left( \cdot \right)$ denotes the function of the contour error calculation. Specifically, as shown in Figure 3 for the PCB-ILCC method, Equation (6) is modified as Equation (7) to represent the calculation of the contour error ${\mathsf{\epsilon }}_j$:

$${\mathsf{\epsilon }}_j=ctrerr \left({\mathrm{H}}_j-{\mathrm{R}}_j\right)$$

(7)

This study developed the cycle learning method shown in Equation (8) to design the PCB-ILCC shown in Figure 3:

$${\mathrm{P}}_j={\mathrm{P}}_{j-1}+Z_L+K\left(s\right){ \mathsf{\epsilon }}_{j-1}$$

(8)

where $Z_L$ denotes the vector of the pitch increment and $K\left(s\right)$ denotes the transfer function matrix of the iterative learning contour controllers. $Z_L$ is a constant vector. $K\left(s\right)=diag\left({\left.K_m\left(s\right)\right|}_{m=x,y,z}\right)$ is a diagonal matrix, and the diagonal entries $K_x\left(s\right)$, $K_y\left(s\right)$, and $K_z\left(s\right)$, respectively, denote the transfer functions of the iterative learning contour controllers for the feed drive axes X, Y, and Z. Because ${\mathrm{H}}_j={\mathrm{H}}_{j-1}+Z_L$, ${\mathrm{R}}_j=G\left(s\right){ \mathrm{P}}_j$, the contour error ${\mathsf{\epsilon }}_j$ shown in Equation (7) can be rewritten as Equation (9) by substituting Equation (8) to Equation (7):

$${\mathsf{\epsilon }}_j=ctrerr \left({\mathrm{H}}_{j-1}+Z_L-G\left(s\right){ \mathrm{P}}_{j-1}-G\left(s\right) Z_L-G\left(s\right)K\left(s\right){ \mathsf{\epsilon }}_{j-1}\right)$$

(9)

where $G\left(s\right)$ denotes the transfer function matrix of the feed drive axes. $G\left(s\right)=diag\left({\left.G_m\left(s\right)\right|}_{m=x,y,z}\right)$ is a diagonal matrix, and the diagonal entries $G_x\left(s\right)$, $G_y\left(s\right)$, and $G_z\left(s\right)$ denote the transfer functions of the feed drive axes X, Y, and Z, respectively. Because ${\mathrm{R}}_{j-1}=G\left(s\right){ \mathrm{P}}_{j-1}$ and $Z_L=G\left(s\right) Z_L$ are at a steady state, Equation (9) can be further rewritten as Equations (10) and (11):

$${\mathsf{\epsilon }}_j=ctrerr \left({\mathrm{H}}_{j-1}-{\mathrm{R}}_{j-1}\right)-G\left(s\right)K\left(s\right){ \mathsf{\epsilon }}_{j-1}$$

(10)

$${\mathsf{\epsilon }}_j={\mathsf{\epsilon }}_{j-1}-G\left(s\right)K\left(s\right){ \mathsf{\epsilon }}_{j-1}$$

(11)

Accordingly, from Equation (11), the iterative equation of the contour error ${\mathsf{\epsilon }}_j$ can be obtained as Equation (12):

$${\mathsf{\epsilon }}_j=\left(I-G\left(s\right)K\left(s\right)\right){ \mathsf{\epsilon }}_{j-1},$$

(12)

where $I$ denotes the identity matrix. Therefore, for each feed drive axis, the relationship between the contour error components in cycles $\left(j\right)$ and $\left(j-1\right)$ can be represented as Equation (13):

$${\mathsf{\epsilon }}_{j,m}=\left(1-G_m\left(s\right)K_m\left(s\right)\right){ \mathsf{\epsilon }}_{j-1,m}, m=x,y,z,$$

(13)

where ${\mathsf{\epsilon }}_{j,x}$, ${\mathsf{\epsilon }}_{j,y}$, and ${\mathsf{\epsilon }}_{j,z}$ are the axial components of the contour error ${\mathsf{\epsilon }}_j$ on the X-axis, Y-axis, and Z-axis, respectively. According to Equation (13), for the cycle learning method presented in Equation (8) to achieve convergence, the inequality shown in Equation (14) must be satisfied:

$${‖1-G_m\left(s\right)K_m\left(s\right)‖}_{\infty }<1, m=x,y,z,$$

(14)

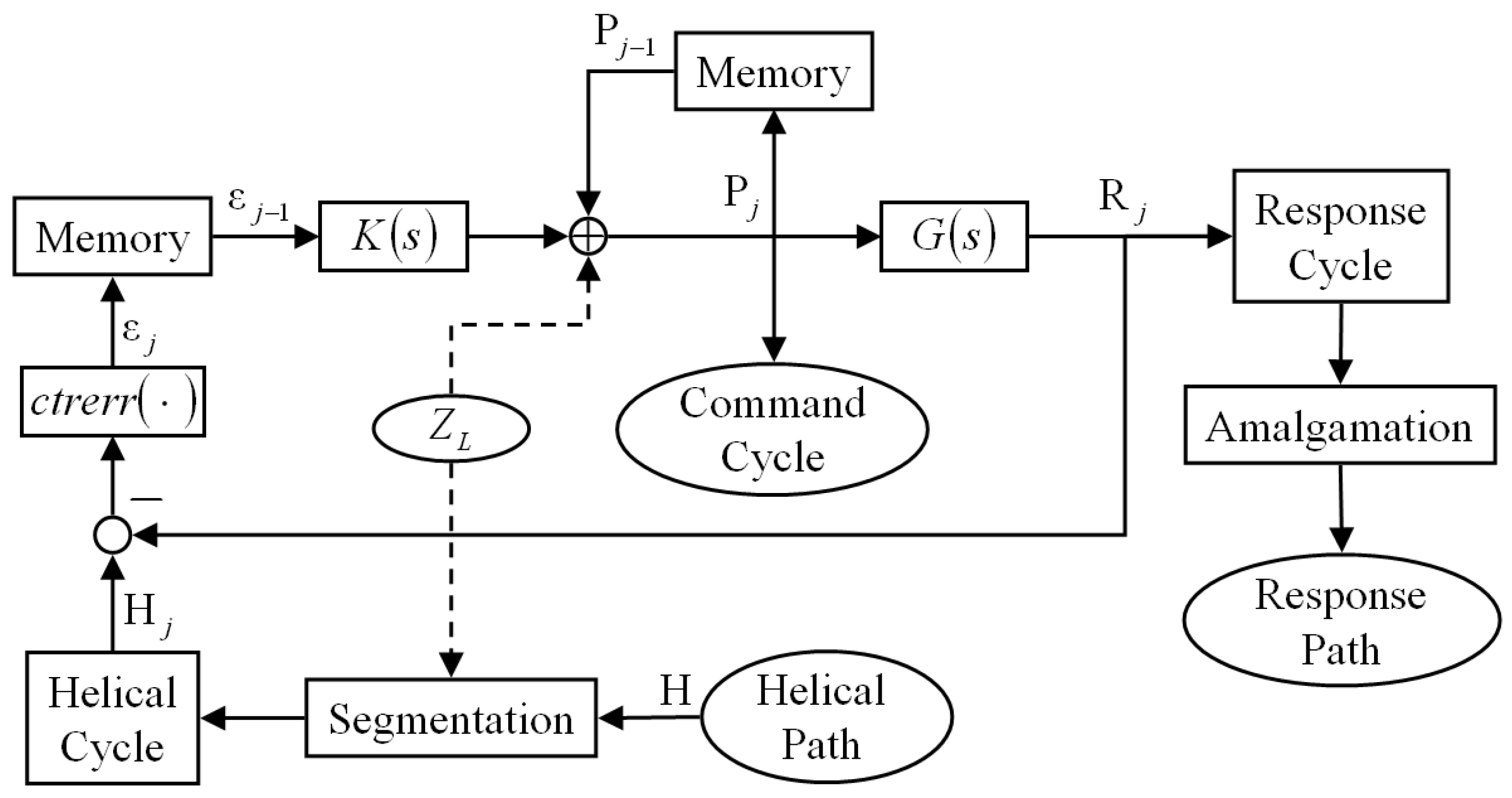
where ${‖ \cdot ‖}_{\infty }$ denotes the infinity norm. Figure 5 shows the PCB-ILCC structure in detail using the cycle learning method; here, the operation of the PCB-ILCC illustrated in Figure 5 can be described as the following steps:

• Step 1: compute the command cycle ${\mathrm{P}}_j$ by combining the recorded command cycle ${\mathrm{P}}_{j-1}$, the filtered contour error $K\left(s\right){ \mathsf{\epsilon }}_{j-1}$, and the pitch increment $Z_L$; here, the command cycle ${\mathrm{P}}_j$ must also be recorded to memory.
• Step 2: feed drive axes perform motions with the command cycle ${\mathrm{P}}_j$ so that the response cycle ${\mathrm{R}}_j$ can be obtained from the motion results.
• Step 3: calculate the contour error ${\mathsf{\epsilon }}_j$ by using the contour error calculation function $ctrerr\left( \cdot \right)$, the helical cycle ${\mathrm{H}}_j$, and the response cycle ${\mathrm{R}}_j$; here, the contour error ${\mathsf{\epsilon }}_j$ must also be recorded to memory.
• Step 4: if the $\left(j\right)$th pitch cycle is not the last cycle, the PCB-ILCC increases the cycle number and then moves to Step 1.

In Figure 5, the pitch cycle number $\left(j\right)$ is increased from $\left(j=1\right)$ (the first cycle); moreover, for $\left(j=1\right)$, the command cycle ${\mathrm{P}}_1={\mathrm{H}}_1$, and the recorded command cycle ${\mathrm{P}}_0$ and the recorded contour error ${\mathsf{\epsilon }}_0$ are both set to be zeros. A conventional proportional–integral controller was employed in this study as the iterative learning contour controller. The proportional and integral control gains were tuned manually according to the influence of the proportional control gain on the rate of convergence and the influence of the integral control gain on the converged contour error. Moreover, the control gains must be tuned to satisfy the inequality shown in Equation (14) to achieve convergence.

4. PMSM Driving Control Design

A PMSM mainly actuates feed drive axes; thus, the PMSM driving control design can significantly affect the motion performance of each feed drive axis and further affects the operating performance of the PCB-ILCC. Considering the dynamic equation of the feed drive axis actuated by the PMSM as Equation (15):

$${\tau }_m=J{\ddot{\theta }}_m+B{\dot{\theta }}_m+{\tau }^{sc}+{\tau }^e,$$

(15)

where $J$ and $B$ denote the equivalent moment of inertia and equivalent viscous friction coefficient, respectively. ${\theta }_m$ denotes the rotating angular position of the PMSM, ${\tau }_m$ and ${\tau }^e$, respectively, denote the driving torque and external disturbance torque of the PMSM, and ${\tau }^{sc}$ as Equation (16) denotes the compound friction torque composed of the static friction torque and Coulomb friction torque:

$${\tau }^{sc}=\left({\tau }^c+\left({\tau }^s-{\tau }^c\right)e^{-{\left(\left|\frac{{\dot{\theta }}_m}{{\omega }_s}\right|\right)}^{\delta }}\right)\cdot \mathit{sgn}\left({\dot{\theta }}_m\right),$$

(16)

where ${\tau }^s$ and ${\tau }^c$ denote the static friction torque and Coulomb friction torque, respectively. ${\omega }_s$ denotes the Stribeck velocity, and $\delta$ denotes the Stribeck shape factor.

Supposing that the feed drive axis would not be influenced by the external disturbance torque (i.e., ${\tau }^e=0$), this study designed the driving control as Equation (17):

$${\tau }_m=\widehat{J}{a}_m+\widehat{B}{\dot{\theta }}_m+{\widehat{\tau }}^{sc},$$

(17)

where $\widehat{J}$ denotes the estimated equivalent moment of inertia, $\widehat{B}$ denotes the estimated equivalent viscous friction coefficient, ${\widehat{\tau }}^{sc}$ denotes the estimated compound friction torque, and $a_m$ denotes the control term required to be further designed. Therefore, by substituting Equation (17) into Equation (15), the dynamic equation can be rewritten as Equation (18):

$$J{\ddot{\theta }}_m=\widehat{J}{a}_m+\left(\widehat{B}-B\right){\dot{\theta }}_m+\left({\widehat{\tau }}^{sc}-{\tau }^{sc}\right)=\widehat{J}{a}_m+\tilde{B}{\dot{\theta }}_m+{\tilde{\tau }}^{sc},$$

(18)

where $\tilde{B}=\widehat{B}-B$ and ${\tilde{\tau }}^{sc}={\widehat{\tau }}^{sc}-{\tau }^{sc}$ denote the estimation errors of the equivalent viscous friction coefficient and compound friction torque, respectively. The estimation error of the equivalent moment of inertia can also be defined as $\tilde{J}=\widehat{J}-J$, and Equation (18) can be rewritten as Equation (19):

$${\ddot{\theta }}_m=J^{-1}\left(\widehat{J}{a}_m+\tilde{B}{\dot{\theta }}_m+{\tilde{\tau }}^{sc}\right)=a_m+J^{-1}\left(\tilde{J}{a}_m+\tilde{B}{\dot{\theta }}_m+{\tilde{\tau }}^{sc}\right)$$

(19)

The uncertainty $\eta$ can be defined as Equation (20):

$$\eta =J^{-1}\left(\tilde{J}{a}_m+\tilde{B}{\dot{\theta }}_m+{\tilde{\tau }}^{sc}\right)$$

(20)

Then, Equation (19) can be rewritten as Equation (21):

$${\ddot{\theta }}_m=a_m+\eta$$

(21)

To overcome the influence of the uncertainty $\eta$, this study designed the control term $a_m$ as shown in Equation (22):

$$a_m={\ddot{\theta }}_d-K_1\left({\dot{\theta }}_m-{\dot{\theta }}_d\right)-K_0\left({\theta }_m-{\theta }_d\right)+\delta a_m,$$

(22)

where ${\ddot{\theta }}_d$, ${\dot{\theta }}_d$, and ${\theta }_d$ denote the commands for the rotating angular acceleration, angular velocity, and angular position of the PMSM, respectively. $K_1>0$ and $K_0>0$ denote the control gains; $\delta a_m$ denotes the additional term and is used to attenuate the influence of the uncertainty. Based on Equations (21) and (22), this study derived the error equation as Equation (23):

$$\left({\ddot{\theta }}_m-{\ddot{\theta }}_d\right)+K_1\left({\dot{\theta }}_m-{\dot{\theta }}_d\right)+K_0\left({\theta }_m-{\theta }_d\right)=\delta a_m+\eta$$

(23)

Moreover, through the definition of the following error vector $e={\left[\begin{array}{cc}\left({\theta }_m-{\theta }_d\right)& \left({\dot{\theta }}_m-{\dot{\theta }}_d\right)\end{array}\right]}^{{\rm T}}$, Equation (23) can be rewritten as Equation (24):

$$\dot{e}=Ae+b\left(\delta a_m+\eta \right),$$

(24)

where $A$ and $b$ denote the error state matrix and uncertain input vector, respectively. Moreover,

$$A=\left[\begin{array}{cc}0& 1\\ -K_0& -K_1\end{array}\right] \mathrm{and} b=\left[\begin{array}{c}0\\ 1\end{array}\right].$$

(25)

Herein, in case the uncertainty $\eta$ is bounded by $\rho$, i.e.,

$$‖\eta ‖<\rho$$

(26)

The additional term $\delta a_m$ can be designed as Equation (27) so that the solution trajectory of the error equation shown in Equation (24) is bounded. The Appendix A shows the detailed derivation.

$$\delta a_m=\left\{\begin{array}{ll}-\rho \frac{b^{T}Pe}{‖b^{T}Pe‖},& ‖b^{T}Pe‖>\sigma \\ -\frac{\rho }{\sigma }{b}^{T}Pe,& ‖b^{T}Pe‖\le \sigma \end{array},\right.$$

(27)

where $\sigma$ denotes a threshold constant. The matrix $A$ in Equation (25) must be a stable matrix. Moreover, matrix $P=P^T>0$ and matrix $Q=Q^T>0$ must satisfy the Lyapunov equation as Equation (28):

$$A^{T}P+PA=-Q$$

(28)

Equations (17), (22), (27) and (28) construct the PMSM driving control designed in this study. Figure 6 shows the control structure developed in this study. The generated commands ${\theta }_d$, ${\dot{\theta }}_d$, and ${\ddot{\theta }}_d$ and the actual responses ${\theta }_m$ and ${\dot{\theta }}_m$ are adopted to calculate the control term $a_m$ and the additional term $\delta a_m$ by using Equation (22) and Equations (27) and (28), respectively. Then, Equation (17) calculates the driving torque ${\tau }_m$ to actuate the feed drive axis through the PMSM. Here, the commands ${\theta }_d$, ${\dot{\theta }}_d$, and ${\ddot{\theta }}_d$ are generated from the axial component of the command cycle, and the actual response ${\theta }_m$ produces the axial component of the response cycle, as shown in Figure 5.

In this study, for simplicity, the matrix $Q$ is designed as $Q=q\cdot I$; where $q$ is a positive and real variable. Therefore, the PMSM driving control includes five control parameters $K_1$, $K_0$, $\rho$, $\sigma$, and $q$. The conservative design of the control parameters generally improves the stability but limits the performance of the PMSM driving control. On the other hand, to improve the performance, the design of the control parameters usually deteriorates the stability of the PMSM driving control. Therefore, due to the control parameters’ design complexity, the control parameters were tuned manually to achieve a balanced performance and stability considering their control characteristics. Referring to Equations (24) and (25), the control parameters $K_1$ and $K_0$ determine the dynamic response of the solution trajectory. Thus, the control parameters $K_1$ and $K_0$ were tuned to rapidly attenuate errors without significant oscillations. Referring to Equation (27), because the threshold constant $\sigma$ affects the chattering phenomenon of the solution trajectory, the threshold constant $\sigma$ was tuned to suppress chattering. Furthermore, the larger the bounded value $\rho$, the more stable control is achieved; however, a large bounded value usually increases the response time and steady-state errors of the PMSM driving control. Referring to the detailed derivation in the Appendix A, the Euclidean norm of the solution trajectory at the steady state (i.e., the magnitude of the error vector at the steady state) is proportional to the product of the bounded value $\rho$ and threshold constant $\sigma$, and is inversely proportional to the control parameter $q$. Therefore, to achieve stable control and improved steady-state errors, the control parameters $\rho$, $\sigma$, and $q$ were tuned repeatedly by reducing the product of the bounded value $\rho$ and threshold constant $\sigma$ and increasing the control parameter $q$.

5. Experimental Results

The PMSM motion control experiment and machine tool thread milling experiment were used to validate the PCB-ILCC approach developed in this study. An industrial computer with a steel chassis, backplane, and CPU card manufactured by Advantech Co., Ltd. was used in this study. The CPU card, which utilized a 3.4-GHz INTEL CORE i7-2600 CPU and 16-Gigabyte memory, is the main component of the industrial computer. The computer used the Linux operating system; moreover, programming language C was used to realize the control system that included a human–machine operating interface, signal measurement, feedback control, and recording and displaying of experimental data. Furthermore, the computer utilized the EtherCAT fieldbus industrial network system for sending control commands to and receiving feedback signals from the PMSM drivers at a sampling period of 0.5 ms so that the feed drive axes perform helical motions. In the experiments, the thread milling path of $\mathrm{M}40\times 3.5$ ISO metric external threads was adopted as the helical path. Here, Equation (29) was used to calculate the helical radius $R_H$:

$$R_H=\frac{1}{2}\left(\left(D_M+D_B\right)-\left(\frac{3\sqrt{3}}{8}\cdot 2\cdot {{\rm P}}_H\right)\right),$$

(29)

where $D_M$, $P_H$, and $D_B$ denote the major diameter, helical pitch of the external thread, and the blade diameter of the thread milling tool, respectively.

The following control structures were adopted in the experiments for validating the feasibility and evaluating the motion performance of the PCB-ILCC approach developed in this study.

• PMSM-PPIC: the proportional–proportional–integral control extensively used in commercialized PMSM drivers and CNC controllers.
• PMSM-DC: the PMSM driving control developed in this study (Section 4).
• PCB-ILCC: the PCB-ILCC (Section 2) with the integration of the CEV estimation and ILCC design (Section 3) and the PMSM driving control (Section 4).

The following performance indices were also adopted:

• AVG: average value.
• SD: standard deviation.
• RMS: root-mean-square value.
• MAX: maximum value.

5.1. PMSM Motion Control Experiment

This study used 1.5 kW commercialized PMSM packs for the motion control experiment, as shown in Figure 7. The PMSM has a rated speed and torque of 2000 rpm and 7.16 Nm, respectively. In addition, the PMSM is coupled to a 23-bit absolute optical encoder that can measure the rotating angular position of the PMSM. This study identified the moment of inertia and the friction parameters of the PMSM through a constant speed experiment and estimation experiment [28].

Table 1. PMSM parameters of the testbench.

Parameters	X-Axis	Y-Axis	Z-Axis
Moment of inertia (kg∙m2)	$0.0016$	$0.0015$	$0.0015$
Viscous friction coefficient (Nm/rad/s)	$0.0074$	$0.0071$	$0.0064$
Static friction torque (Nm)	$0.1037$	$0.1043$	$0.1079$
Coulomb friction torque (Nm)	$0.0890$	$0.0916$	$0.0929$
Stribeck velocity (rad/s)	$0.2588$	$0.3146$	$0.3406$
Stribeck shape factor	$1.5302$	$1.7817$	$1.5339$

shows the identification results.

Figure 8 shows the experimental results of 11 cycles of the helical path. The vertical axis is the RMS of the contour error, and the horizontal axis is the cycle number of the helical path. Since the PMSM does not significantly suffer from external disturbances, for the results of the PMSM-PPIC, the AVG of the RMS variation is $0.129$ rad with an SD of $6.1811\times {10}^{-5}$ rad; hence, the ratio between the SD and AVG is $0.48\%$. Accordingly, the RMS contour error of the PMSM-PPIC is almost unchanged in each cycle of the helical path. Similarly, the RMS contour error is almost unchanged because the PMSM-DC does not perform cycle learning. The AVG of the RMS variation is $0.0012$ rad with an SD of $8.4230\times {10}^{-6}$ rad so that the ratio of the SD and AVG is $0.69\%$. Nevertheless, compared with the PMSM-PPIC, the contour errors of the PMSM-DC were significantly reduced, and the AVG of the RMS variation achieves a rate of reduction of $90.48\%$. The PCB-ILCC can further reduce the RMS contour errors through cycle learning. Figure 8 shows that, after using the PCB-ILCC, the RMS contour error starts to converge at the fourth cycle; the RMS contour error is reduced from $0.0012$ rad (the first cycle) to $5.2681\times {10}^{-4}$ rad (the eleventh cycle), achieving a rate of reduction of $57.61\%$.

Figure 9 shows the magnitude of the CEVs in the last cycle (the eleventh cycle) of Figure 8. Figure 10 compares the different control structures in the AVG, RMS, and MAX errors. The experimental results show that, compared with the PMSM-PPIC, the PMSM-DC significantly reduces contour errors, and the PCB-ILCC can further reduce contour errors. The AVG, RMS, and MAX errors for the PMSM-PPIC are $0.0117$, $0.0129$, and $0.0314$ rad, respectively. As the PMSM-PPIC is susceptible to the influence of PMSM motion dynamics and friction disturbances, the contour errors using the PMSM-PPIC vary considerably. However, because the PMSM-DC and PCB-ILCC use the PMSM driving control developed in this study, which can not only compensate for the PMSM motion dynamics and friction disturbances but can also provide robust performance to PMSM motions, the PMSM-DC and PCB-ILCC have robust control results and small contour errors compared with the PMSM-PPIC. For the PMSM-DC, the AVG error is reduced to $0.0011$ rad at a rate of reduction of $90.74\%$, the RMS error is reduced to $0.0012$ rad at a rate of reduction of $90.50\%$, and the MAX error is reduced to $0.0031$ rad at a rate of reduction of $90.18\%$. Although the PMSM-DC can mitigate the adverse influence of external disturbances, few contour errors remain. Since external disturbances can repeatedly act on the PMSM while performing cycle motions along the helical path, the PCB-ILCC helps reduce contour errors. Compared with the PMSM-PPIC, the rate of reduction of the AVG, RMS, and MAX errors are $96.27\%$, $95.92\%$, and $94.76\%$, respectively. Moreover, compared with the PMSM-DC, the rate of reduction of the AVG, RMS, and MAX errors are $59.72\%$, $57.04\%$, and $46.64\%$, respectively. Therefore, the PMSM motion control experiment can validate that, for the helical path, the PCB-ILCC can effectively reduce contour errors and exhibit performance with robust control and disturbance suppression.

5.2. Machine Tool Thread Milling Experiment

This study utilized the five-axis CNC machining center, as shown in Figure 11, for the thread milling experiment to validate and evaluate the feasibility and performance of the PCB-ILCC approach developed in this study under the cutting force disturbance. The machining center mainly comprises a vertical axis (Z feed drive axis) and two planar axes (X feed drive axis and Y feed drive axis). The vertical axis and planar axes are actuated by PMSMs so that the thread milling tool can perform linear and circular motions. Each feed drive axis is equipped with a ballscrew lead of 10 mm and adopts a 1.5 kW PMSM pack.

Table 2. PMSM-equivalent parameters of feed drive axes.

Parameters	X-Axis	Y-Axis	Z-Axis
Moment of inertia (kg∙m2)	$0.0030$	$0.0026$	$0.0024$
Viscous friction coefficient (Nm/rad/s)	$0.0177$	$0.0514$	$0.0232$
Static friction torque (Nm)	$0.6977$	$0.6228$	$1.9821$
Coulomb friction torque (Nm)	$0.6061$	$0.5680$	$1.1565$
Stribeck velocity (rad/s)	$0.5926$	$2.0243$	$1.2274$
Stribeck shape factor	$1.7386$	$2.1397$	$1.0293$

shows the PMSM-equivalent parameters of the feed drive axes, respectively, identified by the constant speed experiment and estimation experiment [28]. The thread milling experiment used a 90 mm long thread milling tool with a tool holder diameter of 12 mm. The material of the disk-type thread milling blade was tungsten steel. The blade diameter is 20 mm with a blade angle of 60 degrees. The workpiece material is AL6061.

Figure 12 shows the experimental results while performing thread milling operations on the five-axis CNC machining center; here, because the PMSM-DC has been validated to provide superior control results with small contour errors, the PCB-ILCC was compared with the PMSM-PPIC to clarify the control performance between the proposed and conventional control methods under the adverse influence of external disturbances. The vertical axis denotes the RMS contour error of each cycle, and the horizontal axis represents the cycle number of the helical path. Figure 12 illustrates that the RMS contour error of the PMSM-PPIC is almost unchanged and remains at a large value. The AVG of the RMS variation is $10.6930$ μm, the SD is $0.0286$ μm, and the ratio between the SD and AVG is $0.27\%$. Compared with the PMSM-PPIC, although the cutting force makes the RMS contour error fluctuate, the PCB-ILCC still significantly reduces the RMS contour error. The PCB-ILCC achieves that the RMS contour error starts to converge at the fifth cycle and is reduced from $3.0734$ μm (the first cycle) to $1.1055$ μm (the tenth cycle) with a rate of reduction of $64.03\%$.

Figure 13 shows the magnitude of the CEVs in the last cycle (the tenth cycle) of Figure 12. Figure 14 compares the control performance of the PMSM-PPIC and PCB-ILCC. Because of the influence of friction disturbance on each feed drive axis, the contour error of the PMSM-PPIC has been significantly increased at quadrants of circular motion, with the MAX error of $21.7032$ μm. In addition, because of the influence of the cutting force and motion dynamics of each feed drive axis, the suppression of the contour error is limited, and there were larger contour errors while using the PMSM-PPIC; the AVG error is $10.4015$ μm and the RMS error is $10.7086$ μm. Compared with the PMSM-PPIC, the PCB-ILCC can effectively suppress the adverse influence of the cutting force and friction disturbance, and improves the motion dynamics of each feed drive axis. Therefore, the PCB-ILCC can significantly reduce the contour error; the MAX error is reduced to $3.6132$ μm at a rate of $83.35\%$, the RMS error is reduced to $1.1055$ μm with a rate of $89.68\%$, and the AVG error is reduced to $0.9818$ μm with a rate of $90.56\%$. Therefore, the machine tool thread milling experiment indicated that, compared with the PMSM-PPIC, the PCB-ILCC could significantly improve the contour accuracy of the feed drive axes while performing the helical path in thread milling operations.

6. Conclusions

During thread milling operations, the helical contour motion accuracy of feed drive axes is critical because it can significantly affect the accuracy of manufactured threads. The contour control design can improve the contour motion accuracy of feed drive axes; however, the motion dynamics and friction disturbance of each feed drive axis and the cutting force in thread milling operations significantly affect the helical contour motion accuracy of feed drive axes. Although the ILCC can reduce contour errors while feed drive axes perform repeated motions, recording and processing large amounts of data increase the memory usage and the computational burden on the motion control system. Moreover, during the ILCC convergence, producing multiple defective products can lead to wasted materials while increasing manufacturing costs.

Because the helical path is composed of multiple pitch cycles, and feed drive axes are generally influenced similarly by motion dynamics and external disturbances such as the friction disturbance and cutting force during the motions of pitch cycles, the PCB-ILCC is developed to apply the contour error in the previous pitch cycle motion to modify the position command of the current pitch cycle motion so as to not only improve the contour motion accuracy of the feed drive axes while performing a helical path but also deal with the control system problem and thread manufacturing problem induced by applying the ILCC to thread milling operations. To realize the PCB-ILCC, the CEV estimation method must not excessively increase the computational burden, and the ILCC must be easy to implement; in addition, the PMSM driving control must mitigate the adverse influence of motion dynamics and external disturbances acting on the feed drive axes. Therefore, the PCB-ILCC estimated the CEV by referring to the interpolated positions on the helical path, designed the ILCC using a cycle learning method, and designed the PMSM driving control using the robust control method that integrates friction compensation and dynamics compensation.

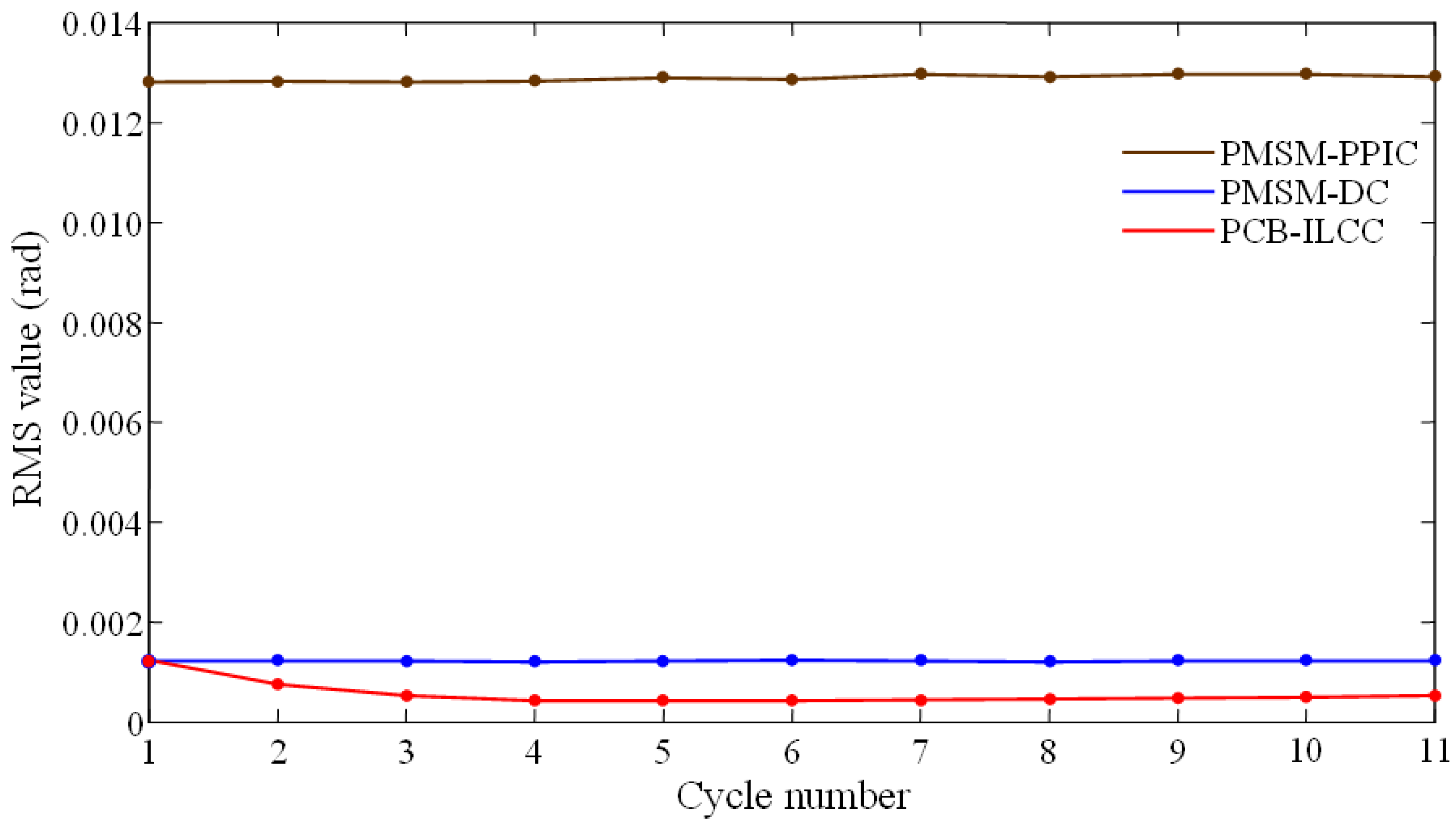
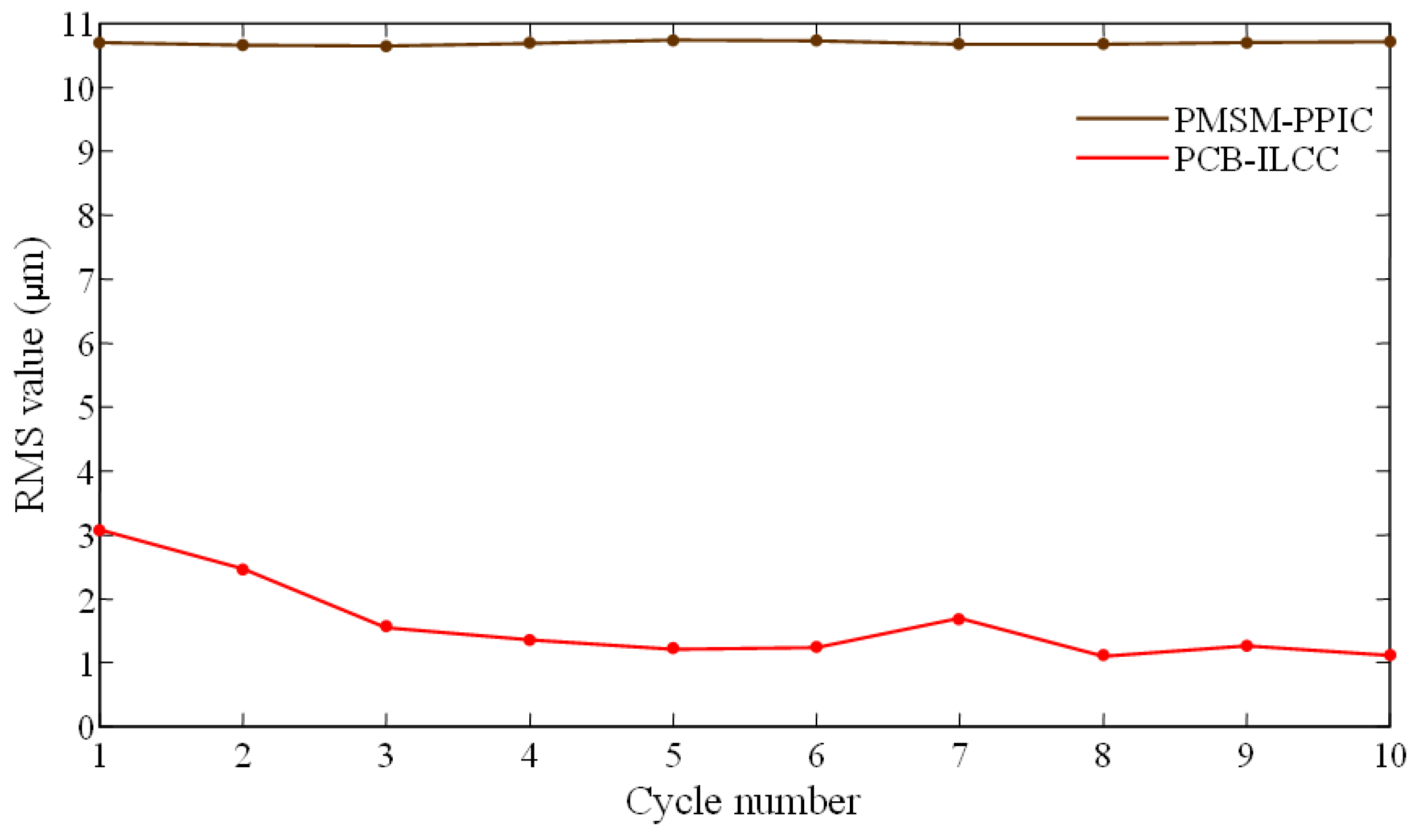
The motion control experiments performed on a testbench validated that the robust PMSM driving control method developed in this study can significantly reduce contour errors compared with the extensively used proportional–proportional–integral control. As proportional–proportional–integral control is susceptible to the influence of PMSM motion dynamics and external disturbances, the contour errors vary considerably. Compared with proportional–proportional–integral control, the PCB-ILCC integrated with the PMSM driving control has robust control results and small contour errors owing to the compensation of PMSM motion dynamics and friction disturbances and the robust performance of PMSM motions. Compared with the extensively used proportional–proportional–integral control, the PCB-ILCC achieves a rate of reduction in the contour errors of over 90%. Moreover, compared with the robust PMSM driving control, the PCB-ILCC can further reduce the contour errors with a rate of reduction of over 40%. Thread milling experiments performed on a five-axis CNC machining center showed that even though the feed drive axes were adversely influenced by the motion dynamics and external disturbances, including the friction disturbance and cutting force, the PCB-ILCC achieved a significant contour error reduction because of the cycle learning method developed in this study. The reduction rate of contour errors when applying the PCB-ILCC reached 80% in thread milling operations compared to proportional–proportional–integral control. Thus, the experimental results validated that the PCB-ILCC can be applied to thread milling operations, effectively improving the helical contour motion accuracy of the feed drive axes.

The PCB-ILCC presented in this paper exhibited improved contour motion accuracy for helical contour motions. Therefore, in the future, the developed PCB-ILCC will be applied to the motion control system of a robotic manufacturing system for manufacturing mechanical parts with a non-circular helix using a robot manipulator. In future studies, some developed approaches in the presented PCB-ILCC must be carefully redesigned. For instance, for the design of the contour error vector estimation, we must consider the curvature variation in the helical path with a non-circular contour. Furthermore, for the design of the iterative learning contour control, we must consider the dynamics of the robot manipulator, and the design of the PMSM driving control must be extended to the design of robotic motion control.