Abstract
With the increasing level of intelligence of marine engines, there is an increasing demand for the online monitoring of engines, and marine NOx emissions have been of great concern. In this paper, a NOx simulation model is developed based on virtual measurement technology, which can calculate and predict NOx emissions based on the current operating state parameters of low-speed two-stroke diesel engines. First, the calibrated 3D simulation model is used to design the experiments to obtain the simulation experimental samples. Based on the NOx generation mechanism and diesel engine work-related parameters, the relevant factors were selected as alternative input parameters for the NOx emission model. The correlation analysis was then performed on the input parameters using the grey relational analysis correlation method and the Pearson correlation coefficient, and the principal component analysis method was used to reduce the dimensionality of the relevant factors by minimizing the loss of important information in reducing the complexity of the whole model. Then, the structure-related parameters of the backpropagation neural network (BPNN) were adaptively optimized using the group method of data handling (GMDH) to improve the accuracy of the NOx soft measurement model. Finally, the developed GMDH–BP model was validated with data and compared with the error evaluation index of BPNN and BPNN optimized by genetic algorithm (GA), and the developed NOx simulation model demonstrated high prediction accuracy under the same hyperparameter settings. The result provides technical support for the subsequent realization of the real-time online monitoring of NOx emissions from low-speed marine diesel engines without NOx sensors.
1. Introduction
Due to the generation mechanism and harmful effects of nitrogen oxides (NOx) in the exhaust emissions of low-speed marine diesel engines, the International Maritime Organization and national regulations have strict NOx emission limits for marine engines. Low-speed marine engines are verified by emission tests to meet these emission regulations before being installed on board ships. However, as marine low-speed engines operate for long periods, environmental changes and the degradation of certain components such as fuel injectors and solenoid valves affect their emission performance. In order to ensure that marine diesel engines can operate efficiently with low emissions under different operating conditions, it is necessary to be able to obtain accurate parameter information during diesel engine operation; as a result, more and more sensors are being installed on marine diesel engines. Among the many sensors, the NOx sensor is a necessary tool for the detection of NOx emissions, which provides NOx data to SCR systems to ensure that all NOx emissions in the exhaust gas are reduced by urea as much as possible. However, in the process of practical application, the NOx sensor needs to be exposed to the engine exhaust gas for a long time, and impurities such as sulfides and particulate matter in the exhaust gas cause the poisoning of sensitive components and reduce the service life. Related papers show that the continuous measurement of ship engine exhaust gas will reduce the service life of NOx sensors to 85 h [1]. Due to the reduced lifetime of NOx sensors, the cost of use and the uncertainty in the application process are increased. In this situation, soft sensors or virtual sensors based on soft measurement techniques are being applied and developed. The basic idea of soft measurement technology to solve the lifetime problem in NOx sensor applications is to predict NOx emissions from diesel engines by modeling the correlation between NOx emissions and other directly measured or easily measurable variables without using NOx sensors directly. According to the principles of modeling NOx simulations, the models can be divided into physical mechanism models and data-driven models [2].
The mechanism-based NOx simulation model is still mainly based on the widely accepted Zeldovich mechanism as the NOx generation model. Based on constructing relevant variables, it can be divided into two categories: (1) Mathematical equations based on the working mechanism of the engine to form a more suitable NOx prediction through the appropriate simplification or additional consideration of the mixing and combustion conditions in the process of NOx formation [3,4,5,6,7,8,9,10]; and (2) use some physical signals (such as in-cylinder pressure, torque, etc.) during the working process of the engine to obtain intermediate variables through signal analysis and processing, and then combine the Zeldovich mechanism to analyze and deduce the generation of NOx to construct NOx predictive models [11,12,13,14,15]. The method of the physical mechanism model needs to be familiar with the formation mechanism of NOx under the characteristics of different models and fuel characteristics and conduct strict physical formula derivation, which can describe the in-cylinder combustion and the formation process of NOx more completely. The solution process often requires iteratively solving mathematical and physical equations, and the results obtained have strong interpretability, but the solution process is complicated. Using empirical equations to simplify the calculation of parameters such as NOx can reduce the computational complexity, but cannot guarantee sufficient accuracy.
The data-driven model uses artificial intelligence algorithms to build a corresponding calculation model to train and learn between input and output, and finally obtain a relatively accurate calculation model. It is considered to be an effective way of solving the prediction of difficult-to-measure physical quantities. This provides new ideas for performance degradation and lifetime prediction. The NOx simulation model based on data-driven construction is less dependent on the mechanism and can achieve satisfactory accuracy under appropriate algorithm selection and optimization. The research on intelligent algorithm modeling of the NOx simulation model mainly focuses on the following: (1) Using different artificial intelligence algorithms (such as artificial neural networks (ANN), deep neural networks (DNN), convolutional neural networks (CNN), long and short-term memory neural networks (LSTM), etc.) and optimization algorithms to construct different models to predict the emissions and characteristic parameters of gasoline engines or medium and high-speed diesel engines [16,17,18,19,20,21,22,23]. (2) Use appropriate algorithms to study the performance characteristics and predicted emissions of dual-fuel engines (such as isoamyl alcohol/gasoline, biodiesel/diesel, etc.) under different fuel ratios [24,25,26,27,28,29]. (3) Research into the promotion and adaptive optimization of artificial intelligence algorithm model prediction abilities [30,31,32,33,34,35,36].
From the modeling characteristics and applications of the physical and data-driven models described above, it is clear that the modeling process of the data-driven model is relatively simple because it does not rely on complex mathematical physical equations based on the working principles of the object. Therefore, it facilitates the exploration of research questions that lack detailed theoretical support, such as the characterization of dual-fuel or new-fuel engines. Many algorithms can use complex computing models and algorithms based on large data sets to achieve high prediction accuracy, which is not conducive to the adaptive expansion of the model and the practical application of the model.
In this paper, a NOx calculation model for marine diesel engines is developed using a data-driven modeling construct. Compared to CNN and DNN, a backpropagation neural network (BPNN) has a simpler structure. After a BPNN learns the data samples, each data undergoes multilayer and multinode repeated operations to realize data regression prediction. Compared with the simple feedforward ANN, BPNN optimizes and adjusts the weight matrix and bias matrix of the neural network by introducing error feedback backpropagation. Selecting an appropriate activation function makes the input and output have a highly nonlinear mapping relationship, and the BPNN can approximate any nonlinear function with arbitrary precision. For non-time series data, such as diesel engine operating conditions, the BPNN is more suitable for the nonlinear regression prediction of multidimensional input and output systems such as diesel engines than LSTM. Meanwhile, to make the structure of the BPNN as simple as possible, the BPNN is optimized using the group method of data handling (GMDH), and the final GMDH–BP model-based NOx calculation model is constructed.
The main contents of this paper are as follows: (a) establishing a three-dimensional simulation model using experimental data and conducting simulation experiments to provide data samples for the NOx calculation model; (b) selecting variables related to NOx emissions from the perspective of mechanism generation, using the grey relational analysis correlation method to initially select influencing factors with strong correlation and using the principal component analysis method to reduce the dimensionality of influencing factors to obtain low-dimensional input data; (c) establishing three computational models to compare the computational accuracy: the GMDH–BPNN NOx computational model using GMDH adaptive optimization of the structure of the BPNN neural network model; the GA–BPNN NOx computational model using the genetic algorithm (GA) to optimize the weights and bias of the BPNN; and, finally, the GMDH–BPNN, GA–BPNN, and unoptimized BPNN models are compared.
2. Materials and Methods
In this paper, the NOx calculation model is constructed as in Figure 1.
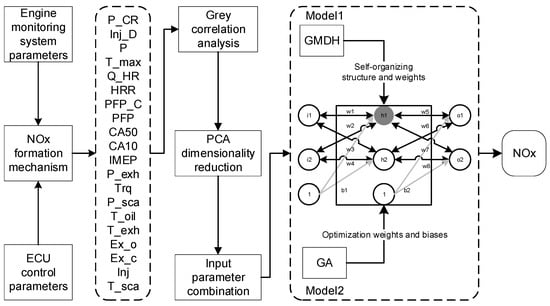
Figure 1.
NOx virtual sensor schematic.
Firstly, from the perspective of control, the relevant factors were initially selected as alternative input parameters for the NOx release model according to the mechanism of NOx formation during diesel engine operation and the controllable factors affecting NOx formation. Then, the Pearson correlation coefficient and grey relational analysis correlation methods are used to correlate the relevant parameters, and principal component analysis is used to reduce the dimensionality of the influencing factors to obtain the input parameter combinations of the model. In this way, the input data can be reduced in dimensionality with the minimum loss of important information, thus reducing the complexity of the whole model. Finally, the structure of the BP neural network is optimized adaptively using GMDH to improve the accuracy of the model. In addition, the weights and biases of the BPNN are optimized using a genetic algorithm and used as a comparison model; and the unimproved BPNN is used as another comparison model.
2.1. Input Parameters Selection
The research object of this paper is a 6EX340EF low-speed two-stroke diesel engine, and some of its parameters are shown in Table 1 below.

Table 1.
Low-speed machine parameters.
Since the research object is a low-speed two-stroke diesel engine, the cost of the bench test is high, and only limited experimental data can be obtained. Table 2 below shows the experimental data under four typical working conditions obtained from the bench test. According to the working principles of marine diesel engines and the complex physical–chemical reaction processes of fluids such as combustible gas mixtures in three-dimensional space, computational fluid dynamics software can be used to create algebraic equations to obtain numerical solutions at discrete time/space points that can accurately calculate the required performance parameters.

Table 2.
6EX340EF typical load experiment data.
The experimental data were used to calibrate the 3D simulation model of the marine diesel engine, and then this model was used to construct orthogonal experimental data to obtain more experimental data. The process of obtaining data is shown in Figure 2 below:
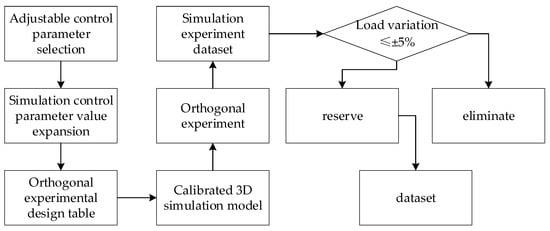
Figure 2.
Dataset source sketch.
According to the data, the NOx content of exhaust emissions produced by the marine low-speed diesel engine burning heavy oil (HFO) is 8.7% according to the mass ratio (NOx/HFO) [37]. The NOx is divided into the thermal type (83.92%), fuel type (11.08%), and fast type (5%) [38]. For the research on the formation mechanism of NOx, the thermal NOx formation explanation of the Zeldovich mechanism is widely recognized. This mechanism clarifies that NOx is produced by the chemical reaction of and in the combustion mixture. Since NOx is a product of combustion, the relevant parameters of the scavenging process, compression, fuel injection, combustion process, and structural characteristics of the marine diesel engine will affect the combustion and then affect the formation of NOx. From the formation mechanism of the thermal NOx chemical reaction, it is known that the distribution of temperature and pressure in the cylinder, the concentration and distribution of oxygen, and the flame propagation rate control the formation of NOx. The impact relationship of structural parameters, initial state parameters, working process parameters, and typical performance characteristic parameters involved in these three conditions in NOx generation are outlined in Figure 3.
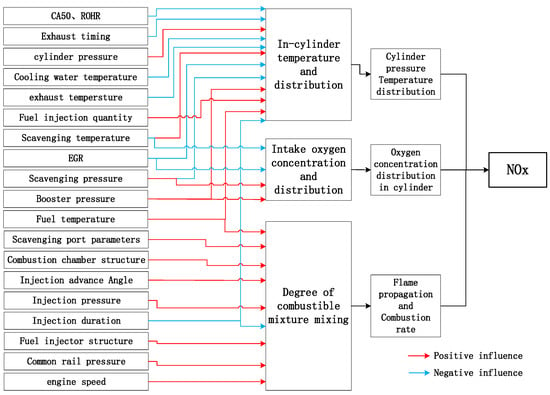
Figure 3.
Influencing factors in the formation of NOx emissions.
Many factors affect the formation of NOx. Selecting appropriate input parameters can reduce the computational complexity of the NOx simulation model and achive higher accuracy. Therefore, it is necessary to further analyze the degree of influence between related factors and NOx formation and describe the correlation quantitatively. Since this paper takes the 6EX340EF engine as the research object, its relevant structural parameters will not change during use, so the correlation with NOx is not considered. A certain number of data samples for the working parameters and performance parameters of the engine under different control parameters are designed by the simulation experiment, and the influencing factors present a normal distribution. Therefore, the commonly used Pearson correlation coefficient and grey relational analysis correlation methods were used to correlate the relevant variables; the results using the Pearson correlation coefficient are shown in Table 3, and the results of the grey relational analysis are shown in Figure 4.

Table 3.
Table of Pearson correlation coefficients between variables and NOx.
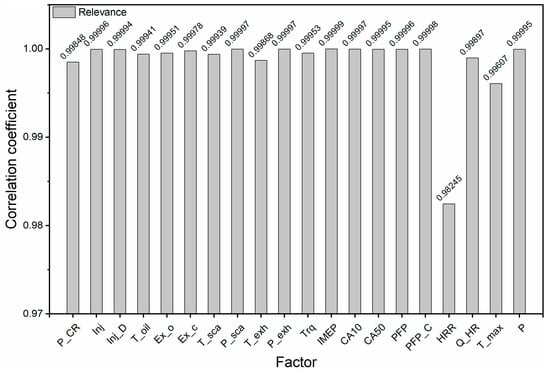
Figure 4.
Gray relational analysis comparison graph.
It can be seen from the correlation coefficients that P_CR, torque, IMEP, PFP, HRR, Q_HR, T_max, and P have a significant positive correlation with NOx. The positive correlations of T_oil, Ex_o, and T_sca are weak. The correlations of Inj, Inj_D, Ex_c, P_sca, T_exh, P_exh, CA50, and CA10 are negative.
From the grey relational analysis correlation graph, it can be seen that all of the analyzed variables are strongly correlated with NOx, and this result has similarities and differences with the Pearson results. To make full use of the information for the relevant parameters and to reduce the number of model input parameters, principal component analysis was used to perform dimensionality reduction for the above 20 parameters. After principal component analysis, the resulting scree plot is shown in Figure 5, and its component coefficient is shown in Table 4. As can be seen from Figure 5, after the 7th principal component, the data tends to flatten out, that is, 20 principal components can be abbreviated to 7 principal components by using the coefficients in Table 4.
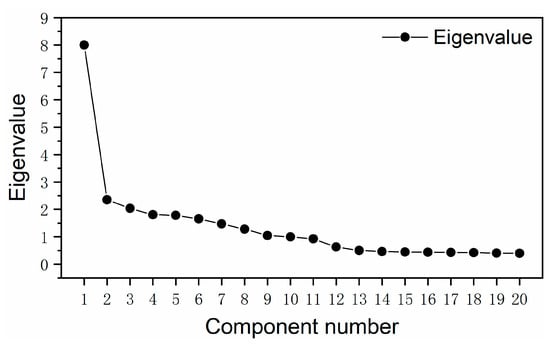
Figure 5.
Principal component analysis scree plot.

Table 4.
Component score coefficient matrix.
2.2. Construction of NOx Simulation Model
The marine diesel engine is a MISO system when NOx is the object of study. This is because the NOx output is influenced not only by the parameters associated with the current cycle but also by those of the previous cycle. Therefore, the complexity and diversity of the physical model and its parameters make it difficult to be simulated and controlled in real-time applications. The BPNN is a typical data-driven model that obtains information by simulating the forward and feedback transmission of signals between neurons and then calculates and predicts NOx.
The GMDH is a heuristic self-organizing method to study the relationship between variables. It can be used to select and classify input parameters to reduce the dimension of input features. For example, when there are three layers and four inputs, the sample architecture of the GMDH algorithm is shown in Figure 6. In Figure 6, there are four inputs (X1, X2, X3, and X4). From these input variables, there are three (X1, X2, and X4) control systems. X3 does not affect classification. The GMDH algorithm selects the important features that have an impact on classification. The GMDH algorithm generates a series of active neurons by cross-combining various input units of the system. Each neuron has the function of selecting the optimal transfer function and then selects several neurons closest to the target variable from the generated generation of neurons. The selected neurons combine to create new ones again, repeating the process of dominance inheritance, survival competition, and evolution until the most complex model is chosen.
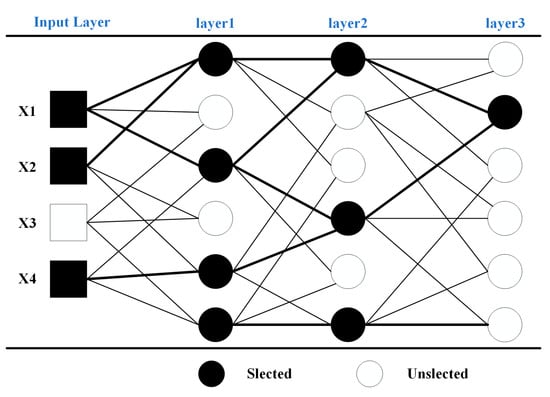
Figure 6.
The architecture of the GMDH algorithm.
The GMDH neural network has the following characteristics: the modeling process is self-organizing control without any initial assumptions; optimized complexity and high-precision prediction; the ability to use the optimal structure of each layer of the self-organizing multilayer neural network, that is, it can automatically retain useful variables and remove redundant variables; automatically selects the optimal number of network layers and the number of neurons per layer.
The BPNN model topology consists of an input layer, an output layer, and several hidden layers. The structure of the BPNN network is shown in Figure 7. Each layer of the BPNN has a specific number of neurons, and the network structure used in this paper can be found in [10,14].
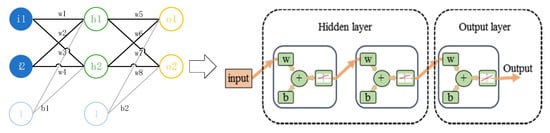
Figure 7.
BPNN structure.
In the forward propagation process, the calculation principle is shown as Equation (1): the output of each layer is multiplied by the input of the layer by the weight plus the bias, and, finally, the nonlinear transmission is realized under the action of the activation function (such as sigmoid, Relu, tanh, et al.). After using the GMDH to determine the structure of the model, the weight and bias of the BPNN are mainly determined. Without using the optimization algorithm, the weight value and bias that meet the accuracy requirements are obtained by repeating the training process.
In Equation (1), is the output of neuron; is the weight between neuron and neuron ; is the bias of neuron .
In the backpropagation, the overall error of groups of training sample data is shown in Equation (2). The gradient descent method is used to update the weight and deviation, and the updated weight and deviation are shown in Equations (3) and (4). Through the forward and backpropagation of errors, the weight and deviation of the neural network are constantly adjusted until a higher accuracy is achieved.
In Equation (2), is the calculated output, is the expected output, and are the weight and bias of the layer.
In this paper, the data samples designed by the simulation experiment are used to train and test the GMDH–BPNN algorithm model. To reflect the prediction performance of GMDH–BPNN, the unimproved BPNN is used as a blank comparison model. In addition, genetic algorithms achieve multiparameter optimization by simulating the inheritance, crossover, compilation, and evolution of populations in nature. Thus, the BPNN, optimized by the genetic algorithm, is used as another comparison model. In each test, the same amounts of data are used in training and testing, but the content of the included data is randomized. After repeated training and testing, the mean value of many test results is selected as the prediction accuracy of the model.
3. Results
In this paper, the regression coefficient (R2), the average relative average error (MAE), and the absolute root-mean-square error (RMSE) of the test set are selected for error evaluation. The three errors of the different calculation models are shown in Table 5. In order to reflect the randomness of NOx data occurrence in practical applications and to calculate the prediction effect of the models, a dotted line plot is used to compare the true and predicted values. The results of the comparisons between the predicted and true values of the three models on the test and training sets are shown in Figure 8, Figure 9 and Figure 10.

Table 5.
Comparison of evaluation parameters of different models.
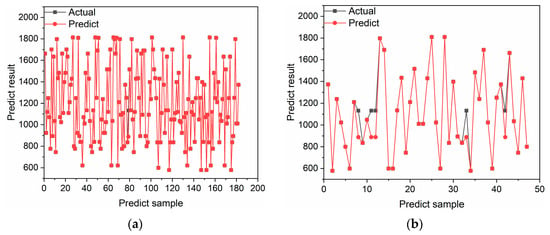
Figure 8.
(a) GMDH–BPNN predictions on the training set; and (b) GMDH–BPNN predictions on the test set.
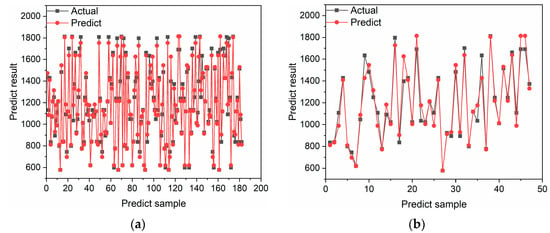
Figure 9.
(a) BPNN predictions on the training set; and (b) BPNN predictions on the test set.
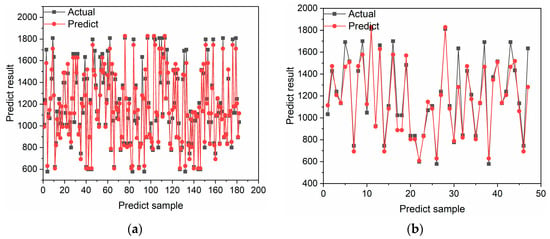
Figure 10.
(a) GA–BPNN predictions on the training set; and (b) GA–BPNN predictions on the test set.
It can be seen from Table 5 that although the error indicators of the three models are not very obvious, the errors are all lower than 10%, and the R2, MAE, and RMSE of the GMDH–BPNN model are all smaller than the other two models. It shows that the fitting degree between the GMDH–BPNN prediction curve and the original data curve is better, the error between each prediction value is also smaller, and the error between the obtained prediction sample and the test sample is smaller.
From the prediction curves of the above three models on the training and test sets, it can be seen that all models can fit the trend of the real NOx values better when changes occur, but the prediction on the extreme value point is still not satisfactory when large abrupt changes occur. This may be due to the small volume of the sample data and the overfitting phenomenon on the training set, resulting in unsatisfactory results on the test set. Meanwhile, since the accuracy of the GMDH–BPNN is slightly higher than that of GA–BPNN, it indicates that for the current data, the structure of the BPNN neural network has slightly more influence on its accuracy than the influence of weights and biases.
4. Discussion
In this paper, principal component analysis is used to reduce the dimensionality of numerous correlated factors, which makes full use of the correlation between the correlated factors and NOx while reducing the dimensionality of the input parameters of the model. The GMDH algorithm is also used to optimize the structure of the model and further reduce the computational effort of the NOx calculation model. Based on the results of this paper, the following studies can be continued in depth.
- (a)
- The sample data used in this paper was small, and the obtained model may not be able to fully explain the performance of the studied model under the target operating conditions.
- (b)
- In order to retain the relevant parameter information as much as possible, 20 relevant parameters were dimensionally reduced in this paper to obtain the input parameters, and subsequent control parameters and easily accessible parameters can be selected as input parameters to facilitate the application of the NOx calculation model to the actual diesel engine.
- (c)
- Based on (b), the NOx calculation model can be integrated with the hardware, which can achieve NOx values without using NOx sensors at all, and the application environment is relatively good and not easily damaged. Further optimization of the accuracy and calculation speed of the NOx calculation model integration in hardware can be performed, which can provide a solution for the online monitoring of marine diesel engine NOx emissions.
5. Conclusions
In this paper, the low-speed marine diesel engine was used as the research object. The input parameters of the computational models were obtained by correlation analysis and principal component analysis of the relevant parameters, and the simulation data were then used to develop and validate the three models. The results show that the prediction errors of the three NOx simulation models, GMDH–BPNN, GA–BPNN, and BPNN can be reduced to 2.296%, 4.678%, and 5.425%, respectively.
Author Contributions
Resources, M.G.; Writing—original draft, S.D.; Writing—review & editing, Q.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study did not require ethical approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
Due to privacy policy requirements, we are unable to provide complete data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Item | Abbreviations |
| nitrogen oxide | NOx |
| selective catalytic reduction | SCR |
| multiple input single output | MISO |
| artificial neural network | ANN |
| deep neural network | DNN |
| convolutional neural network | CNN |
| back propagation neural network | BPNN |
| long short-term memory neural network | LSTM |
| group method of data handling | GMDH |
| genetic algorithm | GA |
| common rail pressure | P_CR |
| fuel injection timing | Inj |
| injection duration | Inj_D |
| fuel temperature | T_oil |
| exhaust valve opening angle | Ex_o |
| exhaust valve closing angle | Ex_c |
| sweep temperature degree | T_sca |
| scavenging manifold pressure | P_sca |
| exhaust temperature | P_exh |
| exhaust pressure | T_exh |
| torque | Tor |
| average effective indicated pressure | IMEP |
| boost pressure | PFP |
| angle of detonation | HRR |
| maximum cylinder temperature | T_max |
| power | P |
| integrated heat release | Q_HR |
| angle of detonation PFP | PFP_C |
References
- Kyrtatos, P.; Barro, C.; Von Rotz, B. Development and Application of a Physically Assisted Virtual Sensor (PVS) for NOx Emissions. In Proceedings of the 29th CIMAC World Congress, Busan, Republic of Korea, 10–14 June 2019. [Google Scholar]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y.; Han, K.; Lee, K.M.; Yu, J.; Min, K. Virtual NOx sensor for Transient Operation in Light-Duty Diesel Engine. In Proceedings of the SAE 2016 World Congress and Exhibition, Detroit, MI, USA, 28 April 2016. [Google Scholar]
- Provataris, S.; Savva, N.; Chountalas, T.; Hountalas, D.T. Prediction of NOx emissions for high speed DI Diesel engines using a semi-empirical, two-zone mode. Energy Convers. Manag. 2017, 153, 659–670. [Google Scholar] [CrossRef]
- Park, W.; Lee, J.; Min, K.; Yu, J.; Park, S.; Cho, S. Prediction of real-time NO based on the in-cylinder pressure in Diesel engines. Proc. Combust. Inst. 2013, 34, 3075–3082. [Google Scholar] [CrossRef]
- Guardiola, C.; Lopez, J.; Martin, J.; García-Sarmiento, D. Semiempirical in-cylinder pressure based model for NOx prediction oriented to control applications. Appl. Therm. Eng. 2011, 31, 3275–3286. [Google Scholar] [CrossRef]
- Carlucci, A.P.; Benegiamo, M.; Camporeale, S.; Ingrosso, D. Improvement of the Control-Oriented Model for the Engine-Out NOx Estimation Based on In-Cylinder Pressure Measurement. In Proceedings of the 13th International Conference on Engines & Vehicles, Napoli, Italy, 10–14 September 2017. [Google Scholar]
- Cho, H.; Fulton, B.; Upadhyay, D.; Brewbaker, T.; van Nieuwstadt, M. In-cylinder pressure sensor–based NO model for real-time application in diesel engines. Int. J. Engine Res. 2018, 19, 293–307. [Google Scholar] [CrossRef]
- Vihar, R.; Baškovič, U.Ž.; Katrašnik, T. Real-time capable virtual NOx sensor for diesel engines based on a two-Zone thermodynamic model. Oil Gas Sci. Technol.–Rev. D’ifp Energ. Nouv. 2018, 73, 11. [Google Scholar] [CrossRef]
- Carra, F.; Ponti, F.; Ravaglioli, V. Validation of a NOx estimation methodology based on the analysis of in-cylinder pressure trace. In Proceedings of the 73rd Conference of the Italian-Thermal-Machines-Engineering-Association (ATI), Pisa, Italy, 12–14 September 2018; pp. 519–526. [Google Scholar]
- Mentink, P.; Escobar-Valdivieso, D.; Forrai, A.; Seykens, X.; Willems, F. Experimental validation of a virtual engine-out NOx sensor for diesel emission control. Int. J. Engine Res. 2019, 20, 1037–1046. [Google Scholar] [CrossRef]
- Finesso, R.; Hardy, G.; Mancarella, A.; Marello, O.; Mittica, A.; Spessa, E. Real-Time Simulation of Torque and Nitrogen Oxide Emissions in an 11.0 L Heavy-Duty Diesel Engine for Model-Based Combustion Control. Energies 2019, 12, 460. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Min, K. Real-time NOx estimation in light duty diesel engine with in-cylinder pressure prediction. Int. J. Engine Res. 2021, 22, 3519–3532. [Google Scholar] [CrossRef]
- Iqbal, M.Y.; Wang, T.; Li, G.X.; Li, S.; Hu, G.; Yang, T.; Gu, F.; Al-Nehari, M. Development and Validation of a Vibration-Based Virtual Sensor for Real-Time Monitoring NOx Emissions of a Diesel Engine. Machines 2022, 10, 594. [Google Scholar] [CrossRef]
- Han, R.; Bohn, C.; Bauer, G. Virtual Engine In-Cylinder Pressure Sensor for Automobiles and Agricultural Tractors. IFAC-Pap. 2020, 53, 543–548. [Google Scholar] [CrossRef]
- Norouzi, A.; Aliramezani, M.; Koch, C.R. A correlation-based model order reduction approach for a diesel engine NOx and brake mean effective pressure dynamic model using machine learning. Int. J. Engine Res. 2021, 22, 2654–2672. [Google Scholar] [CrossRef]
- Bellone, M.; Karayiannidis, Y.; Faghani, E. Comparison of CNN and LSTM for Modeling Virtual Sensors in an Engine. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 2, 2632–2639. [Google Scholar]
- Shin, S.; Lee, Y.; Kim, M.; Park, J.; Lee, S.; Min, K. Deep neural network model with Bayesian hyperparameter optimization for prediction of NOx at transient conditions in a diesel engine. Eng. Appl. Artif. Intell. 2020, 94, 103761. [Google Scholar] [CrossRef]
- Zou, L.; He, C.; Li, Q.; Wang, Y.; Tan, J. Machine learning based particle concentration prediction for diesel engines. Automot. Engines 2020, 2, 84–92. [Google Scholar]
- Jaliliantabar, F.; Najafi, G.; Mamat, R.; Ghobadian, B. Prediction of maximum in-cylinder pressure by adaptive neuro-fuzzy inference system method. In Proceedings of the 5th International Conference on Mechanical Engineering Research (ICMER), Jeju Island, Republic of Korea, 14–16 April 2019. [Google Scholar]
- Saravanakumar, L.; Prakash, R. Validation of performance and emissions of a CI engine fueled with calophyllum inophyllum methyl esters using soft computing technique. Fuel 2020, 266, 117070. [Google Scholar] [CrossRef]
- Dimitrakopoulos, P. Real-Time Virtual Sensor for NOx Emisions and Stoichiometric Air-Fuel Ratio-λ of a Marine Diesel EngineUsing Neural Networks; National Technical University of Athens, School of Naval Architecture and Marine Engineering, National Technical University of Athens: Athens, Greece, 2019; p. 98. [Google Scholar]
- Tsitsilonis, K.-M.; Theotokatos, G. A novel method for in-cylinder pressure prediction using the engine instantaneous crankshaft torque. Proc. Inst. Mech. Eng. Part M-J. Eng. Marit. Environ. 2021, 1, 131–149. [Google Scholar] [CrossRef]
- Falai, A.; Misul, D.A. Data-Driven Model for Real-Time Estimation of NOx in a Heavy-Duty Diesel Engine. Energies 2023, 16, 2125. [Google Scholar] [CrossRef]
- Sharma, P. Gene expression programming-based model prediction of performance and emission characteristics of a diesel engine fueled with linseed oil biodiesel/diesel blends: An artificial intelligence approach. Energy Sources Part A-Recovery Util. Environ. Eff. 2020, 12, 1–15. [Google Scholar] [CrossRef]
- Kenanoğlu, R.; Baltacıoğlu, M.K.; Demir, M.H.; Özdemir, M.E. Performance & emission analysis of HHO enriched dual-fuelled diesel engine with artificial neural network prediction approaches. Int. J. Hydrogen Energy 2020, 45, 26357–26369. [Google Scholar]
- Aydin, M.; Uslu, S.; Celik, M.B. Performance and emission prediction of a compression ignition engine fueled with biodiesel-diesel blends: A combined application of ANN and RSM based optimization. Fuel 2020, 269, 117472. [Google Scholar] [CrossRef]
- Aliramezani, M.; Koch, C.R.; Patrick, R. Phenomenological model of a solid electrolyte NOx and O2 sensor using temperature perturbation for on-board diagnostics. Solid State Ion. 2018, 321, 62–68. [Google Scholar] [CrossRef]
- Sabeghi, M.; Moghiman, M.; Gandomzadeh, D. Experimental study of the effect of HHO gas injection on pollutants produced by a diesel engine at idle speed. Int. J. Hydrogen Energy 2023, 48, 9117–9126. [Google Scholar] [CrossRef]
- Koc, M.A.; Sener, R. Prediction of emission and performance characteristics of reactivity-controlled compression ignition engine with the intelligent software based on adaptive neural-fuzzy and neural-network. J. Clean. Prod. 2021, 318, 128642. [Google Scholar] [CrossRef]
- Arsie, I.; Cricchio, A.; De Cesare, M.; Lazzarini, F.; Pianese, C.; Sorrentino, M. Neural network models for virtual sensing of NOx emissions in automotive diesel engines with least square-based adaptation. Control. Eng. Pract. 2017, 61, 11–20. [Google Scholar] [CrossRef]
- Layhew, Z.S. Investigation of A Neural Network Approach in Modeling and Diagnostics of An Engine-out NOx Sensor; West Virginia University Libraries: Morgantown, WV, USA, 2017. [Google Scholar]
- Kakati, D.; Roy, S.; Banerjee, R. Development of an artificial neural network based virtual sensing platform for the simultaneous prediction of emission-performance-stability parameters of a diesel engine operating in dual fuel mode with port injected methanol. Energy Convers. Manag. 2019, 184, 488–509. [Google Scholar] [CrossRef]
- Uslu, S.; Celik, M.B. Performance and Exhaust Emission Prediction of a SI Engine Fueled with I-amyl Alcohol-Gasoline Blends: An ANN Coupled RSM Based Optimization. Fuel 2020, 265, 116922. [Google Scholar] [CrossRef]
- Chen, T.; Qin, J.; Zhao, H.; Su, Q.; Lv, Y.; Zhong, K.; Wang, Y.; Pei, Y. Prediction of steady-state primary emissions of gasoline engines based on model group prediction method. J. Jilin Univ. (Eng. Ed.) 2020, 51, 1–11. [Google Scholar]
- Yu, Y.; Wang, Y.; Li, J.; Fu, M.; Shah, A.N.; He, C. A Novel Deep Learning Approach to Predict the Instantaneous NOx Emissions from Diesel Engine. IEEE Access 2021, 9, 11002–11013. [Google Scholar] [CrossRef]
- Prado, G.; Rao, Y.; Klerk, A. Nitrogen Removal from Oil: A Review. Energy Fuels 2016, 31, 14–36. [Google Scholar] [CrossRef]
- Joshi, J.B.; Mahajani, V.V.; Juvekar, V.A. Invited Review Absorption of NOX Gases. Chem. Eng. Commun. 1985, 33, 1–92. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).