Angle-Regulating Rule of Guide Vanes of Variable Geometry Turbine Adjusting Mechanism
Abstract
:1. Introduction
2. Rigid–Flexible Coupling Analysis Considering Multiflexible Bodies and Components’ Thermal Deformations
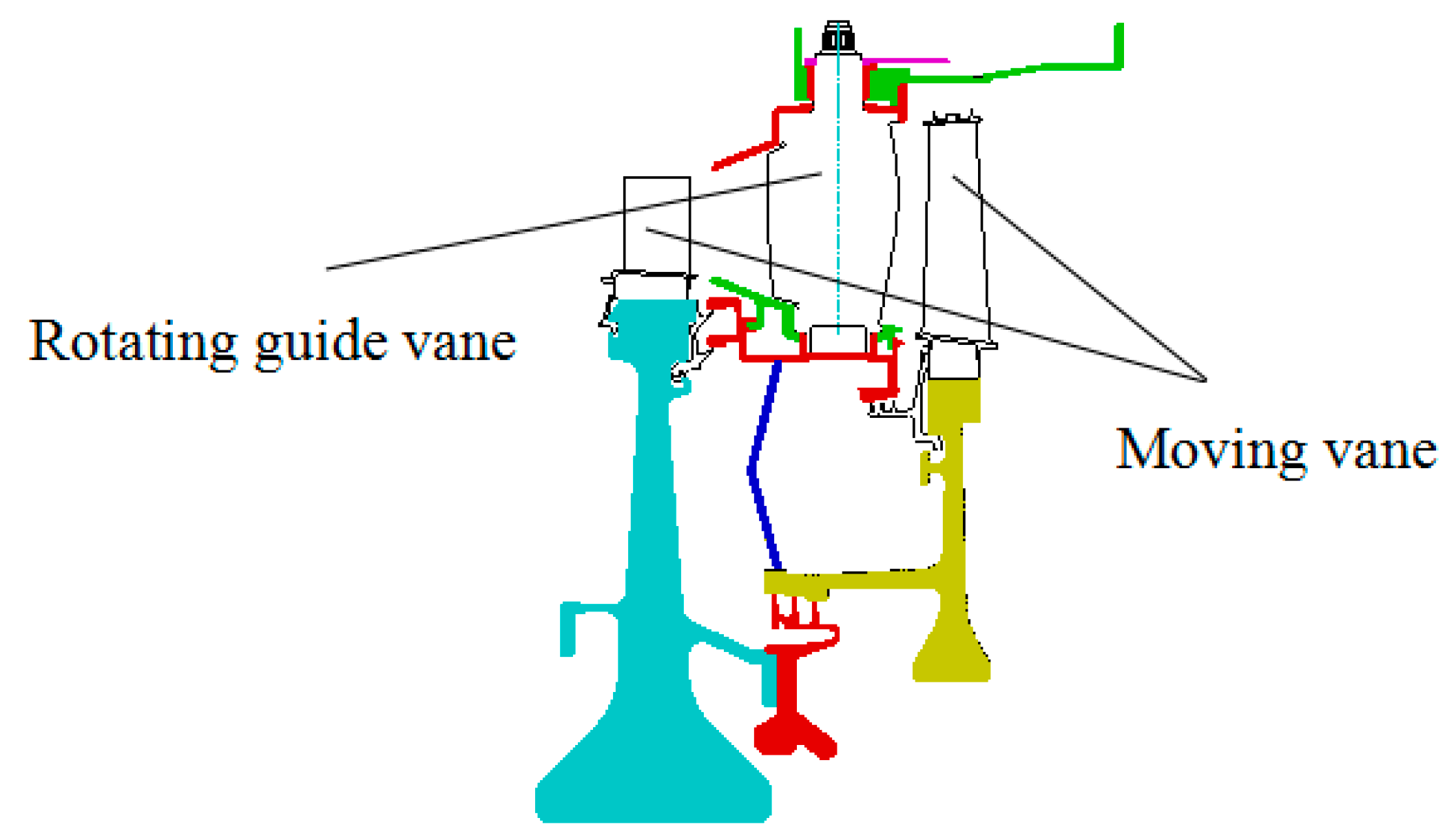
2.1. Computational Model
2.2. Calculation Settings
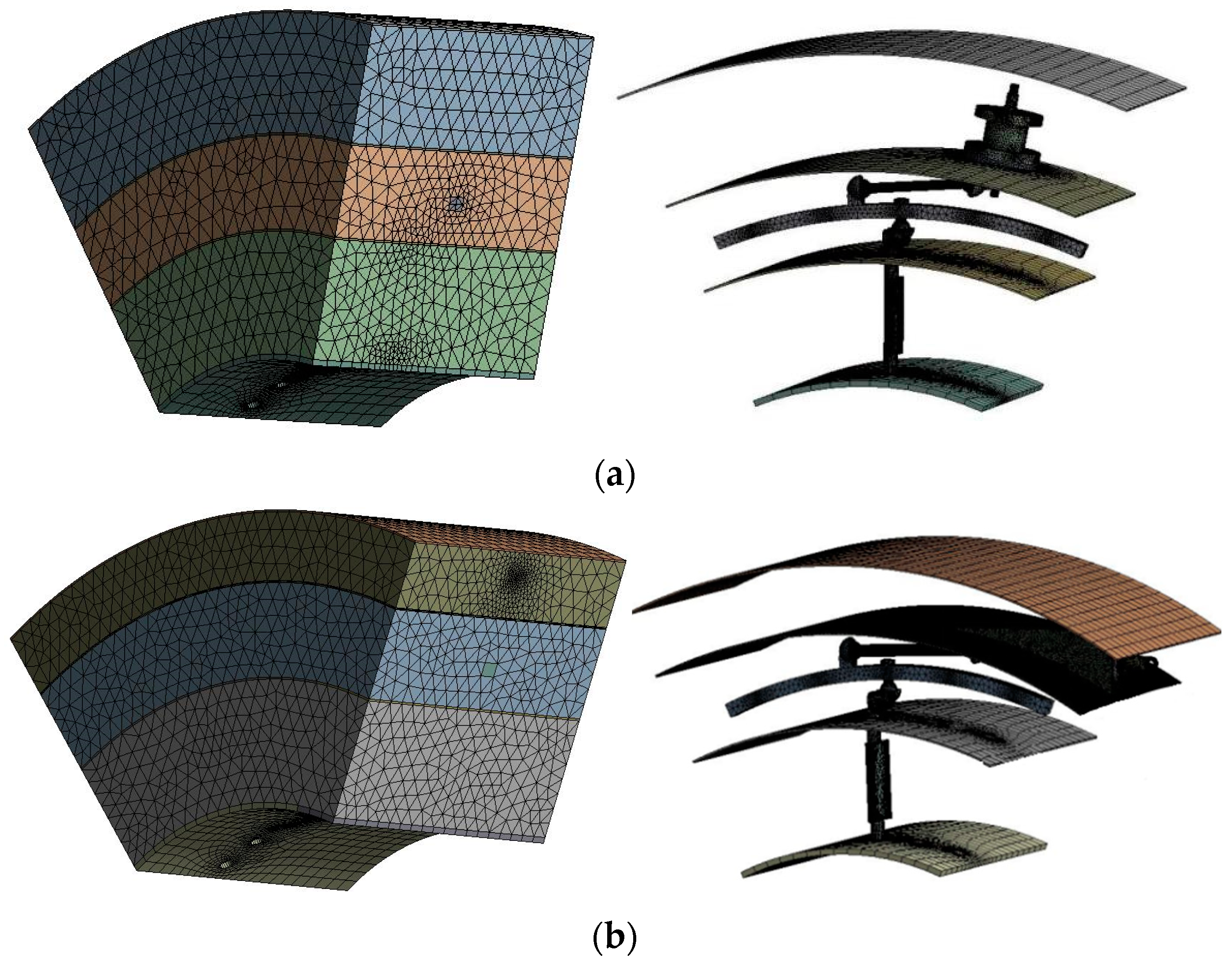
2.3. Meshing
2.4. Material Settings
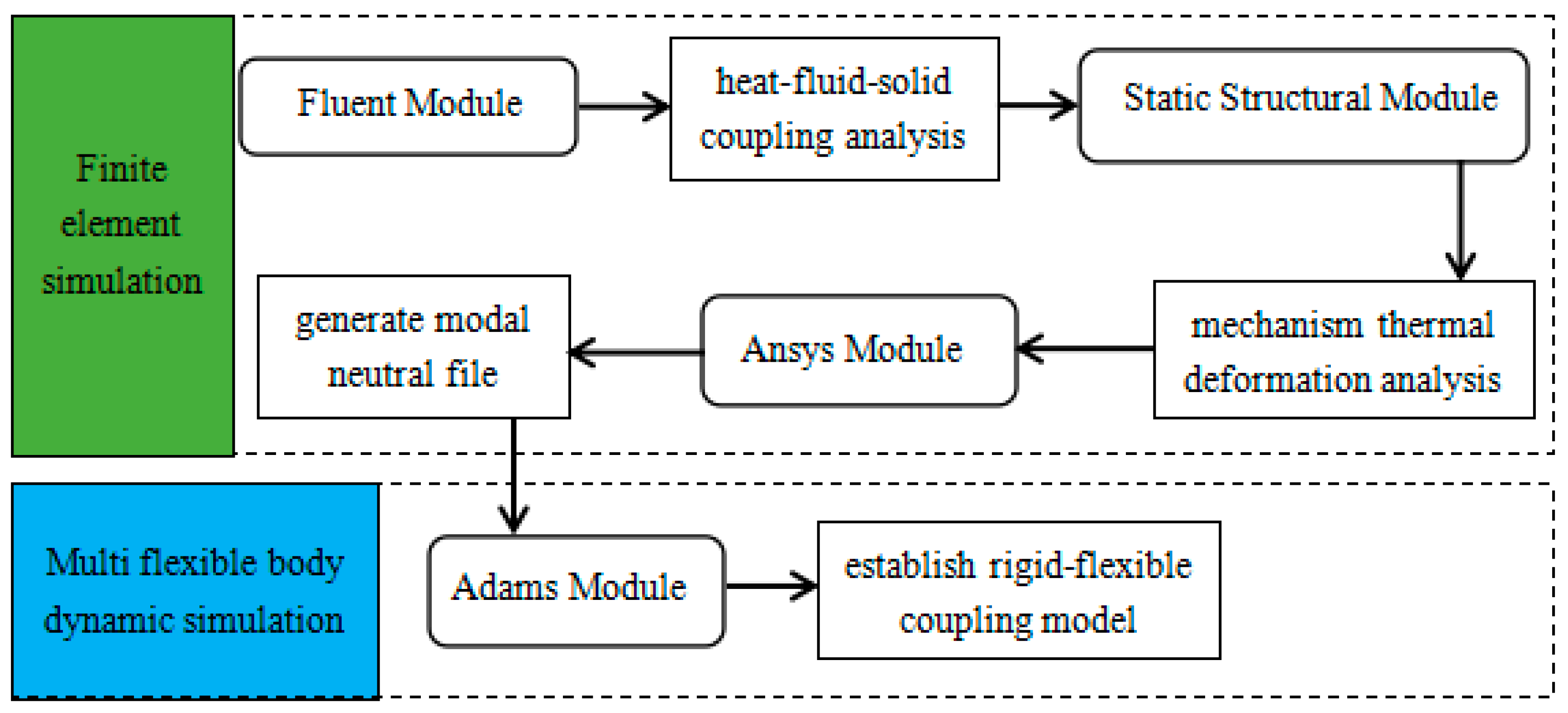
2.5. Calculation Process
3. Results and Discussion
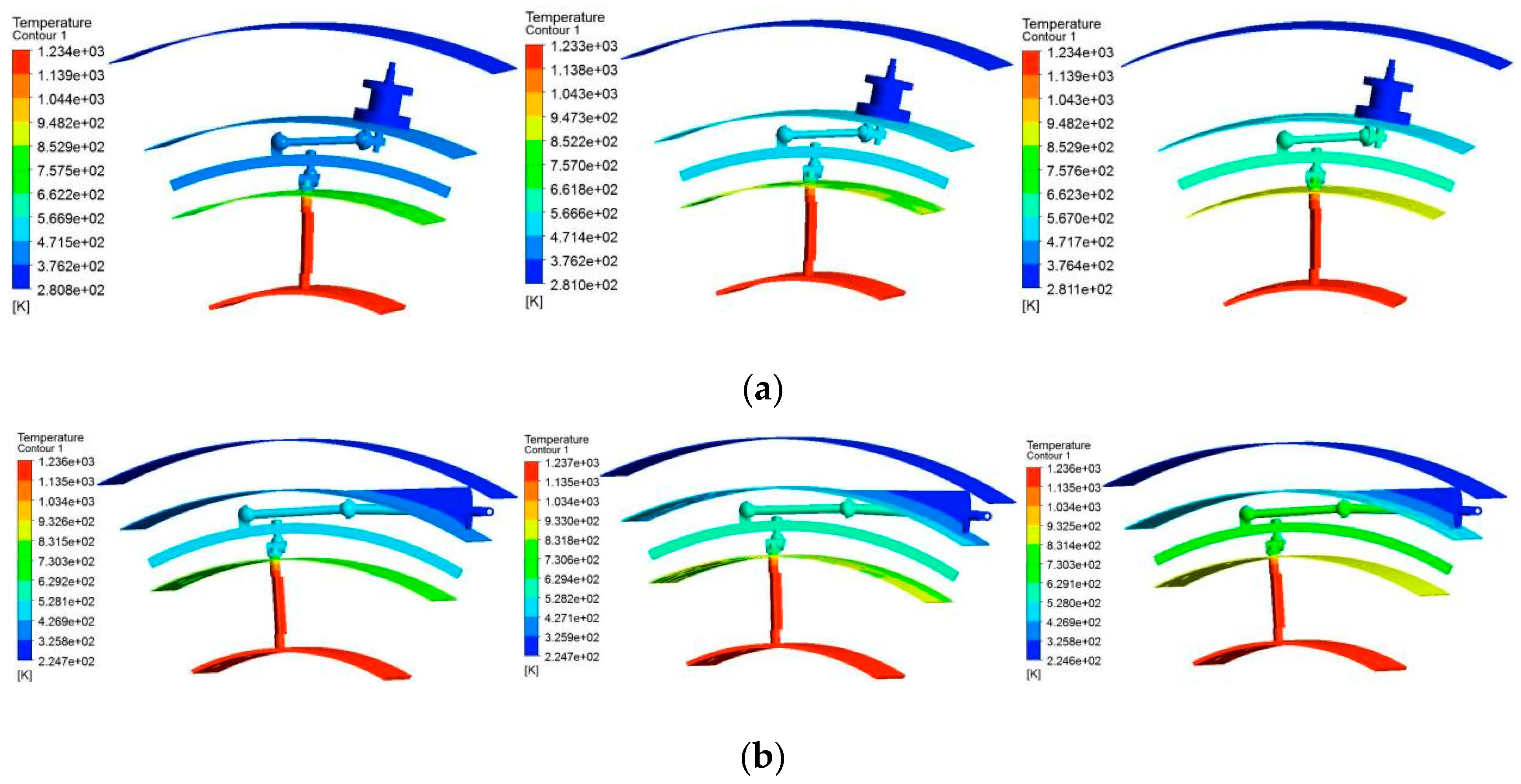
3.1. Temperature Field Analysis
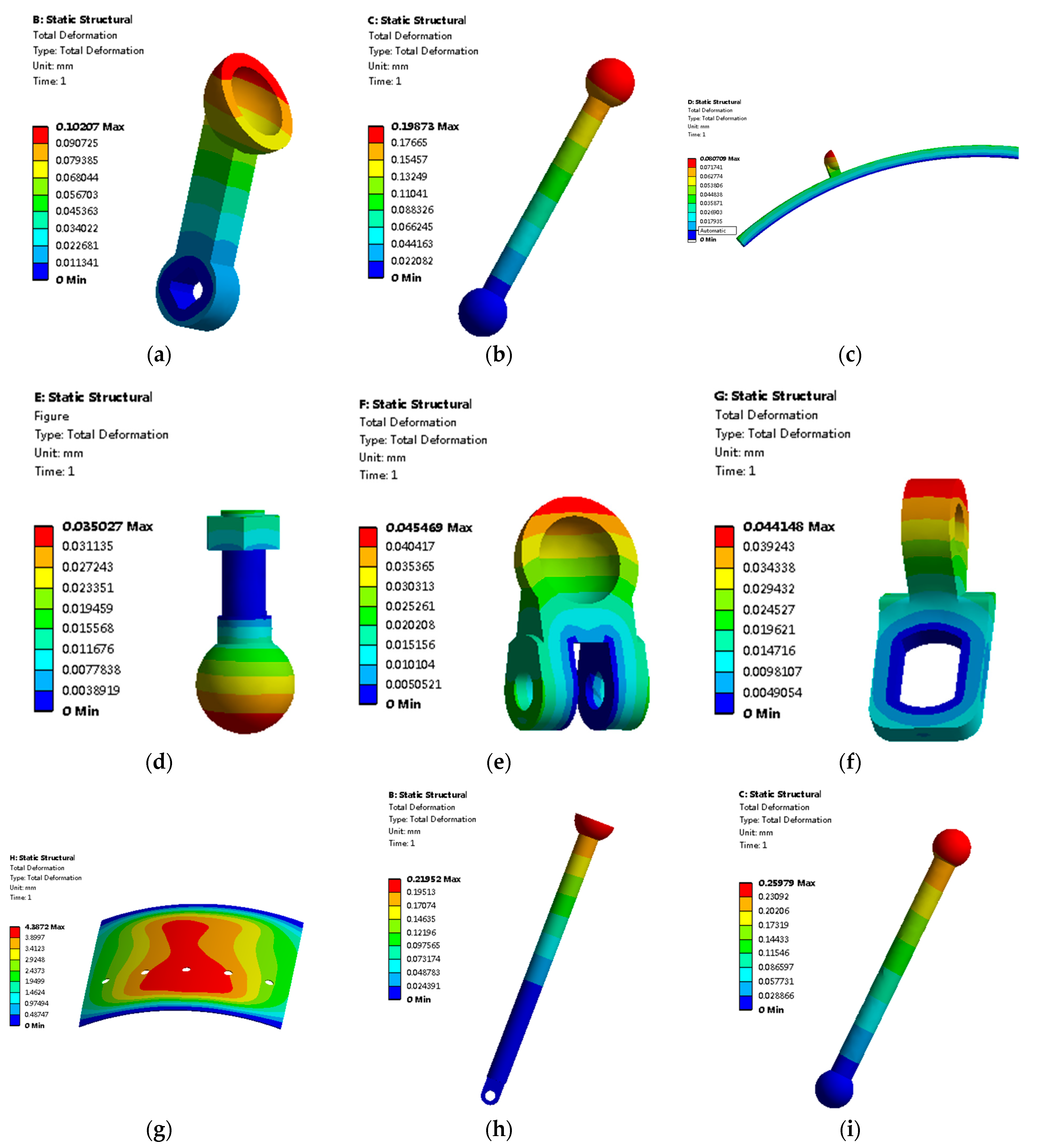
3.2. Thermal Deformation Analysis
3.3. Rigid–Flexible Coupling Models of Two Adjusting Mechanisms with Multiflexible Bodies
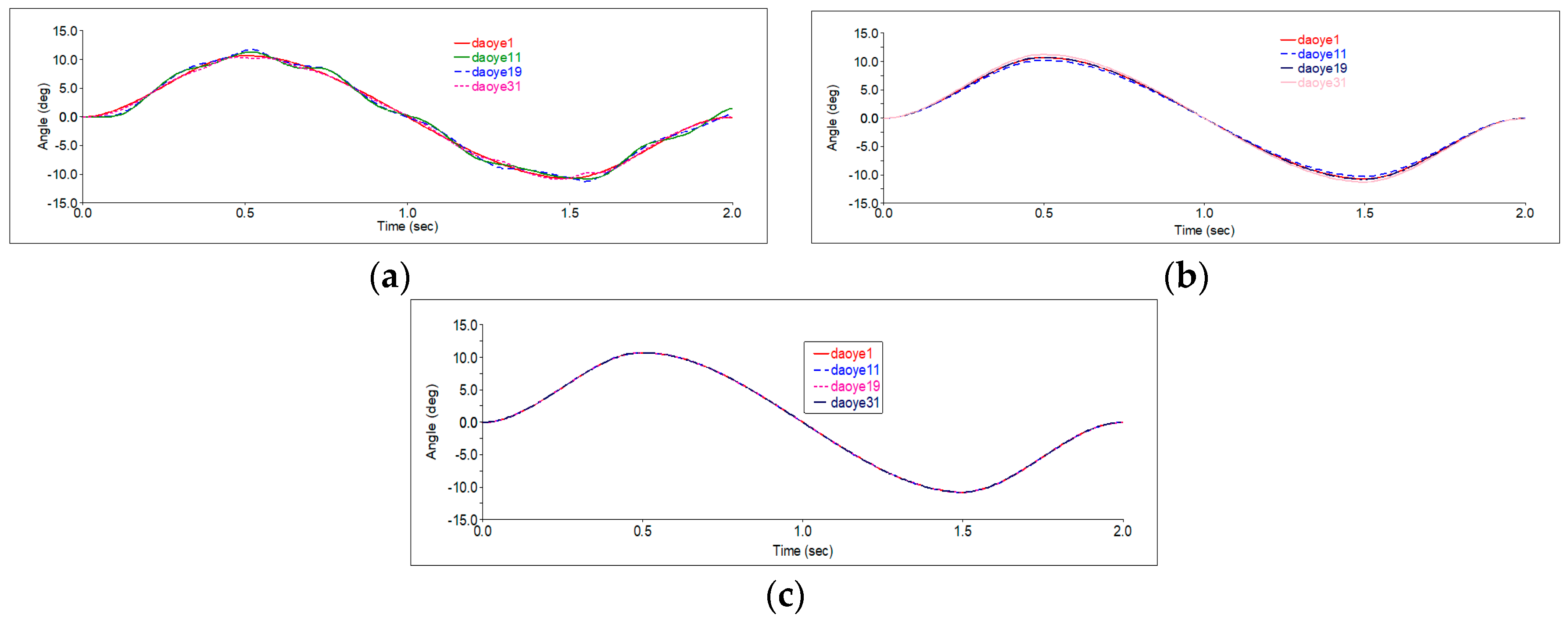
3.4. Influence of Different Driving Modes on Adjusting Mechanism’s Different Guide Vane Angles
3.5. Analysis of Angle-Regulating Rule on Five Guide Vanes with Paddle Rod Adjusting Mechanism
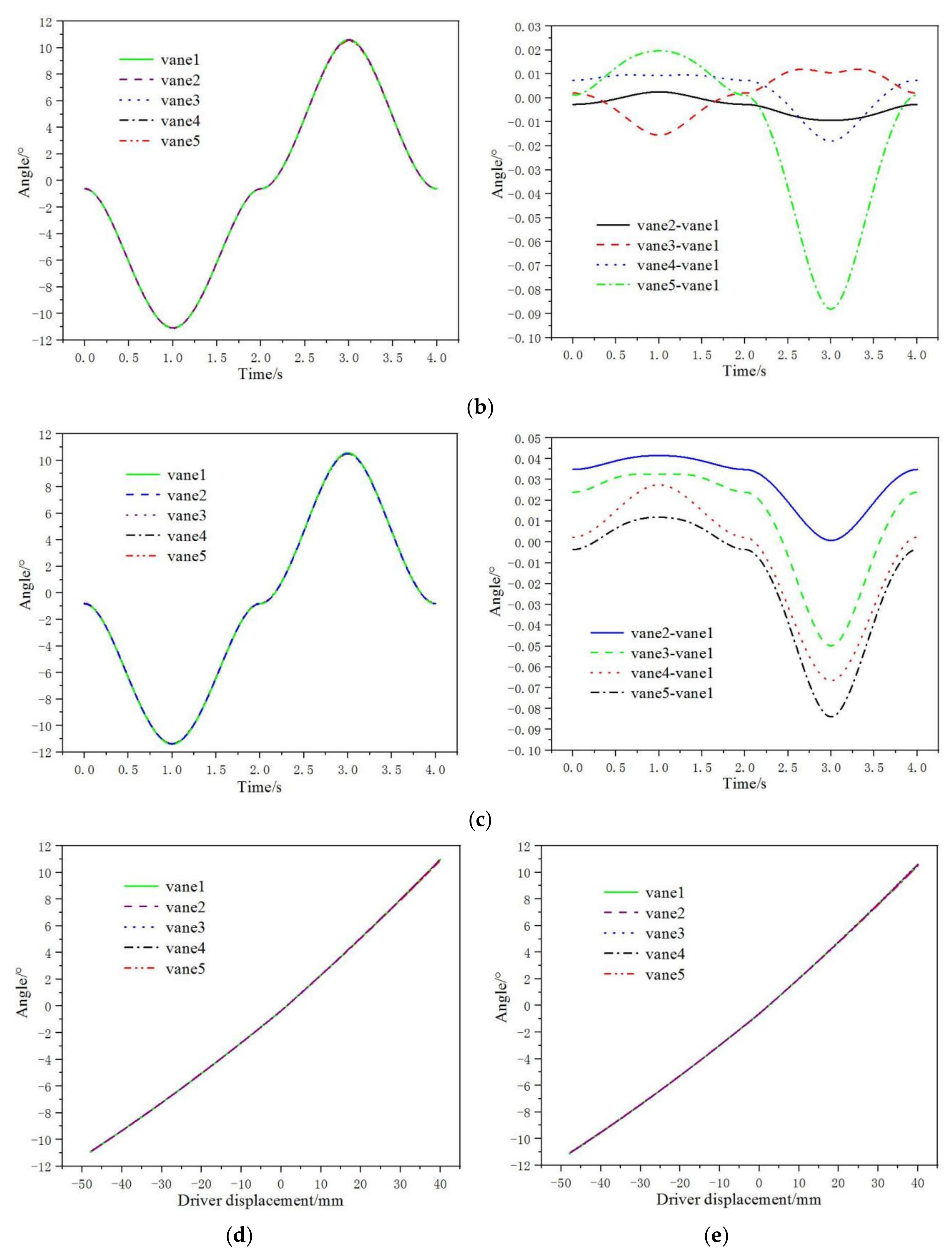
3.6. Analysis of Angle-Regulating Rule on Five Guide Vanes with Push–Pull Rod Adjusting Mechanism
3.7. Influence of Flexible Bodies and Thermal Deformations at Different Temperatures on the Angle-Regulating Rule of Two Adjusting Mechanisms’ Guide Vanes
3.8. Evaluation and Comparison of Two Adjusting Mechanisms
4. Conclusions
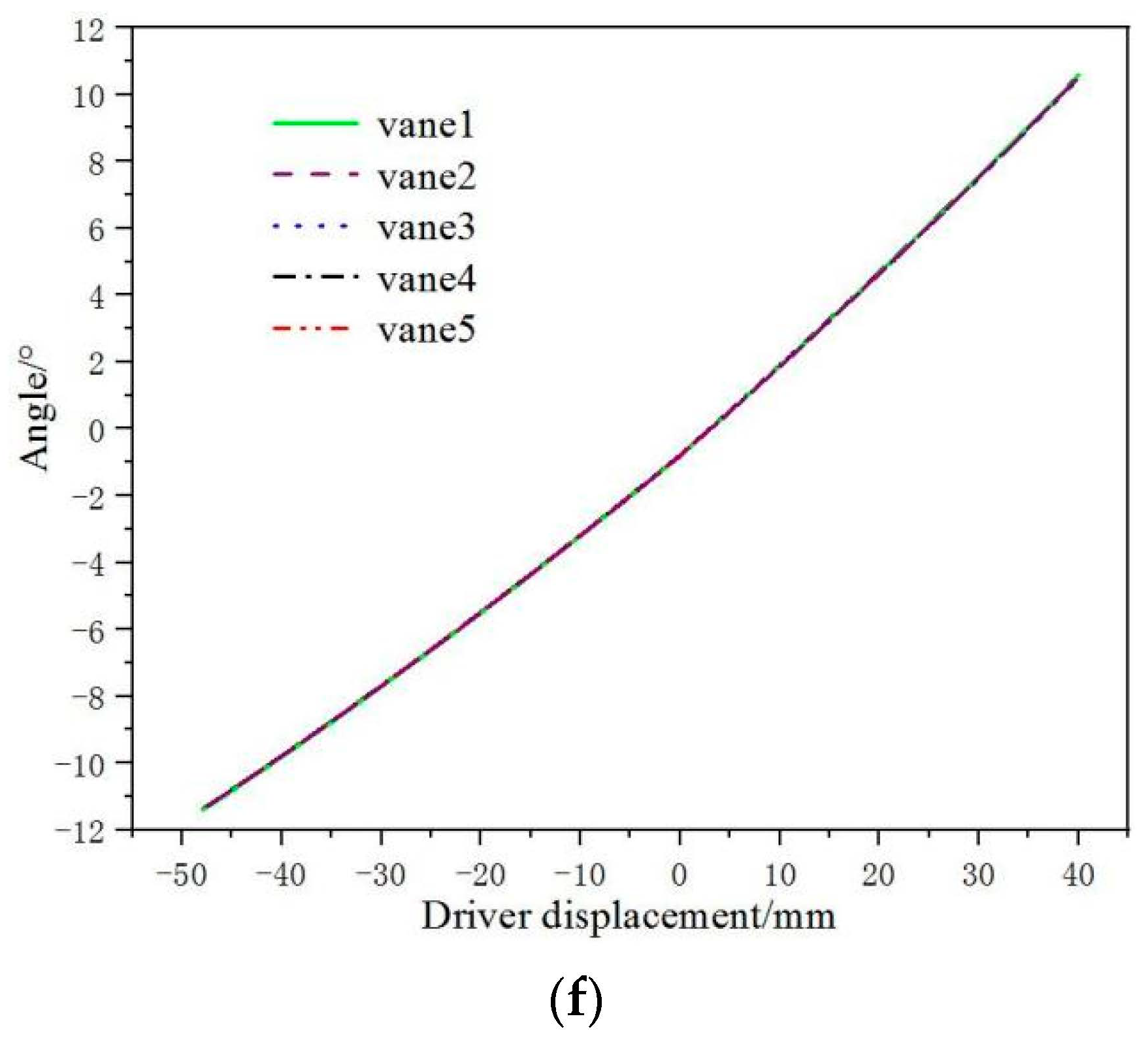
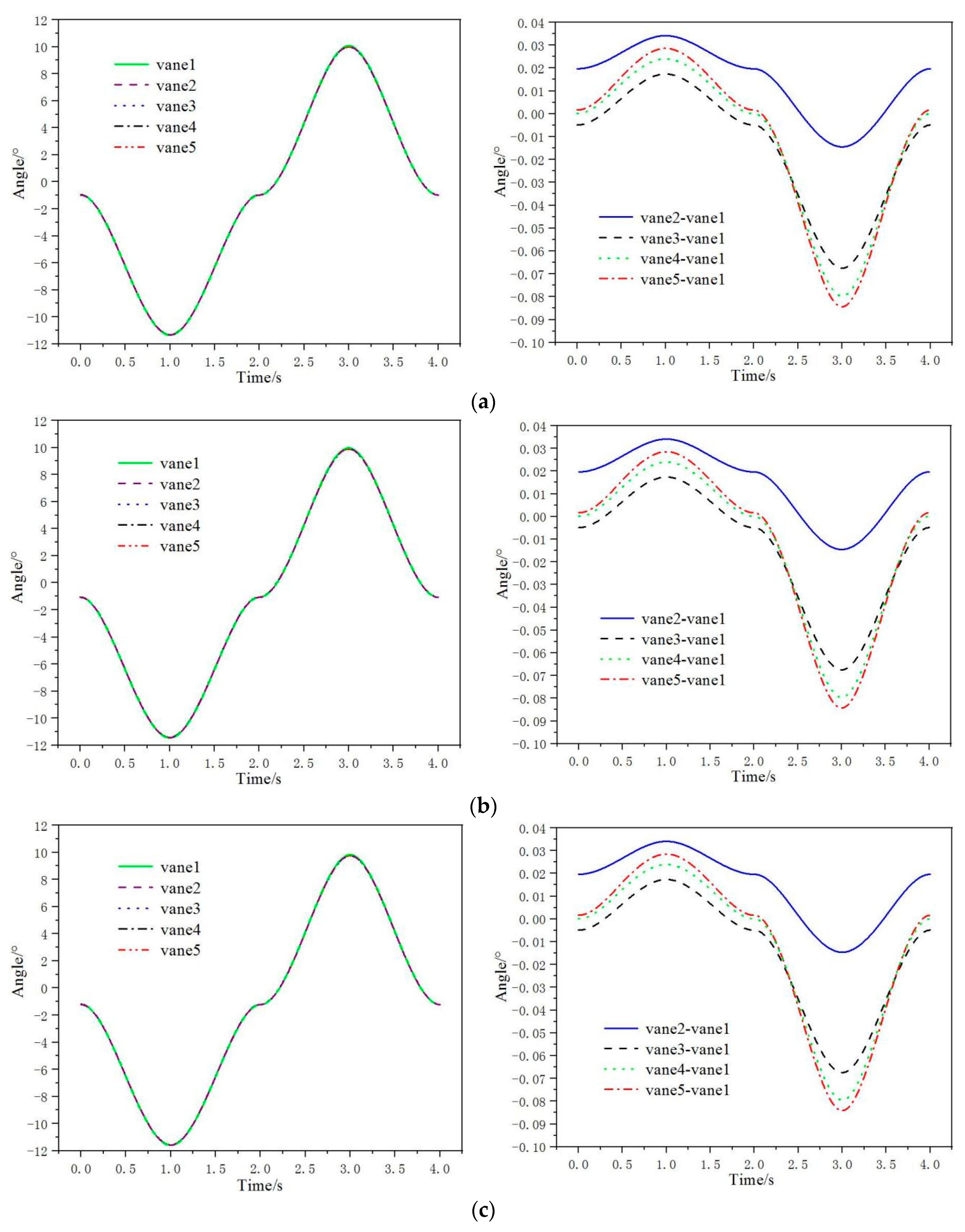
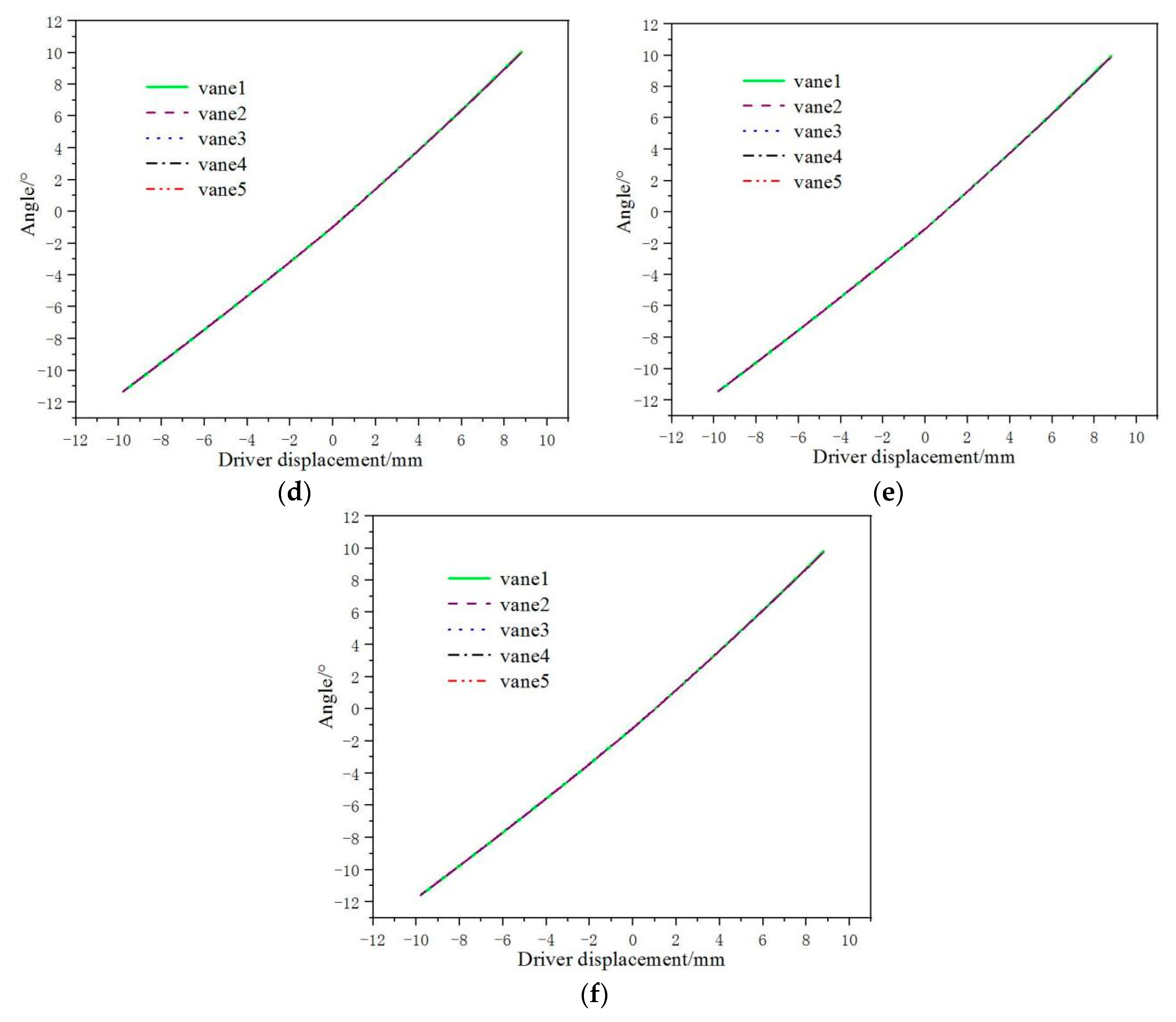
- The angles among different guide vanes of adjusting mechanisms with one driver and two drivers vary greatly. The angle differences can reach 2.3° and 1.9°, respectively. The angle changes among the three drivers’ adjusting mechanism’s different guide vanes are tiny. They are basically a curve track. The guide vanes’ angles are adjusted at the same turbine stage, ensuring ensures the consistency of angle changes among different guide vanes. The regulating rules of the five guide vanes angles of two adjusting mechanisms are basically the same curve track. The maximum difference in deflection angles of different guide vanes is 0.088°. It is much less than the adjusting mechanism’s accuracy requirement of 0.5°.
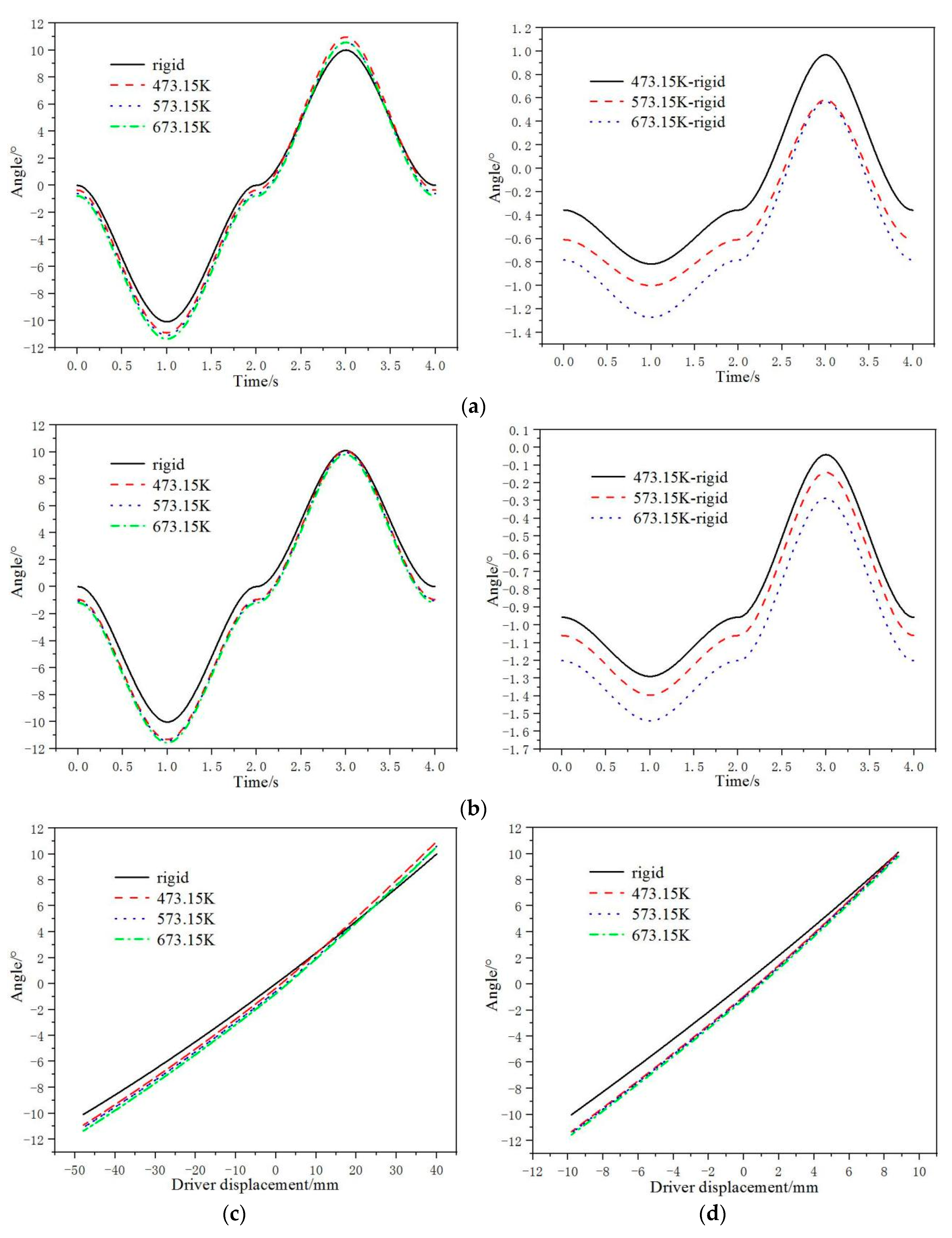
- At the temperature conditions of 473.15K, 573.15K, and 673.15K, each component has high-temperature thermal deformation. The higher the temperature is, the greater the thermal deformation displacement. At 473.15K, 573.15K, and 673.15K, the deflection angle of the guide vane of the multiflexible bodies model deviates from that of the room temperature rigid body model. The higher the temperature is, the greater the deviation. Before making the flexible bodies, the components conduct the thermal deformation analysis. In Figure 9 and Table 5, the higher the temperature, the greater the thermal deformation. The deformed components are made into flexible bodies. The rigid body model is a computational model at room temperature. The components of the rigid body model have no thermal deformations. So there is a deviation in the guide vane angle between the multiflexible bodies model and the rigid body model.
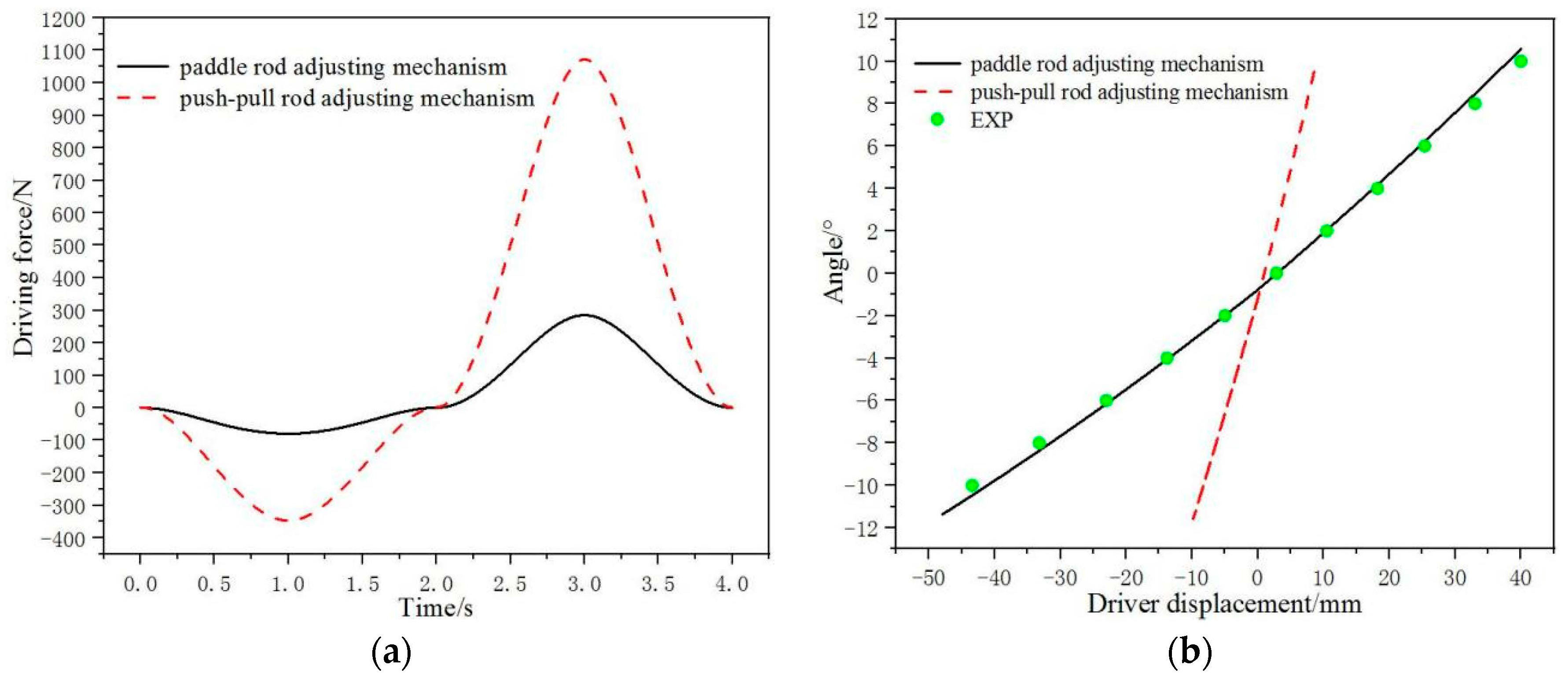
- At 673.15K, the maximum driving force of the paddle rod adjusting mechanism is 284.88N. The maximum driving force of the push–pull rod adjusting mechanism is 1072.27N. In addition, in the whole adjustment process, the driving force of the paddle rod adjusting mechanism is smaller than that of the push–pull rod adjusting mechanism. Because the driving force is small, the deformation of the component is small in the process of movement. It is easier to realize the accurate adjustment of the guide vane angle. During the adjustment process from −10° to +10°, the driving travel of the paddle rod adjusting mechanism is 79 mm. The driving travel of the push–pull rod adjusting mechanism is 17 mm. The larger the driving travel is, the more favorable it is for the guide vane angle to be accurately adjusted and maintained.
- The institute provides the necessary experimental data. The results of the joint computing system are in good agreement with the experimental data. The angle of the guide vane can be accurately adjusted by the paddle rod adjusting mechanism. It is superior to the push–pull rod adjusting mechanism. Furthermore, the production cost of the two adjusting mechanisms is too high. The experimental cycle is also very long. The computational work can result in significant cost savings. The computational work can provide and modify the necessary parameters at the beginning of the design, resulting in much convenience for the design work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Denton, J.D.; Dawes, W.N. Computational fluid dynamics for turbomachinery design. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1998, 213, 107–124. [Google Scholar] [CrossRef]
- Wei, S.; Kun, Z. Design method for high Ma number counter rotating turbine blades. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Boyce, M.P. Gas Turbine Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2011; pp. 841–842. [Google Scholar]
- Wirkowski, P. Modelling the characteristics of axial compressor of variable flow passage geometry, working in the gas turbine engine system. Pol. Marit. Res. 2007, 14, 27–32. [Google Scholar] [CrossRef]
- Hong, S.; Mugabi, J.; Jeong, J.-H. Numerical Study on Vortical Flow Structure and Performance Enhancement of Centrifugal Compressor Impeller. Appl. Sci. 2022, 12, 7755. [Google Scholar] [CrossRef]
- Han, F.; Wang, Z.; Mao, Y.; Tan, J.; Li, W. Flow Control of Radial Inlet Chamber and Downstream Effects on a Centrifugal Compressor Stage. Appl. Sci. 2021, 11, 2168. [Google Scholar] [CrossRef]
- Wang, Z.; Ren, X.; Zhu, W.; Li, X.; Gu, C. Numerical Investigation and Optimization of Variable Guide Vanes Adjustment in a Transonic Compressor. Energies 2023, 16, 567. [Google Scholar] [CrossRef]
- Romagnoli, A.; Martinez-Botas, R.; Rajoo, S. Steady state performance evaluation of variable geometry twin-entry turbine. Int. J. Heat Fluid Flow 2011, 32, 477–489. [Google Scholar] [CrossRef]
- Hadi, Y.; Ali, K.; Mohammad, A.; Behrad, K.; Hiwa, K. Aero-thermal redesign of a high pressure turbine nozzle guide vane. Propuls. Power Res. 2019, 8, 310–319. [Google Scholar]
- Zhang, L.; Cao, G.; Feng, K.; Jia, Y.; Zhang, Z. Improvement of Multi-Hole Airflow Impingement on Flow and Heat Transfer Characteristics Inside a Turbine Vane Cavity. Appl. Sci. 2021, 11, 9924. [Google Scholar] [CrossRef]
- Xu, T.; Shi, D.; Zhang, D.; Xie, Y. Flow and Heat Transfer Characteristics of the Turbine Blade Variable Cross-Section Internal Cooling Channel with Turning Vane. Appl. Sci. 2023, 13, 1446. [Google Scholar] [CrossRef]
- Jin, W.; Mao, Z.; Zhou, S.; Zhang, T.; Hu, Y.; Wu, Z. Research on Multi-Optimal Project of Outlet Guide Vanes of Nuclear Grade Axial Flow Fan Based on Sensitivity Analysis. Appl. Sci. 2022, 12, 3029. [Google Scholar] [CrossRef]
- Xin, J.; Liu, X.; Malik, A.; Liu, H.; Zhao, L.; Kong, X. Investigation of the Flow Field and Aerodynamic Load on Impellers under Guide Vanes with a Self-Induced Slot in Compressor Radial Inlet. Appl. Sci. 2022, 12, 5179. [Google Scholar] [CrossRef]
- José, R.S.; Andrés, O.T.; Juan, A.L.; Natalia, H. Numerical evaluation in a scaled rotor-less nozzle vaned radial turbine model under variable geometry conditions. Appl. Sci. 2022, 12, 7254. [Google Scholar]
- Meng, F.; Li, Y.; Pei, J. Energy Characteristics of Full Tubular Pump Device with Different Backflow Clearances Based on Entropy Production. Appl. Sci. 2021, 11, 3376. [Google Scholar] [CrossRef]
- Yi, X.; Wang, Z.; Liu, S.; Hou, X.; Tang, Q. An Accelerated Degradation Durability Evaluation Model for the Turbine Impeller of a Turbine Based on a Genetic Algorithms Back-Propagation Neural Network. Appl. Sci. 2022, 12, 9302. [Google Scholar] [CrossRef]
- Liang, D.; Jin, D.; Gui, X. Investigation of Seal Cavity Leakage Flow Effect on Multistage Axial Compressor Aerodynamic Performance with a Circumferentially Averaged Method. Appl. Sci. 2021, 11, 3937. [Google Scholar] [CrossRef]
- Szymon, F.; Maciej, C.; Marian, G. Variable geometry in miniature gas turbine for improved performance and reduced environmental impact. Energies 2020, 13, 5230. [Google Scholar]
- Dariusz, K.; Paweł, M.; Andrzej, T. Numerical simulation of two-stage variable geometry turbine. Energies 2021, 14, 5349. [Google Scholar]
- Krzysztof, S.; Damian, O.; Piotr, R.; Emil, M. Numerical investigations of the savonius turbine with deformable blades. Energies 2020, 13, 3717. [Google Scholar]
- Čantrak, D.S.; Janković, N.Z. Turbulence structure and dynamics investigation of turbulent swirl flow in pipe using high-speed stereo PIV data. Energies 2022, 15, 5417. [Google Scholar]
- Li, D.; Qiu, L.; Tao, K.; Zhu, J. Artificial intelligence aided design of film cooling scheme on turbine guide vane. Propuls. Power Res. 2020, 9, 344–354. [Google Scholar] [CrossRef]
- Yang, H.; He, Q.; Huang, X.; Yang, M.; Bi, H.; Wang, Z. Experimental and Numerical Investigation of Rotor–Stator Interaction in a Large Prototype Pump–Turbine in Turbine Mode. Energies 2022, 15, 5523. [Google Scholar] [CrossRef]
- Li, Y.; Song, Y.; Xia, S.; Li, Q. Influence of Guide Vane Slope on Axial-Flow Hydraulic Performance and Internal Flow Characteristics. Energies 2022, 15, 6103. [Google Scholar] [CrossRef]
- Yang, F.; Jiang, D.; Wang, T.; Chang, P.; Liu, C.; Liu, D. Investigation into the Influence of Division Pier on the Internal Flow and Pulsation in the Outlet Conduit of an Axial-Flow Pump. Appl. Sci. 2021, 11, 6774. [Google Scholar] [CrossRef]
- Jesline, J.; Mehrdad, R.; Michel, J.C. Hydraulic performance of a francis turbine with a variable draft tube guide vane system to mitigate pressure pulsations. Energies 2022, 15, 6542. [Google Scholar]
- Vijay Kumar, M.; Subba Reddy, T.; Sarala, P.; Varma, P.S.; Chandra Sekhar, O.; Babqi, A.; Alharbi, Y.; Alamri, B.; Reddy, C.R. Experimental investigation and performance characteristics of francis turbine with different guide vane openings in hydro distributed generation power plants. Energies 2022, 15, 6798. [Google Scholar] [CrossRef]
- Kaddour, T.; Adel, G. Simulation and analysis of vane-blade interaction in a two-stage high-pressure axial turbine. Energy 2019, 172, 1291–1311. [Google Scholar]
- Chen, X.; Chu, W.; Wang, G.; Yan, S.; Shen, Z.; Guo, Z. Effect of span range of variable-camber inlet guide vane in an axial compressor. Aerosp. Sci. Technol. 2021, 116, 106836. [Google Scholar] [CrossRef]
- Lv, M.; Chen, L.; Zhong, Y.; Wang, L. Design and research of swing rod guide vane adjusting mechanism. Modul. Mach. Tool Autom. Manuf. Tech. 2020, 4, 28–32. [Google Scholar]



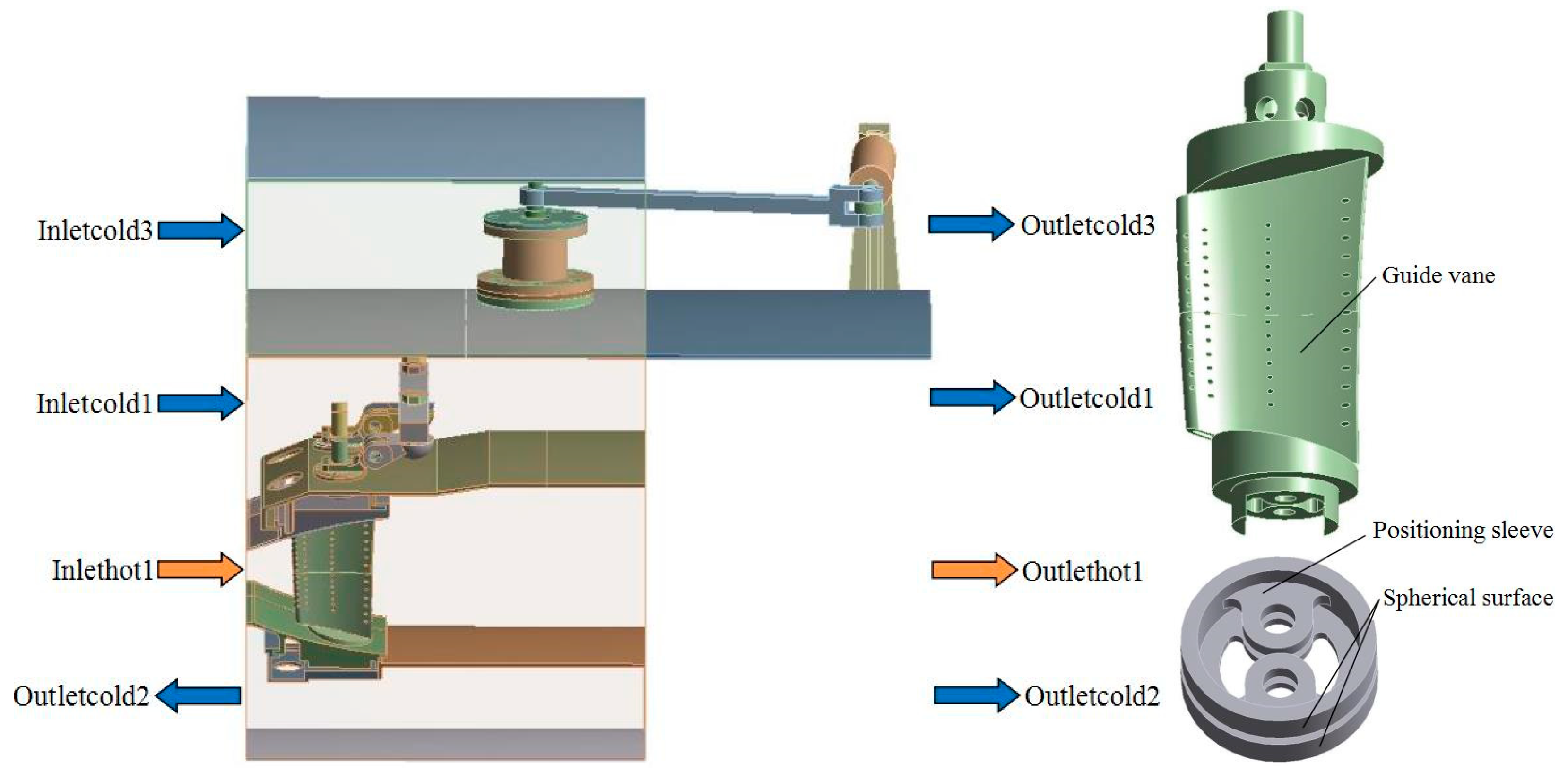



| Name | Type | Temperature/K | Pressure/Pa |
|---|---|---|---|
| Inlethot1 | Pressure inlet | 1273.15 | 657,545.5 |
| Outlethot1 | Pressure outlet | 1204.45 | 494,790.9 |
| Inletcold1 | Pressure inlet | 473.15; 573.15; 673.15 | 657,545.5 |
| Outletcold1 | Pressure outlet | 473.15; 573.15; 673.15 | 494,790.9 |
| Outletcold2 | Pressure outlet | 717.95; 817.95; 917.95 | 494,790.9 |
| Inletcold3 | Pressure inlet | 300 | 111,325 |
| Outletcold3 | Pressure outlet | 300 | 101,325 |
| Parameter Item | Setting |
|---|---|
| Computation domain | Entire fluid domain |
| Fluid type | Compressible gas |
| Turbulence model | k–ε |
| Cascade sides | Periodic boundary |
| Other walls | No slip adiabatic wall |
| TC4 | GH4169 | K417G | 0Cr17Ni4Cu4Nb | 1Cr11Ni2W2MoV | |
|---|---|---|---|---|---|
| 4440 | 8240 | 7850 | 7800 | 7800 | |
| E [Pa] | 8 × 1010 | 1.41 × 1011 | 1.53 × 1011 | 1.7 × 1011 | 1.62 × 1011 |
| μ | 0.37 | 0.33 | 0.3 | 0.3 | 0.3 |
| 5.7 × 108 | 1.01 × 109 | 8.25 × 108 | 7.64 × 108 | 8.53 × 108 | |
| 6.2 × 108 | 1.16 × 109 | 9.25 × 108 | 8.05 × 108 | 1.03 × 109 | |
| 691 | 573.4 | 654 | 502 | 595 | |
| 10.3 | 22.8 | 23.86 | 20.1 | 27.2 | |
| α [10−6C−1] | 9.5 | 15.4 | 14.77 | 13.5 | 11.3 |
| Temperature Range [K] | At 473.15K | At 573.15K | At 673.15K |
|---|---|---|---|
| Paddle rod adjusting mechanism | 376.2–852.9 | 471.4–947.3 | 567–1043 |
| Push–pull rod adjusting mechanism | 325.8–831.5 | 427.1–933 | 528–1034 |
| Thermal Deformation [mm] | At 473.15K | At 573.15K | At 673.15K |
|---|---|---|---|
| Paddle | 0.10207 | 0.16592 | 0.23051 |
| Pull rod I | 0.19873 | 0.31913 | 0.44125 |
| Linkage ring | 0.08071 | 0.12971 | 0.17914 |
| Pin | 0.03503 | 0.05705 | 0.07918 |
| Arm I | 0.04547 | 0.07374 | 0.10225 |
| Arm II | 0.04415 | 0.06949 | 0.09513 |
| Inner casing | 4.3872 | 5.0007 | 5.5658 |
| Push rod | 0.21952 | 0.36659 | 0.5137 |
| Pull rod II | 0.25979 | 0.41566 | 0.57294 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Y.; Chen, L.; Wang, X.; Zhao, L.; Bai, H.; Han, B.; Cheng, S.; Luo, J. Angle-Regulating Rule of Guide Vanes of Variable Geometry Turbine Adjusting Mechanism. Appl. Sci. 2023, 13, 6357. https://doi.org/10.3390/app13116357
Zhong Y, Chen L, Wang X, Zhao L, Bai H, Han B, Cheng S, Luo J. Angle-Regulating Rule of Guide Vanes of Variable Geometry Turbine Adjusting Mechanism. Applied Sciences. 2023; 13(11):6357. https://doi.org/10.3390/app13116357
Chicago/Turabian StyleZhong, Yan, Liangyu Chen, Xinyu Wang, Lei Zhao, Haoxi Bai, Bing Han, Shengzhen Cheng, and Jingbo Luo. 2023. "Angle-Regulating Rule of Guide Vanes of Variable Geometry Turbine Adjusting Mechanism" Applied Sciences 13, no. 11: 6357. https://doi.org/10.3390/app13116357
APA StyleZhong, Y., Chen, L., Wang, X., Zhao, L., Bai, H., Han, B., Cheng, S., & Luo, J. (2023). Angle-Regulating Rule of Guide Vanes of Variable Geometry Turbine Adjusting Mechanism. Applied Sciences, 13(11), 6357. https://doi.org/10.3390/app13116357






