Abstract
This study examines the effectiveness of parapets in preventing overtopping failures of small-scale homogeneous reservoir dams under seismic loads. In this study, a parapet covered the entire width of the dam crest and was designed to ensure its weight is transmitted to the dam crest. The test included four modes: initial mode, first seepage, seismic, and second seepage. The results show that without parapets the crack length and width expand significantly in the dam crest during the seismic mode, and the effect was large in the second seepage mode. The crack depth increased by 11.3–24 times during the seismic mode and expanded up to 73.3% of the dam height in the longitudinal direction along the axis of the crack formed in the dam crest during the second seepage mode. These findings suggest that the earthquake weakened the dam body, making it vulnerable to penetration. In contrast, the parapet structure effectively suppressed most of the tensile cracks by increasing the constraint force. Additionally, no crack expansion or tearing occurred during the second seepage mode post-earthquake, indicating improved seismic performance and suppression of seepage deformation.
1. Introduction
Localized torrential rains owing to climate change have caused extreme flooding and resulted in overtopping-induced embankment failure worldwide for the past several years [1,2]. The increasing frequency, duration, and intensity of natural disasters has heightened the importance of future disaster risk management in the community [3,4,5]. In 2020, 41 deaths and damage to 1057 hydraulic facilities were reported in Korea due to torrential rainfall between 24 June and 16 August, the longest such period in history. Additionally, 22 small-scale reservoir dams collapsed during this period [6,7]. Most of the reservoirs that failed were fill-type embankments (H ≤ 15 m) built over 50 years ago, with their failure caused by overtopping. Figure 1 shows the relationship between the August rainfall and reservoir failure in Korea between 2010 and 2020. Rainfall in 2020 (657 mm), which caused the failure of small reservoir dams, was the highest during the 2010–2020 period. Although rainfall in 2002 (688 mm) and 2003 (684.2 mm) was higher than that in 2020, only one to two reservoir failures were reported. However, by 2020, 85.6% of reservoirs aged above 50 years had collapsed, with earth-fill dams accounting for 99.8% of all reservoirs [8], implying that overtopping was not the only trigger for dam failure. Table 1 shows the causes of reservoir dam failures for the 2010–2020 period, with most failures attributed to torrential rainfall. Some failures were also caused by piping defects due to aging conduits. Although determining the exact cause of dam failure is difficult, it is evident that the failures occurred in dams over 50 years old, potentially because of construction and maintenance issues linked to the prevalence of homogeneous reservoir dams built under poor social conditions during the Japanese colonial period and the Korean War (1930–1970) [9]. Most small reservoirs constructed during this time lacked proper flood protection and control measures or maintenance, increasing the risk of dam failure today. In addition, overflow accounted for the highest failure rate (35.9%) in fill-dam-failure statistics [10], with such failures often attributed to unfavorable physical soil conditions, including compacted soil, soil moisture, and clay content. These conditions can lead to flooding as water levels rise uncontrollably due to soil erosion or structural defects [11,12]. These findings suggest that preventing flooding in old reservoirs, which continue to increase every year, is difficult when torrential rains exceed the designed flood level.
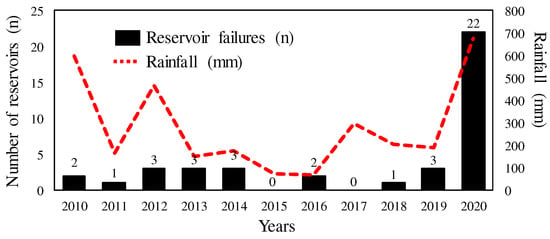
Figure 1.
Relationship between rainfall and reservoir failure (Korea).

Table 1.
Causes of failure of reservoir dams during 2010–2020.
Given the above background information, the present study evaluates the effectiveness of dam reinforcement and flood prevention by constructing a parapet structure on the dam crest. Although a few parapet-designed reservoir dams exist, most of them are concrete or rock-fill dams. An example of an earthen dam, such as the one studied here, is the San Luis Dam in California, USA; its dam parapet wall is made of reinforced concrete and is 14 feet high and 4 feet wide. In some cases, parapets are designed only in certain sections of the dam crest along the upstream slope [13], whereas in this study, the parapet covers the entire width of the dam crest and is designed to ensure that its own weight is transmitted to the dam crest.
The anticipated structural effects of constructing parapets on dam crests include the following: (a) The trapezoidal shape of dams can provide better water pressure resistance and load distribution, which helps crack suppression inside the embankment. The weight of the parapet can also restrain the seepage progression. (b) In Japan, most small-scale earth dams with sandy soil embankments have suffered damage because of earthquakes; even a 5.4 magnitude earthquake can cause embankment failure [14]. Parapets can improve seismic performance by preventing the displacement generated from the dam body. A centrifugal model test was conducted in this study to investigate this effect. Building full-scale circular dams can be expensive and time-consuming; however, centrifugal models can simulate such structures on a smaller scale. By rotating the model, a force similar to gravity is applied in the central direction, allowing the model to produce a deformation that approximates a circular shape. Previous studies have used centrifugal models to evaluate embankment deformation, hydraulic behavior, and reinforcement effects in soft ground or various ground conditions during earthquakes [15,16]. One closely related study describes the characteristics of water pressure changes during an earthquake in a fill dam [17]. While the existing literature provides valuable suggestions for future experimental directions, it typically relies on single-shot experiments that do not link seepage and seismic behavior. In the context of centrifugal model experiments for hydraulic facilities, continuously considering the infiltration problem applied to the embankment can closely simulate field conditions.
This study is novel because it focuses on linking seepage and seismic experiments to provide a more comprehensive understanding of potential issues that may arise in reservoir dams. Furthermore, the effectiveness of the parapet on the dam crest is evaluated.
2. Materials and Methods
2.1. Centrifugal Model Test
A centrifugal model test was conducted to match the stress state due to the material weight in a 1/N scale model (hm) made of the same material and density as the prototype (hp). By introducing a centrifugal force equivalent to NG (G: gravitational acceleration, 9.8 m/s2) in the model, a gravitational field becomes N times stronger than that of the Earth’s gravity, thus enabling a direct comparison of the stresses in the model and the prototype. To obtain the same stress state of the prototype and model, the following relationship applies:
hm/hp = 1/N
Table 2 lists the similarity law applied to the centrifugal model test [18]. The centrifugal model test device used in the experiment was an accelerator with a rotational radius of 1.5 m; the dimensions of the model container, called the “rigid box”, were 45 × 45 × 30 cm.

Table 2.
Similarity law in the centrifugal model test.
2.2. Scenario Setting
Reservoir dams are vulnerable to changes in water levels during construction and maintenance. Therefore, simple experiments are required that can provide realistic conditions to accurately simulate potential hazards such as heavy rainfall or earthquakes. Initially, the dam model is in a state where no load or pressure is applied, and experiments must be conducted to bring the material closer to saturation. The flood level is applied to the upstream water level under the assumption that the embankment saturation state is reached when the pore water pressure in the downstream embankment zone increases. Based on the initial model, the study confirms the hydraulic behavior in the first infiltration mode, stress behavior during seismic motion, and state changes in the dam model during the second infiltration mode after the earthquake in each mode. The study comprises four processes, with each experimental mode classified as either with or without parapet, as shown in Figure 2.
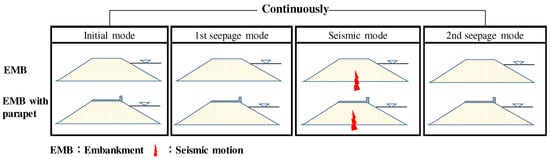
Figure 2.
Scenario setting.
2.3. Modeling and Experimental Conditions
The reservoir dam prototype was a homogeneous small-scale reservoir with a height of 6 m, dam crest width of 4 m, and slopes of 1:1.2 and 1:1.3 on the downstream and upstream sides, respectively. Figure 3 shows the design conditions applied to the model dam construction. A silicon mat (thickness: approximately 2 cm) was installed at the boundary between the model dam and foundation to ensure seepage only within the embankment. The foundation was 15 cm deep, comprising hard sand with over 95% compaction. Accelerometers and three water pressure gauges were used to measure seepage and seismic behavior. Additionally, three small pumps were used to circulate water and maintain the upstream water level during the experiment. The small pump was designed to pass water only through a wire mesh to prevent failure due to soil mixing. The parapet was made of cement with dimensions of 30 × 20 × 200 mm (height × width × depth) and a weight of 2.07 kg. The upstream water level was applied to the viscous fluid. For 100% saturated soils, the physical properties of the soil, such as strength and stiffness, are not affected by viscous fluids [19].
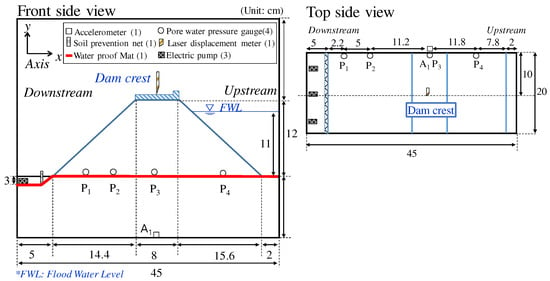
Figure 3.
Design conditions and cross-sectional drawings for the model dam.
In the centrifugal model test, instantaneous failure may occur owing to comparatively fast seepage flow caused by massive gravitational acceleration. Consequently, the viscous fluid was designed to have the same viscosity (50 G) as that of the scale factor of the model. For monitoring equipment, an action camera was placed in front of the model to observe cracks caused by the weight of the parapet structure and deformation of the dam. Additionally, DIPP-Motion V image analysis software was used to numerically track the deformation of the model dam after centrifugal loading [20]. For image analysis, a marker was assigned to the model image captured by the camera and used to calculate the deformation displacement before and after the experiment by tracking the RGB value of a specified pixel. Displacement can be measured and described in both longitudinal and transverse directions.
2.4. Construction Materials
Weathered granite, predominantly sandy soil, has often been used as construction material for embankments, contingent on the construction environment. Depending on the degree of rock weathering, the distribution of components such as sand, silt, and gravel, can exhibit a wide range of properties and may have low stability compared to other soil types [21]. In this experiment, weathered granite soil was selected, considering that small-scale earth dams constructed in the past had abundant sandy soil [14]. Figure 4 shows the grain size distribution of the weathered granite soils. In the laboratory test, weathered granite soil exhibited horizontal permeability (kh) of 7.45 × 10−6 m/s and a specific gravity (Gs) of 2.65. The maximum dry unit weight (𝛾d max) was 1.89 (t/m3) and the optimum water-content ratio (wopt) at this time was 7.5%. Generally, weathered granite soil has a permeability in the range of 10−4 m/s (sandy soils) to 10−6 m/s (silty soils) [22]; thus, the coefficient of permeability measured in the laboratory is considered suitable as a construction material. However, it should be noted that differences in materials and construction methods used may result in potential variability between the strength calculated using laboratory tests and field tests [23]. This variability suggests possible limitations in evaluating the stability of the dam body with a reduced model.
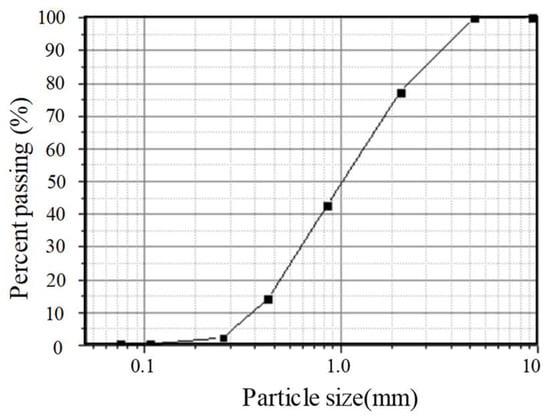
Figure 4.
Grain size distribution of construction material.
As this study aimed to investigate the effect of seepage and seismic behavior on the reservoir dam condition, the calculation of the dam safety factor is not included. Therefore, in this experiment, the mechanical parameters of dam building materials, such as material strength, modulus of elasticity, tensile strength, and compressive strength, were not considered while calculating the safety factor for reservoir dams or parapet structures.
2.5. Input Seismic Motion
Korea is located on the Eurasian Plate, and earthquakes of magnitude (M) 3 or higher have been recorded since digital measurement began in 1978. According to the earthquake classification, M 4.1–5.0 (9%), M 5.1 or greater (2%), and M 3.1–4.0 (88%) have been recorded to date [24]. The maximum possible earthquake on the Korean Peninsula is estimated to be M 6.5. However, unlike newly constructed dams, small aging earth dams may be vulnerable to infiltration and earthquakes due to poor construction environments. The construction materials of old reservoir dams in Korea have problems such as high sand content, high slope angle (about 1:1.5), and no seismic design. In Japan, old small earth dams with high sand content have been damaged and collapsed in an M 5.4 earthquake, suggesting that an M 6.5 earthquake could be too strong for identifying seepage and stress behavior in small old reservoir dams. Therefore, to avoid exaggerated test results, this experiment determined an acceleration of 1.1 m/s2 (approximately 0.1 g) based on the collapse history of a small-scale earth dam that experienced M 5.4 (0.1 g) acceleration in Japan [14]. Figure 5 illustrates the input seismic motion used in this study. It is crucial to select the right earthquake motion records that minimize variables in the test results due to the scale model of the earth dam to obtain accurate test results [25,26]. A sine wave was used to monitor the behavior of the small earth dam at a specific frequency in a basic experiment. Although sine waves produce more severe conditions in terms of the number of load cycles, they enable effective monitoring of the structure’s behavior, which is useful for comparing the effects of different seismic motion types on the behavior of structures and soils. During the experiment, 50 G was applied for 0.4 s. The scale of the prototype is 20 s. The sine wave’s amplification gradually increased and remained constant at maximum acceleration for a period before gradually decreasing. This gradual increase in amplitude prevented abrupt changes in the load that may create shock or impact and affect the structure or sensors used for measurement. Gradually increasing load allows the structure and instrumentation to adjust to the changes in a more controlled manner, enabling a more accurate measurement of the response.
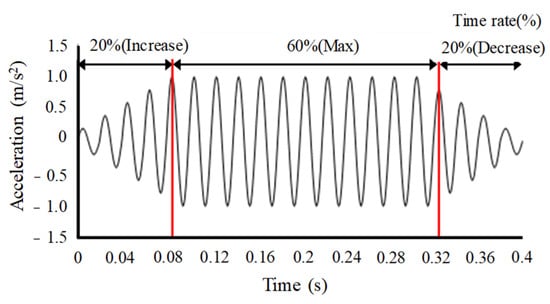
Figure 5.
Input seismic motion.
3. Results and Discussion
3.1. Deformation Shape and Displacement
Considering overtopping failure is related to the embankment state, deformation was observed inside the embankment zone along the parapet and dam crest. Figure 6 and Figure 7 show the conditions without and with a parapet, respectively. In Figure 6a, only the upstream flood water level (h = 11 cm) is set as the initial condition of the model dam; Figure 6b illustrates the condition in which only seepage is applied under 50 G; Figure 6c depicts the condition in which an earthquake with an acceleration of 1.0 (m/s) is applied after penetration; Figure 6d shows the condition of seepage after the earthquake.

Figure 6.
EMB model deformation: (a) initial mode, (b) 1st seepage mode, (c) seismic mode, and (d) 2nd seepage mode (unit: mm).

Figure 7.
Parapet model deformation: (a) initial mode, (b) 1st seepage mode, (c) seismic mode, and (d) 2nd seepage mode (unit: mm).
In the EMB model, as with the first seepage mode, a deformation of 3 mm depth was evident in the downstream dam crest, indicating vulnerability at the top of the downstream slope. In the seismic mode, a settlement of 8–13 mm occurred from the center of the dam crest to the top of the downstream slope, indicating the widening of the vulnerable area formed in the first seepage mode. As the top of the downstream slope was located at the narrow cross-sectional area, it may have been vulnerable to hydraulic pressure or seismic stress. In the second seepage mode, it extended to 73.3% of the embankment height, i.e., the depth from the dam crest (32 mm), along the crack axis formed in the seismic mode. Additionally, a crack depth of approximately 20 mm was observed in the center of the downstream slope. These findings suggest that after an earthquake, the dam body may experience accelerated durability degradation, leading to conditions in which cracks can easily expand, which could significantly threaten the stability of earth dams if left without any maintenance.
The first seepage mode in the parapet model was similar to that in the EMB model, as a slight deformation of 3–4 mm depth was evident at the top of the downstream slope. However, deformation was not observed in seismic mode, indicating a large difference from the EMB model. These results suggest that the parapet’s weight acted on the dam crest and suppressed the deformation. Additionally, no other cracks or deformations were observed in the second seepage mode; therefore, it is believed that the effect of parapet weight also suppressed penetration. The deformation results suggest that the top of the downstream slope is vulnerable to pore water pressure and earthquakes. The displacement of the model dam, presented in Figure 8, was computed using DIPP-Motion V image analysis software. Displacement calculations were performed for Section A (downstream slope), B (dam crest), and C (upstream slope), as shown in the figure, with the maximum displacement values for each section listed in Table 3.
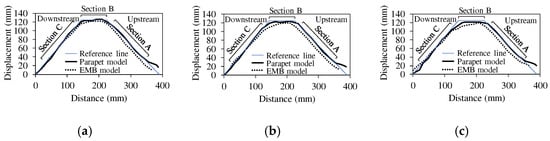
Figure 8.
Displacement comparison in the EMB model and parapet model: (a) 1st seepage mode, (b) seismic mode, and (c) 2nd seepage mode.

Table 3.
Maximum value of displacement extracted from Section A, B, C (unit: mm).
The upstream slope of the EMB model experienced a settlement of 11–14 mm, which remained constant until the seismic and second seepage modes. In contrast, the parapet model exhibited minimal displacement in all modes, probably due to the weight of the structure slowing down the seepage rate. During the seismic mode, the dam crest of the EMB model experienced a rapid increase in settlement resulting in a displacement more than twice that of the first seepage mode. This displacement continued to increase after the earthquake, indicating the significant effect of earthquakes on the hydraulic deformation of the dam. During the experiment, the downstream slope swelled slightly in the transverse direction; however, the displacement due to earthquakes or pore water pressure was relatively small in all modes.
In contrast, the parapet model exhibited a relatively stable tendency with a gentle increase in displacement in all modes. Interestingly, no lateral displacement occurred due to the slip phenomenon, despite no measures being implemented to prevent slip between the parapet and the dam crest because the parapet designed in this study had a structural shape that made it difficult for displacement to occur. Additionally, as a constant weight was applied to the entire width of the dam crest, the dam crest damage through the lateral movement of the parapet was difficult. This finding suggests that parapet load was distributed across the entire area of the dam crest, helping suppress lateral displacement.
3.2. Dam Crest Cracks
The deformation and displacement results of the model indicate that a vulnerable section developed in the dam crest. Figure 9 and Figure 10 show the dam-crest cracks in the EMB and parapet models, respectively. The EMB model exhibited long lateral cracks in the primary seepage mode, adjacent to the upstream dam crest. In the seismic mode, cracks developed along the lateral axis, appearing similar to the cracks caused by actual earthquakes in earth dams [27,28]. There was no change in the crack shape in the second seepage mode compared to the seismic mode, although a widening and deepening was evident. Additionally, the crack shapes increased in the downstream direction, implying that the deformation caused by the pore water pressure inside the dam acted in the direction of the dam crest. Consequently, further discussion is required regarding the effect of continuous hydraulic deformation on the inner stability of the dam after an earthquake.

Figure 9.
EMB model: (a) initial mode, (b) 1st seepage mode, (c) seismic mode, and (d) 2nd seepage mode (unit: mm).

Figure 10.
Parapet model: (a) initial mode, (b) 1st seepage mode, (c) seismic mode, and (d) 2nd seepage mode (unit: mm).
In the parapet model, the parapet was removed to confirm the effect of the parapet in detail, and the dam crest crack shape was observed. In the dam crest, no cracking was observed for all scenarios used in this study. Clearly, the parapet (W: 2.07 kg) improved the seismic performance by increasing the constraint force of the dam crest, even at a weight level of approximately 18% of the model dam (W: 11.2 kg).
Figure 11 illustrates the length, width, and depth of the cracks, with crack size calculated based on the first seepage mode. The crack length generated in the first seepage mode increased by 2.1–2.4 times in the seismic mode. In the second seepage mode, the expansion of the crack length was insignificant as it increased by approximately 1.1 times. The crack width generated in the first seepage mode increased by 5.0–8.0 times in the seismic mode. In the second seepage mode, the expansion of the crack width was insignificant as it increased by about 1.2 times. The crack length and crack width results showed that the earthquake rather than the hydraulic pressure affected dam crest cracks. In contrast, crack depth showed a different pattern compared to crack length and width. The crack depth increased continuously after the earthquake, ranging from 11.3 to 24 times in the seismic mode and 22.5 to 48.0 times in the second seepage mode, enlarging the deformation caused by the pore water pressure in the embankment.
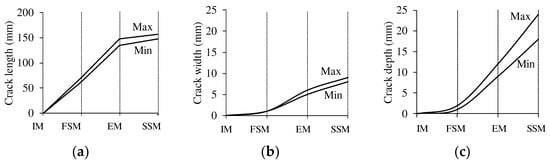
Figure 11.
Dam crest crack size: (a) crack length, (b) crack depth, and (c) crack width. IM: initial mode; FSM: 1st seepage mode; EM: seismic mode; SSM: 2nd seepage mode.
The following conditions can be inferred from the shape and size of the cracks on the dam crest:
- In the case of cracks remaining at the dam crest, large-scale tensile cracks can be caused by loading in the crack direction during an earthquake.
- The increase in crack depth after the earthquake indicates that the deformation continues owing to the pore water pressure in the embankment, suggesting that stabilization measures and management of embankments after an earthquake are necessary.
In the parapet model, after removing the parapet, the condition of the dam crest was inspected under the first seepage mode, seismic mode, and second seepage mode. Unlike the EMB model, no tearing or crack expansion was observed in the dam crest; therefore, no crack size was recorded.
The parapet model results show that, even if seepage continues after an earthquake, the embankment stabilizes in the long term owing to the pressing effect.
3.3. Pore-Water-Pressure Variation
The results of the deformation, displacement, and crack depth of the body and the dam crests show that the pore water pressure after an earthquake is critical for stability. Consequently, a comparison was conducted for pore-water-pressure changes in the embankment before and after the earthquake. In particular, the pore water pressure from reaching 50 G in each mode to the point at which 50 G ended (15 min) was compared for the EMB and parapet models. Figure 12 illustrates the comparison results for the pore water pressure between the EMB and parapet models.
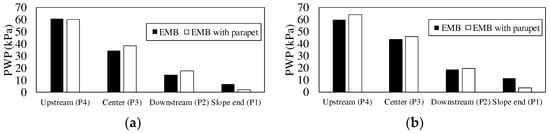
Figure 12.
Comparison of pore water pressure between the EMB and parapet models: (a) 1st seepage mode and (b) 2nd seepage mode.
In this comparison, the pore water pressure of the upstream side (P4) of the first seepage mode was the same. However, in the EMB model, the pore water pressure at the center of the embankment (P3) and the downstream side (P2) was relatively lower, whereas the slope end (P1) was relatively higher. This result is attributed to the relatively lower pore water pressure at P3 and P2 as the EMB model infiltrated to the end of the slope in the first seepage mode.
The increase in P1 indicates that seepage water in the embankment rapidly reached the slope end. In the parapet model, P1 showed a remarkably low pore water pressure, indicating that the seepage rate at the end of the slope was relatively slow during the same time, with the infiltration progress inhibited by the parapet’s weight.
In the second seepage mode, both the EMB and parapet models exhibited pore-water-pressure change patterns similar to the first seepage mode for P4, P3, P2, and P1. However, the pore-water-pressure levels increased for all, compared to the first seepage mode. Thus, it can be considered that the pore water pressure measured in the first seepage mode increased after the earthquake, in which the dam body changed to a more porous condition. The only difference between the first and second seepage modes was the change in pore water pressure for P4. In the second seepage mode, P4 of the EMB model showed a relatively lower pore water pressure than that of the parapet model. This result suggests that infiltration in the embankment progressed rapidly in the EMB model, despite the increase in pore water pressure in both the EMB model and the parapet model.
In contrast, in the parapet model, P4 and P3 showed an increase in pore water pressure of 6–8 kPa compared to the first seepage mode, whereas P2 and P1 showed an increase of 2–3 kPa, with the change in pore water pressure considered insignificant. As a result, the parapet model was found to have a suppressing effect on seepage flow in the dam body after an earthquake. The slope end is an area where the self-weight of the embankment is relatively small due to the trapezoidal shape of the embankment, making it a structurally vulnerable area for erosion. As the parapet induces low pore water pressure at the end of the slope, it provides a reinforcing effect in terms of disaster prevention.
4. Conclusions
This study aimed to assess the effectiveness of a parapet in preventing overtopping of a small reservoir dam. A centrifugal model test with a 50 G acceleration was used to examine two models: the EMB model and the parapet model. The state change of the reservoir dam was analyzed in four modes: initial, first seepage, seismic, and second seepage. The study found that even minor cracks in the dam crest can lead to significant damage under seismic load, with the cracks increasing in length, width, and depth. The pore water pressure after the earthquake was also found to be higher than that of existing reservoir dams, leaving them vulnerable to deformation. However, introducing a parapet suppressed the cracks and deformation of the dam crest, which improved the seismic performance of the dam body and delayed seepage flow. The parapet’s pressing effect increased the constraint force of the dam crest, which stabilized the reservoir dam and improved its disaster preparedness capabilities because the parapet with a certain weight was designed to press the entire area of the dam ridge with its own weight, unlike general parapets only designed at the end of the dam ridge. Nonetheless, the study was conducted only for M 5.4 earthquakes; therefore, higher-intensity seismic behavior still needs to be confirmed through more experiments. Furthermore, it would be worth exploring the penetration and deformation inhibition based on the quantitative weight change of the parapet that covers the dam crest.
Author Contributions
Software, S.Y.; investigation, Y.-H.L., S.Y., H.-S.S. and J.-J.K.; writing—review and editing, Y.-H.L., H.-K.H., H.-S.S. and J.-J.K.; project administration, supervision, and conceptualization, D.-W.L. and T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the project “Development of Slope Disaster Vulnerability Assessment based on Empirical Experiments(Ⅲ)” (No. NDMI-PR-2023-07-02) from the National Disaster Management Research Institute (NDMI), and the National Research Foundation of Korea (NRF) grant funded by the Ministry of Science, ICT and Future Planning of the South Korean Government (Grant No. NRF-2019R1C1C1007100).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available from the corresponding author upon reasonable request.
Acknowledgments
The reservoir information used in this study is based on data from the Korea Rural Community Corporation. In addition, the technology for the centrifugal model experiments was supported by the Disaster Prevention Laboratory of Kansai University in Japan. In this regard, the authors thank both institutions for their contributions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tabari, H. Climate Change Impact on Flood and Extreme Precipitation Increases with Water Availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef] [PubMed]
- UNESCO. Science for a Water Secure World in a Changing Environment, Draft IHP-IX Strategic Plan; Ninth Phase of the Intergovernmental Hydrological Programme: Paris, France, 2021; Volume 2021, Available online: https://en.unesco.org/sites/default/files/ihp-ic-xxiv-ref.1_ihp-ix_strategic_plan.pdf (accessed on 6 January 2021).
- IPCC The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H.; Castelletti, A.; Magliocca, N. Future Drought Risk in Africa: Integrating Vulnerability, Climate Change, and Population Growth. Sci. Total Environ. 2019, 662, 672–686. [Google Scholar] [CrossRef] [PubMed]
- Hosseinzadehtalaei, P.; Tabari, H.; Willems, P.; Data, S.-B. Satellite-Based Data Driven Quantification of Pluvial Floods over Europe Under Future Climatic and Socioeconomic Changes. Sci. Total Environ. 2020, 721, 137688. [Google Scholar] [CrossRef] [PubMed]
- Korea Rural Community Corporation (KRC). Establishment of Condition Evaluation Criteria for Precise Safety Diagnosis and Precise Safety Inspection of Agricultural Reservoirs; Korea Rural Community Corporation (KRC): Naju-si, Republic of Korea, 2020. (In Korean) [Google Scholar]
- Ministry of the Interior and Safety (MOIS). 2020 Annual Natural Disaster Report; Smithsonian Institution: Sejong, Republic of Korea, 2020. (In Korean)
- Ministry of Agriculture, Food and Rural Affairs (MAFRA). Statistical Yearbook of Land and Water Development for Agriculture; Ministry of Agriculture, Food and Rural Affairs (MAFRA): Sejong-si, Republic of Korea, 2021. Available online: https://rawris.ekr.or.kr/stastics/pdf/2021.pdf (accessed on 26 April 2023). (In Korean)
- Lee, Y.-H.; Ryu, J.H.; Lee, T.H.; Shim, J.W.; Kim, C.-H.; Lee, D.-W. Failure Behavior Attributed to Internal Erosion Caused by Conduit Cracks in Homogeneous Embankment. Appl. Sci. 2022, 12, 6305. [Google Scholar] [CrossRef]
- Foster, M.A.; Fell, R.; Spannagle, M. The Statistics of Embankment Dam Failures and Accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Hanson, G.J.; Cook, K.R.; Hunt, S.L. Physical modeling of overtopping erosion and breach formation of cohesive embankments. Trans. ASAE 2005, 48, 1783–1794. [Google Scholar] [CrossRef]
- Morris, M.W.; Kortenhaus, A.; Visser, P.J. Modeling Breach Initiation and Growth FLOODsite Rep. t06-08-02. FLOODsite Consortium. 2009. Available online: http://www.floodsite.net/html/partner_area/project_docs/t06_08_01_breach__execsumm_v3_5_p01.pdf (accessed on 26 April 2023).
- Seo, M.-W.; Ha, I.S.; Kim, Y.-S.; Olson, S.M. Behavior of Concrete-Faced Rockfill Dams During Initial Impoundment. J. Geotech. Geoenviron. Eng. 2009, 135, 1070–1081. [Google Scholar] [CrossRef]
- Tani, S. Behavior of Large Fill Dams During Earthquake and Earthquake Damage. Engineering 2000, 20, 223–229. [Google Scholar] [CrossRef]
- Okamura, M.; Tamamura, S. Seismic Stability of Embankment on Soft Soil Deposit. Int. J. Phys. Modell. Geotech. 2011, 11, 50–57. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Xu, J.; Wang, F.; Wang, B.; Li, Q. Dynamic Behavior of Polymer Antiseepage Wall for Earth Dam by Centrifuge Test. Int. J. Geomech. 2018, 18, 0001294. [Google Scholar] [CrossRef]
- Adapa, G.; Takada, Y.; Ueda, K.; Uzuoka, R. Dynamic Centrifuge Model Tests on Embankment with Different Upstream Conditions. In Proceedings of the 7th Asia and the Pacific Conference on Unsaturated Soils (AP-UNSAT2019), Nagoya, Japan, 23–25 August 2019; Volume 7, pp. 531–540. [Google Scholar] [CrossRef]
- Tobita, T.; Iai, S.; von der Tann, L.; Yaoi, Y. Application of the Generalised Scaling Law to Saturated Ground. Int. J. Phys. Modell. Geotech. 2011, 11, 138–155. [Google Scholar] [CrossRef]
- Chaney, R.; Demars, K.; Dewoolkar, M.; Ko, H.; Stadler, A.; Astaneh, S. A Substitute Pore Fluid for Seismic Centrifuge Modeling. Geotech. Test. J. 1999, 22, GTJ11111J. [Google Scholar] [CrossRef]
- Digital Image Technology (DITECT). 2D/3D Motion Analysis Software (DIPP-Motion V). Available online: https://www.ditect.co.jp/en/software/dipp_motionv.html (accessed on 26 April 2023).
- Onitsuka, K.; Yoshitake, S.; Nanri, M. Mechanical Properties and Strength Anisotropy of Decomposed Granite Soil. Soils Found. 1985, 25, 14–30. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.W.; Santamarina, J.C. The Hydraulic Conductivity of Sediments: A Pore Size Perspective. Eng. Geol. 2018, 233, 48–54. [Google Scholar] [CrossRef]
- Kim, S.-G.; Choi, W.-H.; Kim, Y.-H.; Shin, J.-W.; Kim, B.-J. Investigation of compressive Strength Characteristics of Hardfill Material and Seismic Stability of Hard. Appl. Sci. 2023, 13, 2492. [Google Scholar] [CrossRef]
- Korea Meteorological Administraion (KMA). Seismological Annual Report. 2020. Available online: https://www.kma.go.kr/download_01/earthquake/earthquake_2020.pdf (accessed on 26 April 2023). (In Korean)
- Kayhan, A.H.; Demir, A.; Palanci, M. Multi-functional Solution Model for Spectrum Compatible Ground Motion Record Selection Using Stochastic Harmony Search Algorithm. Bull. Earthq. Eng. 2022, 20, 6407–6440. [Google Scholar] [CrossRef]
- Kim, M.-K.; Lee, S.-H.; Choo, Y.W.; Kim, D.-S. Seismic Behaviors of Earth-Core and Concrete-Faced Rock-Fill Dams by Dynamic Centrifuge Tests. Soil Dyn. Earthq. Eng. 2011, 31, 1579–1593. [Google Scholar] [CrossRef]
- Kobayashi, A.; Murakami, A. Seismic Crack Investigation in an Earth Dam by Centrifugal Loading Test. In Dam Engineering; IntechOpen: London, UK, 2018; pp. 1–16. [Google Scholar] [CrossRef]
- Adapa, G.; Ueda, K.; Uzuoka, R. Seismic Stability of Embankments with Different Densities and Upstream Conditions Related to the Water Level. Soils Found. 2021, 61, 185–197. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).