Abstract
Location science is used to determine the optimal geographical placement of primary care resources with operations research models. In determining the optimal placement, we account for the objectives of both patients and physicians. These objectives and the methods used to address them differ between daytime and after-hours settings. These time settings are treated separately since primary care services are typically limited during after-hours operations. Three solution approaches are considered to address both time settings: independent, sequential, and simultaneous. The independent approach is based on the p-Median problem, and the other two approaches use modified forms of the p-Median. Three case studies are examined by applying these models to census data from Nova Scotia. Solving the daytime and after-hours problem simultaneously consistently yields the best results while considering facility-sharing constraints.
1. Introduction
Primary healthcare is the first step in treatment for most non-emergency health issues, and patients need to be able to easily access primary health services. Access to health services can be measured in many ways (e.g., geographically, financially, or timeliness), but when planning health resource locations, distance between patients and services is a typical measure of access [1]. Normally, patients have greater difficulty accessing health services as distance increases; thus, it is valuable to patients to reduce distance to services. Distance-based access can be optimised by modelling different objectives, such as minimising the average distance between patients and services, minimising the maximum distance travelled by any patient, or maximising the percentage of patients within an acceptable distance from the nearest service.
It is possible to predict locations where general practitioners (GPs) or primary care practices (PCPs) will most effectively improve patient access based on these measures. In regions where there is a shortage of GPs, this represents an opportunity to determine where recruited physicians will be most effective at meeting needs for services. It is also a common problem in many countries that certain types of areas such as rural or urban hot spots are underserved per capita by primary care services [2]. In these cases, it is also valuable to determine the optimal placement of existing or additional GPs to promote balanced access.
While meeting demands for patient service is crucial, it is also important to consider physician preferences for practice location, hours of service, and style of practice and the trade-offs with patient preferences for access [3]. For example, physicians typically prefer to have a large number of patients as part of their clinic (often referred to as the clinic’s panel size) to ensure consistent work, but not so large as to be overwhelming; however, patients may prefer to be in smaller panels so their GPs have more frequent available appointments. GPs may also prefer working with multiple physicians rather than independently. This has the potential to improve access to patients through shared delivery of services or coverage of after-hours demand.
In many areas, primary care services are provided differently during daytime and nighttime hours. Typically, when night services are offered by PCPs, physicians will pool panels to allow them breaks from working while covering for each other [4,5]. While this means a greater panel size, fewer physicians, and greater distances for patients, this is typically acceptable since the expectation of services during night is lower and fewer patients use them. While there are optimisation models for primary care service locations, none are known to account for dual services such as the day and night primary care system. Usually, only-day services are considered, or day and night hours are considered separately. By accounting for both service periods within the same model, trade-offs between patient and provider preferences can be considered and improvements to patient and physician satisfaction can be obtained.
2. Materials and Methods
To address the issue of optimally locating health resources, operations research provides robust mathematical models which consider different objectives and constraints. Broadly, the objective is to ensure that patients are as close to primary care as possible and the main constraint is the number of healthcare facilities available. A model which reflects these characteristics is the p-Median problem (see (Daskin & Maass, 2015) [6] for reference). The p-Median is typically used to locate p facilities among a set of specified locations I to minimise the average distance between demand and the nearest facility, and it has been recognised as a staple model for healthcare facility location problems [7]. In this paper, the p-Median problem is modified to accommodate facilities operating during multiple time settings.
2.1. Multiple Time Setting p-Median Problem
The p-Median problem is typically used in one time setting. However, the problem under consideration covers multiple related time settings: regular and after-hours primary care. Regular care is typically conducted during the daytime during normal working hours. After-hours care is delivered outside of regular hours, usually at night and very early or late in the day. These time settings are mutually exclusive and primary care facilities may operate with different properties in each time setting. Thus, the p-Median problem is altered to address multiple time settings in one OR model. This allows decisions to be made while considering the costs in both time settings simultaneously. The notation used for this model is detailed in Table 1 and Equations (1)–(13).

Table 1.
Multiple Time Setting p-Median Notation.
In this modification of the p-Median problem, a primary and secondary set of facilities is simultaneously located to minimise the distance to demand in a primary and secondary time setting. In this case, the primary facilities are located in the regular time setting, and the secondary facilities are located in the after-hours time setting. A constraint added to the standard p-Median problem to create the modified problem is that the number of secondary facilities must be less than or equal to the number of primary facilities. This constraint is founded on the assumption that there are no more primary care practices open during the after-hours time setting than during the regular time setting.
This limitation also requires a second constraint. Secondary facilities must share locations with primary facilities. This satisfies the assumption that the same facilities are used for regular and after-hours care, which is expected to be more cost-effective (and typical of real-world settings) than opening facilities separately for each setting. Together, these constraints ensure that after-hours facilities must share locations with regular facilities.
In the multiple time setting p-Median notation, an apostrophe () is used to denote variables relating to the secondary setting. Note that (2), (4), (6), (10) and (12) are identical to constraints from the p-Median problem. Additionally, each of these constraints have been duplicated ((3), (5), (7), (11) and (13), respectively) to constrain the secondary facilities identically to the primary facilities. Constraint (8) has also been added to restrict the sites of secondary facilities to be shared with primary facilities, and Constraint (9) has been added so that the number of secondary facilities must be no greater than the number of primary facilities.
A weight variable, W, has also been added to the after-hours term in the objective function. This variable allows for a linear discount rate to be applied to adjust the relative cost of travel between time settings. For example, if policy dictates that after-hours travel is half as costly for patients, incorporates this preference. If travel in either time setting is considered equally costly, assigns equal weight to travel in both settings. Increasing W is expected to bias facility locations toward after-hours demand locations if demand differs between the regular and after-hours settings. This variable is proposed for the purpose of adjusting relative cost between time settings, but a sensitivity analysis of this variable is not within the scope of this paper.
2.2. Solution Approaches
To address both the regular and after-hours needs of patients, both time settings must be considered by the model. Three approaches for addressing both settings are proposed in this section. The first solves both time settings independently, which gives the best case scenario for each. The second approach solves the time settings sequentially, and locations selected in one setting are then required in the other time setting. This approach is expected to be more reflective of how a decision is made in practice. The final approach simultaneously solves both time settings to find the best compromise solution. This approach is expected to be the best method for optimally locating facilities in both settings while also considering facility use constraints.
2.2.1. Independent Approach
In this approach, each time setting is considered independently. The standard p-Median problem is used to solve the regular and after-hours time settings with no shared locations. This approach is effectively a simplified version of the multiple time setting p-Median described above and can be implemented by relaxing all secondary time setting constraints and removing the latter term from the objective function. Formally, this can be stated as follows:
This approach is less cost-effective with respect to practical costs because it places facilities for use in either regular or after-hours care rather than sharing facilities between time settings. However, this approach is expected to provide a lower bound for each time setting. Since this approach is the least constrained, it should provide the lowest overall cost in terms of patient travelling distance. This is because approaches with additional constraints cannot possibly be solved with a lower cost.
2.2.2. Sequential Approach
For this approach, the standard p-Median problem is used to solve for one time setting, and the solution for that time setting constrains the other time setting. This is more robust than the independent approach, since the results of one time setting are used to constrain the other. This is expected to more closely model the real-world use of primary care facilities.
The sequential approach differs depending on which time setting is solved first. If the regular setting is solved first, the solution set of regular hour facility locations becomes the set of possible locations for the after-hours p-Median problem. For example, consider a situation where three facilities are to be placed during the regular setting, two are to be located after-hours, and the nodes are possible facility locations. If the model locates facilities at nodes 1, 2, and 3 in the regular setting, then the after-hours setting facilities must be placed among nodes 1, 2, and 3 only.
The process for the sequential model when the regular setting is solved first (abbreviated as “RtA”) is as follows:
- Solve the standard p-Median problem for the regular setting (identical to the independent approach for the regular setting).
- Create a set () of nodes from the solution containing nodes where regular time setting facilities are located.
- Solve a p-Median problem for the after-hours using instead of I as the set of possible facility locations.
If the after-hours problem is solved first, the nodes selected for after-hours facilities must be included in the regular setting solution. For example, consider a situation where one facility is located for the after-hours setting and three are located in the regular setting. If the model locates a facility at node 2 in the after-hours setting, then a facility must also be set at node 2 in the regular setting solution. This is enforced by a constraint (shown by Equation (15)) added to the regular hours problem so that regular hours facilities must be located at nodes where there are after-hours facilities. Note that this constraint requires that there must be at least as many regular facilities as after-hours facilities.
The process for the sequential model when the after-hours setting is solved first (abbreviated as “AtR”) is as follows:
- Solve the standard p-Median problem for the after-hours setting (identical to the independent approach for the after-hours setting).
- Solve a p-Median problem for the regular setting with additional constraint (15).
This approach should yield more practical results than the independent approach due to practical costs of setting up additional facilities for either time setting. However, this approach does not consider the second time setting when solving for the first, and it should be more constrained than an approach which considers both time settings simultaneously.
2.2.3. Simultaneous Approach
This approach is modelled by the multiple time setting p-Median problem ((1)–(13)). This method considers both time settings simultaneously, rather than one before the other. It is expected that this will provide a better overall result than the sequential method, since all possible location choices are considered in one problem rather than being constrained by a previous problem which is ”blind” to the overall objective. For example, a desirable solution in one time setting may place facilities away from demand in the other time setting because the model is unaware of the details of the other time setting. By considering both time settings at the same time, this issue is avoided. While this approach is more constrained than the independent one, it provides a more realistic solution to the practical problem.
2.3. Model Formulation and Verification
The model was written in Python 3.7.3 using Jupyter Notebook [8,9]. The linear program (LP) was implemented using the PuLP LP modeller [10], and a Python class was written with PuLP to formulate and solve p-Median problems when given the problem parameters. The Python class was tested by solving a set of previously solved p-Median problems from J. E. Beasley’s OR-Library [11]. Once this class was confirmed to solve standard p-Median problems correctly, additional elements were added to the class to allow it to solve each of the solution approaches. Due to excessive processing time on the default solver (CBC), the Python code was used to formulate problems which were solved using the commercial solver Gurobi [12].
3. Results
To test how the models perform with real-world data, three case studies were completed using 2011 Canadian census data in the province of Nova Scotia [13]. The models were tested in the most densely populated region of Nova Scotia, Halifax, as well as a more rural area, Cape Breton. Lastly, the models were tested on a hypothetical setting where Cape Breton data were altered to create a large discrepancy between regular and after-hours demand.
3.1. Data
The parameters for nodes, unit supply costs between nodes, and demand at each node were derived from the census data. Census dissemination areas (DAs) were used as the nodes of the model. Dissemination areas are the smallest geographical unit published by Statistics Canada. They are stable geographical areas typically populated by 400 to 700 people. The centroid of each DA was computed and used for possible facility locations. The population of each DA was used as the demand at each node for both time settings (except for the modified case study). The travel distance between nodes was considered the cost between nodes. The distance between nodes was the shortest distance between every pair of nodes in the Nova Scotia road network. That is, the cost between nodes is the shortest distance one could travel via the Nova Scotia road network, not the naïve Euclidean distance between points. Distance calculations between each DA are provided by McNamara [14]. Note that this method assumes travel distance within one node to be zero; for example, if a primary care practice is located at node i, patients within node i are assumed to travel a distance of 0 to this practice.
The dissemination areas selected to represent Halifax and Cape Breton were those contained within the Halifax Census Metropolitan Area (CMA) and the Cape Breton Census Agglomeration (CA). CMAs and CAs are geographical regions used by the census to indicate which DAs belong to a larger community. They are defined by regions where one or more adjacent municipalities are centred on a population core. For a CA, this means a core consisting of at least 10,000 people. A CMA must have a total population of more than 100,000 with at least 50,000 living within the core. For example, a CMA could have a core of 75,000 residents with 30,000 people living in surrounding municipalities. Images of these dissemination areas within Nova Scotia have been created using ArcMap, shown in Figure 1.
Figure 1.
Nova Scotia with Halifax (center) and Cape Breton (upper-right) Dissemination Areas Highlighted.
By using population to model demand in both settings, demand is identical during the day and after hours as the census data do not distinguish population locations by time of day. To test the effect of geographical differences in demand between regular and after-hours settings, a hypothetical setting and a data set were created by modifying the census data. This data set was used to simulate a scenario where a large portion of people moved from urban areas to rural areas after hours. This may mimic a large population’s commute to urban areas from rural areas for work. A cluster of DAs around Sydney (the most densely populated part of Cape Breton) was chosen to represent an urban area, and 25% of the population in these DAs was distributed proportionally among the remaining DAs after hours to create the hypothetical setting. This was performed by rounding the population in urban DAs to 75% and then increasing each remaining DA proportionately so that the total number of people remained the same.
3.2. Case Studies
For each geographical test setting, the four solution approaches were run for differing numbers of regular and after-hours facilities. The total cost of each scenario (which can be expressed as the sum of all distances between each person and their primary care in kilometres) was recorded, along with the individual costs of the regular and after-hours settings.
3.2.1. Halifax
In the Halifax setting, there are 594 DAs and a total demand of 390,096 people. Figure 2 displays the geography of the included DAs.
Figure 2.
Halifax Dissemination Areas.
Tests were run for increments of 5, 20, 40, 60, and 200 regular facilities, with after-hours facilities increased in fifths. For example, the 60 regular facilities scenario was considered with 12, 24, 36, 48, and 60 after-hours facilities. In total, facility placement scenarios were tested for each solution approach.
Table 2 contains the results for each solution approach (independent, sequential, and simultaneous) and the time periods for one scenario in the Halifax setting. There are two rows for the sequential approach since this approach differs between regular to after hours (RtA) and after hours to regular (AtR). In the scenario used for this example, sixty facilities are located for the regular setting, and twelve are located for the after-hours setting.

Table 2.
Halifax Total Cost (km).
By dividing the results in Table 2 by the total demand, the average distance travelled by each person is calculated, as shown in Table 3.

Table 3.
Halifax Average Cost Per Person (km).
The lower the results are, the better the solution. This is because a lower overall cost means that the demand (people in this case) need to travel less distance on average. It is expected that as p and increase, the cost will go down. This is because locating more facilities allows facilities to be more spread out and closer to demand on average. This can be seen in Figure 3, which plots the cost in the independent setting against the number of facilities. This applies to both settings and each approach. If facilities are added, the cost is expected to decrease.
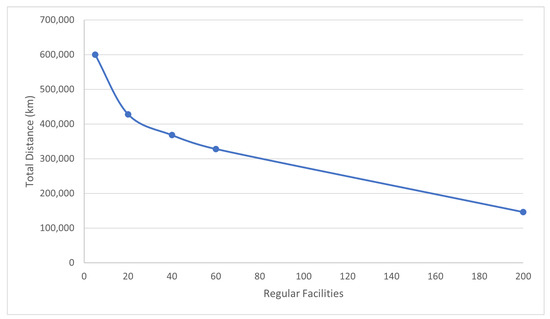
Figure 3.
Halifax Regular Setting Independent Approach Cost by number of Facilities.
In all cases, the least constrained approach, the independent approach, has the lowest costs, while the sequential approaches have higher costs than the simultaneous approach. A sample is shown in Table 4, where the independent approach is treated as the base case to calculate the difference in other cases.

Table 4.
Halifax Total Cost (km per person).
These results suggest that the approaches perform as expected relative to the degree to which they are each constrained.
3.2.2. Halifax Approach Results
The total costs of the independent approach for different values of and p are shown in Figure 4. Each series on the chart represent the ratio of after-hours facilities to the quantity of regular facilities p. For example, each point of the blue series labelled 0.2 represents a scenario where one fifth of the regular facilities are placed during the after-hours.
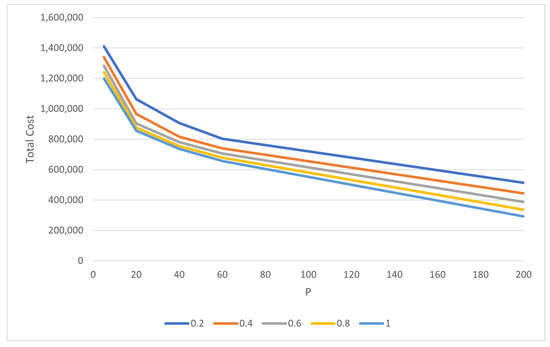
Figure 4.
Minimum cost of p facilities for different ratios of (specified in legend). Independent approach in the Halifax setting is shown.
It is expected that the total cost is reduced as facilities are added. This is because greater numbers of facilities allow for solutions that reduce the average distance between demand and facilities, and this is demonstrated in Figure 4. It is also evident that increasing the ratio of to p decreases total cost. In the case of the independent approach, this simply means adding more facilities to the after-hours p-Median problem, so a reduced cost is expected. Finally, it appears from the graph that the addition of more facilities has a decreasing marginal reduction in cost. That is, the benefit from each new facility decreases as the number of facilities being placed increases.
The trends of decreasing cost and decreasing marginal improvement in cost are apparent for each approach, and plotting the results from each approach produces very similar graphs to Figure 4. This indicates that these effects tend to be present for any of the tested approaches when locating facilities.
3.2.3. Halifax Approach Comparison
Each approach broadly exhibits similar behaviours as the number of facilities to be located increases, but it is also appropriate to compare how each approach performs relative to each other. As expected, the independent approach has the lowest cost, and the simultaneous approach has a lower bound than the sequential approaches. This can be seen in Figure 5, where each series shows the percent increase in costs compared with the independent approach for five different scenarios. This is calculated with the formula (approach cost – independent cost)/independent cost.
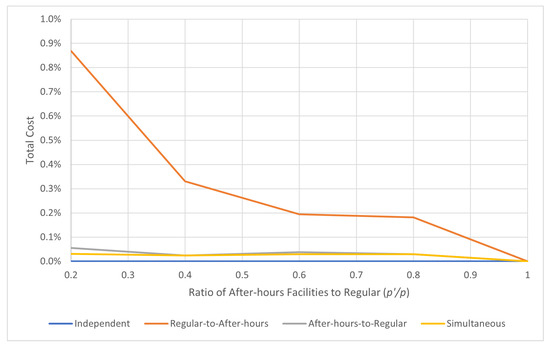
Figure 5.
Percent cost increase of each approach compared with independent approach (p = 60).
One trend that is apparent in Figure 5 is that each approach converges to the same cost as the number of after-hours facilities approaches the number of regular facilities. This makes sense when considering the data used for this case study. The demand at each node is considered to be the same during both the regular and after-hours time settings, so the differentiating factor between problems in each setting is the number of facilities being placed. If the number of facilities being placed is identical, then the problems being solved will be identical for these case data. This is not a phenomenon that would be expected if demand differs between time periods, and this is not expected to be observed in the third case study.
The phenomenon of the independent approach providing the best cost followed by the simultaneous approach is consistent across each scenario. In some cases, the RtA approach yields lower costs than the AtR, but in most cases, the AtR approach is better. However, both are consistently worse than the simultaneous approach. Although the relative difference in total cost is small, the results are important as the most commonly used approach in practice, RtA, is consistently the worst.
3.3. Cape Breton
Cape Breton is a less densely populated area of Nova Scotia than Halifax. The Cape Breton census agglomeration contains 101,619 people in 197 DAs, which are shown in Figure 6.
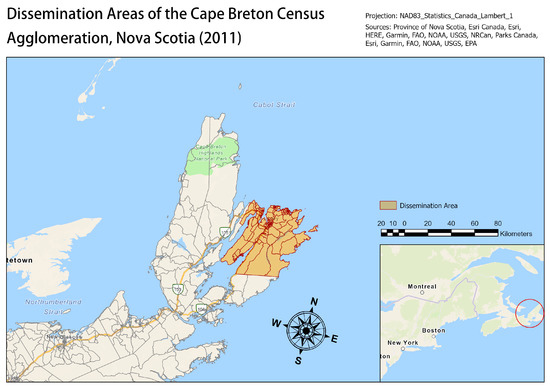
Figure 6.
Cape Breton Dissemination Areas.
Similar tests to the Halifax case study were performed for Cape Breton with the hypothesis that a lower density area may show different results. However, the tests demonstrate very similar effects and are omitted from these results for brevity.
3.4. Cape Breton Modified
In the modified Cape Breton setting, there are still 101,619 people, and 197 DAs with the same geography. However, a set of urban DAs shown in Figure 7 have reduced after-hours demand by 25%, and other DAs have proportionally increased after-hours demand.
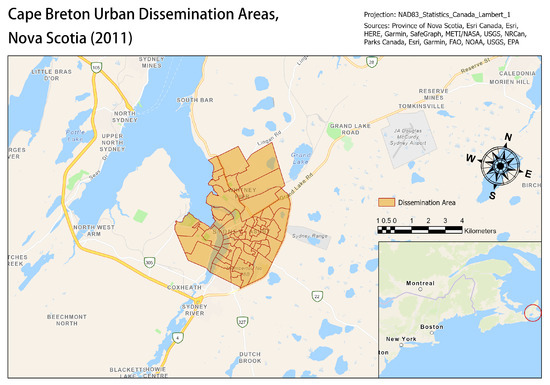
Figure 7.
Cape Breton Urban Dissemination Areas.
Plotting the test results for the independent solution approach (Figure 8) produces a very similar graph to the other geographical settings. Like in the Halifax setting, total cost decreases with p and , as does the marginal utility of each additional facility.
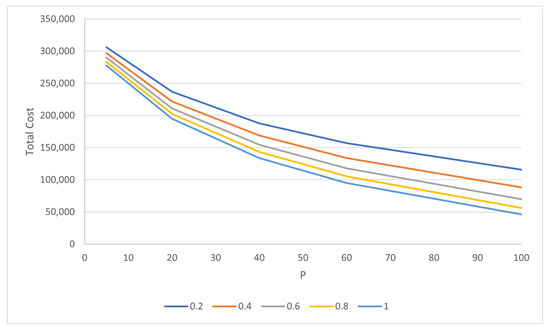
Figure 8.
Minimum cost of p facilities for different ratios of (specified in legend). Independent approach in the Cape Breton Modified setting is shown.
Also similar to the Halifax setting, solution approaches increase in cost as the degree of constraint increases. As expected, the independent approach has the lowest cost, and the simultaneous approach has a lower bound for the sequential approaches. This can be seen in Figure 9.
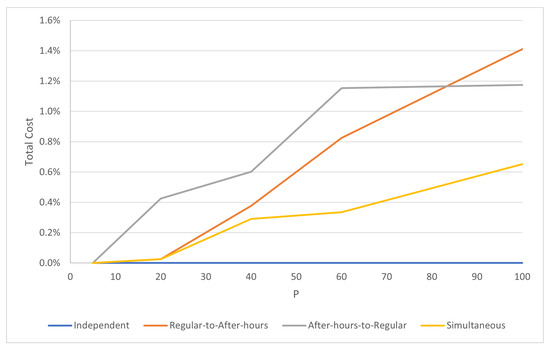
Figure 9.
Cape Breton modified percent cost increase for each approach compared with independent approach ( = 1).
In the Halifax tests, there was no difference between solution approaches when = 1. This was expected since demand did not differ between the regular and after-hours time settings, and thus, the facility-sharing constraints would have no effect when the same number of facilities are placed in both time settings. However, Figure 9 demonstrates that differing demand between time settings affects the effectiveness of each solution approach.
An interesting result is that the non-independent solutions become relatively less effective as the number of facilities increases. This suggests that the constraints that cause facilities to be shared across time settings become more constraining as the number of facilities increases. While the actual solution cost decreases as the number of facilities increases, this effect may contribute to the decreasing marginal efficiency of additional facilities.
4. Discussion
In the Halifax setting, the absolute distance travelled differed little (less than 1% difference) between solution approaches when using the same number of facilities. In terms of distance travelled per person, the largest difference in cost was in the magnitude of tens of meters, which may be considered marginal when looking at a population of hundreds of thousands of people.
However, this result is unsurprising when considering certain details of the study. Foremost, the demand assigned at each node was considered to be the same for both the day and after hours. The difference between settings is the number of facilities located, and the difference between models are the constraints used to restrict facility location. When most of the model parameters are homogeneous across the time setting, it is logical that each approach results in a similar cost.
It is also necessary to consider that the region of study contains urban and rural areas with very different population densities. While the total solution cost may not have changed much on average per person between approaches, this is likely not distributed equally among demand. If a large portion of this cost discrepancy was due to lower distance travelled by people in rural areas, this could mean a much larger difference for those people since there are fewer of them than the urban population. This could mean that the model has a more pronounced effect on the rural population than is apparent when considering urban demand in the average denominator. It is also worth noting that the large portion of people who live in the dense, urban part of Halifax will never be more than a kilometer or two away from a PCP, and optimising for geospatial access is likely best applied to rural demand, where the population density is lower and services are farther away.
Another important result is that each solution approach performs relatively as expected. The independent approach represents a naive scenario where both the day and after-hours facility locations can be treated independently with no cost, and this approach always had the lowest total cost. Conversely, the more constrained approaches had higher costs, with the most constrained approaches (the sequential RtA and AtR approaches) resulting in higher cost solutions. While this was expected, an interesting result was that which sequential approach was better depended on the test conditions. The regular-to-after-hours approach yielded worse results in most cases, which is noteworthy since this is the most likely real-world method for determining facility locations.
For the Halifax tests, each solution approach provided the same result when the number of regular and after-hours facilities were the same. Since the demand in these tests was identically located across both time settings, it makes sense since the same solution would be identical for both settings. However, in the modified Cape Breton setting. this was not the case. Since the demand differed between time settings in these tests, a difference could be observed in the efficacy of each approach (seen in Figure 9).
4.1. Limitations
There are some limitations of the data used in the case study that could be improved upon for more accurate modelling of primary care needs in Nova Scotia. One problem is how the cost parameter assumes that travel distance is an equal measure of access for all patients under all circumstances. The values of are based on minimum road distance from one DA centroid to another, but the time and location are factors that may change how accessible this distance is for a patient. For example, travelling across a dense city during rush hour is likely to take much longer than travelling the same distance in a rural setting late in the evening. A measure of time travelled may be a better metric for measuring access, including the time taken for different forms of available transport in the area.
Another issue with the values is that demand assigned to the same node is assumed to travel no distance. That is, . This assumption may be robust in the case of very small DAs where the distance from the centroid to any edge is negligible. However, as DA size increases, the distance that a patient might have to travel within the DA also increases. A possible improvement may be to calculate the average distance within a DA from the centroid to each other point and to use this value as the intranodal travel distance for each node. While the number of facilities to be placed is fixed in the p-Median formulations used in this study, this would be particularly important to address in a model that considers the number of facilities as a decision variable. Since every additional facility allows demand at the same node to travel no distance when , this may unrealistically incentivise adding facilities to reduce distance.
Finally, an analysis for was excluded from the Halifax case study. This is because the results for these tests were highly variable. It is likely that this is a discretisation effect and that the low number of facilities yielded very different adjacent solutions. Sampling more cases may improve the interpretability of the results, but this effect may be unavoidable for low values of p.
4.2. Future Research
This case study indicates that the simultaneous approach is an effective method of addressing both the regular and after-hours time settings when considering practical facility location constraints. However, there are other considerations when addressing this problem that should be considered in future work. These points are outside of the scope of this research but may be important to consider in the context of developing real-world policy for primary care resource allocation.
Firstly, the p-Median problem was determined to be an appropriate OR model for demonstrating the merits of considering multiple time settings simultaneously. Particularly since the case studies cover populations with varying densities, the objective of the p-Median to minimise all distance travelled is desirable when compared with the other models that were considered. In other contexts, the p-center problem, the location set covering problem (LSCP), or the maximum covering location problem (MCLP) may be more appropriate [15,16,17]. Respectively, the objectives of these models are to minimise the greatest distance travelled by any customer, to minimise the number of facilities needed to cover a population (coverage meaning ensuring no one from the population is further than a specified distance), and to maximise the number of customers within a specific distance of a facility. These models are compatible with the simultaneous approach to treating the regular and after-hours settings, and there may be scenarios where these are more appropriate than the p-Median problem. It may also be of interest to use different models in different time settings for unique objectives. For example, the p-Median could be more appropriate during regular hours when there are more facilities available, but if there are only a small number of after-hours facilities, the LSCP might be better able to maximise the number of people who have access to a facility if they need it. This would provide a solution where regular facilities provide an optimal solution for the average patient, and the number of people who are far from after-hours facilities would be minimised. The p-center problem may be of particular interest for improving accessibility in rural areas since it provides an equitable solution by reducing the greatest distances travelled.
Another potential adjustment to the models used for primary care facility location is to incorporate capacitated facilities. The models in this work have no specific regard for capacity; that is, the PCPs may be considered to have larger or smaller panel sizes than individual GPs typically have. However, this may still accurately reflect clinics where multiple GPs share a space, thus collectively treating more patients within the same facility. Many GPs prefer to work in practices with several other physicians, and realistically, this is the case for many PCPs. Rather than placing individual facilities with no regard for capacity, a model which places facilities with multiple GPs that can handle a constrained panel range may yield more insight into facility location strategies which strictly satisfy physician preferences.
It may also be appropriate to relax facility location constraints and instead add facility costs to control the number of facilities opened. While it is clear that adding more facilities will always allow for solutions with lower distances between demand and facilities, this does not account for the economic costs of additional facilities. A multi-criteria decision analysis may help determine the cost-effectiveness of the number of facilities available. Since the marginal improvement in patient distance travelled decreases as the number of facilities increases, this suggests that there is a point where the gains in accessibility are outweighed by the additional facility costs. A model which replaces facility location constraints with facility costs may also provide more effective solutions for both the regular and after-hours. It is intuitive to assume that it is cost-effective for after-hours care to use the same facilities as regular care, but there may be cases where this is not the best solution. By allowing for these facilities to be separated at the expense of a higher economic cost, a model could potentially provide a better trade-off between economic cost and patient access than if it were constrained to sharing facilities between time settings. It may also be appropriate to examine the effects of the weighting variable, W, on the model. By decreasing or increasing W, solutions that decrease distances during regular service or after hours, respectively, should be favoured.
While census population data were used to model demand for primary care services in this case studies, this information does not necessarily provide an accurate representation of demand in different areas. Of particular importance, the census data do not capture the disparity across individuals in demand for healthcare, nor is the geographical shift in population between time settings measured well by the census. Given that this information may not be easily obtained, a possible approach to testing how these factors could affect results with the available data may be to make adjustments to demand in different areas using demography. For example, an area’s average demand may be increased or decreased by a factor derived from the deviation from median age or income. For demand differences across time settings, further changes could be made, as was performed for the modified Cape Breton case study.
The case studies used a greenfield approach, but it may be of interest to compare solutions to real-world conditions. The difference between optimal facility locations suggested by the model and actual PCPs may reveal factors that have been unaccounted for. Alternatively, discrepancy could demonstrate the utility of this work in planning health services.
To conclude, more research is needed on after-hours primary care, but it is possible to improve patient access to care by considering regular and after-hours care simultaneously in facility location problems. In particular, this research is expected to benefit rural Canadians at a significant distance from primary care providers. By improving the spatial accessibility of health services, the use of these services and health outcomes are likely to improve.
Author Contributions
Conceptualisation, J.C.C., P.T.V. and M.T.; methodology, J.C.C., P.T.V. and M.T.; software, J.C.C.; validation, J.C.C.; formal analysis, J.C.C., P.T.V. and M.T.; investigation, J.C.C.; resources, J.C.C.; data curation, J.C.C.; writing—original draft preparation, J.C.C.; writing—review and editing, J.C.C., P.T.V. and M.T.; visualisation, J.C.C.; supervision, P.T.V. and M.T.; project administration, J.C.C.; funding acquisition, P.T.V. and M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grants RGPIN 2019 05680 and RGPIN-2020-05825.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data presented in this study are available from the authors upon request.
Acknowledgments
The primary author is grateful to Melanie Reuter-Oppermann for guidance in developing an understanding in location analysis and modelling techniques, and to Jacob Macpherson for advice in geographical software.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| GPs | General Practitioners |
| PCPs | Primary Care Practices |
| OR | Operations Research |
| RtA | Regular to After hours |
| AtR | After hours to Regular |
| LP | Linear Program |
| CBC | COIN-OR Branch and Cut |
| DA | Dissemination Area |
| CMA | Census Metropolitan Area |
| CA | Census Agglomeration |
| LSCP | Location Set Covering Problem |
| MCLP | Maximum Covering Location Problem |
References
- Guagliardo, M.F. Spatial accessibility of primary care: Concepts, methods and challenges. Int. J. Health Geogr. 2004, 3, 3. [Google Scholar] [CrossRef] [PubMed]
- Morgan, J.S.; Graber-Naidich, A. Small system dynamics model for alleviating the general practitioners rural care gap in Ontario, Canada. Socio-Econ. Plan. Sci. 2019, 66, 10–23. [Google Scholar] [CrossRef]
- Güneş, E.D.; Yaman, H.; Çekyay, B.; Verter, V. Matching patient and physician preferences in designing a primary care facility network. J. Oper. Res. Soc. 2014, 65, 483–496. [Google Scholar] [CrossRef]
- O’Malley, A.S.; Samuel, D.; Bond, A.M.; Carrier, E. After-Hours Care and its Coordination with Primary Care in the U.S. J. Gen. Intern. Med. 2012, 27, 1406–1415. [Google Scholar] [CrossRef] [PubMed]
- Crighton, E.J.; Bordman, R.; Wheler, D.; Franssen, E.; White, D.; Bovett, M.; Drummond, N.; North Toronto Primary Care Research Network (Nortren). After-hours care in Canada: Analysis of the 2001 National Family Physician Workforce Survey. Can. Fam. Physician Med. Fam. Can. 2005, 51, 1504–1505. [Google Scholar] [CrossRef]
- Daskin, M.S.; Maass, K.L. The p-median problem. In Location Science; Springer: Cham, Switzerland, 2015; pp. 21–45. [Google Scholar]
- Güneş, E.D.; Nickel, S. Location Problems in Healthcare; Springer International Publishing: Cham, Switzerland, 2015; Chapter 21; pp. 555–579. [Google Scholar] [CrossRef]
- Python Software Foundation. Python. 2019. Available online: https://www.python.org/downloads/release/python-373/ (accessed on 1 December 2019).
- Jupyter Team. Jupyter Notebook. 2015. Available online: https://docs.jupyter.org/en/latest/ (accessed on 1 December 2019).
- Roy, J.S.; Mitchell, S.A. PuLP. 2019. Available online: https://pypi.org/project/PuLP/ (accessed on 1 December 2019).
- Beasley, J.E. OR-Library. 2018. Available online: http://people.brunel.ac.uk/~mastjjb/jeb/orlib/pmedinfo.html (accessed on 1 March 2020).
- Gurobi Optimization LLC. Gurobi Optimizer Reference Manual. 2023. Available online: https://www.gurobi.com (accessed on 1 January 2023).
- Statistics Canada. Dissemination Area Boundary File, 2011 Census; Statistics Canada Catalogue No. 92-160-X; Statistics Canada: Ottawa, ON, Canada, 2021. [Google Scholar]
- McNamara, L.; Vanberkel, P.; Petrie, D.; Carter, A. An Application and Framework for Evaluating Emergency Department Networks using Location Analysis and Geographic Information Systems. Comput. Ind. Eng. 2020, 149, 106766. [Google Scholar] [CrossRef]
- Calik, H.; Labbé, M.; Yaman, H. p-Center Problems. In Location Science; Springer International Publishing: Cham, Switzerland, 2015; pp. 79–92. [Google Scholar] [CrossRef]
- ReVelle, C.; Toregas, C.; Falkson, L. Applications of the Location Set-covering Problem. Geogr. Anal. 2010, 8, 65–76. [Google Scholar] [CrossRef]
- Church, R.L.; ReVelle, C. The maximal location covering problem. Pap. Reg. Sci. 1974, 32, 101–118. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).