LFDC: Low-Energy Federated Deep Reinforcement Learning for Caching Mechanism in Cloud–Edge Collaborative
Abstract
1. Introduction
- (1)
- Creating a system model for the cache environment that combines cloud and edge, including network, cache performance, DRL, and energy-consumption models, and proposing a new objective function of the cache energy efficiency ratio to balance performance and energy consumption.
- (2)
- Designing a new federated deep reinforcement learning method that dynamically adjusts cloud aggregation and edge training or decision making to reduce energy consumption while ensuring cache efficiency.
- (3)
- Presenting a series of simulation experiments that demonstrate the effectiveness of the proposed strategies in reducing the training energy consumption of the system while maintaining cache performance.
2. Related Works
3. System Model and Problem Formulation
3.1. Networks Model
3.2. Cache Performance Model
3.3. Np-Complete Proof
3.4. Drl Energy Consumption Model
3.5. Problem Formulation
4. Low-Energy Federated Deep Reinforcement Learning for Caching
4.1. Local DRL Model Design
| Algorithm 1 Local DDQN process for caching. |
|
4.2. Federated Mechanism
| Algorithm 2 Dynamic low-power federated DRL for caching (LFDC). |
Initialized process in BSs:
|
5. Simulation Experiments
- (1)
- Centralized DRL: A DDQN model is deployed in the cloud to train and make decisions on global dynamic caching.
- (2)
- Distributed DRL: A DDQN model is deployed in each BS, which is trained and makes decisions based on local data.
- (3)
- FedAvg: A DDQN model is deployed in each BS and aggregated and distributed through the federated averaging method.
5.1. Simulation Setting
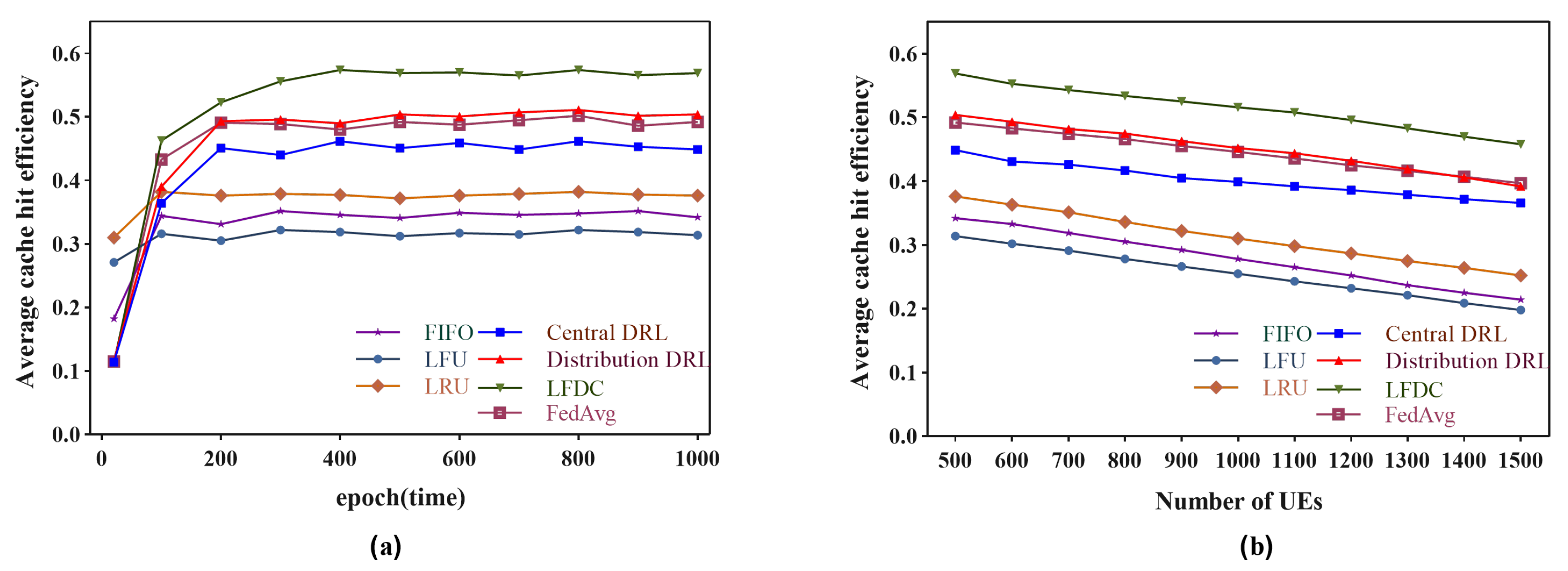
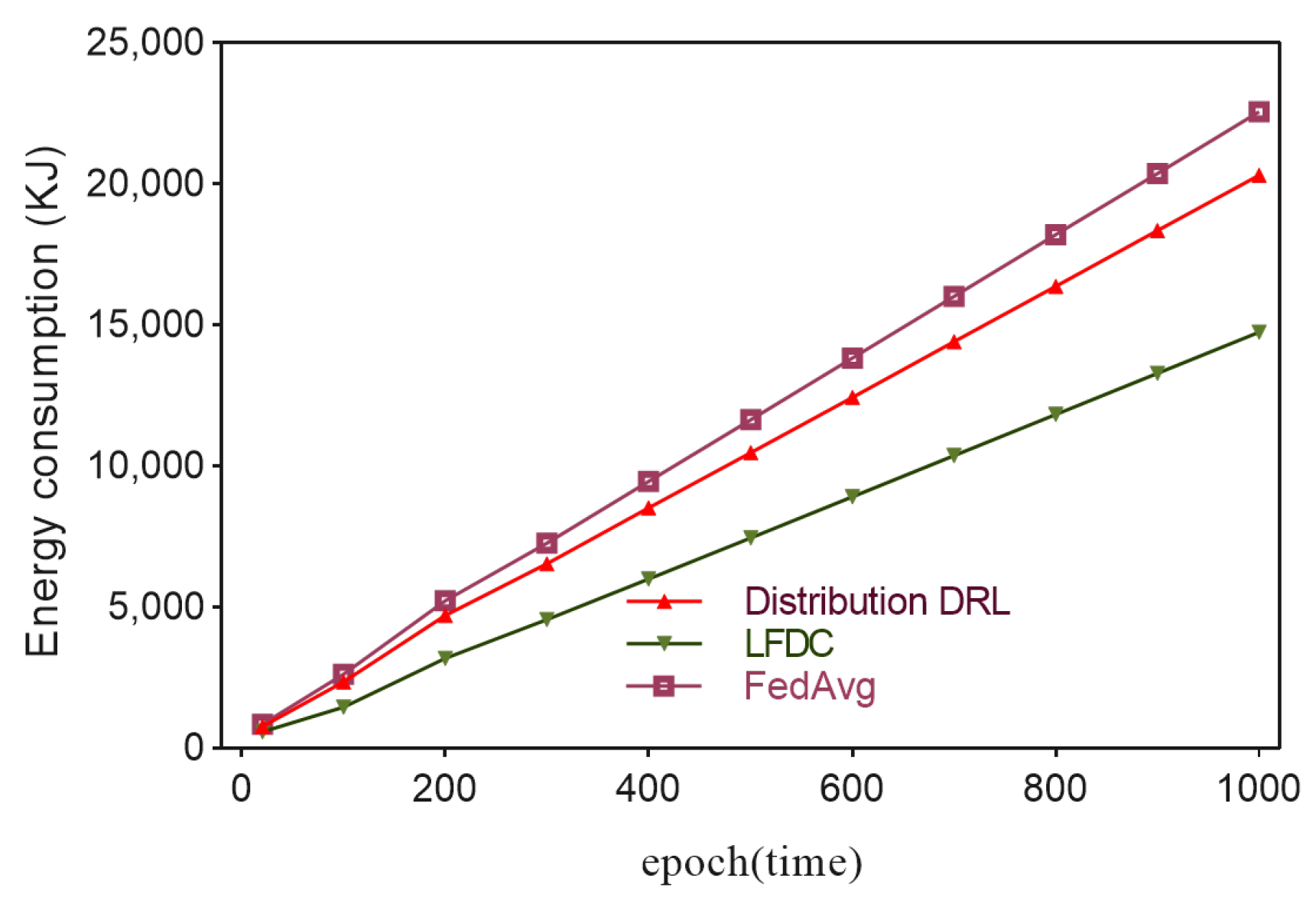
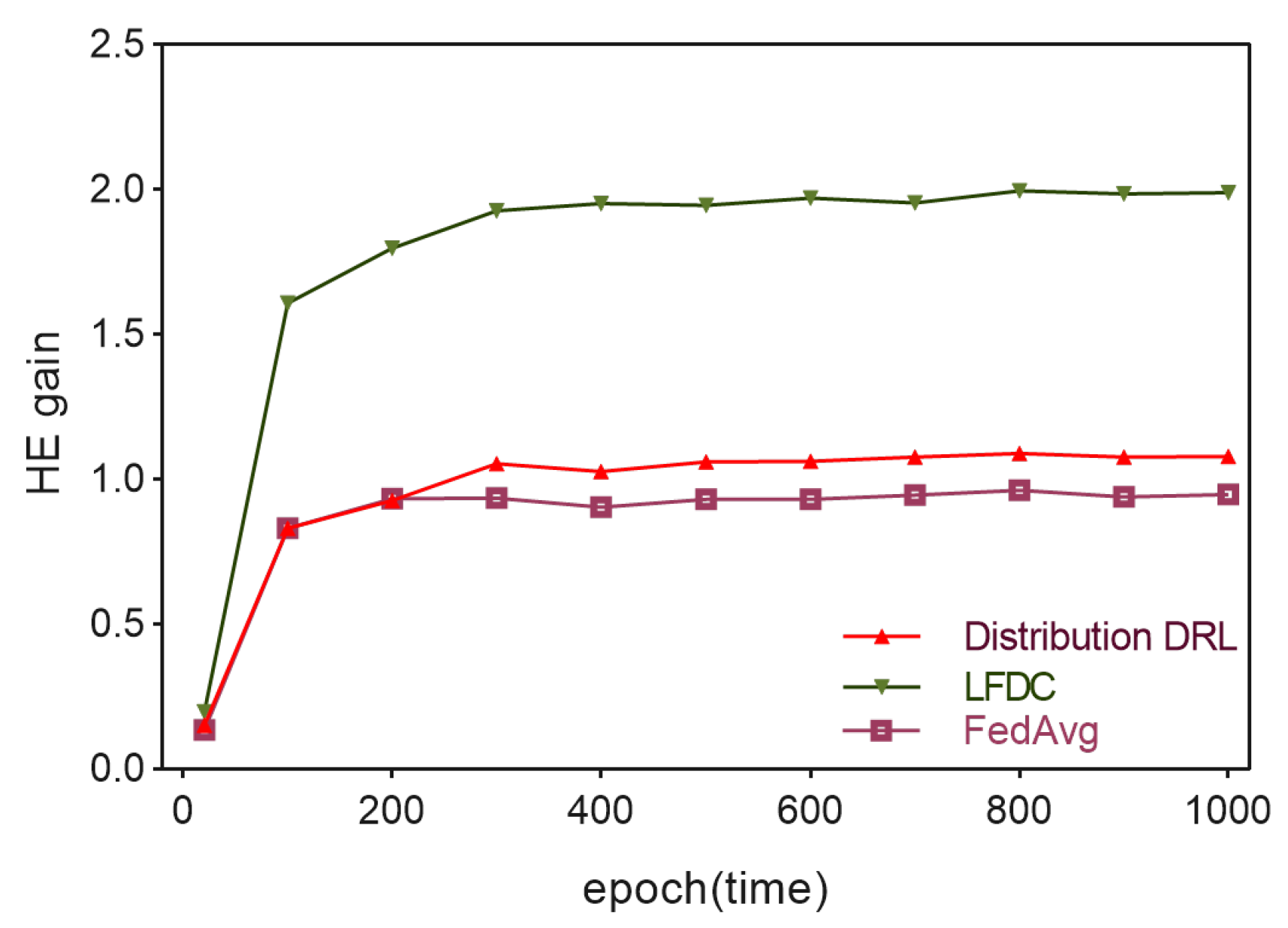
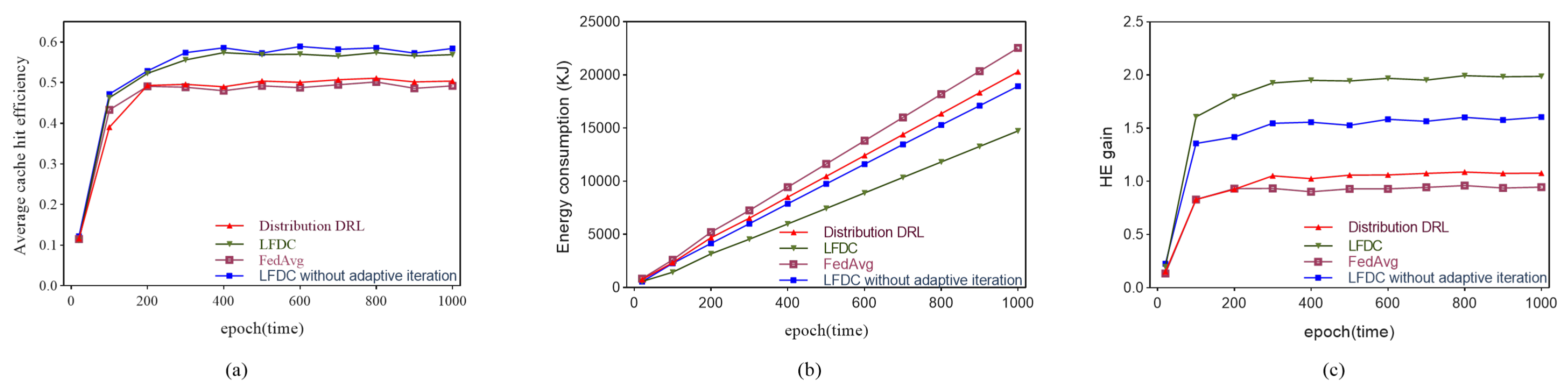
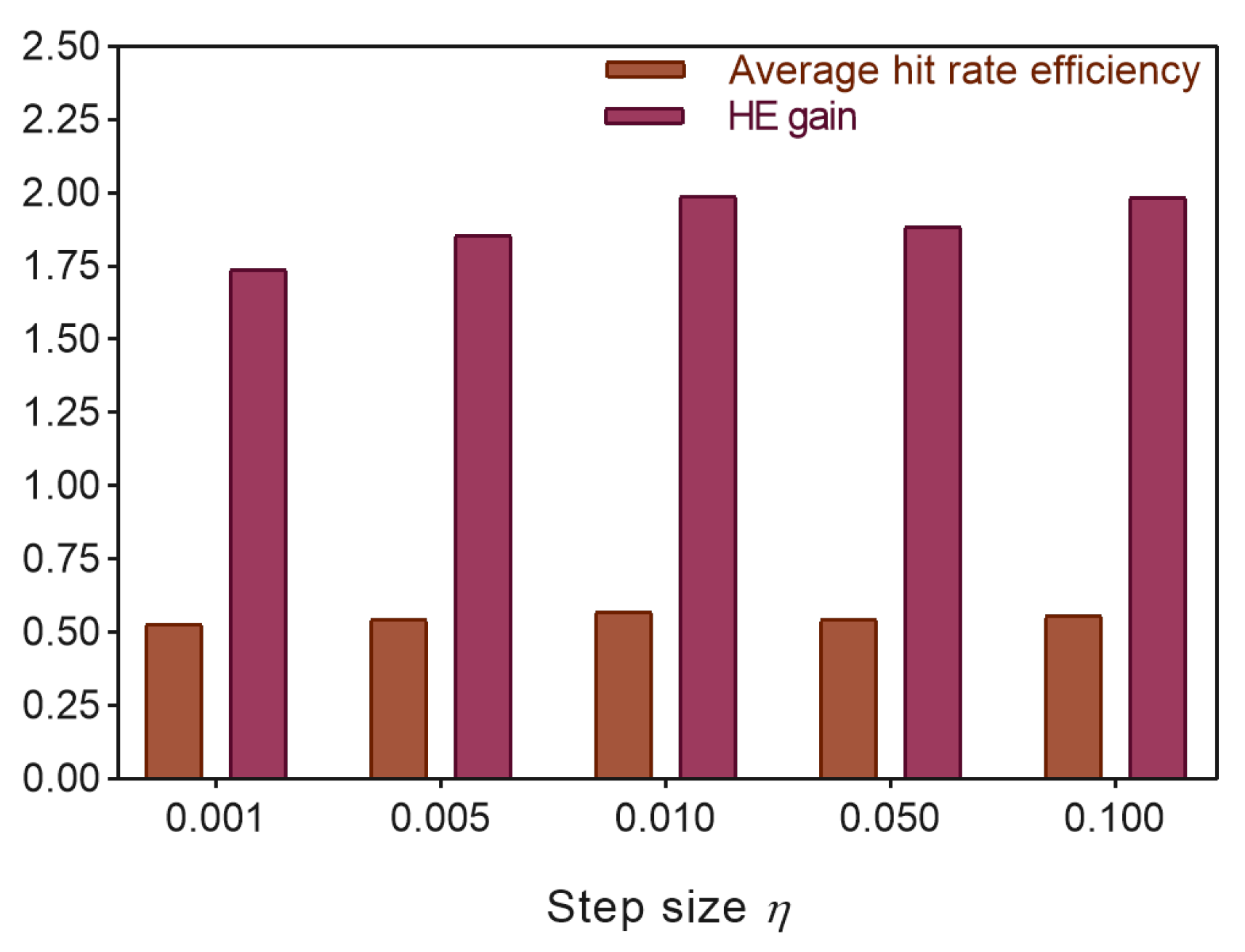
5.2. Evaluation Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, M.; Sharma, S.C.; Goel, A.; Singh, S.P. A comprehensive survey for scheduling techniques in cloud computing. J. Netw. Comput. Appl. 2019, 143, 1–33. [Google Scholar] [CrossRef]
- Shi, W.; Sun, H.; Cao, J.; Zhang, Q.; Liu, W. Edge computing: An emerging computing model for the Internet of everything era. J. Comput. Res. Dev. 2017, 54, 907G924. [Google Scholar]
- Ren, J.; He, Y.; Yu, G.; Li, G.Y. Joint communication and computation resource allocation for cloud-edge collaborative system. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Ding, C.; Zhou, A.; Liu, Y.; Chang, R.N.; Hsu, C.H.; Wang, S. A cloud-edge collaboration framework for cognitive service. IEEE Trans. Cloud Comput. 2020, 10, 1489–1499. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Li, K.; Han, Z.; Leung, V.C. Collaborative multi-tier caching in heterogeneous networks: Modeling, analysis, and design. IEEE Trans. Wirel. Commun. 2017, 16, 6926–6939. [Google Scholar] [CrossRef]
- Wang, X.; Chen, M.; Taleb, T.; Ksentini, A.; Leung, V.C. Cache in the air: Exploiting content caching and delivery techniques for 5G systems. IEEE Commun. Mag. 2014, 52, 131–139. [Google Scholar] [CrossRef]
- Sheng, M.; Xu, C.; Liu, J.; Song, J.; Ma, X.; Li, J. Enhancement for content delivery with proximity communications in caching enabled wireless networks: Architecture and challenges. IEEE Commun. Mag. 2016, 54, 70–76. [Google Scholar] [CrossRef]
- Zhao, X.; Yuan, P.; Tang, S. Collaborative edge caching in context-aware device-to-device networks. IEEE Trans. Veh. Technol. 2018, 67, 9583–9596. [Google Scholar] [CrossRef]
- Sun, Y.; Peng, M.; Mao, S. Deep reinforcement learning-based mode selection and resource management for green fog radio access networks. IEEE Internet Things J. 2018, 6, 1960–1971. [Google Scholar] [CrossRef]
- Yuan, W.; Yang, M.; He, Y.; Wang, C.; Wang, B. Multi-reward architecture based reinforcement learning for highway driving policies. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3810–3815. [Google Scholar]
- Li, J.; Gao, H.; Lv, T.; Lu, Y. Deep reinforcement learning based computation offloading and resource allocation for MEC. In Proceedings of the 2018 IEEE wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Li, Y.; Hu, S.; Li, G. CVC: A collaborative video caching framework based on federated learning at the edge. IEEE Trans. Netw. Serv. Manag. 2021, 19, 1399–1412. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Li, X.; Leung, V.C.; Taleb, T. Federated deep reinforcement learning for internet of things with decentralized cooperative edge caching. IEEE Internet Things J. 2020, 7, 9441–9455. [Google Scholar] [CrossRef]
- Yan, H.; Chen, Z.; Wang, Z.; Zhu, W. DRL-Based Collaborative Edge Content Replication with Popularity Distillation. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Chien, W.C.; Weng, H.Y.; Lai, C.F. Q-learning based collaborative cache allocation in mobile edge computing. Future Gener. Comput. Syst. 2020, 102, 603–610. [Google Scholar] [CrossRef]
- Wang, S.; Tuor, T.; Salonidis, T.; Leung, K.K.; Makaya, C.; He, T.; Chan, K.S. Adaptive Federated Learning in Resource Constrained Edge Computing Systems. IEEE J. Sel. Areas Commun. 2018, 37, 1205–1221. [Google Scholar] [CrossRef]
- Ahmed, M.; Traverso, S.; Giaccone, P.; Leonardi, E.; Niccolini, S. Analyzing the performance of LRU caches under non-stationary traffic patterns. arXiv 2013, arXiv:1301.4909. [Google Scholar]
- Rossi, D.; Rossini, G. Caching performance of content centric networks under multi-path routing (and more). Relatório Técnico Telecom ParisTech 2011, 2011, 1–6. [Google Scholar]
- Jaleel, A.; Theobald, K.B.; Steely, S.C., Jr.; Emer, J. High performance cache replacement using re-reference interval prediction (RRIP). ACM SIGARCH Comput. Archit. News 2010, 38, 60–71. [Google Scholar] [CrossRef]
- Poularakis, K.; Iosifidis, G.; Tassiulas, L. Approximation algorithms for mobile data caching in small cell networks. IEEE Trans. Commun. 2014, 62, 3665–3677. [Google Scholar] [CrossRef]
- Poularakis, K.; Llorca, J.; Tulino, A.M.; Taylor, I.; Tassiulas, L. Joint service placement and request routing in multi-cell mobile edge computing networks. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 10–18. [Google Scholar]
- Yang, L.; Cao, J.; Liang, G.; Han, X. Cost aware service placement and load dispatching in mobile cloud systems. IEEE Trans. Comput. 2015, 65, 1440–1452. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J. Optimal probabilistic caching in heterogeneous IoT networks. IEEE Internet Things J. 2020, 7, 3404–3414. [Google Scholar] [CrossRef]
- Wang, X.; Han, Y.; Leung, V.C.; Niyato, D.; Yan, X.; Chen, X. Convergence of edge computing and deep learning: A comprehensive survey. IEEE Commun. Surv. Tutorials 2020, 22, 869–904. [Google Scholar] [CrossRef]
- Gu, J.; Wang, W.; Huang, A.; Shan, H.; Zhang, Z. Distributed cache replacement for caching-enable base stations in cellular networks. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2648–2653. [Google Scholar]
- Rathore, S.; Ryu, J.H.; Sharma, P.K.; Park, J.H. DeepCachNet: A proactive caching framework based on deep learning in cellular networks. IEEE Netw. 2019, 33, 130–138. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Y. Deep reinforcement learning-based collaborative video caching and transcoding in clustered and intelligent edge B5G networks. Wirel. Commun. Mob. Comput. 2020, 2020, 6684293. [Google Scholar] [CrossRef]
- Neglia, G.; Leonardi, E.; Iecker, G.; Spyropoulos, T. A swiss army knife for dynamic caching in small cell networks. arXiv 2019, arXiv:1912.10149. [Google Scholar]
- Neglia, G.; Carra, D.; Michiardi, P. Cache policies for linear utility maximization. IEEE/ACM Trans. Netw. 2018, 26, 302–313. [Google Scholar] [CrossRef]
- Ricardo, G.I.; Tuholukova, A.; Neglia, G.; Spyropoulos, T. Caching policies for delay minimization in small cell networks with coordinated multi-point joint transmissions. IEEE/ACM Trans. Netw. 2021, 29, 1105–1115. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, L.; Li, W.; Fu, X. Efficient multi-user computation offloading for mobile-edge cloud computing. IEEE/ACM Trans. Netw. 2015, 24, 2795–2808. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, Y.; Shi, G.; Poor, H.V. Optimizing resource-efficiency for federated edge intelligence in IoT networks. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 86–92. [Google Scholar]
- Yang, Z.; Chen, M.; Saad, W.; Hong, C.S.; Shikh-Bahaei, M. Energy efficient federated learning over wireless communication networks. IEEE Trans. Wirel. Commun. 2020, 20, 1935–1949. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, J.; Letaief, K.B. Dynamic computation offloading for mobile-edge computing with energy harvesting devices. IEEE J. Sel. Areas Commun. 2016, 34, 3590–3605. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- van Hasselt, H. Double Q-Learning. IEEE Intell. Syst. 2010, 23. [Google Scholar]
- Yu, S.; Chen, X.; Zhou, Z.; Gong, X.; Wu, D. When deep reinforcement learning meets federated learning: Intelligent multitimescale resource management for multiaccess edge computing in 5G ultradense network. IEEE Internet Things J. 2020, 8, 2238–2251. [Google Scholar] [CrossRef]
- Zhong, C.; Gursoy, M.C.; Velipasalar, S. A deep reinforcement learning-based framework for content caching. In Proceedings of the 2018 52nd Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 21–23 March 2018; pp. 1–6. [Google Scholar]
- McMahan, H.B.; Moore, E.; Ramage, D.; y Arcas, B.A. Federated Learning of Deep Networks using Model Averaging. arXiv 2016, arXiv:1602.05629. [Google Scholar]
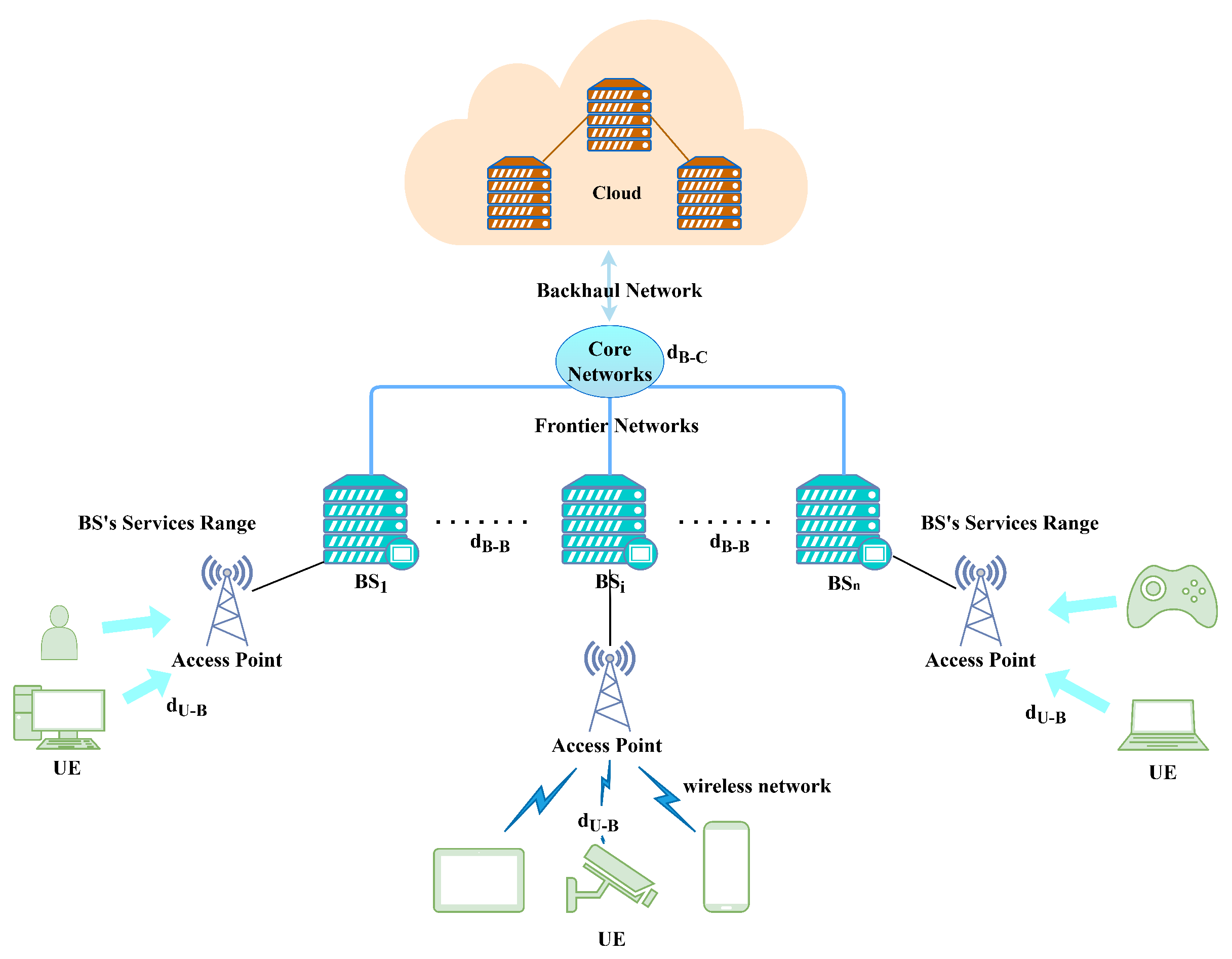
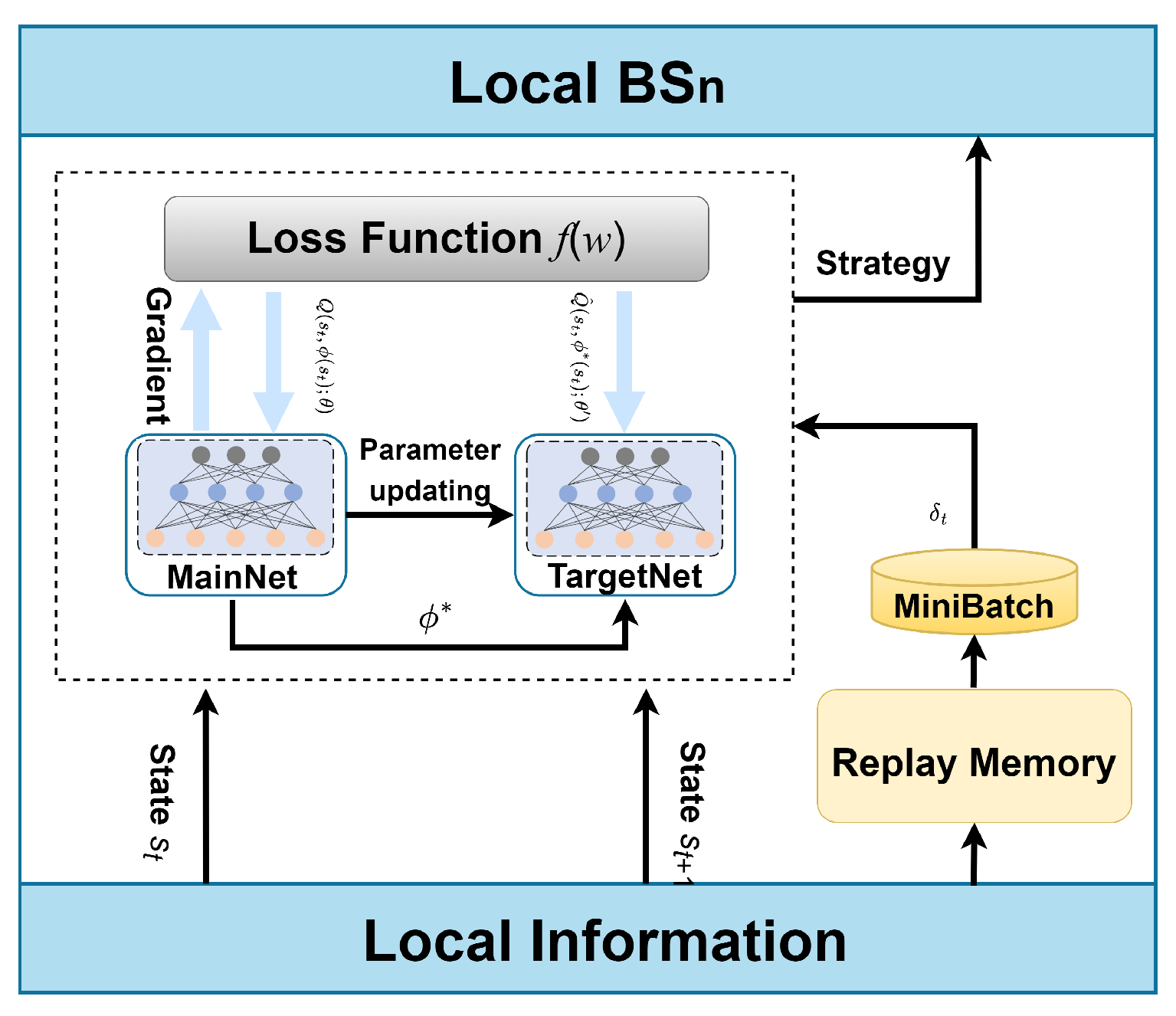
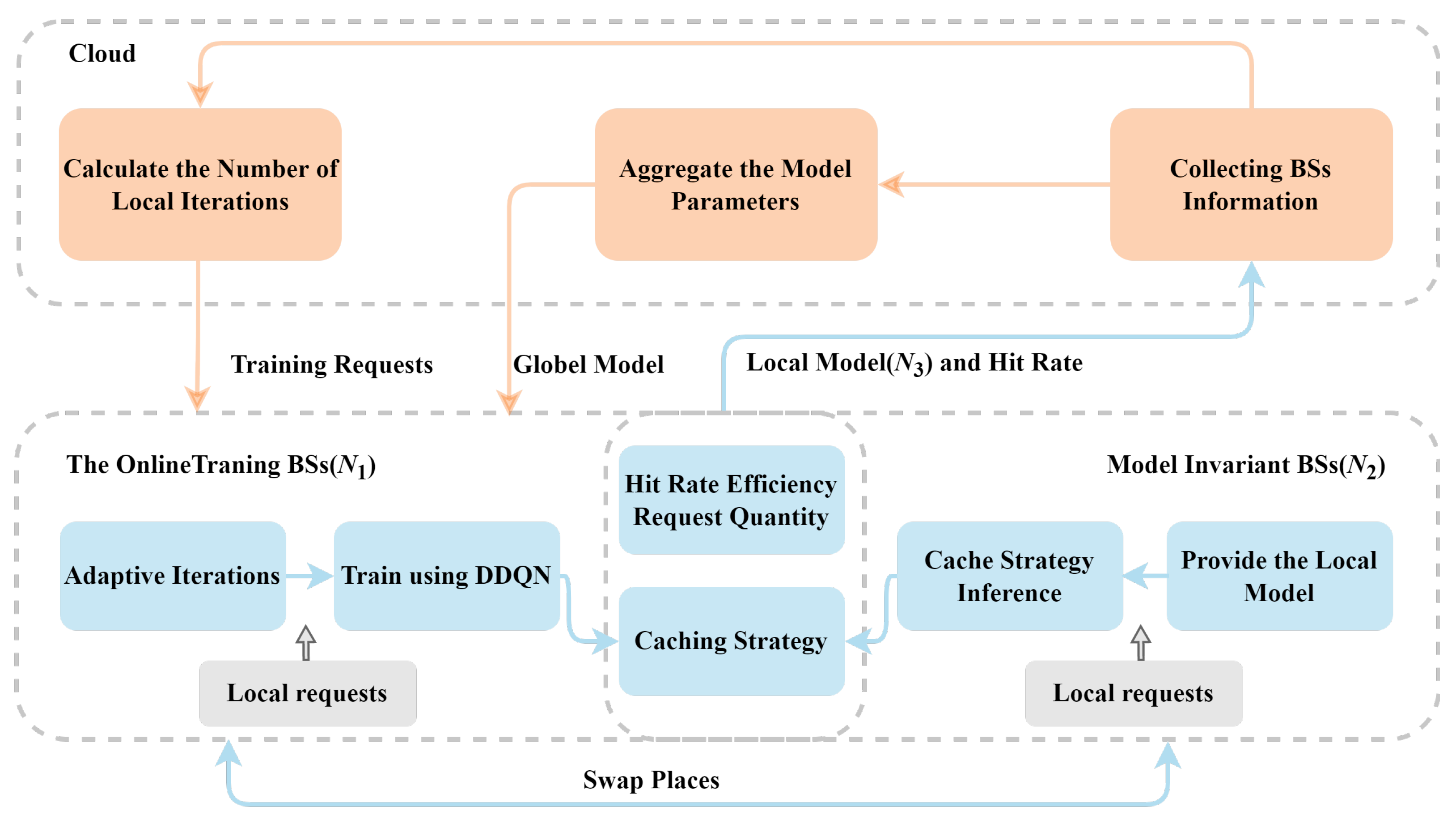
| Notation | Description |
|---|---|
| Set of BSs | |
| Set of UEs | |
| Set of content | |
| Epochs of federated learning/caching decision. | |
| ,, | Transmission rate between UEs and BSs, BSs and Cloud, BSs and BSs. |
| , | The size of the content in BSn, the size of the content f. |
| UE u preferences for content f. | |
| , | Number of requests from UE u, number of requests received by BSn. |
| , | The cache hit efficiency of BSn in epoch t, The cache hit efficiency of system in epoch t. |
| , | The energy consumption respectively, of local learning and upload in epoch t. |
| The system energy consumption for learning in epoch t. | |
| The caching state. | |
| The caching decision. | |
| The Double Deep Q-Network (DDQN) reward. | |
| The loss function of local training. | |
| gradient update formula for . | |
| The weight factor for adaptive iteration times. | |
| Amount of data for a single training session in BSn in epoch t. |
| Parameter | Value | Description |
|---|---|---|
| T | 1000 | Number of global epoch |
| 10 | Number of initial local iterations | |
| 20 cycles/bit | CPU cycles per bit for training one data sample | |
| 4 GHz | Computation capacity of BSs | |
| 500 W | Transmit power of BSn | |
| B | 20 MHz | Channel bandwidth of BSs downlink |
| 1000 Mbps | Transmission speed between cloud and BSs | |
| 1 Gbps | Transmission speed between BSs | |
| 10 Mbit | Content size | |
| Effective capacitance coefficient of BSn | ||
| bit | Parameter size of model | |
| 0.9 | Discount factor | |
| 0.01 | Step size | |
| 0.1 | State transition probability |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Hu, Z.; Zheng, M.; Liang, Y.; Xiao, H.; Zheng, H.; Xu, A. LFDC: Low-Energy Federated Deep Reinforcement Learning for Caching Mechanism in Cloud–Edge Collaborative. Appl. Sci. 2023, 13, 6115. https://doi.org/10.3390/app13106115
Zhang X, Hu Z, Zheng M, Liang Y, Xiao H, Zheng H, Xu A. LFDC: Low-Energy Federated Deep Reinforcement Learning for Caching Mechanism in Cloud–Edge Collaborative. Applied Sciences. 2023; 13(10):6115. https://doi.org/10.3390/app13106115
Chicago/Turabian StyleZhang, Xinyu, Zhigang Hu, Meiguang Zheng, Yang Liang, Hui Xiao, Hao Zheng, and Aikun Xu. 2023. "LFDC: Low-Energy Federated Deep Reinforcement Learning for Caching Mechanism in Cloud–Edge Collaborative" Applied Sciences 13, no. 10: 6115. https://doi.org/10.3390/app13106115
APA StyleZhang, X., Hu, Z., Zheng, M., Liang, Y., Xiao, H., Zheng, H., & Xu, A. (2023). LFDC: Low-Energy Federated Deep Reinforcement Learning for Caching Mechanism in Cloud–Edge Collaborative. Applied Sciences, 13(10), 6115. https://doi.org/10.3390/app13106115





