Minimum Variance Distortionless Response—Hanbury Brown and Twiss Sound Source Localization
Abstract
1. Introduction
2. MVDR-HBT Localization Principle
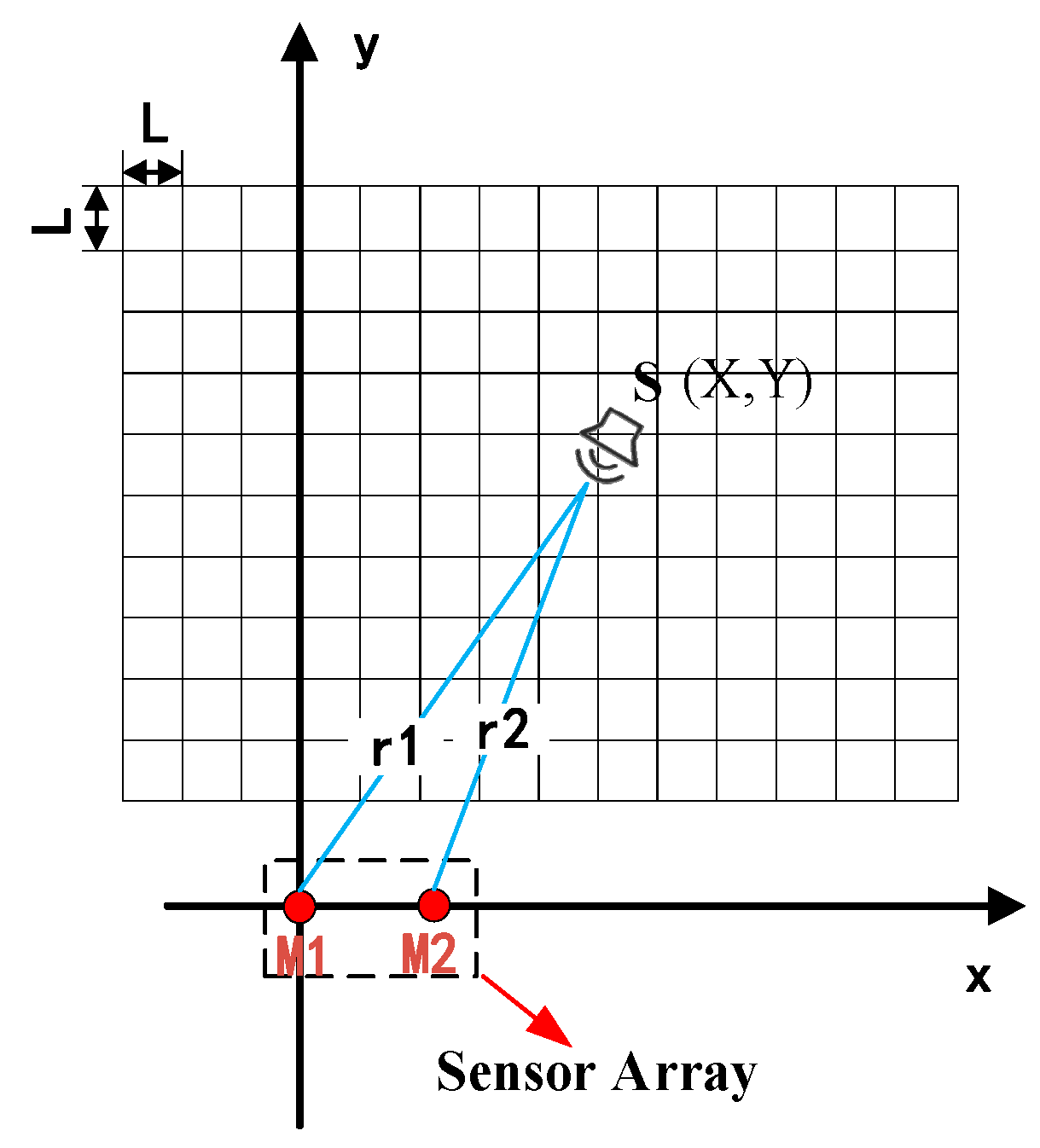
2.1. Principle of Narrowband Sound Source Localization Using MVDR-HBT
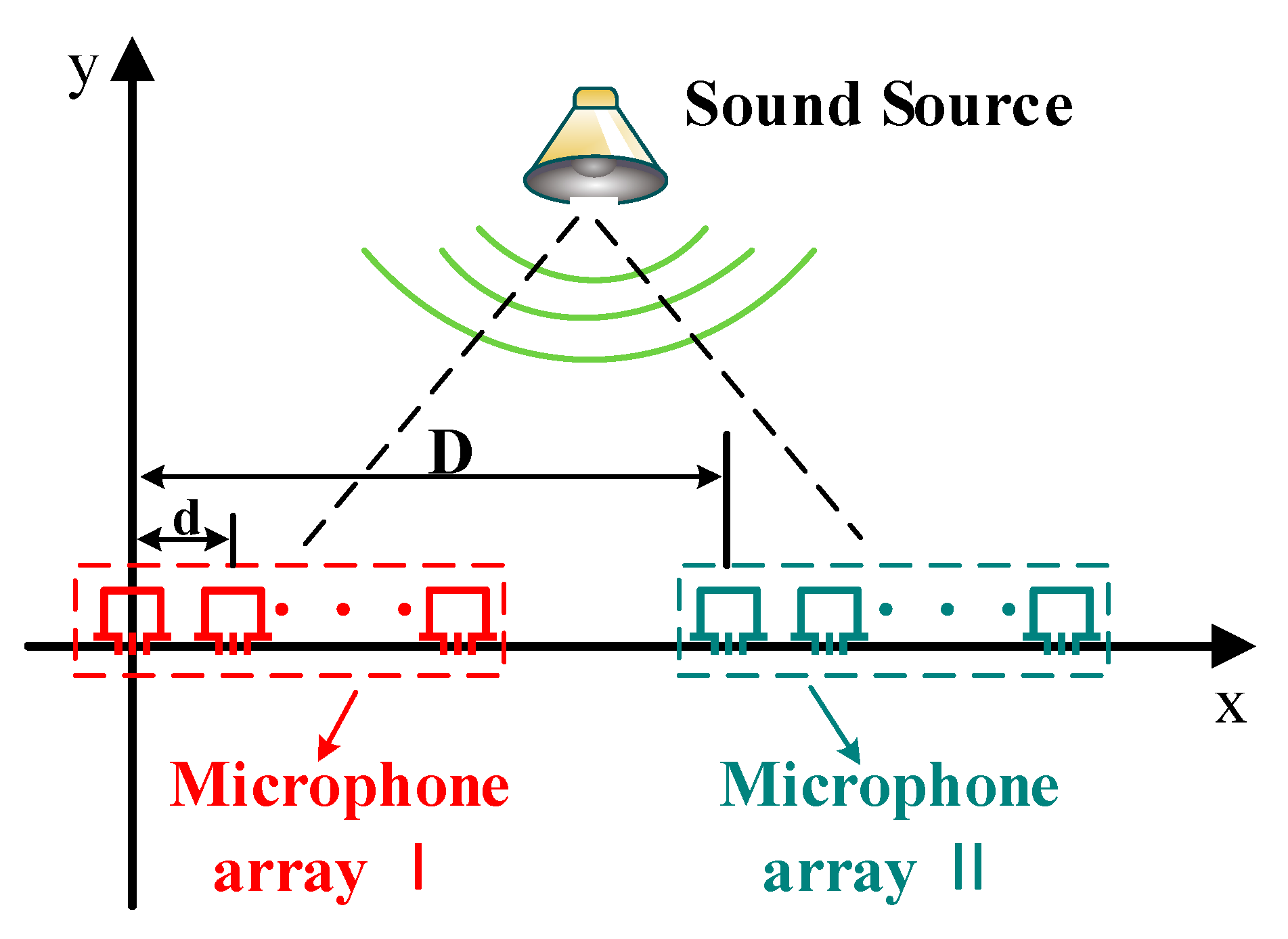
2.2. Principle of Broadband Sound Source Localization Using MVDR-HBT
3. Simulation Analysis
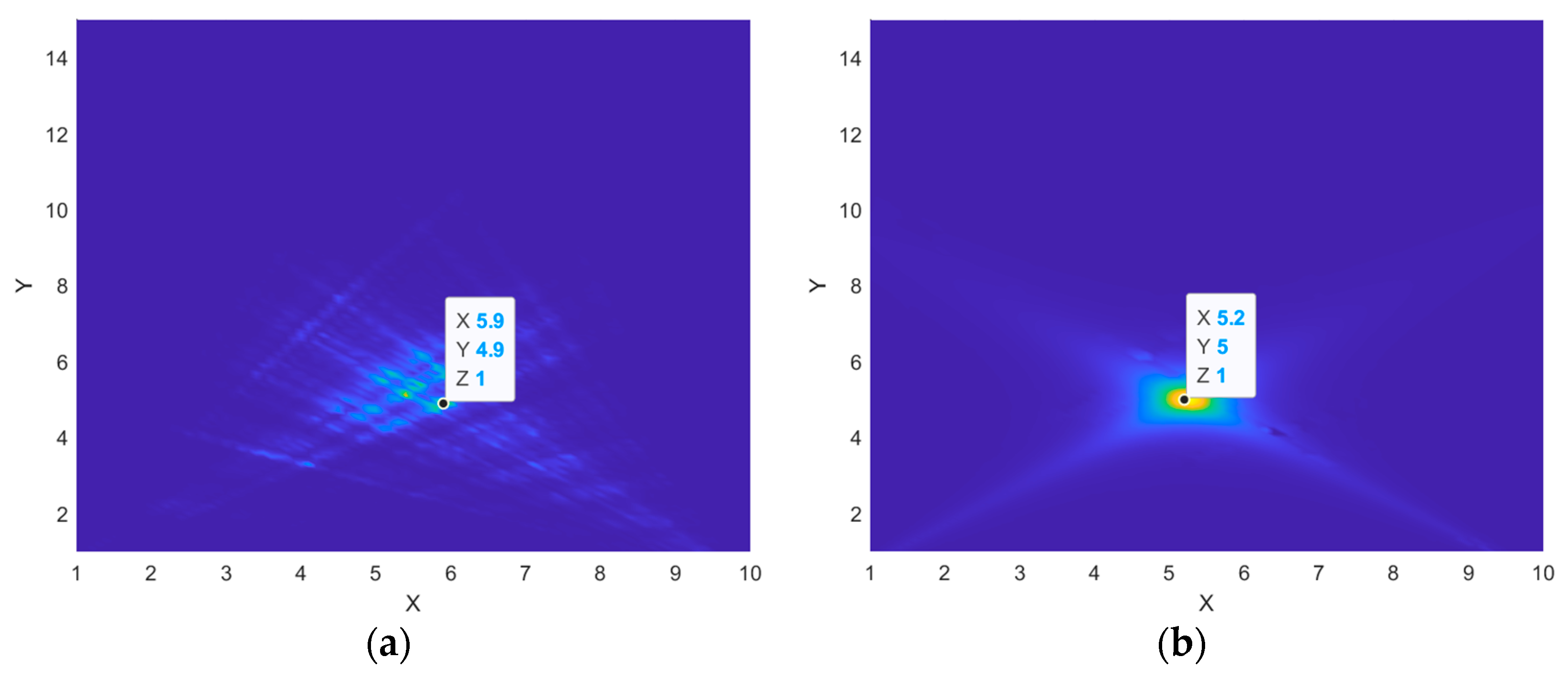
3.1. SNR
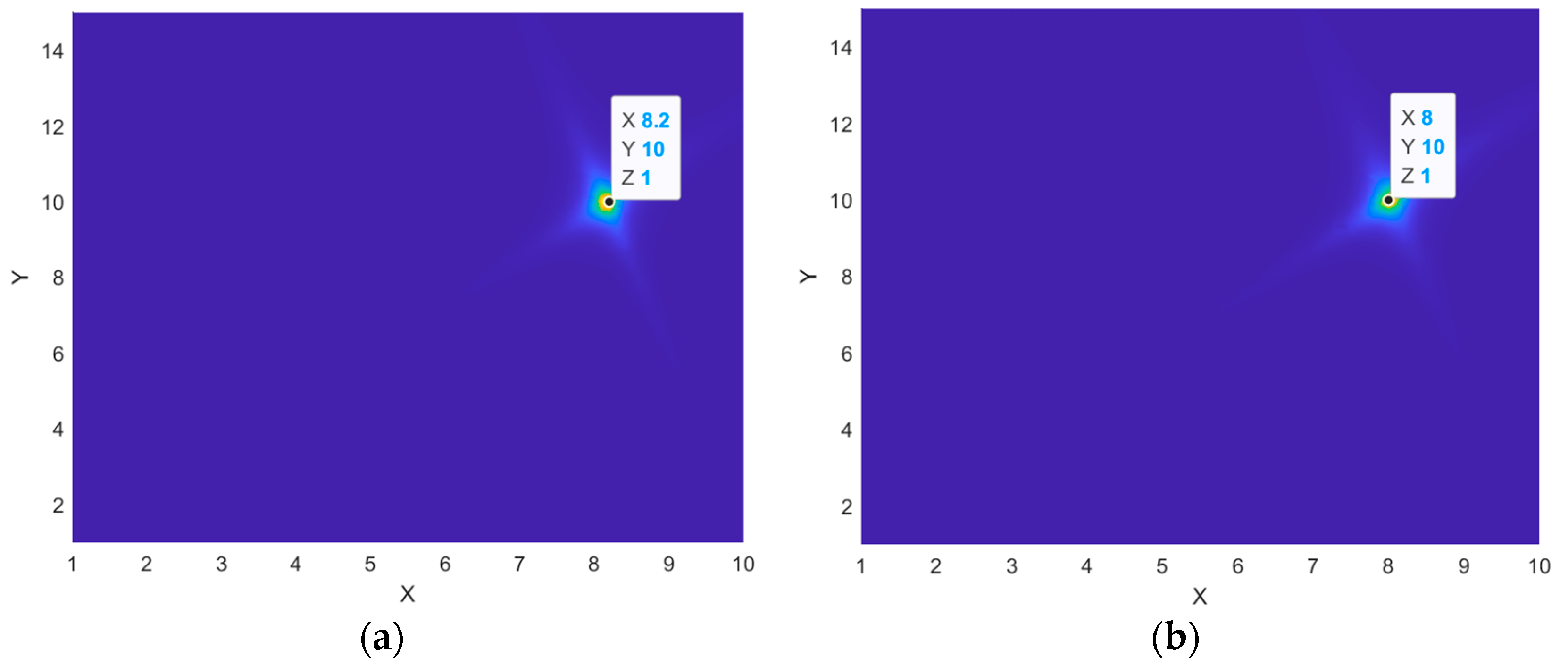
3.2. Distance to Sound Source Target
3.3. Frequency
4. The Sound Source Detection Experiment
4.1. SNR
4.2. Distance to Sound Source Target
4.3. Frequency
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liaquat, M.U.; Munawar, H.S.; Rahman, A.; Qadir, Z.; Kouzani, A.Z.; Mahmud, M.A.P. Localization of sound sources: A systematic review. Energies 2021, 14, 3910. [Google Scholar] [CrossRef]
- Moravec, M.; Badida, M.; Mikušová, N.; Sobotová, L.; Švajlenka, J.; Dzuro, T.J.S. Proposed options for noise reduction from a wastewater treatment plant: Case study. Sustainability 2021, 13, 2409. [Google Scholar] [CrossRef]
- Fiebig, W.; Dąbrowski, D. Use of acoustic camera for noise sources localization and noise reduction in the industrial plant. Arch. Acoust. 2020, 45, 111–117. [Google Scholar]
- Yang, X.; Xing, H.; Ji, X. Sound source omnidirectional positioning calibration method based on microphone observation angle. Complexity 2018, 2018, 2317853. [Google Scholar] [CrossRef]
- Miao, F.; Yang, D.; Wen, J.; Lian, X. Vibration. Moving sound source localization based on triangulation method. J. Sound Vib. 2016, 385, 93–103. [Google Scholar] [CrossRef]
- Thomas, B.; Hunter, A. Coherence-induced bias reduction in synthetic aperture sonar along-track micronavigation. IEEE J. Ocean. Eng. 2021, 47, 162–178. [Google Scholar] [CrossRef]
- Fayad, Y.; Wang, C.; Cao, Q. Electronics. Temporal-spatial subspaces modern combination method for 2D-DOA estimation in MIMO radar. J. Syst. Eng. Electron. 2017, 28, 697–702. [Google Scholar]
- Jin, B.; Xu, X.; Zhu, Y.; Zhang, T.; Fei, Q. Single-source aided semi-autonomous passive location for correcting the position of an underwater vehicle. IEEE Sens. J. 2019, 19, 3267–3275. [Google Scholar] [CrossRef]
- Liu, G.; Yuan, S.; Wu, J.; Zhang, R. A sound source localization method based on microphone array for mobile robot. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 1621–1625. [Google Scholar]
- Chen, G.; Xu, Y. A sound source localization device based on rectangular pyramid structure for mobile robot. J. Sens. 2019, 2019, 4639850. [Google Scholar] [CrossRef]
- Ximing, D.; Wenzhong, L.; Peng, L.; Mingru, G.; Fufu, W. Speaker tracking based on microphone cross arry in the smart conference system. In Proceedings of the 2014 IEEE International Conference on Consumer Electronics-China, Shenzhen, China, 9–13 April 2014; pp. 1–4. [Google Scholar]
- Asp, F.; Jakobsson, A.-M.; Berninger, E. The effect of simulated unilateral hearing loss on horizontal sound localization accuracy and recognition of speech in spatially separate competing speech. Hear. Res. 2018, 357, 54–63. [Google Scholar] [CrossRef]
- Gierlich, R. Joint estimation of spatial and motional radar target parameters by multidimensional spectral analysis. In Proceedings of the 2015 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; pp. 95–101. [Google Scholar]
- Rahman, S.; Arifianto, D.; Dhanardono, T. Localization of underwater moving sound source based on time delay estimation using hydrophone array. J. Phys. Conf. Ser. 2016, 776, 012075. [Google Scholar] [CrossRef]
- Xu, J.; Gao, C.; Liu, H.; Yuan, X.; Dong, Y.; Liu, L. Sound Source Localization of Firearms Based on TDOA Optimization Algorithm. In Proceedings of the 2022 Global Reliability and Prognostics and Health Management (PHM-Yantai), Yantai, China, 13–16 October 2022; pp. 1–5. [Google Scholar]
- Shi, W.; Li, Y.; Zhao, L.; Liu, X. Controllable sparse antenna array for adaptive beamforming. IEEE Access 2019, 7, 6412–6423. [Google Scholar] [CrossRef]
- Lafta, N.A.; Hreshee, S.S. Modified Multiple Signal Classification Algorithm for WSNs Localization. In Proceedings of the 2020 3rd International Conference on Engineering Technology and its Applications (IICETA), Najaf, Iraq, 6–7 September 2020; pp. 56–61. [Google Scholar]
- Chang, H.; Li, W. Correction-based diffusion LMS algorithms for secure distributed estimation under attacks. Digit. Signal Process. 2020, 102, 102735. [Google Scholar] [CrossRef]
- Knapp, C.; Carter, G. The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 320–327. [Google Scholar] [CrossRef]
- Mu, W.; Qu, W.; Liu, G.; Zou, Z.; Liu, P. A study on beamforming location method with improved search strategy. Appl. Acoust. 2017, 36, 298–304. [Google Scholar]
- Dam, H.Q.H.; Nordholm, S. Source separation employing beamforming and SRP-PHAT localization in three-speaker room environments. Vietnam J. Comput. Sci. 2017, 4, 161–170. [Google Scholar] [CrossRef]
- Salvati, D.; Drioli, C.; Foresti, G.L.J.S.P. Sensitivity-based region selection in the steered response power algorithm. Signal Process. 2018, 153, 1–10. [Google Scholar] [CrossRef]
- Liu, M.; Hu, J.; Zeng, Q.; Jian, Z.; Nie, L. Sound source localization based on multi-channel cross-correlation weighted beamforming. Micromachines 2022, 13, 1010. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Cai, X.; Yu, D.; Qiao, Z.; Dong, H.; Wu, M. Sound Source Localization Methods Based on Lagrange-Galerkin Spherical Grid. In Proceedings of the 2021 IEEE International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Qingdao, China, 2–4 July 2021; pp. 665–670. [Google Scholar]
- Hahn, W.; Tretter, S. Optimum processing for delay-vector estimation in passive signal arrays. IEEE Trans. Inf. Theory 1973, 19, 608–614. [Google Scholar] [CrossRef]
- Liu, M.; Nie, L.; Li, S.; Jia, W. Passive positioning of sound target based on HBT interference. AIP Adv. 2019, 9, 105120. [Google Scholar] [CrossRef]
- Brown, R.H.; Twiss, R.Q.; Sciences, P. Interferometry of the intensity fluctuations in light. II. An experimental test of the theory for partially coherent light. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1958, 243, 291–319. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Wolfel, M.; McDonough, J. Minimum variance distortionless response spectral estimation. IEEE Signal Process. Mag. 2005, 22, 117–126. [Google Scholar] [CrossRef]





| SNR (dB) | Method | Position (m) | Results (m) | Errors (m) | Relative Positioning Error (%) | Percentage Decrease in Error (%) |
|---|---|---|---|---|---|---|
| −10 | HBT | (5, 5) | (5.9, 4.9) | (0.9, −0.1) | 12.81% | 9.98% |
| MVDR-HBT | (5.2, 5) | (0.2, 0) | 2.83% | |||
| −5 | HBT | (5.3, 4.7) | (0.3, −0.3) | 6.00% | 4.59% | |
| MVDR-HBT | (5.1, 5) | (0.1, 0) | 1.41% | |||
| 0 | HBT | (5.1, 5) | (0.1, 0) | 1.41% | 1.41% | |
| MVDR-HBT | (5, 5) | (0, 0) | 0 |
| SNR (dB) | Method | Position (m) | Results (m) | Errors (m) | Relative Positioning Error (%) | Percentage Decrease in Error (%) |
|---|---|---|---|---|---|---|
| −10 | HBT | (5, 5) | (5.9, 4.9) | (0.9, −0.1) | 12.81% | 9.98% |
| MVDR-HBT | (5.2, 5) | (0.2, 0) | 2.83% | |||
| HBT | (8, 10) | (7.6, 10.6) | (−0.4, 0.6) | 5.63% | 3.88% | |
| MVDR-HBT | (8.1, 9.8) | (0.1, −0.2) | 1.75% | |||
| −5 | HBT | (5, 5) | (5.3, 4.7) | (0.3, −0.3) | 6.00% | 4.59% |
| MVDR-HBT | (5.1, 5) | (0.1, 0) | 1.41% | |||
| HBT | (8, 10) | (7.6, 9.6) | (−0.4, −0.4) | 4.42% | 2.86% | |
| MVDR-HBT | (8.2, 10) | (0.2, 0) | 1.56% |
| SNR (dB) | Frequency (Hz) | Method | Position (m) | Results (m) | Errors (m) | Relative Positioning Error (%) |
|---|---|---|---|---|---|---|
| −5 | 600 | HBT | (8, 10) | (7.6, 9.6) | (−0.4, −0.4) | 4.42% |
| MVDR-HBT | (8.2, 10) | (0.2, 0) | 1.56% | |||
| 600, 700 | HBT | (7.8, 9.5) | (−0.2, −0.5) | 4.21% | ||
| MVDR-HBT | (8.1, 10.1) | (0.1, 0.1) | 1.10% | |||
| 600, 700, 800 | HBT | (8.1, 10.3) | (0.1, 0.3) | 2.47% | ||
| MVDR-HBT | (8, 10) | (0, 0) | 0% |
| SNR (dB) | Method | Position (m) | Distance (m) | Real Incident Direction (°) | Estimating the Direction of Arrival of the Signal (°) | Angular Deviation (°) |
|---|---|---|---|---|---|---|
| 0 | MVDR-HBT | (2.5, 2) | 3.20 | 51.34 | 52.43 | 1.09 |
| HBT | 53.62 | 2.28 | ||||
| MVDR-HBT | (5, 5) | 7.07 | 45.0 | 48.24 | 3.24 | |
| HBT | 48.95 | 3.95 | ||||
| −5 | MVDR-HBT | (2.5, 2) | 3.20 | 51.34 | 53.47 | 2.13 |
| HBT | 54.63 | 3.29 | ||||
| MVDR-HBT | (5, 5) | 7.07 | 45.0 | 48.74 | 3.74 | |
| HBT | 49.47 | 4.47 |
| Frequency (Hz) | Method | Position (m) | Distance (m) | Real Incident Direction (°) | Estimating the Direction of Arrival of the Signal (°) | Angular Deviation (°) |
|---|---|---|---|---|---|---|
| 200~2000 | MVDR-HBT | (2.5, 2) | 3.20 | 51.34 | 50.57 | 0.77 |
| HBT | 52.82 | 1.48 | ||||
| MVDR-HBT | (5, 3) | 5.83 | 59.04 | 61.33 | 2.29 | |
| HBT | 55.85 | 3.19 | ||||
| MVDR-HBT | (5, 5) | 7.07 | 45.0 | 47.78 | 2.78 | |
| HBT | 48.43 | 3.43 | ||||
| MVDR-HBT | (6, 8) | 10 | 36.87 | 33.70 | 3.17 | |
| HBT | 32.91 | 3.96 |
| Frequency (Hz) | Method | Position (m) | Distance (m) | Real Incident Direction (°) | Estimating the Direction of Arrival of the Signal (°) | Angular Deviation (°) |
|---|---|---|---|---|---|---|
| 600 | MVDR-HBT | (2.5, 2) | 3.20 | 51.34 | 53.13 | 1.79 |
| HBT | 53.75 | 2.41 | ||||
| MVDR-HBT | (5, 5) | 7.07 | 45.0 | 48.58 | 3.58 | |
| HBT | 49.39 | 4.39 | ||||
| 200~2000 | MVDR-HBT | (2.5, 2) | 3.20 | 51.34 | 50.57 | 0.77 |
| HBT | 52.82 | 1.48 | ||||
| MVDR-HBT | (5, 5) | 7.07 | 45.0 | 47.78 | 2.78 | |
| HBT | 48.43 | 3.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Qu, S.; Zhao, X. Minimum Variance Distortionless Response—Hanbury Brown and Twiss Sound Source Localization. Appl. Sci. 2023, 13, 6013. https://doi.org/10.3390/app13106013
Liu M, Qu S, Zhao X. Minimum Variance Distortionless Response—Hanbury Brown and Twiss Sound Source Localization. Applied Sciences. 2023; 13(10):6013. https://doi.org/10.3390/app13106013
Chicago/Turabian StyleLiu, Mengran, Shanbang Qu, and Xuhui Zhao. 2023. "Minimum Variance Distortionless Response—Hanbury Brown and Twiss Sound Source Localization" Applied Sciences 13, no. 10: 6013. https://doi.org/10.3390/app13106013
APA StyleLiu, M., Qu, S., & Zhao, X. (2023). Minimum Variance Distortionless Response—Hanbury Brown and Twiss Sound Source Localization. Applied Sciences, 13(10), 6013. https://doi.org/10.3390/app13106013





