A New Insight into Reliability Data Modeling with an Exponentiated Composite Exponential-Pareto Model
Abstract
1. Introduction
2. Related Work
2.1. The Composite Distributions
2.2. A Generalized Family of Exponentiated Composite Distributions
2.2.1. Moments
2.2.2. Survival Function
2.2.3. Hazard Function
2.2.4. Quantile Function
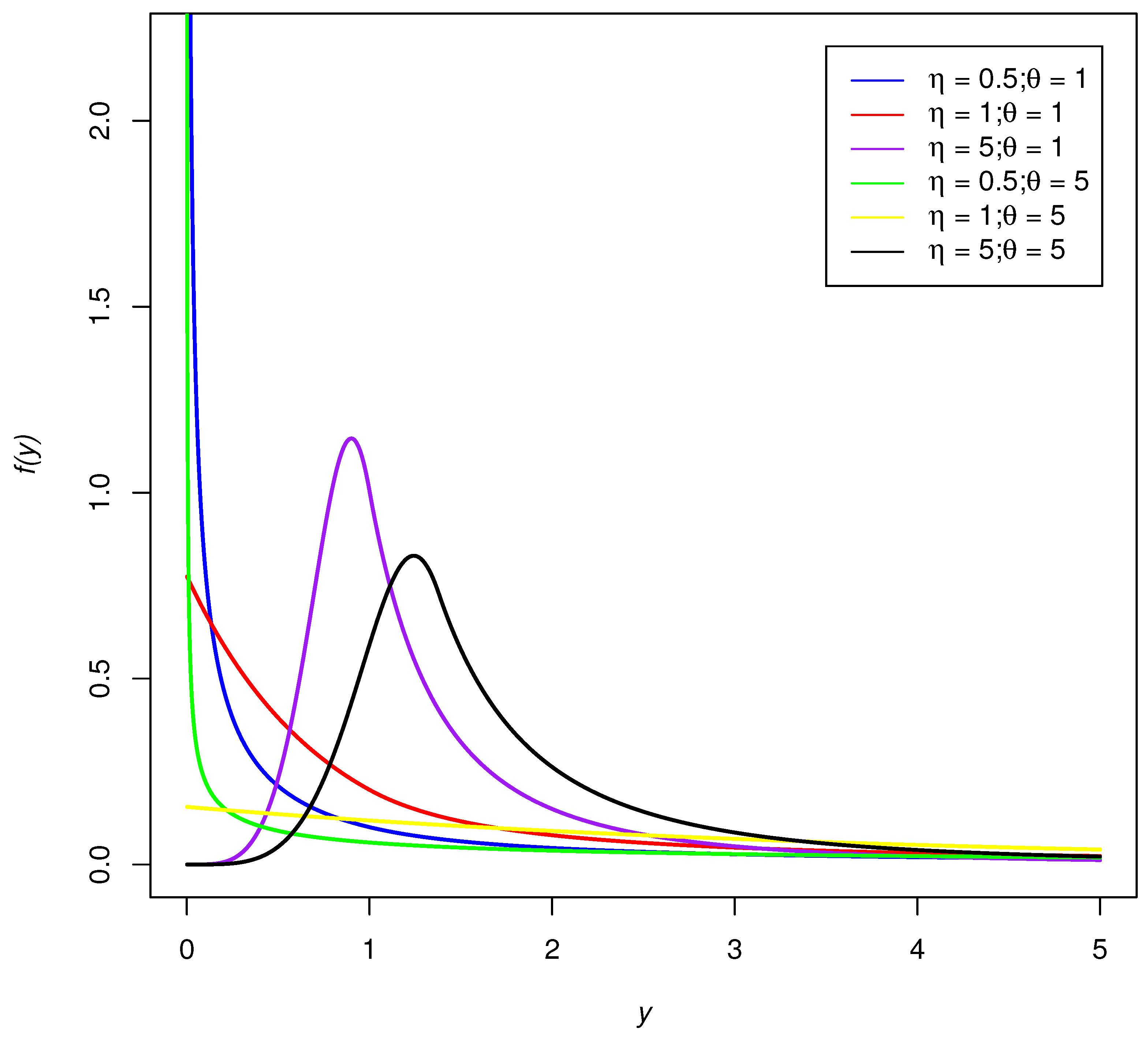
3. Special Model: Exponentiated Exponential-Pareto Distribution (EEP)
3.1. Mode
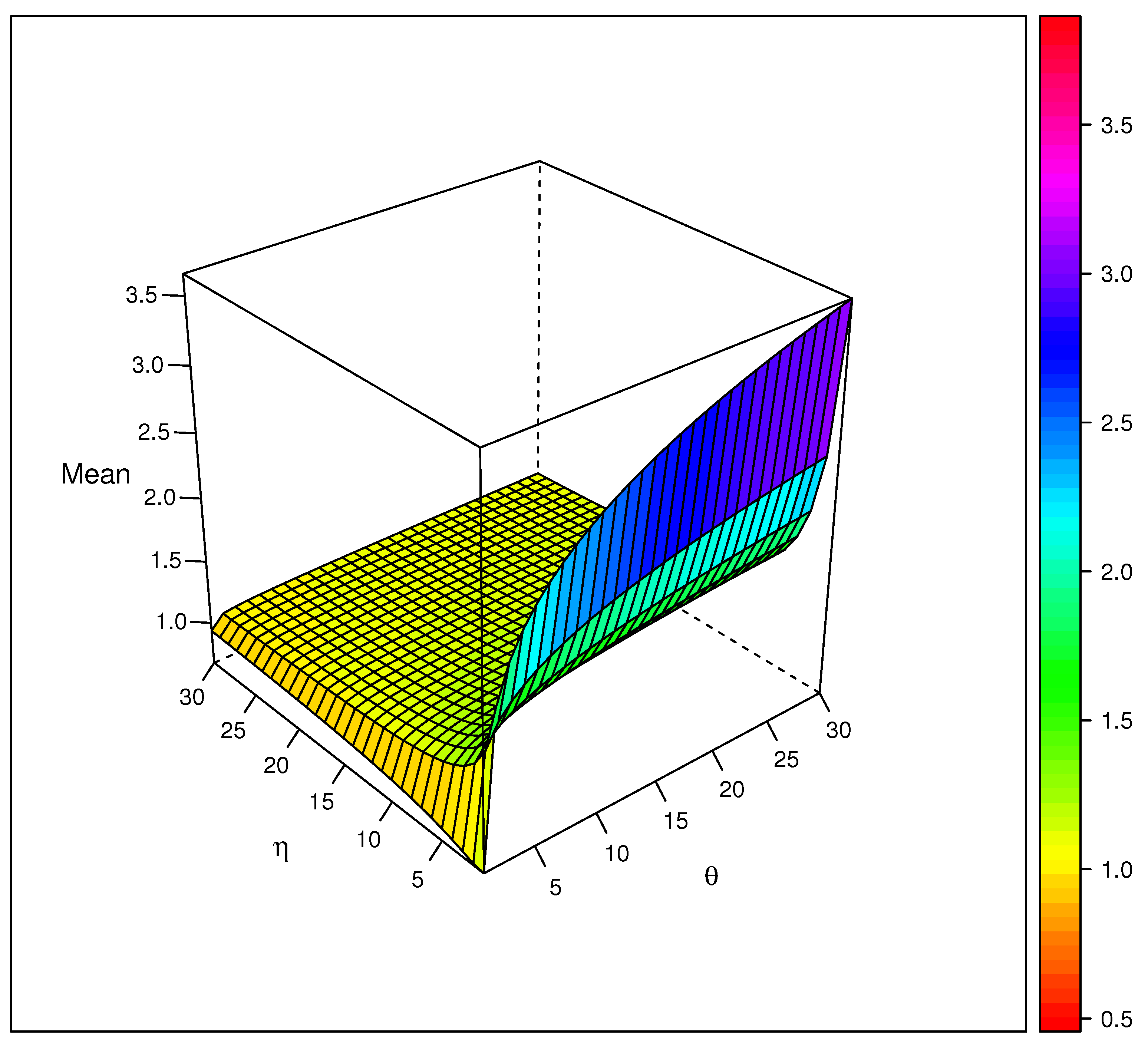
3.2. Moments
3.3. Survival Function and Tail Properties
3.4. Hazard Function
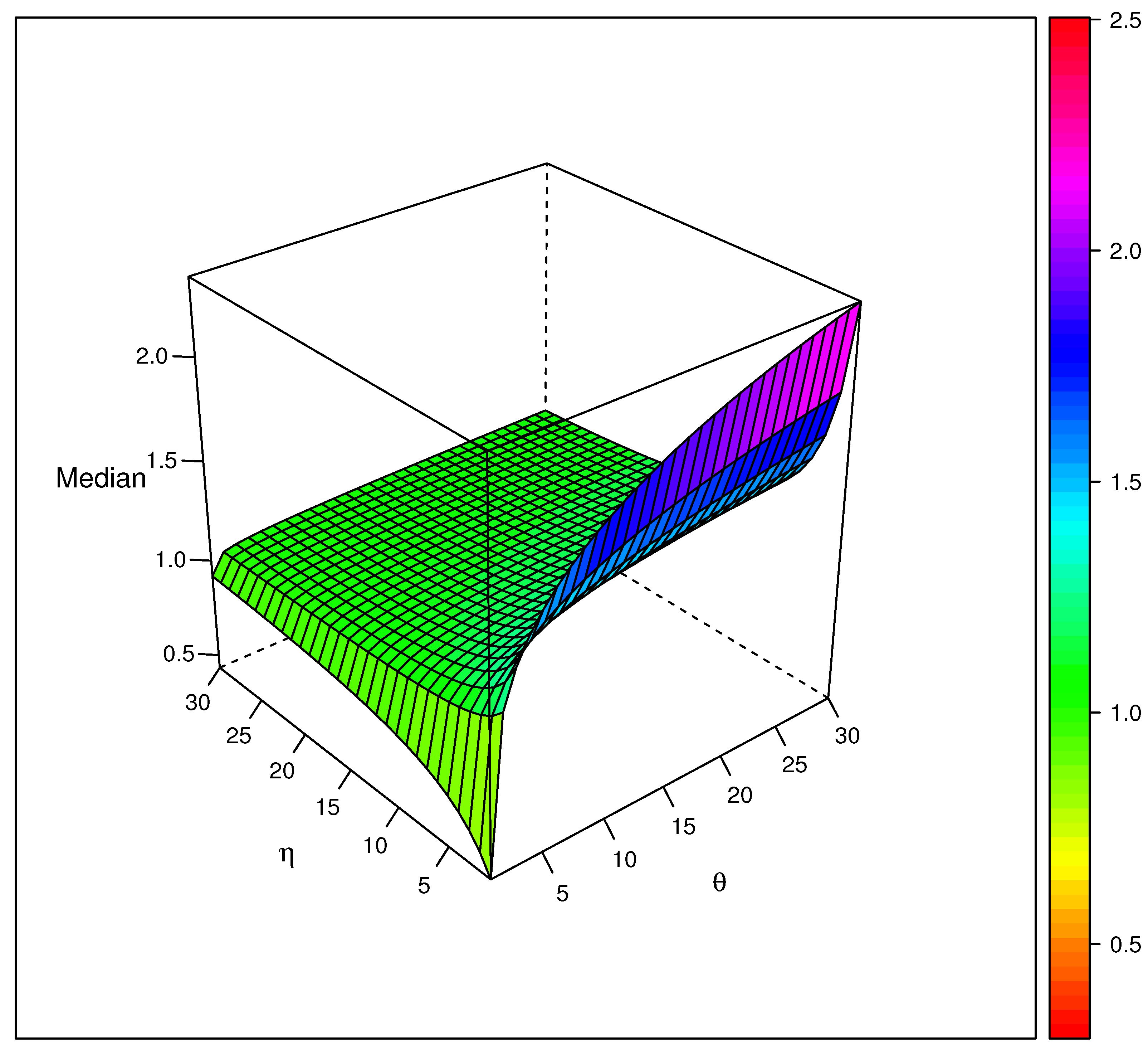
3.5. Quantile Function
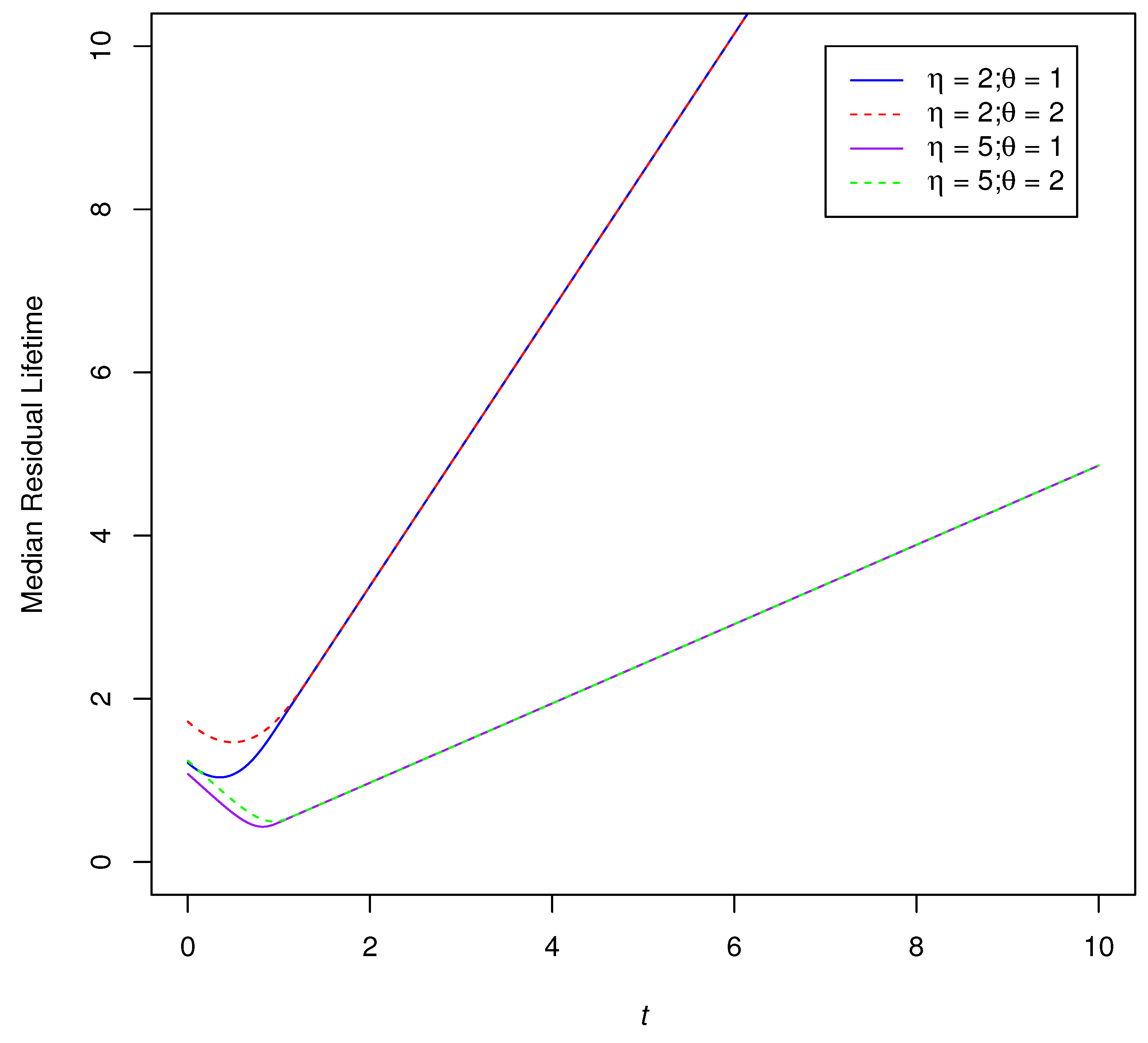
3.6. Median Residual Lifetime
4. Parameter Estimation
Parameter Search for Two-Parameter EEP Distributions
- Arrange the observations in the sample in increasing order such that .
- For , maximize the objective function and obtain … correspondingly.
- Start from , check the condition . If this is true, then and are the estimates for and . If not, go to the next step.
- For , check the condition . If this is true, then and are the estimates for and . Repeat this procedure until the correct m is detected. With the correct m, the corresponding and are the estimates for and .
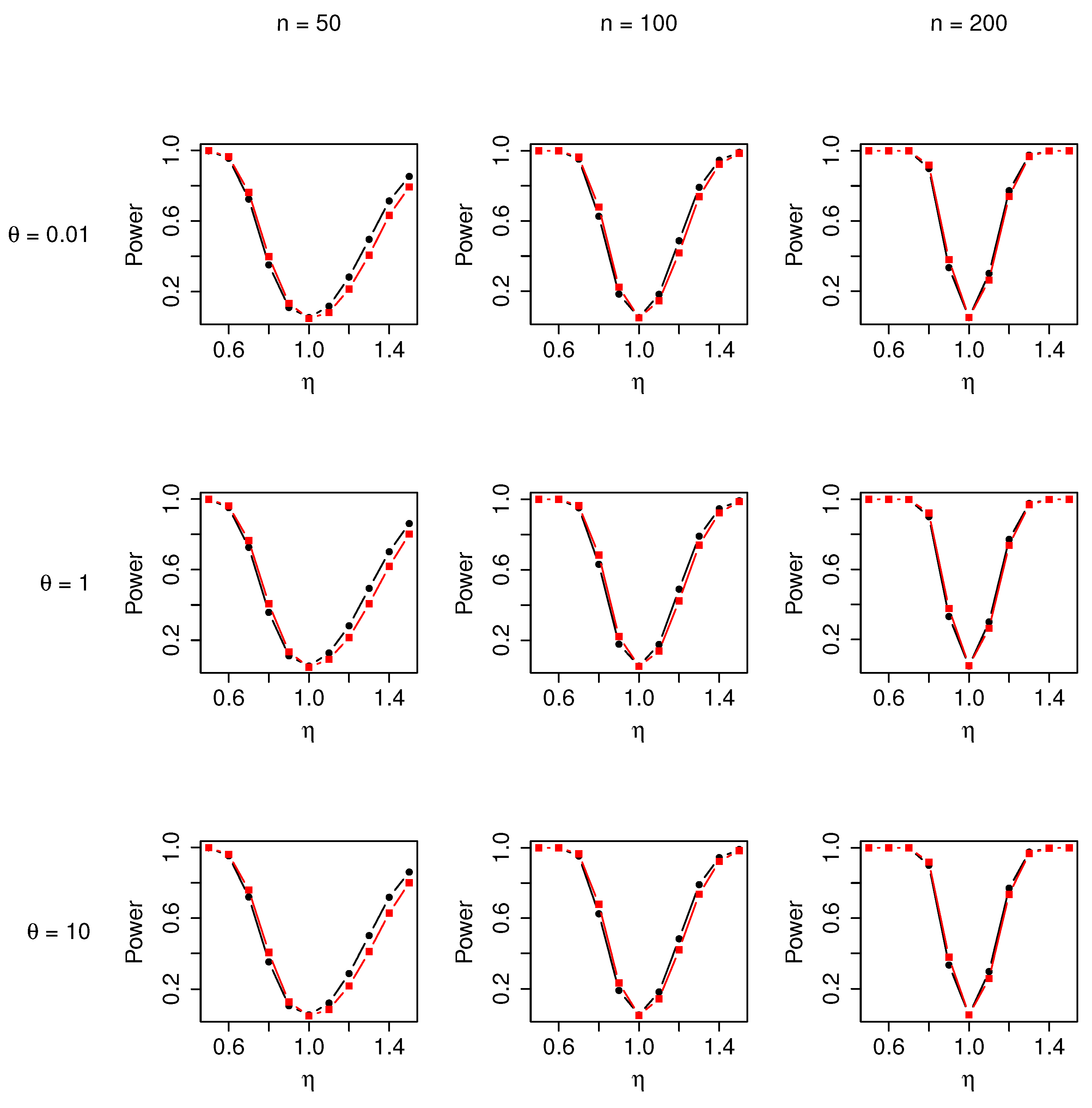
5. Goodness-of-Fit Tests with Simulation Studies
- Three different sample sizes: .
- Four different true values: .
- Eleven true values: .
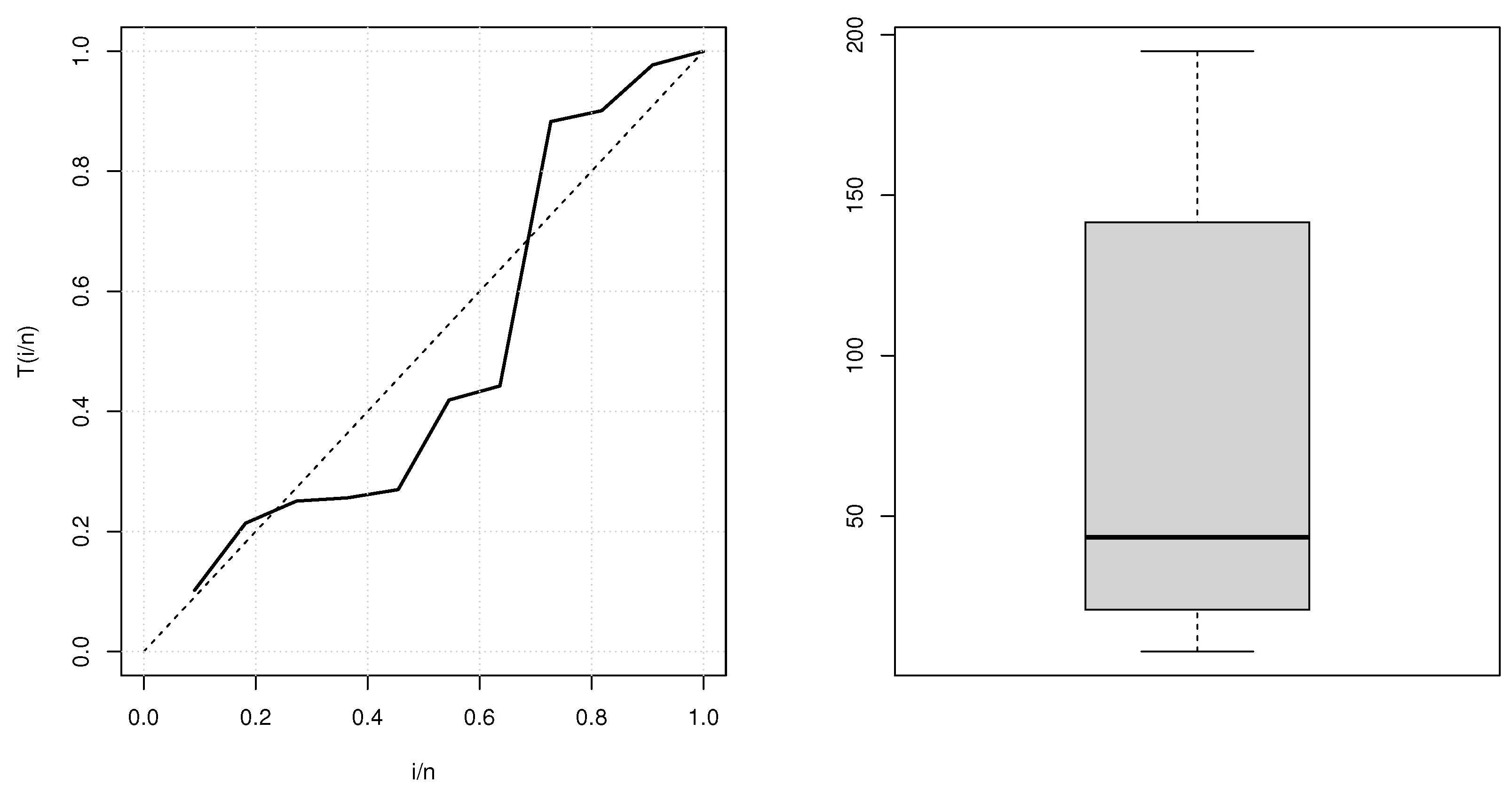
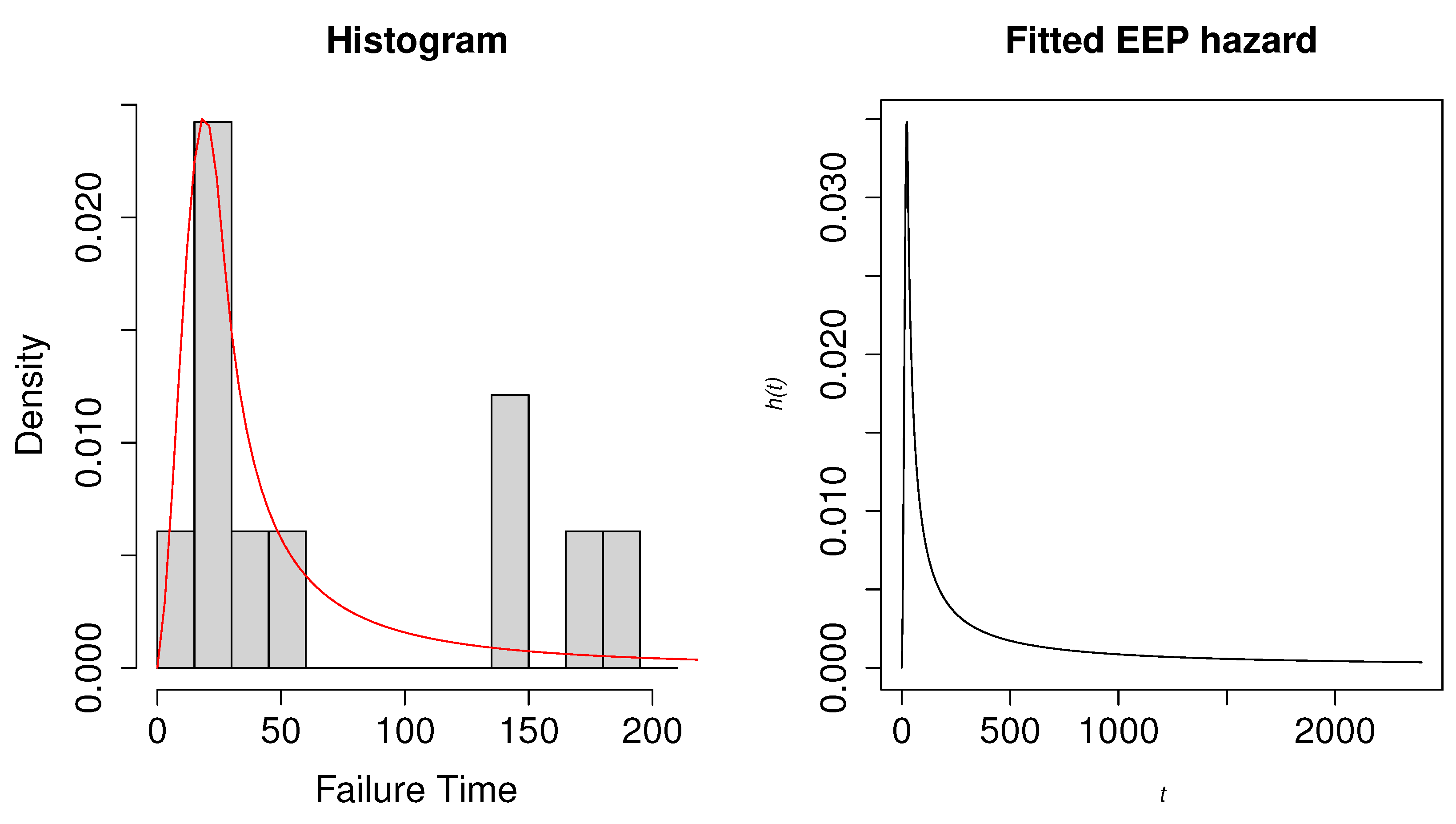
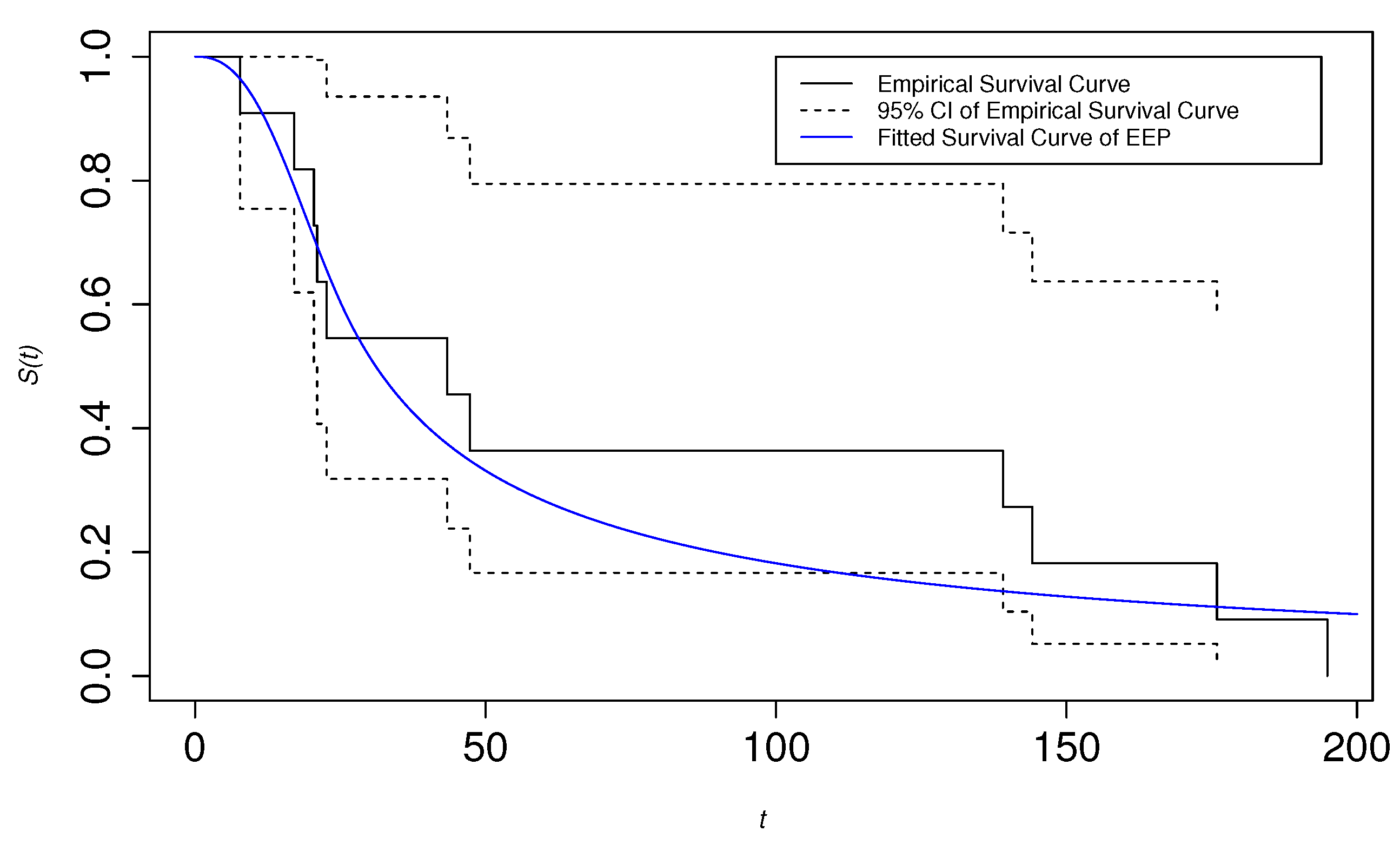
6. Application to Real Data
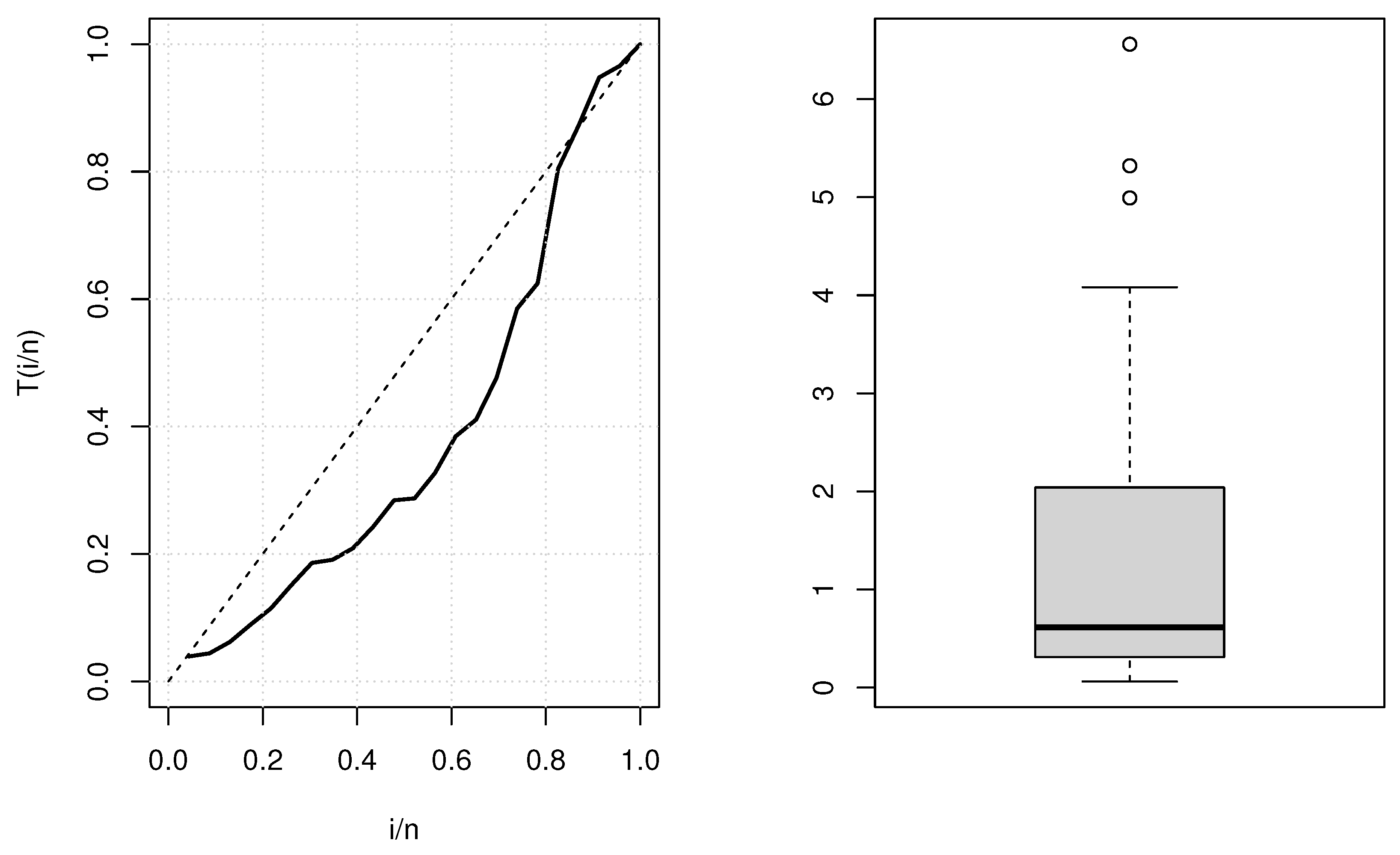
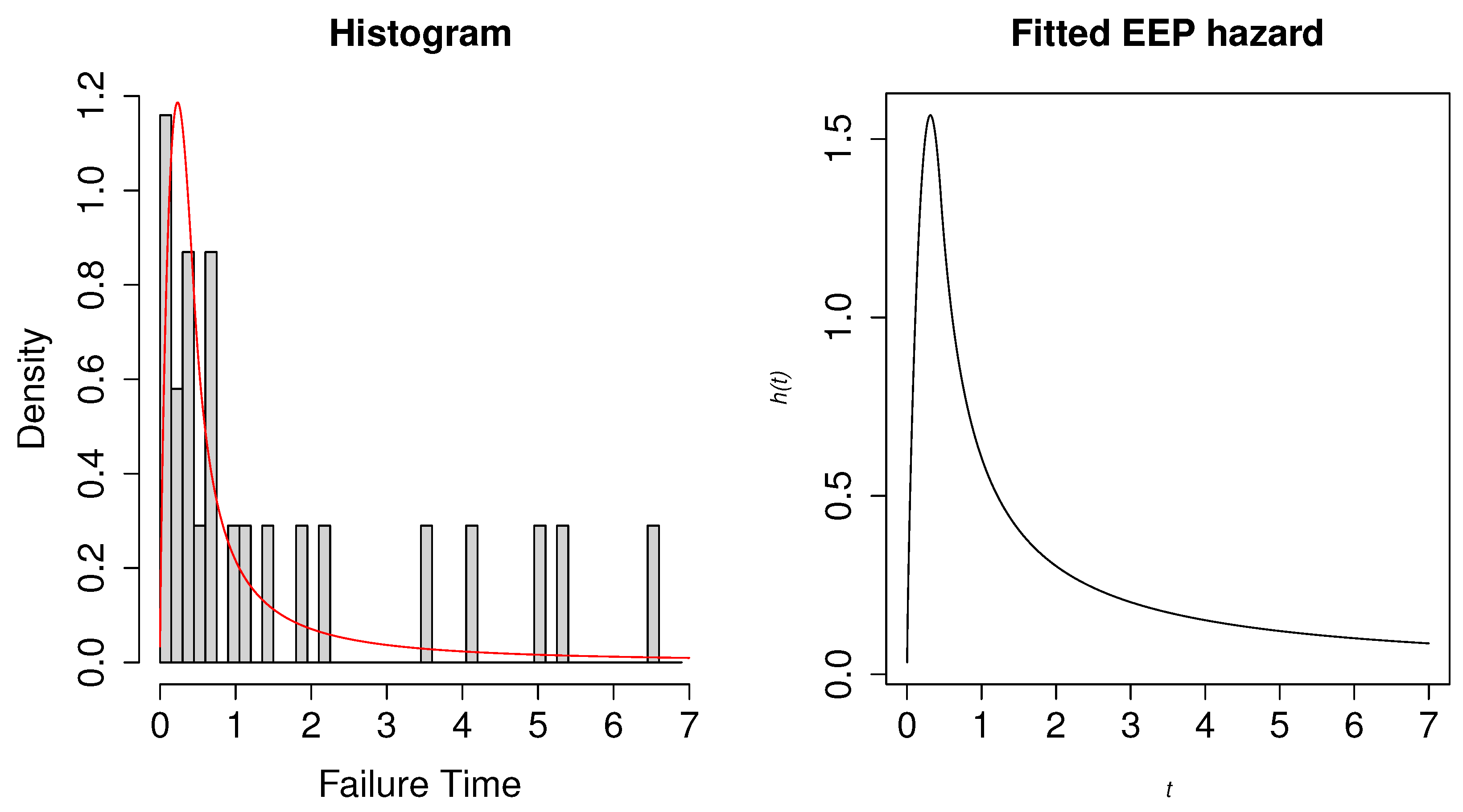
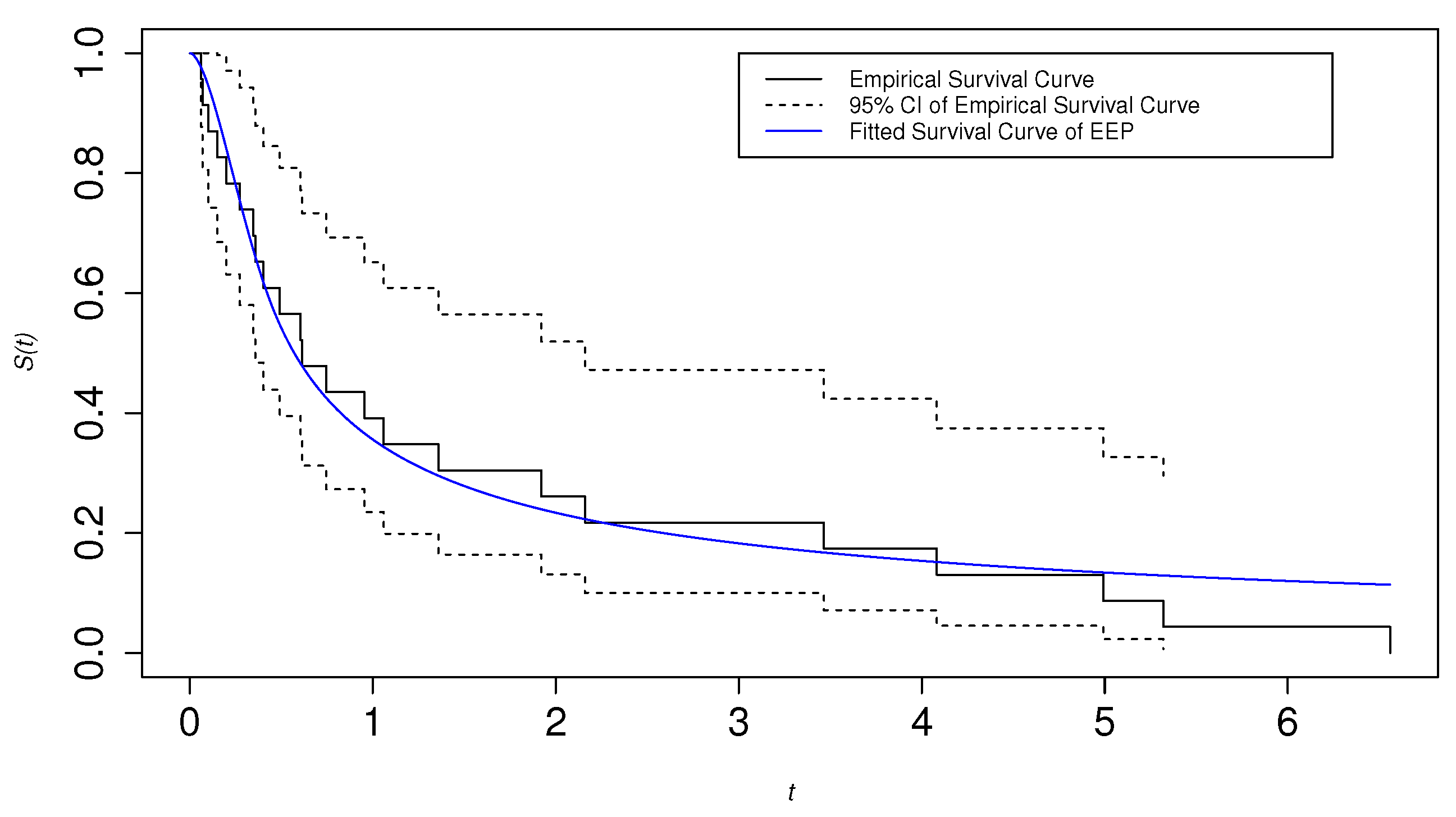
6.1. Second Reactor Pump Data
6.2. Electrical Breakdown of An Insulating Fluid
7. Concluding Remark and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UBT | Upside-down bathtub-shaped |
| GEC | Generalized exponentiated composite distributions |
| Probability density function | |
| CDF | Cumulative distribution function |
| EP | Exponential-Pareto distribution |
| EEP | Exponentiated exponential-Pareto distribution |
| LRT | Likelihood ratio test |
| MLE | Maximum likelihood estimates |
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| AICc | Corrected Akaike information criterion |
| cAIC | Consistent Akaike information criterion |
| KS | Kolmogorov–Smirnoff |
References
- Bennett, S. Log-Logistic Regression Models for Survival Data. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1983, 32, 165–171. [Google Scholar] [CrossRef]
- Prentice, R.L. Exponential Survivals with Censoring and Explanatory Variables. Biometrika 1973, 60, 279–288. [Google Scholar] [CrossRef]
- Prentice, R.L. Linear Rank Tests with Right Censored Data. Biometrika 1978, 65, 167–179. [Google Scholar] [CrossRef]
- Efron, B. Logistic Regression, Survival Analysis, and the Kaplan-Meier Curve. J. Am. Stat. Assoc. 1988, 83, 414–425. [Google Scholar] [CrossRef]
- Langlands, A.O.; Pocock, S.J.; Kerr, G.R.; Gore, S.M. Long-term survival of patients with breast cancer: A study of the curability of the disease. Br. Med. J. 1979, 2, 1247–1251. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.K.; Singh, S.K.; Singh, U. A new upside-down bathtub shaped hazard rate model for survival data analysis. Appl. Math. Comput. 2014, 239, 242–253. [Google Scholar] [CrossRef]
- de Gusmão, F.R.S.; Ortega, E.M.M.; Cordeiro, G.M. The generalized inverse Weibull distribution. Stat. Pap. 2011, 52, 591–619. [Google Scholar] [CrossRef]
- Khan, M.S.; King, R. A New Class of Transmuted Inverse Weibull Distribution for Reliability Analysis. Am. J. Math. Manag. Sci. 2014, 33, 261–286. [Google Scholar] [CrossRef]
- Domma, F.; Condino, F.; Popović, B.V. A new generalized weighted Weibull distribution with decreasing, increasing, upside-down bathtub, N-shape and M-shape hazard rate. J. Appl. Stat. 2017, 44, 2978–2993. [Google Scholar] [CrossRef]
- Sharma, V.K.; Singh, S.K.; Singh, U.; Agiwal, V. The inverse Lindley distribution: A stress-strength reliability model with application to head and neck cancer data. J. Ind. Prod. Eng. 2015, 32, 162–173. [Google Scholar] [CrossRef]
- Sharma, V.K.; Singh, S.K.; Singh, U.; Merovci, F. The generalized inverse Lindley distribution: A new inverse statistical model for the study of upside-down bathtub data. Commun. Stat. Theory Methods 2016, 45, 5709–5729. [Google Scholar] [CrossRef]
- Maurya, S.; Singh, S.; Singh, U. A New Right-Skewed Upside Down Bathtub Shaped Heavy-tailed Distribution and its Applications. J. Mod. Appl. Stat. Methods 2021, 19, eP2888. [Google Scholar] [CrossRef]
- Liu, B.; Ananda, M.M.A. Analyzing insurance data with an exponentiated composite Inverse-Gamma Pareto Model. Commun. Stat. Theory Methods 2022. [Google Scholar] [CrossRef]
- Liu, B.; Ananda, M.M.A. A Generalized Family of Exponentiated Composite Distributions. Mathematics 2022, 10, 1895. [Google Scholar] [CrossRef]
- Scollnik, D.P.M. On composite lognormal-Pareto models. Scand. Actuar. J. 2007, 2007, 20–33. [Google Scholar] [CrossRef]
- Cooray, K.; Ananda, M.M.A. Modeling actuarial data with a composite lognormal-Pareto model. Scand. Actuar. J. 2005. [Google Scholar] [CrossRef]
- Teodorescu, S.; Vernic, R. A composite Exponential-Pareto distribution. Ann. “Ovidius” Univ. Constanta Math. Ser. 2006, XIV, 99–108. [Google Scholar]
- Teodorescu, S.; Vernic, R. Some Composite ExponentialPareto Models for Actuarial Prediction. J. Econ. Forecast. 2009, 12, 82–100. [Google Scholar]
- Preda, V.; Ciumara, R. On Composite Models: Weibull-Pareto and Lognormal-Pareto. A comparative study. J. Econ. Forecast. 2006, 3, 32–46. [Google Scholar]
- Cooray, K. The Weibull–Pareto Composite Family with Applications to the Analysis of Unimodal Failure Rate Data. Commun. Stat. Theory Methods 2009, 38, 1901–1915. [Google Scholar] [CrossRef]
- Deng, M.; Aminzadeh, M.S. Bayesian predictive analysis for Weibull-Pareto composite model with an application to insurance data. Commun. Stat. Simul. Comput. 2022, 51, 2683–2709. [Google Scholar] [CrossRef]
- Aminzadeh, M.S.; Deng, M. Bayesian predictive modeling for Inverse Gamma-Pareto composite distribution. Commun. Stat. Theory Methods 2019, 48, 1938–1954. [Google Scholar] [CrossRef]
- Grün, B.; Miljkovic, T. Extending composite loss models using a general framework of advanced computational tools. Scand. Actuar. J. 2019, 2019, 642–660. [Google Scholar] [CrossRef]
- Nadarajah, S. Exponentiated Pareto distributions. Statistics 2005, 39, 255–260. [Google Scholar] [CrossRef]
- Sablica, L.; Hornik, K. mistr: A Computational Framework for Mixture and Composite Distributions. R J. 2020, 12, 283–299. [Google Scholar] [CrossRef]
- Shrahili, M.; Kayid, M. Modeling extreme value data with an upside down bathtub-shaped failure rate model. Open Phys. 2022, 20, 484–492. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bozdogan, H. Mixture-Model Cluster Analysis Using Model Selection Criteria and a New Informational Measure of Complexity. In Proceedings of the First US/Japan Conference on the Frontiers of Statistical Modeling: An Informational Approach: Volume 2 Multivariate Statistical Modeling; Bozdogan, H., Sclove, S.L., Gupta, A.K., Haughton, D., Kitagawa, G., Ozaki, T., Tanabe, K., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 69–113. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Bozdogan, H. Model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
- Suprawhardana, M.S.; Sangadji, P. Total Time on Test Plot Analysis for Mechanical Components of the Rsg-Gas Reactor. Atom Indones 1999, 25, 81–90. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A.; Pascual, F.G. Statistical Methods for Reliability Data; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]

| Sample Size (n) | LRT | Wald’s Test | |||
|---|---|---|---|---|---|
| 0.01 | 0.0110 | 0.0536 | 0.0107 | 0.0484 | |
| 0.0125 | 0.0496 | 0.0105 | 0.0477 | ||
| 0.0095 | 0.0499 | 0.0101 | 0.0503 | ||
| 0.1 | 0.0094 | 0.0514 | 0.0087 | 0.0443 | |
| 0.0108 | 0.0529 | 0.0104 | 0.0519 | ||
| 0.0112 | 0.0495 | 0.0113 | 0.0517 | ||
| 1 | 0.0116 | 0.0537 | 0.0111 | 0.0469 | |
| 0.0120 | 0.0542 | 0.0121 | 0.0523 | ||
| 0.0100 | 0.0484 | 0.0113 | 0.0508 | ||
| 10 | 0.0120 | 0.0544 | 0.0095 | 0.0490 | |
| 0.0104 | 0.0523 | 0.0103 | 0.0495 | ||
| 0.0121 | 0.0518 | 0.0127 | 0.0523 | ||
| 2.160, 0.150, 4.082, 0.746, 0.358, 0.199, 0.402, 0.101, 0.605, 0.954, |
| 1.359, 0.273, 0.491, 3.465, 0.070, 6.560, 1.060, 0.062, 4.992, 0.614, |
| 5.320, 0.347, 1.921 |
| Model | Estimates | LRT Statistic (p-Value) | Wald Statistic (p-Value) | KS Statistic (p-Value) |
|---|---|---|---|---|
| EEP | 6.32602 (0.01190) | 4.45271 (0.03485) | 0.13043 (0.9924) | |
| EP | - | - | 0.26087 (0.4218) |
| Model | p | AIC | AIC3 | AICc | CAIC |
|---|---|---|---|---|---|
| EEP | 2 | 72.29528 | 74.29528 | 72.89528 | 76.56627 |
| EP | 1 | 76.62130 | 77.62130 | 76.81178 | 78.75679 |
| Generalized Heavy-Tailed Pareto | 3 | 69.86288 | 72.86288 | 71.12604 | 76.26936 |
| Weighted Weibull–Pareto Composite | 4 | 69.71532 | 73.73368 | 71.95590 | 78.27566 |
| 7.74, 17.05, 20.46, 21.02 22.66, 43.40, |
| 47.30, 139.07 144.12, 175.88, 194.90 |
| Model | Estimates | LRT Statistic (p-Value) | Wald Statistic (p-Value) | KS Statistic (p-Value) |
|---|---|---|---|---|
| EEP | 4.08993 (0.04314) | 7.090596 (0.008) | 0.54545 (0.0758) | |
| EP | - | - | 0.90909 (0.0002254) |
| Model | p | AIC | AIC3 | AICc | CAIC |
|---|---|---|---|---|---|
| EEP | 2 | 121.6466 | 123.6466 | 123.1466 | 124.4424 |
| EP | 1 | 126.7372 | 127.7372 | 127.1816 | 128.1351 |
| Generalized Heavy-Tailed Pareto | 3 | 123.4848 | 125.2912 | 125.7197 | 126.4848 |
| Weighted Weibull–Pareto Composite | 4 | 125.2129 | 129.2129 | 131.8795 | 130.8045 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Ananda, M.M.A. A New Insight into Reliability Data Modeling with an Exponentiated Composite Exponential-Pareto Model. Appl. Sci. 2023, 13, 645. https://doi.org/10.3390/app13010645
Liu B, Ananda MMA. A New Insight into Reliability Data Modeling with an Exponentiated Composite Exponential-Pareto Model. Applied Sciences. 2023; 13(1):645. https://doi.org/10.3390/app13010645
Chicago/Turabian StyleLiu, Bowen, and Malwane M. A. Ananda. 2023. "A New Insight into Reliability Data Modeling with an Exponentiated Composite Exponential-Pareto Model" Applied Sciences 13, no. 1: 645. https://doi.org/10.3390/app13010645
APA StyleLiu, B., & Ananda, M. M. A. (2023). A New Insight into Reliability Data Modeling with an Exponentiated Composite Exponential-Pareto Model. Applied Sciences, 13(1), 645. https://doi.org/10.3390/app13010645






