Online SOPDT Model Identification Method Using a Relay
Abstract
1. Introduction
- (a)
- First-order inertia plus dead time (FOPDT);
- (b)
- An integrating model with time delay;
- (c)
- Second-order inertia plus dead time.
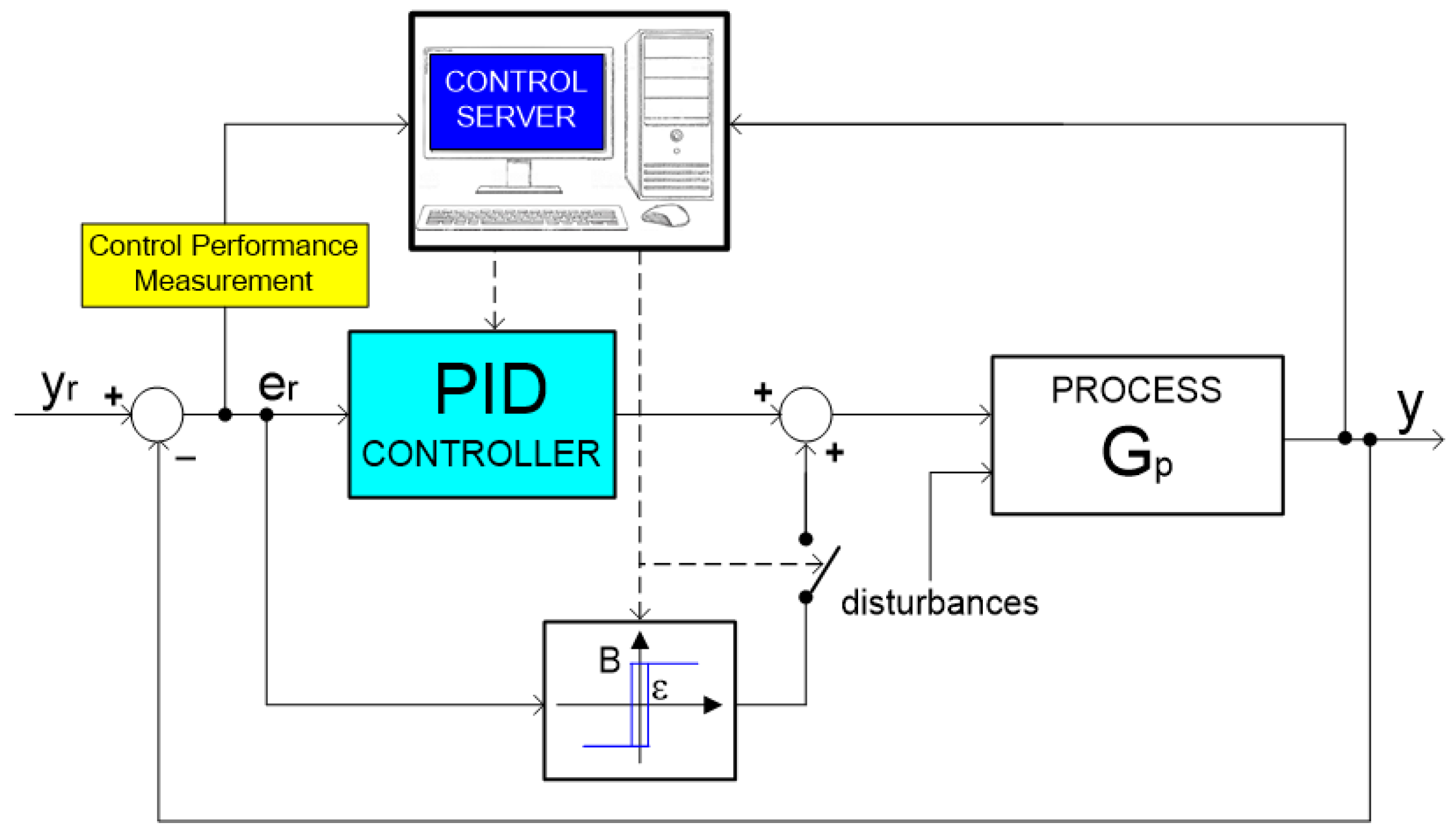
2. Description of the Method
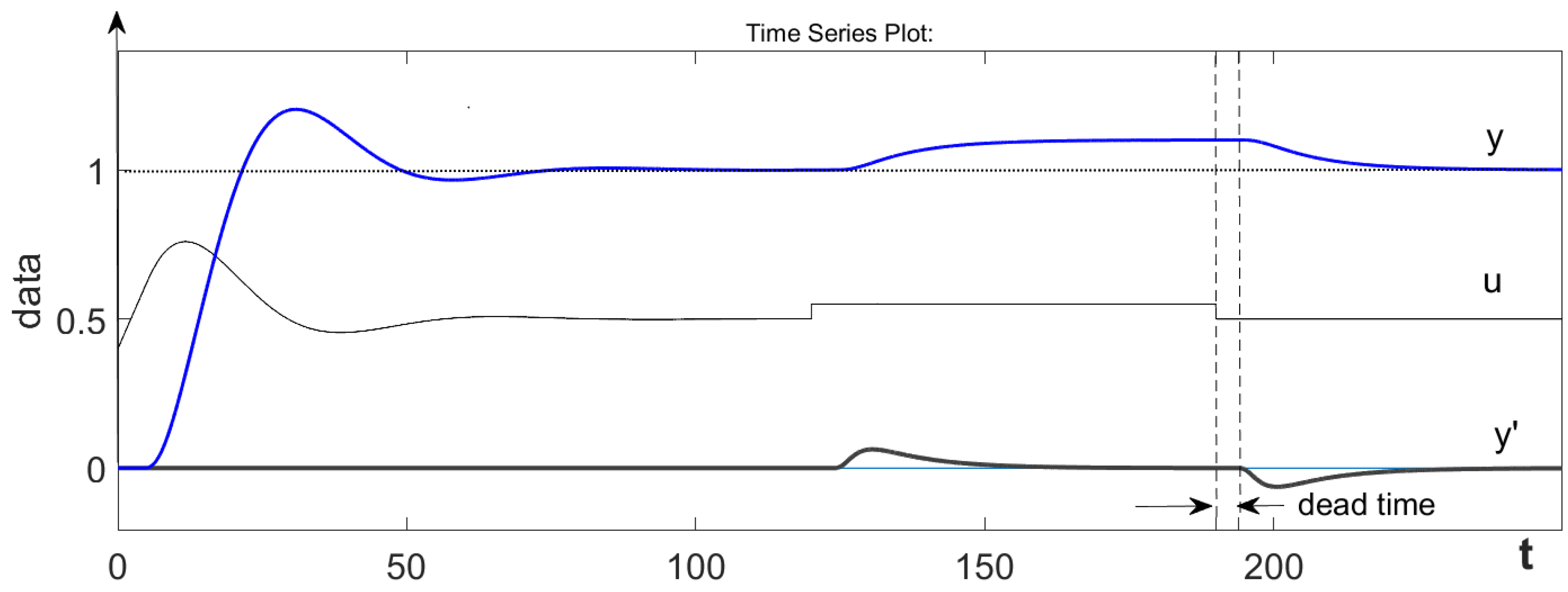
2.1. Identification Experiment
2.2. Determination of the Steady-State Gain
2.3. Measurement of the Time-Delay Constant
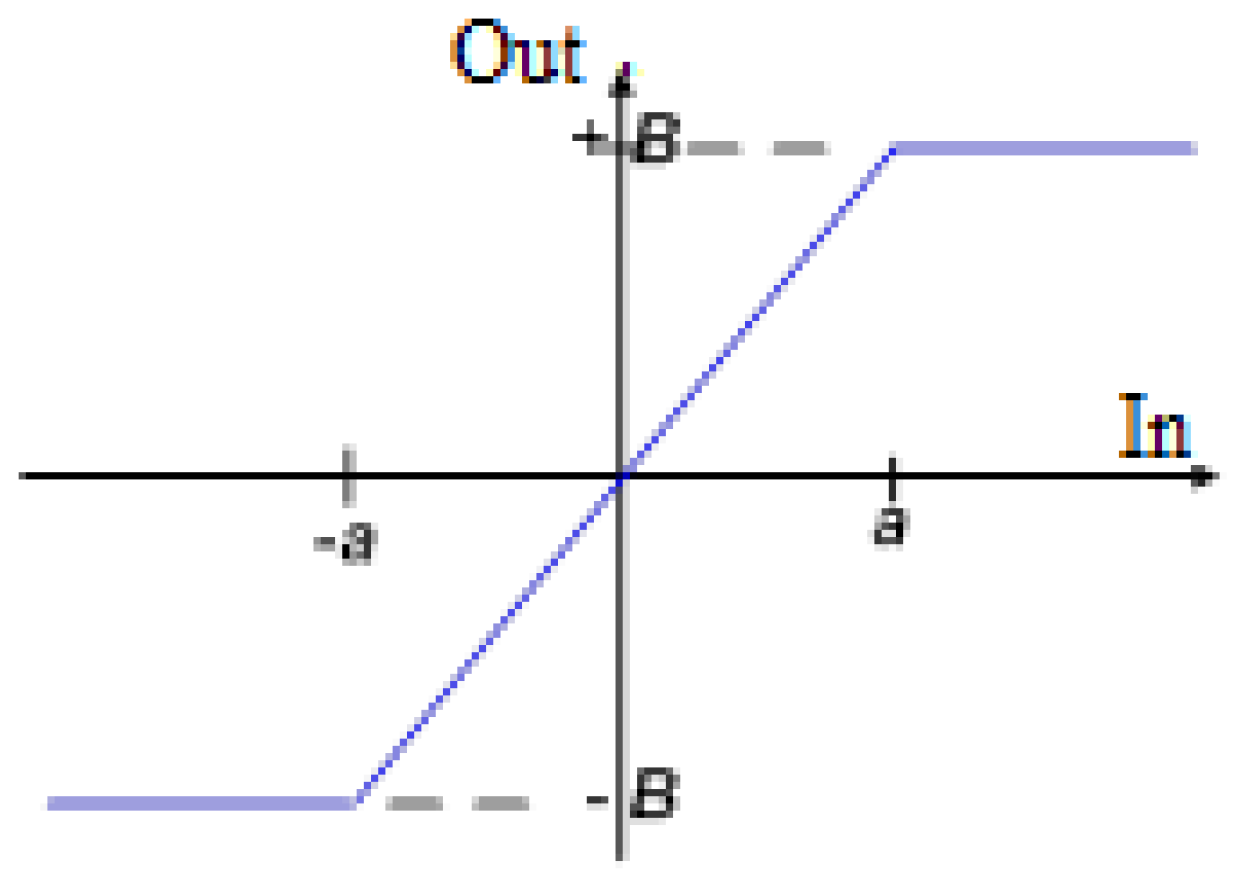
2.4. Determination of Limit Cycle Parameters
2.5. Calculation of the Time Constants
3. Simulation Results and Discussion
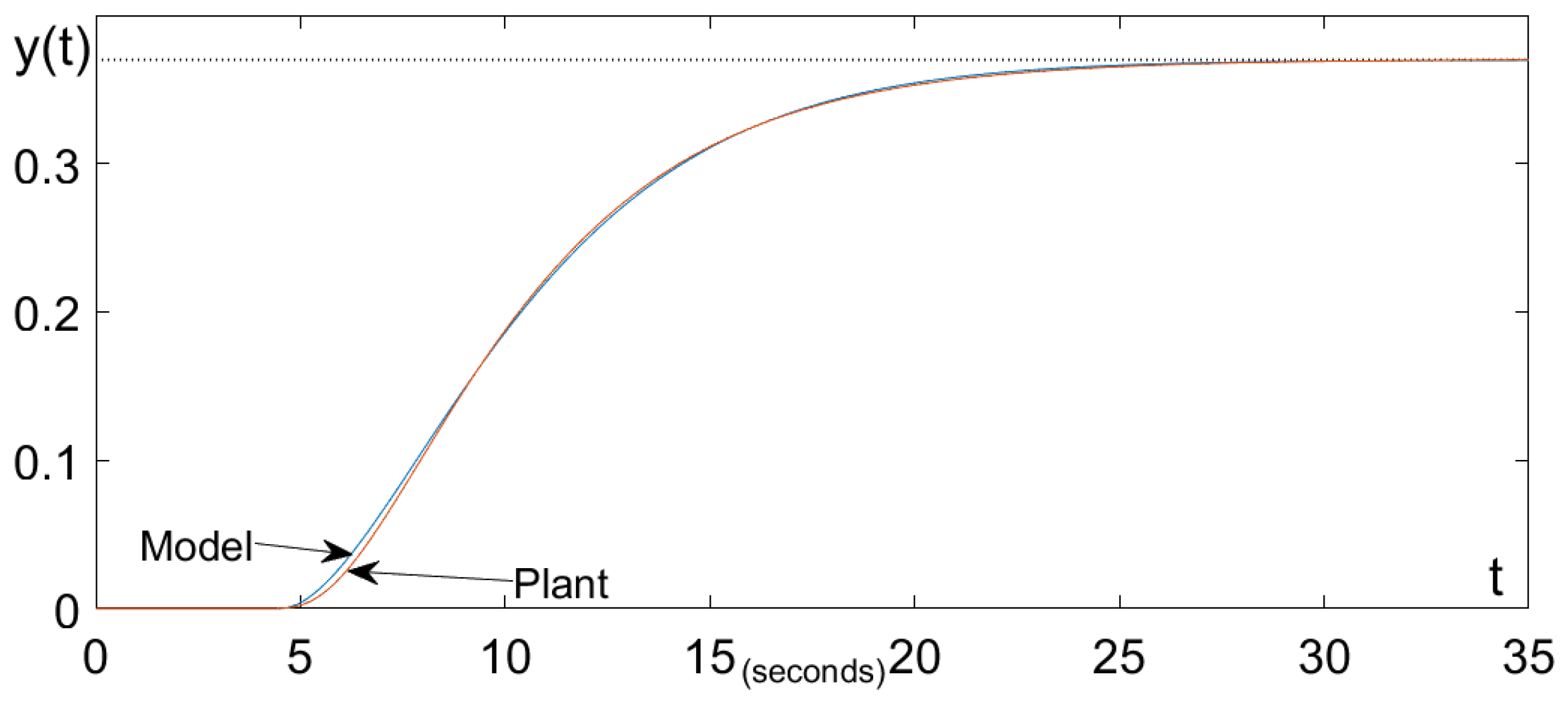
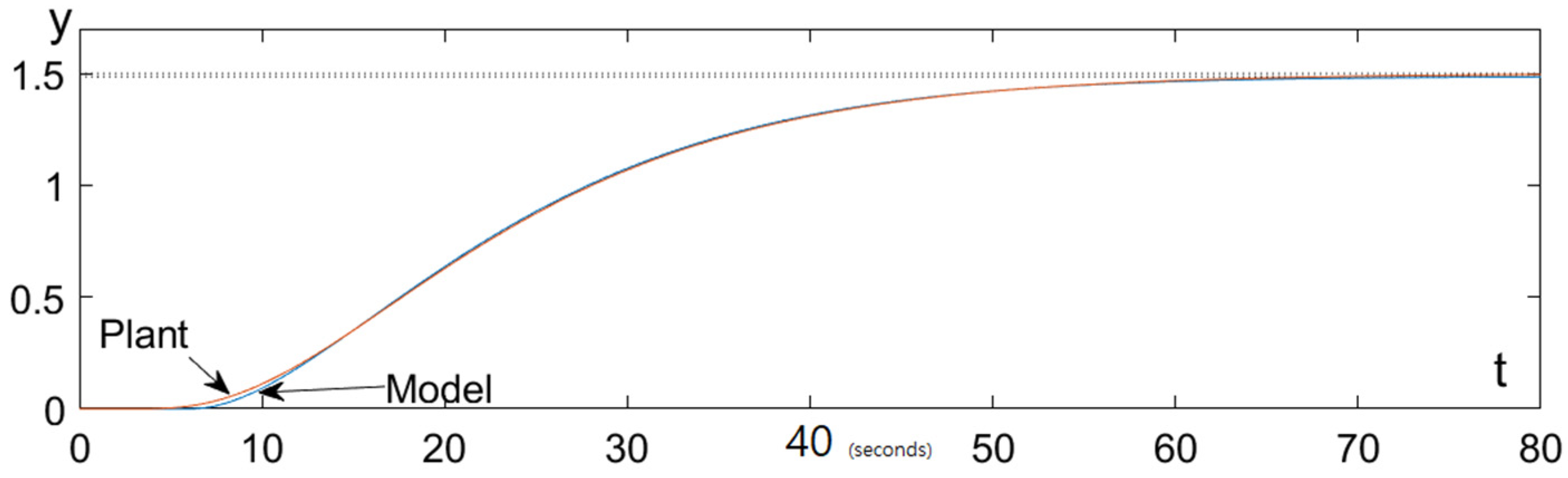
3.1. Identification of the Second-Order Time-Delayed Plant
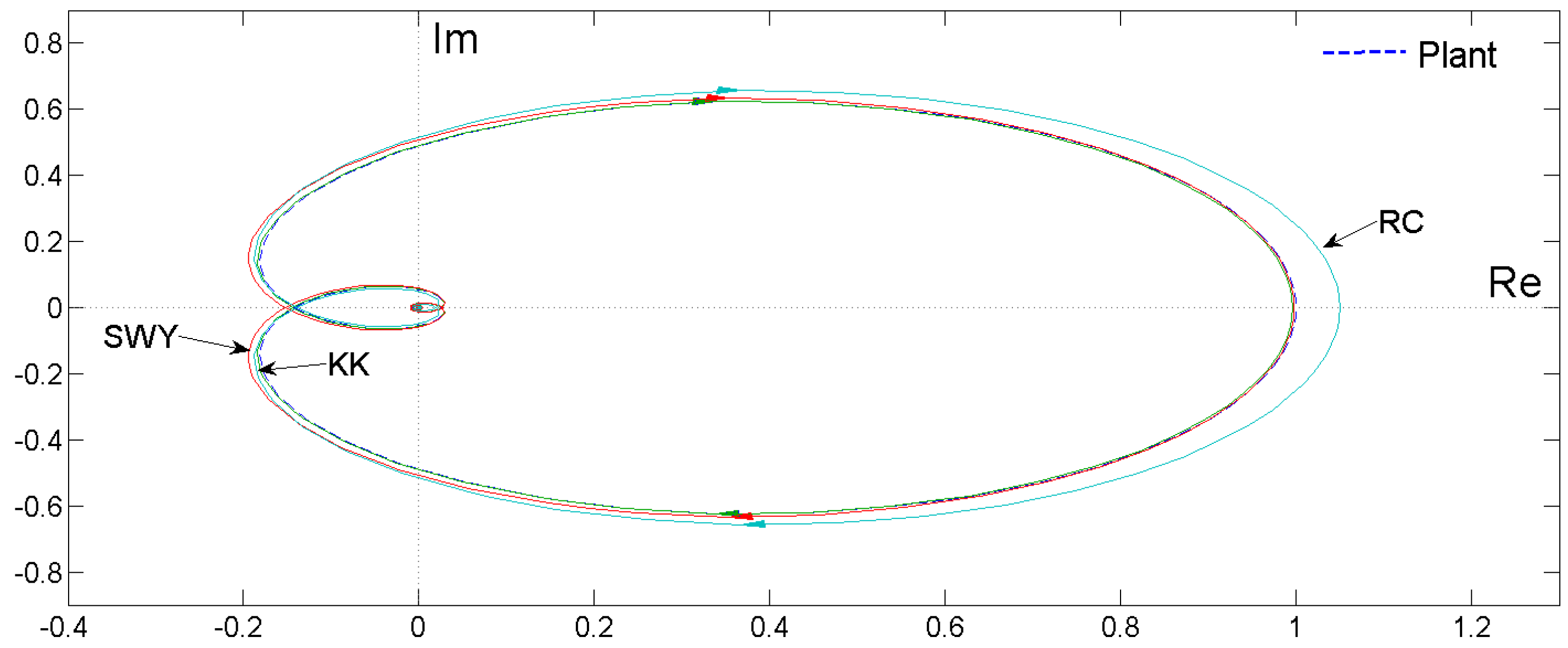
3.2. Comparision with Other Methods
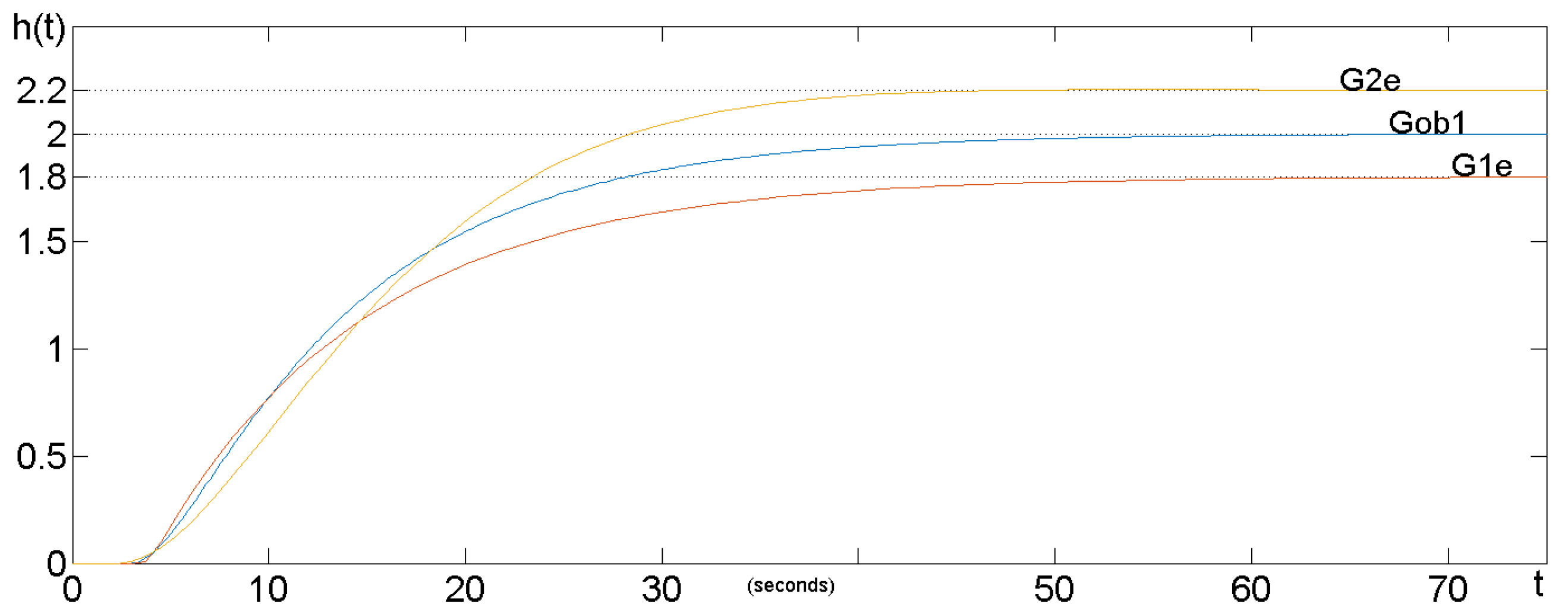
3.3. Robustness
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sato, T.; Hayashi, I.; Horibe, Y.; Vilanova, R.; Konishi, Y. Optimal Robust PID Control for First- and Second-Order Plus Dead-Time Processes. Appl. Sci. 2019, 9, 1934. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Q.-G.; Huang, H.-P. A tutorial review on process identification from step or relay feedback test. J. Process Control 2013, 23, 1597–1623. [Google Scholar] [CrossRef]
- Åstrom, K.J.; Hågglund, T. Automatic tuning of simple regulators with specifications on phase and amplitude margins. Automatica 1984, 20, 645–651. [Google Scholar] [CrossRef]
- Srinivasan, K.; Chidambaram, M. Modified relay feedback method for improved system identification. Comput. Chem. Eng. 2003, 27, 727–732. [Google Scholar] [CrossRef]
- Majhi, S. Relay based identification of process with time delay. J. Process Control 2007, 17, 93–100. [Google Scholar] [CrossRef]
- Wang, Q.-G.; Zhang, Y. Robust identification of continuous systems with dead-time from step responses. Automatica 2001, 37, 377–390. [Google Scholar] [CrossRef]
- Shin, G.W.; Song, Y.J.; Lee, T.B.; Choi, H.K. 2007. Genetic algorithm for identification of time-delay systems from step responses. Int. J. Control. Autom. Syst. 2007, 5, 79–85. [Google Scholar]
- Hofreiter, M.; Hornachova, A. Process Identification Using Relay Shifting Method for Auto Tuning of PID Controller. MATEC Web Conf. 2019, 292, 01015. [Google Scholar] [CrossRef][Green Version]
- Bajarangbali, R.; Majhi, S.; Pandey, S. Identification of FOPDT and SOPDT Process Dynamics Using Closed Loop Test. ISA Trans. 2014, 53, 1223–1231. [Google Scholar] [CrossRef]
- Pandey, S.; Majhi, S. Limit cycle based identification of second order processes with time delay. In 2016 Indian Control Conference (ICC); IIT: Hyderabad, India, 2016; Volume 2, pp. 438–773. [Google Scholar]
- Majhi, S.; Atherton, D.P. Autotuning and controller design for processes with small time delays. IEE Proc. Control Theory Appl. 1999, 146, 415–424. [Google Scholar] [CrossRef]
- Atherton, D.P.; Majhi, S. Plant parameter identification under relay control. In Proceedings of the 37th IEEE Conference on Decision and Control, Tampa, FL, USA, 18 December 1998; pp. 1272–1277. [Google Scholar]
- Ramakrishnan, V.; Chidambaram, M. Estimation of a SOPTD transfer function model using a single asymmetrical relay feedback test. Comput. Chem. Eng. 2003, 27, 1779–1784. [Google Scholar] [CrossRef]
- Wang, Q.G.; Hang, C.C.; Bi, Q. Process frequency response estimation from relay feedback. Control. Eng. Pract. 1997, 5, 1293–1302. [Google Scholar] [CrossRef]
- Wang, Q.G.; Zhang, Y.; Guo, X. Robust closed-loop identification with application to auto-tuning. J. Process Control. 2001, 11, 519–530. [Google Scholar] [CrossRef]
- Kaya, I.; Atherton, D.P. Parameter estimation from relay autotuning with asymmetric limit cycle data. J. Process Control 2001, 11, 429–439. [Google Scholar] [CrossRef]
- Li, W.; Eskinat, E.; Luyben, W.L. An improved autotune identification method. Ind. Eng. Chem. Res. 1991, 30, 1530–1541. [Google Scholar] [CrossRef]
- Sanchez, J.; Guinado, M.; Dormido, S.; Visioli, A. An Improved Relay-based Identification Approach based on Asymmetric Oscillations. IFAC PapersOnLine 2018, 51, 468–473. [Google Scholar] [CrossRef]
- Kasi, V.R.; Majhi, S.; Gogoi, A.K. Identification and PID tuning techniques for stable and unstable SOPDT processes. Int. J. Dynam. Control 2018, 6, 1194–1206. [Google Scholar] [CrossRef]
- Ghorai, P.; Majhi, S.; Pandey, S. 2018. A real-time approach for dead-time plant transfer function modelling based on relay autotuning. Int. J. Dyn. Control 2018, 6, 950–960. [Google Scholar] [CrossRef]
- dos Santos, J.B.M.; Barros, P.R. 2010. A Simple Identification Technique for Second-Order plus Time-Delay Systems. IFAC Proc. Vol. 2010, 43, 188–193. [Google Scholar] [CrossRef]
- Shen, S.H.; Yu, H.D.; Yu, C.C. Use of Saturation-Relay Feedback for Autotune Identification. Chem. Eng. Sci. 1996, 51, 1187–1198. [Google Scholar] [CrossRef]
- Hang, C.C.; Åstrom, K.J.; Wang, Q.G. Relay feedback auto-tuning of process controllers—A tutorial review. J. Process Control 2002, 12, 143–162. [Google Scholar] [CrossRef]
- Prokop, R.; Korbel, J.; Matušú, R. 2005. Relay-based autotuning: A second order algebraic design. In IEEE International Workshop on Intelligent Signal Processing; Faro; IEEE International Workshop on Intelligent Signal Processing: Piscataway, NJ, USA, 2005; pp. 98–103. [Google Scholar] [CrossRef]
- Padmasree, R.; Chidambaram, M. Identification of transfer function model for unstable system with a zero. In Proceedings of the International Conference on Control, Instrumentation and Information Communication, Kolkata, India, 13 December 2001; pp. 37–40. [Google Scholar]
- Shen, S.H.; Wu, J.S.; Yu, C.C. Use of biased-relay feedback for system identification. AIChe J. 1996, 42, 1174–1180. [Google Scholar] [CrossRef]
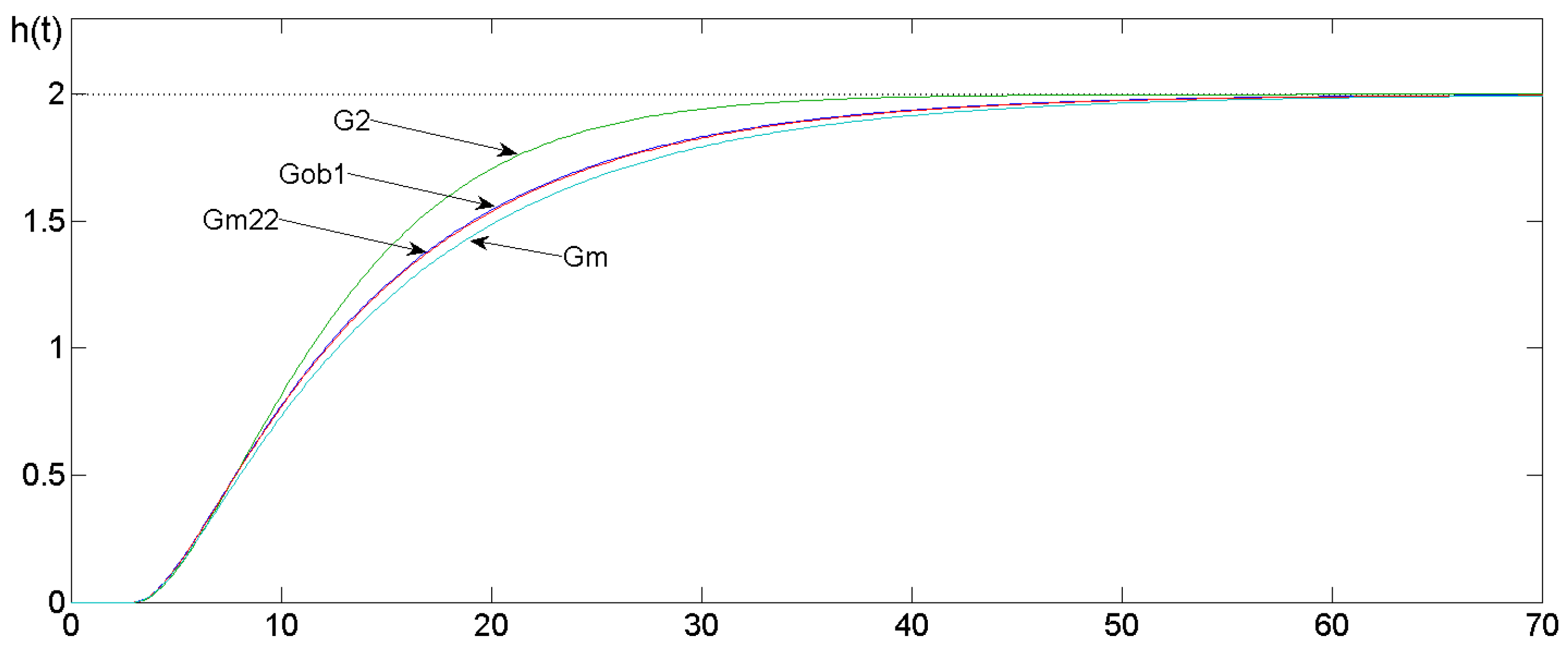
| Km | θ | T1 | T2 | I | |
|---|---|---|---|---|---|
| Plant | 1 | 2 | 1 | 10 | 0 |
| Ramakrishnan and Chidambaram | 1.05 | 1.814 | 1.217 | 9.766 | 0.4603 |
| Li, Eskinat, and Luyben | 0.853 | 2.0 | 1.15 | 7.416 | 1.122 |
| Bajarangbali, Majhi, and Pandey | 0.9923 | 2.0 | 1.0105 | 9.899 | 0.05974 |
| Shen, Wu, and Yu | 0.998 | 2.0 | 1.044 | 9.14 | 0.07201 |
| Presented method | 0.996 | 2.01 | 0.992 | 9.775 | 0.03274 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kula, K.S. Online SOPDT Model Identification Method Using a Relay. Appl. Sci. 2023, 13, 632. https://doi.org/10.3390/app13010632
Kula KS. Online SOPDT Model Identification Method Using a Relay. Applied Sciences. 2023; 13(1):632. https://doi.org/10.3390/app13010632
Chicago/Turabian StyleKula, Krzysztof S. 2023. "Online SOPDT Model Identification Method Using a Relay" Applied Sciences 13, no. 1: 632. https://doi.org/10.3390/app13010632
APA StyleKula, K. S. (2023). Online SOPDT Model Identification Method Using a Relay. Applied Sciences, 13(1), 632. https://doi.org/10.3390/app13010632






