Abstract
Microwave ablation, as an emerging method for treating lung cancer, has been widely used because of its advantages, such as being less invasive and having fewer side effects compared with other therapies, such as surgery and chemotherapy. The key to microwave ablation is to destroy the tumor tissue while minimizing the damage caused to the surrounding healthy tissues. Based on the heat transfer model of porous media, a two-dimensional simulation model of a spherical tumor surrounded by healthy tissue is established in this paper. The effects of tumor diameter, tumor porosity, and microwave ablation power on the highest temperature, ablation area, and volume of the tumor tissue were studied by using the software COMOSL Multiphysics. The results show that the porous heat transfer model is more practical than the Pennes biological heat transfer model. The tumor diameter and the tumor porosity have a great influence on the maximum temperature, the ablation area and volume. In this study, a more realistic model of microwave ablation of lung tumors was established, and the ablation results were predicted accurately, which provided the basic reference data for the selection of clinical therapeutic parameters of microwave ablation of lung tumors. To a certain extent, it can ensure that the ablation area completely covers the tumor and reduces the risk of tumor recurrence, which is of great significance in the accurate treatment of pulmonary tumors by microwave ablation.
1. Introduction
Cancer is considered to be one of the leading causes of death, hindering the possibility of a global increase in life expectancy [1]. Lung cancer is a malignant tumor with the highest morbidity and mortality rate in the world, which seriously threatens the life and health of human beings [2]. At present, microwave ablation is widely used as an emerging treatment method for parenchymal tumors of the liver, kidney, lung, thyroid, etc., which has the advantages of less trauma, precise positioning, and rapid and efficient inactivation of tumor cells compared with surgery and chemotherapy [3,4]. The principle of microwave ablation is to insert the microwave antenna into the tumor under the guidance of CT or MRI [5]. The microwave antenna focuses the microwave energy on the tumor, and the tumor tissue will reach a high temperature of 60 °C–150 °C in a short time, enabling a complete necrosis to achieve the goal of treatment of tumors [6,7]. The key to microwave ablation is to destroy the tumor tissue while minimizing the damage caused to the surrounding healthy tissues. More importantly, tumor and normal tissue properties differ greatly, which may have an impact on therapeutic ablation. In this case, a biological heat transfer model close to the clinical effect was constructed for microwave ablation to evaluate the influence of tumor and normal tissue heterogeneity on the efficacy and analyze the temperature distribution and thermal injury volume. It is very important to predict the final ablation area and volume according to the tumor size, which is beneficial to the accurate treatment of microwave ablation of lung tumors.
For this reason, various biological heat transfer models have been developed over the years, starting with the Pennes equation. Pennes biological heat transfer equation is the simplest biological heat equation and is widely used for modeling heat transfer in biological tissues during thermotherapy [8]. However, the Pennes heat transfer equation has the disadvantage of neglecting the direction of blood flow and the reverse flow arrangement of the arteries and veins. This equation assumes thermal equilibrium between venous blood and tissue and assumes a constant arterial temperature of 37 °C [9,10]. This is unrealistic in thermal ablation. Biological tissues are complex structures composed of cells of different sizes and microvascular beds. According to the porous medium theory, it can be divided into different phases coexisting in the same domain, namely the “tissue phase” and the “blood phase”. The former consists of cells and intercellular spaces, while the latter represents the vasculature that permeates the entire tissue [11,12]. During microwave ablation, the more blood vessels there are, the more heat is carried away by blood flow [13]. Therefore, the higher the degree of vascularization of biological tissues, the more it is necessary to use them as porous media in the model, for example, for the liver and lung [14]. At the same time, the heat transfer model using a porous media theory is established with fewer assumptions, so the porous theory is gradually applied to the biological heat transfer model, and a porous media heat transfer model is established. Alzahrani et al. [15] used the eigenvalue technique to study the effects of weak, normal, and strong thermal conductivity on displacement, temperature, stress, and volume fraction fields in two-dimensional porous media. Su et al. [16] established a theoretical model of porous media in an intermittent microwave heating process and considered the changes in electromagnetic energy, phase transition, and large deformation. Chaichanyut et al. [17] developed the porous liver model, including a solid tumor, based on the porous medium model and the generalized two-phase lag (DPL) model. Zhang et al. [18] analyzed the thermoelastic response of skin tissue during laser irradiation. However, few studies have considered the lung as a porous medium and investigated whether differences in lung tumors have an impact on the results of microwave ablation.
There is a lack of basic reference data for microwave ablation of lung tumors, and the selection of treatment parameters (ablation time and power) that are only based on experience is prone to inadequate or excessive ablation. Therefore, it is necessary to establish a model which is closer to the actual situation of lung tissue, and the results of this model can provide help for obtaining more accurate ablation parameters.
In this study, microwave ablation of a spherical tumor surrounded by healthy lung tissue was simulated, and heat transfer in porous media was modeled, based on the local thermal equilibrium equation. The maximum temperature obtained by Pennes heat transfer equation and the porous medium heat transfer equation are compared. At the same time, the effects of different tumor diameters, different tumor porosities, and different microwave ablation powers on the therapeutic effect of microwave ablation of lung tumors were analyzed from three aspects: the highest temperature of the tissue, the volume of ablation, and the size of the ablation area. The final ablation area and volume can be predicted more accurately by using the porous heat transfer model, and thus the ablation parameters can be determined, which is beneficial to the accurate treatment of microwave ablation of lung tumors.
2. Materials and Methods
In this section, the heat transfer of porous lung tissue during microwave ablation is analyzed by using the finite element method coupled with the heat transfer equation, the electromagnetic equation, and the transient momentum equation. Related geometric models and equations are described in the following sections.
2.1. Model Geometry
The geometry of the model is shown in Figure 1a. It consists of ideal cylindrical lung tissue with a radius of 30 mm and a height of 80 mm, which includes a spherical tumor (the diameter of the tumor is 1.4 cm, 2.0 cm, and 2.6 cm, respectively). Also, it is assumed that both the lung and the tumor are isotropic and homogeneous tissues. In microwave ablation, a microwave antenna is inserted into the tumor to release energy into the tumor tissue (insertion depth of 70.5 mm). A single slot antenna with a diameter of 1.79 mm was built with three parts: inner conductor, dielectric and outer conductor, encapsulated in a catheter made of polytetrafluoroethylene (PTFE). Figure 1b shows the microwave antenna structure. Since the ablation area in lung tissue is axisymmetric, the geometry of this model is simplified to a two-dimensional axisymmetric model to reduce the computational time.
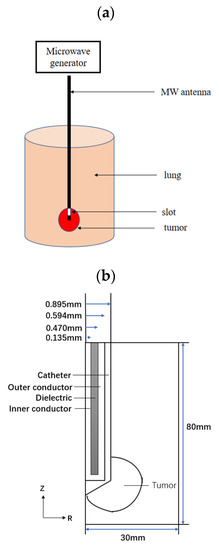
Figure 1.
Model geometry: (a) 3D porous model (b) 2D axisymmetric model.
2.2. Mathematical Models
In this study, after establishing the geometric model, the material properties are set, the heat transfer equation and electromagnetic equation are coupled, and then the transient momentum equation is combined. The ablation parameters are set. The temperature distribution, ablation zone size and ablation volume of the porous lung tissue containing the tumor are calculated using the finite element method. The scheme of the numerical simulation is shown in Figure 2.
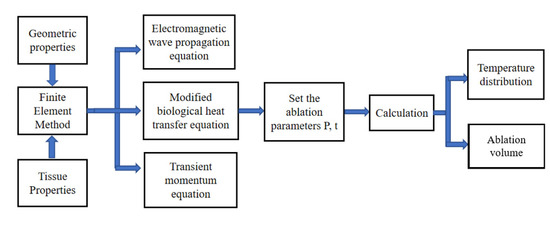
Figure 2.
The scheme of the numerical simulation.
To solve the temperature distribution within the lung tissue, the Pennes biological heat transfer equation was modified based on porous media. According to the porous medium theory, the lung tissue can be considered as two phases coexisting in the same domain: the solid phase (tissue), consisting of tissue cells and intercellular spaces, and the liquid phase (blood), representing the blood flowing through the tissue [19]. In addition, using the local thermal equilibrium assumption, blood and lung tissue are considered to have the same temperature.
2.2.1. Electromagnetic Field Analysis
The electromagnetic wave propagation equations are calculated using Maxwell’s set of equations and are reduced to a general form [20]. The equations are shown as follows:
where = 8.8542 × 10−12 F/m is the permittivity of free space, is the relative permittivity (, is the electric conductivity (S/m), is the relative permeability and is the free space wave number (m−1), is magnetic field strength (A/m).
The microwave energy is emitted from the slot of the microwave antenna and propagated into the porous lung tissue. The boundary conditions for the analysis considering electromagnetic wave propagation are:
- In the microwave antenna dielectric inlet, specify an input microwave power.
- Z-axis as the axis of symmetry.
- The outer boundary along the lung tissue is considered the radiation boundary [21].
- 4.
- The microwave antenna outer and inner conductors are regarded as ideal dielectric [21].
2.2.2. Blood flow Analysis
This study investigates blood flow and heat transfer based on the following hypotheses:
- Incompressible Navier-Stokes equations for simulating laminar flow in blood vessels [21].
- Tissues and blood have the same temperature, i.e., local thermal equilibrium [21].
- Phase changes and chemical reactions occurring within the porous lung tissue are not considered [21].
Darcy’s law is further extended to obtain the Brinkman equation for the study of the blood flow of porous lung tissue. The transient momentum equation is then used. The temperature distribution in porous lung tissue can be obtained by solving the two equations separately [21].
The controlling equation for blood flow in porous lung tissue is as follows [22]:
Continuous equations
Momentum equation
In the equation, represents the blood velocity (m/s); is the porosity i.e., the ratio of vascular volume to tissue volume; is the pressure (Pa); is the blood viscosity, = 3.78 × 10−7 m²/s; is the coefficient of thermal expansion, = 1 × 10−4; is the permeability (m²).
Boundary condition
- Application of axisymmetric boundaries for blood flow analysis [21].
- 2.
- The boundary of the blood analysis is considered as an open boundary condition [21].
2.2.3. Heat Transfer Analysis
The Pennes biological heat transfer equation is shown below [8]:
where T, ρ, C and k are the temperature (°C), density (kg/m3·s), specific heat (J/kg·K) and thermal conductivity (W/m·K) of the tissue, respectively, wb, cb, Tb are the blood perfusion rate (kg/m3·s), specific heat of blood (J/kg·K) and blood temperature (°C), respectively, and Qmet (W/m3) is the heat generated by tissue metabolism. Qext is the external heat source, i.e., the energy generated by microwaves (W/m3). The metabolic heat production (Qmet) is usually neglected; the external heat source (Qext) is shown below:
The Pennes biological heat transfer equation was modified to obtain a heat transfer model based on porous media. The local thermal equilibrium assumption is also used, and the temperature field of the lung tissue can be obtained by calculation, considering that the blood and the lung tissue have the same temperature [23]. The equation is shown as follows:
where φ is the porosity of porous media, subscripts eff, s, and b represent the effective value, solid phase (i.e., lung tissue), and liquid phase (i.e., blood).
Boundary condition
- Application of axisymmetric boundary for heat transfer analysis [24].
- 2.
- The initial temperature of the porous lung was set to 37 °C [24].
- 3.
- Consider only the heat transfer from the lung tissue without considering the microwave antenna. Consider the outer boundary of the lung tissue as insulation [24].
2.2.4. Heat Damage Model
The Arrhenius equation uses the temperature of the tissue at the time of ablation, the time to reach this temperature, and the associated kinetic parameters to represent the thermal damage to the tissue associated with the thermal degradation of the protein. This thermal damage calculation model can more accurately assess the size of the damaged area after ablation. The equation is shown below [25]:
where T is the temperature at any point in the model area, A is the frequency factor, is the activation energy for the irreversible damage reaction, and R is the universal gas constant. Ω describes the degree of thermal damage of the tissue in time t. It is generally considered that irreversible thermal damage occurs in the tissue when Ω = 1. Therefore, the boundary of Ω = 1 is usually taken as the effective range of ablation. In our study, A = 7.39 × 1039 s−1 and E = 2.577 × 105 J mol−1 are for healthy lung tissue, while A = 3.247 × 1043 s−1 and E = 2.814 × 105 s−1 are for a lung tumor [21].
2.3. Calculation Method
A two-dimensional axisymmetric model of the microwave antenna and lung tissue is established in this paper. The electromagnetic wave equation, heat transfer equation, and transient momentum equation are coupled and solved by using COMSOL Multiphysics 5.5 software. The dielectric, thermal properties and porosity of the lung tissue were assumed to remain constant. In the simulation, according to the characteristics of the electromagnetic field and temperature field, the boundary conditions are set, the grid is divided, and the solver is set.
For transient numerical simulation, it is necessary to determine the number of meshes used in the calculation, independent of the calculation results. Therefore, the mesh independence is verified, and the optimal mesh number is determined. Temperature is a key parameter in the numerical simulation of microwave ablation of lung tissue. Therefore, we take the temperature distribution at 5 mm of the antenna to verify the grid independence. The grid is divided into 8451, 14,976, 20,471, 27,234, and 32,371 by automatic partition. Finally, we choose the 20,471 grid number for calculation. The electromagnetic field module is set to a steady state, and the frequency domain, and the output microwave frequency is set to 2450 MHz. For the heat transfer model, the temperature changes with time, so it is set as a transient solver, the solution time is 360 s,the time step is set to 1 s. Table 1 lists the values of the relevant properties of lung tissue, tumor tissue and blood in the simulations [21,24]. Table 2 lists the values of the relevant parameters of the microwave antenna used in the simulations.

Table 1.
The dielectric and thermal properties of tissue, blood and tumor [21,24].

Table 2.
The dielectric properties of a single-slot MW antenna [24].
3. Results
We will present the results of the study in four aspects: model verification, the effect of tumor size, the effect of tumor porosity, and the effect of microwave ablation power.
3.1. Model Verification
Planche et al. [26] performed microwave ablation experiments on living pigs. The ablation power was set at 60 W, and the ablation was guided by a single-needle microwave antenna for 15 min. To verify the accuracy of the porous heat transfer model, we keep the simulation conditions consistent with those studied by Planche et al.: an ablation power of 60 W, ablation time of 15 min, and tumor radius of 1 cm.
The tissue temperatures obtained in the simulation for the porous model and the biological heat transfer model were compared with those obtained from in vivo experiments by Planche et al. Table 3 demonstrates the tissue temperatures for the three cases at a distance of 20 mm from the microwave antenna. The tissue temperatures of the porous heat transfer model were 86.8 °C, 95.3 °C, 98.6 °C, and 103.8 °C for microwave ablation times of 8 min, 10 min, 11 min, and 12 min, respectively, and the tissue temperatures of the Pennes biological heat transfer model were 90.2 °C, 98.4 °C, 103.0 °C, and 108.4 °C, respectively. The tissue temperature in the porous heat transfer model is slightly lower than that in the Pennes heat transfer model. The possible reason is that there are pores in the porous model, and the pores are filled with blood flow; the blood flow will take away some heat. It can be seen from Table 4 that the error between the calculated tissue temperature by the porous heat transfer model and the experimental one is less, which verifies the correctness of the simulation model.

Table 3.
Maximum temperature of lung tissue under different conditions.

Table 4.
Mean absolute percentage errors between simulation and experimental results.
3.2. Effect of Tumor Diameter
The temperature distribution of the lung tissue with tumor diameters of 1.4 cm, 2.0 cm, and 2.6 cm, porosity of lung tissue () is 0.7, porosity of tumor tissue () is 0.6, at P = 10 W and t = 360 s is shown in Figure 3a–c, respectively. It can be seen that the ablation areas of the tissues are all nearly oval, and the temperature of the tissues at the slot of the microwave antenna is the highest. The highest temperatures reached by the ablated lung tissue were 89.4 °C, 87.3 °C, and 86.1 °C for tumor diameters of 1.4, 2.0, and 2.6 cm, respectively. The lung tissue temperatures obtained in the numerical simulation are closer to the temperature distribution in the study by Keangin et al. [21]. Observing Figure 3a, we found that the ablation area completely covered the tumor, whereas, in Figure 3b,c, the ablation area sizes are much smaller than the tumors. Therefore, we believe that P = 10 W, t = 360 s is sufficient to completely ablate a tumor with a diameter of 1.4 cm, whereas tumors with the diameters of 2.0 cm and 2.6 cm would require increased ablation power or ablation time in order to be completely ablated.
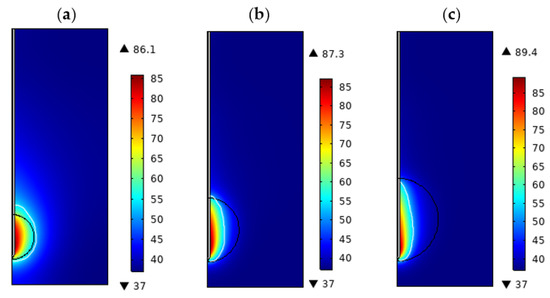
Figure 3.
Temperature distribution of porous lung tissue at different tumor diameters (P = 10 W, t = 300 s, = 0.7, = 0.6): (a) d = 1.4 cm, (b) d = 2.0 cm. (c) d = 2.6 cm.
We used Ω = 1 as the ablation zone boundary, and the tissue ablation volume can be obtained by surface integration of the two-dimensional region [26]. Table 5 shows the maximum temperature reached, the transverse and longitudinal diameter of the ablation zone, and the ablation volume of tumors with different diameters. As the tumor diameter increased from 1.4 cm to 2.6 cm, the maximum temperature reached by the tissue decreased from 89.4 °C to 86.1 °C, the transverse diameter of the ablation zone decreased from 1.30 cm to 0.76 cm, the longitudinal diameter increased from 1.82 cm to 2.19 cm, and the ablation volume increased from 2.34 cm3 to 2.52 cm3, which indicates the influence of tumor size on the ablation. The effect of tumor size on ablation was mainly reflected in the transverse diameter of the ablation area, and the increase of tumor diameter would limit the heat transmission in the transverse direction but had little effect on the ablation volume.

Table 5.
Ablation temperature, ablation area and ablation volume for different diameter tumors.
3.3. Effect of Tumor Porosity
Since the human body is a thermostatic regulating system, the temperature of the blood is automatically regulated during microwave ablation to maintain a stable value of body temperature [27]. On the one hand, the core temperature of the arterial blood is changed to achieve the purpose of regulating the blood temperature, and on the other hand, the porosity of the biological tissue is changed. This is achieved by increasing the porosity of biological tissues at higher temperatures and decreasing the porosity of biological tissues at lower temperatures. The change in the porosity of biological tissues further affects the change in their effective thermal conductivity, thus achieving the purpose of regulating body temperature [26]. Meanwhile, tissues under different physiological conditions have different porosities, which can affect the temperature of tissues during microwave ablation and influence the final ablation effect. Therefore, it is of great practical significance to study the effect of tumor tissue porosity on ablation.
Figure 4a–c show the temperature distribution of porous lung tissue with tumor tissue porosities of 0.5, 0.6, and 0.7, at P = 10 W and t = 360 s, respectively [21]. It can be seen from the figure that tumor tissues with different porosities have the same temperature distribution, but there are some temperature differences. As the tumor porosity increases, the maximum temperature reached by the ablated tissue gradually decreases. From the figure, we can see that the transverse diameter of the ablation area is decreasing. We also noticed that when the tumor was 2.0 cm in diameter, the tumor could not be completely ablated, regardless of the porosity (0.5,0.6, or 0.7, P = 10 W, t = 360 s).
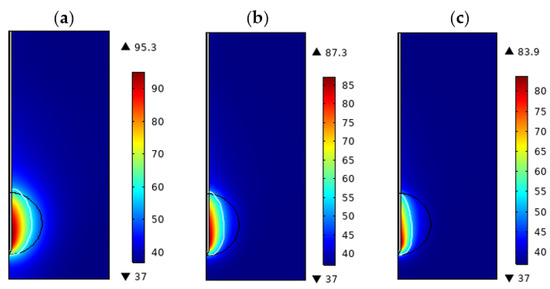
Figure 4.
Temperature distribution of porous lung tissue at different porosity of tumor (P = 10 W, t = 300 s, d = 2.0 cm, = 0.7): (a) = 0.5 (b) = 0.6 (c) = 0.7.
Table 6 shows the maximum temperature, ablation zone transverse and longitudinal diameter, and ablation volume of tumors with different porosities. The maximum temperature decreased from 95.3 °C to 83.9 °C when the tumor porosity increased from 0.5 to 0.7, the transverse and longitudinal diameter of the ablation zone both decreased; the transverse diameter from 1.23 cm to 0.62 cm, and the longitudinal diameter from 2.02 cm to 1.82 cm. At the same time, the transverse diameter decreased more than the longitudinal diameter. The ablation volume decreased from 2.94 cm3 to 1.80 cm3. The greater the porosity is, the greater the risk of incomplete ablation of the tumor. Therefore, when tissue lesions exist, the effect of the tissue porosity change on the ablation effect should be considered and the ablation parameters should be adjusted in time.

Table 6.
Ablation temperature, ablation area and ablation volume of tumors with different porosities.
3.4. Effect of Microwave Ablation Power
In microwave ablation, ablation power is one of the most important factors on the ablation effect [28]. Figure 5a–c show the temperature distribution of the lung tissue for = 0.7, = 0.6, d = 2.0 cm, at t = 360 s, and ablation powers of 10 W, 20 W, and 30 W, respectively. It can be seen from the figure that the higher the power of microwave ablation is, the higher the highest temperature of the tissue is, and the transverse and longitudinal diameter of the ablation area is also increasing. As seen in Figure 5c, at P = 30 W, t = 360 s, the tumor was not completely ablated, so we believe that further adjustment of ablation parameters is required if the tumor with a diameter of 2.0 cm is to be completely ablated. Table 7 shows the values of the transverse and longitudinal diameter of the ablation zone, and the ablation volume under different ablation powers when the ablation power was increased from 10 W to 30 W; the maximum temperature increased from 87.3 °C to 142 °C, the transverse diameter of the ablation zone increased from 0.92 cm to 1.40 cm, the longitudinal diameter increased from 1.88 cm to 2.11 cm, and the ablation volume increased from 2.28 cm3 to 4.06 cm3. The higher the ablation power, the higher the maximum temperature of the tissue, and the larger the ablation area and volume.
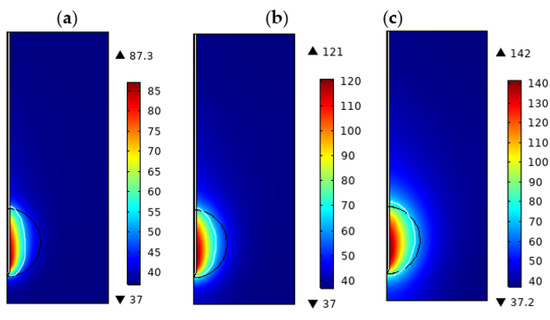
Figure 5.
Temperature distribution of porous lung tissue at different ablation powers. (t = 300 s, d = 2.0 cm, = 0.6, = 0.7): (a) P = 10 W (b) P = 20 W (c) P = 30 W.

Table 7.
Ablation temperature, ablation area and ablation volume at different ablation powers.
4. Discussion
In order to ensure that the tumor tissue is completely destroyed and to minimize the damage to the surrounding healthy tissues, a model that more closely fits the actual lung tissue is needed. Pennes biological heat transfer equation does not take into account the porous characteristics of lung tissue and ignores the influence of blood flow [9]. The difference between the lung tissue temperature obtained using the Pennes heat transfer equation and the temperature achieved in the actual ablation in the simulation is large, which will have a certain impact on the ablation efficacy. Therefore, it is important to establish a heat transfer model based on porous lung tissue in microwave ablation.
In this paper, a biological heat transfer model based on porous lung tissue was established, and microwave ablation of lung tissue containing tumor tissue was simulated using the finite element method. The effects of tumor diameter, tumor porosity, and microwave ablation power on the ablation effect of porous lung tissue were investigated in terms of tissue temperature distribution, ablation zone, and ablation volume. The results showed that as the tumor diameter increased, the tissue temperature and the longitudinal diameter of the ablation zone decreased, while the ablation volume did not change significantly. The greater the porosity of tumor tissue, the lower the tissue temperature, and the lower the ablation area and ablation volume. The tissue temperature, ablation area, and ablation volume will increase with the increase of ablation power. Therefore, increasing the ablation power can ensure a certain degree of complete ablation of the tumor.
The larger the diameter of the tumor, the more abundant the blood vessels deep inside it, the more heat is taken away by the blood flow in the vessels, and the temperature reached by the tumor tissue is subsequently reduced. Since the coaxial single-slot antenna mainly transfers energy along the direction of antenna insertion, it is not conducive to the ablation of large-size tumors in the lateral direction, and the transverse diameter of the ablation zone is consequently reduced, so the treatment difficulty increases. Tehrani et al. [29] showed that in smaller tumors, the cell death process occurs faster; the percentage of dead cancer cells also decreases by 20% when the tumor diameter increases, and the treatment of large tumors are more difficult than that of small tumors, in agreement with the findings of our study. One of the most important properties of biological porous tissue is the blood volume fraction, i.e., porosity; the greater the tumor porosity, the more blood vessels in the tissue, the more heat is taken away by blood flow, and the lower the temperature reached by the tissue, which further affects the size of the ablation zone and ablation volume. Andreozz et al. [25] showed that the tissue temperature and ablation zone were much lower at a tumor porosity of 0.23 than at a porosity of 0.07, which also indicates that tumor porosity affects ablation efficacy. In our study, when the ablation power was increased from 10 W to 30 W, the maximum temperature reached by the tissue increased from 87.3 °C to 142.0 °C, and the ablation volume increased from 2.28 cm3 to 4.06 cm3, and the possibility of complete ablation of the tumor increased, so we believe that the risk of tumor recurrence can be reduced to some extent by appropriately increasing the ablation power.
Meanwhile, the porosity changes from the central to the marginal regions of the tumor [29]. However, in the present study, we considered the tumor tissue porosity as a constant value to simplify the study, which is one of the limitations of our study. Also, the variation of electrical properties as well as thermal properties of lung and tumor tissues with temperature was not considered in the numerical simulation. Although the porous model in this paper considers the vascular distribution and blood flow inside the lung tissue, it adopts the local thermal equilibrium equation to study, ignoring the temperature difference between the lung tissue and the blood and the heat exchange existing between them during the actual ablation process. Therefore, in the subsequent study of the porous heat transfer model, the local thermal non-equilibrium equation should be used to consider the heat transfer process of lung tissue, which will be closer to the actual microwave ablation.
To ensure that the tumor tissue is ablated and the risk of recurrence is reduced, in subsequent studies, we will consider the safety boundary of the ablation area in the simulation and will consider the difference in tumor porosity in the clinical application to better provide surgical planning.
5. Conclusions
To ensure that the tumor tissue is destroyed and to minimize the damage to the surrounding healthy tissue, it is necessary to establish a more accurate model of lung tissue and obtain more accurate ablation parameters according to this model. In this paper, a biological heat transfer model based on porous media is established, and the microwave ablation of lung tissue containing tumor tissue is simulated by the finite element method. The effects of tumor diameter, tumor porosity, and microwave ablation power on the microwave ablation of porous lung tissue were studied in terms of tissue temperature distribution, ablation area, and ablation volume. The results showed that with the increase of tumor diameter, the tissue temperature and the longitudinal diameter of the ablation area decreased, but the ablation volume did not change significantly. The larger the tumor porosity, the lower the tissue temperature, and the smaller the ablation area and volume. Tissue temperature, ablation area, and ablation volume increased with the increase of ablation power. Therefore, increasing the power of ablation can ensure that the tumor is ablated to some extent. This paper provides the basic reference data for clinical treatment parameters of microwave ablation of lung tumors, which is beneficial to improve the treatment scheme. Fathalla et al. [1] used DETECT-LC, an automatic segmentation method based on the threshold, to construct a three-dimensional tumor volume and reduce the burden of clinicians. In the future, we will also consider the three-dimensional reconstruction of tumors to obtain more generalized clinical treatment parameters.
Author Contributions
X.M., idea proposal, data analysis, simulation, writing-original manuscript preparation, review and editing; Q.N., supervision, conceptualization, investigation, project administration, funding acquisition, visualization, validation, writing—review and editing; N.W., conceptualization, review of the manuscript; S.B. conceptualization, review of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Fundation of China (31771021), Beijing Municiple Natural Science Fundation (3162006) and Jiangsu Science and Technology Department (Jiangsu Science and Technology Committee) (BE2017758).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fathalla, K.M.; Youssef, S.M.; Mohammed, N. DETECT-LC: A 3D Deep Learning and Textural Radiomics Computational Model for Lung Cancer Staging and Tumor Phenotyping Based on Computed Tomography Volumes. Appl. Sci. 2022, 12, 6318. [Google Scholar] [CrossRef]
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef] [PubMed]
- Alexander, E.S.; Dupuy, D.E. Lung Cancer Ablation: Technologies and Techniques. Semin. Interv. Radiol. 2013, 30, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Vogl, T.J.; Nour-Eldim, N.A.; Albrecht, M.H.; Kaltenbach, B.; Hohenforst-Schmidt, W.; Lin, H.; Panahi, B.; Eichler, K.; Gruber-Rouh, T.; Roman, A. Thermal ablation of lung tumors: Focus on microwave ablation. Rofo 2017, 189, 828–843. [Google Scholar] [CrossRef] [PubMed]
- Heidari, A.; Toumaj, S.; Navimipour, N.J.; Unal, M. A privacy-aware method for COVID-19 detection in chest CT images using lightweight deep conventional neural network and blockchain. Comput. Biol. Med. 2022, 145, 105461. [Google Scholar] [CrossRef]
- Zhai, F.; Nan, Q.; Zhang, H.J. Review of microwave ablation antenna for atrial fibrillation. Beijing Biomed. Eng. 2013, 32, 95–100. [Google Scholar]
- Andreozzi, A.; Iasiello, M.; Tucci, C. An overview of mathematical models and modulated-heating protocols for thermal ablation. Adv. Heat Transf. 2020, 52, 489–541. [Google Scholar]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Okajima, J.; Maruyama, S.; Takeda, H.; Komiya, A. Dimensionless solutions and general characteristics of bioheat transfer during thermal therapy. J. Therm. Biol. 2009, 34, 377–384. [Google Scholar] [CrossRef]
- Abraham, J.P.; Sparrow, E.M. A thermal-ablation bioheat model including liquid-to-vapor phase change, pressure-and necrosis-dependent perfusion, and moisture-dependent properties. Int. J. Heat Mass Transf. 2007, 50, 2537–2544. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. A novel local thermal non-equilibrium model for biological tissue applied to multiple-antennas configurations for thermal ablation. Numer. Heat Transf. Part A Appl. 2020, 79, 111–121. [Google Scholar] [CrossRef]
- Nakayama, A.; Kuwahara, F. A general bioheat transfer model based on the theory of porous media. Int. J. Heat Mass Transf. 2008, 51, 3190–3199. [Google Scholar] [CrossRef]
- Khaled AR, A.; Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 2003, 46, 4989–5003. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. The role of porous media in biomedical engineering as related to magnetic resonance imaging and drug delivery. Heat Mass Transf. 2006, 42, 939–953. [Google Scholar] [CrossRef]
- Alzahrani, F.; Hobiny, A.; Abbas, I.; Marin, M. An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry 2020, 12, 848. [Google Scholar] [CrossRef]
- Su, T.; Zhang, W.; Zhang, Z.; Wang, X.; Zhang, S. Numerical Investigation of the Deformable Porous Media Treated by the Intermittent Microwave. Processes 2021, 9, 757. [Google Scholar] [CrossRef]
- Chaichanyut, M.; Tungjitkusolmun, S. Microwave ablation using four-tine antenna: Effects of blood flow velocity, vessel location, and total displacement on porous hepatic cancer tissue. Comput. Math. Methods Med. 2016, 2016, 4846738. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y.; Yang, J. Thermoelastic behavior of skin tissue induced by laser irradiation based on the generalized dual-phase lag model. J. Therm. Biol. 2021, 100, 103038. [Google Scholar] [CrossRef]
- Zhang, Y.; Qian, Z.; Guo, J.; Hu, G.; Zhao, J. Simulation on temperature distribution of effective lesion area for tumor microwave ablation thermotherapy. Acta Biophys. Sin. 2012, 28, 763–770. [Google Scholar] [CrossRef]
- Kee, R.J.; Coltrin, M.E.; Glarborg, P. Chemically Reacting Flow: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Keangin, P.; Rattanadecho, P. A numerical investigation of microwave ablation on porous liver tissue. Adv. Mech. Eng. 2018, 10, 1687814017734133. [Google Scholar] [CrossRef]
- Brinkman, H.C. On the permeability of media consisting of closely packed porous particles. Flow Turbul. Combust. 1949, 1, 81–86. [Google Scholar] [CrossRef]
- Rattanadecho, P.; Keangin, P. Numerical study of heat transfer and blood flow in two-layered porous liver tissue during microwave ablation process using single and double slot antenna. Int. J. Heat Mass Transf. 2013, 58, 457–470. [Google Scholar] [CrossRef]
- Gao, X.; Tian, Z.; Cheng, Y.; Geng, B.; Chen, S.; Nan, Q. Experimental and numerical study of microwave ablation on ex-vivo porcine lung. Electromagn. Biol. Med. 2019, 38, 249–261. [Google Scholar] [CrossRef] [PubMed]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G. Numerical investigation of a thermal ablation porous media-based model for tumoral tissue with variable porosity. Computation 2021, 9, 50. [Google Scholar] [CrossRef]
- Planché, O.; Teriitehau, C.; Boudabous, S.; Robinson, J.M.; Rao, P.; Deschamps, F.; Farouil, G.; De Baere, T. In vivo evaluation of lung microwave ablation in a porcine tumor mimic model. Cardiovasc. Interv. Radiol. 2013, 36, 221–228. [Google Scholar] [CrossRef]
- Selmi, M.; Bin Dukhyil, A.A.; Belmabrouk, H. Numerical analysis of human cancer therapy using microwave ablation. Appl. Sci. 2019, 10, 211. [Google Scholar] [CrossRef]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Pennes’ bioheat equation vs. porous media approach in computer modeling of radiofrequency tumor ablation. Sci. Rep. 2021, 11, 5272. [Google Scholar] [CrossRef]
- Tehrani MH, H.; Soltani, M.; Kashkooli, F.M.; Raahemifar, K. Use of microwave ablation for thermal treatment of solid tumors with different shapes and sizes—A computational approach. PLoS ONE 2020, 15, e0233219. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).