Investigation of Beat Wave Propagation along Lossy Dielectric Bar for Wind Tunnel Microwave Experiments
Abstract
1. Introduction
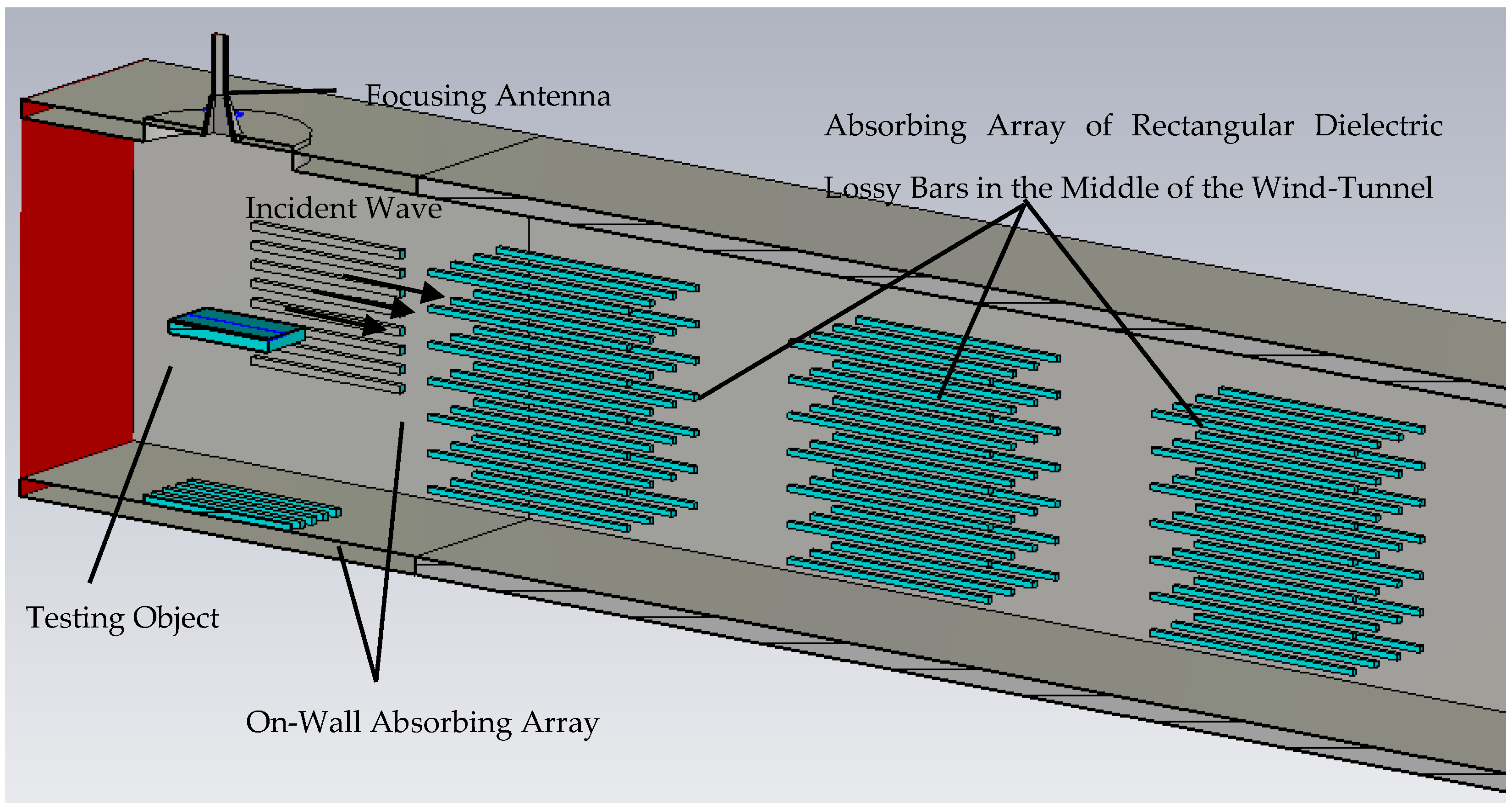
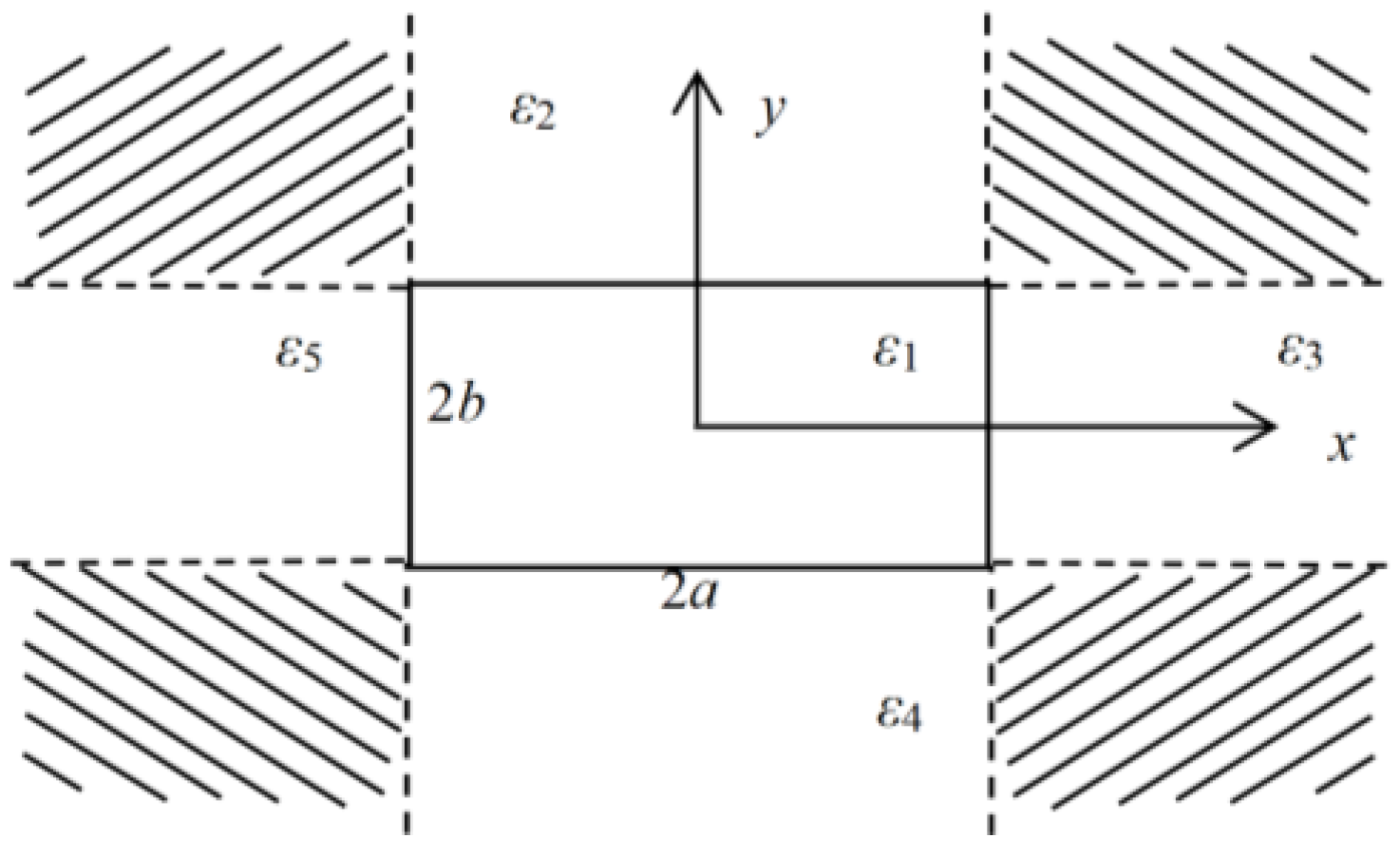
2. Problem Description
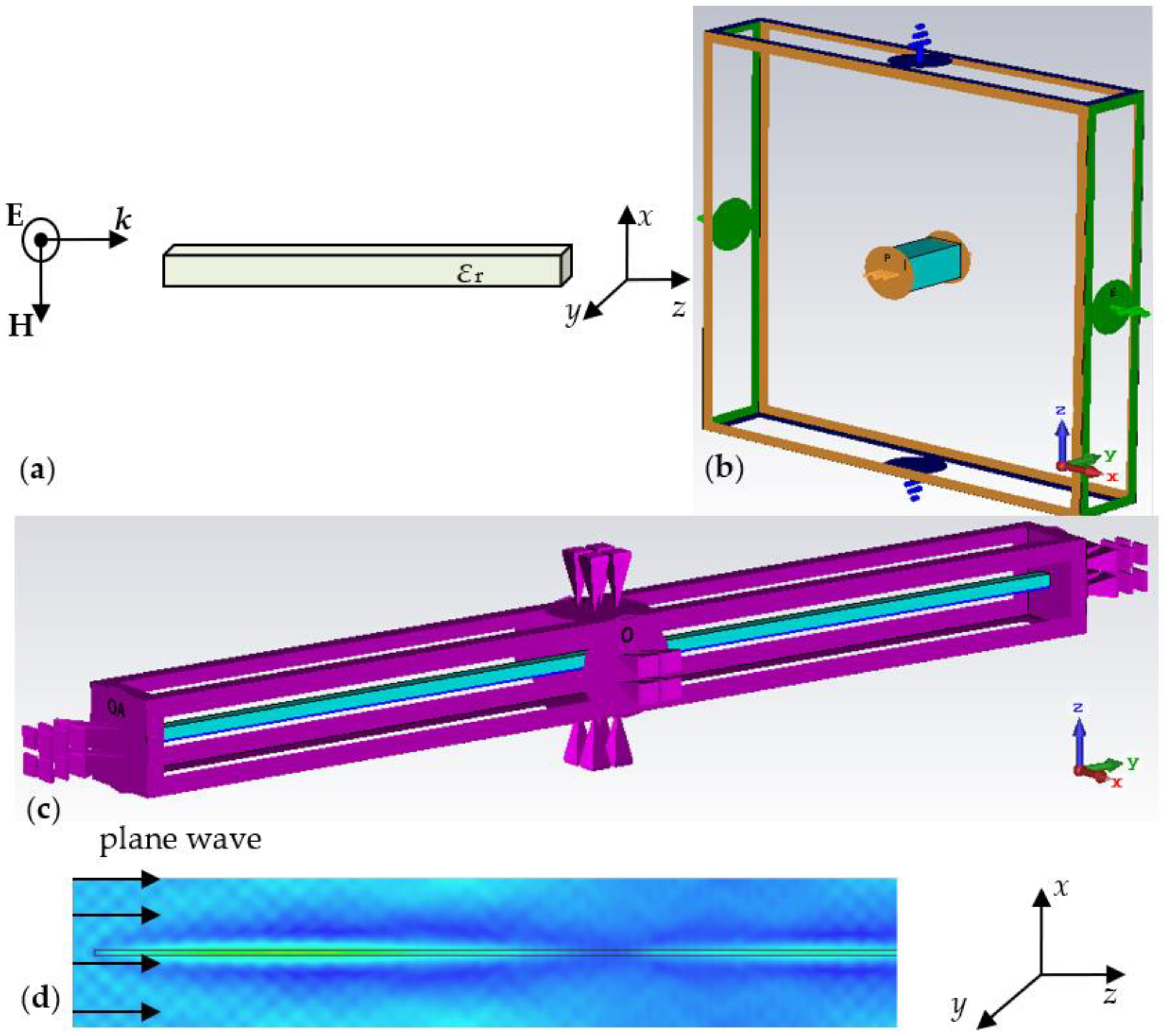
2.1. Beat wave Propagation along Dielectric Bar
2.2. Mismatch between Plane Wave and Guided Modes
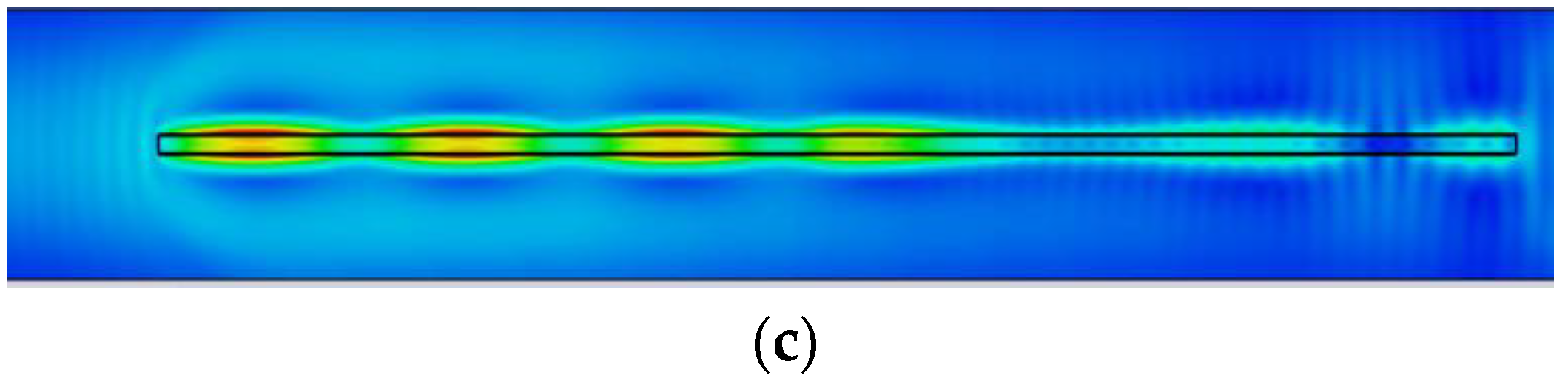
3. Mode Analysis of Beat Wave Pattern
3.1. Guided Wave and Leaky Wave
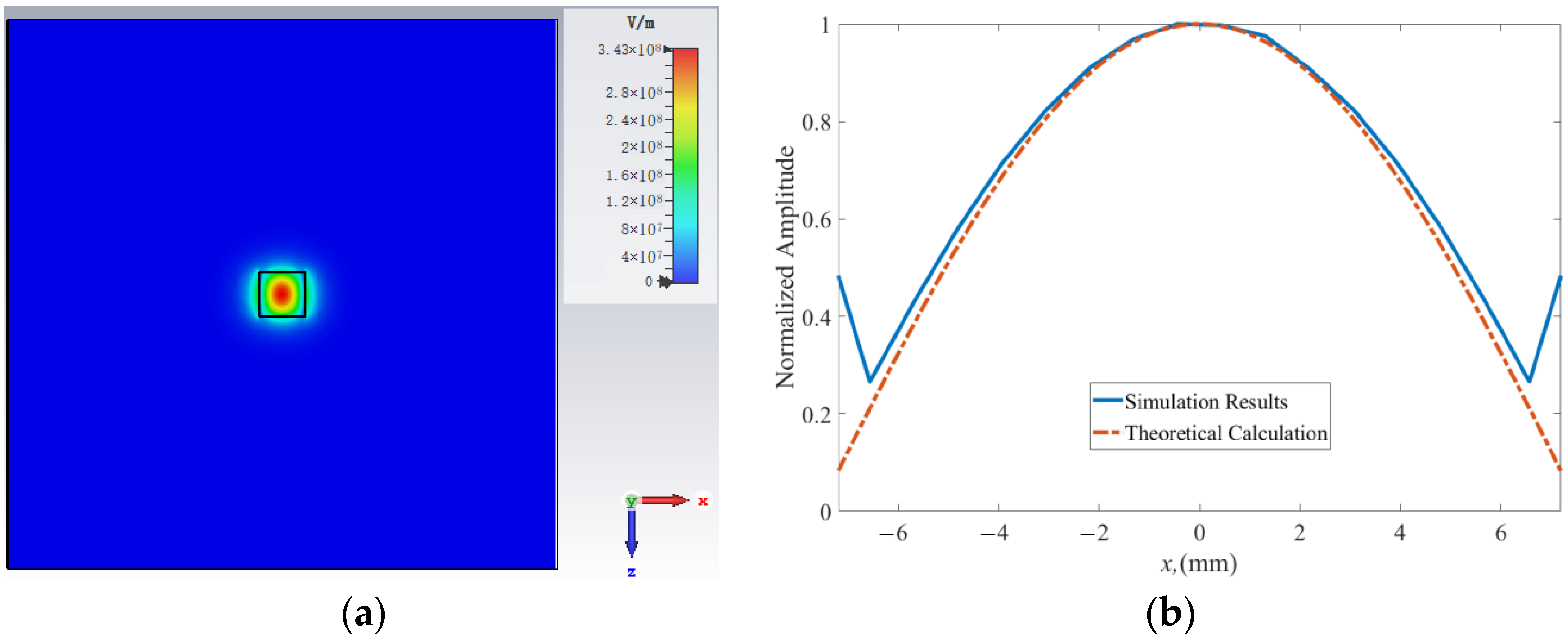
3.2. Analysis of Propagation Characteristics of Guided Wave
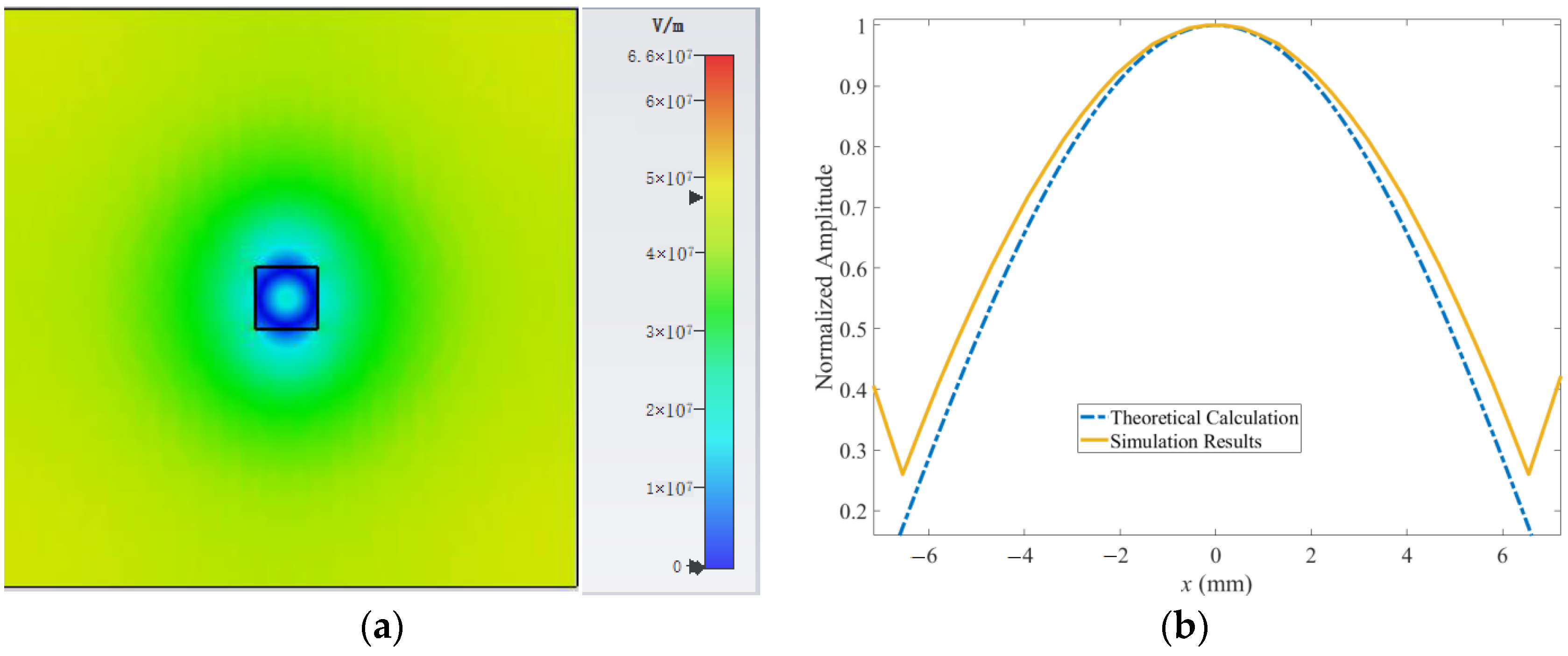
3.3. Analysis of Propagation Characteristics of Leaky Wave
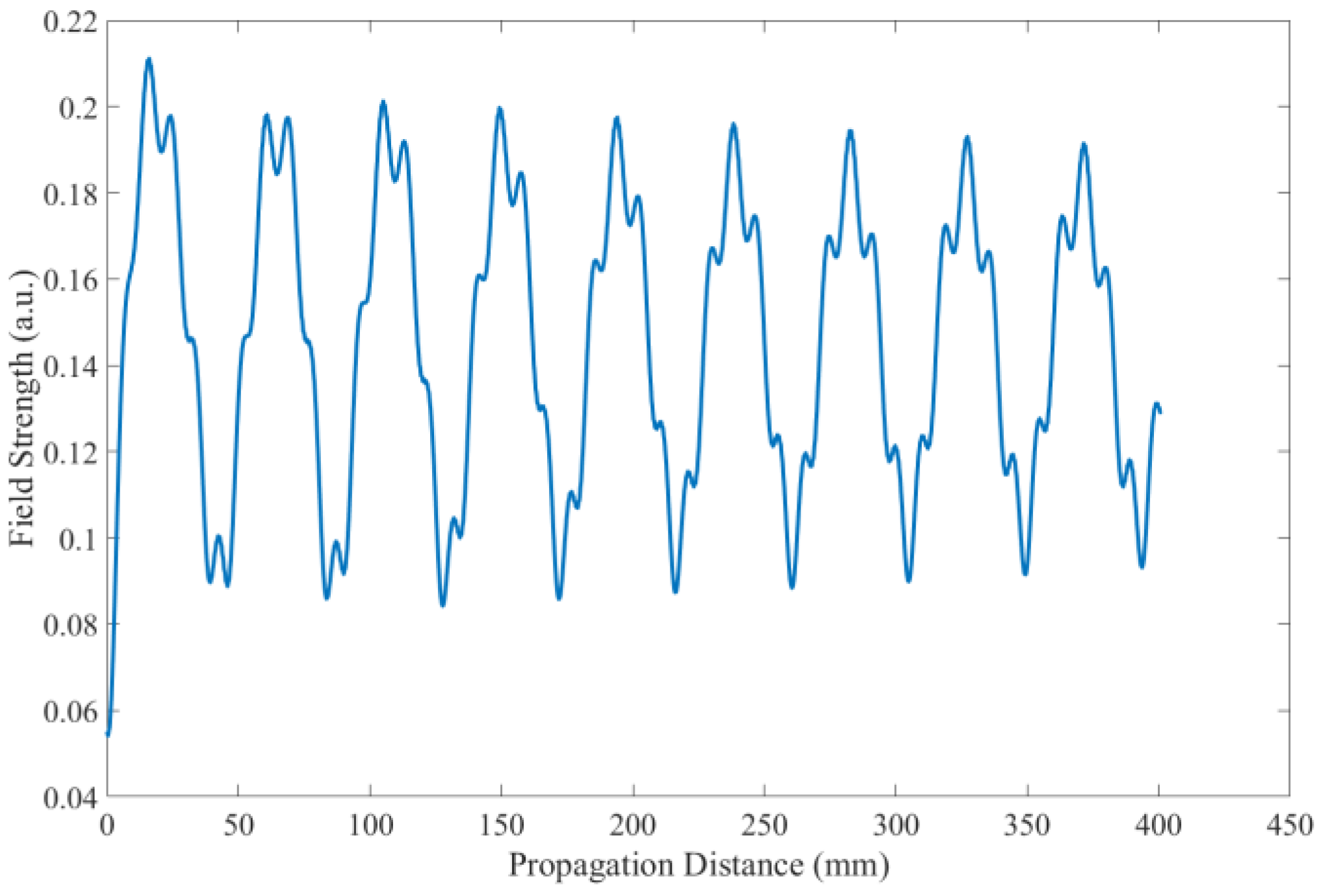
3.4. Period Length of Field Distribution
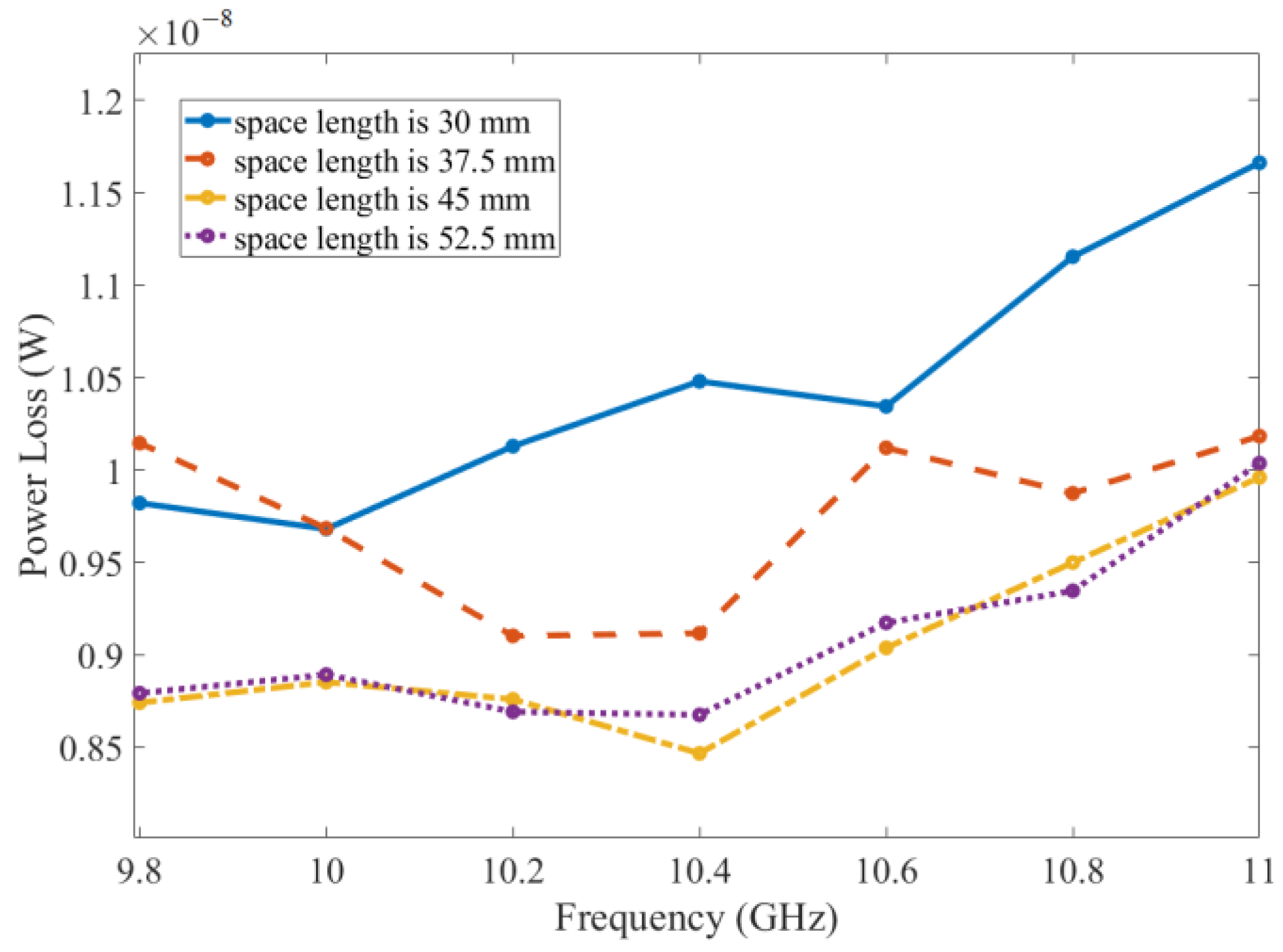
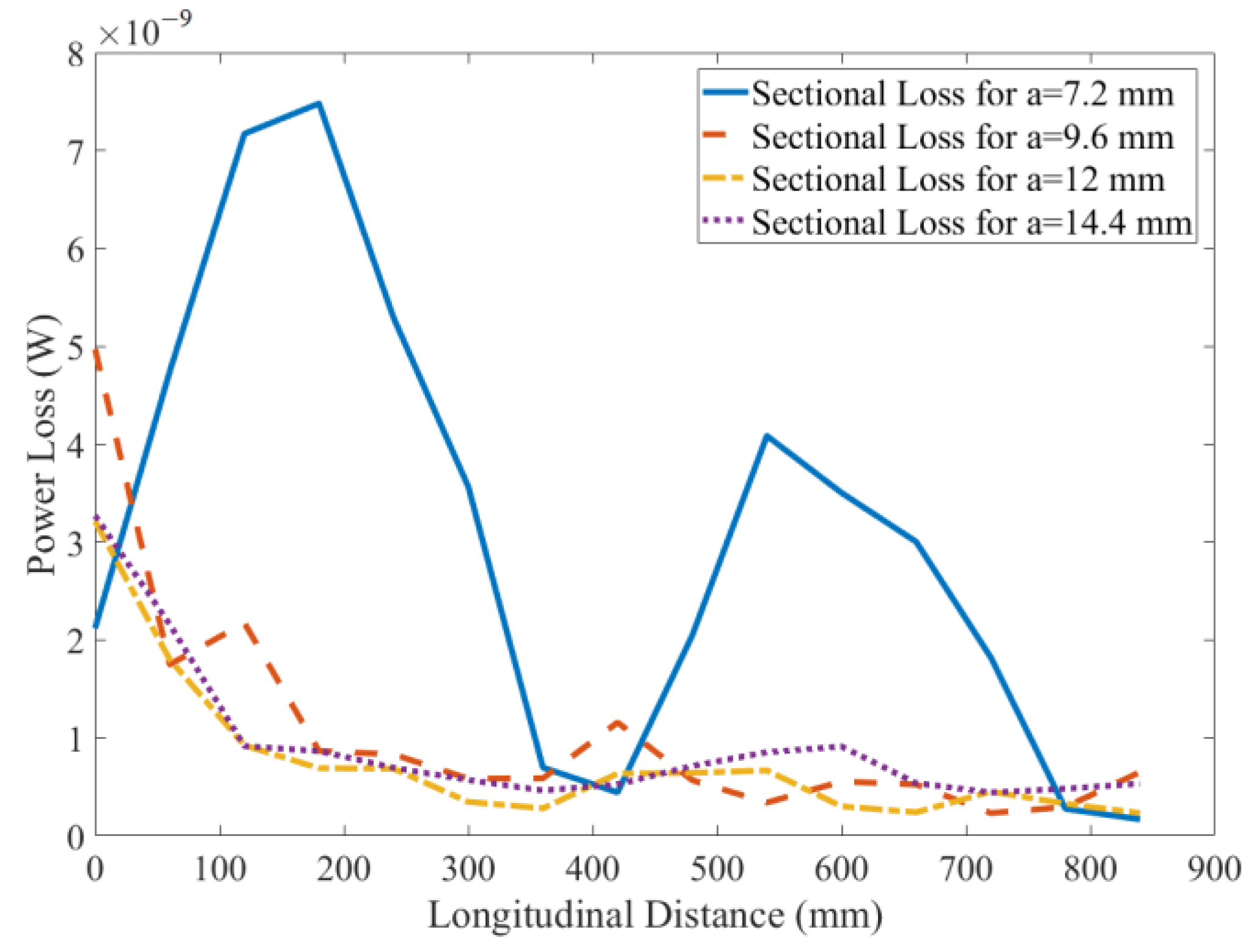
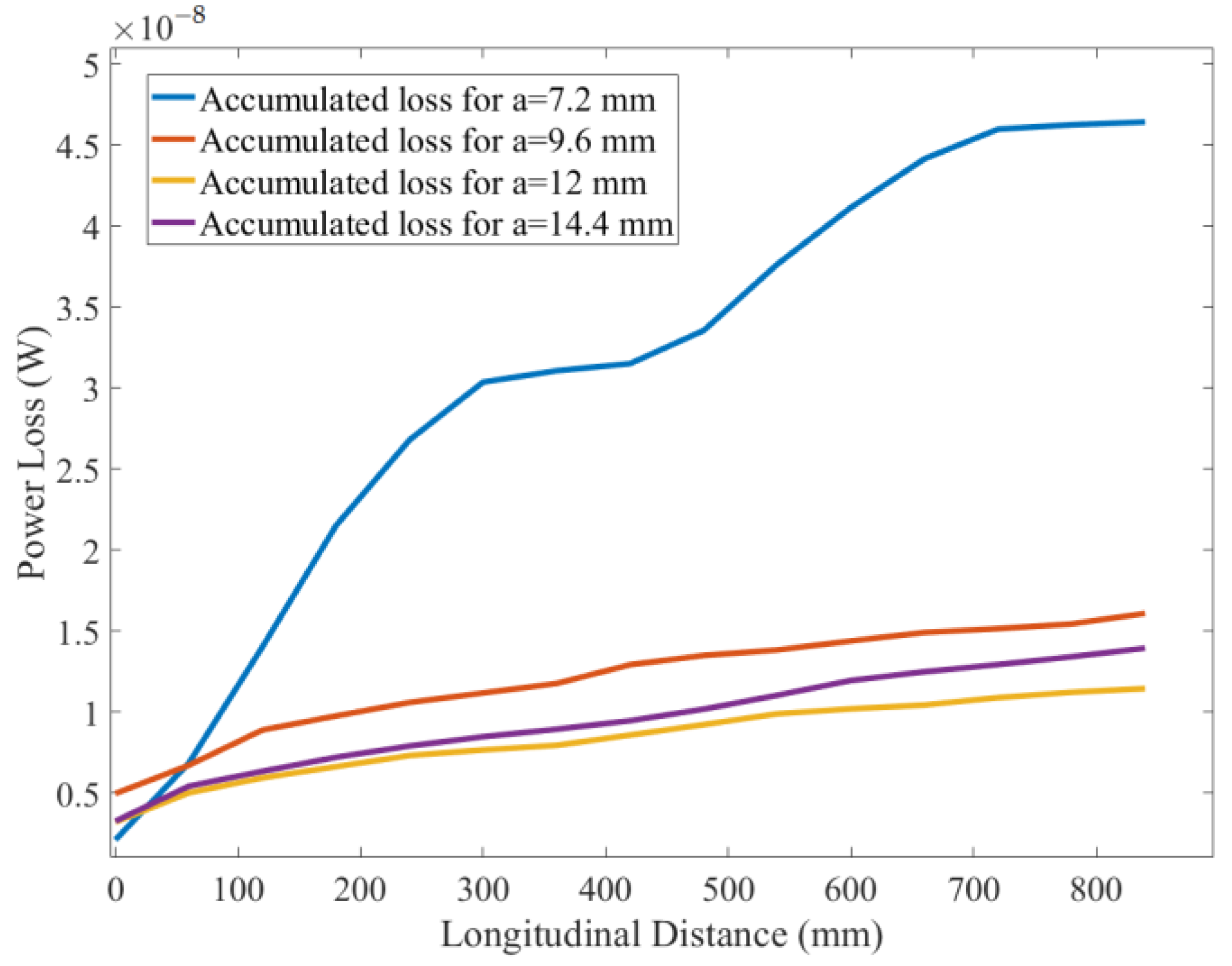
4. Absorbing Array Design and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Wang, Y.; Bin, L.I. Application of High Power Microwave Weapons in Air Defense. Electron. Sci. Technol. 2011, 24, 128–131. [Google Scholar]
- Yang, D.; Chen, C.; Teng, Y.; Li, S.; Li, X.; Tan, W.; Zhu, X.; Zhang, L.; Sun, J.; Su, J. Investigation of damage traces on the SWS of the RBWO with a low guiding magnetic field. Phys. Plasmas 2021, 28, 053101. [Google Scholar] [CrossRef]
- Gunin, A.V.; Klimov, A.I.; Korovin, S.D.; Kurkan, I.K.; Pegel, I.V.; Polevin, S.D.; Roitman, A.M.; Rostov, V.V.; Stepchenko, A.S.; Totmeninov, E.M. Relativistic X-band BWO with 3-GW output power. IEEE Trans. Plasma Sci. 1998, 26, 326–331. [Google Scholar] [CrossRef]
- Ansari, M.A.; Thottappan, M. Design and Simulation of Dual-Band Nonuniform Relativistic Backward Wave Oscillator Using a Bragg Structure as Its RF Circuit and Reflector-Cum-Mode Converter. IEEE Trans. Electron. Devices 2020, 67, 1814–1818. [Google Scholar] [CrossRef]
- Jacob, J.; Chia, L.H.L.; Boey, F.Y.C. Thermal and non-thermal interaction of microwave radiation with materials. J. Mater. Sci. 1995, 30, 5321–5327. [Google Scholar] [CrossRef]
- Gabriel, C.; Gabriel, S.; Grant, E.H.; Grant, E.H.; Halstead, B.S.J.; Mingos, D.M.P. Dielectric parameters relevant to microwave dielectric heating. Chem. Soc. Rev. 1998, 27, 213–219. [Google Scholar] [CrossRef]
- Hotta, M.; Hayashi, M.; Lanagan, M.T.; Agrawal, D.K.; Nagata, K. Complex permittivity of graphite, carbon black and coal powders in the ranges of X-band frequencies (8.2 to 12.4 GHz) and between 1 and 10 GHz. ISIJ Int. 2011, 51, 1766–1772. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, E.; Zhang, J.; Yu, C.; Zheng, H.; Guo, G. A broadband variable-temperature test system for complex permittivity measurements of solid and powder materials. Rev. Sci. Instrum. 2018, 89, 024701. [Google Scholar] [CrossRef]
- Michael, D.; Mingos, P.; Baghurst, D.R. Tilden Lecture. Applications of microwave dielectric heating effects to synthetic problems in chemistry. Chem. Soc. Rev. 1991, 20, 1–47. [Google Scholar] [CrossRef]
- Razzaq, T.; Kremsner, J.M.; Kappe, C.O. Investigating the existence of nonthermal/specific microwave effects using silicon carbide heating elements as power modulators. J. Org. Chem. 2008, 73, 6321–6329. [Google Scholar] [CrossRef]
- Li, E.; Gao, Y.; Zhang, Y.; Gao, C.; Zheng, H.; Zeng, Z. Nonlinear behavior of microwave semiconductor materials measured under a strong electromagnetic environment using a compressed rectangular resonant cavity. Appl. Phys. A-Mater. Sci. Process. 2017, 123, 415–423. [Google Scholar] [CrossRef]
- Miyakoshi, J. Cellular and molecular responses to radio-frequency electromagnetic fields. Proc. IEEE 2013, 101, 1494–1502. [Google Scholar] [CrossRef]
- Wait, J.R. Scattering of a Plane Wave from a Circular Dielectric Cylinder at Oblique Incidence. Can. J. Phys. 1955, 33, 189–195. [Google Scholar] [CrossRef]
- Wu, R.B.; Chen, C.H. On the Variational Reaction Theory for Dielectric Waveguides. IEEE Trans. Microw. Theory Tech. 1985, 33, 477–483. [Google Scholar]
- Coves, A.; Gimeno, B.; Blas, A.A.S.; Vidal, A.; Boria, V.E.; Andres, M.V. Three-Dimensional Scattering of Dielectric Gratings Under Plane-Wave Excitation. IEEE Antennas Wirel. Propag. Lett. 2003, 2, 215–218. [Google Scholar] [CrossRef]
- Yang, Y.; Castaneda, J.A.; Alexopoulos, N.G. An Integral Equation Analysis of an Infinite Array of Rectangular Dielectric Waveguides. IEEE Trans. Microw. Theory Tech. 1990, 38, 873–880. [Google Scholar] [CrossRef]
- Goell, J.E. A Circular-Harmonic Computer Analysis of Rectangular Dielectric Waveguides. Bell Syst. Tech. J. 1969, 48, 2133–2160. [Google Scholar] [CrossRef]
- Marcatilli, E.A.J. Dielectric rectangular waveguide and directional coupler for integrated optics. Bell Syst. Tech. J. 1969, 48, 2071–2102. [Google Scholar] [CrossRef]
- Kaufman, R.G.; Hulse, G.; Vezzetti, D.J.; Munowitz, M.; Stair, K.; Bird, T. Observation and analysis of spatial beats in a multimode dielectric optical waveguide. Appl. Opt. 1992, 31, 4920–4922. [Google Scholar] [CrossRef]
- Kang, M.; Park, J.; Lee, I.M.; Lee, B. Floating dielectric slab optical interconnection between metal-dielectric interface surface plasmon polariton waveguides. Opt. Express 2009, 17, 676–687. [Google Scholar] [CrossRef]
- Marcuse, D. Investigation of coupling between a fiber and an infinite slab. J. Light. Technol. 1989, 7, 122–130. [Google Scholar] [CrossRef]
- Hu, J.; Menyuk, C.R. Understanding leaky modes: Slab waveguide revisited. Adv. Opt. Photonics 2009, 1, 58–106. [Google Scholar] [CrossRef]



| Frequency (GHz) | Theoretical Value (rad/m) | Simulation Result (rad/m) | Relative Error (%) |
|---|---|---|---|
| 10 | 326.7 | 352.9 | −7.42 |
| 10.2 | 338.6 | 363.0 | −6.71 |
| 10.4 | 350.9 | 372.9 | −5.90 |
| 10.6 | 360.8 | 382.7 | −5.74 |
| 10.8 | 375.0 | 392.9 | −4.55 |
| 11 | 387.0 | 403.2 | −4.00 |
| Frequency (GHz) | Theoretical Value (rad/m) | Simulation Result (rad/m) | Relative Error (%) |
|---|---|---|---|
| 10 | 198.2 | 209.4 | −5.38 |
| 10.2 | 202.9 | 213.6 | −5.02 |
| 10.4 | 207.9 | 217.8 | −4.55 |
| 10.6 | 211.0 | 222.0 | −4.95 |
| 10.8 | 215.6 | 226.2 | −4.71 |
| 11 | 220.1 | 230.4 | −4.45 |
| Frequency (GHz) | Theoretical Value (mm) | Eigenmode Simulation (mm) | FDTD Simulation (mm) |
|---|---|---|---|
| 10 | 48.9 | 43.8 | 43.9 |
| 10.2 | 46.3 | 42.1 | 42.1 |
| 10.4 | 43.9 | 40.5 | 40.4 |
| 10.6 | 41.9 | 39.1 | 39.2 |
| 10.8 | 39.4 | 37.7 | 37.7 |
| 11 | 37.6 | 36.4 | 36.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, R.; Peng, X.; Yang, Y.; Xiong, N.; Tao, Y.; Wu, J.; Liu, D. Investigation of Beat Wave Propagation along Lossy Dielectric Bar for Wind Tunnel Microwave Experiments. Appl. Sci. 2023, 13, 619. https://doi.org/10.3390/app13010619
Bao R, Peng X, Yang Y, Xiong N, Tao Y, Wu J, Liu D. Investigation of Beat Wave Propagation along Lossy Dielectric Bar for Wind Tunnel Microwave Experiments. Applied Sciences. 2023; 13(1):619. https://doi.org/10.3390/app13010619
Chicago/Turabian StyleBao, Rong, Xin Peng, Yin Yang, Neng Xiong, Yang Tao, Jifei Wu, and Dawei Liu. 2023. "Investigation of Beat Wave Propagation along Lossy Dielectric Bar for Wind Tunnel Microwave Experiments" Applied Sciences 13, no. 1: 619. https://doi.org/10.3390/app13010619
APA StyleBao, R., Peng, X., Yang, Y., Xiong, N., Tao, Y., Wu, J., & Liu, D. (2023). Investigation of Beat Wave Propagation along Lossy Dielectric Bar for Wind Tunnel Microwave Experiments. Applied Sciences, 13(1), 619. https://doi.org/10.3390/app13010619






