Photomechanical Solid Polymers: Model for Pressure and Strain Induced by Photoisomerization and Photo-Orientation
Abstract
1. Introduction
2. Model for Pressure and Strain Induced by Photoisomerization
2.1. Dynamics of Volume Change and Pressure Build-up
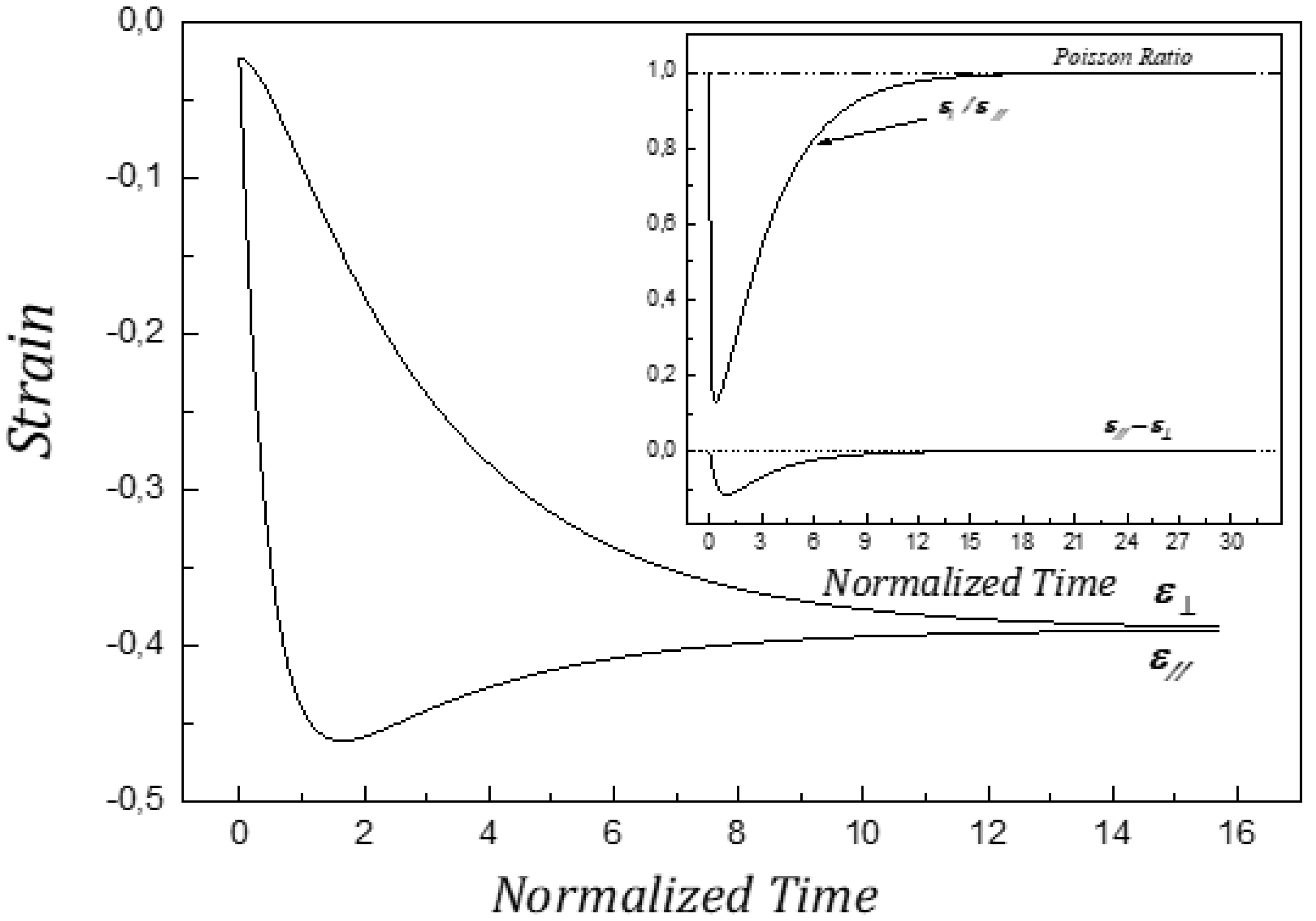
2.2. Strain Induced by Photo-Orientation
3. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sekkat, Z. Enhancement of molecular mobility in solid polymers by light: Fundamentals and applications. Appl. Phys. B Lasers Opt. 2022, 128, 19. [Google Scholar] [CrossRef]
- Sekkat, Z. Model for athermal enhancement of molecular mobility in solid polymers by light. Phys. Rev. E 2020, 102, 032501. [Google Scholar] [CrossRef] [PubMed]
- Karageorgiev, P.; Neher, D.; Schulz, B.; Stiller, B.; Pietsch, U.; Giersig, M.; Brehmer, L. From anisotropic photo-fluidity towards nanomanipulation in the optical near-field. Nat. Mater. 2005, 4, 699. [Google Scholar] [CrossRef] [PubMed]
- Fang, G.J.; Maclennan, J.E.; Yi, Y.; Glaser, M.A.; Farrow, M.; Korblova, E.; Walba, D.M.; Furtak, T.E.; Clark, N.A. Athermal photofluidization of glasses. Nat. Commun. 2013, 4, 1521. [Google Scholar] [CrossRef] [PubMed]
- Vapaavuori, J.; Laventure, A.; Bazuin, C.G.; Lebel, O.; Pellerin, C. Submolecular plasticization induced by photons in azobenzene materials. J. Am. Chem. Soc. 2015, 137, 13510. [Google Scholar] [CrossRef]
- Moujdi, S.; Rahmouni, A.; Mahfoud, T.; Nesterenko, D.V.; Halim, M.; Sekkat, Z. Surface relief gratings in azo-polymers revisited. J. Appl. Phys. 2018, 124, 213103. [Google Scholar] [CrossRef]
- Gotze, W.; Sjogren, L. Relaxation processes in supercooled liquids. Rep. Prog. Phys. 1992, 55, 241. [Google Scholar] [CrossRef]
- Sekkat, Z.; Dumont, M. Photoassisted poling of azo dye doped polymeric films at room temperature. Appl. Phys. B 1992, 54, 486–489. [Google Scholar] [CrossRef]
- Sekkat, Z.; Dumont, M. Poling of polymer films by photoisomerization of azo dye chromophores. Mol. Cryst. Liq. Cryst. Sci. Technol. B 1992, 2, 359–362. [Google Scholar]
- Rahmouni, A.; Bougdid, Y.; Moujdi, S.; Nesterenko, D.V.; Sekkat, Z. Photoassisted holography in azo dye doped polymer films. J. Phys. Chem. B 2016, 120, 11317. [Google Scholar] [CrossRef]
- Maeda, M.; Ishitobi, H.; Sekkat, Z.; Kawata, S. Polarization storage by nonlinear orientational hole burning in azo dye-containing polymer films. Appl. Phys. Lett. 2004, 85, 351–353. [Google Scholar] [CrossRef]
- Shi, Y.; Steier, W.H.; Yu, L.; Chen, M.; Dalton, L.R. Large stable photoinduced refractive index change in a nonlinear optical polyester polymer with disperse red side groups. Appl. Phys. Lett. 1991, 58, 1131–1133. [Google Scholar] [CrossRef]
- Rochon, P.; Gosselin, J.; Natansohn, A.; Xie, S. Optically induced and erased birefringence and dichroism in azoaromatic polymers. Appl. Phys. Lett. 1992, 60, 4–5. [Google Scholar] [CrossRef]
- Rochon, P.; Batalla, E.; Natansohn, A. Optically induced surface gratings on azoaromatic polymer films. Appl. Phys. Lett. 1995, 66, 136–138. [Google Scholar] [CrossRef]
- Kim, D.Y.; Tripathy, S.K.; Li, L.; Kumar, J. Laser-induced holographic surface relief gratings on nonlinear optical polymer films. Appl. Phys. Lett. 1995, 66, 1166–1168. [Google Scholar] [CrossRef]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Materials. 2015, 14, 1087–1098. [Google Scholar] [CrossRef]
- Kuzyk, M.G.; Dawson, N.J. Photomechanical materials and applications: A tutorial. Adv. Opt. Photonics 2020, 12, 847–1011. [Google Scholar] [CrossRef]
- Lovrien, R. The photoviscosity effect. Proc. Natl. Acad. Sci. USA 1967, 57, 236–242. [Google Scholar] [CrossRef]
- Agolini, F.; Gay, F.P. Synthesis and properties of azoaromatic polymers. Macromolecules 1970, 3, 349–351. [Google Scholar] [CrossRef]
- White, T.J. Light to work transduction and shape memory in glassy, photoresponsive macromolecular systems: Trends and opportunities. J. Polym. Sci. B Polym. Phys. 2012, 50, 877–880. [Google Scholar] [CrossRef]
- Serak, S.; Tabiryan, N.; Vergara, R.; White, T.J.; Vaia, R.A.; Bunning, T.J. Liquid crystalline polymer cantilever oscillators fueled by light. Soft Matter. 2010, 6, 779–783. [Google Scholar] [CrossRef]
- Ikeda, T.; Mamiya, J.I.; Yu, Y. Photomechanics of liquid-crystalline elastomers and other polymers. Angew. Chem. Int. Ed. 2007, 46, 506–528. [Google Scholar] [CrossRef] [PubMed]
- Ada-Ioana, B.; Martella, D.; Nocentini, S.; Parmeggiani, C.; Rafael, T.; Wiersma, D.S. Light-Powered Microrobots: Challenges and Opportunities for Hard and Soft Responsive Microswimmers. Adv. Intell. Sysyt. 2021, 3, 2000256. [Google Scholar]
- Sekkat, Z.; Knoll, W. Photoisomerization and photo-orientation of azo dye in films of polymer: Molecular interaction, free volume, and polymer structural effects. In Photoreactive Organic Thin Films; Academic Press: Cambridge, MA, USA, 2002; pp. 107–143. [Google Scholar]
- Sekkat, Z. Optical tweezing by photomigration. Appl. Opt. 2016, 55, 259–268. [Google Scholar] [CrossRef] [PubMed]
- Sekkat, Z. Vectorial motion of matter induced by light fueled molecular machines. OSA Continuum. 2018, 1, 668–681. [Google Scholar] [CrossRef]
- Nesterenko, D.V.; Moujdi, S.; Hayashi, S.; Sekkat, Z. Simulation of photochemically induced motion of matter in gradient light fields. J. Appl. Phys. 2020, 127, 243106. [Google Scholar] [CrossRef]
- Irie, M.; Hirano, Y.; Hashimoto, S.; Hayashi, K. Photoresponsive polymers. 2. Reversible solution viscosity change of polyamides having azobenzene residues in the main chain. Macromolecules 1981, 14, 262–267. [Google Scholar] [CrossRef]
- Irie, M.; Menju, A.; Hayashi, K. Photoresponsive polymers. Reversible solution viscosity change of poly (methyl methacrylate) having spirobenzopyran side groups. Macromolecules 1979, 12, 1176–1180. [Google Scholar] [CrossRef]
- Zhou, B.; Bernhardt, E.; Bhuyan, A.; Ghorbanishiadeh, Z.; Rasmussen, N.; Lanska, J.; Kuzyk, M.G. Theoretical and experimental studies of photomechanical materials. J. Opt. Soc. Am. B 2019, 36, 1492–1517. [Google Scholar] [CrossRef]
- Finkelmann, H.; Nishikawa, E.; Pereira, G.G.; Warner, M. A new opto-mechanical effect in solids. Phys. Rev. Lett. 2001, 87, 015501. [Google Scholar] [CrossRef]
- Corbett, D.; Xuan, C.; Warner, M. Deep optical penetration dynamics in photobending. Phys. Rev. E 2015, 92, 013206. [Google Scholar] [CrossRef] [PubMed]
- Corbett, D.; Van Oosten, C.L.; Warner, M. Nonlinear dynamics of optical absorption of intense beams. Phys. Rev. A 2008, 78, 013823. [Google Scholar] [CrossRef]
- Yu, Y.; Nakano, M.; Ikeda, T. Directed bending of polymer film by light. Nature 2003, 425, 145. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Nakano, M.; Shishido, A.; Shiono, T.; Ikeda, T. Alignment modulation of azobenzene-containing liquid crystal systems by photochemical reactions. Chem. Mater. 2004, 16, 1637. [Google Scholar] [CrossRef]
- Sekkat, Z.; Wood, J.; Knoll, W. Reorientation mechanism of azobenzenes within the trans .fwdarw. cis photoisomerization. J. Phys. Chem. 1995, 99, 17226–17234. [Google Scholar] [CrossRef]
- Yasumatsu, D.; Sekkat, Z.; Kawata, S. Pure photoorientation of azo dye in polyurethanes and quantification of orientation in spectrally overlapping isomers. J. Phys. Chem. B 2002, 106, 12407–12417. [Google Scholar]
- Sperling, L.H. Introduction to Physical Polymer Science; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Tanchak, O.M.; Barrett, C.J. Light-induced reversible volume changes in thin films of azo polymers: The photomechanical effect. Macromolecules 2005, 38, 10566–10570. [Google Scholar] [CrossRef]
- Wang, D.H.; Wie, J.J.; Lee, K.M.; White, T.J.; Tan, L.-S. Impact of backbone rigidity on the photomechanical response of glassy, azobenzene-functionalized polyimides. Macromolecules 2014, 47, 659–667. [Google Scholar] [CrossRef]
- Kondo, M.; Yu, Y.; Ikeda, T. How does the intial alignment of mesogens affect the photo-induced bending behavior of liquid-crystalline elastomers. Angew. Chem. Int. Ed. 2006, 45, 1378–1382. [Google Scholar] [CrossRef]
- Sekkat, Z.; Wood, J.; Geerts, Y.; Knoll, W. A Smart Ultra-thin Photochromic Layer. Langmuir 1995, 11, 2856. [Google Scholar] [CrossRef]
- White, T.J. Photomechanical Materials, Composites, and Systems: Wireless Transduction of Light into Work; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Cviklinski, J.; Tajbakhsh, A.R.; Terentjev, E.M. UV isomerization in nematic elastomers as a route to photo-mechanical transducer. Eur. Phys. J. E 2002, 9, 427–434. [Google Scholar] [CrossRef] [PubMed]
- Tabiryan, N.; Serak, S.; Dai, X.-M.; Bunning, T. Polymer film with optically controlled form and actuation. Opt. Express 2005, 13, 7442–7448. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekkat, Z. Photomechanical Solid Polymers: Model for Pressure and Strain Induced by Photoisomerization and Photo-Orientation. Appl. Sci. 2023, 13, 321. https://doi.org/10.3390/app13010321
Sekkat Z. Photomechanical Solid Polymers: Model for Pressure and Strain Induced by Photoisomerization and Photo-Orientation. Applied Sciences. 2023; 13(1):321. https://doi.org/10.3390/app13010321
Chicago/Turabian StyleSekkat, Zouheir. 2023. "Photomechanical Solid Polymers: Model for Pressure and Strain Induced by Photoisomerization and Photo-Orientation" Applied Sciences 13, no. 1: 321. https://doi.org/10.3390/app13010321
APA StyleSekkat, Z. (2023). Photomechanical Solid Polymers: Model for Pressure and Strain Induced by Photoisomerization and Photo-Orientation. Applied Sciences, 13(1), 321. https://doi.org/10.3390/app13010321




