A Full Loading-Based MVDR Beamforming Method by Backward Correction of the Steering Vector and Reconstruction of the Covariance Matrix
Abstract
1. Introduction
2. Conventional Diagonal Loading Methods
3. The Proposed Method
3.1. Framework of the Proposed Method
3.2. The Improved GLC Method
3.2.1. Full Loading of the Covariance Matrix
3.2.2. Solution of the Non-Negative Shrinkage Parameters
3.3. Backward Correction of the Steering Vector of the Target Source
3.4. Reconstruction of the Covariance Matrix
3.5. MVDR Beamforming
3.6. DOA Deduction through the Spatial Response Power and Iteration
- Step 1: Calculate the CMOS RXX through Equation (3);
- Step 2: Calculate the loaded covariance matrix RIGLC through Equation (10);
- Step 3: Correct the steering vector of the target source through Equation (15) and normalize it;
- Step 4: Reconstruct the covariance matrix Rrec through Equation (16), and normalize it;
- Step 5: Calculate the weighting vector wproposed through Equation (20);
- Step 6: Calculate the spatial response power ψ(ϑ) through Equation (21) and derive a new DOA of the target source;
- Step 7: Update the DOA of the target source and return to Step 2 to repeat the procedures from Step 2 to Step 6 until the derived DOA of the target source is converged.
4. Simulations and Analysis
4.1. Simulation Setup
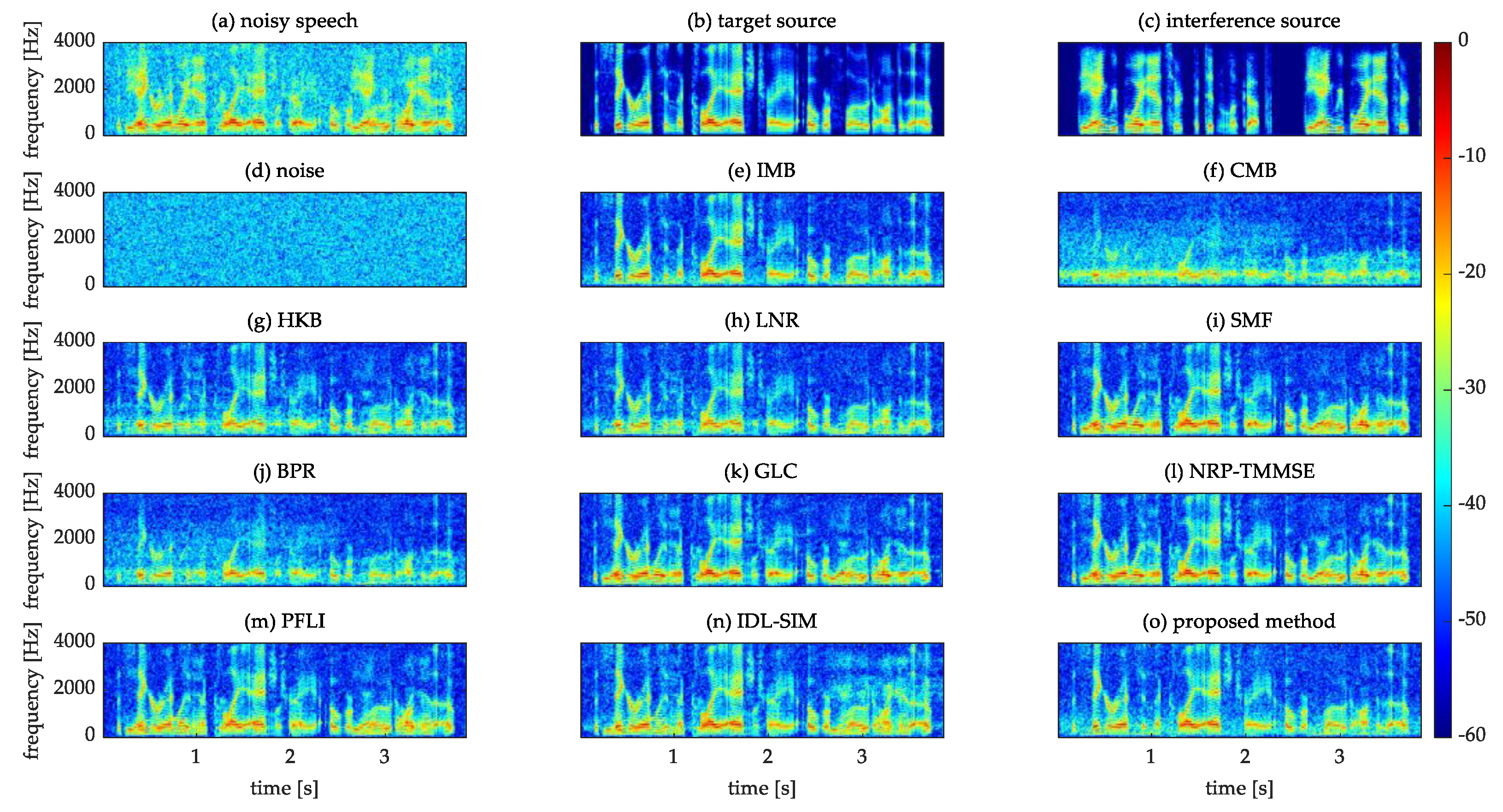
4.2. Comparison of Spectrograms
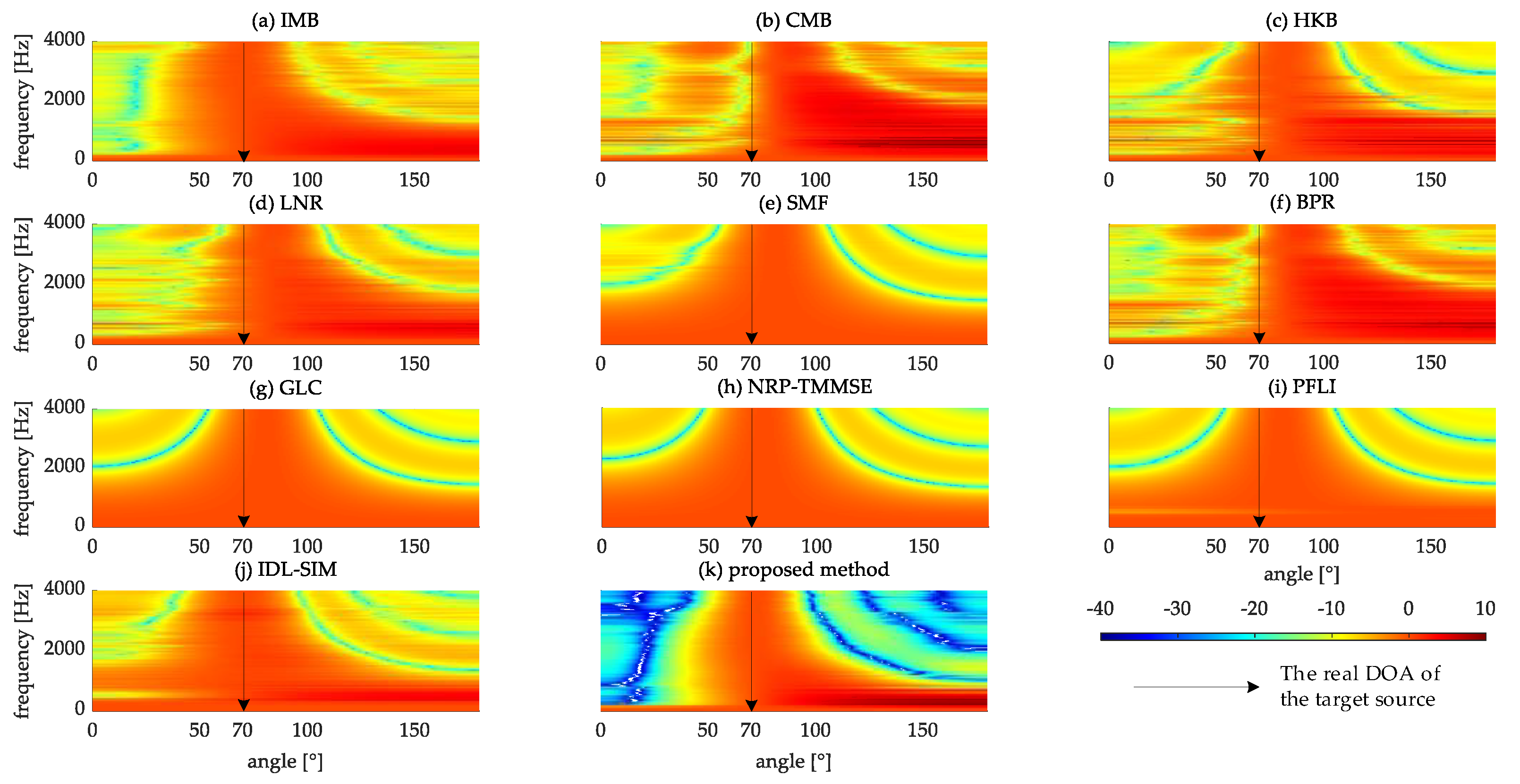
4.3. Comparison of Beampatterns
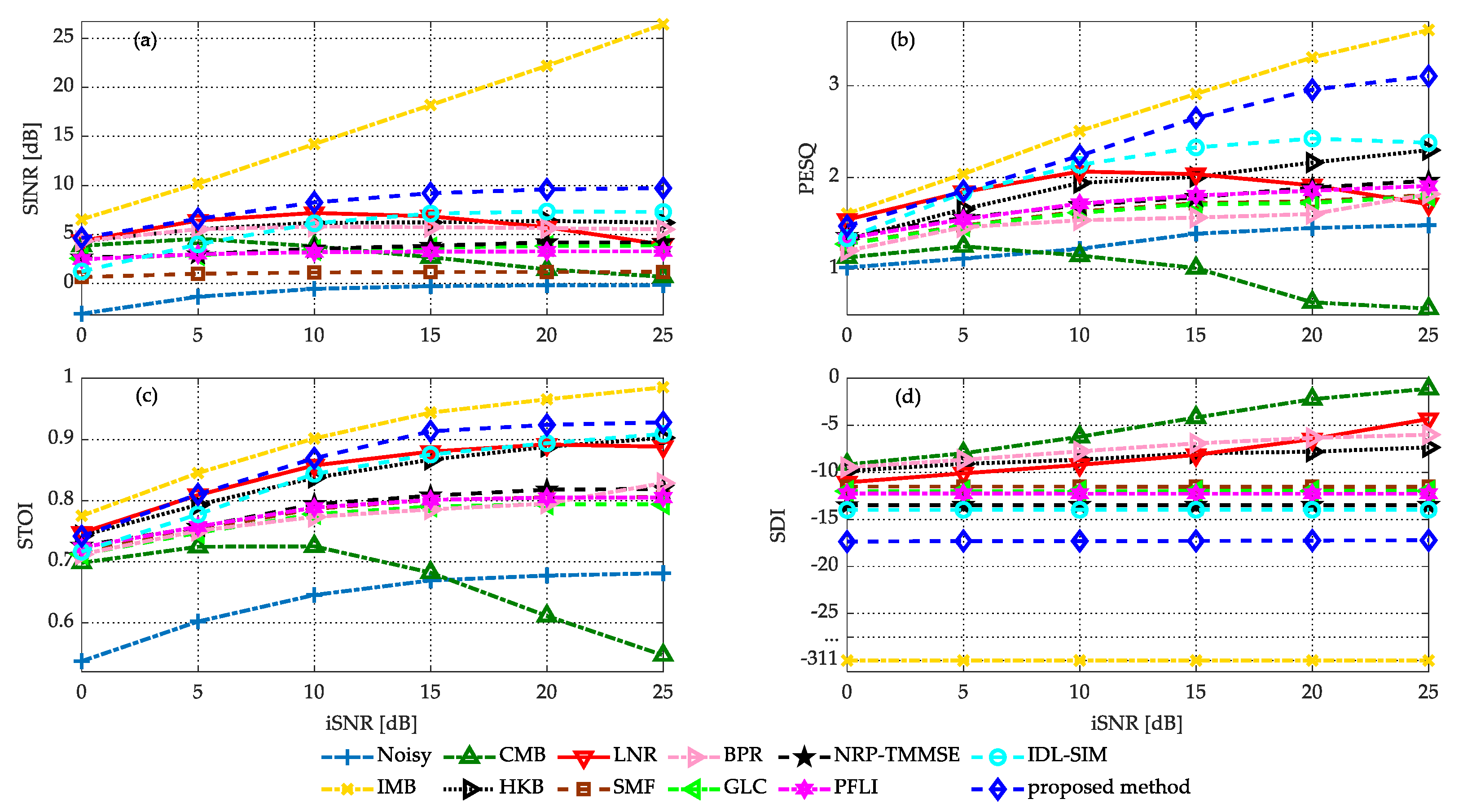
4.4. Comparison of Evaluation Measures
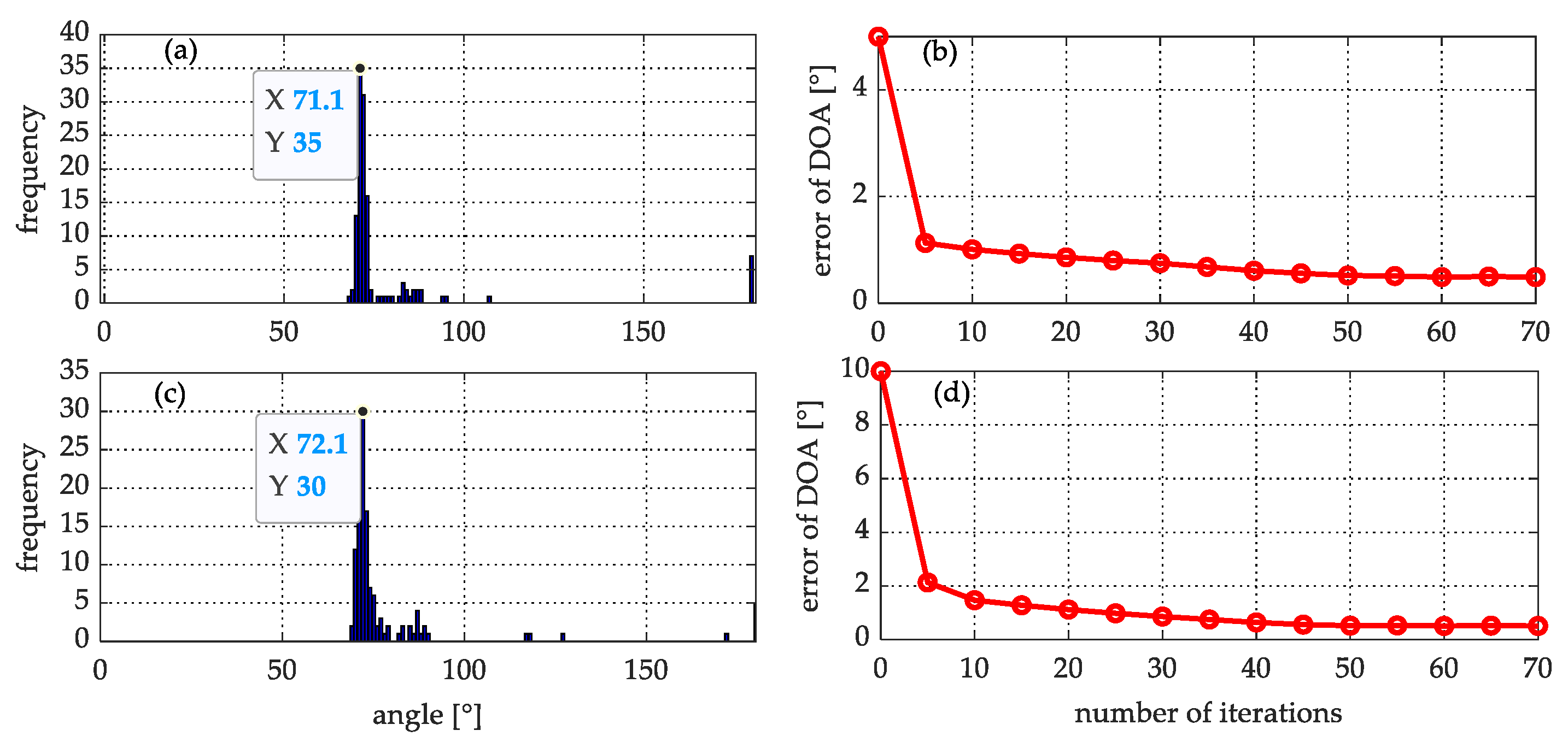
4.5. Verification of the DOA Deduction through the Spatial Response Power
4.6. Performance Analysis of the Optimization Modules
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zoltowski, M. On the performance analysis of the MVDR beamformer in the presence of correlated interference. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 945–947. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. Microphone Array Signal Processing; Springer-Verlag: Berlin, Germany, 2008; pp. 52–54. [Google Scholar]
- Souden, M.; Benesty, J.; Affes, S. A Study of the LCMV and MVDR Noise Reduction Filters. IEEE Trans. Signal Process. 2010, 58, 4925–4935. [Google Scholar] [CrossRef]
- Vorobyov, S.A. Principles of minimum variance robust adaptive beamforming design. Signal Process. 2013, 93, 3264–3277. [Google Scholar] [CrossRef]
- Pan, C.; Chen, J.; Benesty, J. Performance Study of the MVDR Beamformer as a Function of the Source Incidence Angle. IEEE/ACM Trans. Audio Speech Lang. Process. 2013, 22, 67–79. [Google Scholar] [CrossRef]
- Gu, Y.; Leshem, A. Robust Adaptive Beamforming Based on Interference Covariance Matrix Reconstruction and Steering Vector Estimation. IEEE Trans. Signal Process. 2012, 60, 3881–3885. [Google Scholar] [CrossRef]
- Zhao, Y.; Jensen, J.; Jensen, T.; Chen, J.; Christensen, M. Experimental Study of Robust Acoustic Beamforming for Speech Acquisition in Reverberant and Noisy Environments. Appl. Acoust. 2020, 170, 107531. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Wang, Z. On robust Capon beamforming and diagonal loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kannard, R.W.; Baldwin, K.F. Ridge Regression: Some Simulations. Communications in Statistics-Theory and Methods; Marcel Dekker Inc.: New York, NY, USA, 1975; Volume 4, pp. 105–123. [Google Scholar]
- Carlson, B. Covariance matrix estimation errors and diagonal loading in adaptive arrays. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 397–401. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, A.; Yang, Q. Robust Adaptive Beamforming Based on Conjugate Gradient Algorithms. IEEE Trans. Signal Process. 2016, 64, 6046–6057. [Google Scholar] [CrossRef]
- Mahadi, M.; Ballal, T.; Moinuddin, M.; Al-Naffouri, T.; Al-Saggaf, U. A Robust LCMP Beamformer with Limited Snapshots. In Proceedings of the 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2021; pp. 1831–1835. [Google Scholar]
- Du, L.; Li, J.; Stoica, P. Fully Automatic Computation of Diagonal Loading Levels for Robust Adaptive Beamforming. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 449–458. [Google Scholar] [CrossRef]
- Ke, Y.; Zheng, C.; Peng, R.; Li, X. Robust Adaptive Beamforming Using Noise Reduction Preprocessing-Based Fully Automatic Diagonal Loading and Steering Vector Estimation. IEEE Access 2017, 5, 12974–12987. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Jin, M.; Ding, S. Parameter-Free Landweber Iteration Method for Robust Adaptive Beamforming. Circuits Syst. Signal Process. 2019, 39, 2716–2729. [Google Scholar] [CrossRef]
- Jin, W.; Jia, W.; Yao, M. Iterative Diagonally Loaded Sample Matrix Inverse Robust Adaptive Beamforming. J. Electron. Inform. Technol. 2012, 34, 1120–1125. [Google Scholar]
- Huang, Y.; Zhou, M.; Vorobyov, S.A. New Designs on MVDR Robust Adaptive Beamforming Based on Optimal Steering Vector Estimation. IEEE Trans. Signal Process. 2019, 67, 3624–3638. [Google Scholar] [CrossRef]
- Zhuang, J.; Ye, Q.; Tan, Q.; Ali, A.H. Low-complexity variable loading for robust adaptive beamforming. Electron. Lett. 2016, 52, 338–340. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, X.; Zhang, A. A simple tridiagonal loading method for robust adaptive beamforming. Signal Process. 2018, 157, 103–107. [Google Scholar] [CrossRef]
- Muhammad, M.; Li, M.; Abbasi, Q.H.; Goh, C.; Imran, M.A. Adaptive Diagonal Loading Technique to Improve Direction of Arrival Estimation Accuracy for Linear Antenna Array Sensors. IEEE Sensors J. 2022, 22, 10986–10994. [Google Scholar] [CrossRef]
- Chen, P.; Gao, J.; Wang, W. Linear Prediction-Based Covariance Matrix Reconstruction for Robust Adaptive Beamforming. IEEE Signal Process. Lett. 2021, 28, 1848–1852. [Google Scholar] [CrossRef]
- Pezeshki, A.; Van Veen, B.D.; Scharf, L.L.; Cox, H.; Nordenvaad, M.L. Eigenvalue Beamforming Using a Multirank MVDR Beamformer and Subspace Selection. IEEE Trans. Signal Process. 2008, 56, 1954–1967. [Google Scholar] [CrossRef]
- Zhou, M.; Ma, X.; Shen, P.; Sheng, W. Weighted Subspace-Constrained Adaptive Beamforming for Sidelobe Control. IEEE Commun. Lett. 2019, 23, 458–461. [Google Scholar] [CrossRef]
- Feng, Y.; Liao, G.; Xu, J.; Zhu, S.; Zeng, C. Robust adaptive beamforming against large steering vector mismatch using multiple uncertainty sets. Signal Process. 2018, 152, 320–330. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, Z.; Liao, G.; Jing, G.; Ma, T. An RCB-Like Steering Vector Estimation Method Based on Interference Matrix Reduction. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 636–646. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, Y. Complex Quadratic Optimization and Semidefinite Programming. SIAM J. Optim. 2006, 16, 871–890. [Google Scholar] [CrossRef]
- Garofolo, J.S.; Lamel, L.; Fisher, W.M.; Fiscus, J.G.; Pallett, D.S. DARPA TIMIT Acoustic-Phonetic Continous Speech Corpus CD-ROM. In NIST Speech disc 1-1.1. NASA STI/Recon Technical Report N 93, 27403; NASA: Washington, DC, USA, 1993. [Google Scholar]
- Cheng, R.; Bao, C.; Cui, Z. MASS: Microphone Array Speech Simulator in Room Acoustic Environment for Multi-Channel Speech Coding and Enhancement. Appl. Sci. 2020, 10, 1484. [Google Scholar] [CrossRef]
- Rix, A.W.; Beerends, J.G.; Hollier, M.P.; Hekstra, A.P. Perceptual evaluation of speech quality (PESQ)-A new method for speech quality assessment of telephone networks and codecs. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Salt Lake City, UT, USA, 7–11 May 2001; pp. 749–752. [Google Scholar] [CrossRef]
- Taal, C.H.; Hendriks, R.C.; Heusdens, R.; Jensen, J. An Algorithm for Intelligibility Prediction of Time–Frequency Weighted Noisy Speech. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2125–2136. [Google Scholar] [CrossRef]


| Methods | Diagonal Loading | Methods | Diagonal Loading |
|---|---|---|---|
| HKB | LNR | ||
| SMF | BPR | ||
| GLC | NRP-TMMSE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Bao, C. A Full Loading-Based MVDR Beamforming Method by Backward Correction of the Steering Vector and Reconstruction of the Covariance Matrix. Appl. Sci. 2023, 13, 285. https://doi.org/10.3390/app13010285
Zhou J, Bao C. A Full Loading-Based MVDR Beamforming Method by Backward Correction of the Steering Vector and Reconstruction of the Covariance Matrix. Applied Sciences. 2023; 13(1):285. https://doi.org/10.3390/app13010285
Chicago/Turabian StyleZhou, Jing, and Changchun Bao. 2023. "A Full Loading-Based MVDR Beamforming Method by Backward Correction of the Steering Vector and Reconstruction of the Covariance Matrix" Applied Sciences 13, no. 1: 285. https://doi.org/10.3390/app13010285
APA StyleZhou, J., & Bao, C. (2023). A Full Loading-Based MVDR Beamforming Method by Backward Correction of the Steering Vector and Reconstruction of the Covariance Matrix. Applied Sciences, 13(1), 285. https://doi.org/10.3390/app13010285





