Abstract
It is important to detect the defect of products efficiently in modern industrial manufacturing. Image processing is one of common techniques to achieve defect detection successfully. To process images degraded by noise and lower contrast effects in some scenes, this paper presents a new energy functional with background fitting, then deduces a novel model which approximates to estimate the smoothed background and performs the nonlinear diffusion on the residual image. Noise removal and background correction can be both successfully achieved while the defect feature is preserved. Finally, the proposed method and some other comparative methods are performed on several experiments with some classical degraded images. The numerical results and quantitative evaluation show the efficiency and advantages of the proposed method.
1. Introduction
Image processing has become more and more important in many fields, such as machine vision, geological prospecting, medical imaging, defect detection, and so on. In the past decades, many methods have been presented based on different views, and nonlinear diffusion is one of the most important techniques for the solid mathematical physics foundation [1,2,3]. Different from the uniform diffusion (holds the same velocity along any direction), nonlinear diffusion can be applied to describe lots of complex natural phenomenons. Nonlinear diffusion models are often driven by partial differential equations (PDEs) which can be derived by minimizing an energy functional and computing the Euler–Lagrange equation [4,5].
Perona and Malik (PM) proposed a nonlinear diffusion model with a fixed edge stop velocity function related to the local gradient mode [6]. It can be applied to achieve some denoising tasks with homogeneous features and noise; however, it is difficult to efficiently govern the diffusion process for some more complex cases. Rudin, Osher and Fatemi (ROF) proposed the classical total variation model to recover noisy images by minimizing a geometric energy functional [1]. The diffusion can be performed only along the edge to preserve the image features and remove the noise.
Though these traditional methods have been reported to work well in many cases, they are still found to show some unfavorable phenomena, such as the staircase effect, loss of texture features, and so on [7,8]. Especially in many industrial scenes, the lighting condition is limited, inhomogeneous and easy to be disturbed so that the observed images are often low-contrast, have an inhomogeneous background and are serious polluted. It is often not a good idea to directly apply the traditional models to these degraded images for defect detection since the mentioned unfavorable effects often become worse in such situations.
Defects detection is often implemented on the images captured by some vision devices, which are effected by some objective factors, such as noise level, brightness, background gray distribution, size and shape of the defects. Lots of efforts have been made to present novel models or algorithms based on different starting points and proper assumptions. Saitoh [9] presented a machine vision scheme for the inspection of brightness unevenness in LCD panel surfaces. An edge detection algorithm and a genetic algorithm were used to identify discontinuous points and extract the boundary of anomalous brightness region, respectively. Kim et al. [10] presented an adaptive multiple-level threshold method based on the statistical characteristics of the local area to segment spot-type defects from the background surface. Ng revised the Otsu method for selecting optimal threshold values for both unimodal and bimodal distributions and tested the performance on common defect detection applications [11]. Krummenacher proposed two machine learning methods to automatically detect the wheel defects, which automatically learn different types of wheel defects and predict during normal operation if a wheel has a defect or not [12].
In recent years, with different views or assumptions, several improved nonlinear diffusion models were presented for different tasks about image processing and defect detection. Tsai and Chao took a non-negative decreasing function with an annealing gradient threshold as the diffusion coefficient, and then proposed a novel anisotropic diffusion model (TCAD) to detect subtle defects embedded in inhomogeneous textures [13]. Chao and Tsai introduced a weighted diffusion function and a generalized diffusion coefficient function respectively to the classical PM model for defect detection in low-contrast surface images [14,15]. These two models both carry out a smoothing process for faultless areas and perform a sharpening process for defect areas. Based on the directional Laplacian, Wang et al. proposed a modified version (MPM) of the original Perona–Malik model [16]. A weighted Laplacian was incorporated in the PM model to perform the diffusion along the edge direction of the original image. Prasath and Vorotnikov proposed a weighted and balanced anisotropic diffusion scheme for image denoising and restoration [17]. Maiseli and Gao presented a robust edge detector based on an anisotropic diffusion-driven process [18]. In this model, noise suppression and edge enhancement are achieved respectively by anisotropic diffusion and the edge-sensitive detector.
Xu et al. [19] contributed a new filter by introducing a semi-adaptive threshold to an anisotropic diffusion process. In detail, a Gaussian filter is applied to recognize corrupted pixels in noise-free pixels and then a semi-adaptive threshold function is introduced to the diffusion coefficient for noise removal and edge preservation. Malarvela et al. found that the local probability value of image gray can be applied to adjust the indication degree of a low edge gradient in the feature space of a noisy image, similar to the action of an adaptive threshold parameter [20]. They proposed an improved anisotropic diffusion model which can adaptively adjust the implication of the image edge gradient in the diffusion process. More research studies about defect detection and image denoising related to other techniques refer to some recent papers [21,22,23,24,25].
Based on the above, it can be found most research focuses on designing novel diffusion patterns or using the observed information in new schemes. However, in complex scenes, inconsistent background and features should be properly treated for efficient defect detection. The gradient, Laplacian and some other geometric metrics are often used to describe the observed image features, and they are easily disturbed by an uneven background. In this paper, a novel hybrid energy based on L1 and L2 is introduced to a constrained optimization problem. Then the corresponding Euler–Lagrange equations are derived to form a nonlinear diffusion with a smoothed background estimation, which can remove the noise and preserve more details of the defect features.
This paper is organized as follows. In Section 2, the basic fundamentals of defect detection and nonlinear diffusion are introduced. Then the proposed model based on a novel hybrid functional is introduced in Section 3; the algorithm and numerical scheme are also presented. Section 4 shows the experiments and results.
2. Basis and Fundamentals
Image degradation is a common situation in transmitting image information and recording digital images, but in many practical applications, high-quality images are necessary, so effective methods to improve and recover degraded images are worthy of our study. In this section, we will briefly describe some important image denoising models based on partial differential equations and anisotropic diffusion.
2.1. Nonlinear Diffusion
Perona and Malik proposed a classical nonlinear diffusion model based on the linear diffusion (or heat equation) [6], and the diffusion process can be represented by a partial differential equation:
where refers to the image at time t, div means the divergence operator, means the spatial gradient of the image at time t, and k denotes a threshold linked to the features strength. This partial differential equation can be derived by minimizing a related energy functional:
Here means a diffusion velocity, and it can be replaced by other function as necessary.
In the PM model, the diffusion velocity is determined by a fixed pattern at each iteration, which reduces the diffusion as the gradient module increases to protect the edges present in the image. Some degraded images can be successfully recovered by solving the above equation with a proper initial condition and boundary condition, even if the artifacts still occur in the result due to the instability of the diffusion process.
The total variation model (TV) is another representative one of nonlinear diffusion models, and it was first proposed by Rudin, Osher and Fatami [1]. The bounded variation (BV) function is introduced to denote the ideal image and then the discontinuities edge can be well-preserved when removing the noise. This model has been widely applied to many other fields as a regularization technique [26]. It can be denoted as
Here, f denotes the observed degraded image and is a Lagrangian multiplier which balances different terms. It can be obtained by minimizing a combined energy functional
Differing from the diffusion controlling mechanism of the PM model, the TV model prevents smoothing across the edge everywhere, even if in an almost plain area. For preserving the discontinuous edge and smoothing the approximately flat area, it is often necessary to carefully design numerical schemes with a small time step.
Based on the TV model and the PM model, lots of research has been presented to improve the results at different views [3,27,28,29]. The CTAD model [30] was presented to treat the restoration tasks on astronomical images. The local variance of the image gray is embedded in the diffusion velocity of the model for an adaptive process. Specifically, the advanced diffusion velocity is denoted as
where is the local variance of gray levels in a proper neighborhood.
A weighted Laplacian was incorporated the modified Perona–Malik model, where the directional Laplacian diffuses the image along the edge direction of the original image [16]. In this model, the diffusion is designed along a unit directional vector , and the noise can be suppressed by the weighted Laplace operator. The related partial differential equation can be denoted as
where , denotes a small positive constant and f is the observed degraded image.
Malarvel et al. proposed a modified model that introduces both a probability value and gradient of local image gray to reduce the noise and smooth the noise-free part adaptively [20]. Thee diffusion velocity can be denoted as
Here parameter k should be a positive fixed constant, and it is related to the strength to denoise and enhance the edge. The input variable p is related to the local gray distribution, and it can be calculated based on image I.
In this paper, we will first introduce several fields related to smoothed estimation and edge information, and then present a novel dynamic mechanism based on them to better determine the diffusion velocity for improvements of the denoising results.
2.2. Some Evaluation Metrics
To measure the qualities of image processing results, some metrics are often applied to calculate the evaluation values. The general evaluation metrics include but are not limited to mean square error (MSE), peak signal-to-noise ratio (PSNR), entropy (ET) and structural similarity (SSIM).
The dissimilarity between the referenced image and the result image can be measured by MSE, which means the loss of image quality. Assume that the image size is , MSE can be calculated as
The PSNR can be defined as
Here, L means the gray level. The lower the MSE, the lesser the error, and MSE is inversely proportional to PSNR.
The entropy is a measure widely applied in many fields such as data mining and image processing. A lesser entropy value implies lesser disorder. The common Shannon entropy (10) can be used to evaluate the disorder degree or variance of a result image:
Here, means the gray ratio on the ith bin of the normalized image histogram.
SSIM measures the image quality by computing the similarity between the result image and reference image. The SSIM value is limited in and a larger value indicates that the result image is more similar to the original one.
where and represent the average pixels of the two images, and represent the standard variance of I and u, is the covariance, and constant .
3. The Proposed Method
In many complex scenes, image will suffer from inconsistent noise and varying lighting condition, which leads to a nonuniform background. Traditional models can often successfully treat the consistent degradation and uniform background (no or little change in each parts) while being deficient for inconsistent cases. For example, the noise strength is very different in some parts of the image area, the edge consists of some strong parts and some weak parts, and the background gray of some parts are at different levels (inconsistent background). Here, we focus on the image degraded by Gaussian white noise and an inconsistent background.
In this paper, a background gray surface is introduced to the observation model for complex scenes, and then a novel functional based on the combination of L1 and L2 energy is presented to modify the traditional total variation energy. Then, novel nonlinear diffusion equations can be derived to remove the noise and separate the inconsistent background by minimizing the energy functional.
3.1. A Novel Energy Functional
The existence of an inconsistent background (which different in parts) is disadvantageous for treating the polluted and low-contrast image. More exactly, many geometric terms (such as gradient, Laplacian, etc.) are unavoidable to be polluted by not only noise, but also the inconsistent background. Accurate estimation of the background can help to remove the noise and enhance the image quality more efficiently. The observation can be generally denoted as , and a simple example is shown in the first row of Figure 1. Here, f is the observed image polluted by Gaussian white noise n with variance and inconsistent background v, and I is the clear version of f. Assume that v is almost smooth everywhere, then a novel energy functional is presented as
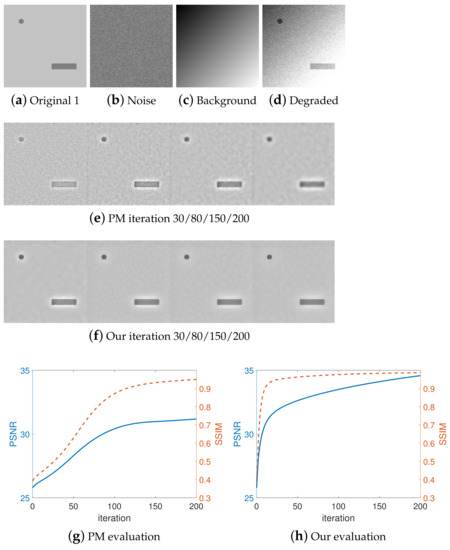
Figure 1.
Traditional result and our result on artificial image 1.
It can be found that the first term means the total variation of the ideal image I. The second term is the energy of the gradient field of background v and the minimization can be linked to solve a smoothing version of v. The third term is the total variation of , and the minimization means an edge-preserved process. and are both weight factors to balance these terms.
Based on the observation model, the variance prior of the noise can be related to a fitting functional . In a dynamic minimization process, it can limit the solved not far away from the observation f. Then an optimization problem to determine can be denoted as
Apply the Lagrange method and then the above problem is equivalent to an unconstrained optimization problem, that is
Here, means a Lagrange multiplier to combine the geometric energy and the fitting error. Apply the following Euler–Lagrange equations to compute the gradient flow of (13), and introduce the artificial term , the final evolution equations can be obtained as (14)
In the evolution, the first equation will preserve the features, including defects to be detected due to the two total variation diffusion terms. The second equation is mainly to approximate the ideal background v while features are well-protected.
Set the homogeneous Neumann boundary condition on , that is
where means the normal vector on the boundary . Set the initial condition in
then Equation (14) can be solved by some numerical methods, such as finite difference.
Here, means an initial estimation of the background. Figure 1 shows the traditional evolution and the proposed evolution on an artificial image with two suspect areas. The first row shows the original image, the noise, the inconsistent background and the degraded image. As shown in Figure 1d, the clear image is polluted by Gaussian noise (Signal to Noise Ratio, SNR = 20) and an inconsistent background. The top-left seems underexposed, and the bottom-right looks overexposed. With PM model performance, the noise removal and edge preservation can be well balanced under the influence of an inconsistent background (as shown in Figure 1e). Applying our model on the degraded image, noise and inconsistent background are both reduced while the edge is preserved (as shown in Figure 1f). The PSNR curve and SSIM curve are shown in Figure 1g,h.
3.2. Numerical Scheme
In this paper, the spatial domain is discretized by a grid domain and the time interval is discretized as . Then the numerical solution of at can be denoted as .
Apply the minmod scheme [1] to approximate the TV diffusion terms, and apply central difference to approximate all other differential term, then an efficient numerical scheme for the proposed model (14) can be denoted as
Here, is denoted as
and the Lagrange multipliers can be determined by
or
After discretization of the boundary condition and initial condition by the central difference scheme, the numerical algorithm can be implemented efficiently.
4. Experiments and Results
In this section, the proposed method will be performed on some experiments for detailed evaluation. The test images are shown in Figure 2 and the first two are artificial ones. The subsequent four are randomly selected from classical image datasets, such as miscellaneous of USC-SIPI (http://sipi.usc.edu/database/, accessed on 1 September 2022). The last six are collected from real industrial scenes.

Figure 2.
Test images.
Different Gaussian white noise and background surfaces will be acted on the first three test images for their degraded version, which will be processed by the proposed method and other comparative methods, such as PM [6], TV [1], CTAD [30], mPM (modified PM) [16], Malarvel [20], and so on. The last three will be processed respectively to verify the performance of the proposed method on actual data.
4.1. Experiment 1: Artificial Images Test
To evaluate the performance of the proposed method working on different degradation levels, in this experiment, Gaussian noise at different levels (SNR = 12, 14, 16, 18, 20) and a inhomogeneous background surface are added to two artificial images respectively as shown in Figure 3a. The same initial estimation of the restoration image without an inhomogeneous background is configured to solve the five models.

Figure 3.
Results of test on artificial image 1.
The results achieved by different methods are shown in Figure 3b–f and Figure 4b–f. The one to five columns refer the results of PM, TV, CTAD, Malarvel, and our method. It is found that the noise can be reduced to some extent in different levels by each method. The treatment effects of the four traditional methods are affected by an inhomogeneous background and lead to lower evaluations. Benefit from the background fitting mechanism, the proposed model can achieve better results.

Figure 4.
Results of test on artificial image 2.
The results are evaluated by two metrics (PSNR and SSIM) for full comparison. It can be found that the proposed method achieves the best performance in each degradation level. About the artificial image 1, our PSNR is on average 6.88% higher than the other four methods, while the SSIM is at least 2.05% higher than the traditional results. More details refer to Figure 3g,h and Table 1. A similar situation can be found on the test of artificial image 2, as shown in Figure 4 and Table 2. The iteration numbers are shown in Figure 5. Fewer iterations are required by our method.

Table 1.
Results evaluation on artificial image 1.

Table 2.
Results evaluation on artificial image 2.
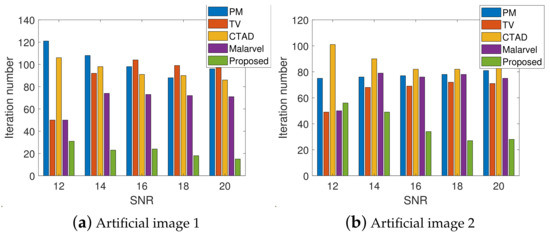
Figure 5.
Iteration numbers.
4.2. Experiment 2: Natural Images Test
In this experiment, a more inhomogeneous artificial background is added to the two natural images with five levels of noise (SNR = 12, 14, 16, 18, 20) as shown in Figure 6a, Figure 7a, Figure 8a and Figure 9a.

Figure 6.
Results of Fruits image in Experiment 2.

Figure 7.
Results of House image in Experiment 2.

Figure 8.
Results of dogs image in Experiment 2.

Figure 9.
Results of plane image in Experiment 2.
The four natural images results achieved by different methods are shown in Figure 6b–f, Figure 7b–f, Figure 8b–f and Figure 9b–f. Each column refers the results of a method; one to five refer to the results of PM, TV, CTAD, Malarvel, and our method. It is found that the noise can be reduced to some extent in different levels by each method. However, the deficiency in treating the inhomogeneous background prevented the four traditional methods from achieving satisfying results. The proposed model was found to be more successful in obtaining high quality results.
PSNR and SSIM of the results are listed in Table 3, Table 4, Table 5 and Table 6. It can be found that the proposed method achieves the best performance in each degradation level. Our method achieves significant improvements of PSNR (at least 9.97% in average on the Fruits image and 7.44% on the House image) for the well treatments on an inhomogeneous background. A similar situation can be found about SSIM; in fact, our results are at least 1.15% larger on the Fruits image and 1.14% larger on the House image than other methods. The advancement of the performance can be also found in tests on the Dogs image and Plane image.

Table 3.
Fruits image experiment results evaluation.

Table 4.
House image experiment results evaluation.

Table 5.
Dogs image experiment results evaluation.

Table 6.
Plane image experiment results evaluation.
The iteration numbers are shown in Figure 10. Fewer iterations are required by our method.
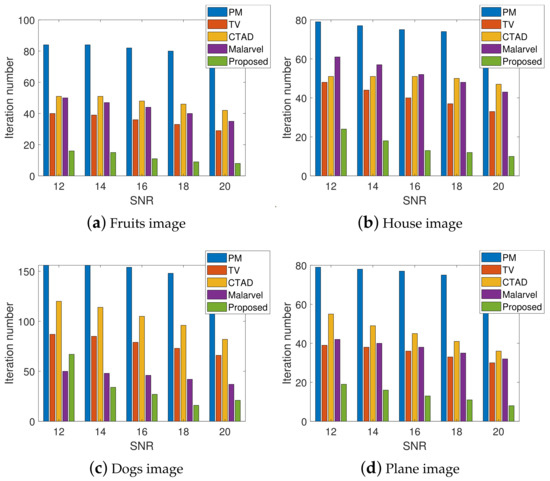
Figure 10.
Iteration numbers.
4.3. Experiment 3: Industrial Images Test
In this experiment, the five methods are applied to process six industrial images with some defects as shown in Figure 2g–l.
The six defect images results achieved by different methods are shown in Figure 11a–f. There is no reference image that can be applied to calculate PSNR or SSIM, so the standard variance (STD) and entropy will be applied to evaluate the results.

Figure 11.
Results of Industrial images in Experiment 3.
It is difficult to locate the defect in the original version of industrial image 1 directly by vision. After the five methods applied on indust1, the defect becomes clearer than the original, and it can be found that the proposed result is better than others (as shown in Figure 11a). The inhomogeneous background is removed from the main part of our result, while it can still be found in other results.
The suspect defect in the second image is very weak in vision, and it is also difficult to be found. The traditional methods strengthen the background difference between top part and bottom part. In this situation, it is disadvantageous to find a weak defect deeply hidden in a part of the background for the over-smoothing on each part. Our method excludes the inhomogeneous background, and the weak defect is more significant than other results (as shown in Figure 11b).
Though the main defects in the last four images are easy to be found and all the methods treat it well, some small features (maybe defects in other scenes) are smoothed in the results of PM, TV and CTAD. It seems that the Malarvel’s model better protects the features than our model because it preserves abundant details (suspect area). In fact, most of them are unnecessary details or noise; it may result in a more expensive check cost.
STD and entropy of the results are listed in Table 7. It can be found that the proposed method achieves the minimal STD or entropy on each image, that is, the results show less confusion and more regularity in the view of information theory.

Table 7.
Industrial image experiment results evaluation.
5. Conclusions
Many research studies have been presented to improve the image quality for defect detection, and very few of them take the inconsistent background into account. From our results, it is difficult for traditional models to treat some defect images well for the effects of inconsistent backgrounds. This paper presents novel nonlinear diffusion equations to achieve smoothed background estimation and denoising. It is helpful to improve the image quality for defect detection tasks, especially in some low-contrast cases. The numerical results and quantitative evaluation show the efficiency and advantages of proposed method. More efforts can be made to develop advanced models and algorithms for more practical solutions.
Author Contributions
Conceptualization, T.Y. and B.Z.; resources, B.X.; data curation, W.W.; writing—original draft preparation, B.X. and B.Z.; writing—review and editing, T.Y. and B.X.; visualization, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by Sichuan Science and Technology Program (No. 2021YJ0084) and Xi’an Science and Technology Plan Project (No. 2022JH-RGZN-0073).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to thank the anonymous reviewers for their insightful comments that helped improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Mumford, D.B.; Shah, J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 1989, 42, 577–685. [Google Scholar] [CrossRef]
- Prasath, V.S.; Vorotnikov, D.; Pelapur, R.; Jose, S.; Seetharaman, G.; Palaniappan, K. Multiscale Tikhonov-total variation image restoration using spatially varying edge coherence exponent. IEEE Trans. Image Process. 2015, 24, 5220–5235. [Google Scholar] [CrossRef] [PubMed]
- Gelfand, I.M.; Silverman, R.A. Calculus of Variations; Courier Corporation: North Chelmsford, MA, USA, 2000. [Google Scholar]
- Aubert, G.; Kornprobst, P.; Aubert, G. Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations; Springer: Berlin/Heidelberg, Germany, 2006; Volume 147. [Google Scholar]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Chan, T.; Esedoglu, S.; Park, F.; Yip, A. Recent developments in total variation image restoration. Math. Model. Comput. Vis. 2005, 17, 17–31. [Google Scholar]
- Chen, Q.; Montesinos, P.; Sun, Q.S.; Heng, P.A. Adaptive total variation denoising based on difference curvature. Image Vis. Comput. 2010, 28, 298–306. [Google Scholar] [CrossRef]
- Saitoh, F. Boundary extraction of brightness unevenness on LCD display using genetic algorithm based on perceptive grouping factors. In Proceedings of the 1999 International Conference on Image Processing (Cat. 99CH36348), Kobe, Japan, 24–28 October 1999; Volume 2, pp. 308–312. [Google Scholar]
- Kim, W.S.; Kwak, D.M.; Song, Y.C.; Choi, D.H.; Park, K.H. Detection of spot-type defects on liquid crystal display modules. In Key Engineering Materials; Trans Tech Publ.: Bach, Switzerland, 2004; Volume 270, pp. 808–813. [Google Scholar]
- Ng, H.F. Automatic thresholding for defect detection. Pattern Recognit. Lett. 2006, 27, 1644–1649. [Google Scholar] [CrossRef]
- Krummenacher, G.; Ong, C.S.; Koller, S.; Kobayashi, S.; Buhmann, J.M. Wheel defect detection with machine learning. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1176–1187. [Google Scholar] [CrossRef]
- Tsai, D.M.; Chao, S.M. An anisotropic diffusion-based defect detection for sputtered surfaces with inhomogeneous textures. Image Vis. Comput. 2005, 23, 325–338. [Google Scholar] [CrossRef]
- Chao, S.M.; Tsai, D.M. An anisotropic diffusion-based defect detection for low-contrast glass substrates. Image Vis. Comput. 2008, 26, 187–200. [Google Scholar] [CrossRef]
- Chao, S.M.; Tsai, D.M. Anisotropic diffusion with generalized diffusion coefficient function for defect detection in low-contrast surface images. Pattern Recognit. 2010, 43, 1917–1931. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, J.; Chen, W.; Zhang, W. Image denoising using modified Perona–Malik model based on directional Laplacian. Signal Process. 2013, 93, 2548–2558. [Google Scholar] [CrossRef]
- Prasath, V.S.; Vorotnikov, D. Weighted and well-balanced anisotropic diffusion scheme for image denoising and restoration. Nonlinear Anal. Real World Appl. 2014, 17, 33–46. [Google Scholar] [CrossRef]
- Maiseli, B.J.; Gao, H. Robust edge detector based on anisotropic diffusion-driven process. Inf. Process. Lett. 2016, 116, 373–378. [Google Scholar] [CrossRef]
- Xu, J.; Jia, Y.; Shi, Z.; Pang, K. An improved anisotropic diffusion filter with semi-adaptive threshold for edge preservation. Signal Process. 2016, 119, 80–91. [Google Scholar] [CrossRef]
- Malarvel, M.; Sethumadhavan, G.; Bhagi, P.C.R.; Kar, S.; Saravanan, T.; Krishnan, A. Anisotropic diffusion based denoising on X-radiography images to detect weld defects. Digit. Signal Process. 2017, 68, 112–126. [Google Scholar] [CrossRef]
- Czimmermann, T.; Ciuti, G.; Milazzo, M.; Chiurazzi, M.; Roccella, S.; Oddo, C.M.; Dario, P. Visual-based defect detection and classification approaches for industrial applications—A survey. Sensors 2020, 20, 1459. [Google Scholar] [CrossRef]
- Cao, W.; Liu, Q.; He, Z. Review of pavement defect detection methods. IEEE Access 2020, 8, 14531–14544. [Google Scholar] [CrossRef]
- Mak, K.L.; Peng, P.; Yiu, K.F.C. Fabric defect detection using morphological filters. Image Vis. Comput. 2009, 27, 1585–1592. [Google Scholar] [CrossRef]
- Malarvel, M.; Singh, H. An autonomous technique for weld defects detection and classification using multi-class support vector machine in X-radiography image. Optik 2021, 231, 166342. [Google Scholar] [CrossRef]
- Luo, Q.; Fang, X.; Liu, L.; Yang, C.; Sun, Y. Automated visual defect detection for flat steel surface: A survey. IEEE Trans. Instrum. Meas. 2020, 69, 626–644. [Google Scholar] [CrossRef]
- Ogada, E.A.; Guo, Z.; Wu, B. An alternative variational framework for image denoising. In Abstract and Applied Analysis; Hindawi: London, UK, 2014; Volume 2014. [Google Scholar]
- Blomgren, P.; Chan, T.F.; Mulet, P.; Wong, C.K. Total variation image restoration: Numerical methods and extensions. In Proceedings of the International Conference on Image Processing, Santa Barbara, CA, USA, 26–29 October 1997; Volume 3, pp. 384–387. [Google Scholar]
- Gilboa, G.; Sochen, N.; Zeevi, Y.Y. Texture preserving variational denoising using an adaptive fidelity term. In Proceedings of the VLsM, Nice, France, 2003; Volume 3. [Google Scholar]
- Pang, Z.F.; Zhou, Y.M.; Wu, T.; Li, D.J. Image denoising via a new anisotropic total-variation-based model. Signal Process. Image Commun. 2019, 74, 140–152. [Google Scholar] [CrossRef]
- Chao, S.M.; Tsai, D.M. Astronomical image restoration using an improved anisotropic diffusion. Pattern Recognit. Lett. 2006, 27, 335–344. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).