Elastic Scattering Time–Gated Multi–Static Lidar Scheme for Mapping and Identifying Contaminated Atmospheric Droplets

Abstract

Numerical simulations are performed to determine the angular dependence of the MIe scattering cross-section intensities of pure water droplets and pollutants such as contaminated water droplets and black carbon as a function of the wavelength of the incident laser light, complex refractive index, and size of the scatterer. Our results show distinct scattering features when varying the various scattering parameters, thereby allowing the identification of the scattering particle with specific application to the identification of atmospheric pollutants including black carbon. Regardless of the type of scatterer, the scattering intensity is nearly uniform with a slight preference for forward scattering when the size of the particle is within 20% of the incident laser’s wavelength. The scattering patterns start to exhibit distinguishable features when the size parameter equals 1.77, corresponding to an incident laser wavelength of 0.355 μm and a particle radius of 0.1 μm. The patterns then become increasingly unique as the size parameter increases. Based on these calculations, we propose a time-gated lidar scheme consisting of multiple detectors that can rotate through a telescopic angle and be placed equidistantly around the scattering particles to collect the backscattered light and a commercially available Q-switched laser system emitting at tunable laser wavelengths. By using a pulsed laser with 10-ns pulse duration, our scheme could distinguish scattering centers that are at least 3 m apart. Our scheme called MIe Scattering Time-gated multi-Static LIDAR (MISTS–LIDAR) would be capable of identifying the type of atmospheric pollutant and mapping its location with a spatial resolution of a few meters.

1. Introduction

The air quality of highly urbanized cities is a major environmental and health concern as large amounts of air pollutants are produced rapidly by various anthropogenic activities. Along with carbon dioxide, short-lived climate pollutants (SLCP) including black carbon, methane, tropospheric ozone, and sulfate are responsible for up to 45% of the current global warming [1]. In addition, particulate matter (PM) pollution, especially when the size of the particle is smaller than 2.5 μm in diameter, is especially dangerous to human health as it can be inhaled into the deepest portions of the lungs. The main components of PM pollution are usually black carbon and sulfate. Non-volatile particulate matter such as sulfate, crustal material, and black carbon are already easily measured by a variety of techniques [2,3]. However, semi-volatile particulate matter such as ammonium nitrate, some organic materials, and water is more difficult to monitor. This is mainly because semi-volatile matter can escape from the particle samples during and after sampling for chemical analysis [4,5].

The scattering of light incident on the particles depends on the physical properties of these particles, such as their average size and composition [6,7]. Particles whose sizes are much smaller than the wavelength of the incident light are described through Rayleigh scattering whereas MIe scattering is more appropriate for particles whose diameter is similar to or larger than the wavelength of the incident light [8,9]. By evaluating the MIe scattering of light by the particles through the collection of scattered light from multiple angles, the physical properties of the particles can be deduced. The collection of scattered light can be accomplished by using a single detector that sweeps through an arc about the illuminated particles, a technique called differential light scattering [10]. Alternatively, instead of using a single detector, multiple detectors can be placed equidistantly around the scattering particles such that the scattered light can be collected simultaneously at multiple angles. This technique called multiangle light scattering is faster than differential light scattering and is, therefore, one of the most widely used techniques for collecting the scattered light [11,12]. In both techniques, the physical properties of the scattering particles are deduced from the angular dependence of the average intensity of the scattered light. However, the dependence of the scattering cross section on the wavelength of the incident light, the complex refractive index of the scatterer, the absorption coefficient of the scatter, and size of the scatter has not been investigated yet, especially in the context of lidar monitoring of particulate matter in the atmosphere. In this work, we perform numerical simulations to determine the angular dependence of the MIe scattering cross-section of pure water droplets, contaminated water droplets and black carbon as a function of the wavelength of the incident laser light, complex refractive index of the scatterer, and size of the scatterer. Most atmospheric particles are not spherical. Thus, the prediction of their scattering properties using Mie theory is a crude approximation [13]. To account for the complexity of atmospheric particles, other groups have used more sophisticated light scattering models such as the T-Matrix method for aggregates and colloid particles [14,15,16,17], the Discrete Dipole Approximation for irregularly shaped particles [18,19] or Hybrid approaches for facet particles [20,21]. Dynamic light scattering (DLS) can also analyze the size of particles and determine the size distribution profile of small particles in suspension, even though multiple measurements are needed to obtain a smooth correlation function and a reasonable average particle size [22]. DLS utilizes a continuous wave laser source to perform measurements with a duration of several tens of seconds, making it inappropriate for time-gated measurement techniques. Mie theory was used in this work as a first step to validate the time-gated multi-static lidar scheme for obtaining the angular dependence of the MIe scattering cross-section as a function of the wavelength of the incident laser light, complex refractive index of the scatterer, and size of the scatterer. Our results show distinct scattering features when varying the various scattering parameters, thereby allowing the identification of the scattering particle. We further propose a time-gated lidar scheme for experimentally validating the simulations to obtain the angular MIe scattering cross sections as a function of the wavelength of the incident laser light, a complex refractive index of the scatterer, and the diameter of the scatter. Although we only present results for the three mentioned particles, our scheme can also be extended to other pollutants. This will enable the development of a database of MIe scattering cross-sections for in-situ identification of the pollutants that are present in the atmosphere. Our proposed scheme, which we call MIe Scattering Time–gated multi–Static LIDAR (MISTS–LIDAR), will have specific application to the identification of atmospheric pollutants including black carbon.

2. Simulation Method

Upon interaction with incident radiation, oscillations of charges within a particle result in the scattering of that incident radiation. In addition, part of the incident radiation may be extinguished through absorption within the particle. The particle in this case has a complex refractive index. The interaction of a particle with the incident radiation using the Mie theory uses Maxwell’s equations to derive the incident, scattered and internal fields where an electromagnetic plane wave is scattered by a particle. For simplicity, the particle is initially modeled as an independent isotropic, homogeneous, dielectric sphere. Scattering from both spherical and non-spherical particles appear to be spherical in the far field, and therefore, the particles can be treated as spheres in the far-field approximation [23]. The expressions for the incident, scattered and internal fields take the form of an infinite series expansion of vector spherical harmonics from which cross sections, efficiency factor, and intensity distribution in a particle can be derived. The complete derivation can be found in textbooks discussing Mie theory of scattering, for instance [24,25,26,27,28,29]. J.R. Frisvad has also given a detailed derivation of the solution to the phase function of a spherical particle when scattering electromagnetic plane waves [30]. Here, we summarize the key parameters used for our MIe scattering calculations. To compute the amplitude of the scattered fields, the key parameters are the Mie coefficients a_n and b_n as described by Equations (1) and (2).

$$a_n=\frac{m^2{j}_n\left(mx\right){\left[x{j}_n\left(x\right)\right]}^{\prime }-j_n\left(x\right){\left[mx{j}_n\left(mx\right)\right]}^{\prime }}{m^2{j}_n\left(mx\right){\left[x{h}_n^{\left(1\right)}\left(x\right)\right]}^{\prime }-h_n^{\left(1\right)}\left(x\right){\left[mx{j}_n\left(mx\right)\right]}^{\prime }}$$

(1)

$$b_n=\frac{j_n\left(mx\right){\left[x{j}_n\left(x\right)\right]}^{\prime }-j_n\left(x\right){\left[mx{j}_n\left(mx\right)\right]}^{\prime }}{j_n\left(mx\right){\left[x{h}_n^{\left(1\right)}\left(x\right)\right]}^{\prime }-h_n^{\left(1\right)}\left(x\right){\left[mx{j}_n\left(mx\right)\right]}^{\prime }}$$

(2)

In these equations, m is the complex refractive index of the scattering particle relative to the surrounding air medium and x is the size parameter. The size parameter is further defined to be equal to

$$x=\frac{2\pi a}{\lambda }$$

(3)

where a is the radius of the scattering particle and $\lambda$ is the wavelength of the incident radiation. The functions $j_n\left(z\right)$ and $h_n^{\left(1\right)}\left(z\right)$ are spherical Bessel functions of the order n where n is an integer (n = 1, 2, …) and of the given arguments, z = x or z = mx. The Bessel function $h_n^{\left(1\right)}\left(z\right)$ can further be defined as

$$h_n^{\left(1\right)}\left(z\right)=j_n\left(z\right)+i{y}_n\left(z\right)$$

(4)

where the relationships between Bessel and spherical Bessel functions are given by

$$j_n\left(z\right)=\sqrt{\frac{\pi }{2z}{J}_{n+0.5}\left(z\right)}$$

(5)

$$y_n\left(z\right)=\sqrt{\frac{\pi }{2z}{Y}_{n+0.5}\left(z\right)}$$

(6)

The primes (′) mean derivatives with respect to the argument x or mx, which follow from the spherical Bessel functions themselves as

$${\left[z{j}_n\left(z\right)\right]}^{\prime }=z{j}_{n-1}\left(z\right)-n{j}_n\left(z\right)$$

(7)

$${\left[z{h}_n^{\left(1\right)}\left(z\right)\right]}^{\prime }=z{h}_{n-1}^{\left(1\right)}\left(z\right)-n{h}_n^{\left(1\right)}\left(z\right)$$

(8)

Calculations of the spherical Bessel functions were conducted in MATLAB, with the size parameter (x) as the input. In this case, the radius of the scattering particle and the wavelength of the excitation light were used to calculate the size parameter according to Equation (3). For determining the effect of the wavelength, the radius of the scattering particle was fixed while the input wavelength was changed. Similarly, for determining the effect of the particle size, the wavelength was fixed while the radius of the scattering particle was changed. This allows us to explore the effects of particle size, the complex refractive index of the particle relative to the surrounding air medium, and the wavelength of the incident radiation on the intensity and the polar distribution of MIe scattering by pure water, contaminated water, and black carbon. Such effects have not been explored yet in the context of lidar monitoring of particulate matter in the atmosphere. Pure water refers to pristine water droplets without any contamination while contaminated water refers to water droplets containing a mixture of waste, dirt, or chemicals.

The wavelength of the incident radiation was chosen to be 1.064 μm, 0.532 μm, and 0.355 μm. These wavelengths were chosen because these are the fundamental, second, and third harmonics of a commercial neodymium (Nd)-based laser system such as Nd:YAG or Nd:YVO₄. Such laser systems are typically used in conventional lidar monitoring stations and were, therefore, chosen for our simulations. The complex refractive indices of pure water, contaminated water and black carbon at the chosen excitation wavelengths are summarized in

Table 1. Complex refractive index of contaminated water and black carbon at the 1.064, 0.532, and 0.355 μm wavelengths of the incident radiation.

Scatterer	Wavelength of Incident Radiation (μm)
	1.064	0.532	0.355
Pure Water [33,34]	1.327 + i2.89 × 10−6	1.334 + i1.32 × 10−9	1.343 + i6.5 × 10−9
Contaminated Water [35]	1.54 + i0.015	1.54 + i0.015	1.54 + i0.015
Black Carbon [36]	1.95 + i0.79	1.77 + i0.63	1.70 + i0.64

. The contaminated water considered in this case contains a mixture of ammonium sulfate and carbon. The radii of the scattering particles that we considered in our calculations, along with the corresponding size parameters obtained from Equation (5) are summarized in

Table 2. Size parameter, x for different values of particle radius and incident wavelength.

λ (μm)	1.064	0.532	0.355
a (μm)
0.1	0.59	1.18	1.77
0.5	2.95	5.91	8.85
1.25	7.38	14.76	22.12

. The radii 0.1 μm, 0.5 μm and 1.25 μm were chosen since these are approximately the average sizes (diameter) of particulate matter, for example, black carbon (0.085 μm to 0.5 μm) and PM2.5 (≤2.5 μm) [31]. MIe scattering is also the more appropriate model compared to Rayleigh scattering when the particle size is larger than around 10% of the wavelength of the incident radiation. Accordingly, the minimum particle radius for MIe scattering to be valid is around 0.1 μm given the longest laser wavelength considered in our work, which is 1.064 μm [32].

After calculating the Mie coefficients ($a_n$ and $b_n$), the scattering efficiency $Q_{sca}$ and backscattering efficiency $Q_b$ are calculated using

$$Q_{sca}=\frac{2}{x^2}{\sum }_{n=1}^{\infty }\left(2n+1\right)\left({\left|a_n\right|}^2+{\left|b_n\right|}^2\right)$$

(9)

$$Q_b=\frac{1}{x^2}{\left|{\sum }_{n=1}^{\infty }\left(2n+1\right){\left(-1\right)}^n\left(a_n-b_n\right)\right|}^2$$

(10)

where n is the number of expansion terms in those infinite series. The infinite series was truncated after n_max = x + 4x^1/3 + 2 terms as proposed by Bohren and Huffman [24]. The x in n_max also refers to the size parameter given in Equation (3).

The detailed shape of the angular scattering pattern is obtained by solving the scattering phase functions that describe the scattered field, E_S. The scattered far field in spherical coordinates (E_Sθ, E_Sϕ) is given by

$$E_{S\theta }=\frac{e^{ikr}}{-ikr}\cos \varphi ·S_2\left(\cos \theta \right)$$

(11)

$$E_{S\varphi }=\frac{e^{ikr}}{ikr}\sin \varphi ·S_1\left(\cos \theta \right)$$

(12)

where $E_{S\theta }$ is the far-field component in the scattering plane defined by the incident and scattered directions and $E_{S\varphi }$ is the orthogonal component. The angle ϕ is the angle between the incident electric field and the scattering plane. $S_1\left(\cos \theta \right)$ and $S_2\left(\cos \theta \right)$ are the scattering phase functions that describe the angular scattering patterns and hence the polar distribution of MIe scattering by pure water, contaminated water, and black carbon. The scattering amplitudes are given by

$$S_1\left(cos\theta \right)={\sum }_{n=1}^{\infty }\frac{2n+1}{n\left(n+1\right)}\left(a_n{\pi }_n+b_n{\tau }_n\right)$$

(13)

$$S_2\left(cos\theta \right)={\sum }_{n=1}^{\infty }\frac{2n+1}{n\left(n+1\right)}\left(a_n{\tau }_n+b_n{\pi }_n\right)$$

(14)

It is the functions ${\pi }_n$ and ${\tau }_n$ in these spherical harmonics that describe the angular scattering patterns of the incident light upon encountering the particulate matter. The functions ${\pi }_n$ and ${\tau }_n$ follow from the recurrence relations

$${\pi }_n=\frac{2n-1}{n-1}cos\theta · {\pi }_{n-1}-\frac{n}{n-1}{\pi }_{n-2}$$

(15)

$${\tau }_n=n·cos\theta · {\pi }_n-\left(n+1\right){\pi }_{n-1}$$

(16)

The angular intensity distribution obtained from Equations (13)–(16) and the backscattering efficiency obtained from Equation (10) were plotted using Matlab. The calculations using the Mie theory as described above take in the complex refractive index, particle size and wavelength of excitation light as input parameters. The particles in the calculations are assumed to be independent single scatterers with spherical shapes excited by a homogeneous plane wave. In future work, the Mie theory can be extended to coated [37] and multilayer particles such as droplets with surface and/or internal contaminants [38].

3. Results and Discussion

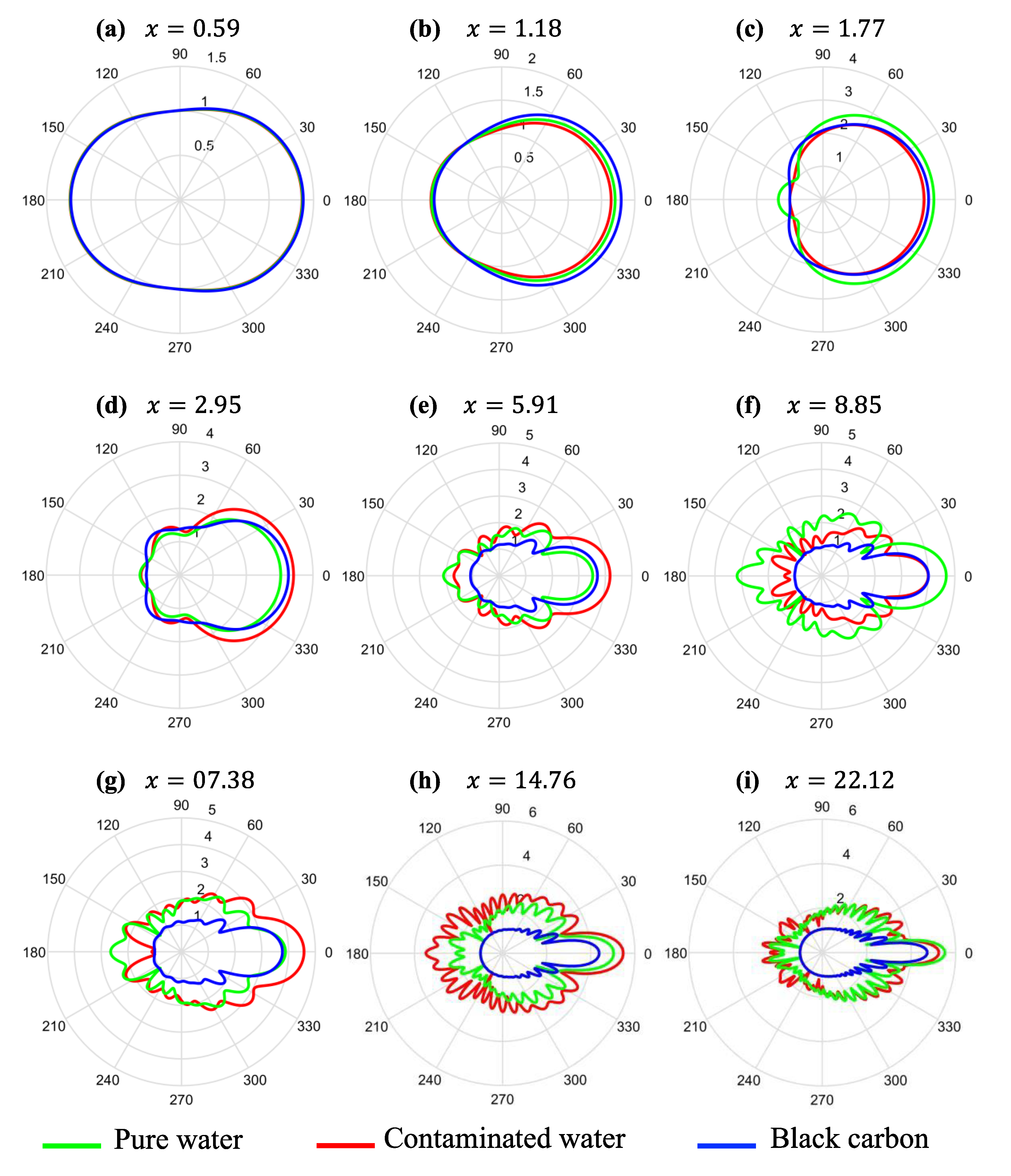
Figure 1a–i show the cross-sectional scattering intensity patterns from pure water, contaminated water, and black carbon, respectively. These patterns were calculated using Equations (13) to (16), where the angle θ is from 0 to 2π. In the calculations, the particles are assumed to be independent. The indices (a) to (i) refer to each of the size parameters in Table 2 where (a) $x$= 0.59, (b) $x$= 1.18, (c) $x$= 1.77, (d) $x$= 2.95, (e) $x$= 5.91, (f) $x$= 8.85, (g) $x$= 7.38, (h) $x$= 14.76, and (i) $x$ = 22.12. Therefore, each of the size parameters captures the effect of particle radius and incident wavelength on the intensity pattern of the scattered incident light. The patterns are plotted in polar coordinates from 0 to 360° where backscattering is towards the 180°–angle (towards the left) and forward scattering is towards the 0 or 360°–angle (towards the right). The intensity is plotted in a log₁₀ scale to emphasize the salient features of the scattering patterns. For all three particles, the scattering intensity is nearly uniform with a slight preference for forward scattering when the size of the particle is within 20% of the incident laser’s wavelength, for example (a) $x$ = 0.59, (b) $x$ = 1.18, and (c) $x$ = 1.77 where the particle size is 0.1 μm and the wavelength is (a) 1.064 μm and (b) 0.532 μm. The cross-sectional scattering intensity patterns for pure water, contaminated water, and black carbon also appear to be similar, especially when $x$= 0.59 (Figure 1a) where it appears to be indistinguishable. As the size parameter increases because of the particle becoming bigger and the laser wavelength becoming shorter, forward scattering is favored with the forward scattering intensity becoming confined within a narrower polar distribution. The scattering patterns from pure water, contaminated water, and black carbon start to exhibit distinguishable features, especially from the back-scattered light when $x$= 1.77. The patterns then become increasingly unique as the value of $x$ increases. These results show that for small particle sizes, shorter laser lidar wavelengths should be used to distinguish between the particles. As the size of the particle increases, there is more flexibility in using longer laser lidar wavelengths to distinguish between the particles. Interestingly, when the particle size is 1.25 μm, a laser lidar wavelength of 0.532 μm (Figure 1h) gives a similar scattering intensity pattern as a laser lidar wavelength of 0.355 μm (Figure 1i). Using either laser lidar wavelength gives clearly distinguishable scattering intensity patterns that can differentiate between pure water, contaminated water, and black carbon. This result is important economically since it is cheaper and easier to use the second harmonics (0.532 μm wavelength) instead of the third harmonics (0.355 μm wavelength) of Nd-based laser systems. The second harmonic also has a higher light intensity compared to the third harmonic. The unique scattering patterns demonstrated by different particulate matter could serve as fingerprints that can be used to identify the scattering particle. Calculation of the cross-sectional scattering intensity patterns could be extended to other types of pollutants as well. By doing so, a database of atmospheric pollutants and their corresponding scattering patterns can be created.

To make the database of pollutants more accurate, we need to obtain and compare the scattering cross-sections of typical scattering sources in the real experiment. The database could then be used to identify the pollutants in the atmosphere during practical environmental monitoring exercises, whereby actual scattering patterns are collected in–situ. These are then scanned against the scattering patterns in the database to identify the scattering particle. To capture the actual scattering patterns, we propose a MIe Scattering Time-gated multi-Static LIDAR (MISTS–LIDAR) scheme. Bistatic lidar operation has been reported previously, whereby the detector (receiver) is spaced at a far distance from the source (transmitter) so that angular scattering measurements can be made [39,40]. The MISTS–LIDAR scheme extends the concept of bistatic lidar a step further by implementing multiple detectors that can rotate through a small angle. By rotating each of the multiple detectors through an angle of 0 to 180°, the cross-sectional scattering intensity patterns that were initially simulated could be recreated. 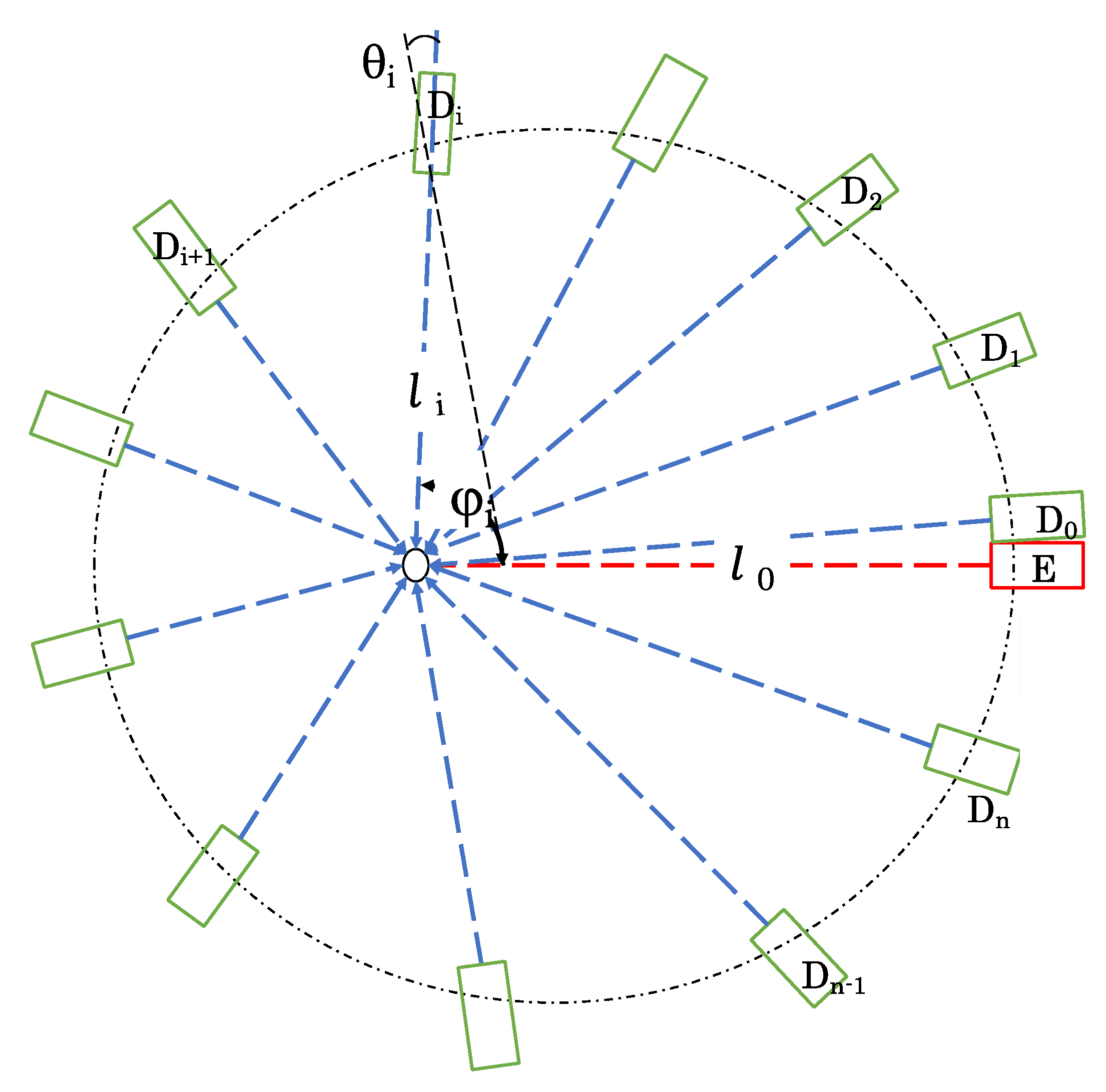The top view of the schematic diagram of the proposed MISTS–LIDAR experimental set-up is shown in Figure 2.

A scattering center, for example, a smoke being emitted by a factory, is illuminated by a commercially available pulsed Q-switched laser (E), such as an Nd:YAG or Nd:YVO₄ laser. The importance of the laser being pulsed will be discussed later. The laser emission can be sequentially tuned to its fundamental (1.064 μm), second (0.532 μm), or third (0.355 μm) harmonic wavelengths. The laser light source is located at a distance l₀ from the scattering center. Furthermore, the laser is at a lower elevation compared to the scattering center such that the laser beam is directed upward toward the scattering center. The backscattered laser light is then collected by a set of multiple telescope detectors (D₀ to D_n). The collected light then creates the MIe scattering intensity profiles, which will then be compared against the database to identify the type of scattering particle present in the scattering center that is being observed. The number of telescope detectors is correlated to the angular scattering cross-section. For example, for x = 0.59 or 1.18 (Figure 1a,b), at least four telescope detectors will be needed to recreate the cross-sectional scattering intensity patterns. The number of telescope detectors increases as the size parameter also increases. This is because as the size parameter increases, the scattering intensity patterns also become more complex, as shown in Figure 1. The telescope detectors are placed at known distances around the scattering center. Each detector can rotate through a telescopic angle 0 < θ_i < π so that the detector (Di) that is tilted at an angle θ_i has a distance l_i from the scattering center. By scanning the detectors through a range of angles, the polar plot showing the angular dependence of the scattering cross-section intensity (such as the scattering patterns in Figure 1) can be obtained. The scattering pattern that is collected using MISTS–LIDAR will then be scanned against the scattering intensity patterns in the database to identify the particles present in the scattering center. In practice, multiple scattering centers emitting the same pollutant particle could be present within the vicinity, for instance within a 10–100 km radius. To collect and identify the correct scattering pattern that originated from the scattering center being monitored, a time gate will be used. Using a time gate requires that the laser source is pulsed. The principle behind this time gate is illustrated in Figure 3. If l₀ is the known distance from the laser to the scattering particle source S₀, and l_i is the distance from the scattering particle to the ith detector, then the time it takes to reach detector Di will be

$$t_i=\frac{l_0+l_i}{c}$$

(17)

where c is the speed of light. Owing to the pulsed emission of the incident laser source, scattering from surrounding sources will arrive at the detector at different time intervals. For instance, if a pulsed laser light with a 10-ns pulse duration is scattered by the pollutant particles from a scattering center, then the estimated spatial resolution of the time gate is around 3 m. Meaning, the minimum distance between the scattering centers should be 3 m for MISTS–LIDAR to correctly assign the collected scattering patterns to the correct scattering center. The spatial resolution can be improved to 1.5 m if the laser that is used has a pulse duration of 5 ns.

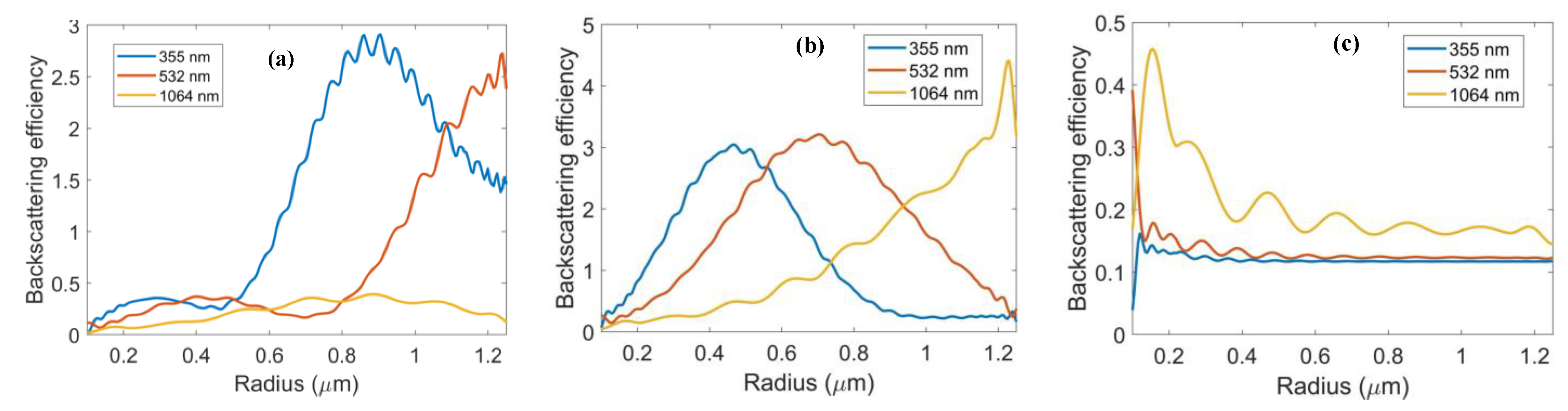
Since the telescope detectors in Figure 2 collect the Mie backscattering and recreate the back-scattered intensity profile, the back-scattering intensities are further analyzed by plotting the intensities as a function of the size of the scatterer for different incident laser wavelengths. The backscattering intensities for pure water, contaminated water, and black carbon are shown in Figure 4a–c, respectively. The results show that the backscattering intensities are unique for each of the scattering particles regardless of particle size and laser wavelength. For pure water, backscattering is more efficient for larger droplets with radii from about 0.5 μm and as the size increases, longer wavelength laser light would also be better. Light having 355 nm wavelength would be appropriate for droplet sizes that are at least 0.6 μm. On the hand, a laser operating at 532 nm wavelength would be an appropriate light source for droplet sizes that are at least 0.8 μm. A laser operating at 1064 nm can be used for bigger droplet sizes as well, but the results in Figure 4a show that in this instance 532 nm wavelength would be a better choice. For contaminated water, a laser operating at 355 nm wavelength will be appropriate for droplet sizes smaller than about 0.5 μm. As Figure 4b shows, higher backscattering efficiency is achieved with 355 nm wavelength for these small droplet sizes. On the other hand, more efficient backscattering can be observed from droplet sizes between 0.5 μm and 1.0 μm when the wavelength of the illuminating light is 532 nm. For bigger droplet sizes whose radii are more than 1.0 μm, 1064 nm will yield the highest backscattering intensity. For black carbon, the smaller the particle size is, the higher the backscattering intensity. Moreover, the backscattering intensity increases as the wavelength of the illuminating laser becomes longer. Results in Figure 4c show that as the particle radius increases beyond about 0.6 μm, 1064 nm wavelength light will yield higher backscattering efficiencies, and therefore, this longer wavelength light will be more practical to use. These results highlight that particle size and the wavelength of the illuminating light are important parameters to consider in optimizing the backscattering intensities that will be collected by the telescope detectors. Moreover, the different backscattering intensities manifested by pure water, contaminated water and black carbon confirm that the MIe scattering intensity patterns can be used to distinguish between different scattering particles.

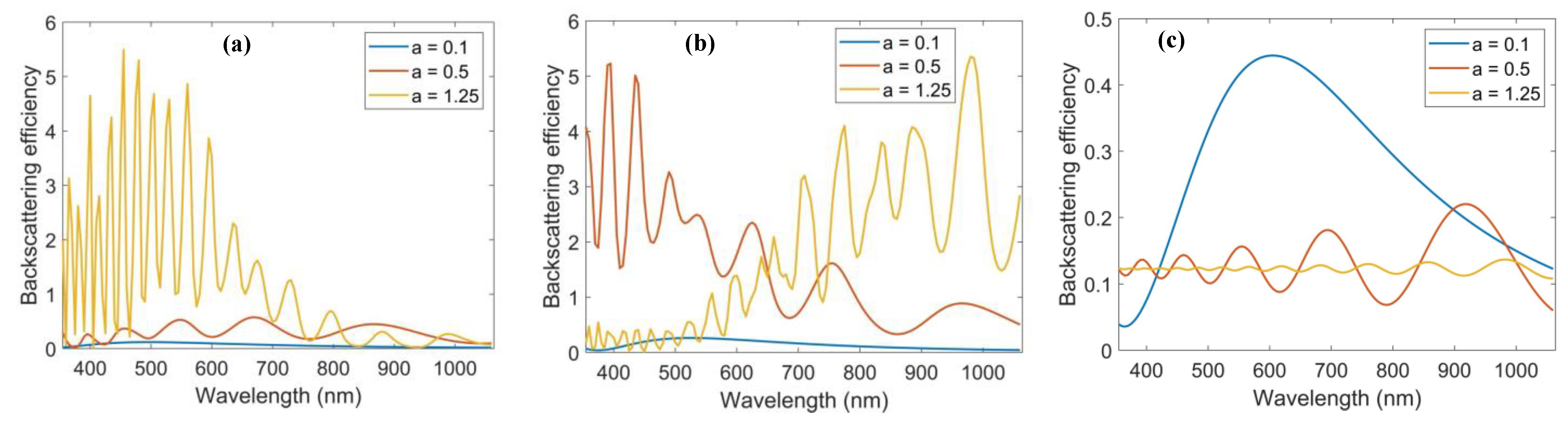
Since the backscattering intensity depends on the wavelength of the illuminating laser light, the backscattering intensity profiles for pure water, contaminated water, and black carbon were also obtained as a function of the wavelength of the illuminating laser light for different particle radii where a = 0.1 μm, 0.5 μm, and 1.25 μm. Figure 5a–c show the scattering intensity profiles for pure water, contaminated water, and black carbon, respectively. For pure water, backscattering is more efficient when the wavelength of the laser light is shorter. A shorter wavelength is particularly useful when the radius is 0.1 μm because the backscattering intensity appears to be featureless but the intensity peaks when the wavelength is about 500 nm. For the radius of 0.5 μm, the backscattering intensity shows a periodic pattern. As the radius is further increased to 1.25 μm, backscattering becomes more intense, especially for short-wavelength light. For contaminated water, backscattered light from 0.1 μm-radius also appears to be featureless with an intensity peak around 500 nm wavelength. When the radius is increased to 0.5 μm, the intensity of backscattered light also increases, with the maximum intensity being achieved also at a shorter wavelength. These results show that when the size of the scatterer is small, shorter wavelength light is needed to elicit more efficient backscattering. For bigger scatterers, such as when the radius is 1.25 μm, longer wavelength light results in a higher backscattering intensity. For both pure and contaminated water, backscattering becomes more efficient as the size of the scatterer increases. On the other hand, the intensity of backscattered light is highest for smaller black carbon particles although the scattered light still appears featureless when the radius is 0.1 μm. When the size increases to 0.5 μm, longer wavelength light results in more efficient backscattering. Interestingly, an opposite trend is observed between pure water and black carbon. Specifically, for pure water, the backscattered intensity increases as the size increases while for black carbon, the backscattered intensity decreases as the size increases. Similar to the scattering profiles as a function of size, the wavelength-dependent backscattering intensity profiles are also unique to the scattering particle regardless of the size of the particle. We note that the fluctuations observed in the backscattering efficiency plots in Figure 4 and Figure 5 are due to the behavior of the scattering particles acting as a Mie resonator [41].

The unique scattering intensity profiles allow the identification of the scattering particle. These results illustrate the concept behind our proposed MISTS–LIDAR scheme. The concept could also be extended to mixed particles with varying shapes and refractive indices by looking at the angular (θ) dependence of the cross-sectional scattering intensity patterns along the vertical (ϕ) direction where varying polarization is expected to result in variations in the scattering intensity patterns. Experimental verification of our calculation results using the MISTS-LIDAR system will be performed in future work.

4. Conclusions

In summary, the polar MIe scattering intensity patterns from pure water droplets, contaminated water droplets and black carbon aggregates were simulated for various size parameters determined by the 1.064-μm, 0.532-μm, and 0.355-μm wavelengths of the illuminating laser light and the 0.1-μm, 0.5-μm, and 1.25-μm radii of the scattering particle. The effect of the scatterer’s complex refractive index was also considered in the simulations. As the size parameter increases because of the particle becoming bigger and the laser wavelength becoming shorter, the scattering patterns from pure water, contaminated water, and black carbon exhibit distinguishable features that become increasingly unique. Likewise, the scattering intensity profiles are unique to the scattering particle. The unique scattering patterns and intensity profiles could serve as fingerprints that can be used to identify the scattering particle. To capture the actual scattering patterns in-situ, a MIe Scattering Time–gated multi–Static LIDAR (MISTS–LIDAR) scheme was proposed. The MISTS–LIDAR consists of a pulsed laser illumination source and a series of telescope detectors positioned around a scattering center. By scanning the detectors through a range of angles, the angular dependence of the scattering cross-section can be obtained. The scattering pattern that was collected using MISTS–LIDAR will then be scanned against the scattering intensity patterns in the database to identify the particles present in the scattering center. The pulsed laser operation serves as a time gate that would exclude the detection of scattering from other scattering centers. Although the simulations focused on pure water, contaminated water and black carbon, MISTS–LIDAR could be extended to other types of pollutants, enabling the development of a database of atmospheric pollutants and their corresponding scattering patterns. The database could then be used in the in-situ identification of various pollutants in the atmosphere during practical environmental monitoring events. The present work used Mie theory as a crude approximation as a first step in verifying the proposed time-gated multi-static scheme. In future work, the Mie theory can be extended to coated and multilayer particles such as droplets with surface and/or internal contaminants. The T-Matrix method for aggregates and colloid particles, the Discrete Dipole Approximation for irregularly shaped particles, and Hybrid approaches for facet particles will also be considered.