Effects of Vibration on Adjacent Pipelines under Blasting Excavation
Abstract
1. Introduction
2. Experimental Design of Blasting Vibration
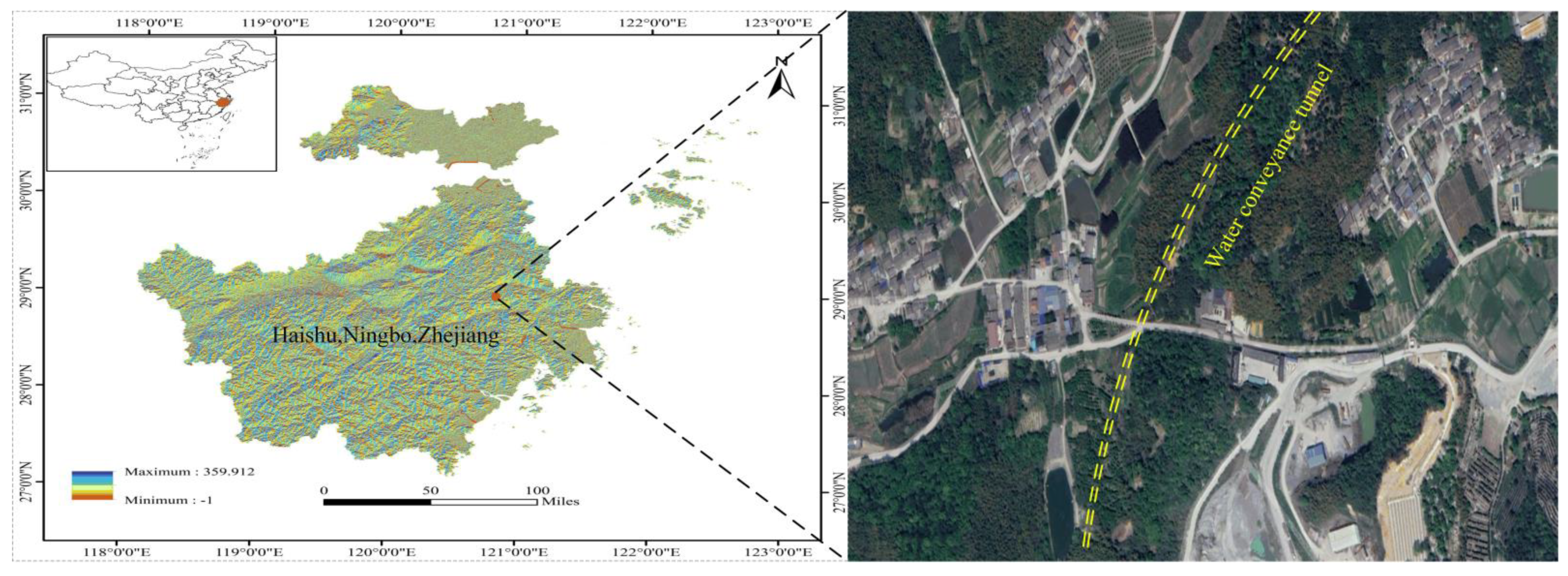
2.1. Background and Blasting Parameters
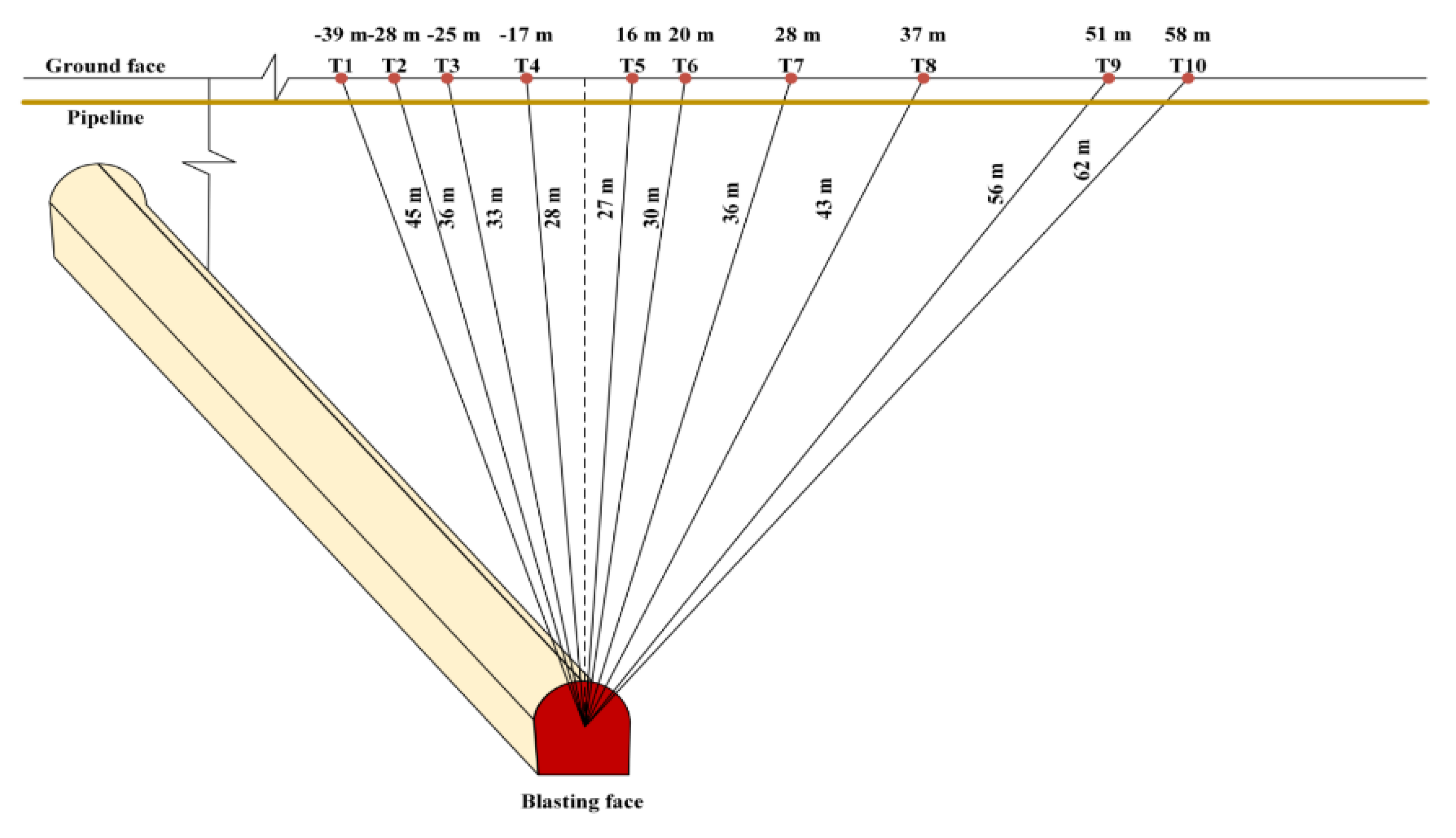
2.2. Layout of the Measurement Point
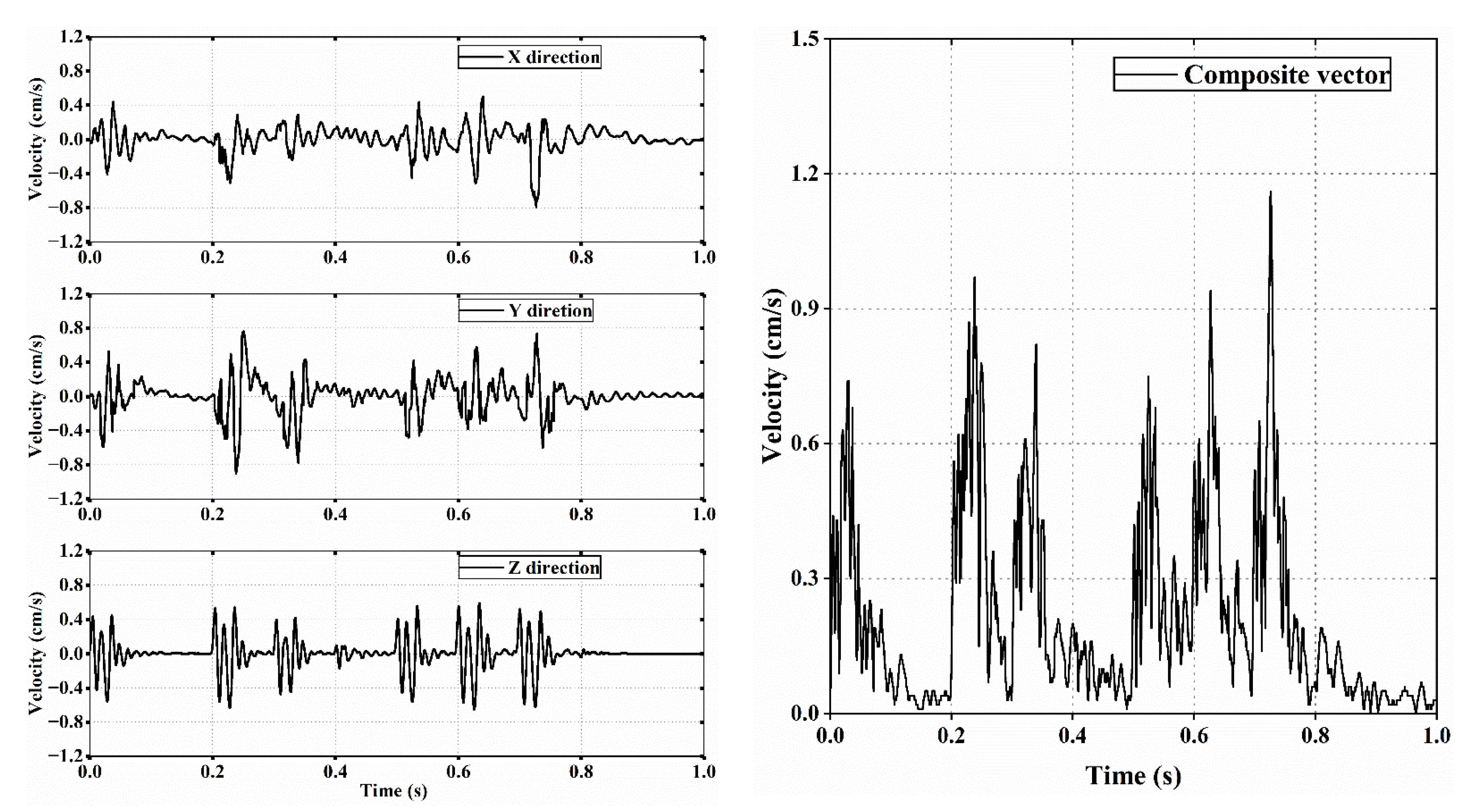
2.3. Monitoring Results Analysis
3. Blast Vibration Attenuation Law
4. Numerical Simulation and Dynamic Response Analysis
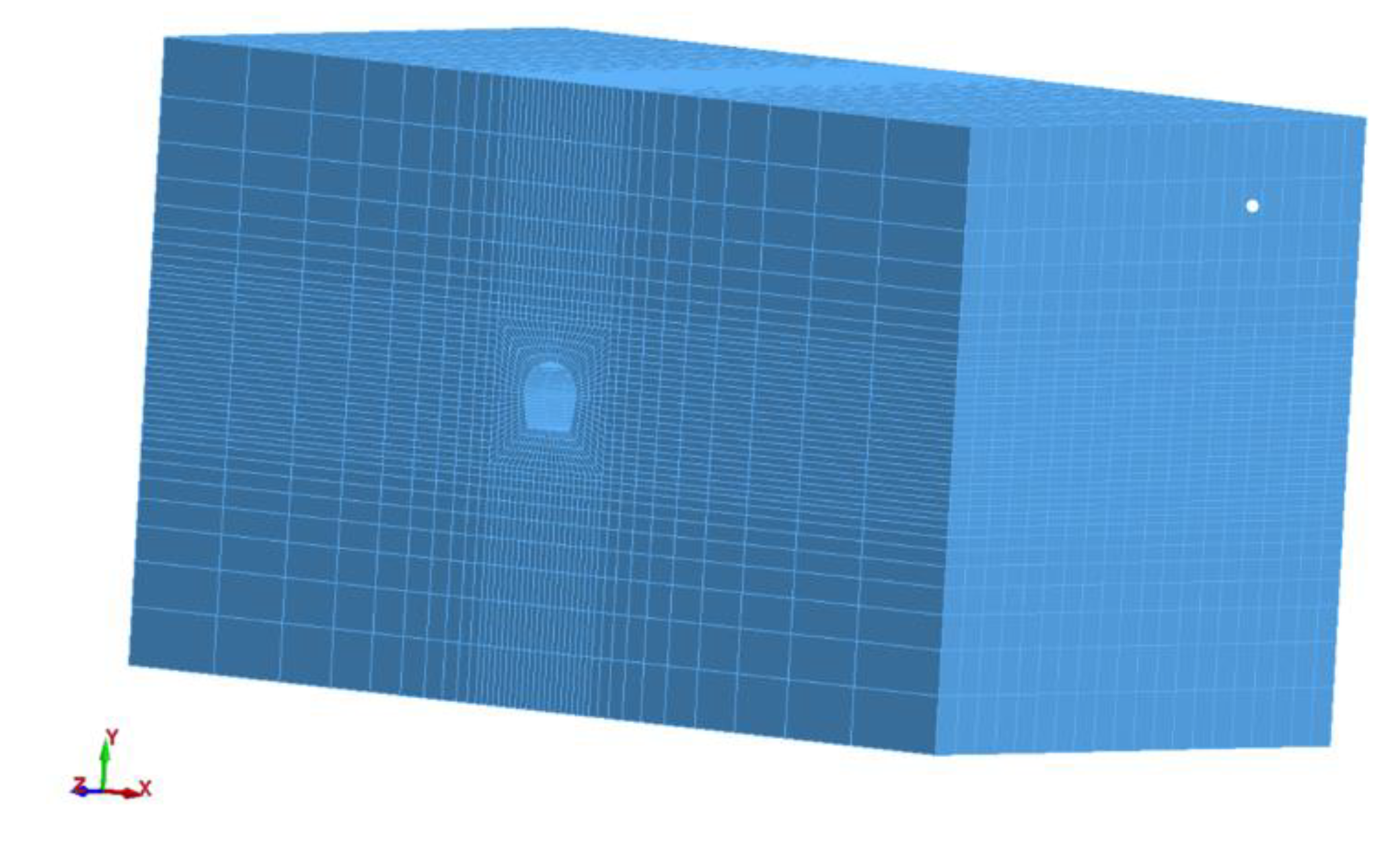
4.1. Model Parameter and Set Up
4.2. Blasting Load Application
4.3. Numerical Calculation and Verification
4.4. Pipeline Dynamic Response Analysis
5. Soil Vibration Response above the Buried Pipeline
5.1. Soil Vibration Response above the Buried Pipe
5.2. Pipeline Dynamic Response Characteristics
5.3. Soil Response Characteristics around the Pipeline
5.4. Security Criteria Analysis
6. Conclusions
- (1)
- A three-dimensional numerical model considering in situ stress was established. The triangular equivalent load method was used to reflect the explosion effect. The reasonableness of the model was verified based on a comparative analysis of the field-monitoring results and a solution using the empirical equation of stress wave theory. The results show the error of the PPV is within a reasonable range (≤7.69%) with high simulation accuracy.
- (2)
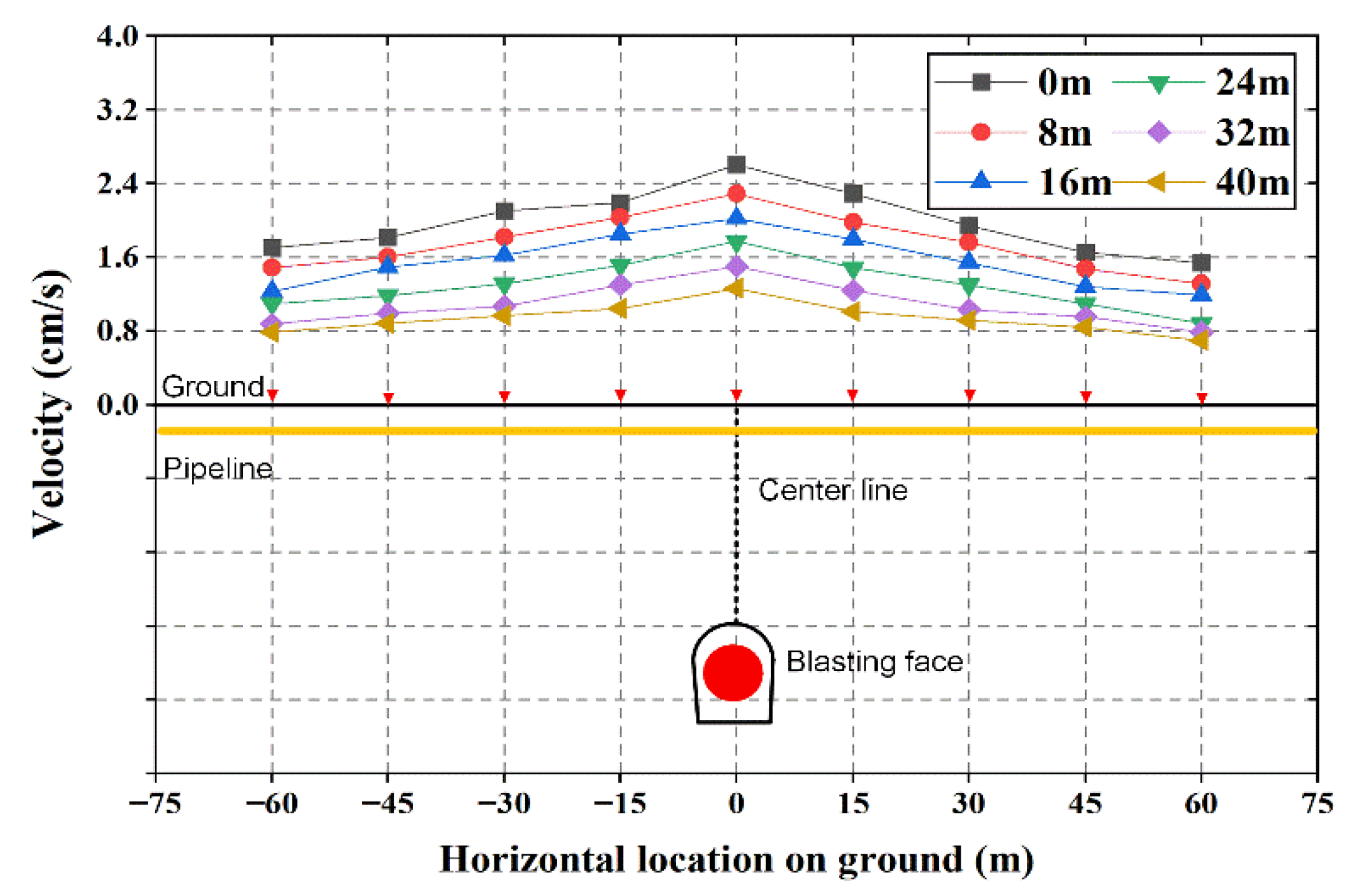
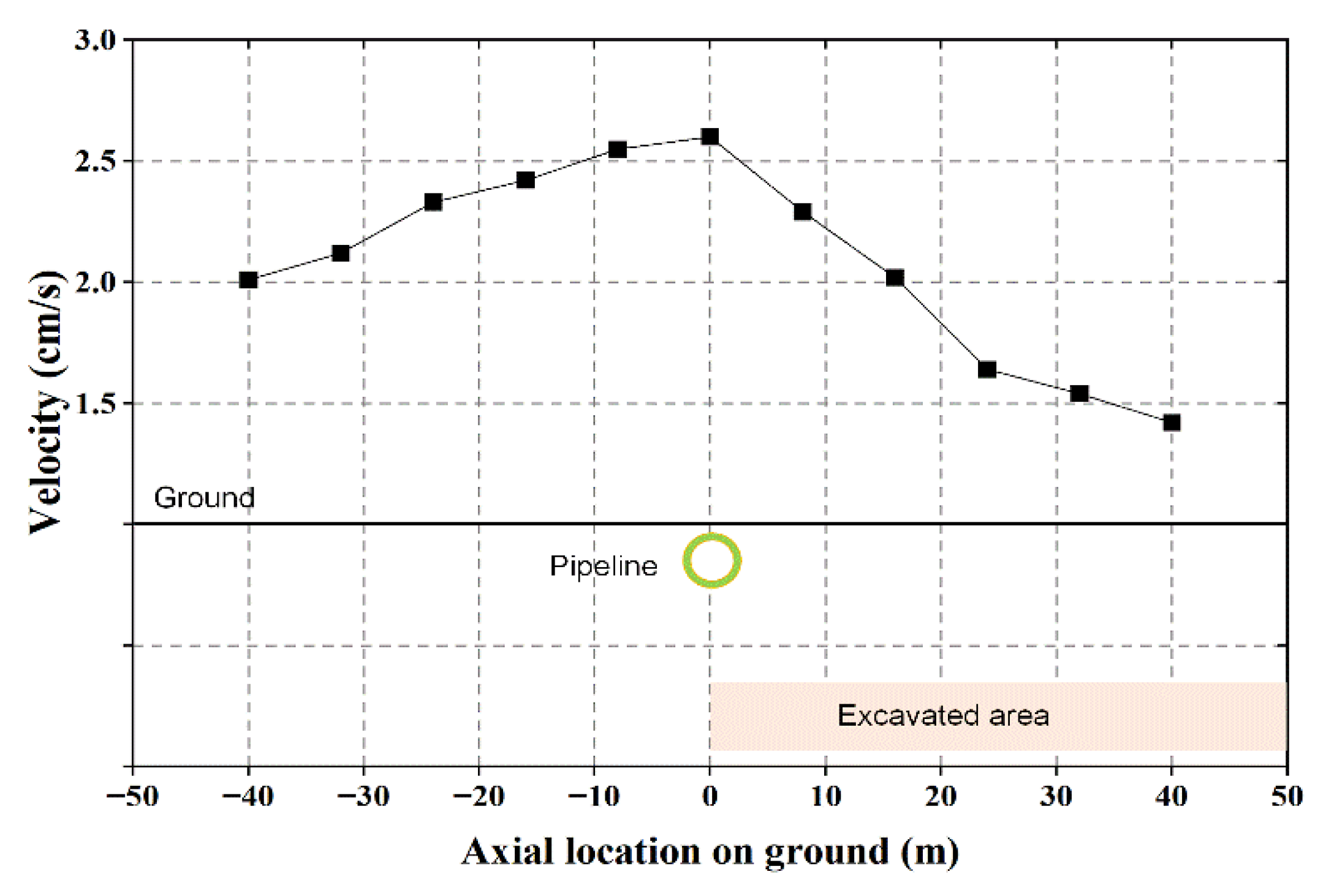
- The PPV results for each construction condition show the PPV decays exponentially with increasing horizontal and axial distances. The maximum PPV appeared at the horizontal distance of 0 m from the explosion source when the axial distance was 0 m with a value of 2.6 cm/s. The minimum PPV appeared at the horizontal distance of 60 m from the explosion source when the axial distance was 40 m with a value of 0.7 cm/s. In addition, the axial vibration velocity distribution results indicate a significant cavity amplification effect above the excavation area, which should be seriously considered in future research.
- (3)
- The PPV distribution results at the pipe cross-section indicate the PPV on the blast side was more significant than that behind the blast side when the blast vibration was transmitted to the pipeline. The maximum PPV value appeared nearest to the source of the explosion, and the minimum value appeared farthest from the blast source.
- (4)
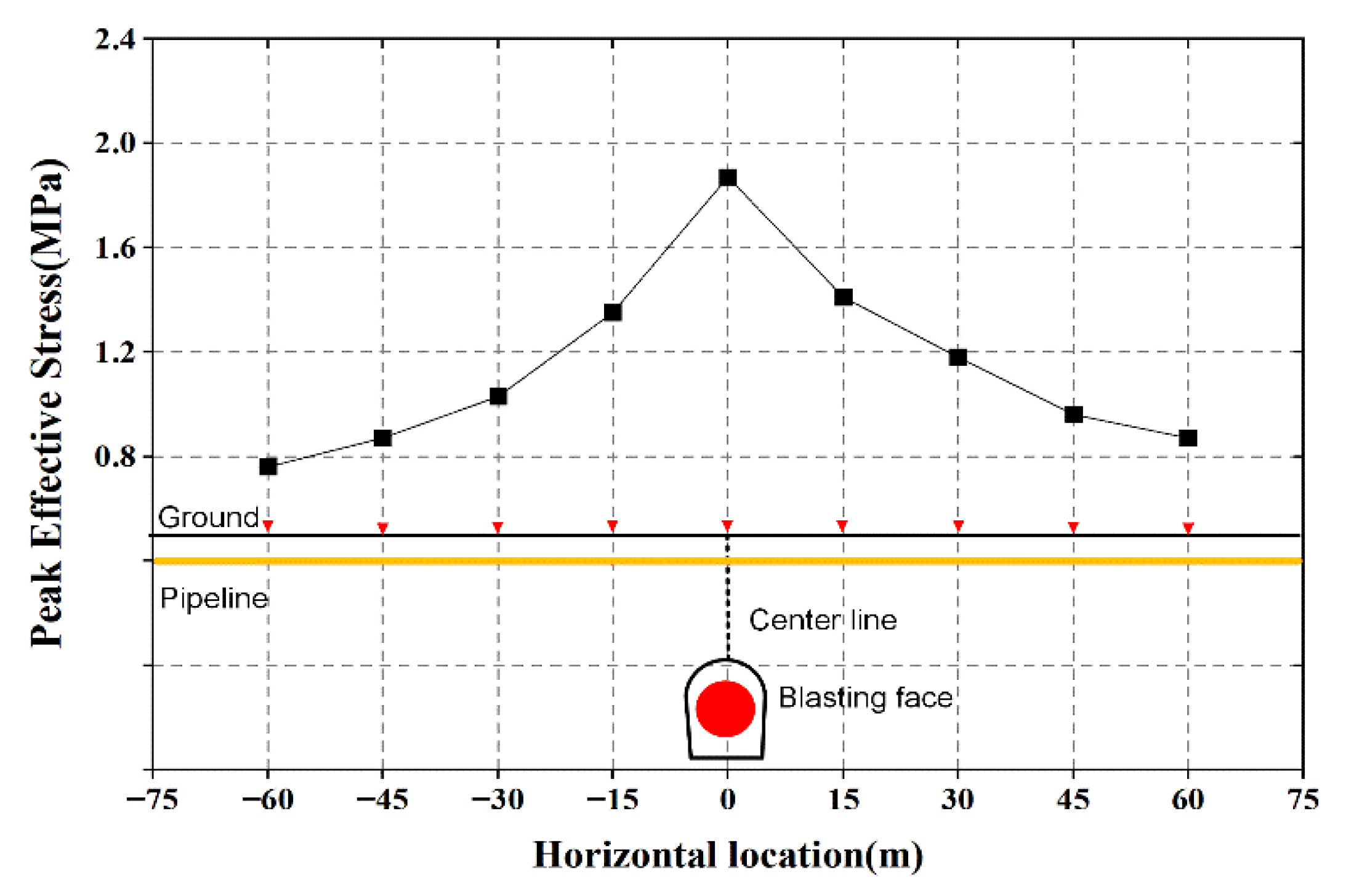
- The PES occurring had exponential decay on both sides of the blast source with increasing horizontal distance from the blast source. The PES results of the pipe sections under different construction conditions show the PES of the lower part of the pipe section was significantly lower than that of the upper part due to the interaction between the soil and the pipe. In addition, the maximum PES value at the cross-section (1.53 MPa) when in a hazardous situation (pipe directly above the blast source) was less than the safe threshold (≤4.6 MPa). This indicates the blast vibration will not affect the normal service of the buried pipeline.
- (5)
- This paper effectively reflects blast vibration propagation law by proposing an effective PPV prediction model for pipelines which applies a dimension and composition analysis combined with numerical simulation and field-monitoring results. This prediction model may guide the subsequent development of a reasonable blasting scheme. In addition, this study proposes an empirical safety criteria formula for the scientific implementation of safety assessments for subsequent construction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Zhou, C.; Remennikov, A.; Wu, T.; Lu, S.; Xia, Y. Dynamic response and safety control of civil air defense tunnel under excavation blasting of subway tunnel. Tunn. Undergr. Space Technol. 2021, 112, 103879. [Google Scholar] [CrossRef]
- Yu, H.; Yuan, Y.; Yu, G.; Liu, X. Evaluation of influence of vibrations generated by blasting construction on an existing tunnel in soft soils. Tunn. Undergr. Space Technol. 2014, 43, 59–66. [Google Scholar] [CrossRef]
- Singh, P.K.; Roy, M.P. Damage to surface structures due to blast vibration. Int. J. Rock Mech. Min. Sci. 2010, 47, 949–961. [Google Scholar] [CrossRef]
- Xia, Y.; Jiang, N.; Zhou, C.; Sun, J.; Luo, X.; Wu, T. Dynamic behaviors of buried reinforced concrete pipelines with gasketed bell-and-spigot joints subjected to tunnel blasting vibration. Tunn. Undergr. Space Technol. 2021, 118, 104172. [Google Scholar] [CrossRef]
- Xia, Y.; Jiang, N.; Zhou, C.; Meng, X.; Luo, X.; Wu, T. Theoretical solution of the vibration response of the buried flexible HDPE pipe under impact load induced by rock blasting. Soil Dyn. Earthq. Eng. 2021, 146, 106743. [Google Scholar] [CrossRef]
- Xia, Y.; Jiang, N.; Zhou, C.; Luo, X. Safety assessment of upper water pipeline under the blasting vibration induced by Subway tunnel excavation. Eng. Fail. Anal. 2019, 104, 626–642. [Google Scholar] [CrossRef]
- Wu, T.; Jiang, N.; Zhou, C.; Luo, X.; Li, H.; Zhang, Y. Experimental and numerical investigations on damage assessment of high-density polyethylene pipe subjected to blast loads. Eng. Fail. Anal. 2022, 131, 105856. [Google Scholar] [CrossRef]
- Jiang, N.; Gao, T.; Zhou, C.; Luo, X. Effect of excavation blasting vibration on adjacent buried gas pipeline in a metro tunnel. Tunn. Undergr. Space Technol. 2018, 81, 590–601. [Google Scholar] [CrossRef]
- Zhong, D.; Gong, X.; Han, F.; Li, L. Monitoring the Dynamic Response of a Buried Polyethylene Pipe to a Blast Wave: An Experimental Study. Appl. Sci. 2019, 9, 1663. [Google Scholar] [CrossRef]
- Abedi, A.S.; Hataf, N.; Ghahramani, A. Analytical solution of the dynamic response of buried pipelines under blast wave. Int. J. Rock Mech. Min. Sci. 2016, 88, 301–306. [Google Scholar] [CrossRef]
- Nyman, D.J.; Dowding, C.H.; Oriard, L.L. Evaluation of Close-in Blasting Effects on Welded Steel Pipelines. In Proceedings of the 7th International Pipeline Conference, Calgary, AB, Canada, 29 September–3 October 2008. [Google Scholar]
- Kouretzis, G.P.; Bouckovalas, G.D.; Gantes, C.J. Analytical calculation of blast-induced strains to buried pipelines. Int. J. Impact Eng. 2007, 34, 1683–1704. [Google Scholar] [CrossRef]
- Esparza, E.D.; Westine, P.S.; Wenzel, A.B. Pipeline Response to Buried Explosive Detonations; American Gas Association: Arlington, VA, USA, 1981. [Google Scholar]
- Mokhtari, M.; Alavi Nia, A. A parametric study on the mechanical performance of buried X65 steel pipelines under subsurface detonation. Arch. Civ. Mech. Eng. 2015, 15, 668–679. [Google Scholar] [CrossRef]
- Mokhtari, M.; Alavi Nia, A. The application of CFRP to strengthen buried steel pipelines against subsurface explosion. Soil Dyn. Earthq. Eng. 2016, 87, 52–62. [Google Scholar] [CrossRef]
- Almahakeri, M.; Moore, I.D.; Fam, A. Numerical Study of Longitudinal Bending in Buried GFRP Pipes Subjected to Lateral Earth Movements. J. Pipeline Syst. Eng. Pract. 2017, 8, 04016012. [Google Scholar] [CrossRef]
- Jiang, N.; Zhu, B.; Zhou, C.; Luo, X.; Li, H.; Wu, T.; Lyu, G. Safety criterion of gas pipeline buried in corrosive saturated soft soil subjected to blasting vibration in a coastal metro line. Thin-Walled Struct. 2022, 180, 109860. [Google Scholar] [CrossRef]
- Zhu, B.; Jiang, N.; Zhou, C.; Luo, X.; Li, H.; Chang, X.; Xia, Y. Dynamic interaction of the pipe-soil subject to underground blasting excavation vibration in an urban soil-rock stratum. Tunn. Undergr. Space Technol. 2022, 129, 104700. [Google Scholar] [CrossRef]
- Qu, Y.; Li, Z.; Zhang, R.; Qin, Y.; Zhang, D. Dynamic performance prediction and influencing factors analysis of buried polyethylene pipelines under subsurface localized explosion. Int. J. Press. Vessel. Pip. 2021, 189, 104252. [Google Scholar] [CrossRef]
- Giannaros, E.; Kotzakolios, T.; Kostopoulos, V. Blast response of composite pipeline structure using finite element techniques. J. Compos. Mater. 2015, 50, 3459–3476. [Google Scholar] [CrossRef]
- Parviz, M.; Aminnejad, B.; Fiouz, A. Numerical simulation of dynamic response of water in buried pipeline under explosion. KSCE J. Civ. Eng. 2017, 21, 2798–2806. [Google Scholar] [CrossRef]
- Langhaar, H.L. Dimensional Analysis and Theory of Models; Wiley: New York, NY, USA, 1951. [Google Scholar]
- Jiang, N.; Zhou, C.; Lu, S.; Zhang, Z. Propagation and prediction of blasting vibration on slope in an open pit during underground mining. Tunn. Undergr. Space Technol. 2017, 70, 409–421. [Google Scholar] [CrossRef]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Yang, J.-C.; Liu, K.-W.; Li, X.-D.; Liu, Z.-X. Stress initialization methods for dynamic numerical simulation of rock mass with high in-situ stress. J. Cent. South Univ. 2020, 27, 3149–3162. [Google Scholar] [CrossRef]
- Lyu, G.; Zhou, C.; Jiang, N. Experimental and Numerical Study on Tunnel Blasting Induced Damage Characteristics of Grouted Surrounding Rock in Fault Zones. Rock Mech. Rock Eng. 2022. [Google Scholar] [CrossRef]
- Fickett, W.; Davis, W.C. Detonation; University of California Press: Berkeley, CA, USA, 1979. [Google Scholar]
- Henrych, J.; Major, R. The Dynamics of Explosion and Its Use; Elsevier Scientifific Pub. Co.: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Wang, W.L. Drilling Blasting; Coal Industry Press: Beijing, China, 1984. (In Chinese) [Google Scholar]
- Yang, S.Y. Foundations of Dynamics in Rock Blasting; China Coal Industry Publishing House: Beijing, China, 1991. (In Chinese) [Google Scholar]
- Persson, P.A.; Holmberg, R.; Lee, J. Rock Blasting and Explosives Engineering; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Lu, W.; Yang, J.; Yan, P.; Chen, M.; Zhou, C.; Luo, Y.; Jin, L. Dynamic response of rock mass induced by the transient release of in-situ stress. Int. J. Rock Mech. Min. Sci. 2012, 53, 129–141. [Google Scholar] [CrossRef]
- Ji, L.; Zhou, C.; Lu, S.; Jiang, N.; Li, H. Modeling study of cumulative damage effects and safety criterion of surrounding rock under multiple full-face blasting of a large cross-section tunnel. Int. J. Rock Mech. Min. Sci. 2021, 147, 104882. [Google Scholar] [CrossRef]
- Ji, L.; Zhou, C.; Lu, S.; Jiang, N.; Gutierrez, M. Numerical Studies on the Cumulative Damage Effects and Safety Criterion of a Large Cross-Section Tunnel Induced by Single and Multiple Full-Scale Blasting. Rock Mech. Rock Eng. 2021, 54, 6393–6411. [Google Scholar] [CrossRef]
- GB/T13295-2013; Ductile Iron Pipes, Fittings and Accessories for Water or Gas Applications. AQSIQ: Beijing, China, 2013.





| Hole Type | Hole Number | Blasting Segment Number | Hole Depth (cm) | Charge per Hole (kg/hole) | Total Charge (kg) |
|---|---|---|---|---|---|
| Empty hole | 1 | 210 | |||
| Cut hole | 4 | 1 | 190 | 2.4 | 9.6 |
| Relief hole | 4 | 2 | 190 | 1.8 | 7.2 |
| Auxiliary hole | 12 | 3, 4 | 170 | 1.8 | 21.6 |
| Perimeter hole | 15 | 5, 6 | 170 | 0.9 | 13.5 |
| Bottom hole | 4 | 7 | 170 | 1.8 | 7.2 |
| Sum | 39 | 59.1 |
| Points | Horizontal Distance | Distance from the Source (m) | PPV (cm/s) | |||
|---|---|---|---|---|---|---|
| X | Y | Z | Resultant | |||
| T1 | −39 | 45 | 0.62 | 0.73 | 0.54 | 1.10 |
| T2 | −28 | 36 | 0.69 | 0.79 | 0.57 | 1.20 |
| T3 | −25 | 33 | 0.73 | 0.84 | 0.62 | 1.27 |
| T4 | −17 | 28 | 0.77 | 0.86 | 0.68 | 1.33 |
| T5 | 16 | 27 | 0.79 | 0.90 | 0.65 | 1.36 |
| T6 | 20 | 30 | 0.71 | 0.83 | 0.59 | 1.24 |
| T7 | 28 | 36 | 0.66 | 0.77 | 0.52 | 1.15 |
| T8 | 37 | 43 | 0.59 | 0.71 | 0.46 | 1.03 |
| T9 | 51 | 56 | 0.42 | 0.54 | 0.40 | 0.79 |
| T10 | 58 | 62 | 0.39 | 0.50 | 0.36 | 0.72 |
| Variables | Symbol | Dimension |
|---|---|---|
| Displacement | μ | L |
| Peak particle velocity | v | LT−1 |
| Particle vibration acceleration | a | LT−2 |
| Main frequency | f | T−1 |
| Charges | Q | M |
| Distance from blast source | r | L |
| Depth of blast source | d | L |
| Density of surrounding rock | ρ | ML−3 |
| Phase velocity | c | LT−1 |
| Time | t | T |
| Direction | Correlation Coefficient | |
|---|---|---|
| X | 0.82 | |
| Y | 0.85 | |
| Z | 0.83 | |
| Resultant | 0.89 |
| Size of the Grid (cm) | T3 | T4 | T5 | T6 | - |
|---|---|---|---|---|---|
| Velocity (cm/s) | Velocity (cm/s) | Velocity (cm/s) | Velocity (cm/s) | Time (h) | |
| 10–25 | 1.16 | 1.27 | 1.28 | 1.12 | 58 |
| 25–50 | 1.21 | 1.25 | 1.32 | 1.21 | 29 |
| 50–75 | 1.26 | 1.29 | 1.35 | 1.17 | 14 |
| 50–100 | 1.24 | 1.31 | 1.34 | 1.20 | 5 |
| 75–100 | 1.29 | 1.28 | 1.41 | 1.19 | 1.2 |
| Results of field monitoring | 1.27 | 1.33 | 1.36 | 1.24 | - |
| Parameters | Units | Type | ||
|---|---|---|---|---|
| Pipeline | Surface Soil | Sintered Tuff | ||
| Density | g/cm3 | 7.62 | 1.64 | 2.712 |
| Elastic modulus | GPa | 200 | 0.07 | 53.56 |
| Shear modulus | GPa | 60 | 6.37 × 10−3 | 18.34 |
| Cohesion | MPa | 0.08 | 6.4 | |
| Tensile stress | MPa | 275 | 0.02 | 2.7 |
| Poisson’s ratio | 0.28 | 0.30 | 0.28 | |
| Frictional angle | ° | 37 | 47 | |
| Points | PPV of Numerical Simulation (cm/s) | PPV of Monitoring (cm/s) | Error Rate % | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | X | Y | Z | Resultant | ||
| T1 | 0.65 | 0.76 | 0.57 | 1.15 | 0.62 | 0.73 | 0.54 | 1.10 | 4.35 |
| T2 | 0.71 | 0.84 | 0.59 | 1.25 | 0.69 | 0.79 | 0.57 | 1.20 | 4.00 |
| T3 | 0.76 | 0.87 | 0.65 | 1.33 | 0.73 | 0.84 | 0.62 | 1.27 | 4.51 |
| T4 | 0.79 | 0.89 | 0.72 | 1.39 | 0.77 | 0.86 | 0.68 | 1.33 | 4.32 |
| T5 | 0.81 | 0.92 | 0.68 | 1.40 | 0.79 | 0.90 | 0.65 | 1.36 | 2.86 |
| T6 | 0.74 | 0.87 | 0.63 | 1.30 | 0.71 | 0.83 | 0.59 | 1.24 | 4.62 |
| T7 | 0.71 | 0.82 | 0.56 | 1.22 | 0.66 | 0.77 | 0.52 | 1.15 | 5.74 |
| T8 | 0.62 | 0.75 | 0.49 | 1.09 | 0.59 | 0.71 | 0.46 | 1.03 | 5.50 |
| T9 | 0.46 | 0.58 | 0.42 | 0.85 | 0.42 | 0.54 | 0.40 | 0.79 | 7.06 |
| T10 | 0.42 | 0.53 | 0.39 | 0.78 | 0.39 | 0.50 | 0.36 | 0.72 | 7.69 |
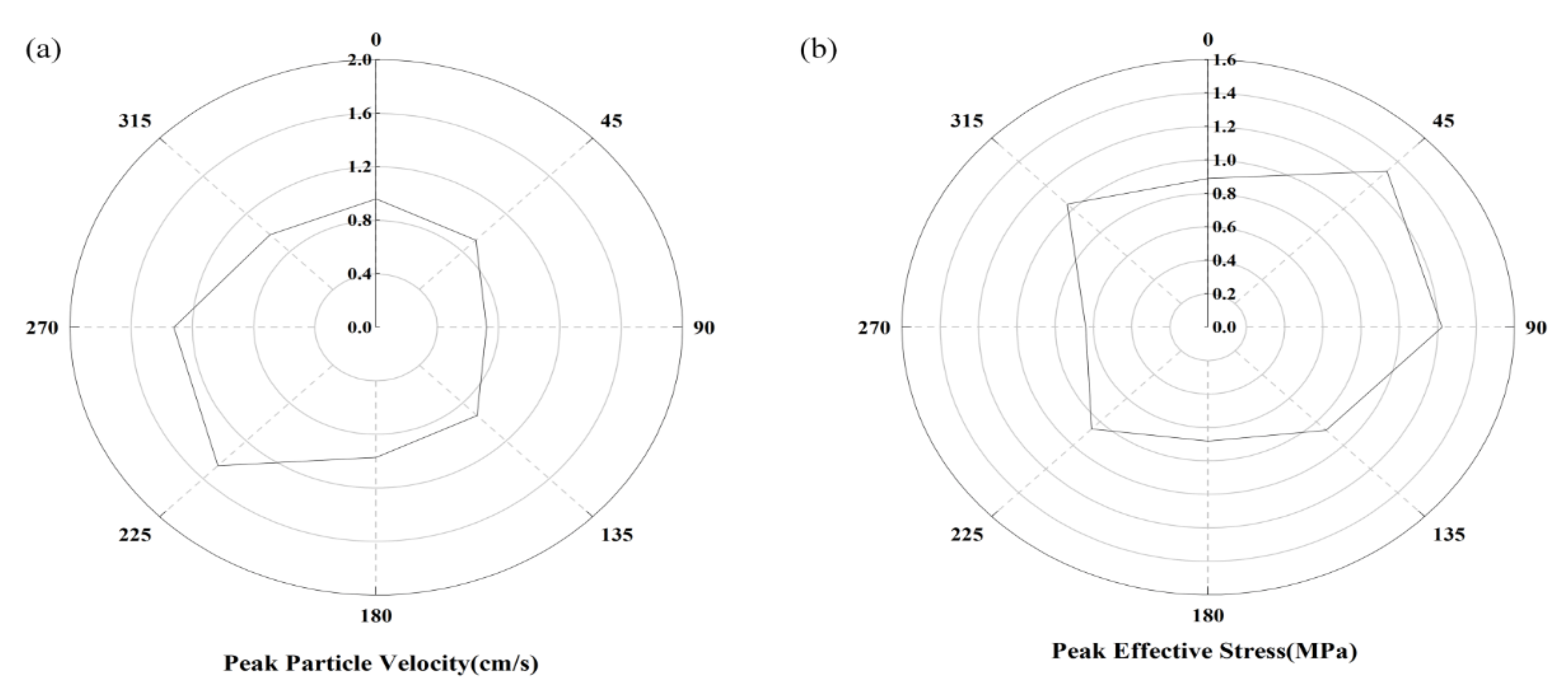
| Angle (°) | |||
|---|---|---|---|
| 0 | 2.463 × 10−3 | 0.72 | 292.341 |
| 45 | 5.008 × 10−3 | 1.53 | 305.514 |
| 90 | 2.745 × 10−3 | 0.94 | 342.475 |
| 135 | 1.476 × 10−3 | 0.57 | 386.271 |
| 180 | 3.569 × 10−3 | 1.25 | 350.233 |
| 225 | 1.393 × 10−3 | 0.42 | 301.486 |
| 270 | 1.938 × 10−3 | 0.63 | 325.158 |
| 315 | 3.532 × 10−3 | 1.16 | 328.453 |
| Average | 328.991 |
| Horizontal Distance | PES of Simulation (MPa) | PPV of Simulation (cm/s) | PPV Predicted by Equation (11) | Error Rate of PPV (%) |
|---|---|---|---|---|
| 0 | 1.87 | 2.60 | 2.58 | 0.77 |
| 8 | 1.48 | 2.29 | 2.31 | 0.87 |
| 16 | 1.20 | 2.02 | 2.03 | 0.50 |
| 24 | 1.05 | 1.77 | 1.69 | 4.52 |
| 32 | 0.84 | 1.50 | 1.48 | 1.33 |
| 40 | 0.65 | 1.26 | 1.22 | 3.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, T.; Wu, M.; Jia, L.; Xie, L.; Wu, L. Effects of Vibration on Adjacent Pipelines under Blasting Excavation. Appl. Sci. 2023, 13, 121. https://doi.org/10.3390/app13010121
Qin T, Wu M, Jia L, Xie L, Wu L. Effects of Vibration on Adjacent Pipelines under Blasting Excavation. Applied Sciences. 2023; 13(1):121. https://doi.org/10.3390/app13010121
Chicago/Turabian StyleQin, Tiange, Mingze Wu, Lin Jia, Lingli Xie, and Li Wu. 2023. "Effects of Vibration on Adjacent Pipelines under Blasting Excavation" Applied Sciences 13, no. 1: 121. https://doi.org/10.3390/app13010121
APA StyleQin, T., Wu, M., Jia, L., Xie, L., & Wu, L. (2023). Effects of Vibration on Adjacent Pipelines under Blasting Excavation. Applied Sciences, 13(1), 121. https://doi.org/10.3390/app13010121






