Form Finding of Asymmetric Cable Network Reflector with Flexible Ring Truss
Abstract
:1. Introduction
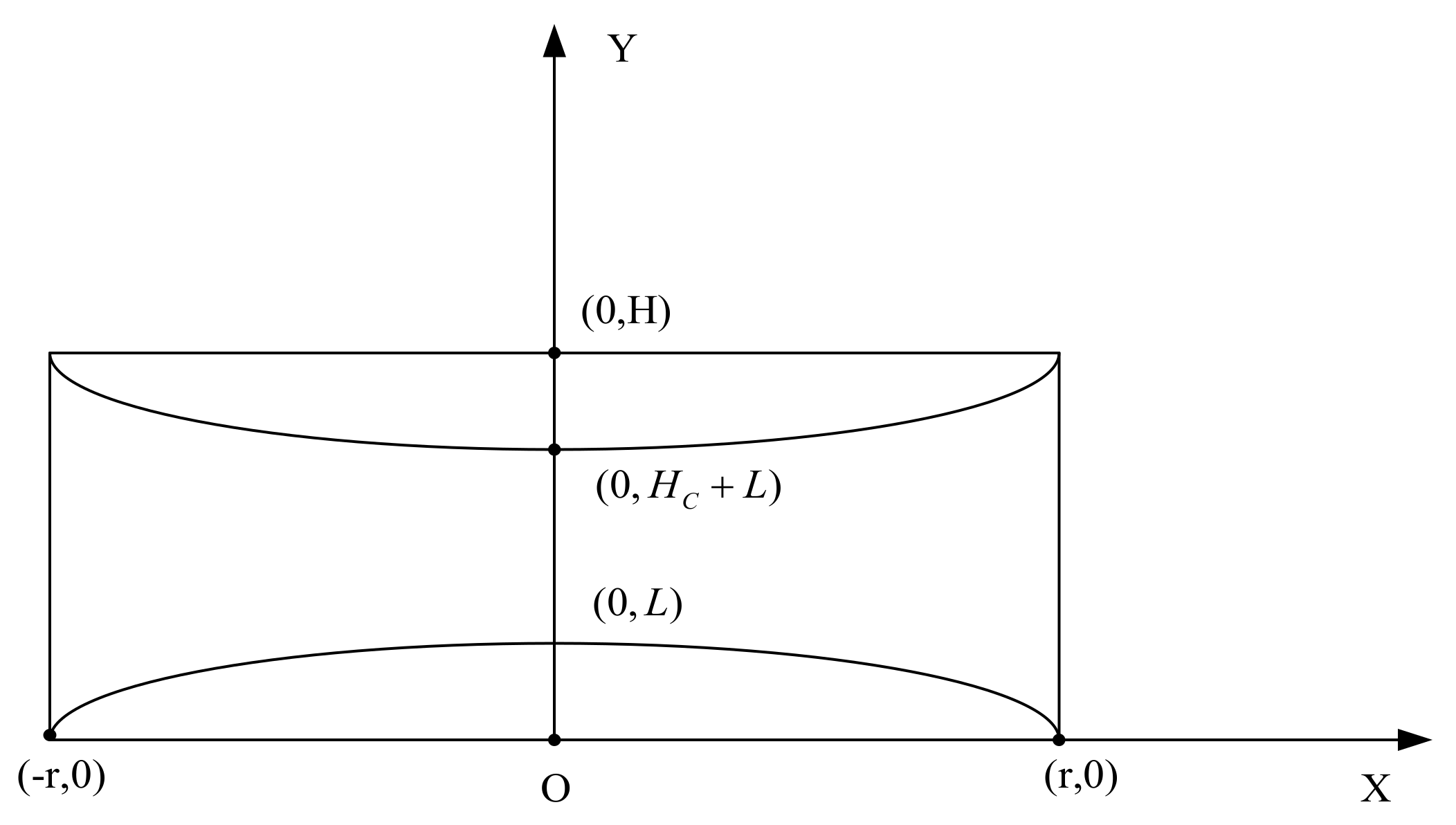
2. Form-Finding Method for Asymmetric Cable Network Reflector
2.1. Equilibrium Equation
2.2. The Optimal Design of the Pre-Stress in Cable Nets
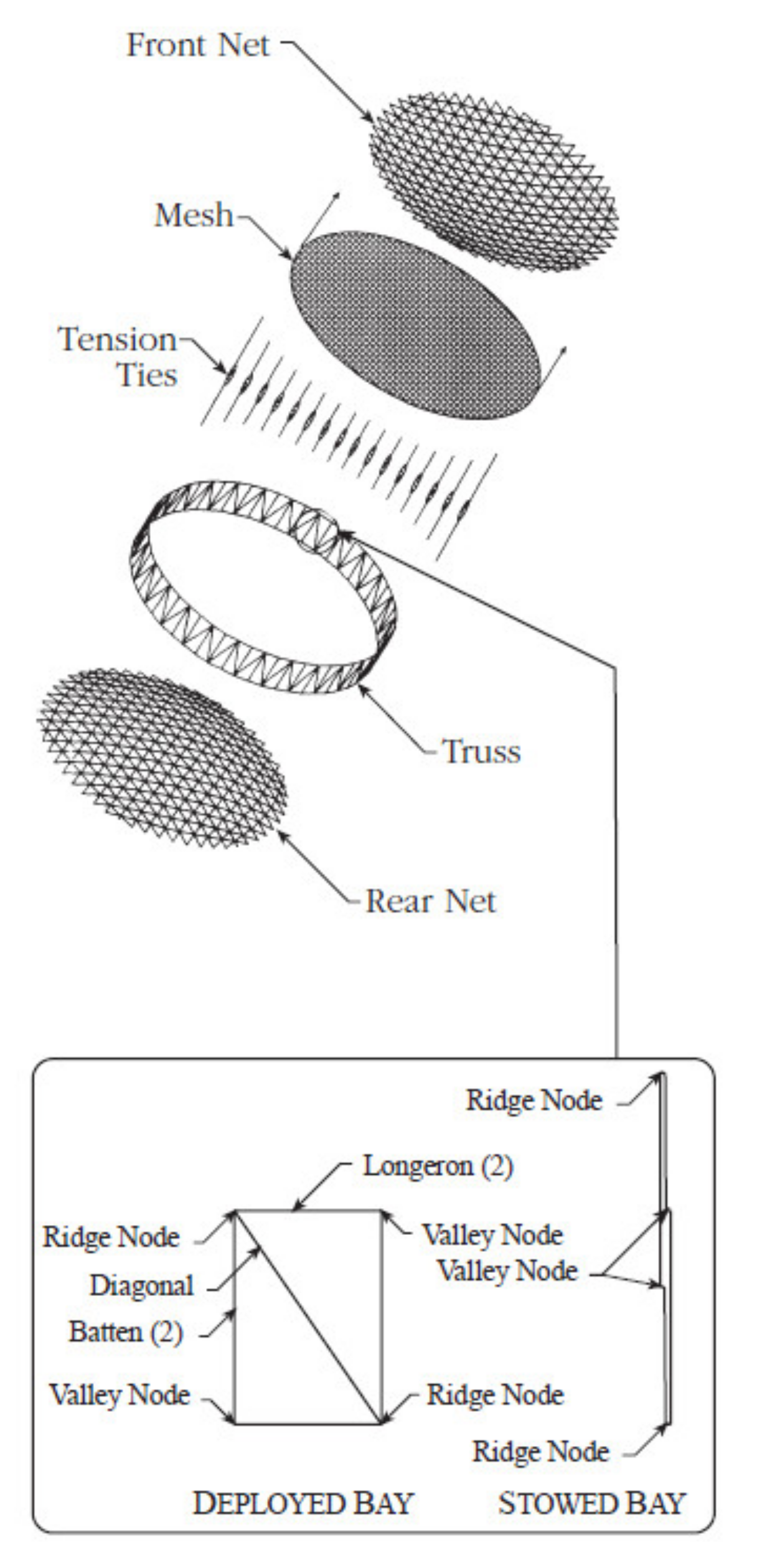
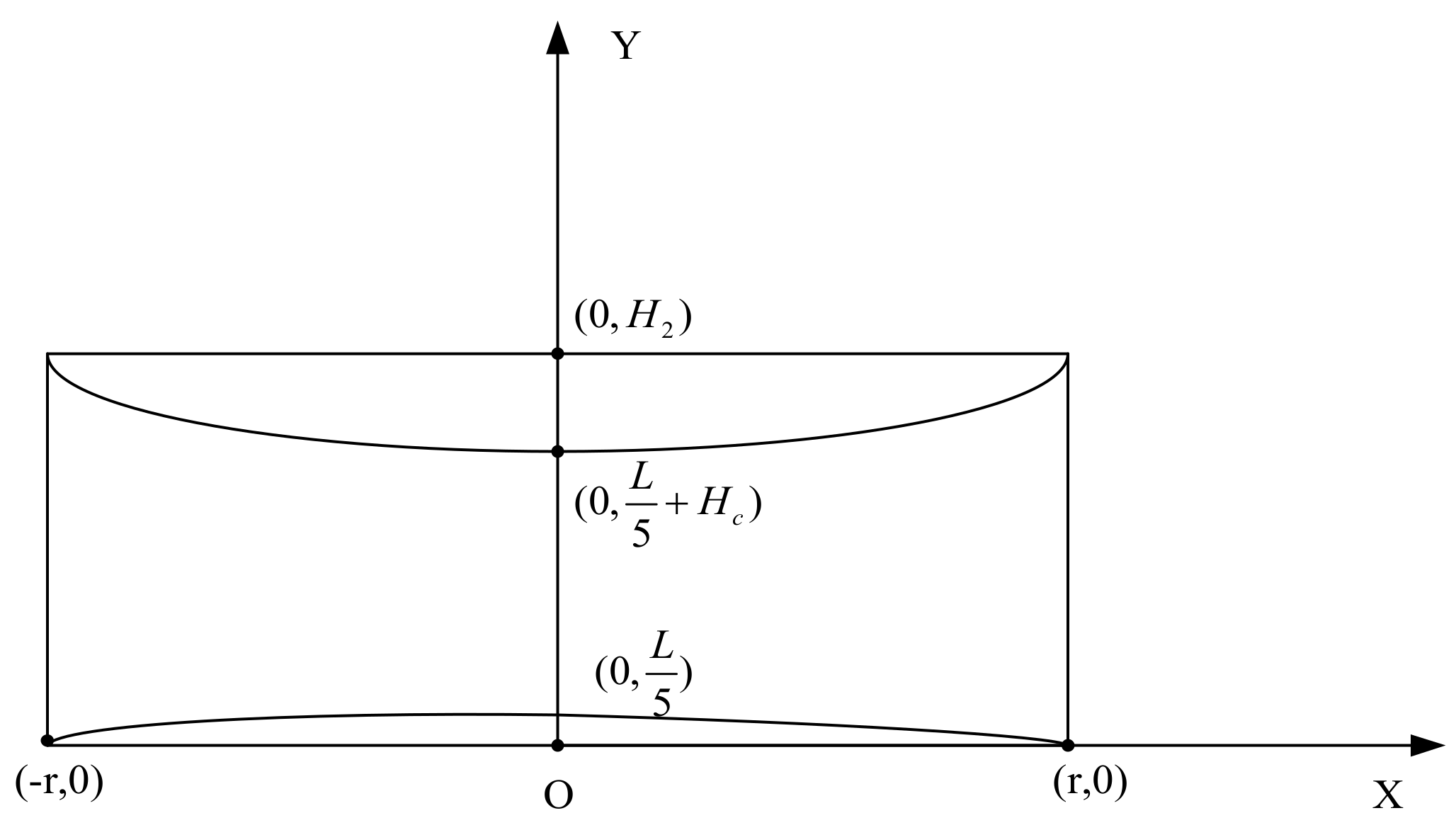
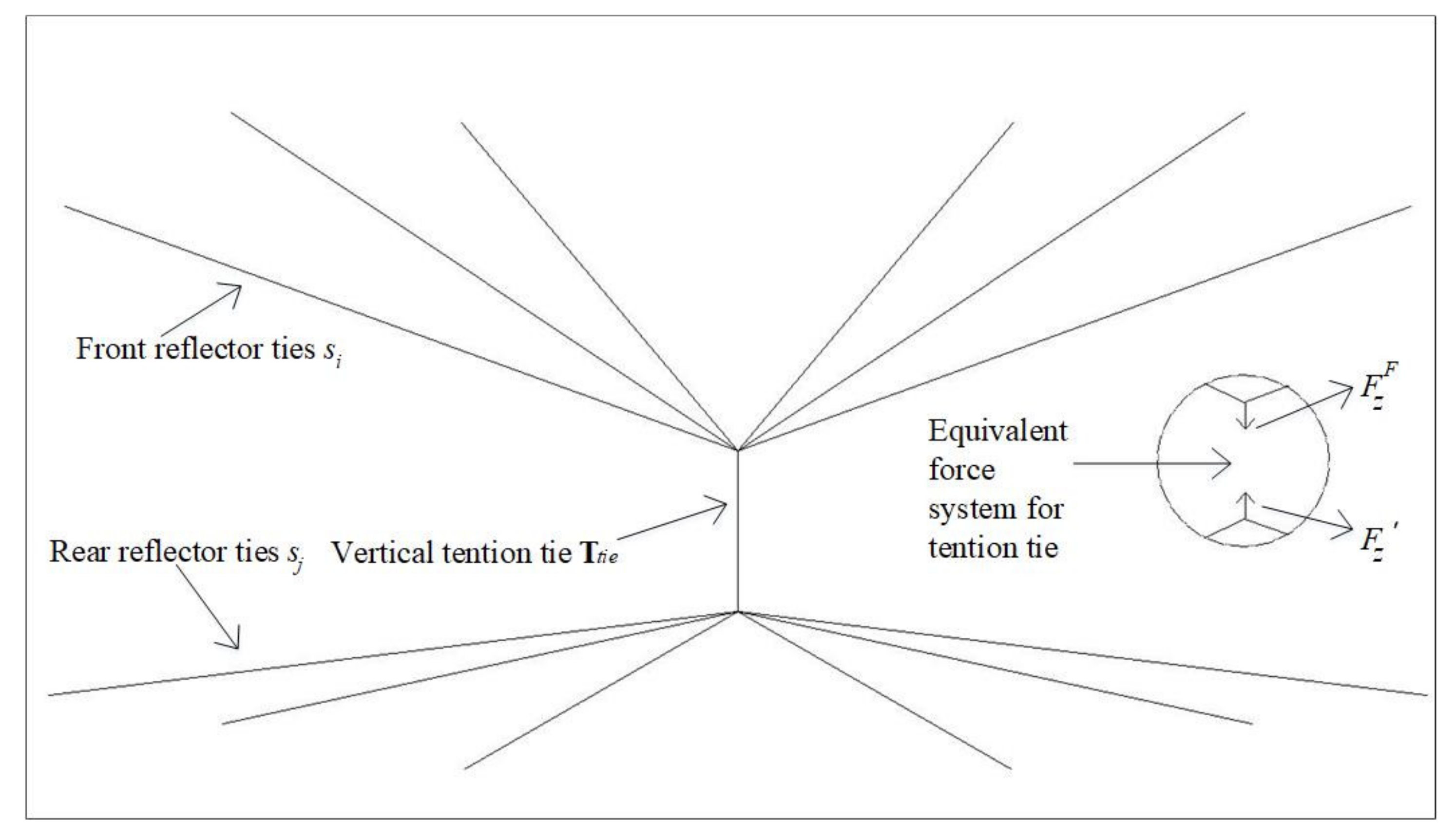
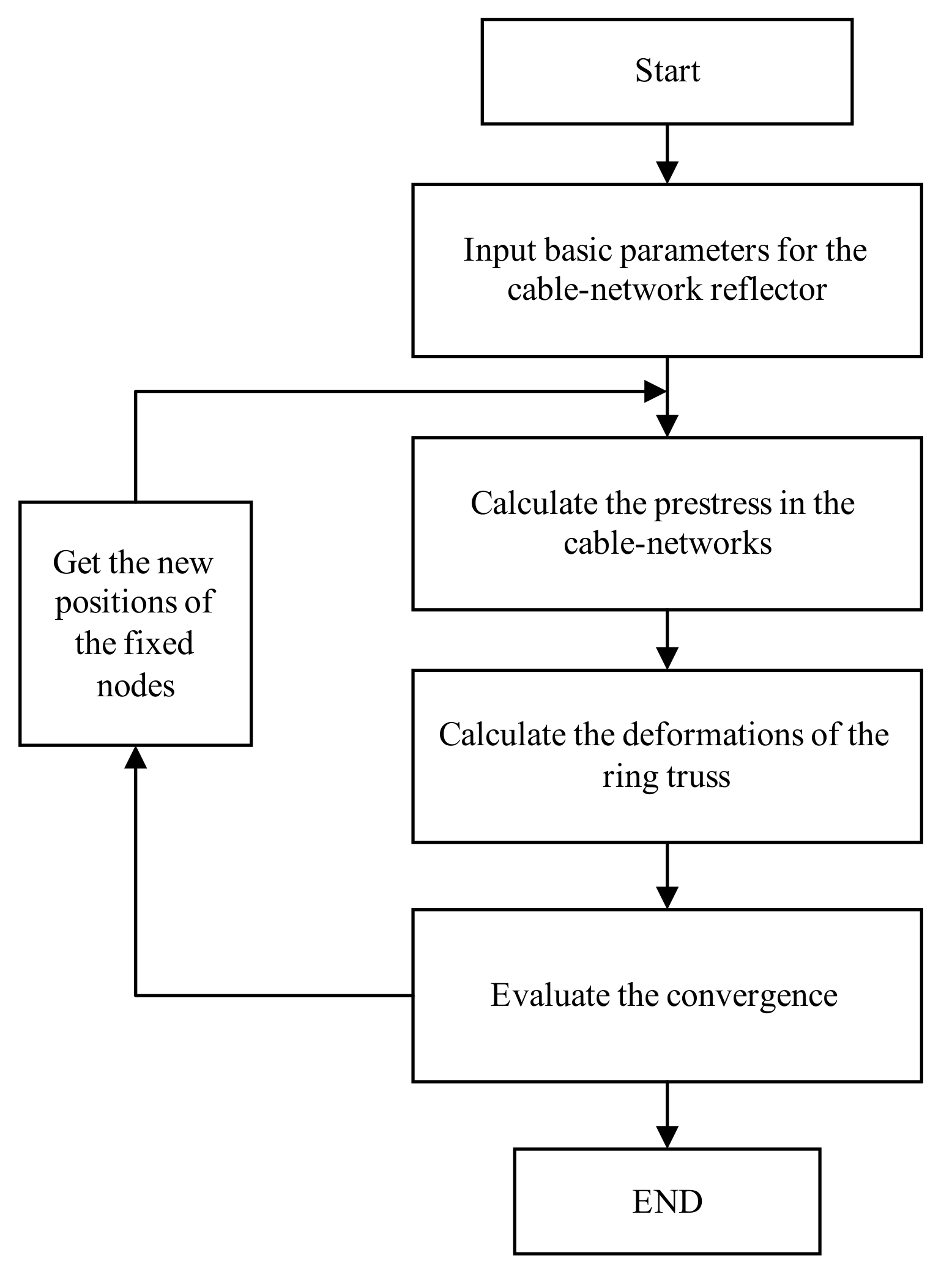
3. Form-Finding Method Considering the Deformation of Flexible Ring Truss
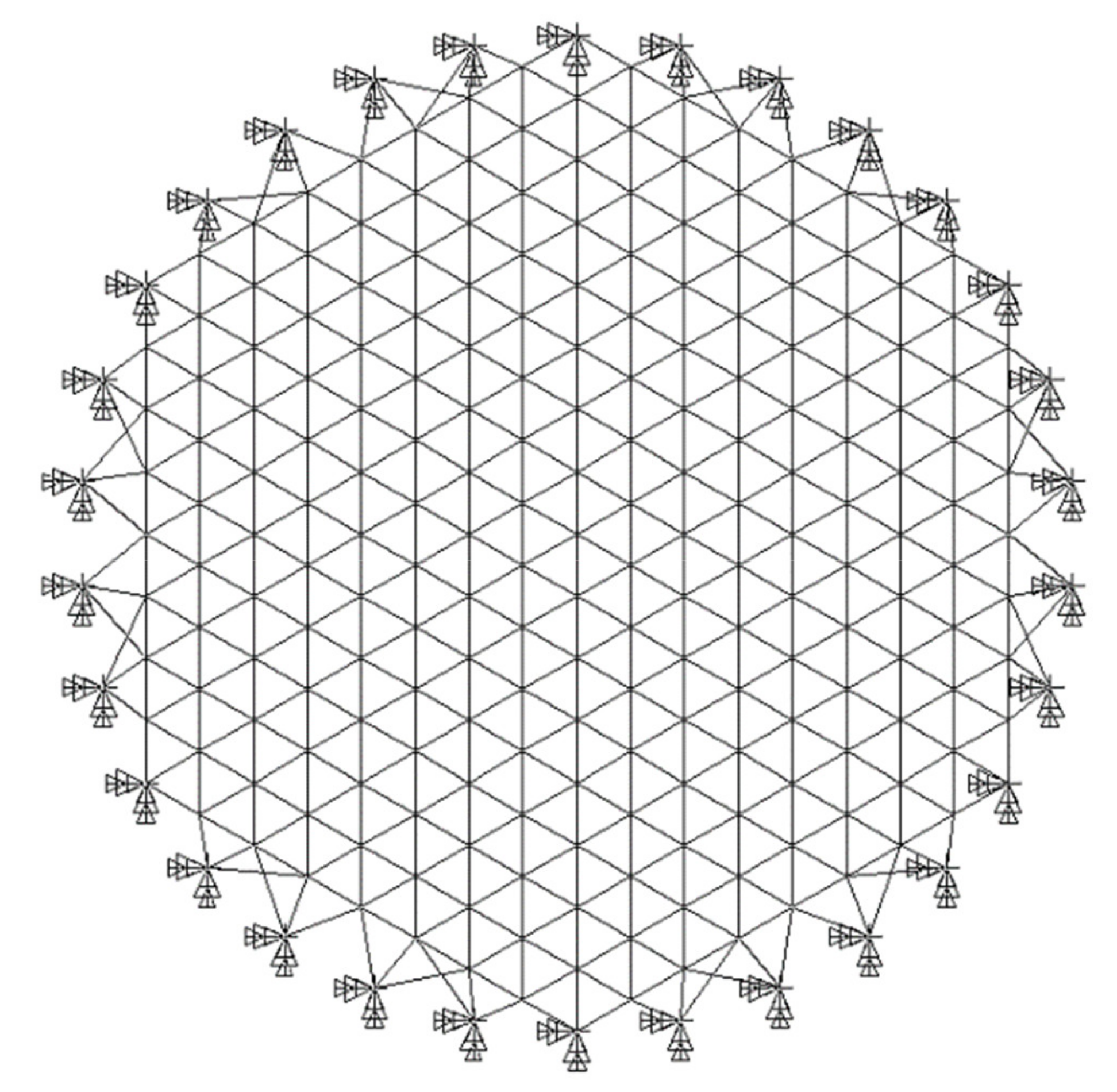
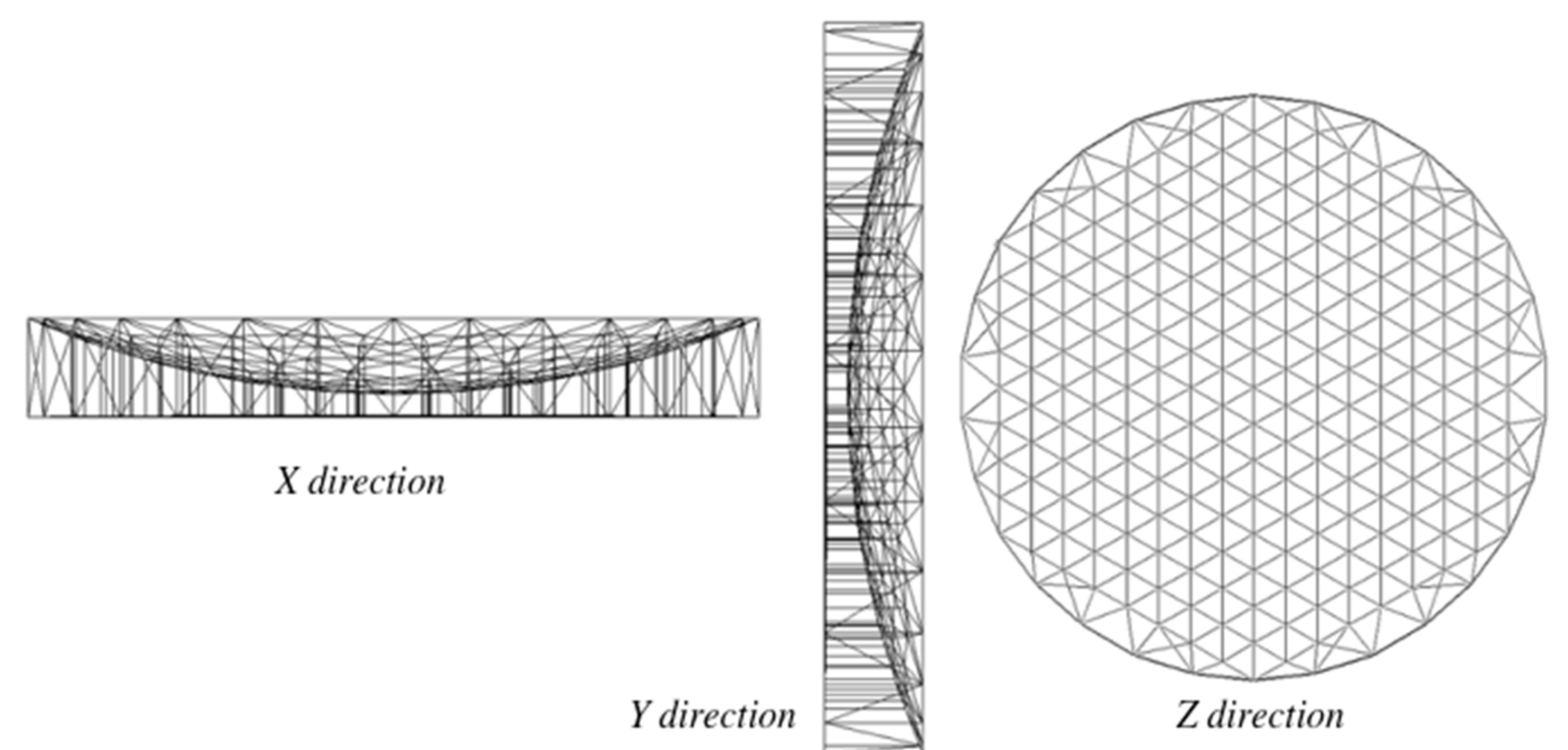
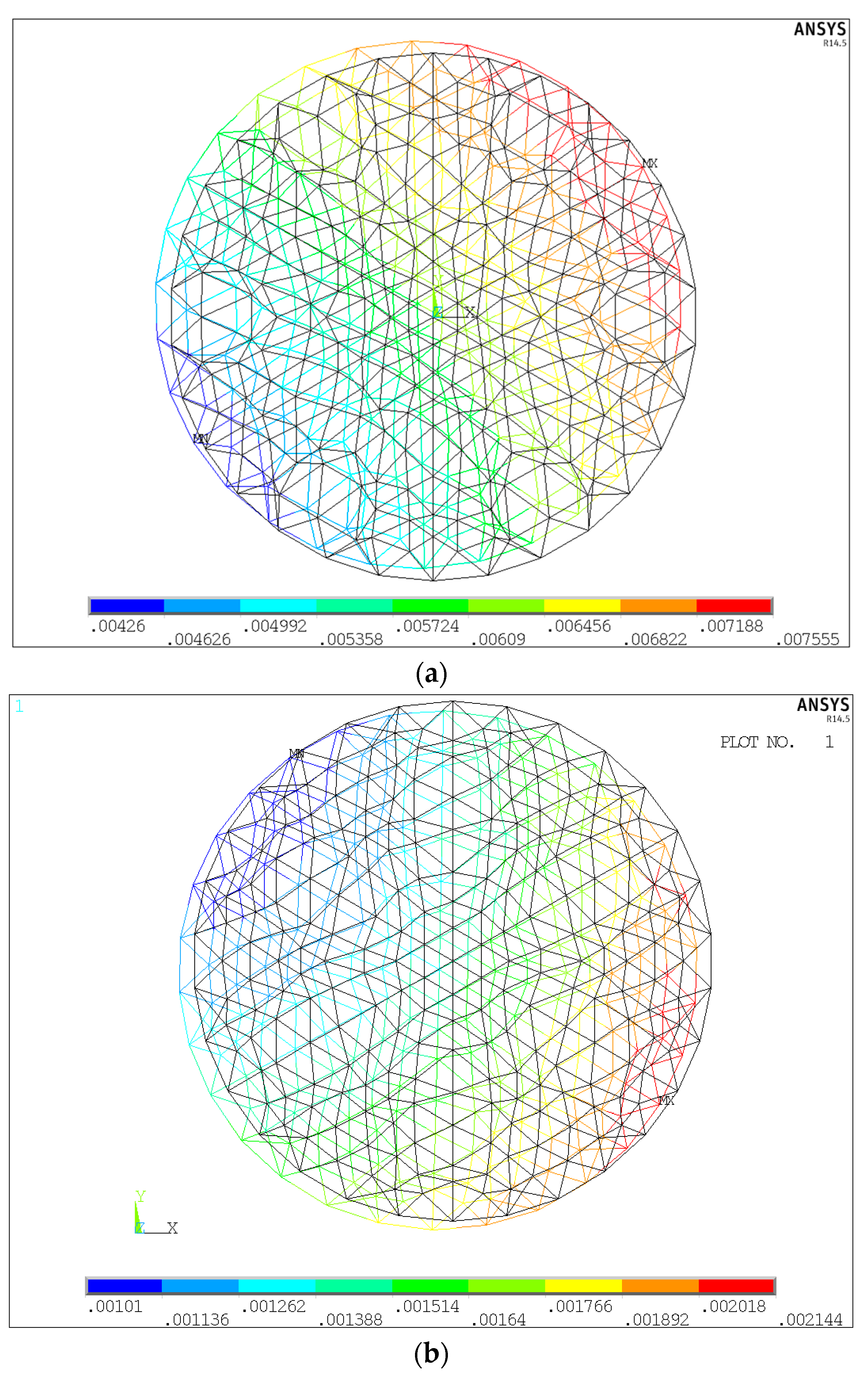
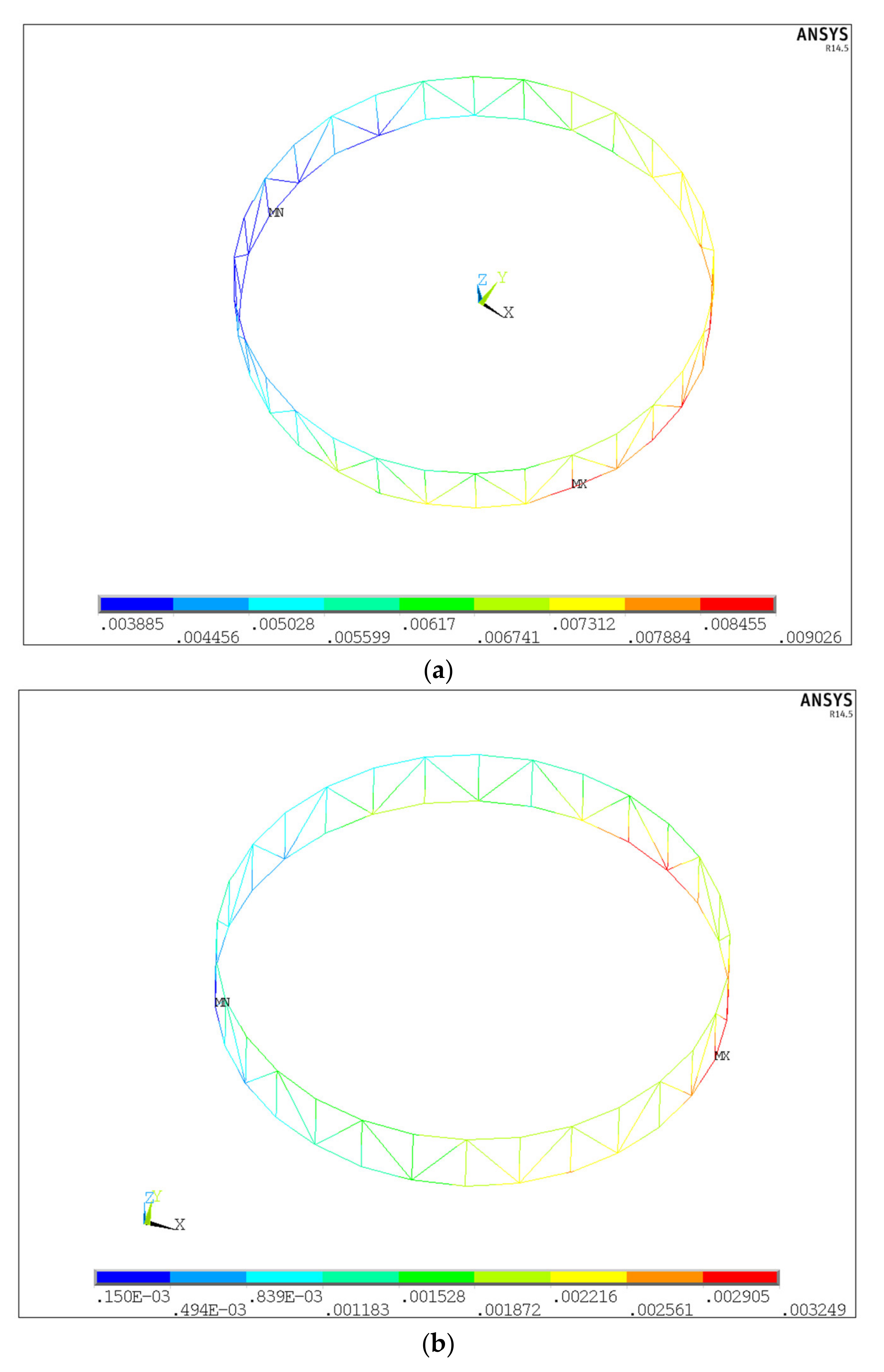
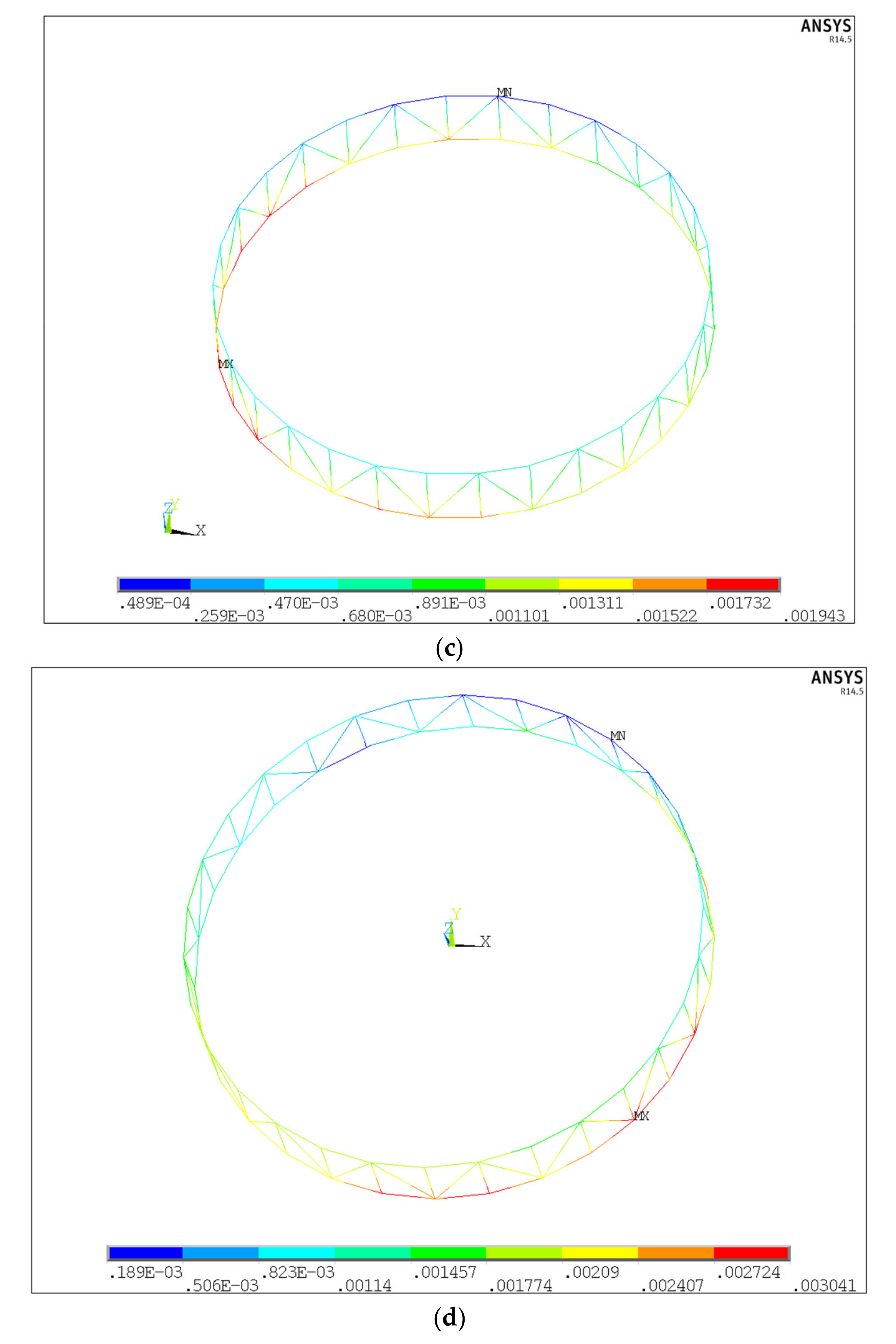
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mileski, P.; Kornblith, J. Lightweight Deployable Antenna System. U.S. Patent 5,091,732, 25 February 1992. [Google Scholar]
- Takano, T.; Miura, K.; Natori, M.; Hanayama, E.; Inoue, T.; Noguchi, T.; Miyahara, N.; Nakaguro, H. Deployable antenna with 10-m maximum diameter for space use. IEEE Trans. Antennas Propag. 2004, 52, 2–11. [Google Scholar] [CrossRef]
- Salama, M.; Lou, M.; Fang, H. Deployment of inflatable space structures-a review of recent developments. In Proceedings of the 41st Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, GA, USA, 3–6 April 2000; p. 1730. [Google Scholar]
- Freeland, R.E.; Bilyeu, G.D.; Veal, G.R.; Steiner, M.D.; Carson, D.E. Large inflatable deployable antenna flight experiment results. Acta Astronaut. 1997, 41, 267–277. [Google Scholar] [CrossRef]
- Tabata, M.; Fujii, K.; Shintate, K.; Ozawa, S. Deployable antenna. U.S. Patent 20,120,193,498, 30 January 2012. [Google Scholar]
- Pellegrino, S. Deployable Structures; Springer: Berlin/Heidelberg, Germany, 2014; Volume 412. [Google Scholar]
- Thomson, M.W. The Astromesh deployable reflector. In Proceedings of the Antennas and Propagation Society International Symposium, Orlando, FL, USA, 11–16 July 1999; pp. 1516–1519. [Google Scholar]
- Tibert, A.G.; Pellegrino, S. Deployable tensegrity reflectors for small satellites. J. Spacecr. Rocket. 2002, 39, 701–709. [Google Scholar] [CrossRef] [Green Version]
- Tabarrok, B.; Qin, Z. Nonlinear-Analysis of Tension Structures. Comput. Struct. 1992, 45, 973–984. [Google Scholar] [CrossRef]
- Tang, Y.Q.; Li, T.J.; Ma, X.F. Form Finding of Cable Net Reflector Antennas Considering Creep and Recovery Behaviors. J. Spacecr. Rocket. 2016, 53, 610–618. [Google Scholar] [CrossRef]
- Tabata, M.; Yamamoto, K.; Inoue, T.; Noda, T.; Miura, K. Shape adjustment of a flexible space antenna reflector. J. Intell. Mater. Syst. Struct. 1992, 3, 646–658. [Google Scholar] [CrossRef]
- Fazli, N.; Abedian, A. Design of tensegrity structures for supporting deployable mesh antennas. Sci. Iran. 2011, 18, 1078–1087. [Google Scholar] [CrossRef] [Green Version]
- Mobrem, M. Methods of analyzing surface accuracy of large antenna structures due to manufacturing tolerances. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, Virginia, 7–10 April 2003; p. 1453. [Google Scholar]
- Tanaka, H. Surface error estimation and correction of a space antenna based on antenna gainanalyses. Acta Astronaut. 2011, 68, 1062–1069. [Google Scholar] [CrossRef]
- Shi, H.; Yang, B.; Fang, H. Offset-feed surface mesh generation for design of space deployable mesh reflectors. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013; p. 1526. [Google Scholar]
- Meguro, A.; Harada, S.; Watanabe, M. Key technologies for high-accuracy large mesh antenna reflectors. Acta Astronaut. 2003, 53, 899–908. [Google Scholar] [CrossRef]
- Tang, Y.Q.; Li, T.J.; Ma, X.F. Pillow Distortion Analysis for a Space Mesh Reflector Antenna. AIAA J. 2017, 55, 3206–3213. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Deng, H. Form-finding analysis and active shape adjustment of cable net reflectors with PZT actuators. J. Aerosp. Eng. 2012, 27, 575–586. [Google Scholar] [CrossRef]
- Wang, Z.W.; Li, T.J.; Cao, Y.Y. Active shape adjustment of cable net structures with PZT actuators. Aerosp. Sci. Technol. 2013, 26, 160–168. [Google Scholar] [CrossRef]
- Yan, B.; Wang, K.; Kang, C.X.; Zhang, X.N.; Wu, C.Y. Self-Sensing Electromagnetic Transducer for Vibration Control of Space Antenna Reflector. IEEE/ASME Trans. Mechatron. 2017, 22, 1944–1951. [Google Scholar] [CrossRef]
- Xun, G.B.; Peng, H.J.; Wu, S.N.; Wu, Z.G. Active Shape Adjustment of Large Cable-Mesh Reflectors Using Novel Fast Model Predictive Control. J. Aerosp. Eng. 2018, 31, 04018038. [Google Scholar] [CrossRef]
- Tanaka, H.; Shimozono, N.; Natori, M.C. A design method for cable network structures considering the flexibility of supporting structures. Trans. Jpn. Soc. Aeronaut. Space Sci. 2008, 50, 267–273. [Google Scholar] [CrossRef] [Green Version]
- Maddio, P.D.; Meschini, A.; Sinatra, R.; Cammarata, A. An optimized form-finding method of an asymmetric large deployable reflector. Eng. Struct. 2019, 181, 27–34. [Google Scholar] [CrossRef]
- Li, T.; Zuowei, W.; Deng, H. Mesh reflector antennas: Form-finding analysis review. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013; p. 1576. [Google Scholar]
- Liu, W.; Li, D.X.; Yu, X.Z.; Jiang, J.P. Exact mesh shape design of large cable-network antenna reflectors with flexible ring truss supports. Acta Mech. Sin. 2014, 30, 198–205. [Google Scholar] [CrossRef]
- Li, T.J.; Jiang, J.; Deng, H.Q.; Lin, Z.C.; Wang, Z.W. Form-finding methods for deployable mesh reflector antennas. Chin. J. Aeronaut. 2013, 26, 1276–1282. [Google Scholar] [CrossRef] [Green Version]
- Tran, H.C.; Lee, J. Self-stress design of tensegrity grid structures with exostresses. Int. J. Solids Struct. 2010, 47, 2660–2671. [Google Scholar] [CrossRef] [Green Version]
- Linkwitz, K.; Schek, H.-J. Einige bemerkungen zur berechnung von vorgespannten seilnetzkonstruktionen [Some comments on the calculation of pre-tensioned cable network constructions]. Ing. Arch. 1971, 40, 145–158. (In German) [Google Scholar] [CrossRef]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Michalewicz, Z. Evolution strategies and other methods. In Genetic Algorithms+ Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1996; pp. 159–177. [Google Scholar]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Ribeiro Filho, J.L.; Treleaven, P.C.; Alippi, C. Genetic-algorithm programming environments. Computer 1994, 27, 28–43. [Google Scholar] [CrossRef]



| Material Parameter | Material Properties | Elastic Modulus (GPa) | Diameter (m) | ||
|---|---|---|---|---|---|
| Cable network | Kevlar49 | 137.07 | 1440 | 0.002 | |
| Ring truss | Carbon Fiber 60J | 588 | 1940 | inner | outer |
| 0.018 | 0.02 | ||||
| The Initial Reflector Data | Present Approach | |||
|---|---|---|---|---|
| 1st Iteration | 2nd Iteration | 3rd Iteration | ||
| Max–min distributed tension in the front reflector (N) | 17.06/3.53 | 27.39/6.40 | 22.24/5.70 | 27.90/5.00 |
| Max–min tension ratio of cable net | 4.82 | 4.28 | 3.90 | 5.58 |
| Free nodal position error (m) | 7.56 × 10−3 | 2.14 × 10−3 | 0.76 × 10−3 | 1.95 × 10−3 |
| Improvement of surface accuracy | — | 71.69% | 89.95% | 74.21% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Luo, Y.; Zhang, X. Form Finding of Asymmetric Cable Network Reflector with Flexible Ring Truss. Appl. Sci. 2022, 12, 4508. https://doi.org/10.3390/app12094508
Hu Z, Luo Y, Zhang X. Form Finding of Asymmetric Cable Network Reflector with Flexible Ring Truss. Applied Sciences. 2022; 12(9):4508. https://doi.org/10.3390/app12094508
Chicago/Turabian StyleHu, Zifan, Yajun Luo, and Xinong Zhang. 2022. "Form Finding of Asymmetric Cable Network Reflector with Flexible Ring Truss" Applied Sciences 12, no. 9: 4508. https://doi.org/10.3390/app12094508
APA StyleHu, Z., Luo, Y., & Zhang, X. (2022). Form Finding of Asymmetric Cable Network Reflector with Flexible Ring Truss. Applied Sciences, 12(9), 4508. https://doi.org/10.3390/app12094508





