Definition and Determination of Fin Substitution Factors Accelerating Thermal Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Temperature-Dependent Properties of Air
2.2. Analytical Formulas
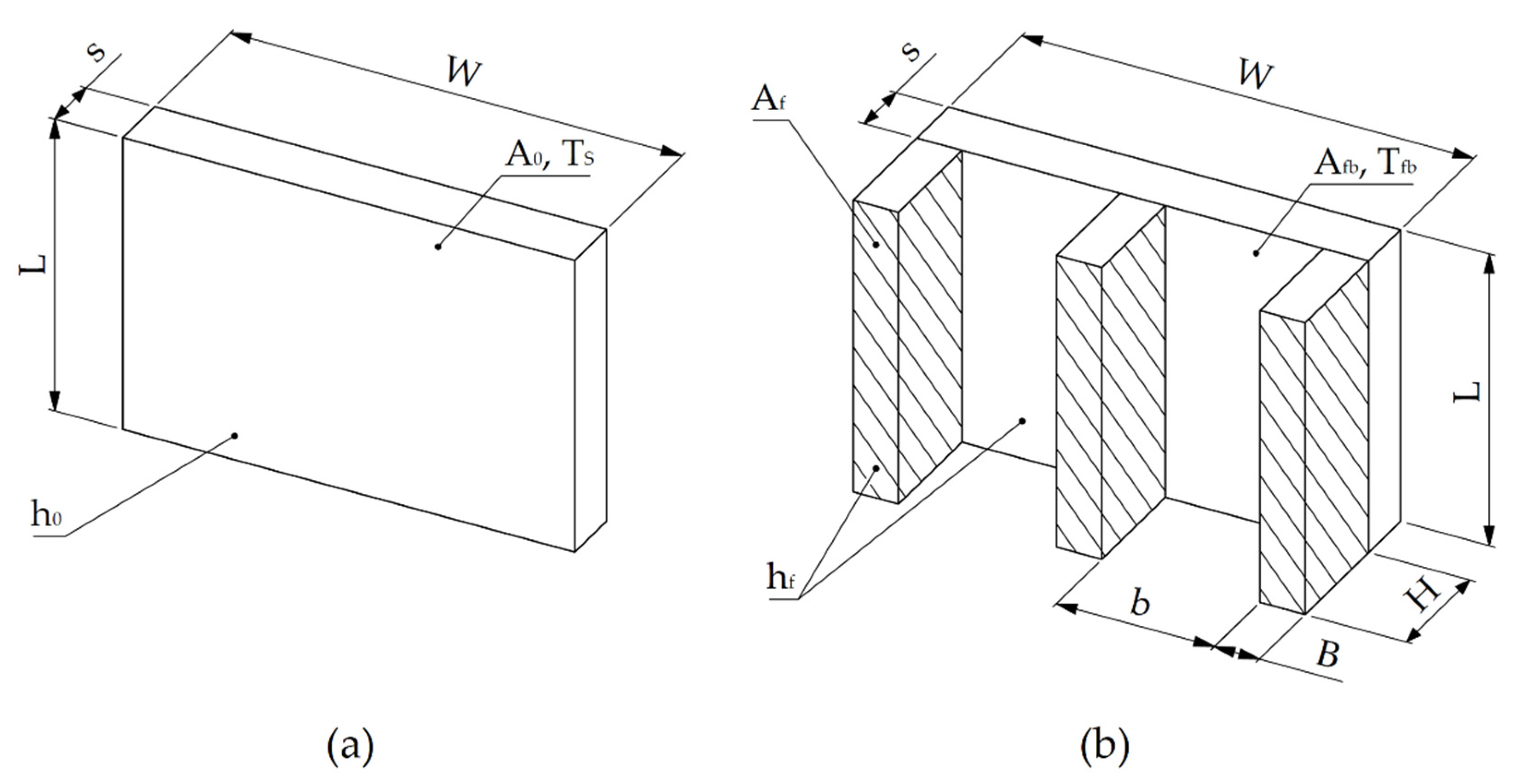
2.2.1. Surfaces of the Smooth and Finned Surface
2.2.2. Parameters for Plates
2.2.3. Parameters for Vertical Rectangular Finned Arrays
2.3. Hardware and Software
2.4. CFD Simulation Modeling
2.5. Solid-State Simulation Modeling
3. Results
3.1. Definition of the Fin Substitution Factor
- Identical temperatures exist for the smooth surface and the fin base
- Identical heat flows of the smooth and the ripped surfaces
3.2. Method for Determining Fin Substitution Factor
- Shape of the fins
- Orientation of the finned array
- Type of surrounding fluid
- Type of the thermal boundary conditions
- Geometric dimensions of the finned array
- Fluid and Material parameters
- Values of the thermal boundary conditions
- Determination of the case-specific, temperature-dependent air properties
- Calculation of the surfaces of the smooth base body and the finned array
- Calculation of the parameters of the smooth surface
- Calculation of the finned array parameters
- Determination of the FSFi vector
3.3. Case Study: Natural Convection on Vertical Rectangular Finned Arrays
3.3.1. Specifications
- Shape of the fins: rectangular
- Orientation of the finned array: vertical
- Type of surrounding fluid: air
- Type of the thermal boundary conditions: constant temperature
3.3.2. Objectives
3.3.3. Determination of the Calculation Path for Vertical Rectangular Finned Arrays
3.3.4. Validation
4. Discussion and Conclusions
- FSFs were determined based solely on geometric ratios, and the heat conduction showed the largest deviations both overall and concerning low-level parameters. Thus, these calculation paths were unsuitable.
- The same applies to the calculation paths, which consider all three components. Looking at all, the results FSFA,η,h,EL were the exception, as this calculation path was among the five most accurate ones.
- The paths considering the geometric and heat transfer components gave the best results. Four of the five most accurate calculation paths were among these concerning the overall mean deviation and the overall standard deviation. The FSFA,h,Ro1 path had the best results for low fin base temperatures. There was no single calculation path for higher temperatures and different fin heights that turned out to be particularly accurate. The performance of the FSFA,h,El, FSFA,h,Ai, FSFA,h,Ba and FSFA,h,Ro1 paths were very similar for these parameters. For longer fin lengths and almost all examined fin spacing, the FSFA,h,Ai path was the best one.
- The FSFA,h,Ai path gave the best results with an 8% overall mean deviation and an overall standard deviation of 0.5. For this reason, this calculation path is recommended for the analytical determination of the FSF for vertical rectangular finned arrays considering natural convection with air as surrounding fluid and an isothermal boundary condition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A0 | area smooth surface |
| Afa | area finned array |
| Afb | area fin base |
| Af | area of all fins |
| Af,cs | cross-sectional area of one fine |
| Af,s | area of one fin |
| B | fin width |
| b | fin spacing |
| Bi | Biot number |
| cRo | Rohsenow parameter |
| CRo | Rohsenow parameter |
| CFD | Computational fluid dynamics |
| cp | specific heat capacity |
| FEM | Finite-Element-Method |
| FSF | fin substitution factor |
| g | acceleration of gravity |
| H | fin hight |
| h | heat transfer coefficient |
| h0 | heat transfer coefficient smooth surface |
| hf | heat transfer coefficient finned array |
| kfluid | conductivity fluid |
| kf | conductivity fins |
| L | fin length |
| Lspe | specific length |
| n | number of fins |
| Nu | Nusselt number |
| Pf | perimeter of one fin |
| Pr | Prandtl number |
| Q0 | Heat flux smooth surface |
| QCFD | Heat flux flow simulation |
| Qf | Heat flux finned array |
| QFEM+FSF | Heat flux solid-state simulation |
| Ra | Rayleigh number |
| s | base plate thickness |
| T∞ | ambient temperature |
| TS | surface temperature |
| Tfb | fin base temperature |
| W | base plate width |
| y+ | dimensionless wall distance |
| α | thermal diffusivity |
| β | thermal expansion coefficient |
| ηf | fin efficiency |
| μ | fin parameter |
| ν | kinematic viscosity |
| ρ | density |
References
- Senapati, J.R.; Dash, S.K.; Roy, S. Numerical investigation of natural convection heat transfer from vertical cylinder with annular fins. Int. J. Therm. Sci. 2017, 111, 146–159. [Google Scholar] [CrossRef]
- Senapati, J.R.; Dash, S.K.; Roy, S. Numerical investigation of natural convection heat transfer over annular finned horizontal cylinder. Int. J. Heat Mass Transf. 2016, 96, 330–345. [Google Scholar] [CrossRef]
- Wong, S.-C.; Lee, W.-Y. Numerical study on the natural convection from horizontal finned tubes with small and large fin temperature variations. Int. J. Therm. Sci. 2019, 138, 116–123. [Google Scholar] [CrossRef]
- Mehrtash, M.; Tari, I. A correlation for natural convection heat transfer from inclined plate-finned heat sinks. Appl. Therm. Eng. 2013, 51, 1067–1075. [Google Scholar] [CrossRef]
- Tari, I.; Mehrtash, M. Natural convection heat transfer from inclined plate-fin heat sinks. Int. J. Heat Mass Transf. 2013, 56, 574–593. [Google Scholar] [CrossRef]
- Shen, Q.; Sun, D.; Xu, Y.; Jin, T.; Zhao, X. Orientation effects on natural convection heat dissipation of rectangular fin heat sinks mounted on LEDs. Int. J. Heat Mass Transf. 2014, 75, 462–469. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Livine, A.S. Introduction to Heat Transfer, 5th ed.; John Wily & Son: New York, NY, USA, 2007; pp. 348–372. [Google Scholar]
- Clapp, M. A Designer’s Guide to CFD, 1st ed.; NAFEMS: Hamilton, ON, Canada, 2019. [Google Scholar]
- Xu, Y.; Yang, J.; Xu, C.; Wang, W.; Ma, Z. Thermal analysis on NAC-STC spent fuel transport cask under different transport conditions. Nucl. Eng. Des. 2013, 265, 682–690. [Google Scholar] [CrossRef]
- Leber, A.; Graf, W.; Hüggenberg, R. Validation of CFD-methods to predict heat transfer and temperatures during the transport and storage of casks under a cover. In Proceedings of the 14th International Symposium on the Packaging and Paper Transportation of Radioactive Materials (PATRAM), Berlin, Germany, 20–24 September 2004. [Google Scholar]
- Stratmann, W.; Hages, P. Analysis of removal of residual decay heat from interim storage facilities by means of the CFD program FLUENT. In Proceedings of the 14th International Symposium on the Packaging and Paper Transportation of Radioactive Materials (PATRAM), Berlin, Germany, 20–24 September 2004. [Google Scholar]
- ANSYS Inc. ANSYS FLUENT 2020 R2: ANSYS FLUENT User´s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- VDI Heat Atlas, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [CrossRef]
- Karwa, R. Heat and Mass Transfer, 2nd ed.; Springer Nature: Singapore, 2020. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H.S. Correlating equations for laminar and turbulent free convection from a vertical plate. Int. J. Heat Mass Transf. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- Marek, R.; Nitsche, K. Praxis der Wärmeübertragung, 5th ed.; Carl Hanser Verlag: München, Germany, 2019; pp. 192–194. [Google Scholar]
- Kraus, A.D.; Aziz, A.; Welty, J. Extended Surface Heat Transfer, 1st ed.; John Wily & Son: New York, NY, USA, 2001; pp. 190–207. [Google Scholar]
- Elenbaas, W. Heat dissipation of parallel plates by free convection. Physica 1942, 9, 1–28. [Google Scholar] [CrossRef]
- Auhara, T. Heat Transfer due to Natural Convection from Parallel Vertical Plates. Trans. Jpn. Soc. Mech. Engr. 1963, 29, 903–909. [Google Scholar] [CrossRef][Green Version]
- Bar-Cohen, A.; Rohsenow, W.M. Thermally Optimum Spacing of Vertical, Natural Convection Cooled, Parallel Plates. J. Heat Transf. 1984, 106, 116–123. [Google Scholar] [CrossRef]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. Handbook of Heat Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1998; pp. 4.1–4.40. [Google Scholar]
- Olsson, C.-O. Prediction of Nusselt Number and Flow Rate of Buoyancy Driven Flow Between Vertical Parallel Plates. J. Heat Transf. 2004, 126, 97–104. [Google Scholar] [CrossRef]
- Wu, T.; Lei, C. On numerical modelling of conjugate turbulent natural convection and radiation in a differentially heated cavity. Int. J. Heat Mass Transf. 2015, 91, 454–466. [Google Scholar] [CrossRef]
- Jeong, H.M.; Lee, Y.H.; Ji, M.K.; Bae, K.Y.; Chung, H.S. Natural convection heat transfer estimation from a longitudinally finned vertical pipe using CFD. J. Mech. Sci. Technol. 2009, 23, 1517–1527. [Google Scholar] [CrossRef]
- Yazicioğlu, B.; Yüncü, H. Optimum fin spacing of rectangular fins on a vertical base in free convection heat transfer. Heat Mass Transf. 2006, 44, 11–21. [Google Scholar] [CrossRef]
- Sathe, A.; Sanap, S.; Dingare, S.; Sane, N. Thermal Analysis of Vertical Plate Fin Heat Sink. E3S Web Conf. 2020, 170, 01022. [Google Scholar] [CrossRef]
- Güvenç, A.; Yüncü, H. An experimental investigation on performance of fins on a horizontal base free convective heat transfer. Heat Mass Transf. 2001, 37, 409–416. [Google Scholar] [CrossRef]


| T (K) | ρ (kg/m3) | ν (kg/m s) | k (W/m K) | cp (J/kg K) | β (1/K) |
|---|---|---|---|---|---|
| 273 | 1.276 × 100 | 1.722 × 10−5 | 2.436 × 10−2 | 1.006 × 103 | 3.674 × 10−3 |
| 293 | 1.189 × 100 | 1.821 × 10−5 | 2.587 × 10−2 | 1.006 × 103 | 3.421 × 10−3 |
| 373 | 9.333 × 10−1 | 2.190 × 10−5 | 3.162 × 10−2 | 1.011 × 103 | 2.684 × 10−3 |
| 473 | 7.359 × 10−1 | 2.605 × 10−5 | 3.823 × 10−2 | 1.025 × 103 | 2.115 × 10−3 |
| 573 | 6.075 × 10−1 | 2.981 × 10−5 | 4.442 × 10−2 | 1.045 × 103 | 1.745 × 10−3 |
| Parameter | Setting | Parameter | Setting |
|---|---|---|---|
| Solution Method | Residuals | ||
| Pressure-Velocity-Coupling | Coupled | continuity | 10−6 |
| Spatial Discretization | x-velocity | 10−6 | |
| Gradient | Least Square Cell Based | y-velocity | 10−6 |
| Pressure | PRESTO! | z-velocity | 10−6 |
| Momentum | Second Order Upwind | energy | 10−6 |
| Turbulent Kinetic Energy | Second Order Upwind | k | 10−6 |
| Specific Dissipation Rate | Second Order Upwind | ω | 10−6 |
| Energy | Second Order Upwind | ||
| Pseudo Transient |
| Low-Level Parameters | Unit | Value |
|---|---|---|
| W | mm | 180 |
| s | mm | 5 |
| B | mm | 3 |
| kfin | W/m K | 130 |
| Tamb | K | 293 |
| H | mm | 12.5/25/50/100 |
| L | mm | 125/250/500 |
| b | mm | 8.8/14.7/32.4/56 |
| n | - | 4/6/11/16 |
| Tfb | K | 303/323/373/423/473 |
| FSF | Overall | Tfb (K) | H (mm) | L (mm) | b (mm) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 303 | 323 | 373 | 423 | 473 | 12.5 | 25 | 50 | 100 | 125 | 250 | 500 | 8.8 | 14.7 | 32.4 | 56.0 | ||
| FSFA | 14.12 | 21.62 | 17.74 | 12.97 | 9.83 | 8.45 | 17.28 | 13.89 | 11.97 | 13.35 | 8.17 | 12.52 | 21.68 | 23.43 | 14.06 | 9.63 | 9.37 |
| FSFA,η,EL | 12.86 | 17.93 | 12.57 | 9.41 | 10.55 | 13.84 | 15.78 | 11.97 | 11.77 | 11.91 | 10.65 | 11.47 | 16.45 | 19.80 | 11.98 | 9.53 | 10.12 |
| FSFA,η,Ai | 12.67 | 17.95 | 12.59 | 9.25 | 10.20 | 13.37 | 15.84 | 12.01 | 11.61 | 11.24 | 10.44 | 11.27 | 16.30 | 19.75 | 11.83 | 9.24 | 9.88 |
| FSFA,η,Ba | 12.82 | 17.92 | 12.55 | 9.36 | 10.49 | 13.78 | 15.78 | 11.96 | 11.73 | 11.81 | 10.61 | 11.43 | 16.42 | 19.85 | 11.94 | 9.44 | 10.04 |
| FSFA,η,Ro1 | 12.35 | 18.00 | 12.64 | 9.00 | 9.59 | 12.55 | 15.94 | 12.08 | 11.32 | 10.07 | 10.06 | 10.96 | 16.04 | 19.75 | 11.55 | 8.68 | 9.42 |
| FSFA,η,Ro1.32 | 13.42 | 17.89 | 12.63 | 9.94 | 11.51 | 15.12 | 15.61 | 11.87 | 12.30 | 13.90 | 11.24 | 12.02 | 17.00 | 20.02 | 12.54 | 10.32 | 10.79 |
| FSFA,η,Ol1 | 13.42 | 17.99 | 12.72 | 9.98 | 11.44 | 14.96 | 15.64 | 11.91 | 12.32 | 13.82 | 11.22 | 12.00 | 17.05 | 20.12 | 12.69 | 10.26 | 10.61 |
| FSFA,η,Ol1.32 | 14.94 | 18.13 | 13.14 | 11.51 | 13.83 | 18.08 | 15.29 | 11.87 | 14.02 | 18.56 | 12.70 | 13.58 | 18.53 | 20.48 | 14.37 | 12.42 | 12.48 |
| FSFA,h,EL | 9.64 | 15.62 | 13.99 | 8.41 | 4.62 | 5.57 | 12.85 | 9.20 | 7.49 | 9.01 | 9.92 | 9.66 | 9.33 | 8.75 | 11.51 | 10.16 | 8.14 |
| FSFA,h,Ai | 8.04 | 12.15 | 9.88 | 4.64 | 4.94 | 8.59 | 10.40 | 8.29 | 7.50 | 5.97 | 8.00 | 7.74 | 8.39 | 7.82 | 8.74 | 8.75 | 6.84 |
| FSFA,h,Ba | 9.51 | 15.51 | 13.44 | 7.98 | 4.57 | 6.06 | 12.80 | 9.19 | 7.47 | 8.59 | 9.74 | 9.34 | 9.46 | 9.16 | 11.62 | 9.70 | 7.56 |
| FSFA,h,Ro1 | 9.65 | 6.53 | 4.09 | 6.95 | 12.18 | 18.50 | 9.80 | 10.49 | 12.12 | 6.19 | 9.34 | 8.58 | 11.02 | 9.25 | 8.42 | 10.41 | 10.52 |
| FSFA,h,Ro1.32 | 17.92 | 23.84 | 23.33 | 18.99 | 14.01 | 9.44 | 21.87 | 17.02 | 13.97 | 18.83 | 18.87 | 18.53 | 16.37 | 14.68 | 21.94 | 18.22 | 16.86 |
| FSFA,h,Ol1 | 16.73 | 22.89 | 21.52 | 17.45 | 12.76 | 9.00 | 20.39 | 15.71 | 13.20 | 17.60 | 17.68 | 16.91 | 15.59 | 11.92 | 22.67 | 17.75 | 14.56 |
| FSFA,h,Ol1.32 | 33.61 | 35.83 | 37.27 | 35.34 | 31.71 | 27.87 | 36.95 | 32.92 | 30.29 | 34.27 | 35.91 | 34.13 | 30.77 | 22.28 | 39.48 | 37.53 | 35.14 |
| FSFA,η,h,EL | 11.58 | 11.91 | 9.42 | 8.49 | 11.46 | 16.62 | 11.52 | 9.20 | 11.62 | 13.97 | 8.70 | 10.26 | 15.79 | 12.79 | 12.08 | 11.50 | 9.95 |
| FSFA,η,h,Ai | 12.71 | 9.42 | 7.98 | 9.69 | 15.12 | 21.37 | 9.89 | 9.73 | 14.03 | 17.21 | 9.01 | 11.24 | 17.89 | 13.81 | 12.62 | 12.75 | 11.68 |
| FSFA,η,h,Ba | 11.83 | 12.06 | 9.29 | 8.57 | 11.97 | 17.25 | 11.54 | 9.31 | 12.04 | 14.43 | 8.84 | 10.33 | 16.32 | 12.89 | 12.30 | 11.77 | 10.36 |
| FSFA, η,h,Ro1 | 18.25 | 9.21 | 9.44 | 16.56 | 24.17 | 31.87 | 10.41 | 14.04 | 22.63 | 25.92 | 13.95 | 16.47 | 24.32 | 18.02 | 16.76 | 19.12 | 19.11 |
| FSFA,η,h,Ro1.32 | 13.53 | 19.45 | 16.72 | 11.95 | 9.78 | 9.75 | 19.73 | 13.18 | 10.08 | 11.13 | 13.75 | 12.39 | 14.45 | 13.23 | 15.56 | 13.44 | 11.90 |
| FSFA,η,h,Ol1 | 13.47 | 19.14 | 15.88 | 11.60 | 10.00 | 10.74 | 18.34 | 12.81 | 10.72 | 12.01 | 12.88 | 12.05 | 15.48 | 13.78 | 15.85 | 13.27 | 10.98 |
| FSFA,η,h,Ol1.32 | 25.78 | 31.66 | 30.62 | 26.30 | 21.80 | 18.51 | 34.80 | 28.26 | 21.44 | 18.62 | 30.41 | 25.55 | 21.38 | 18.26 | 29.64 | 28.37 | 26.83 |
| FSF | Overall | Tfb (K) | H (mm) | L (mm) | b (mm) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 303 | 323 | 373 | 423 | 473 | 13 | 25 | 50 | 100 | 125 | 250 | 500 | 8.8 | 14.7 | 32.4 | 56.0 | ||
| FSFA | 1.40 | 2.06 | 1.43 | 1.07 | 0.91 | 0.80 | 0.44 | 0.70 | 1.22 | 2.13 | 0.77 | 1.20 | 1.78 | 2.19 | 0.82 | 0.44 | 0.33 |
| FSFA,η,EL | 1.18 | 1.75 | 0.91 | 0.56 | 0.63 | 0.77 | 0.42 | 0.66 | 1.13 | 1.86 | 0.81 | 1.07 | 1.46 | 1.95 | 0.81 | 0.42 | 0.35 |
| FSFA,η,Ai | 1.17 | 1.75 | 0.91 | 0.55 | 0.60 | 0.74 | 0.42 | 0.66 | 1.13 | 1.85 | 0.80 | 1.06 | 1.45 | 1.93 | 0.78 | 0.40 | 0.35 |
| FSFA,η,Ba | 1.19 | 1.77 | 0.91 | 0.56 | 0.63 | 0.77 | 0.42 | 0.66 | 1.13 | 1.87 | 0.81 | 1.08 | 1.47 | 1.97 | 0.80 | 0.41 | 0.35 |
| FSFA,η,Ro1 | 1.16 | 1.77 | 0.93 | 0.53 | 0.56 | 0.69 | 0.42 | 0.66 | 1.13 | 1.84 | 0.78 | 1.05 | 1.45 | 1.93 | 0.74 | 0.38 | 0.33 |
| FSFA,η,Ro1.32 | 1.22 | 1.78 | 0.92 | 0.60 | 0.70 | 0.85 | 0.42 | 0.66 | 1.15 | 1.92 | 0.85 | 1.12 | 1.51 | 2.02 | 0.87 | 0.45 | 0.38 |
| FSFA,η,Ol1 | 1.24 | 1.80 | 0.96 | 0.62 | 0.70 | 0.85 | 0.42 | 0.67 | 1.16 | 1.95 | 0.86 | 1.13 | 1.53 | 2.03 | 0.89 | 0.45 | 0.37 |
| FSFA,η,Ol1.32 | 1.32 | 1.82 | 0.99 | 0.73 | 0.85 | 1.02 | 0.42 | 0.67 | 1.19 | 2.05 | 0.96 | 1.22 | 1.61 | 2.12 | 1.06 | 0.54 | 0.43 |
| FSFA,h,EL | 0.55 | 0.51 | 0.50 | 0.44 | 0.39 | 0.40 | 0.23 | 0.31 | 0.49 | 0.69 | 0.63 | 0.50 | 0.45 | 0.68 | 0.59 | 0.46 | 0.26 |
| FSFA,h,Ai | 0.47 | 0.38 | 0.34 | 0.30 | 0.31 | 0.41 | 0.22 | 0.30 | 0.49 | 0.62 | 0.51 | 0.44 | 0.44 | 0.63 | 0.49 | 0.39 | 0.23 |
| FSFA,h,Ba | 0.56 | 0.58 | 0.55 | 0.46 | 0.38 | 0.37 | 0.25 | 0.33 | 0.50 | 0.74 | 0.65 | 0.51 | 0.47 | 0.72 | 0.61 | 0.44 | 0.25 |
| FSFA,h,Ro1 | 0.49 | 0.29 | 0.19 | 0.24 | 0.39 | 0.55 | 0.21 | 0.31 | 0.52 | 0.61 | 0.49 | 0.47 | 0.51 | 0.70 | 0.50 | 0.34 | 0.24 |
| FSFA,h,Ro1.32 | 0.96 | 0.98 | 1.02 | 0.98 | 0.87 | 0.77 | 0.30 | 0.40 | 0.61 | 1.17 | 1.14 | 0.89 | 0.71 | 1.18 | 1.06 | 0.71 | 0.40 |
| FSFA,h,Ol1 | 0.99 | 1.00 | 1.02 | 1.00 | 0.93 | 0.86 | 0.32 | 0.44 | 0.70 | 1.34 | 1.15 | 0.89 | 0.79 | 1.14 | 1.11 | 0.71 | 0.37 |
| FSFA,h,Ol1.32 | 2.07 | 1.91 | 2.08 | 2.17 | 2.11 | 2.01 | 0.47 | 0.72 | 1.22 | 2.51 | 2.44 | 1.90 | 1.53 | 2.39 | 2.43 | 1.47 | 0.85 |
| FSFA,η,h,EL | 0.86 | 0.40 | 0.44 | 0.67 | 0.87 | 1.06 | 0.23 | 0.34 | 0.66 | 1.23 | 0.58 | 0.78 | 1.04 | 1.24 | 0.91 | 0.54 | 0.37 |
| FSFA,η,h,Ai | 0.91 | 0.38 | 0.47 | 0.73 | 0.95 | 1.15 | 0.22 | 0.34 | 0.67 | 1.23 | 0.65 | 0.86 | 1.09 | 1.32 | 0.96 | 0.55 | 0.39 |
| FSFA,η,h,Ba | 0.85 | 0.46 | 0.46 | 0.65 | 0.84 | 1.03 | 0.25 | 0.35 | 0.64 | 1.20 | 0.57 | 0.76 | 1.03 | 1.22 | 0.92 | 0.55 | 0.38 |
| FSFA, η,h,Ro1 | 1.01 | 0.46 | 0.59 | 0.87 | 1.09 | 1.28 | 0.22 | 0.34 | 0.69 | 1.24 | 0.81 | 0.99 | 1.18 | 1.45 | 1.08 | 0.60 | 0.44 |
| FSFA,η,h,Ro1.32 | 0.83 | 0.67 | 0.60 | 0.63 | 0.75 | 0.90 | 0.29 | 0.41 | 0.70 | 1.35 | 0.60 | 0.61 | 0.93 | 1.17 | 0.89 | 0.57 | 0.35 |
| FSFA,η,h,Ol1 | 0.89 | 0.76 | 0.69 | 0.73 | 0.84 | 0.98 | 0.31 | 0.44 | 0.75 | 1.43 | 0.60 | 0.69 | 1.03 | 1.24 | 0.88 | 0.58 | 0.36 |
| FSFA,η,h,Ol1.32 | 1.28 | 1.35 | 1.27 | 1.19 | 1.15 | 1.17 | 0.46 | 0.68 | 1.12 | 2.08 | 1.31 | 0.83 | 1.00 | 1.64 | 1.36 | 0.87 | 0.49 |
| Parameter | Unit | Examples from Literature | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Source | - | [25] | [26] | [27] | ||||||
| s | mm | 5.00 | 25.00 | 4.00 | ||||||
| W | mm | 180.00 | 150.00 | 250.00 | ||||||
| B | mm | 3.00 | 2.00 | 3.00 | ||||||
| H | mm | 25.00 | 50.00 | 15.00 | ||||||
| L | mm | 340.00 | 200.00 | 100.00 | ||||||
| b | mm | 14.70 | 16.50 | 16.00 | ||||||
| n | - | 11.00 | 9.00 | 14.00 | ||||||
| kf | W/m K | 130.00 | 200.00 | 200.00 | ||||||
| T∞ | K | 293.00 | 301.30 | 293.00 | ||||||
| Tfb | K | 314.5 | 339.0 | 360.0 | 314.3 | 333.8 | 351.8 | 323.0 | 338.0 | 353.0 |
| hvp | W/m2 K | 4.37 | 5.34 | 5.86 | 4.01 | 5.12 | 5.73 | 5.68 | 6.27 | 6.70 |
| FSFA,h,Ai | - | 3.66 | 3.64 | 3.62 | 7.01 | 6.94 | 6.89 | 2.85 | 2.83 | 2.82 |
| QCFD | W | 18.48 | 50.20 | 82.26 | 10.99 | 35.89 | 63.54 | 11.06 | 18.76 | 27.50 |
| QFEA+FSF | W | 21.03 | 54.74 | 87.01 | 10.93 | 34.50 | 59.43 | 12.11 | 19.96 | 27.38 |
| Dev. | % | 13.77 | 9.04 | 5.77 | −0.57 | −3.88 | −6.47 | 9.48 | 6.39 | −0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roppel, M.; Rieg, F.; Tremmel, S. Definition and Determination of Fin Substitution Factors Accelerating Thermal Simulations. Appl. Sci. 2022, 12, 4449. https://doi.org/10.3390/app12094449
Roppel M, Rieg F, Tremmel S. Definition and Determination of Fin Substitution Factors Accelerating Thermal Simulations. Applied Sciences. 2022; 12(9):4449. https://doi.org/10.3390/app12094449
Chicago/Turabian StyleRoppel, Matthias, Frank Rieg, and Stephan Tremmel. 2022. "Definition and Determination of Fin Substitution Factors Accelerating Thermal Simulations" Applied Sciences 12, no. 9: 4449. https://doi.org/10.3390/app12094449
APA StyleRoppel, M., Rieg, F., & Tremmel, S. (2022). Definition and Determination of Fin Substitution Factors Accelerating Thermal Simulations. Applied Sciences, 12(9), 4449. https://doi.org/10.3390/app12094449







