1. Introduction
With the continuous development of network communication, many application scenarios such as industrial IoT, vehicular networks, and avionics networks have increasingly higher requirements for real-time and reliable transmission, while traditional Ethernet can no longer meet the requirements of applications. Consequently, a more optimal design of communication systems is needed to achieve deterministic and low end-to-end transmission delay for a massive amount of time-triggered traffic. Traditionally, industry networks adopted a dedicated field bus [
1] to obtain deterministic guarantees for real-time data transmission. What is more, various real-time Ethernet technologies, such as EtherCAT [
2] and TTEthernet [
3] have been proposed to achieve hard real-time guarantees for Ethernet.
In addition, the IEEE 802.1 TSN task group puts forward the concept of a time-sensitive network (TSN) [
4,
5,
6], which intends to build a unified interface that can be used in various fields through standardization to support real-time transmission. TSN supports real-time applications with zero packet loss and bounded end-to-end latency. To achieve bounded delay and low jitter transmission, the TSN task group improves a series of standards [
7] including IEEE 802.1Qbv supporting time-aware shaper to schedule real-time data in a time-triggered mechanism, whereas TSN standards do not cover specific algorithms for routing and scheduling.
The routing and scheduling problem has been proven to be an NP-hard problem, and there are generally directly solving scheduling and search-based scheduling algorithms to solve such problems. Pahleavan proposes two routing and scheduling algorithms based on heuristic algorithms, i.e., a genetic algorithm [
8] and a heuristic list scheduler [
9]. The NEH algorithm proposed in [
10] is a well-established initialization heuristic in genetic algorithms. Additionally, Arestova discusses a design approach for a hybrid genetic algorithm proposed in [
11] which can compete with the well-adapted NEH algorithm. However, all mentioned heuristic algorithms model and optimize routing and scheduling, respectively. Routing selection typically uses the shortest path first (SPF) and load balance first (LBF) algorithms.
Satisfiability Modulo Theories (SMT) and integer linear programming (ILP) mathematical techniques can jointly solve the routing and scheduling problem to meet the timing requirements [
12,
13,
14]. The most common optimization goals include the shortest path and reducing maximum load balancing to improve scheduling success [
15,
16]. The path generated by these algorithms can only ensure a low end-to-end latency of newly added traffic while they cannot guarantee the success rate of added traffic and also cannot confirm whether they have a serious impact on scheduled traffic. Yu [
17] adds a preprocessing stage based on [
13] which removes unnecessary links and generates a subgraph of the network. Additionally, an improved topology pruning is introduced to reduce the scale of the scheduling problem [
18]. Inspired by this approach, we introduce a flow preprocessing step before optimizing on the network side. Nevertheless, existing scheduling algorithms for TT traffic do not address the impact of route planning and time scheduling results on scheduling success, the number of schedulable flows, and the future capacity of the network to carry traffic when the differences between different traffic periods are too large [
15,
19,
20].
1.1. Contributions
The motivation of this paper is to resolve the problem of routing and scheduling of TT traffic considering characteristics of flow period satisfying the deterministic transmission requirements for different network scales and network connectivity. In this paper, an enhanced routing and scheduling approach based on flow classification is explored to maintain the quality of service of applications with different periods. In particular, our contributions to this paper are as follows:
We preprocess the preknown flows and group them based on the period correlation to obtain a delimited set of flows, named flow classification (FC).
Based on the FC, a multiperiod flows routing and scheduling algorithm (MPFRS-FC) adopts the iterated ILP-based scheduling and routing in order to attain high scheduling scalability by flow group, and incrementally adding a flow group to the scheduled procedure is proposed. Additionally, the link pruning after successful scheduling of each flow group in the MPFRS-FC can effectively reduce the search space and execution time.
Furthermore, an adaptive period compensation routing and scheduling algorithm based on FC (APCRS-FC) is designed to tackle the simple or loosely coupled network topology carrying complex periodic TT traffic problems, since multiple disjoint paths need to be found in the MPFRS-FC algorithm to minimize the number of unschedulable flows.
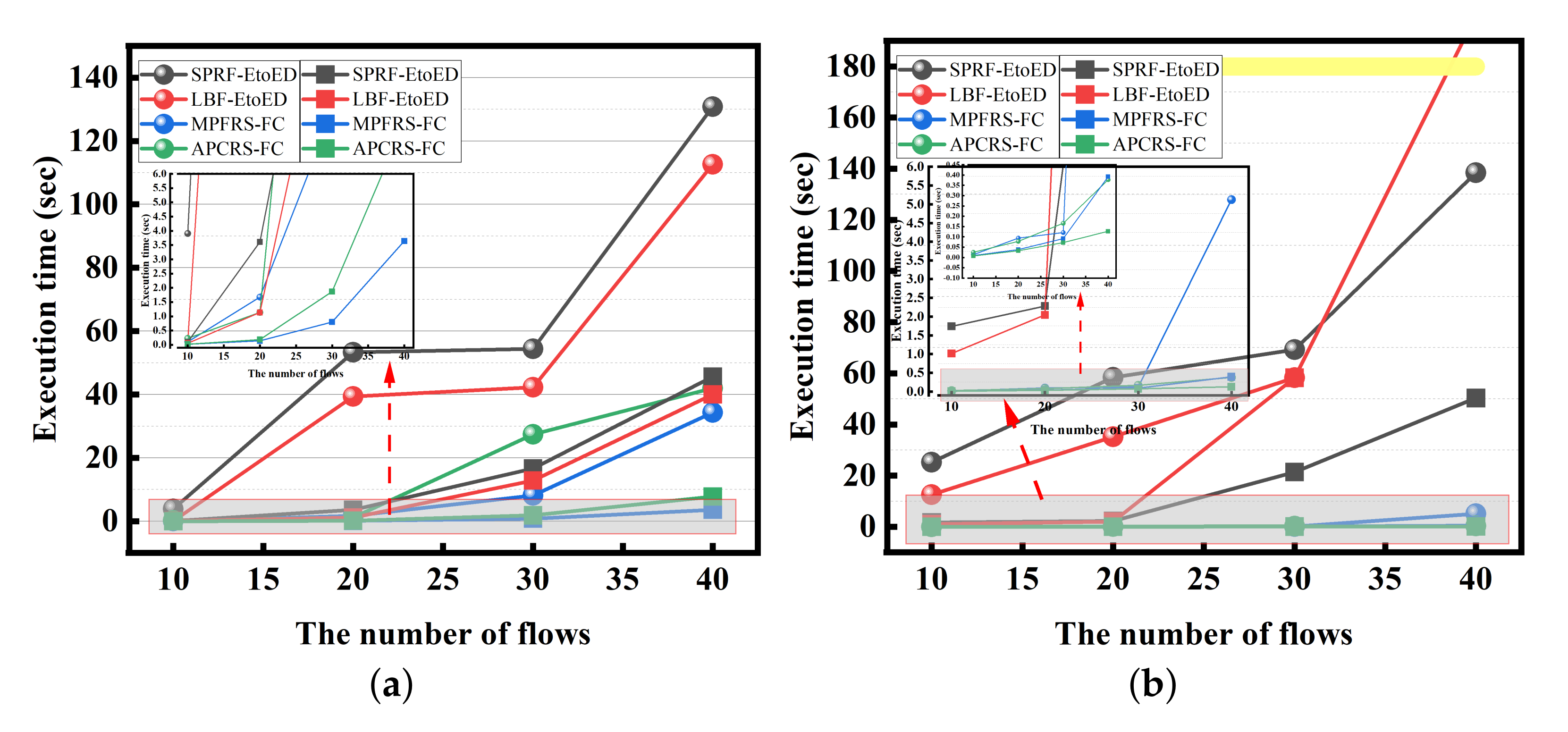
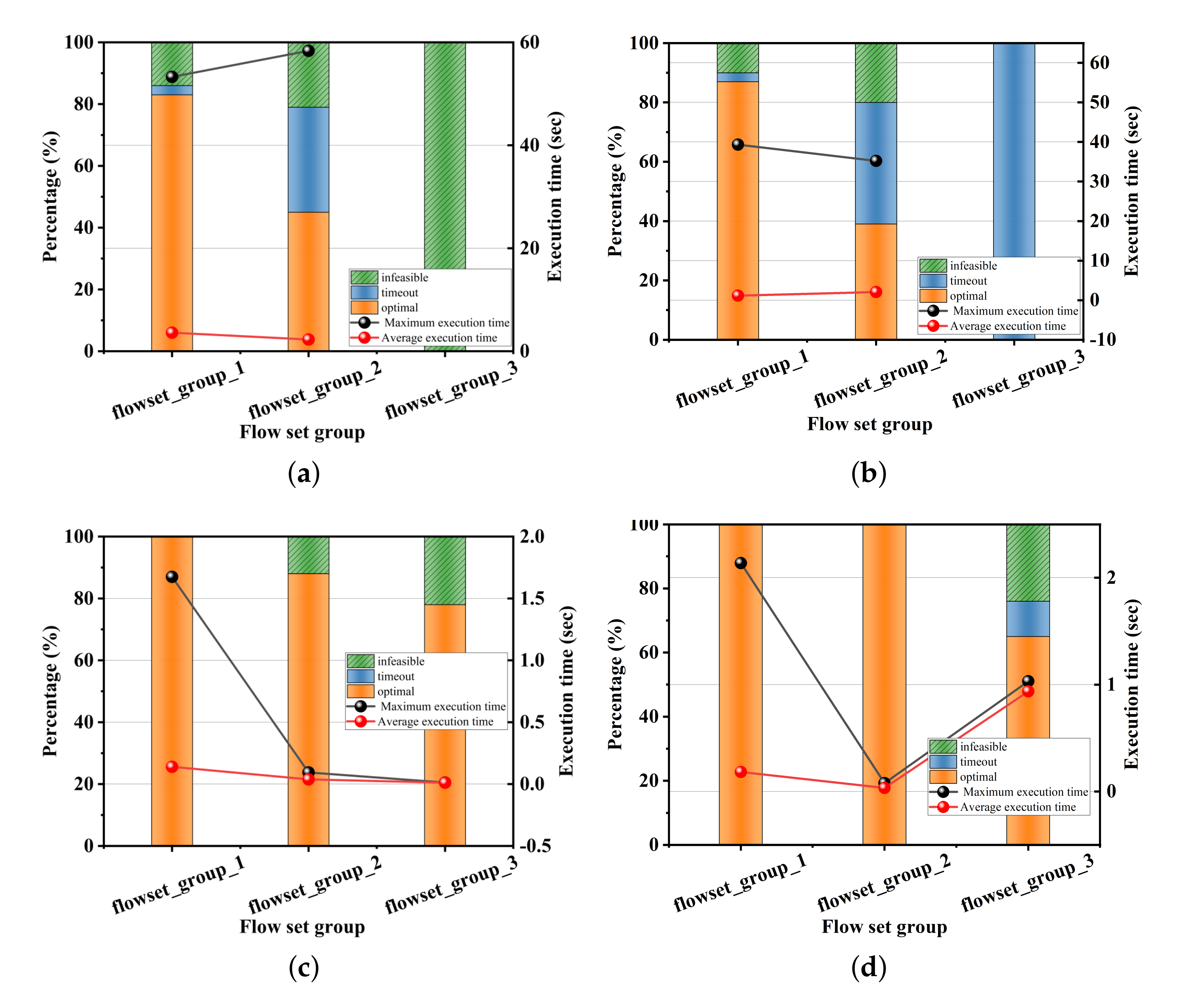
Through evaluations, the paper shows that the proposed algorithm outperforms benchmark routing and scheduling algorithms in terms of scheduling success rate and execution time.
1.2. Outline of the Paper
This remaining paper is structured as follows. The background and related work is discussed in
Section 2. The system model is presented in
Section 3. In
Section 4, we propose MPFRS-FC and APCRS-FC techniques for time-triggered flows to improve scheduling rate and reduce execution time. We present the evaluations of our algorithms with a relevant discussion in
Section 5 and the conclusion in
Section 6, respectively.
2. Background and Related Work
The IEEE TSN standards released IEEE 802.1 Qbv standard [
21] to support the time-triggered mechanism with low bounded latency and jitter guarantees. Before network configuration and operation, a scheduler collects network topo information and timing parameters of time-triggered flows as input and generates a valid scheduling table. Then, it sends down scheduling tables to each switch, and switches periodically perform scheduling table entries to achieve deterministic communication and latency guarantees.
Transmission scheduling in TSN networks to impact real-time performance is a well-researched problem [
22,
23,
24,
25,
26,
27]. The resource allocation mechanism in TSN can be considered from two aspects in general. The first subproblem is the routing algorithm, i.e., how to select a path from source to destination for each flow. The second subproblem is the scheduling method, i.e., when to send which frame to be sent or forwarded.
Concerning the routing subproblem, the optimal objective is to minimize the number of hops for routing traffic traditionally [
28]. However, Laursen et al. proved that the shortest path algorithm is not an excellent routing algorithm for TSN because this approach may result in nonschedulable solutions. Hence, many heuristic routing algorithms are proposed [
8,
9,
10,
11,
29] to determine the route paths with different objective optimization. The work in [
30] proposes a K-shortest path heuristic and a metaheuristic randomized adaptive search procedure to solve the joint routing and scheduling problem for time-triggered traffic. Some existing approaches use the Steiner Tree as the default route [
24,
25]. In the schedule synthesis, a routing and scheduling procedure is devised to improve the schedule success rate. The scheduling procedure is based on the formerly fixed routing, and thus the execution time of the schedule is sharply reduced.
To solve the scheduling problem in TSN, several prior works used mathematical programming Satisfiability Modulo Theories (SMTs) based on solver (Z3) to compute schedules for TTEthernet, profiNET, and IEEE 802.1Qbv [
31,
32,
33,
34]. Additionally, the results in [
12] show that the computational complexity increase exponentially when the number of flows increases linearly. E. Schweissguth et al. [
13] observed that prior works separate the flow routing subproblem from the flow scheduling subproblem. The typical solution is to solve the routing subproblem first and then compute the schedule based on fixed routing results. They formulated routing and scheduling jointly as an ILP problem using a Gurobi optimizer to solve the problem. Nayak et al. [
15] studied how to improve schedulability and proposed an ILP-based algorithm with a maximum scheduled traffic load (MSTL) metric to determine the routing of each TT flow. Dürr and Nayak [
20] address a special problem named no-wait packet scheduling, where the frames are not allowed to wait in the switches. The switch forwards the frame to the next node as soon as it receives the frame. This method avoids the frames jitter by assuming that all flows have the same period, and thus, the problem is restricted to one frame per flow. Jin, Xia et al. [
35] proposed a joint algorithm of appropriate message fragmentation and no-wait scheduling to improve the schedule success rate up to 50% further than previous algorithms. Nayak et al. [
27] propose an approach that schedules the transmission of time-triggered flows only on the hosts. Moreover, authors of [
17,
36,
37] observed the effect of different routing results on scheduling and recommended joint routing and scheduling algorithms to use proper network resources and to target load balancing.
Atallah et al. [
36] considered frame period as a factor of the degree of conflict measured and incrementally added to the schedule; this approach is based on assuming densely connected typologies such that the possible paths between any two nodes outnumber those required for messages exchanged between these nodes. We observed that the above approaches omitted the period correlation between these flows. The approach [
36] does not focus on the correlation between traffic periods. We proposed the flow classification (FC) technique which finds the correlation of multiple flows’ periods to utilize the same links. Based on FC, we proposed the MPFRS-FC algorithm to generate routes based on traffic period characteristics, which is suitable for relatively complex topologies where there are more than two disjoint paths between two end systems that can be transmitted. If during route discovery, flows that are not in the same class must share partial path to reach the destination, then the scheduling step can be terminated early and the newly added flow can be placed in the nonschedulable flow set. This process simplifies the complexity of joint routing and scheduling optimization. Then, the APCRS-FC algorithm is not only appropriate for network topologies with simple or loosely coupled structures but also can further improve the schedulability of the nonschedulable flow set output by the MPFRS-FC algorithm.
3. System Model
In this section, we present the network model and the flows specification assumed throughout this paper. We use uppercase letters for sets, lowercase bold letters for vectors, and object-oriented notation for attributes.
Table 1 summarizes the notation used.
3.1. Network Model
We denote the time-sensitive network (TSN) as a directed graph , where the set is the set of all nodes (end systems and switches) connected by physical links, and the set includes a set of full-duplex physical links or edges. Note that each full-duplex link is regarded as two-directional logical links denoted by ordered pairs and , where the first element is the source and the latter is the destination. and denote the number of nodes and links, respectively.
A physical link is characterized by the tuple , where represents the transmission rate of the link , is the sum of maximum latency which is independent of the scheduling algorithm.
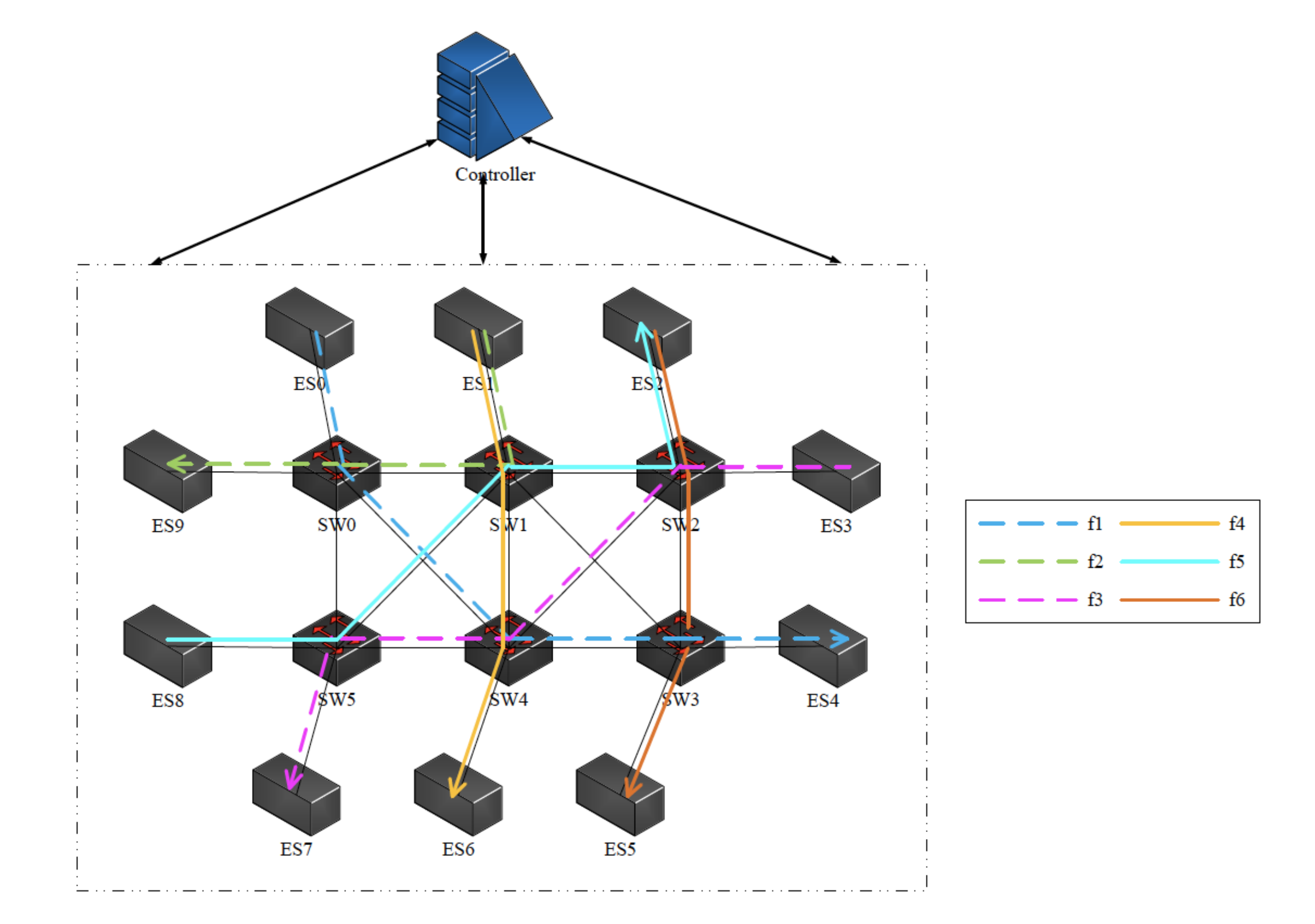
An example of the TSN topology is shown in
Figure 1. Each end system executes one or more types of real-time application that periodically sends flows under firm latency constraints. We assume that the whole network is precisely synchronized, that is, as long as the routes and transmission time slots are properly planned, the flows can be transmitted based on the schedule without conflict links in ideal circumstances. The controller has to gather all network information and all flow information and schedule routes and time slots. A feasible route consists of end systems, switches, and links which the flows traverse. The time slot must be reserved for the links within each flow’s route.
3.2. Flow Specification
The delay-critical applications are modeled as periodic tasks that send recurrent flows grouped in classes. Each flow is transmitted within its period, and the hyper cycle is defined as the least common multiple of the periods of all flows. We consider a set of n unicast time-triggered flows . For simplicity, the multicast case can be split into multiple unicast flows with the same source and different destinations. Each flow is characterized by a 7-tuple, where are the flow’s source and destination node, respectively. is the flow category which affects the selection of routes. defines the frame length in bytes and is the period of the flow. Moreover, denotes the maximum allowed end-to-end delay. We assume that all flows are transmitted simultaneously over the network. When all flows are released, we can safely restrict our attention to the first cycle, called the hyper cycle. denotes the transmission duration of a flow related to the link transmission rate and flow size. Suppose that the size of the flow is 1000 bytes, then the transmission duration of flow sent to 1000 Mb/s link on the port is 8 s. We assume that the unit for and is microsecond.
4. Proposed Solution
We define time-triggered flows with different periods as heterogeneous flows and assume that all links are homogeneous which all have the same characteristics. To facilitate the understanding of our proposed routing and scheduling strategy, we first explain some of the concepts used in it.
Definition 1. (Scheduling Cycle) The length of schedule denoted by is defined as the least common multiple of the periods of all time-triggered flows to be scheduled via the port , which is attached to only one directional link . Definition 2. (Time Slot) The size of one slot denoted by is defined as the greatest common divisor of the periods of all time-triggered flows to be scheduled. Definition 3. (Flow Correlation) The correlation of flow cycles denoted as is defined as the ability of heterogeneous flows to share bandwidth without conflict. We use the number of situations that other flows can be scheduled without conflict as a measure of correlation when one flow already exists in the network. We denote as the number of situations that accommodated flows can coexist with , assuming that flow has been assigned to be transmitted through one link at zero time slot. Proof of Definition 3 The periods of flow and are defined as and , respectively. We assume that the flow has already been scheduled in the network in the earliest iteration. In the overall iterative scheduling algorithm, flow with smaller period is prioritized to reduce the number of iterations, i.e., .
We take the sending instant of flow m as the reference zero point to analyze, for flow , how many combinations of time slots can be available to be scheduled on the same link with the guarantee that the two flows do not conflict.
The offsets of the flow and in the first cycle are and , respectively, and the transmission cycle constraints as well as are satisfied as shown in (15). Then, the locations of time slots to sending or forwarding flow and are and , where and .
The conditions under which collisions occur between two flows transmitting on the same link are
that is, the contention constraints are not satisfied as shown in (
13). The time slot
is defined as
We can obtain that
,
and
are satisfied. Then, the collision condition can be expressed as
Based on Bezout Theorem, if a and b are integers, and , then must be a multiple of d for any integer . In particular, there must exist integers such that . An important corollary is that a sufficient condition for the mutuality of a and b is that there exist integers x and y such that .
Here, is the greatest common divisor of and , additionally, and are two mutually prime numbers, i.e., . There exist integers and such that . Since the time slot location of the offset must be integer multiples of the time slot, is satisfied when and only when and .
The offset of flow in the first cycle cannot be chosen from . Therefore, the number of available time slot combinations is . The definition is proved. □
The traditional routing algorithms (e.g., shortest path algorithm, equal-cost multipath algorithm) are focused on finding the shortest route for each flow, which may result in too many flows traversing the same path simultaneously. Here, we fully consider flow characteristics and explore the valid routes that meet the timing constraint .
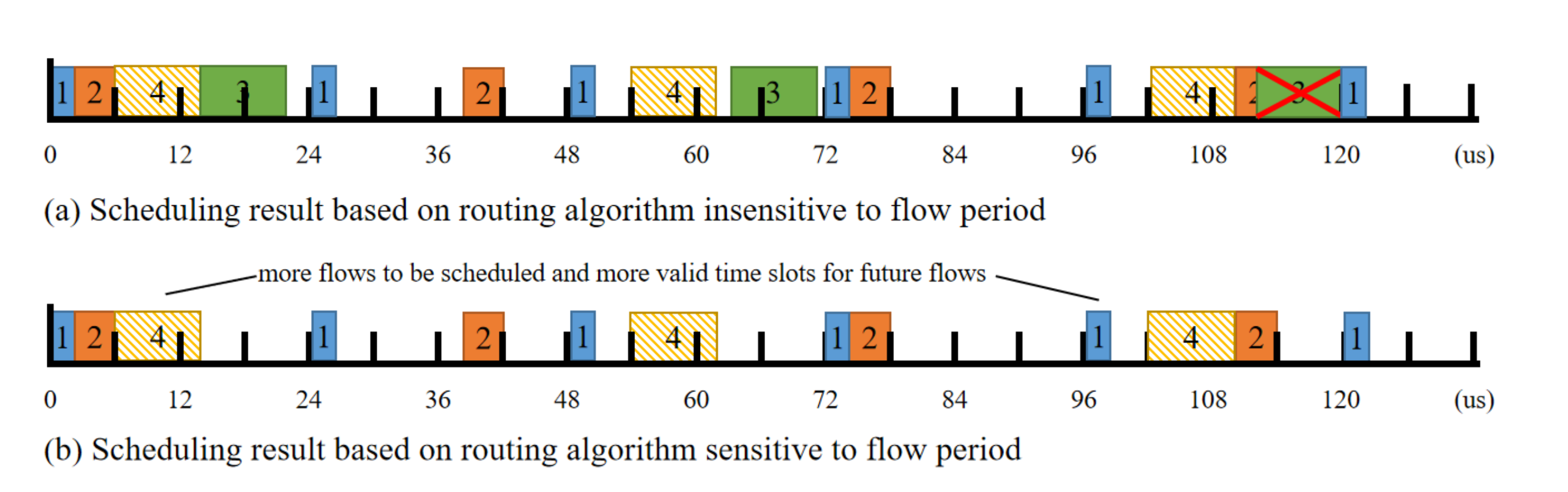
To describe how to optimize the routing and scheduling solution, we give an instance of a scenario with four time-triggered flows traversing through switch
as depicted in
Figure 2. The partition of the time slot represents the time resource reserved on the switch’s output port, since the flow correlation of flow set
is larger than
. From the results of flow correlation, we can find that it is mainly related to the greatest common divisor of flow sets. We can see that
and
congest at time slot 112 in
Figure 3b. Additionally, another option for the transmission starting time slot which is sufficient for the transmission of one frame is 26–30 in one cycle, and it will conflict in the following cycle since
. There is poor flow correlation between them and it is not suitable to pass through the same route. If the flow is scheduled according to the flow sequence, flow
and other flows cannot be scheduled on the same path without conflict, since they did not have a common divisor and the first frame must be sent within their periods. We consider using the flow classification step to classify the flow first and use a separate path scheduling for flows with periods such as
that seriously affect the scheduling cycle. Without loss of generality, flows with a period that is a multiple of 7 are also added to the same route to schedule. There is no need to recall the routing and scheduling algorithm for global planning.
The FC step to group the flows by
can be considered independent of the network topology to increase the correlation of flows passing through the same link. The whole procedure of FC is presented in Algorithm 1. We introduce three categories to group flows with different periods (lines 5–14). The first group has common divisors other than 1. The flows of this group are further classified based on the additional factors of the third group (lines 15–22). The second group flow cycle has an additional factor
. The third group contains the flows that are intermixed with other flow cycles. Flows in this category require a separate path for transmission and cannot share links with other flows. Moreover, flows in the same group can share the same link. The function
can be easily implemented based on the flow class index. Finally, flows in each group are sorted in ascending order (line 24). The FC is a strategy that can be superimposed on any routing and scheduling algorithms based on finer-grained classification.
| Algorithm 1: Flows classification algorithm |
![Applsci 12 04448 i001]() |
Then, we focus on the time-sensitive routing and scheduling constraints as well as the optimization objective, which is used for ILP in the next part.
4.1. Routing Constraints
The route allocation is modeled by binary path variable given as follows.
The route for a flow starts at its source and ends at its destination(s) , hence the number of the outgoing links is exactly one more than the incoming link of has to be active, additionally, the number of destinations over the incoming links of the is one.
For the intermediate nodes
eligible for forwarding
, the flow conservation constraint needs to be satisfied because of the unicast model.
Here, and are the ingoing link and outgoing link of node eligible for routing .
To prevent routing loops in the same flow, the flow
can be forwarded by any node at most once, i.e., each switch receives flows from at most one port.
4.2. Schedule Constraints
We introduce integer decision variable
, which is the offset of the time slot occupied by
in the first cycle with respect to the zero time slot on link
. Another integer variable
is the offset of the transmission window, which is the positive integer multiple of the flow period
. Hence, we can locate time slot position at the beginning of the transmission of the flow
on link
as
. We denote
. To ensure that the constraints on scheduling decision variable work when link
is occupied by flow
, the basic constraint is
where
is an arbitrary but sufficiently large constant.
Contention Constraints: To achieve zero congestion transmission, it is required that all assigned time slots are nonoverlapping. For any two flows
,
, no flow can be sent to the same link at the same time, otherwise, a conflict occurs. The forward time of outgoing ports of each switch does not conflict. We have the condition
Transmission Cycle Constraints: The flow must be transmitted during its cycle and cannot be confused with the next cycle. The transmission start time of the flow
on the link
is constrained by:
Equation (
16) ensures that
and
are invalid when the link
is not reserved for flow
.
Path Order Constraints: Only when the flow is received by the current node, the previous node can start to transmit the next flow. Hence, the constraint is
where
is the one-hop delay of flow
, i.e.,
. This inequality is meaningful only when the flow
passes through the link
, i.e.,
.
No-wait Forwarding Constraints: We assume that each switch forwards a data frame immediately after it is received, while satisfying the path constraint above.
4.3. Application Constraints
The flow
must be fully received by the destination
within the deadline
. The maximum end-to-end latency constraint is defined as follows:
Here, we define as the communication latency of a flow from the source to destinations.
4.4. Objective Function
Flow scheduling needs to optimize transmission performance while meeting the above constraints. Therefore, we construct a cost function to evaluate the routing and scheduling scheme, which consists of different optimization objective functions. For each flow
, its best route
is defined by
which considers each flow have a greater number of scheduling situations and also introduce a user-defined positive integer to limit the hops of each route. The FC-based flow correlation objective intends to carry more flows in the network, additionally, flow classification and sorting can reduce the execution time of the routing and scheduling method.
The objective function of the scheduling model is to minimize the end-to-end flow latencies and the sending start time of the flow, which is defined as
We optimize the sending time of each flow to make the remaining time slots more available. It breaks up a large number of time slices so that some flows with large frame size cannot be scheduled if the model does not consider that.
The overall procedure of the multiperiod flow routing and scheduling algorithms with flow classification (MPFRS-FC) is shown in Algorithm 2. Given a TSN network
G and a flow set F, the output is a mapping
of routes and transmission time slots. In the initialization step, MPFRS-FC groups call the flow classification function so that the paths can be better shared for routing without conflict (line 1). The schedule is built over
iterations and each iteration handles a flow group. The ILP constraints are generated for
, where
. The function
searches for a feasible solution that satisfies the time-sensitive routing, scheduling, and application constraints. Since the next group of flows cannot use the link contained in the path of the current group, we remove the links which the current group of flow passes through from the graph
G and then find the route for the next group of flows (line 11) if the routing or schedule results are empty, i.e. it is infeasible for that flow to be scheduled in the current network.
| Algorithm 2: Multiperiod flow routing and scheduling algorithms with flow classification |
![Applsci 12 04448 i002]() |
Furthermore, we found that in some topologies or some network localities, we could not find multiple disjoint paths and could not implement the MPFRS-FC algorithm to improve the schedule success rate. We can use the MPFRS-FC algorithm to quickly locate groups of unschedulable flows, but we cannot schedule them without conflicting routes.
Therefore, an adaptive period compensation routing and scheduling algorithm with flow classification (APCRS-FC) is designed to handle the simple network architecture. There may not be more than one route to pick between the two end systems in this condition. We add optimal compensated value based on the original period. Flows with class 3 can be carried on the same path as flows with class 1 or 2 in that way. This strategy increases a certain delay but can meet the constraints of its deadline.
As shown in Algorithm 3, the flow preprocessing step is first completed with the setting of the flow set (line 1). We introduce an adaptive variable to compensate for the period that can be scheduled in the current network and is within the deadline for that traffic. The following process is similar to the MPFRS-FC. If the compensated flows cannot be scheduled in this way, we remove them from the flow set to ensure the normal scheduling of other traffic, without wasting search time and space on that unnecessary scheduling.
| Algorithm 3: An adaptive period compensation routing and scheduling with flow classification |
![Applsci 12 04448 i003]() |
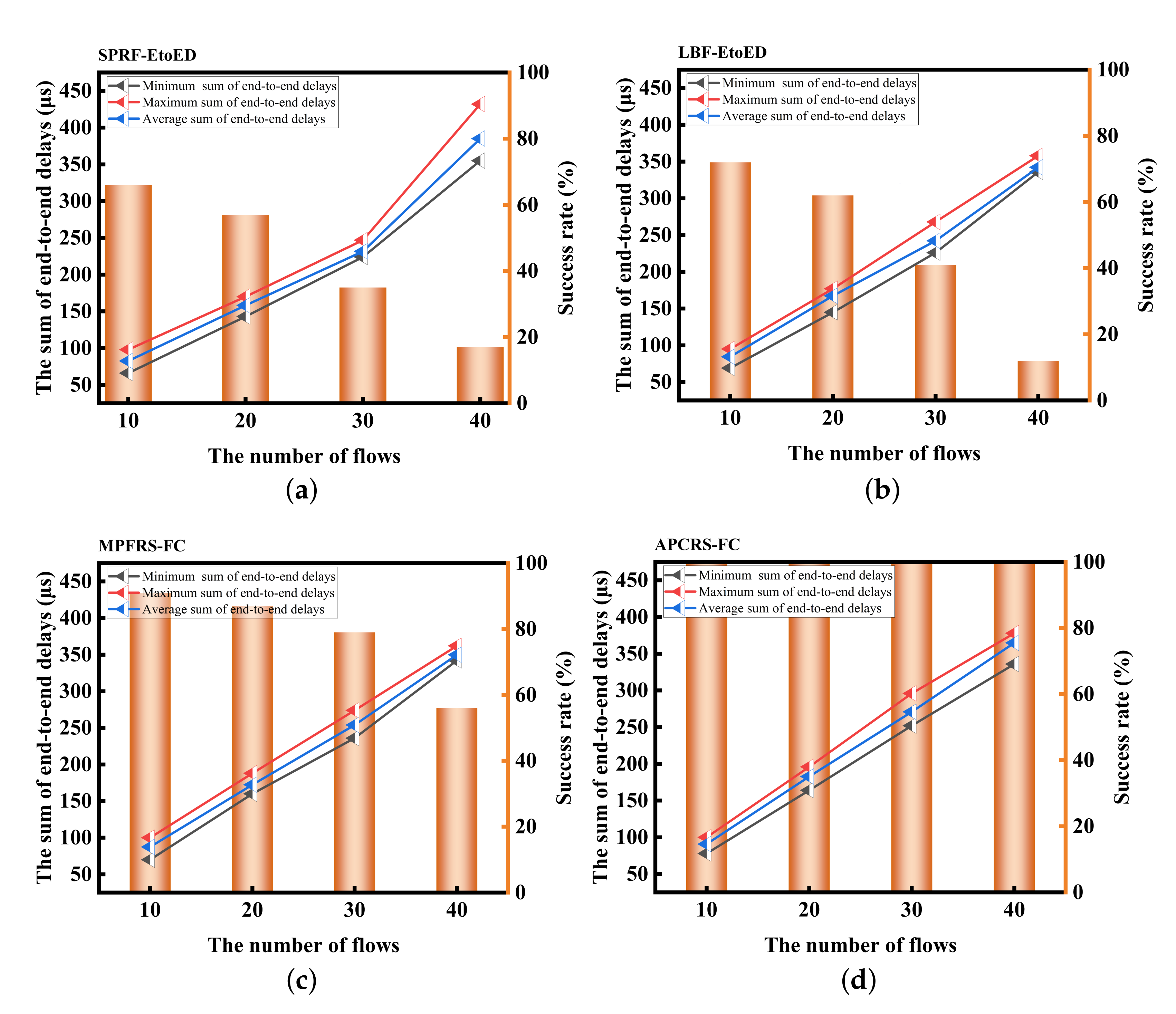
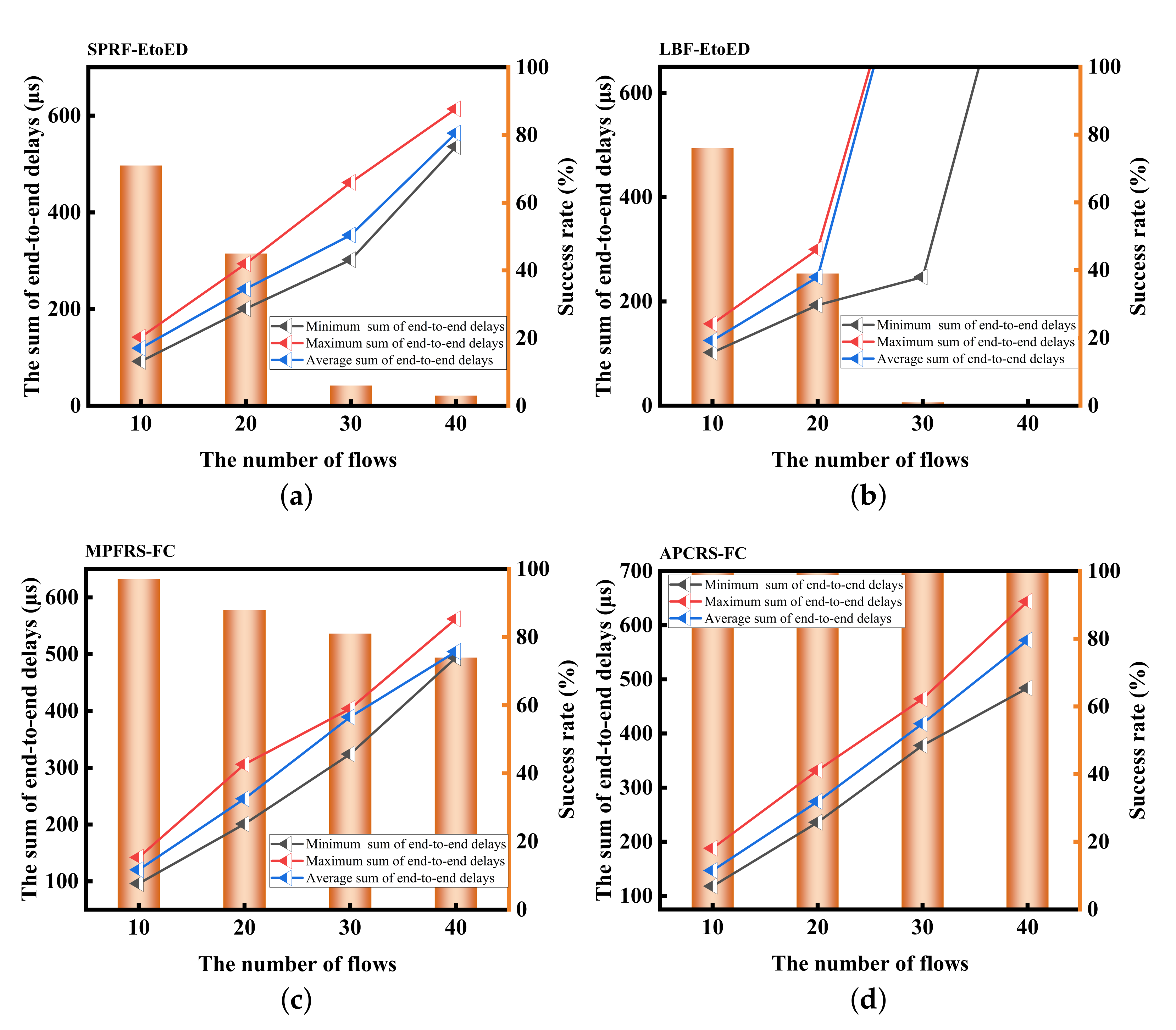
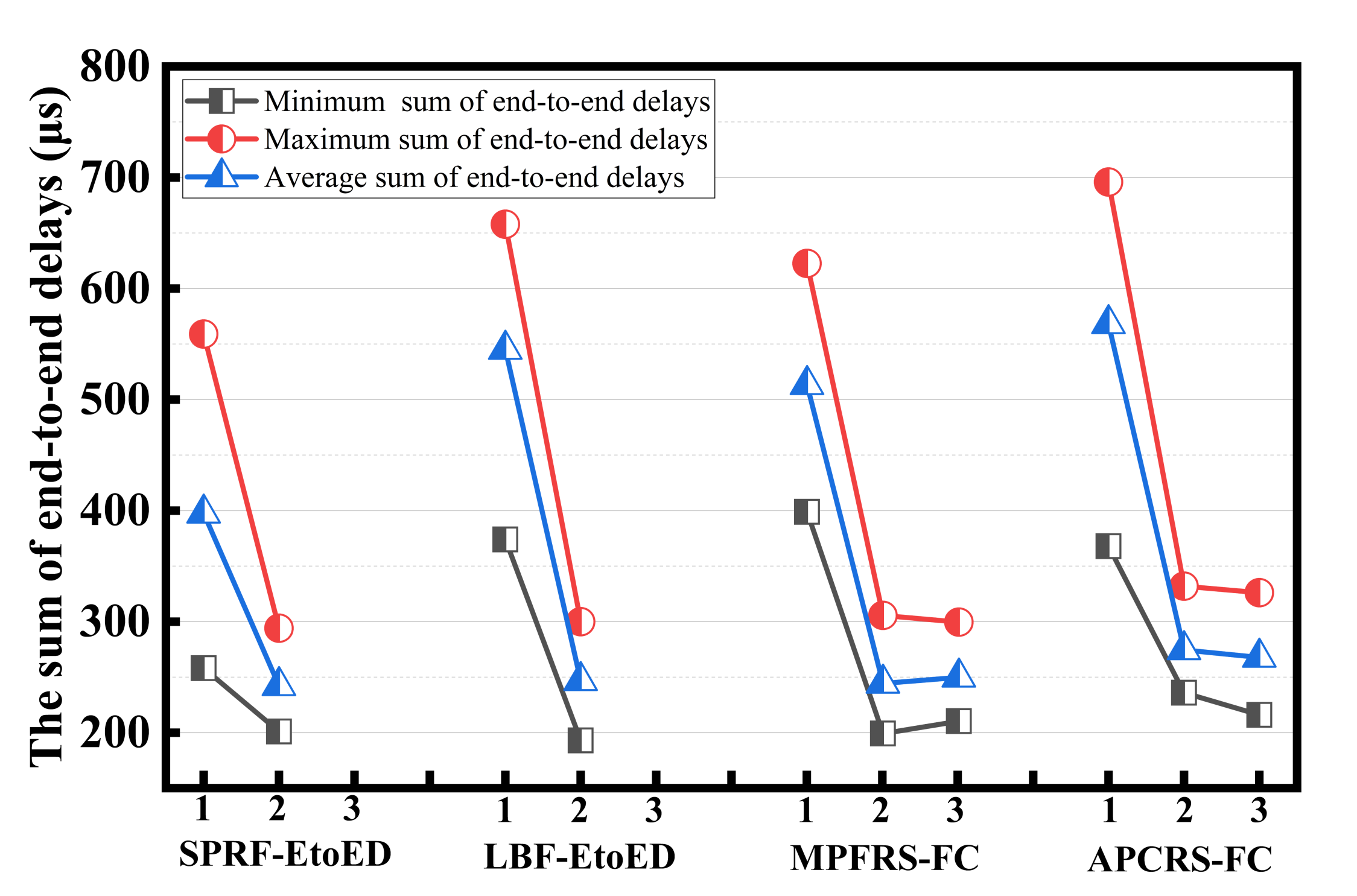
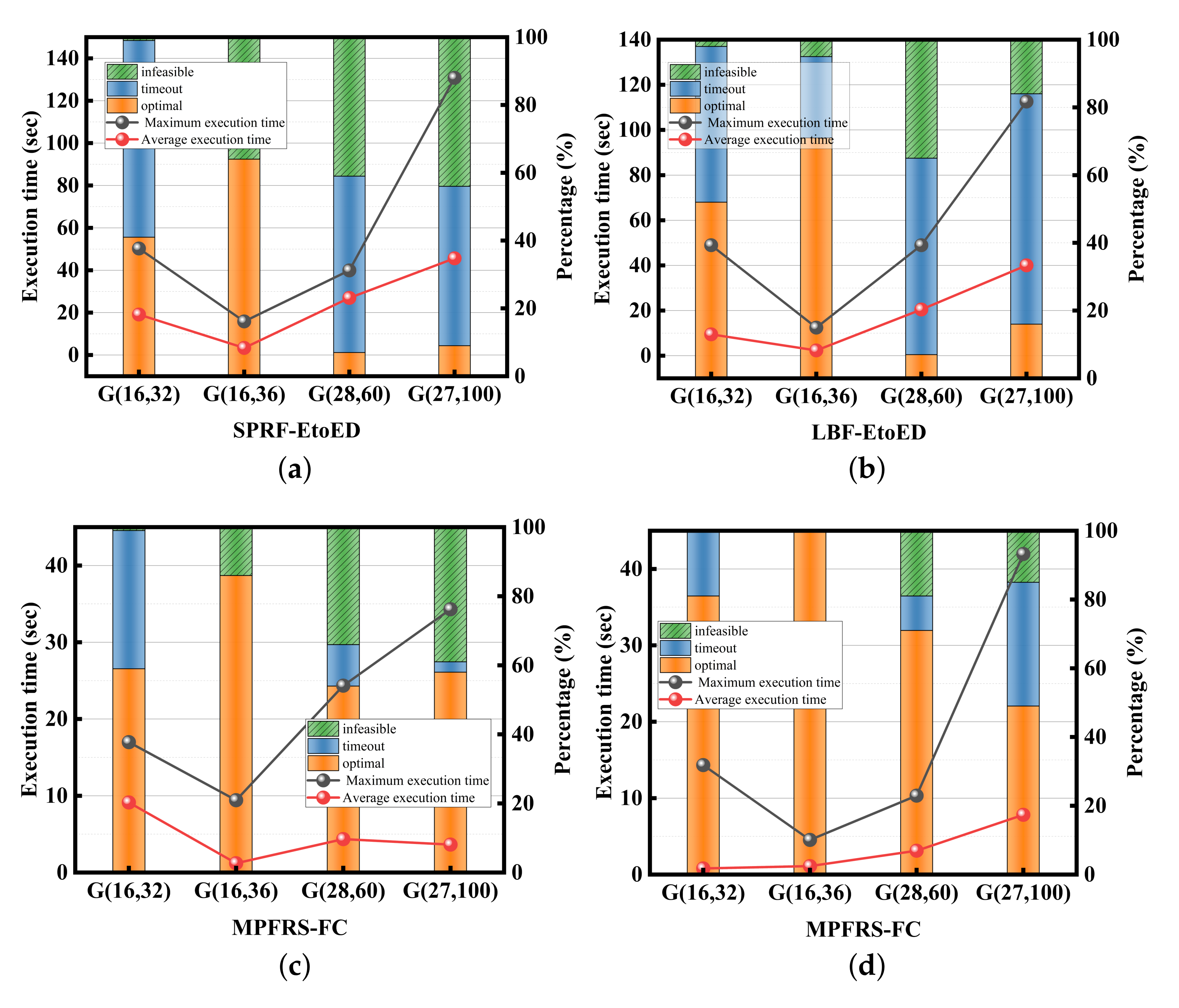
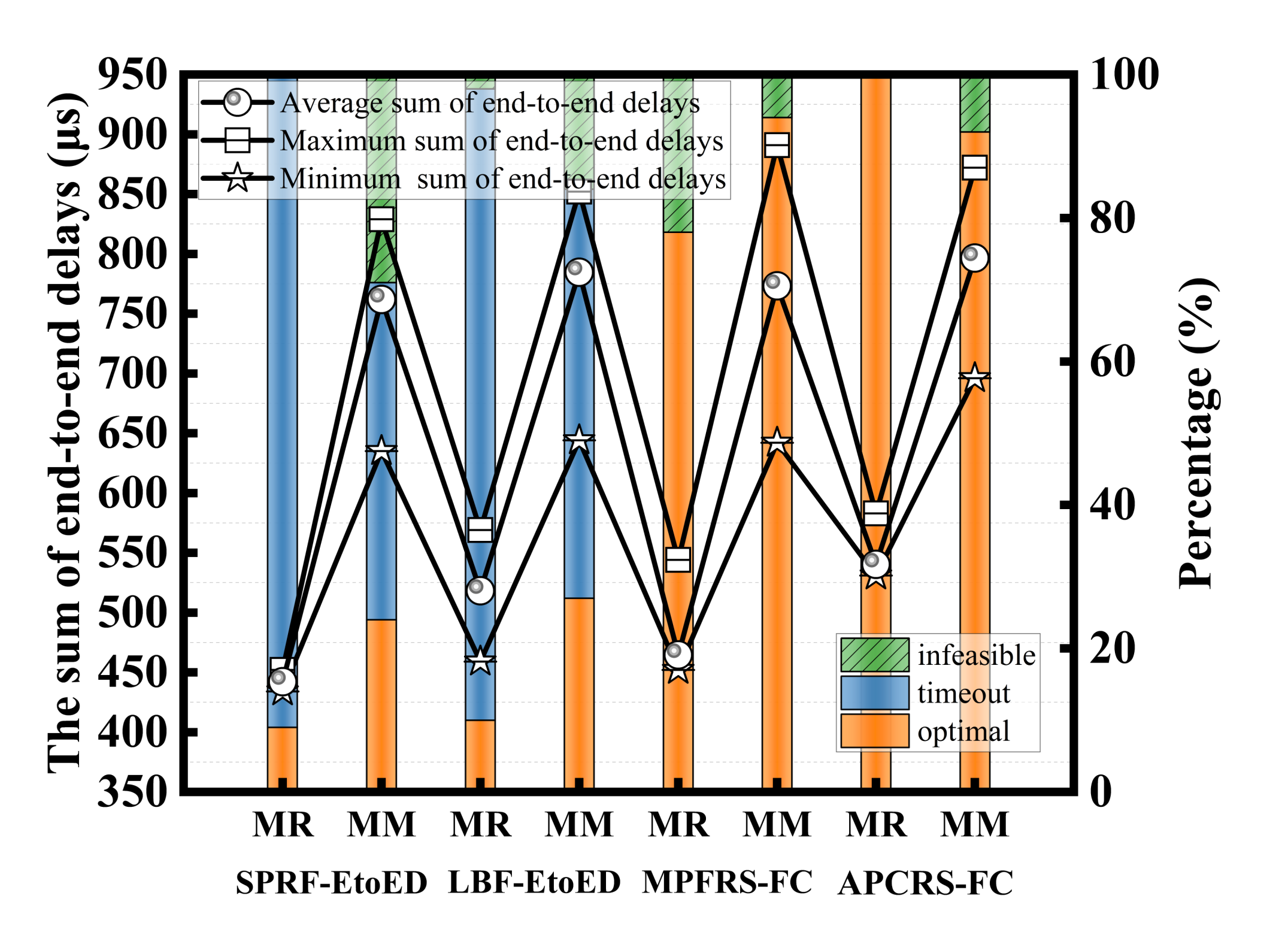
6. Conclusions
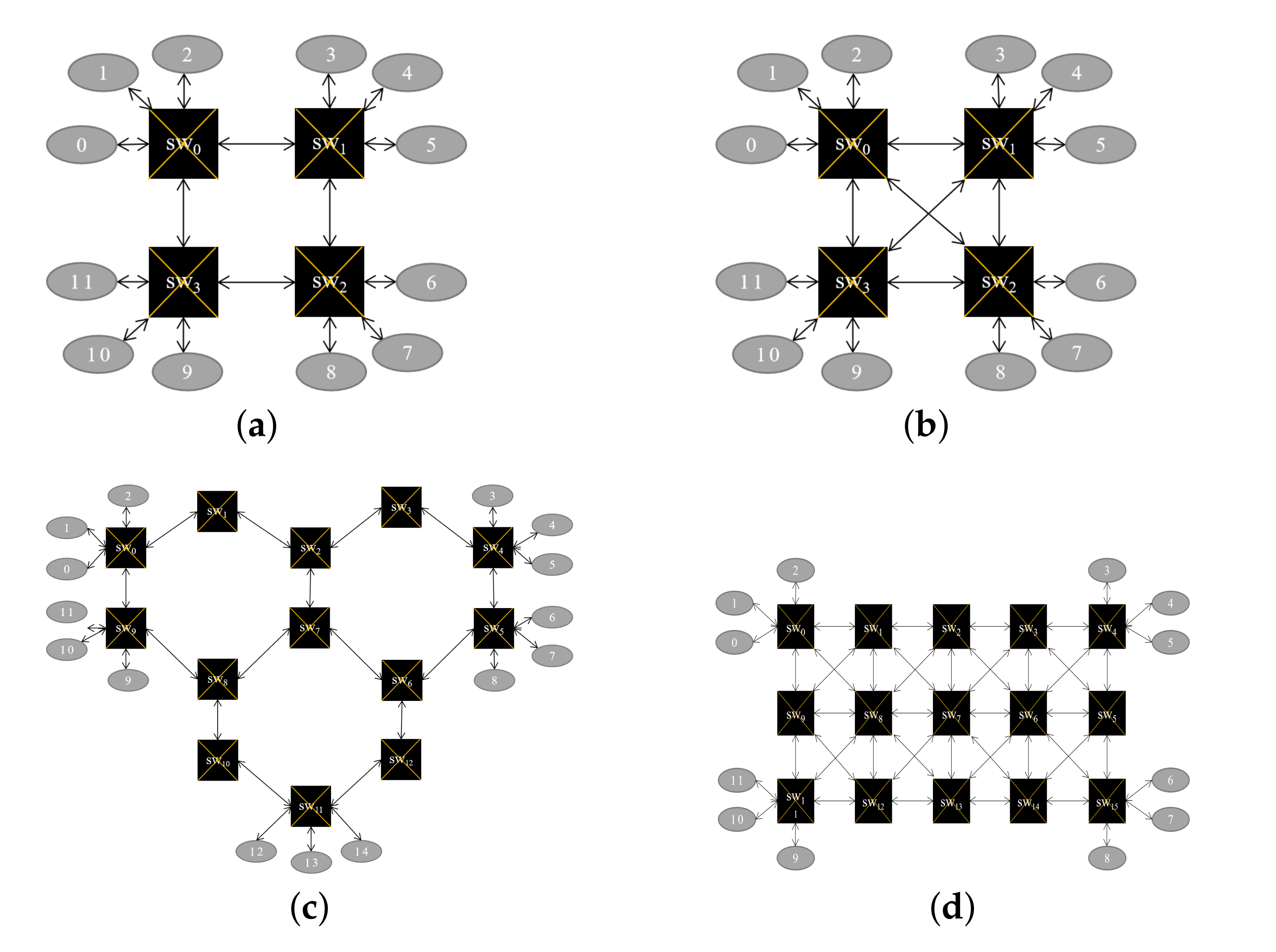
In this article, the flow routing and scheduling problems in time-sensitive networking were studied. A novel method based on the FC step is proposed, which covered a finer-grained classification and the no-wait scheduling of TT flows by ILP techniques. The proposed MPFRS-FC technique covered multidisjoint path routing based on flow period correlation and links pruning to improve the scheduling performance and reduce the execution time of the algorithm. Given the characteristics of different network structures, no disjoint paths can occur in routing. An optimal scheduling method called APCRS-FC was further proposed to add an adaptive period compensation factor to make it possible for flows to increase their schedulability in the network. We designed twelve experiments, each of which used 100 test cases to evaluate the applicability scenarios and scalability of the proposed algorithm, and compared the performance with two baseline algorithms, namely, the SPRF-EtoED algorithm and LBF-EtoED algorithm. The results show the out-performance of the proposed algorithms in handling large traffic load, large differential traffic periods, large network scale, and varied network connectivity scenarios in terms of success rate and execution time. We also calculate the overall end-to-end delays in each method, though both MPFRS-FC and APCRS-FC algorithms increase the end-to-end delay of partial flows, which is not higher than 15% on average. The main reason for this depends on the routing planning, since the scheduling methods are all based on the constraints of no-wait transmission. Partial flows planned by the MPFRS-FC algorithm choose the path that is not the shortest path to the destination node to improve the global scheduling success rate. Furthermore, the APCRS-FC algorithm makes it possible to transmit in the network by compensating the traffic period at the source, which results in some flows having a delay of compensation at the first hop. This latency is accumulated in each hop relative to the original flow. Optimization here depends on a tradeoff between the latency performance of partial flows and the success rate of traffic scheduling. The larger the compensated flow period the greater the impact on the end-to-end delay performance of that flow. It is noticed that MPFRS-FC and APCRS-FC can lower the sum of end-to-end delays in large-scale networks with high traffic loads. In our future work, we would extend the routing and scheduling approach to improve scheduling flexibility by introducing deep reinforcement learning. On the other hand, the issue of converged wired and wireless routing and scheduling in TSN is also an interesting direction.