Abstract
Electric power distribution networks are generally radial in nature, with unidirectional power flows transmitted from the highest voltage levels to the consumption levels. The protection system in these distribution networks is relatively simple and consists mainly of fuses, reclosers (RC) and overcurrent relays (OCRs). The installation of distributed generation (DG) in a network causes coordination problems between these devices, because the power flows are no longer unidirectional and can flow upstream to the substation. For this reason, the work proposed here analyzes the most significant impacts that DG has on the protection devices and proposes an adjustment method for the OCRs based on linear programming (LP) techniques with the aim of improving their response time to the different faults that may occur in the main feeder of the network. The distribution system selected for the study is the IEEE 34 bus system using DIgSILENT 14.1 software for its modeling and Matlab for the adjustment of the overcurrent devices. Results indicate that better coordination between protection devices are achieved if LP is used.
1. Introduction
The current philosophy in the planning, management and control of a radial power distribution network is based on the assumption of the existence of unidirectional power flows, which is transmitted from the highest transport voltage levels to the distribution levels. We can assume that short-circuit currents behave similarly. These assumptions allow for the implementation of relatively simple and inexpensive protection schemes with which a selective operation of the protection system is achieved [1,2]. According to the principles of selectivity [3], only the protection device closest to the fault should operate to clear the fault, leaving the rest of the network energized.
The installation of DGs at medium and low voltage levels changes this fundamental basis. Power flows and short-circuit currents can now have different upstream directions and values [4]. As a consequence, the initial schemes implemented (e.g., main feeder protection) may no longer work or be less effective [1,5].
With the presence of DG the distribution system becomes more active, i.e., both load and generation significantly affect the state of the network [6]. The effects of DG on distribution network devices have been discussed in different literature [4,7]. To reduce them, several “mitigation methods” have been proposed, thus, several authors recommend acting directly on the DG [3,8], e.g., disconnecting it just before fault detection or limiting its power and therefore its effect on the protection system [9], others recommend reconfiguring the network topology [10,11], or the use of fault current limiters (FLCs) [12,13].
In recent years, mitigation methods based on coordination algorithms have been developed using linear programming (LP), non-linear programming (NPL), or genetic algorithms (GA) [14,15,16,17] that either modify the coordination interval time (CTI) between devices, determine the optimal location of the DG [15], or in combination, without compromising the protection system.
Although these methods can be effective, they have some disadvantages and limitations. Therefore, the disconnection of the DG immediately before fault detection proposed in [3,18], can cause asynchronous reconnections and cause severe damage to both the DG and the distribution network, especially at high penetration levels [3,10]. The limitation of the DG capacity proposed in [9] is also undesirable, since it also limits the penetration level and therefore the advantages of its installation close to the consumption points, (loss reduction, improvement of supply quality, etc.). The network reconfiguration suggested in [10,11] is costly and sometimes unfeasible. Finally, the use of current limiters [12,14] entails an additional installation cost that can be prohibitive.
Regarding the use of NLP methods for the determination of the coordination index mentioned in [15] can be very complex, particularly if the number of protection devices and DG’s is high, since the calculation time required to determine their operating parameters will also be high [19,20,21], on the other hand, not always the optimal location point of DG is viability from the perspective of network operation, e.g., availability of power evacuation at the point of common connection (PCC).
The investigations described in [14,16,17], use GA-based optimization algorithms to determine optimal coordination between OCR and distance relays [14]. In [16] a hybrid GA and NLP algorithm is developed to choose the optimal value of DIAL or time multiplier setting (TMS) of all OCR, the use of a continuous genetic algorithm (GAC) faster than GA for the same purpose is developed in [17]. However, all the optimization algorithms described do not consider DG.
In the present work:
- the most significant impacts that DG causes on protection devices are analyzed,
- an adjustment method for OCRs based on LP techniques is proposed,
- the analysis is carried out by using the IEEE 34-node test feeder system modeled in DIgSILENT PowerFactory.
As far as the authors know, it seems that there is a lack of similar studies in the available literature.
2. Effect Caused by the DG on Protective Devices
2.1. Loss of Sensitivity
The problem related to the loss of sensitivity to main feeder protection is often referred to as protection blinding [8]. Installation of DGs in the distribution system can reduce the value of the short-circuit current detected by the protection of the main substation and affect the response time of the circuit breaker, which will depend, to a large extent, on the size and location of the DG within the distribution network.
The loss of sensitivity of the protection device can be analyzed as a function of where the short circuit is located in relation to the location of the DG, distinguishing between short circuits located upstream of the DG and short circuits located downstream of it. Figure 1 shows the topology of a radial distribution network where S.E is the substation, R is the main feeder protection, RC is the automatic recloser, and F is a protection fuse for the branch line.

Figure 1.
Sketch of a short circuit upstream of DG.
For faults located upstream (between the substation—S.E, and the DG), the contribution current of the S.E to the short-circuit is independent of the size of the DG. A three-phase short-circuit is also represented upstream of the DG, for different penetration levels: 17%, 33%, and 50%. In the operating characteristic curves of the time overcurrent (t/i) devices shown in Figure 2, this effect is observed, as the current detected by the relay remains constant at 1.59 kA, regardless of the of penetration level of the DG.
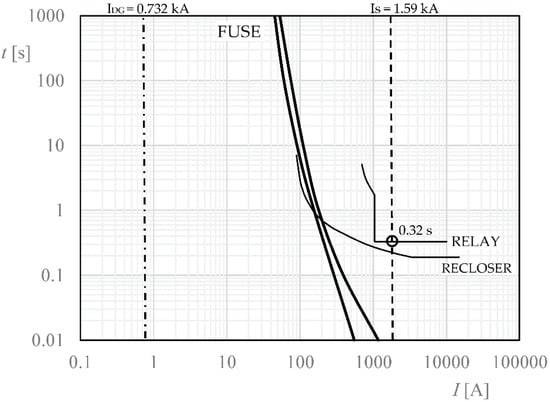
Figure 2.
Short circuit upstream of DG. See also Figure 1.
In contrast, for faults located downstream of the substation and the DG (as shown in Figure 3), it is observed that the current contribution of the DG to the short circuit causes the current measured by the main relay, R, of the S.E to decrease from 1.21 with 17% penetration to 1.14 kA with 50% penetration level of the DG, which represents a 6.1% loss in the sensitivity of the protection device. This effect will cause a delay in the operating time of the protection device, as shown in Figure 4. The extreme case of this effect occurs when the main relay does not detect the fault current, as shown in Figure 5. The maximum value at which the relay stops detecting the fault current appears when the DG is installed close to the substation and under fault conditions at the main feeder [12].
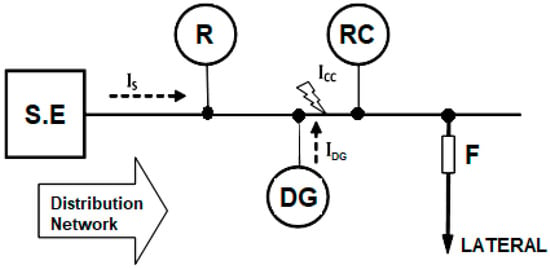
Figure 3.
Sketch of a short circuit downstream of DG.
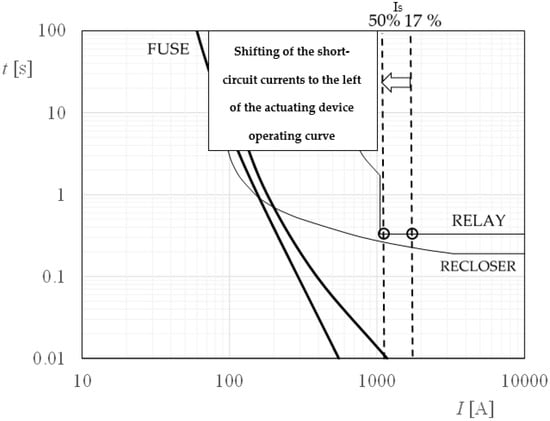
Figure 4.
Short circuit downstream of DG. See also Figure 3.
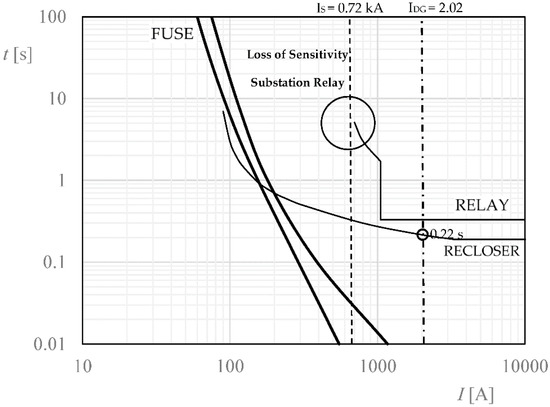
Figure 5.
Short loss of sensitivity substation relay. Loss of sensitivity.
2.2. Loss of Coordination
Under normal operating conditions, protection devices are coordinated in such a way that, in the event of a fault in the network, the main protection acts before backup protection. A large majority of faults occurring in the network are of a temporary nature, the purpose of the recloser, RC, is to try to clear these faults and on the one hand avoid an unnecessary interruption of the electrical service, and on the other hand to safeguard the protection fuse of the branch line under its supervision. Depending on the initial settings of the coordination schemes, and taking into account the size, location, and type of DG installed, it may happen that a temporary fault in a branch line causes the loss of coordination between fuse and recloser, affecting their coordination time due to the additional current with which the DG contributes to the short-circuit. To observe this impact, the situation of temporary fault, ICC, in a branch line (lateral) is shown in Figure 6.
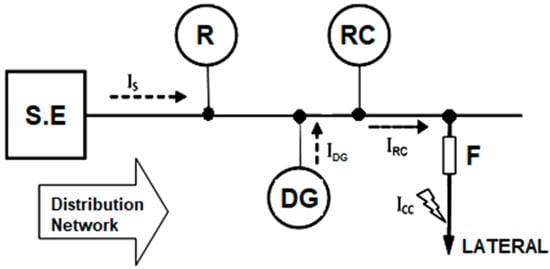
Figure 6.
Short circuit in branch line.
The characteristic t/i trip curves are represented in Figure 7 where the impact called (fuse nuisance blowing) is shown. We can observe how a temporary fault in a branch line causes a loss of coordination between the fuse and the recloser. Thus, the fuse detects a fault current of 0.25 kA and trips in 0.15 s, while the recloser is crossed by a current of 0.650 kA, which would cause it to trip in 0.32 s. This time is higher than the fuse tripping.
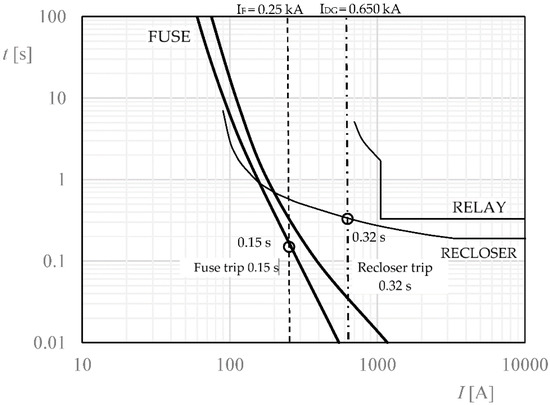
Figure 7.
Failure coordination between recloser, RC, and fuse, F, see also Figure 6.
3. Coordination with Linear Programming
OCRs are currently the most widely used protection devices [13,22], this device generally being used as backup protection. However, in some situations, it may be the only protection. The OCR should act as primary protection by removing faults that occur in the area under its supervision. Only in the event that the primary protection fails to operate should the backup protection initiate tripping. A typical electrical distribution network may consist of hundreds of equipment protection relays. Each relay in the system must be coordinated with the adjacent equipment protection relay. If backup protection is not well coordinated, coordination failure may occur, and therefore, coordination of backup protections is one of the main concerns in the network protection system [13,23]. Generally, protection coordination can be performed by topology [24,25], by optimization methods [26,27], or by expert methods [28]. Topological analysis is used for relay tuning in multiterminal networks, graph theory, and functional approximation techniques are employed to provide the best solution that does not necessarily have to be the optimal one. In optimization methods, some researchers [26,29] use non-linear programming techniques to determine the optimal relay settings, subject to constraints due to coordination and limits of the relay settings themselves. In reference [30], the big M method is proposed to find the optimal value of the OCR time multiplier setting (TMS) in which the stated values of the plug setting are assumed to be known and fixed.
The problem of OCR coordination in the distribution system with DG presence can thus be defined as an optimization problem with constraints. The objective is to minimize the operating time of the relay closest to the place where the fault has occurred. The constraints imposed are due to limits on the operating time of the relay, coordination criteria, and relay characteristics. In this work, the OCR coordination problem in radial distribution systems is formulated as a linear programming (LP) problem with constraints, where the sum of the operating times of the relays in the system for different minimum fault points:
where α and β are OCR shape constants according to Table 1, ki,j is the ratio between the short-circuit current, ICC, and the relay setting current, Iar, regarding relay i with fault in section j, and TMS is the time multiplier setting.

Table 1.
Form constants for the exponential equation IEC [31].
The proposed optimization problem is subjected to the following group of constraints:
- Coordination criterion—The protection coordination criterion establishes the minimum time that must elapse between the operation of the primary protection and the operation of the backup protection. The fault is detected simultaneously by the primary protection, PP, and the secondary protection, PS. To avoid erroneous operation, the PS will only have to operate in case the PP fails. If we define Ri as the primary fault protection at a certain point, j, and Ri+1 as the secondary or backup protection for the same fault. The constraint condition for coordination criteria is:where, ti+1,j is the operation time of the back-up, PS, operation for fault at point j, ti,j is the operation time of PP operation for the same fault, and ∆t is the coordination time interval (CTI).
- Relay operating time limits—The time taken by a relay to detect and isolate a fault produced in its zone of influence must be bounded. This is the constraint imposed by the operating time of the relays:where, ti,min and ti,max are the minimum and maximum operating times of relay i (at any point).
- Time multiplier setting, TMS, limits—The operating time of a relay is directly proportional to the TMS. Therefore:where TMSi,min is the minimum TMS value for relay i and, TMSi,max is maximum value of TMS for relay i. The TMS values usually taken are 0.025–1.2, respectively [32].
- Relay operating characteristics—To extend the work region of the overcurrent relay specified by the standard [33], the relay’s parameters are optimized considering the maximum value of the relay and the minimum value of the relay, as expressed respectively. We consider all relays with the same characteristics:where top is the relay operating time and PSM is the plug setting multiplier (ki,j in Equation (1)). For inverse characteristic curves it is usually α = 0.02 and β = 0.14 [32,33].
The relay setting current, Iar, is determined from the system requirements. Thus, the above equation can be rewritten as:
where:
4. Case Study Results and Discussion
The distribution system selected for the simulations is the one taken from the test feeders of the Distribution System Analysis Subcommittee of the Institute of Electrical and Electronics Engineers (IEEE) [34], shown in Figure 8. The main characteristics of the distribution network on which the short circuits were simulated are the following:
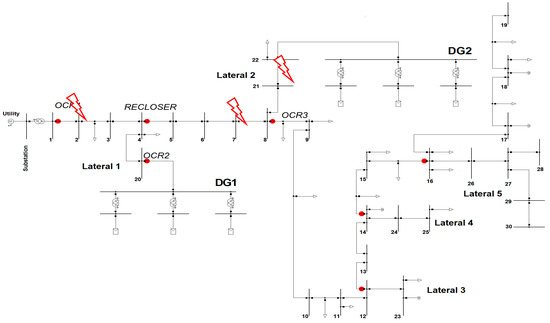
Figure 8.
Modified IEEE 34-node test feeder system [34].
- The voltage across the distribution network is 15 kV.
- The short-circuit power of the external network will be 100 MVA.
- The power demand of the electrical loads connected to the network is 12 MW and load flow analysis they have been considered balanced.
- Overhead network with double circuit with LA-110 conductor. The electrical characteristics of this conductor are shown in [35].
Three-phase and single-phase short circuits were simulated on the distribution network, at busbars 2, 7, and 21, as shown in Figure 8, and with different DG penetration levels ranging from 33% to 50%. A first distributed generation unit, DG1, was installed at busbar 20, whereas a second one, DG2, was installed at busbar 22.
The DG protection device should be properly coordinated with the other protection devices in the distribution network. When a fault occurs on the line to which the DG unit is connected, the DG unit must be disconnected before the protection device on that line is disconnected. This ensures that the DG does not cause disturbances in the operation of the line protections. Furthermore, when a fault occurs on a branch line, the DG must remain in service and will not disconnect before the fault line does [8]. According to this, the coordination criterion shown in Table 2 is proposed.

Table 2.
Coordination criteria according fault location.
The transformation ratio of the current transformers used in the test is 400/5, chosen according to the full-load currents of the system and the short-circuit currents detected by each of the protection devices according to the location of the fault (shown in Table 3).

Table 3.
Short circuit (expressed in amperes, A) detected by the protection devices, for different grounding resistor values, Rf, expressed in ohm.
4.1. Objective Function According to Fault Location
According to the location of the fault, and based on the protection criteria included in Table 2, three objective functions to minimize can be obtained, each of them will result in a different adjustment, an adaptive adjustment.
The scenario analyzed is the three-phase short-circuit scenario with a DG1 penetration level of 17%, the results obtained for the other scenarios can be found in Table A3 in the Appendix A.
Fault 2: OCR2 with OCR1
Fault 7: Recloser with OCR2
Fault 21: OCR3 with recloser
Constraints:
- The minimum operating time of each relay is 0.1 s.
- The normal range of TMS from 0.025 to 1.2.
- Typical CTI setting is 0.3 s.
Coordination criterion
Fault 2: OCR2 with OCR1:
2.27TMS1 − 3.33TMS2 ≥ 0.3
Fault 7: Recloser with OCR2:
3.49TMS2 − 2.21TMSRC ≥ 0.3
Fault 21: OCR3 with Recloser:
4.57TMS3 − 3.23TMSRC ≥ 0.3
Relay operating time limits
Fault 2: OCR2 with OCR1:
2.27TMS1 ≥ 0.1 TMS1 ≤ 0.044
3.33TMS2 ≥ 0.1 TMS2 ≤ 0.030
3.33TMS2 ≥ 0.1 TMS2 ≤ 0.030
Fault 7: Recloser with OCR2:
3.49TMS2 ≥ 0.1 TMS2 ≤ 0.038.
2.21TMSRC ≥ 0.1 TMSRC ≤ 0.045
2.21TMSRC ≥ 0.1 TMSRC ≤ 0.045
Fault 21: OCR3 with recloser:
4.57TMS3 ≥ 0.1 TMS3 ≤ 0.021.
3.23TMSRC ≥ 0.1 TMSRC ≤ 0.030
3.23TMSRC ≥ 0.1 TMSRC ≤ 0.030
The normal range of TMS is from 0.025 to 1.2:
TMS1 ≥ 0.025
TMS2 ≥ 0.025
TMS3 ≥ 0.025
TMSRC ≥ 0.025
TMS2 ≥ 0.025
TMS3 ≥ 0.025
TMSRC ≥ 0.025
4.2. Relay Operating Time Calculation
Using linear programming, the TMS value was calculated as a function of the fault location point.
Substituting the TMS value and the obtained value of the relay constant in Equation (4), we obtain the operating time of each protection relay.
Fault 2: OCR2 with OCR1:
OCR1 top1 = a1(TMS1) = 2.27·0.17 = 0.39 s
OCR2 top2 = a2(TMS2) = 3.33·0.030 = 0.10 s
OCR2 top2 = a2(TMS2) = 3.33·0.030 = 0.10 s
Fault 7: Recloser with OCR2:
OCR2 top2 = a2(TMS2) = 3.49·0.038 = 0.13 s
RECLOSER topRC = aRC(TMSRC) = 2.21·0.11 = 0.24 s
RECLOSER topRC = aRC(TMSRC) = 2.21·0.11 = 0.24 s
Fault 21: OCR3 with Recloser
OCR3 top3 = a3(TMS3) = 4.57·0.065 = 0.30 s
RECLOSER topRC = aRC(TMSRC) = 3.23·0.025 = 0.1 s
RECLOSER topRC = aRC(TMSRC) = 3.23·0.025 = 0.1 s
The values of constants a and TMS and relay operation times top for the rest of the scenarios are shown in Appendix A Table A1 and Table A2. Table A3, shows a comparison of the operation times between the coordination performed in a classical way and with the calculation of adjustments carried out by using LP. Implementing the results obtained in the simulation software, we obtain the following protection schemes shown below.
The classical coordination plots versus linear programming coordination in the case of three-phase short-circuits in the locations described with 17% DG1, are shown in Figure 9, Figure 10 and Figure 11. It can be seen that the response of the OCR protection devices is optimized using the method proposed in this work.
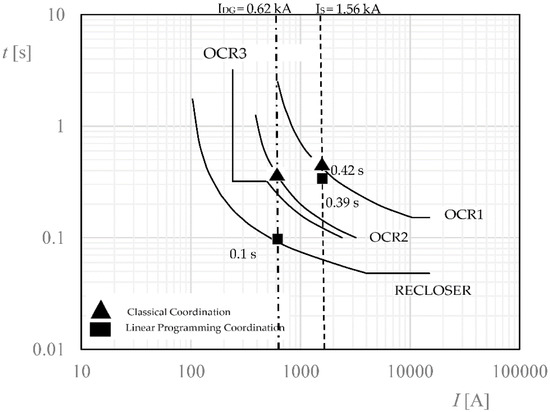
Figure 9.
Short-circuit in F2 with penetration level of DG1 17 %. Classical coordination versus linear programming coordination.
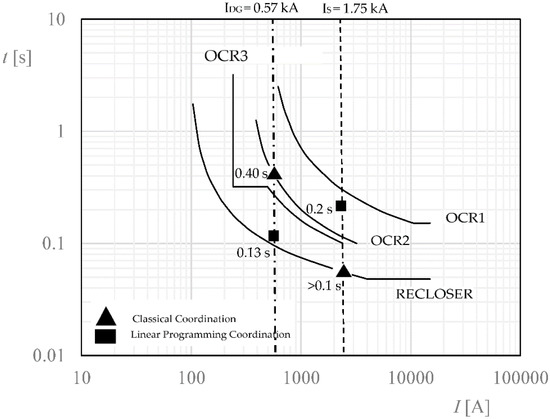
Figure 10.
Short-circuit in F7 with penetration level of DG1 17%. Classical coordination versus al linear programming coordination.
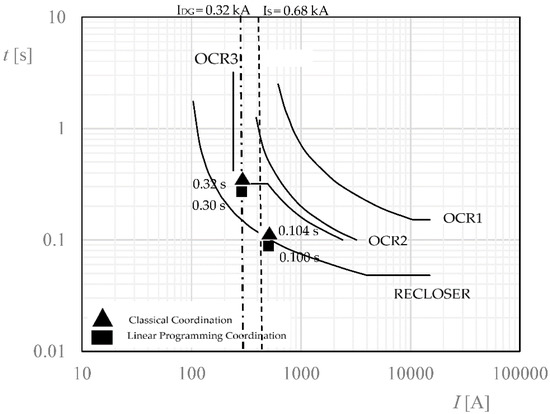
Figure 11.
Short-circuit in F21 with penetration level of DG1 17%. Classical coordination versus linear programming coordination.
5. Conclusions
In this work, a unified protection system that offers double functionality is proposed. The system was proven to be capable of both optimizing the settings of the relays for each network situation.
The performance of the relay has been tested for different DG penetration levels, different types of short-circuit faults (single-phase to ground and three-phase), and different fault zones (faults in the main feeder and the laterals).
The proposed scheme can be implemented in distribution systems using the communication standard IEC61850 [31].
In all the cases studied, the system has proven capable of adapting, in real time, the performance parameters of the relays that protect the faulted line section depending on the operating conditions of the system at the time of the fault.
The proposed protection system has been applied to a distribution system in the presence of DG. The results demonstrate that the protection coordination proposed in this paper is capable of reducing relay operating times by more than 80% compared to classical coordination, which produces a more reliable operation of a network with DG.
Author Contributions
Conceptualization, E.M.G.d.T. and M.I.M.-L.; methodology, D.A.-G., E.M.G.d.T., M.I.M.-L., S.G.-S. and S.P.; software, D.A.-G.; validation, S.G.-S., E.M.G.d.T. and M.I.M.-L.; formal analysis, E.M.G.d.T., M.I.M.-L. and D.A.-G.; investigation, D.A.-G., E.M.G.d.T., M.I.M.-L., S.G.-S. and S.P.; data curation, E.M.G.d.T. and M.I.M.-L.; writing—original draft preparation, D.A.-G., E.M.G.d.T., S.G.-S., M.I.M.-L. and S.P.; writing—review and editing, E.M.G.d.T. and M.I.M.-L.; supervision, S.G.-S., M.I.M.-L. and S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Values of constant relay (ai,j) for the different scenarios analyzed.
Table A1.
Values of constant relay (ai,j) for the different scenarios analyzed.
| F2 | F7 | F21 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Type of Fault | a17% | a33% | a50% | a17% | a33% | a50% | a17% | a33% | a50% | ||
| Three-phase | IOCR1 | 2.27 | 2.27 | 2.27 | 2.52 | 2.58 | 2.59 | 4.96 | 4.92 | 4.89 | |
| IOCR2(DG) | 3.33 | 2.83 | 2.62 | 3.49 | 3.00 | 2.79 | 4.33 | 4.23 | 4.17 | ||
| IOCR3 | - | - | - | - | - | - | 4.57 | 4.51 | 4.47 | ||
| IRC | - | - | - | 2.21 | 2.13 | 2.08 | 3.23 | 3.19 | 3.18 | ||
| Single-phase | Rf = 0 | IOCR1 | 3.59 | 3.38 | 3.23 | 3.72 | 3.54 | 3.47 | 4.25 | 4.30 | 4.31 |
| IOCR2(DG) | 3.13 | 2.62 | 2.4 | 3.22 | 2.74 | 2.54 | 3.83 | 3.90 | 3.86 | ||
| IOCR3 | - | - | - | - | - | 6.55 | 6.35 | 6.27 | |||
| IRC | 3.28 | 3.33 | 3.35 | 2.62 | 2.34 | 2.23 | 3.10 | 3.06 | 3.05 | ||
| Rf = 5 | IOCR1 | 3.51 | 3.39 | 3.34 | 3.68 | 3.63 | 3.62 | 4.29 | 7.78 | 4.32 | |
| IOCR2(DG) | 3.08 | 2.76 | 2.64 | 3.22 | 2.92 | 2.79 | 4.00 | 3.92 | 3.88 | ||
| IOCR3 | - | - | - | - | - | - | 7.14 | 6.97 | 6.88 | ||
| IRC | 3.2 | 3.16 | 3.14 | 2.63 | 2.46 | 2.40 | 3.09 | 3.06 | 3.05 | ||
| Rf = 10 | IOCR1 | 3.65 | 3.61 | 3.61 | 3.79 | 3.8 | 3.92 | 4.30 | 4.32 | 3.91 | |
| IOCR2(DG) | 3.23 | 3.2 | 2.93 | 3.35 | 3.15 | 3.05 | 4.02 | 3.95 | 4.34 | ||
| IOCR3 | - | - | - | - | - | - | 7.83 | 7.61 | 7.56 | ||
| IRC | 3.16 | 3.14 | 3.14 | 2.7 | 2.59 | 2.56 | 3.08 | 3.06 | 3.05 | ||
| Rf = 15 | IOCR1 | 3.8 | 3.78 | 3.8 | 3.9 | 3.93 | 3.97 | 4.32 | 4.34 | 4.35 | |
| IOCR2(DG) | 3.39 | 3.23 | 3.15 | 3.48 | 3.32 | 3.25 | 4.03 | 3.97 | 3.93 | ||
| IOCR3 | - | - | - | - | - | - | 8.56 | 8.33 | 7.78 | ||
| IRC | 3.16 | 3.15 | 3.15 | 2.76 | 2.69 | 2.67 | 3.08 | 3.06 | 3.05 | ||
| Rf = 20 | IOCR1 | 3.91 | 3.91 | 3.92 | 3.99 | 4.03 | 4.06 | 4.33 | 3.99 | 4.37 | |
| IOCR2(DG) | 3.51 | 3.38 | 3.32 | 3.59 | 3.46 | 3.39 | 4.05 | 4.35 | 3.96 | ||
| IOCR3 | - | - | - | - | - | - | 9.36 | 9.14 | 9.07 | ||
| IRC | 3.16 | 3.15 | 3.15 | 2.82 | 2.77 | 2.75 | 3.08 | 3.06 | 3.06 | ||
| Rf = 25 | IOCR1 | 3.99 | 4.00 | 4.02 | 4.06 | 4.11 | 4.13 | 4.34 | 4.37 | 4.38 | |
| IOCR2(DG) | 3.61 | 3.5 | 3.41 | 3.68 | 3.56 | 3.51 | 4.06 | 4.01 | 3.95 | ||
| IOCR3 | - | - | - | - | - | - | 10.2 | 10.0 | 9.93 | ||
| IRC | 3.16 | 3.16 | 3.16 | 2.86 | 2.82 | 2.81 | 3.09 | 3.07 | 3.06 | ||

Table A2.
Relay TMS values for the different scenarios analyzed.
Table A2.
Relay TMS values for the different scenarios analyzed.
| F2 | F7 | F21 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Type of Fault | TMS17% | TMS33% | TMS50% | TMS17% | TMS33% | TMS50% | TMS17% | TMS33% | TMS50% | ||
| Three-phase | IOCR1 | 0.17 | 0.17 | 0.17 | - | - | - | - | -. | - | |
| IOCR2(DG) | 0.03 | 0.04 | 0.04 | 0.04 | 0.03 | 0.04 | - | - | - | ||
| IOCR3 | - | - | - | - | - | - | 0.08 | 0.09 | 0.09 | ||
| IRC | - | - | - | 0.19 | 0.18 | 0.19 | 0.03 | 0.03 | 0.03 | ||
| Single-phase | Rf = 0 | IOCR1 | 0.11 | 0.11 | 0.12 | - | - | - | - | - | - |
| IOCR2(DG) | 0.03 | 0.04 | 0.04 | 0.03 | 0.04 | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | 0.06 | 0.06 | 0.06 | 0.06 | ||
| IRC | - | - | - | 0.15 | 0.14 | 0.03 | 0.03 | 0.03 | 0.03 | ||
| Rf = 5 | IOCR1 | 0.11 | 0.11 | 0.11 | - | - | - | - | - | - | |
| IOCR2(DG) | 0.03 | 0.04 | 0.04 | 0.03 | 0.03 | - | - | - | - | ||
| IOCR3 | - | - | - | - | 0.06 | 0.06 | 0.07 | 0.07 | |||
| IRC | - | - | - | 0.15 | 0.01 | 0.03 | 0.03 | 0.03 | 0.03 | ||
| Rf = 10 | IOCR1 | 0.10 | 0.11 | 0.11 | - | - | - | - | - | - | |
| IOCR2(DG) | 0.03 | 0.03 | 0.04 | 0.03 | 0.03 | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | 0.05 | 0.05 | 0.06 | 0.06 | ||
| IRC | - | - | - | 0.14 | 0.01 | 0.03 | 0.03 | 0.03 | 0.03 | ||
| Rf = 15 | IOCR1 | 0.10 | 0.10 | 0.10 | - | - | - | - | - | - | |
| IOCR2(DG) | 0.03 | 0.03 | 0.03 | 0.03 | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | 0.05 | 0.05 | 0.05 | 0.05 | ||
| IRC | - | - | - | 0.14 | 0.03 | 0.03 | 0.03 | 0.03 | |||
| Rf = 20 | IOCR1 | 0.10 | 0.10 | 0.10 | - | - | - | - | - | - | |
| IOCR2(DG) | 0.03 | 0.03 | 0.03 | 0.03 | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | 0.04 | 0.04 | 0.05 | 0.05 | ||
| IRC | - | - | - | 0.14 | 0.03 | 0.03 | 0.03 | 0.03 | |||
| Rf = 25 | IOCR1 | 0.10 | 0.10 | 0.10 | - | - | - | - | - | - | |
| IOCR2(DG) | 0.03 | 0.03 | 0.03 | 0.03 | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | 0.04 | 0.04 | 0.05 | 0.04 | ||
| IRC | - | - | - | 0.13 | - | 0.03 | 0.03 | 0.03 | 0.03 | ||

Table A3.
Operation time PL coordination versus operation time from classical coordination.
Table A3.
Operation time PL coordination versus operation time from classical coordination.
| F2 | F7 | F21 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type of Fault | top 17% | top 33% | top 50% | top 17% | top 33% | top 50% | top 17% | top 33% | top 50% | |||||||||||
| Type Coordination | C | PL | C | PL | C | PL | C | PL | C | PL | C | PL | C | PL | C | PL | C | PL | ||
| Three-phase | IOCR1 | 0.42 | 0.39 | 0.42 | 0.39 | 0.42 | 0.39 | - | - | - | - | - | - | - | - | - | - | - | - | |
| IOCR2(GD) | 0.20 | 0.20 | 0.19 | 0.10 | 0.15 | 0.08 | 0.20 | 0.13 | 0.20 | 0.10 | 0.20 | 0.10 | - | - | - | - | - | |||
| IOCR3 | - | - | - | - | - | - | - | - | - | - | - | - | 0.42 | 0.38 | 0.42 | 0.40 | 0.42 | 0.40 | ||
| IRC | - | - | - | - | - | - | 0.45 | 0.42 | 0.45 | 0.38 | 0.45 | 0.40 | 0.12 | 0.08 | 0.12 | 0.10 | 0.12 | 0.10 | ||
| Single-phase | Rf = 0 | IOCR1 | 0.42 | 0.39 | 0.43 | 0.37 | 0.42 | 0.39 | - | - | - | - | - | - | - | - | - | - | - | - |
| IOCR2(DG) | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.13 | - | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | - | - | - | - | - | - | - | 0.40 | 0.39 | 0.14 | 0.38 | 0.14 | 0.38 | ||
| IRC | - | - | - | - | - | - | 0.40 | 0.39 | 0.40 | 0.33 | 0.40 | 0.31 | 0.40 | 0.10 | 0.40 | 0.09 | 0.40 | 0.09 | ||
| Rf = 5 | IOCR1 | 0.41 | 0.39 | 0.42 | 0.37 | 0.41 | 0.37 | - | - | - | - | - | - | - | - | - | - | - | - | |
| IOCR2(DG) | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.08 | - | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | - | - | - | - | - | - | - | 0.39 | 0.43 | 0.45 | 0.49 | 0.45 | 0.48 | ||
| IRC | - | - | - | - | - | - | 0.40 | 0.39 | 0.40 | 0.3 | 0.40 | 0.40 | 0.40 | 0.09 | 0.40 | 0.09 | 0.40 | 0.09 | ||
| Rf = 10 | IOCR1 | 0.41 | 0.37 | 0.42 | 0.40 | 0.41 | 0.40 | - | - | - | - | - | - | - | - | - | - | - | - | |
| IOCR2(DG) | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.11 | 0.14 | 0.10 | 0.14 | 0.09 | 0.14 | 0.09 | - | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | - | - | - | - | - | - | - | - | 0.39 | - | 0.46 | - | 0.45 | ||
| IRC | - | - | - | - | - | - | 0.40 | 0.38 | 0.40 | 0.3 | 0.40 | 0.3 | 0.40 | 0.10 | 0.4 | 0.09 | 0.40 | 0.09 | ||
| Rf = 15 | IOCR1 | 0.40 | 0.38 | 0.41 | 0.38 | 0.40 | 0.38 | - | - | - | - | - | - | - | - | - | - | - | - | |
| IOCR2(DG) | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.09 | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.10 | - | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | - | - | - | - | - | - | - | 0.45 | 0.39 | - | 0.42 | - | 0.39 | ||
| IRC | - | - | - | - | - | - | 0.40 | 0.39 | 0.40 | 0.3 | 0.40 | 0.3 | 0.40 | 0.09 | - | 0.09 | - | 0.09 | ||
| Rf = 20 | IOCR1 | 0.40 | 0.39 | 0.41 | 0.39 | 0.40 | 0.39 | - | - | - | - | - | - | - | - | - | - | - | - | |
| IOCR2(DG) | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.11 | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.10 | - | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | - | - | - | - | - | - | - | - | 0.39 | - | 0.46 | - | 0.45 | ||
| IRC | - | - | - | - | - | - | 0.40 | 0.39 | 0.40 | 0.3 | 0.40 | 0.03 | 0.40 | 0.09 | 0.40 | 0.09 | 0.40 | 0.09 | ||
| Rf = 25 | IOCR1 | 0.42 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | - | - | - | - | - | - | - | - | - | - | - | - | |
| IOCR2(DG) | 0.14 | 0.10 | 0.14 | 0.10 | 0.14 | 0.11 | 0.14 | 0.10 | 0.14 | 0.11 | 0.14 | 0.11 | - | - | - | - | - | - | ||
| IOCR3 | - | - | - | - | - | - | - | - | - | - | - | - | - | 0.40 | - | 0.50 | - | 0.40 | ||
| IRC | - | - | - | - | - | - | 0.40 | 0.37 | 0.40 | 0.3 | 0.40 | 0.03 | 0.40 | 0.09 | 0.40 | 0.09 | 0.40 | 0.09 | ||
C—classical coordination; PL—lineal programming coordination.
References
- Dugan, R.C.; McDermott, T.E. Distributed generation. IEEE Ind. Appl. Mag. 2002, 8, 19–25. [Google Scholar] [CrossRef]
- Salman, S.; Rida, I. Investigating the impact of embedded generation on relay settings of utilities electrical feeders. IEEE Trans. Power Deliv. 2001, 16, 246–251. [Google Scholar] [CrossRef]
- Anderson, P.M. Power System Protection; Sons, J.W., Ed.; IEEE Press: Piscataway, NJ, USA, 1998. [Google Scholar]
- Girgis, A.; Brahma, S.M. Effect of distributed generation on protective device coordination in distribution system. In Proceedings of the Large Engineering Systems Conference of Power Engineering, Halifax, NS, Canada, 11–13 July 2001. [Google Scholar]
- Scheepers, M.; van Werven, M.; Mutale, J.; Strbac, G.; Porter, D. Distributed generation in electricity markets, its impact on distribution system operators, and the role of regulatory and commercial arrangements. Int. J. Distrib. Energy Resour. 2006, 2, 35–38. [Google Scholar]
- Jenkins, N. Embedded generation. Power Eng. J. 1995, 9, 145–150. [Google Scholar] [CrossRef]
- Doyle, M.T. Reviewing the impacts of distributed generation on distribution system protection. Power Eng. Soc. Summer Meet. IEEE 2002, 1, 103–105. [Google Scholar]
- Repo, S.; Jarventausta, P.; Maki, K. Protection requirement graph for interconnection of distributed generation on distribution level. Int. J. Energy Issues 2007, 28, 47–64. [Google Scholar]
- Girgis, A.; Fallon, C.M.; Lubkeman, D.L. A fault location technique for rural distribution feeders. IEEE Trans. Ind. Appl. 1993, 29, 1170–1175. [Google Scholar] [CrossRef]
- Das, R. Estimating locations of shunt faults on distribution lines. Master’s Thesis, College of Graduate Studies and Research, University of Saskatchewan, Saskatoon, SK, Canada, 1995. [Google Scholar]
- Das, R.; Sachdev, M.S.; Sidhu, T.S. A technique for estimating locations of shunt faults on distribution lines. In Proceedings of the IEEE WESCANEX 95. Communications, Power, and Computing. Conference Proceedings, Winnipeg, MB, Canada, 15–16 May 1995; Volume 1, pp. 6–11. [Google Scholar]
- Tarek, K.; Girgis, A. Protection Coordination Planning with Distributed Generation. Master’s Thesis, CETC Varennes—Energy Technology and Programs Sector, Varennes, QC, Canada, 2007. [Google Scholar]
- Warrington, A.R.V.C. Protective Relays: Their Theory and Practice; Wiley, J., York, S.N., Eds.; Springer: Cham, Switzerland, 1969. [Google Scholar]
- Sant, M.T.; Paithankar, Y.G. Online digital fault locator foroverhead transmission line. Proc. Inst. Electr. 1979, 126, 1181–1185. [Google Scholar] [CrossRef]
- Sant, M.T.; Paithankar, Y. Fault locator for long ehv transmission lines. Electr. Power Syst. Res. 1983, 6, 305–310. [Google Scholar] [CrossRef]
- Takagi, T.; Yamakoshi, Y.; Yamaura, M.; Kondow, R.; Matsushima, T. Development of a new type fault locator using the One-Terminalvoltage and current data. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 2892–2898. [Google Scholar] [CrossRef]
- Edmond, S., III. Evaluation and development of transmission line fault-locating techniques which use sinusoidal steady-state. Comput. Electr. Eng. 1983, 10, 269–278. [Google Scholar]
- Johns, A.T.; Lai, L.L.; El-Hami, M.; Daruvala, D.J. New approach to directional fault location for overhead power distribution feeders. Gener. Transm. Distrib. IEE Proc. C 1991, 138, 351–357. [Google Scholar] [CrossRef]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 2nd ed.; Prentice Hall: Hoboken, NJ, UK, 2002. [Google Scholar]
- Brand, C.B.K.; Wimmer, W. Design of IEC 61850 Based Substation Automation Systems According to Customer Requirements; Paper b5-103; CIGRE: Paris, France, 2004. [Google Scholar]
- Paithankar, Y.G. Transmission Network Protection: Theory and Practice; Routledge: Oxfordshire, UK, 1997. [Google Scholar]
- Noghabi, A.S.; Sadeh, J.; Mashhadi, H.R. Considering different network topologies in optimal overcurrent relay coordination using a hybrid GA. IEEE Trans. Power Deliv. 2019, 24, 1857–1863. [Google Scholar] [CrossRef]
- Knable, A. A standardized approach to relay coordination. IEEE Winter Power Meet. 1969, 69, 58. [Google Scholar]
- Jenkins, L.; Khicha, H.; Shivakumar, S.; Dash, P. An application of function dependencies to the topological analysis of protection schemes. IEEE Trans. Power Deliv. 1992, 7, 77–83. [Google Scholar] [CrossRef] [Green Version]
- Urdaneta, A.J.; Nadira, R.; Perez Jimenez, L.G. Optimal coordination of directional overcurrent relays in interconnected power systems. IEEE Trans. Power Deliv. 1988, 3, 903–911. [Google Scholar] [CrossRef]
- Chattopadhyay, B.; Sachdev, M.S.; Sidhu, T.S. An on-line relay coordination algorithm for adaptive protection using linear programming technique. IEEE Trans. Power Deliv. 1996, 11, 165–173. [Google Scholar] [CrossRef]
- So, C.W.; Li, K.K. Time coordination method for power system protection by evolutionary algorithm. IEEE Trans. Ind. Appl. 2000, 36, 1235–1240. [Google Scholar] [CrossRef]
- Laway, N.A.; Gupta, H.O. A method for adaptive coordination of overcurrent relays in an interconnected power system. In Proceedings of the Fifth International Conference on Developments in Power System Protection, York, UK, 30 March–2 April 1993; pp. 240–243. [Google Scholar]
- Bedekar, P.; Bhide, S.; Kale, V. Optimum time coordination of overcurrent relays in distribution system using big-m (penalty) method. WSEAS Trans. Power Syst. 2019, 4, 341–350. [Google Scholar]
- IEC 61850-SER; Communication Networks and Systems in Substations. All Parts. IEC Std: Geneva, Switzerland, 2005.
- Soman, S. Lectures on Power System Protection. Module 5, Lecture 19. NPTEL Online. 2010. Available online: www.cdeep.iitb.ac.in (accessed on 26 March 2022).
- Keil, T.; Jager, J. Advanced coordination method for overcurrent protection relays using nonstandard tripping characteristics. IEEE Trans. Power Deliv. 2018, 23, 52–57. [Google Scholar] [CrossRef]
- IEEE. 34 Node Test Feeder; The Institute of Electrical and Electronics Engineers, Inc.: Piscataway, NJ, USA, 2004. [Google Scholar]
- Proyecto Tipo Unión Fenosa Líneas Eléctricas Aéreas de Hasta 20 kV; UFD: Madrid, Spain, 2017.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).