Masonry Spiral Stairs: A Comparison between Analytical and Numerical Approaches
Abstract
:1. Introduction
1.1. The Spiral Stair throughout History: Brief Notes
1.2. Current State of the Research
1.3. Purpose of the Study
2. Materials and Methods
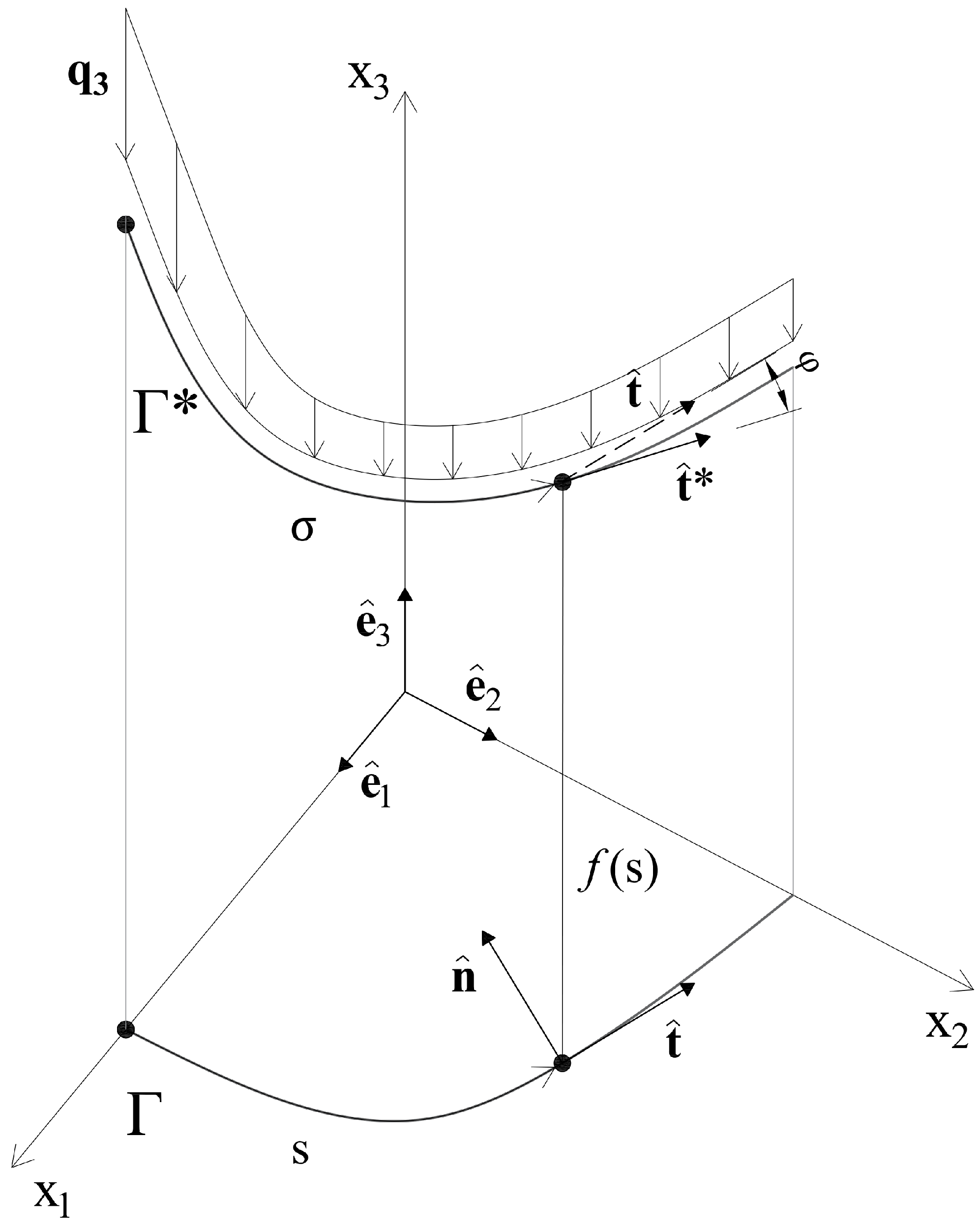
2.1. Linear Arch Static Analysis (LASA)
2.1.1. Geometry
2.1.2. Forces
2.1.3. Solution of the Equilibrium Problem for the Curve *
3. Application to the Case Study
3.1. The Spiral Staircase in the Fortified Tower of Nisida: Geometry and Construction
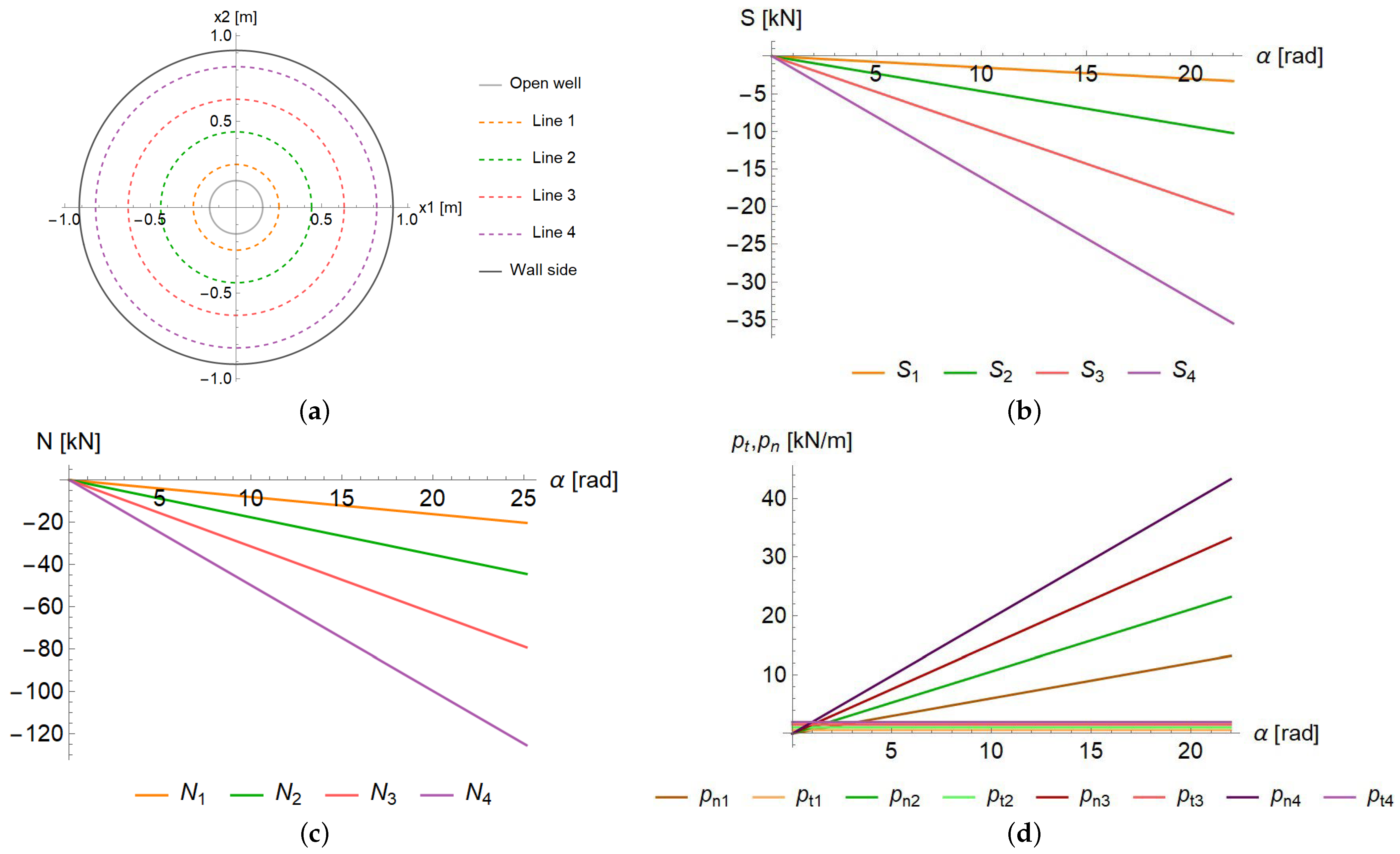
3.2. LASA Equilibrium Solution
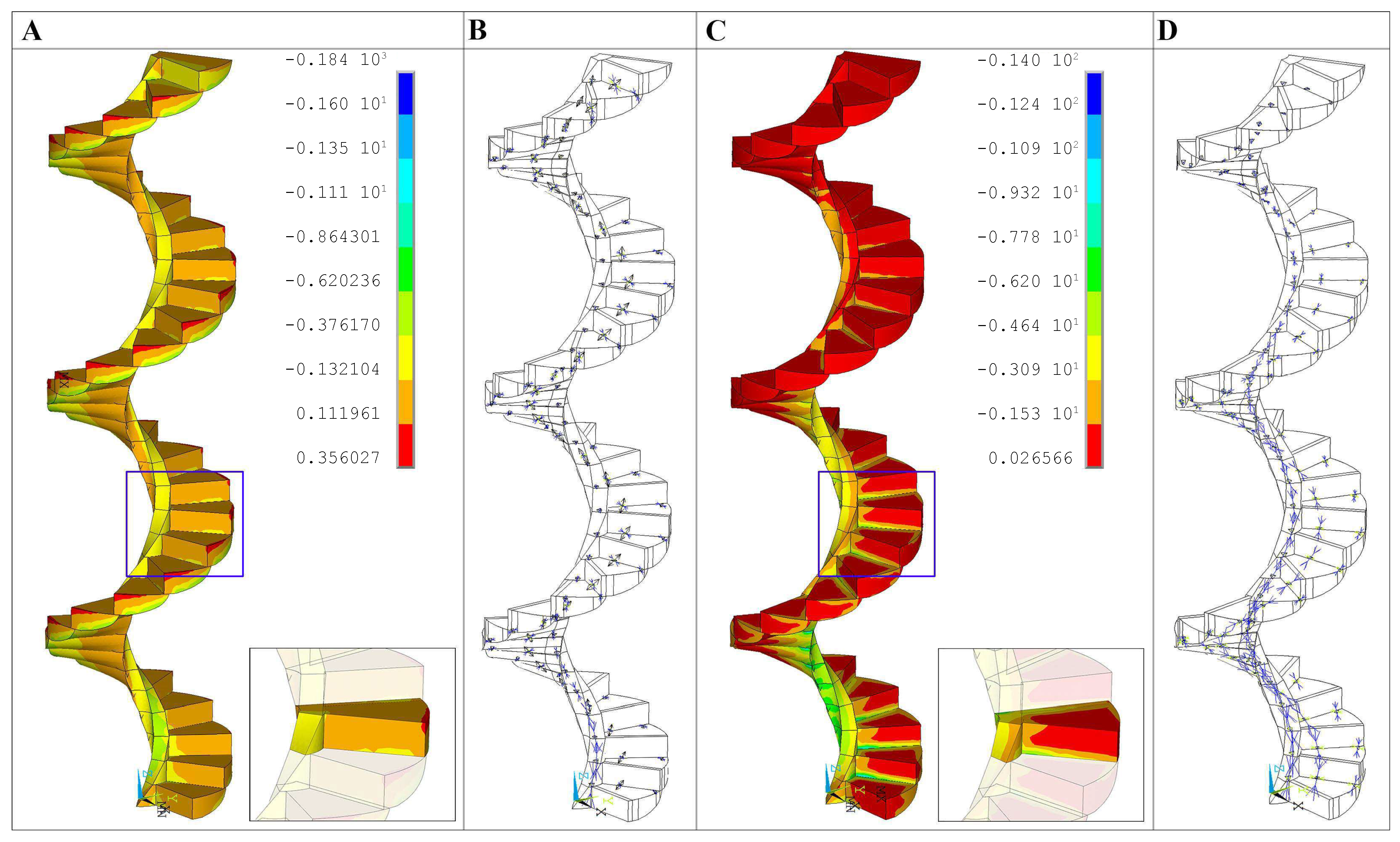
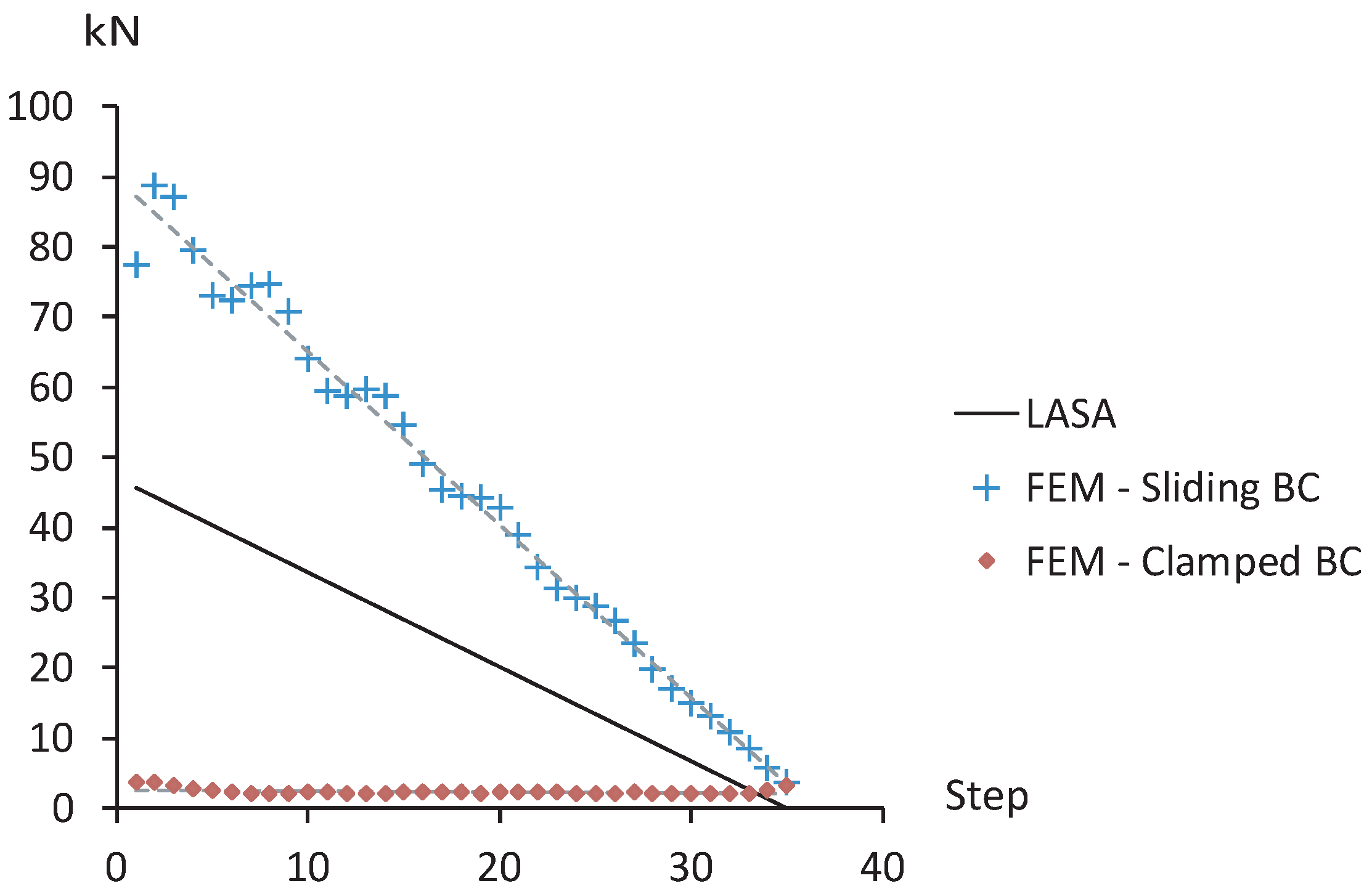
3.3. Analysis with FEM
- Clamped boundary conditions: the base of the first step from the ground is clamped and the horizontal displacements and of the upper step (36th step) are prevented. Each intermediate step is embedded into the outer wall.
- Sliding boundary conditions: the base of the first step from the ground is clamped and the horizontal displacements and of the upper step (36th step) are prevented. Each intermediate step is linked to the outer wall by a sliding condition, i.e., it cannot detach from the wall but it is free to slide along its surface.
Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| LA | Limit Analysis |
| LASA | Linear Arch Static Analysis |
| NT | No-Tension |
| TNA | Thrust Network Analysis |
References
- Choisy, A. L’art de bâtir Chez les Byzantins: Planches; Librairie de la Société Anonyme de Publications Périodiques; Arnaldo Forni Editore: Bologna, Italy, 1883; Volume 1. [Google Scholar]
- Viollet-le Duc, E.E. Dictionnaire Raisonné de L’architecture Française du XIe au XVIe Siècle; Banc Bance: Paris, France, 1854; Volume 1. [Google Scholar]
- Ochsendorf, J. Guastavino Vaulting: The Art of Structural Tile; Princeton Architectural Press: New York, NY, USA, 2010. [Google Scholar]
- Betti, M.; Galano, L.; Vignoli, A. Finite Element Modelling for Seismic Assessment of Historic Masonry Buildings. In Earthquakes and Their Impact on Society; D’Amico, S., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 377–415. [Google Scholar] [CrossRef] [Green Version]
- Rigó, B.; Bagi, K. Discrete element analysis of stone cantilever stairs. Meccanica 2018, 53, 1571–1589. [Google Scholar] [CrossRef]
- Mascolo, I.; Modano, M.; Amendola, A.; Fraternali, F. A Finite Element Analysis of the Stability of Composite Beams with Arbitrary Curvature. Front. Built Environ. 2018, 4, 57. [Google Scholar] [CrossRef] [Green Version]
- Guarracino, F.; Walker, A. Some comments on the numerical analysis of plates and thin-walled structures. Thin-Walled Struct. 2008, 46, 975–980. [Google Scholar] [CrossRef]
- Busool, W.; Eisenberger, M. Exact static analysis of helicoidal structures of arbitrary shape and variable cross section. J. Struct. Eng. 2001, 127, 1266–1275. [Google Scholar] [CrossRef]
- Calladine, C.R. A preliminary Structural Analysis of a Guastavino Spiral Staircase Shell. In History of Structures: Essays in the History of the Theory of Structures in Honour of Jacques Heyman; Instituto Juan de Herrera, Escuela Technica Superior de Arquitectura de Madrid: Madrid, Spain, 2006; Available online: http://publications.eng.cam.ac.uk/364877/ (accessed on 25 March 2022).
- Huerta, S. The analysis of masonry architecture: A historical approach: To the memory of professor Henry J. Cowan. Archit. Sci. Rev. 2008, 51, 297–328. [Google Scholar] [CrossRef] [Green Version]
- Kooharian, A. Limit Analysis of Voussoir (Segmental) and Concrete Archs. J. Amer. Concr. Inst. 1952, 49, 317–328. [Google Scholar]
- Heyman, J. The stone skeleton. Int. J. Solids Struct. 1966, 2, 249–279. [Google Scholar] [CrossRef]
- Fraldi, M.; Gesualdo, A.; Guarracino, F. Influence of actual plastic hinge placement on the behavior of ductile frames. J. Zhejiang Univ. Sci. A 2014, 15, 482–495. [Google Scholar] [CrossRef]
- Iannuzzo, A. Energy based fracture identification in masonry structures: The case study of the church of “Pietà dei Turchini”. J. Mech. Mater. Struct. 2019, 14, 683–702. [Google Scholar] [CrossRef]
- Fortunato, A.; Gesualdo, A.; Mascolo, I.; Monaco, M. P-Bézier energy optimization for elastic solutions of masonry-like panels. Int. J. Mason. Res. Innov. 2021, 7, 113–125. [Google Scholar] [CrossRef]
- Malena, M.; Angelillo, M.; Fortunato, A.; de Felice, G.; Mascolo, I. Arch bridges subject to pier settlements: Continuous vs. piecewise rigid displacement methods. Meccanica 2021, 56, 2487–2505. [Google Scholar] [CrossRef]
- Cennamo, C.; Cusano, C. Roman Masonry Stairways. Geometry, Construction and Stability. In Conference of the Italian Association of Theoretical and Applied Mechanics; Springer: Cham, Switzerland, 2020; pp. 1896–1909. [Google Scholar] [CrossRef]
- Heyman, J. The mechanics of masonry stairs. WIT Trans. Built Environ. 1970, 17. Available online: https://www.witpress.com/elibrary/wit-transactions-on-the-built-environment/17/10699 (accessed on 25 March 2022).
- Price, S.; Rogers, H. James sutherland history lecture-Stone cantilevered staircases. Struct. Eng. 2005, 83, 29–36. [Google Scholar]
- Angelillo, M. The equilibrium of helical stairs made of monolithic steps. Int. J. Archit. Herit. 2016, 10, 675–687. [Google Scholar] [CrossRef]
- De Serio, F.; Angelillo, M.; Gesualdo, A.; Iannuzzo, A.; Zuccaro, G.; Pasquino, M. Masonry structures made of monolithic blocks with an application to spiral stairs. Meccanica 2018, 53, 2171–2191. [Google Scholar] [CrossRef]
- Olivieri, C.; Angelillo, M.; Gesualdo, A.; Iannuzzo, A.; Fortunato, A. Parametric design of purely compressed shells. Mech. Mater. 2021, 155, 103782. [Google Scholar] [CrossRef]
- Fraternali, F.; Angelillo, M.; Fortunato, A. A lumped stress method for plane elastic problems and the discrete-continuum approximation. Int. J. Solids Struct. 2002, 39, 6211–6240. [Google Scholar] [CrossRef]
- Montanino, A.; Olivieri, C.; Zuccaro, G.; Angelillo, M. From Stress to Shape: Equilibrium of Cloister and Cross Vaults. Appl. Sci. 2021, 11, 3846. [Google Scholar] [CrossRef]
- Olivieri, C.; Fortunato, A.; DeJong, M. A new membrane equilibrium solution for masonry railway bridges: The case study of Marsh Lane Bridge. Int. J. Mason. Res. Innov. 2021, 6, 446–471. [Google Scholar] [CrossRef]
- Angelillo, M. Static analysis of a Guastavino helical stair as a layered masonry shell. Compos. Struct. 2015, 119, 298–304. [Google Scholar] [CrossRef]
- Gesualdo, A.; Cennamo, C.; Fortunato, A.; Frunzio, G.; Monaco, M.; Angelillo, M. Equilibrium formulation of masonry helical stairs. Meccanica 2017, 52, 1963–1974. [Google Scholar] [CrossRef]
- García Ares, J.A. Un enfoque para el análisis límite de las escaleras de fábrica helicoidales. In Proceedings of the Actas del Quinto Congreso Nacional de Historia de la Construcción, Burgos, Spain, 7–9 June 2007. [Google Scholar]
- Block, P.P.C.V. Thrust Network Analysis: Exploring Three-Dimensional Equilibrium. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Angelillo, M.; Olivieri, C.; DeJong, M.J. A new equilibrium solution for masonry spiral stairs. Eng. Struct. 2021, 238, 112176. [Google Scholar] [CrossRef]
- Mascolo, I.; Fulgione, M.; Pasquino, M. Lateral torsional buckling of compressed open thin walled beams: Experimental confirmations. Int. J. Mason. Res. Innov. 2019, 4, 150–158. [Google Scholar] [CrossRef]
- Nowak, R.; Kania, T.; Rutkowski, R.; Ekiert, E. Research and TLS (LiDAR) Construction Diagnostics of Clay Brick Masonry Arched Stairs. Materials 2022, 15, 552. [Google Scholar] [CrossRef] [PubMed]
- Cusano, C.; Montanino, A.; Zuccaro, G.; Cennamo, C. Considerations about the static response of masonry domes: A comparison between limit analysis and finite element method. Int. J. Mason. Res. Innov. 2021, 6, 502–528. [Google Scholar] [CrossRef]
- Cusano, C.; Montanino, A.; Olivieri, C.; Paris, V.; Cennamo, C. Graphical and analytical quantitative comparison in the Domes assessment: The case of San Francesco di Paola. Appl. Sci. 2021, 11, 3622. [Google Scholar] [CrossRef]
- Pucher, A. Über der spannungszustand in gekrümmten flächen. Beton Eisen 1934, 33, 298–304. [Google Scholar]
- Cennamo, C.; Cusano, C.; Angelillo, M. The spiral staircase in the fortified tower of Nisida. In Proceedings of the 12th International Conference on Structural Analysis of Historical Constructions—SAHC 2021, Online event, 29 September–1 October 2021. [Google Scholar]
- Adachi, T.; Ogawa, T.; Hayashi, M. Mechanical Properties of Soft Rock and Rock Mass. In Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering, Stockholm, Sweden, 15–19 June 1981; pp. 527–530. [Google Scholar]
- Thompson, M.; Thompson, J. ANSYS Mechanical APDL for Finite Element Analysis; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]


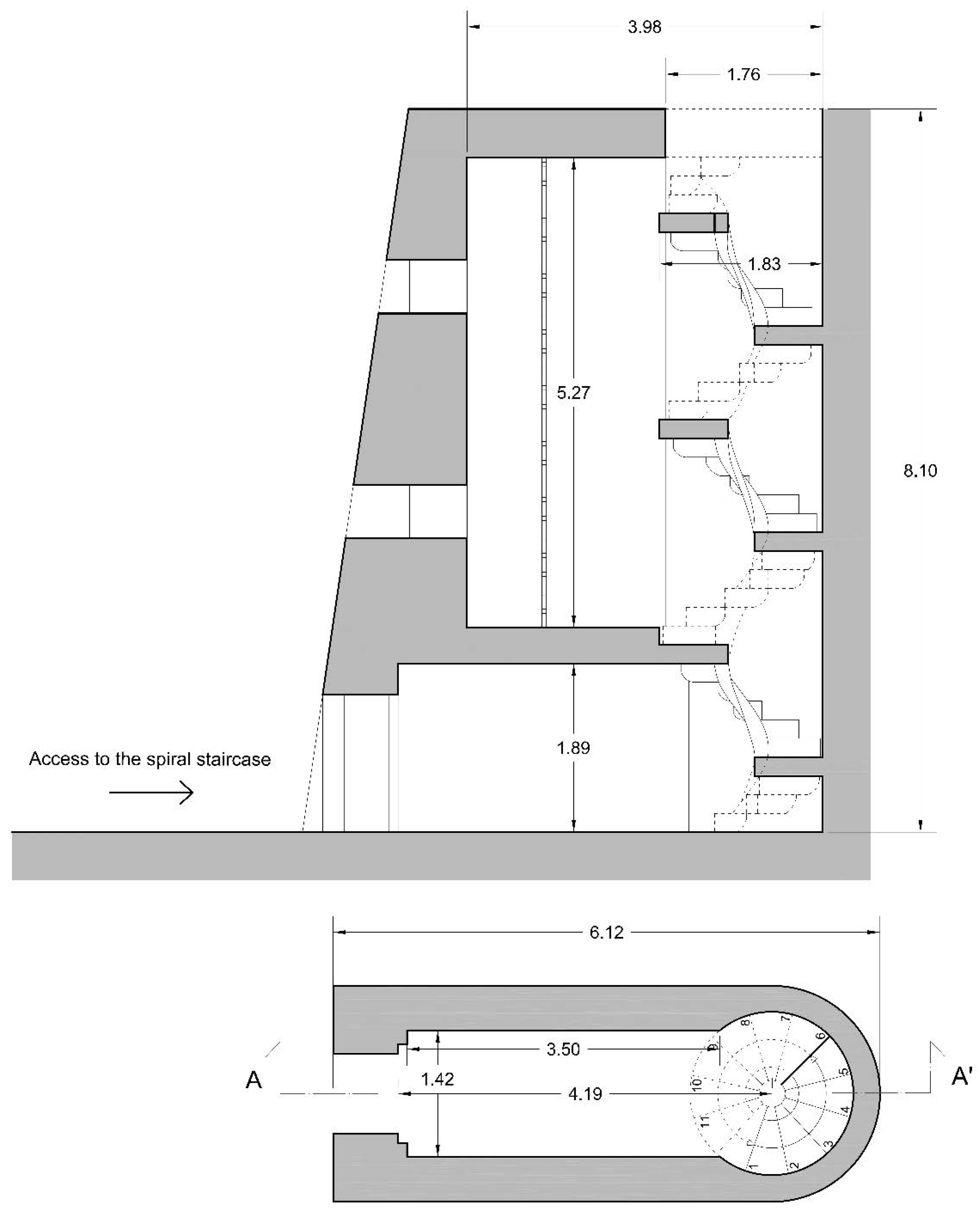
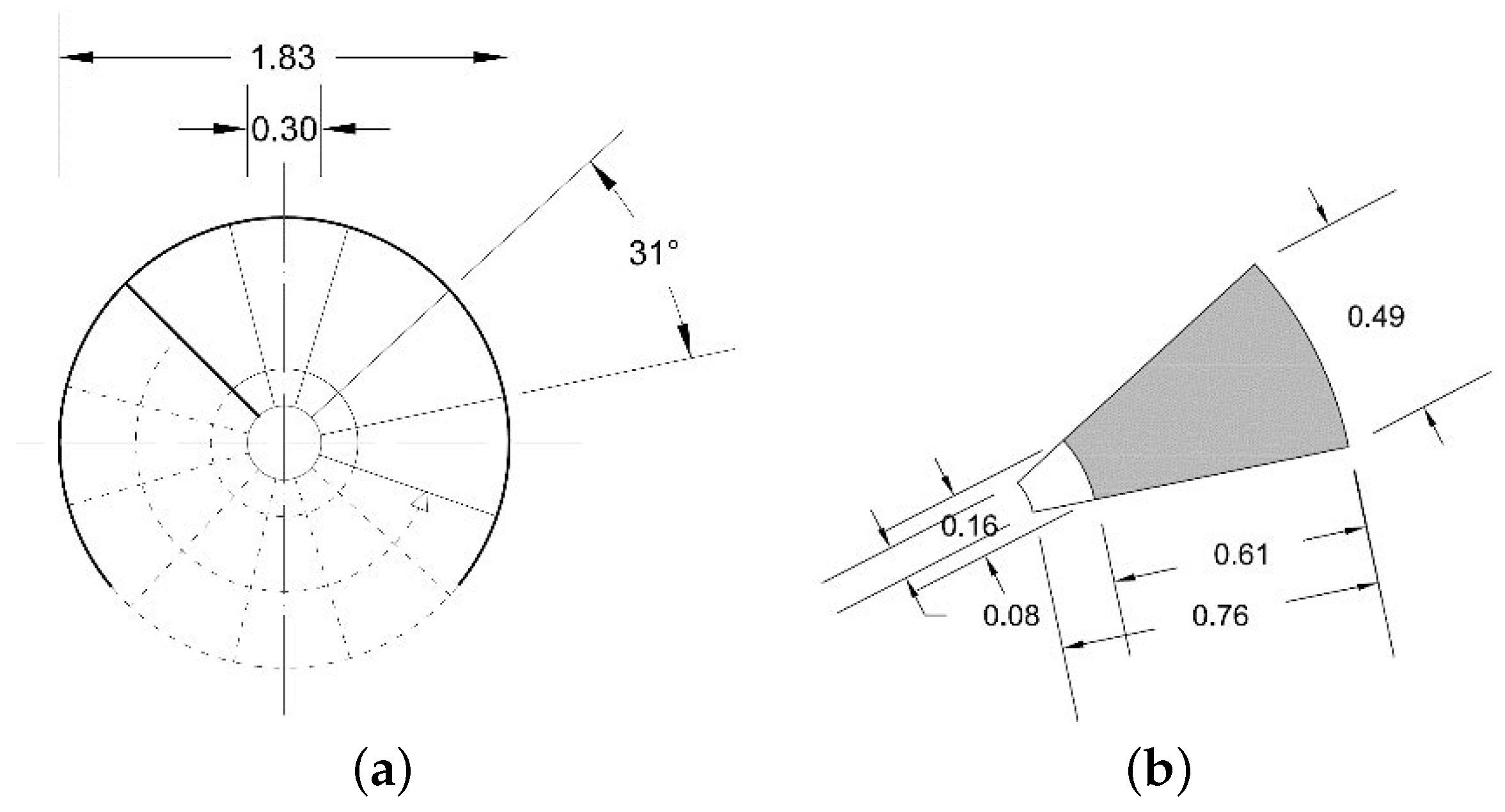
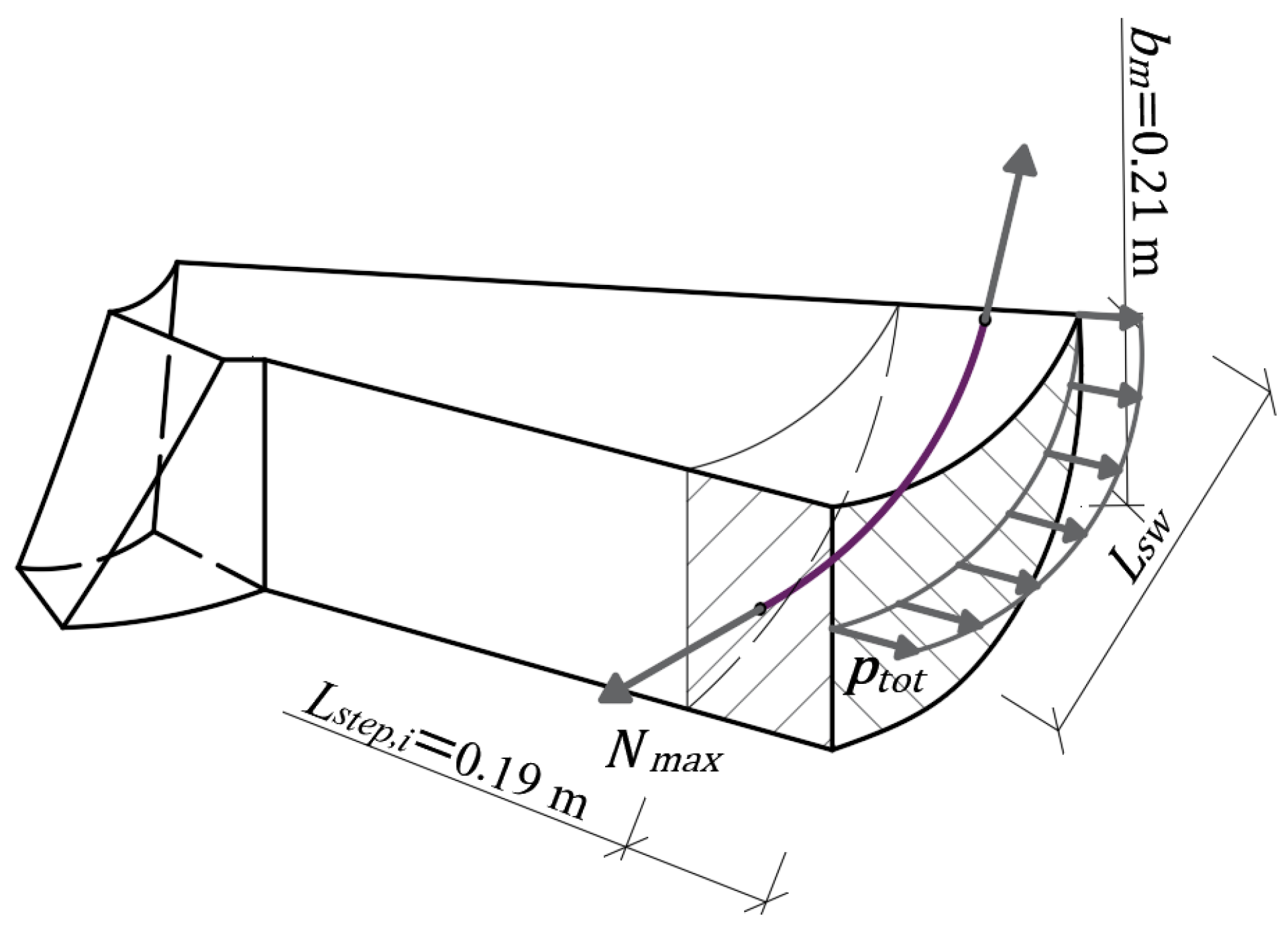
| PLAN | type: | circular |
| rotation: | laevorotatory | |
| staircase diameter: | m | |
| hole (eye) diameter: | m | |
| step angle: | ||
| number of steps: | 36 | |
| STEP | central hole solution: | radial |
| total length (): | m | |
| usable length: | m | |
| minimum width: | m | |
| maximum width: | m | |
| step height: | m | |
| medium height (): | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivieri, C.; Cennamo, C.; Cusano, C.; Cutolo, A.; Fortunato, A.; Mascolo, I. Masonry Spiral Stairs: A Comparison between Analytical and Numerical Approaches. Appl. Sci. 2022, 12, 4274. https://doi.org/10.3390/app12094274
Olivieri C, Cennamo C, Cusano C, Cutolo A, Fortunato A, Mascolo I. Masonry Spiral Stairs: A Comparison between Analytical and Numerical Approaches. Applied Sciences. 2022; 12(9):4274. https://doi.org/10.3390/app12094274
Chicago/Turabian StyleOlivieri, Carlo, Claudia Cennamo, Concetta Cusano, Arsenio Cutolo, Antonio Fortunato, and Ida Mascolo. 2022. "Masonry Spiral Stairs: A Comparison between Analytical and Numerical Approaches" Applied Sciences 12, no. 9: 4274. https://doi.org/10.3390/app12094274
APA StyleOlivieri, C., Cennamo, C., Cusano, C., Cutolo, A., Fortunato, A., & Mascolo, I. (2022). Masonry Spiral Stairs: A Comparison between Analytical and Numerical Approaches. Applied Sciences, 12(9), 4274. https://doi.org/10.3390/app12094274









