Dynamic Analysis of a Wiper Blade in Consideration of Attack Angle and Clarification of the Jumping Phenomenon
Abstract
:1. Introduction
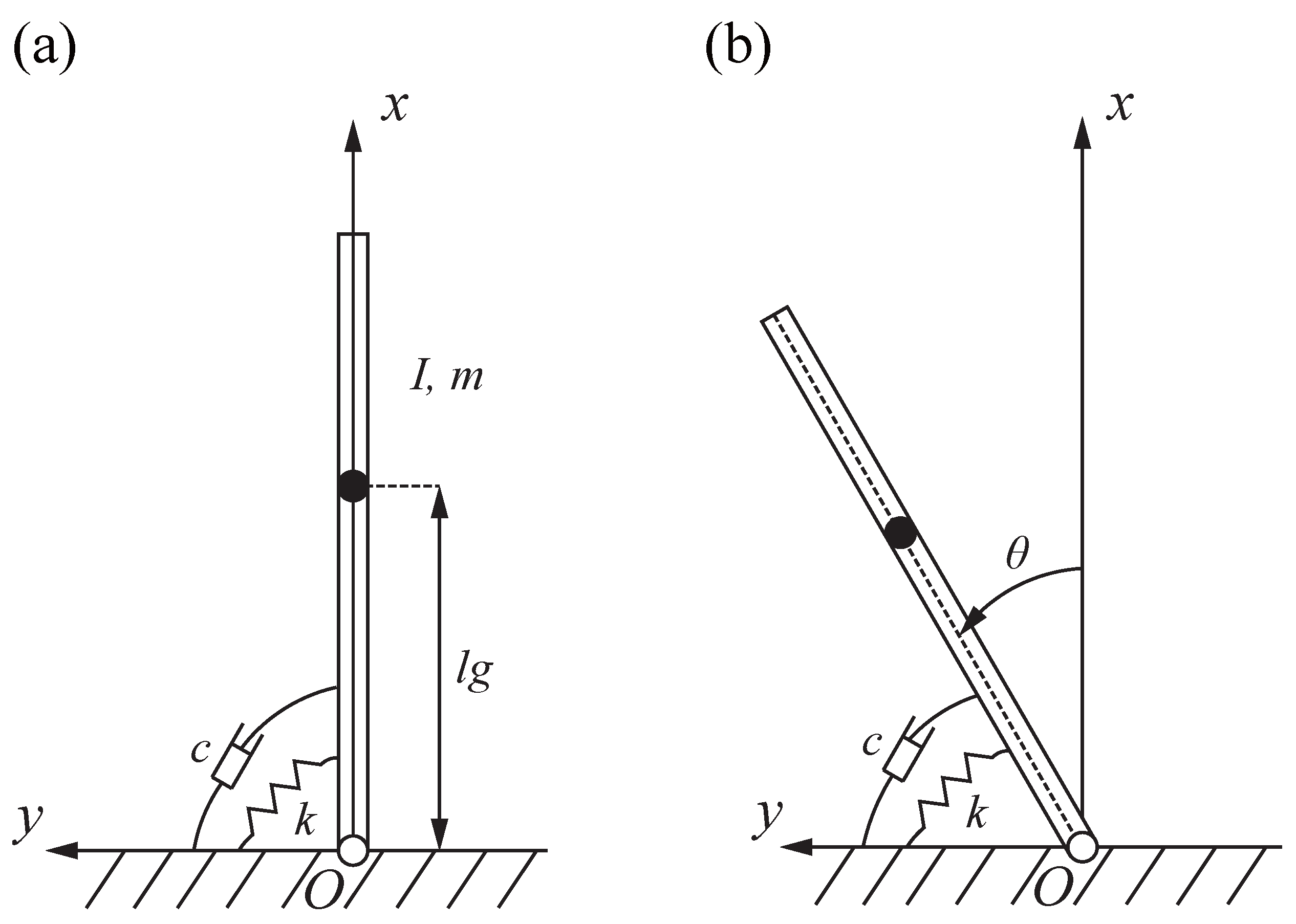
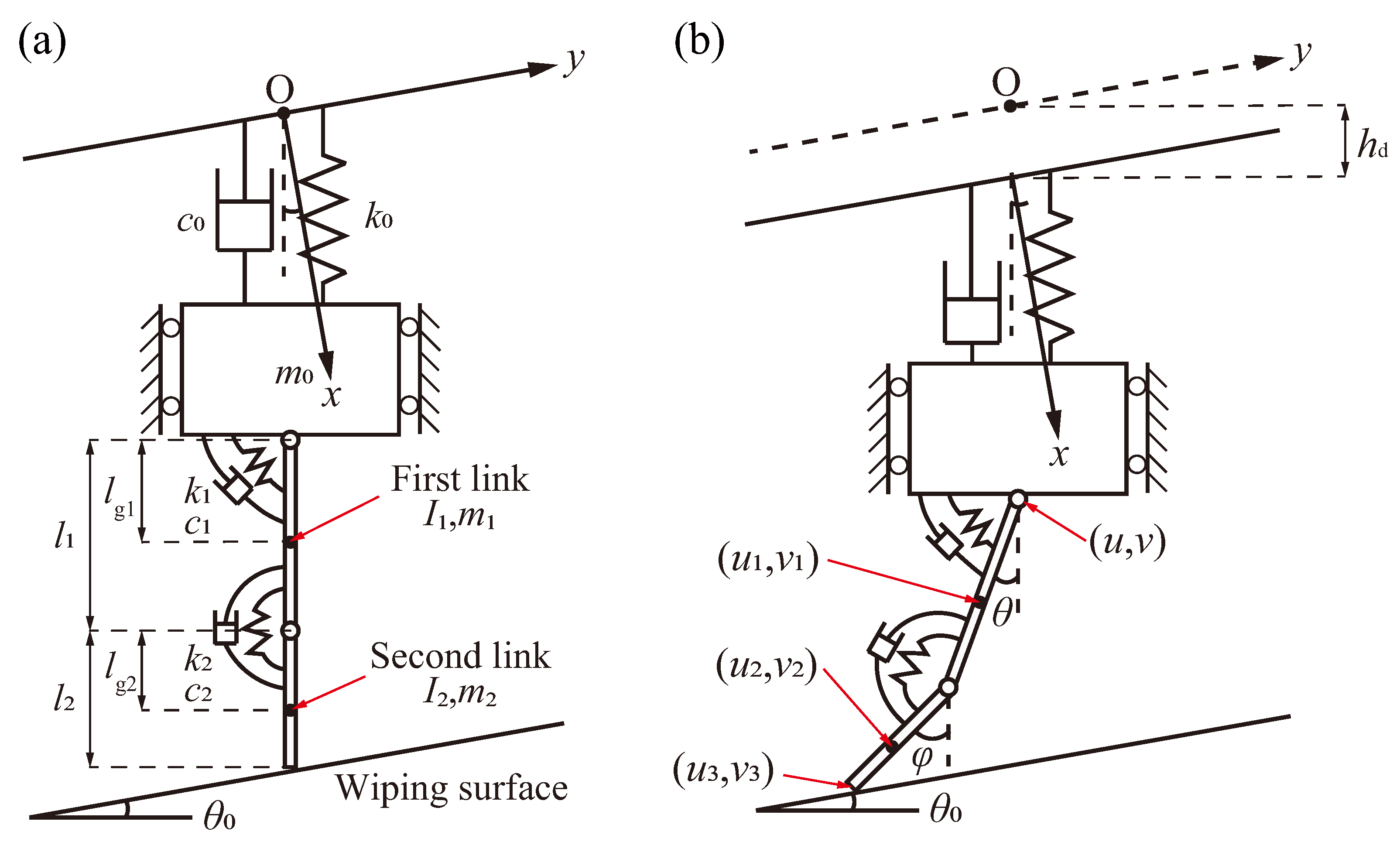
2. Analytical Two-Link Model and Equations of Motion
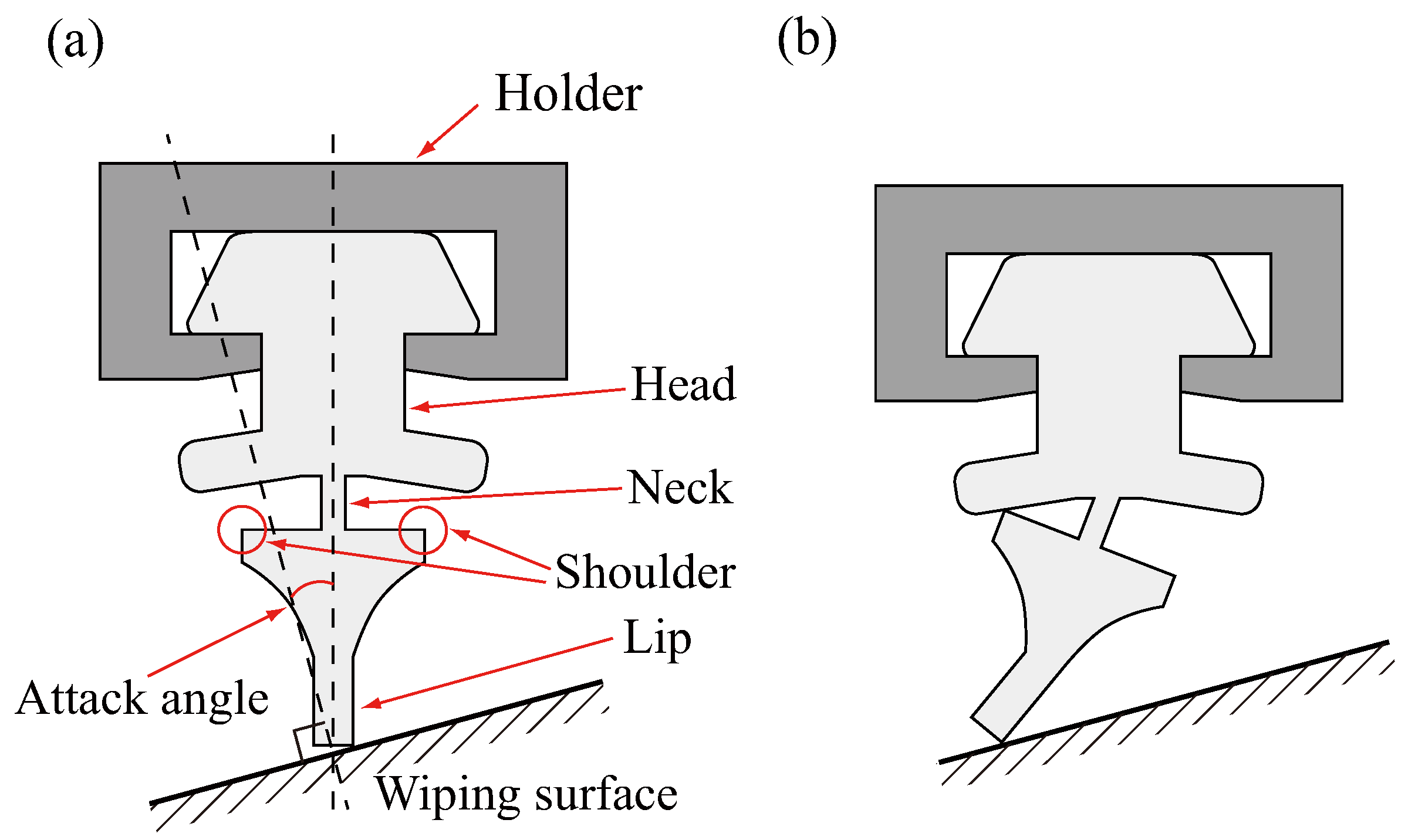
2.1. Analytical Two-Link Model
2.2. Equations of Motion of the Model
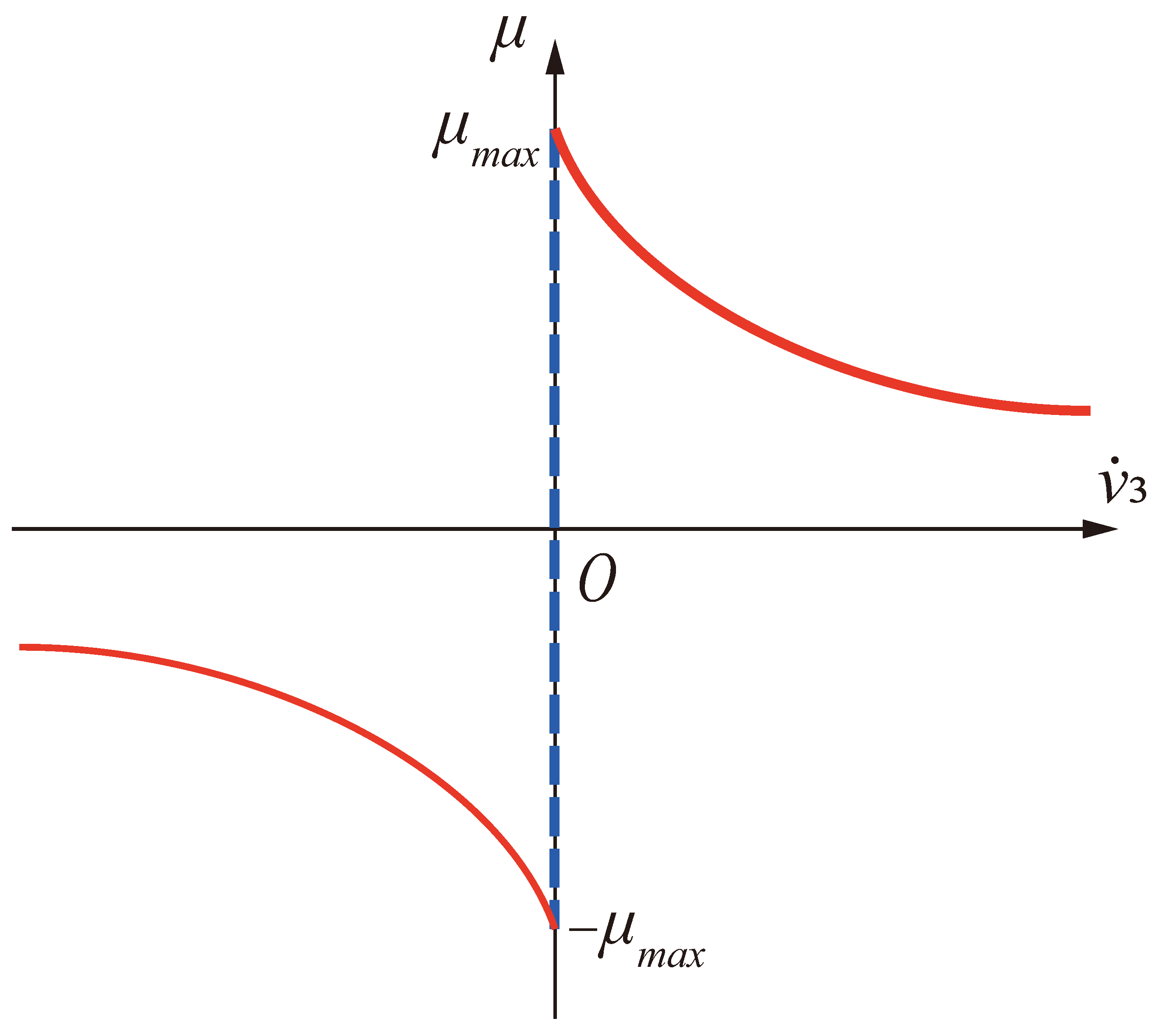
2.3. Friction Models in the Slip and Stick States
3. Numerical Calculation Method in Different States
3.1. Numerical Calculation Method in the Slip State
3.2. Numerical Calculation Method in the Stick State
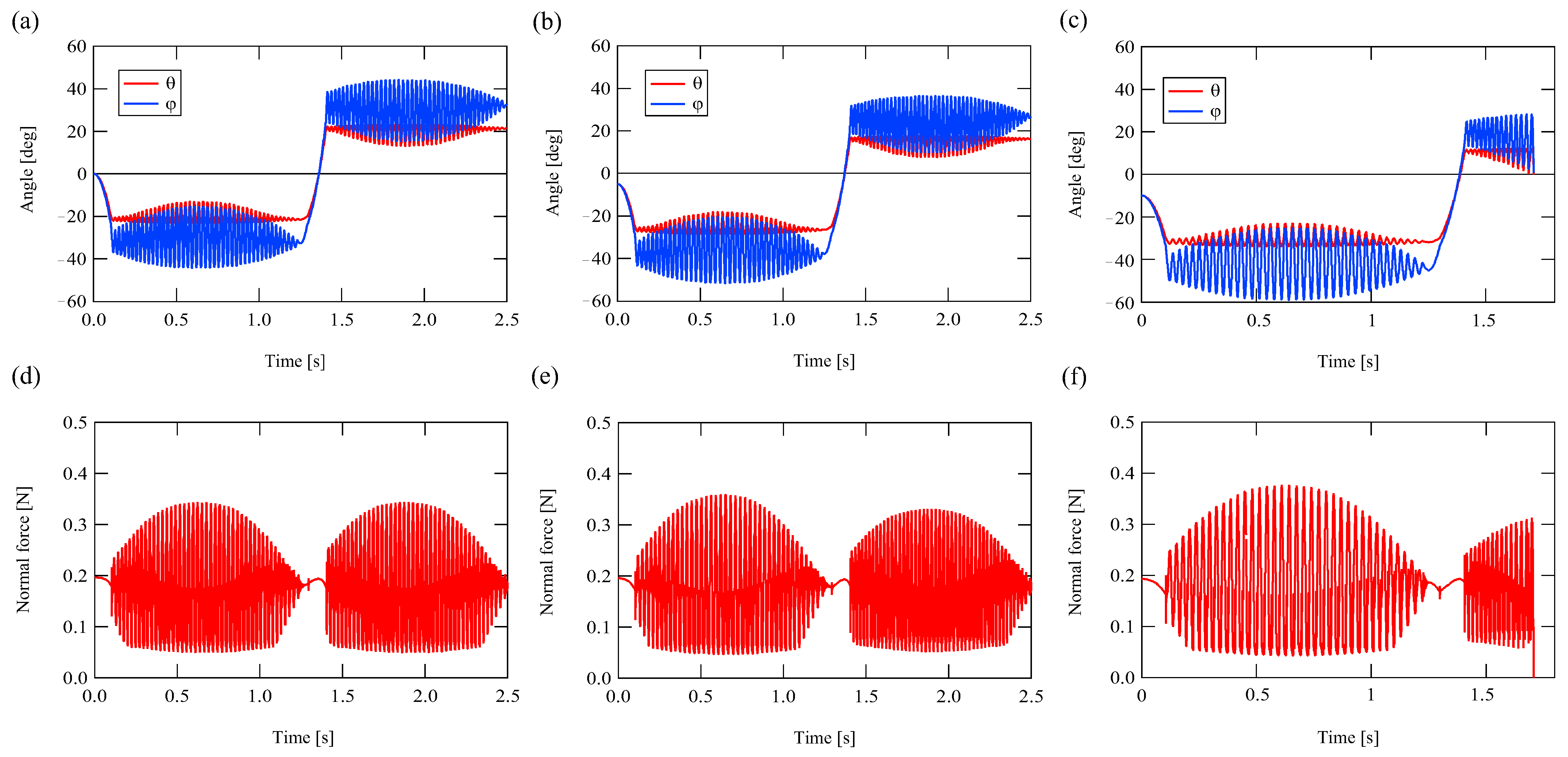
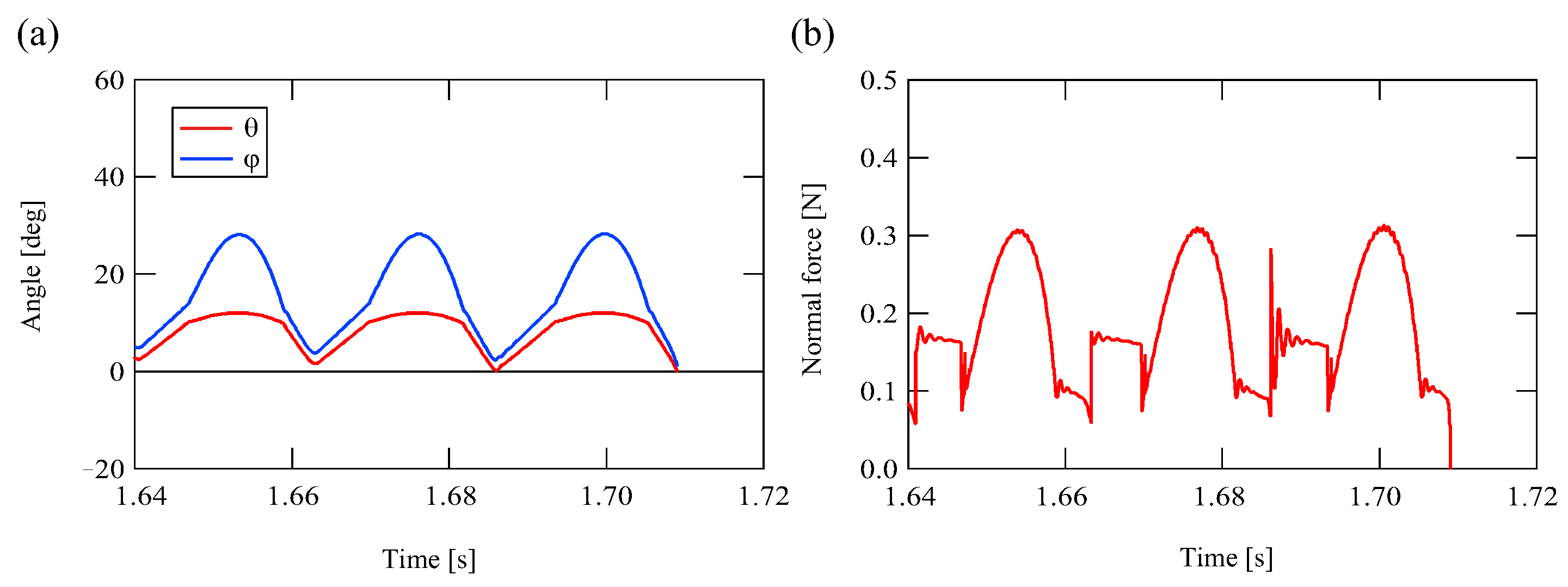
4. Behavior of Wiper Blade
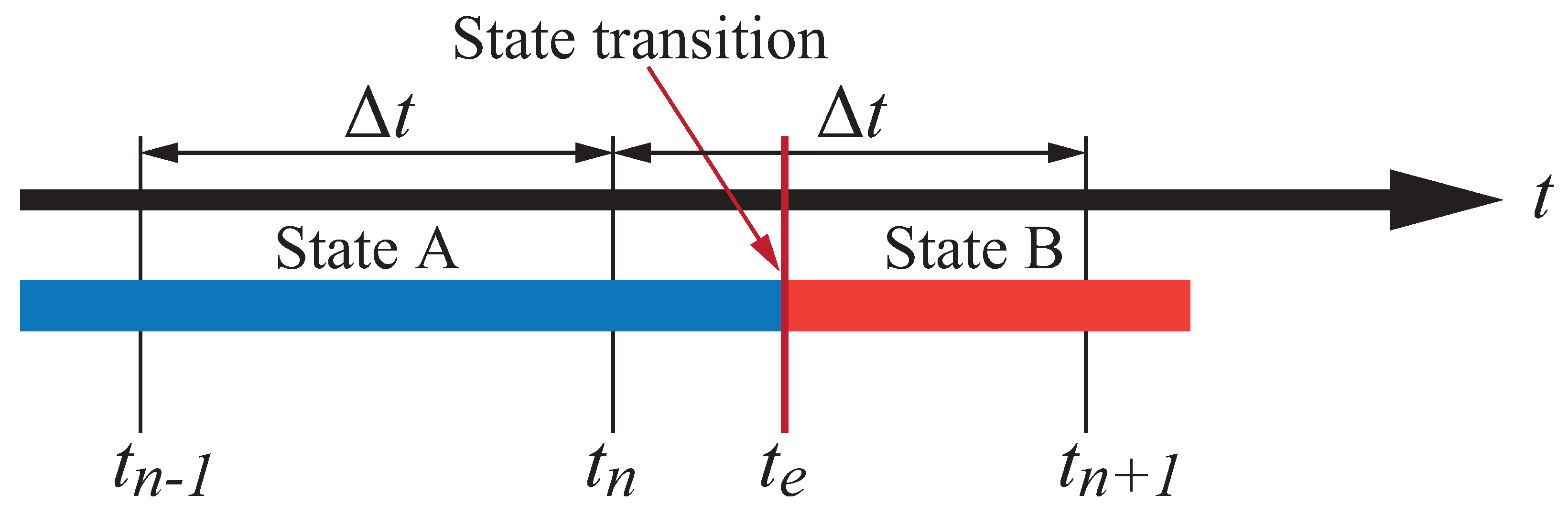
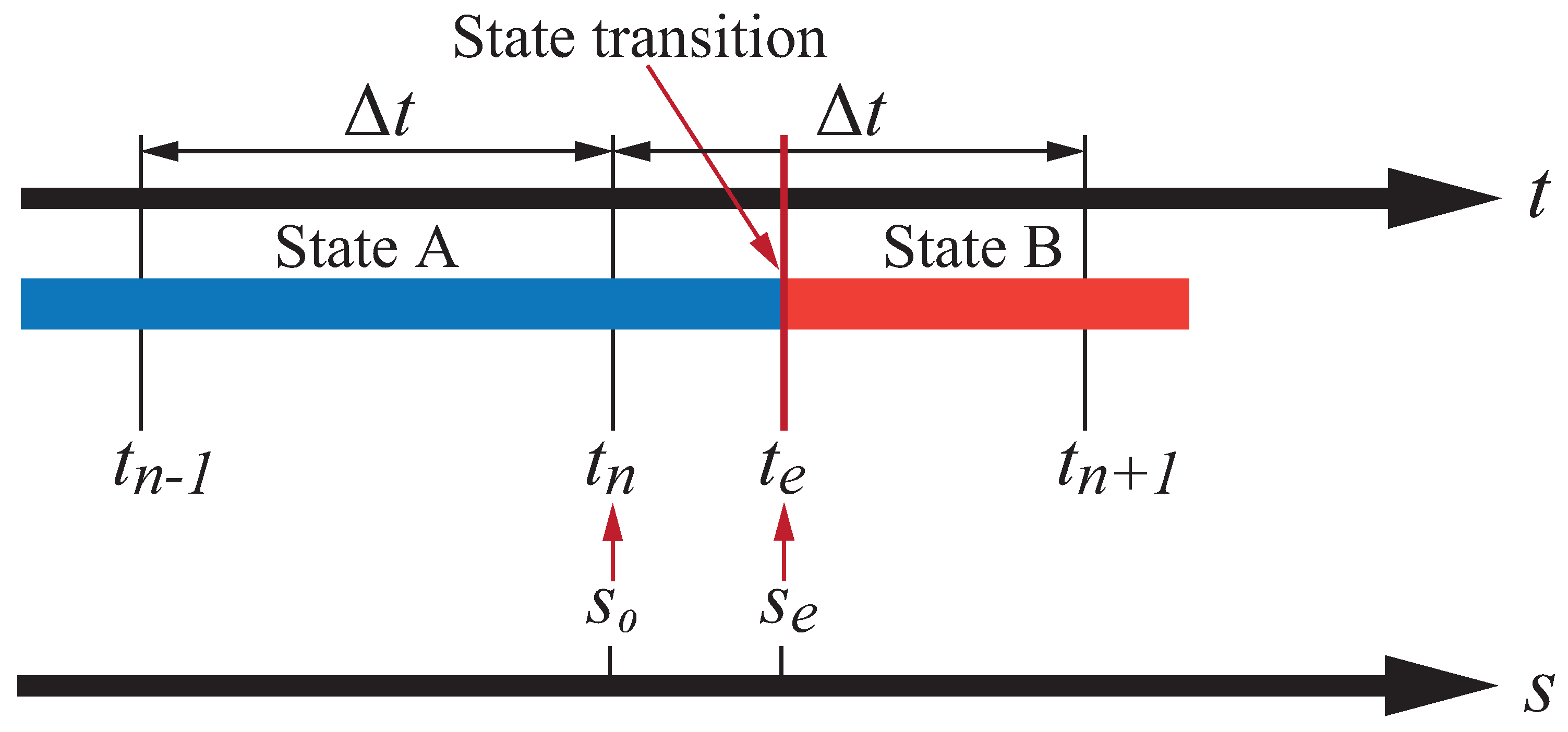
4.1. Employment of the Slack Variable Method to Obtain the Transition Time and State Variables
4.2. Conditions of State Transitions
4.2.1. Transition from Slip to Stick State
4.2.2. Transition from Stick to Slip State
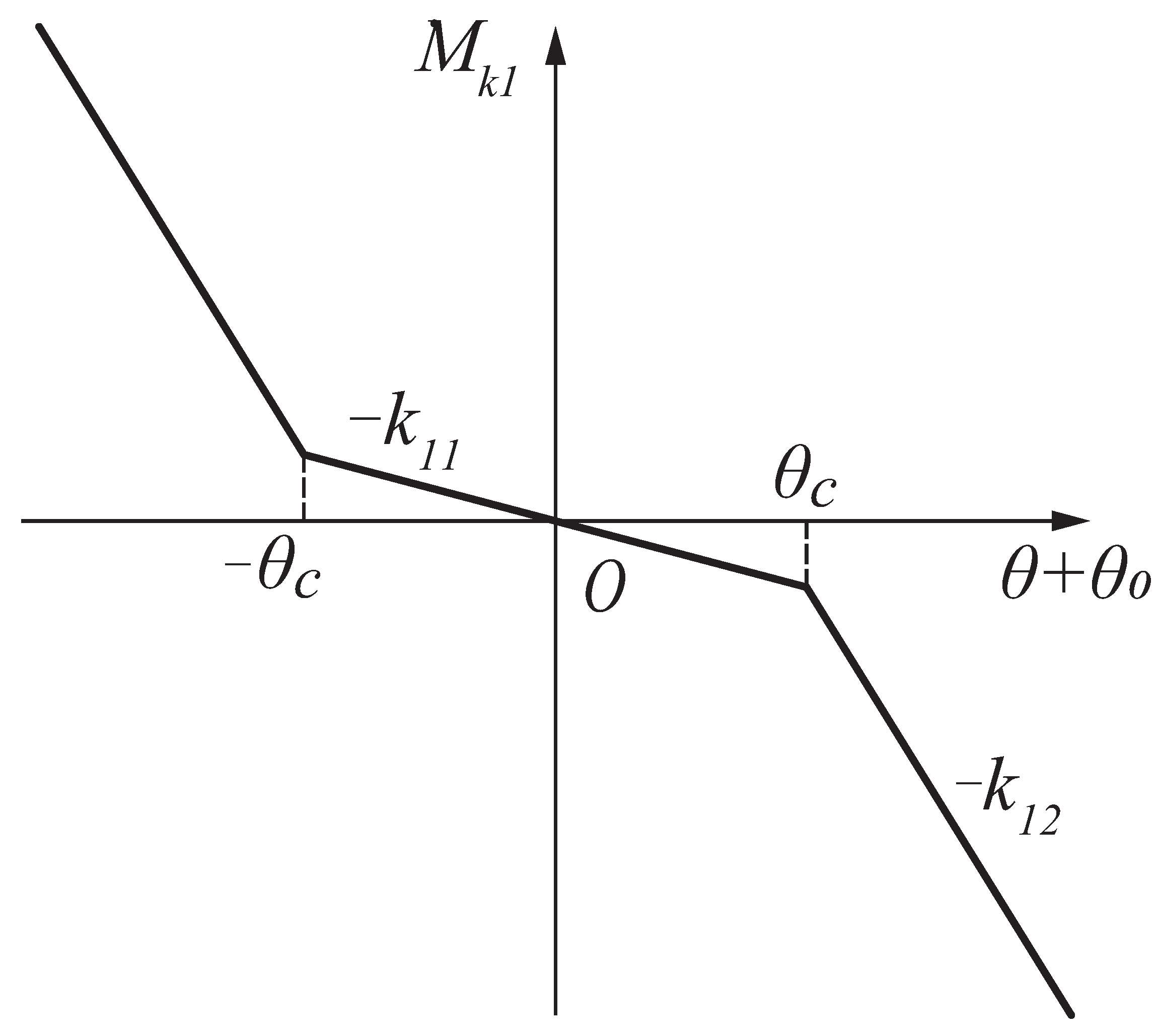
4.2.3. Transition of the Rotational Stiffness
4.3. Numerical Calculation Results
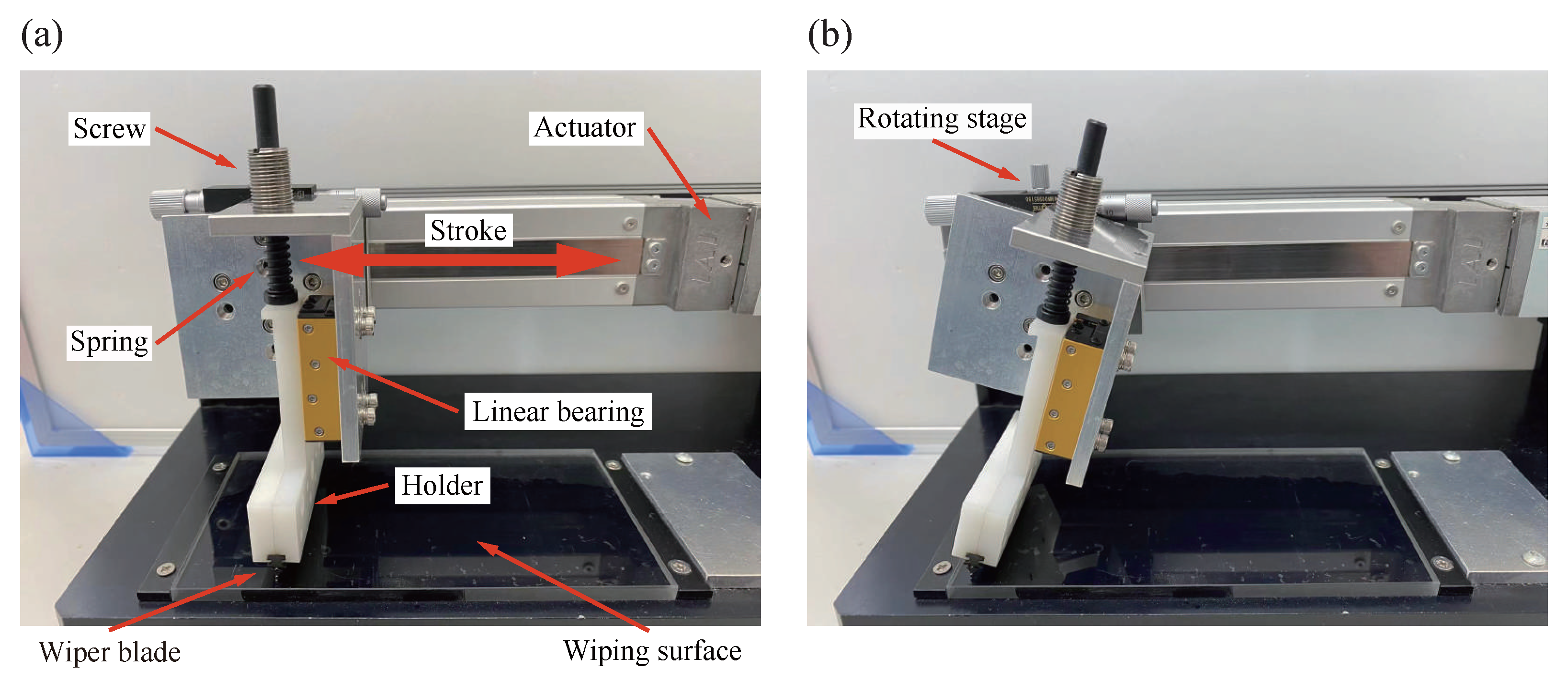
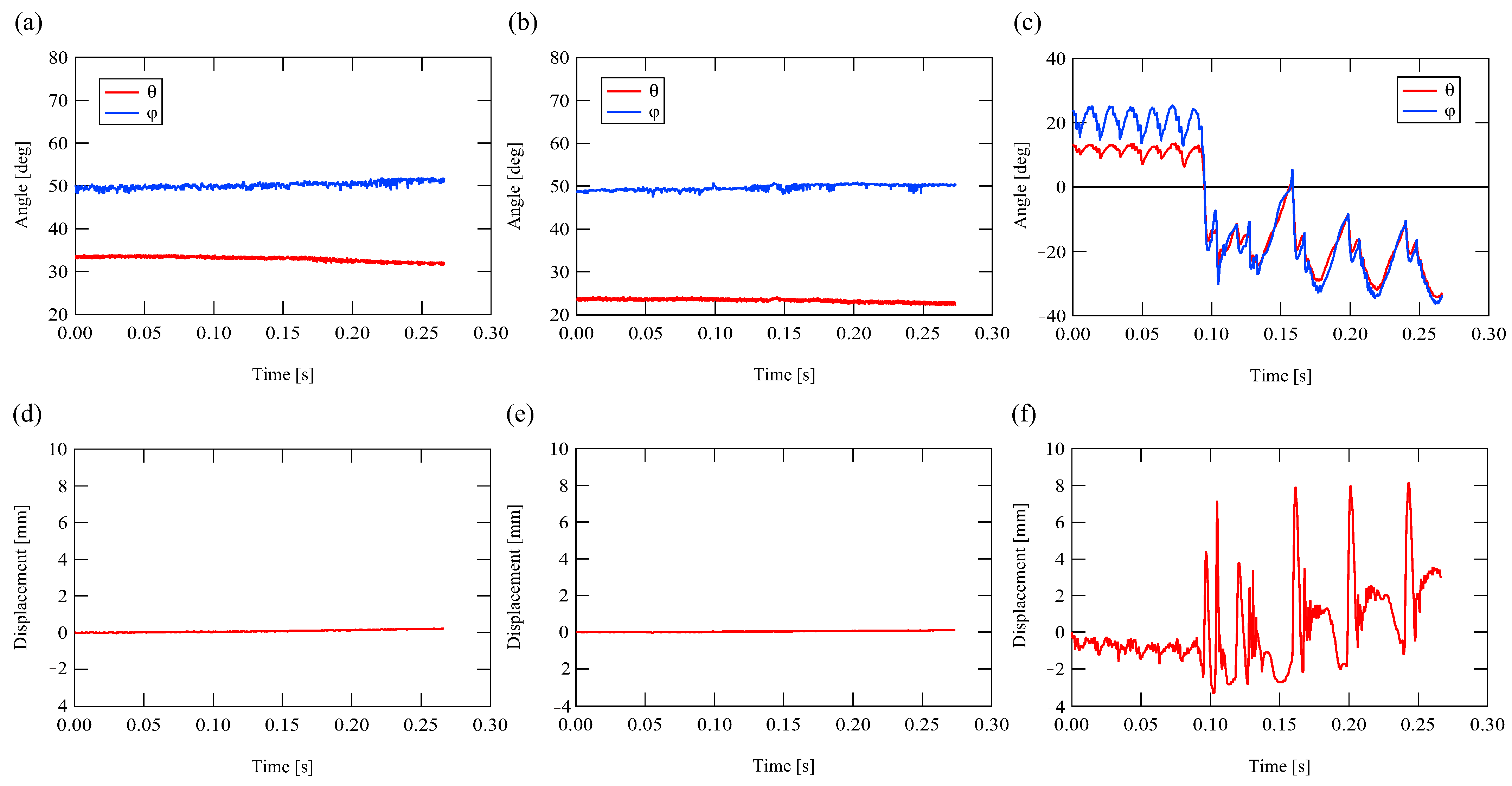
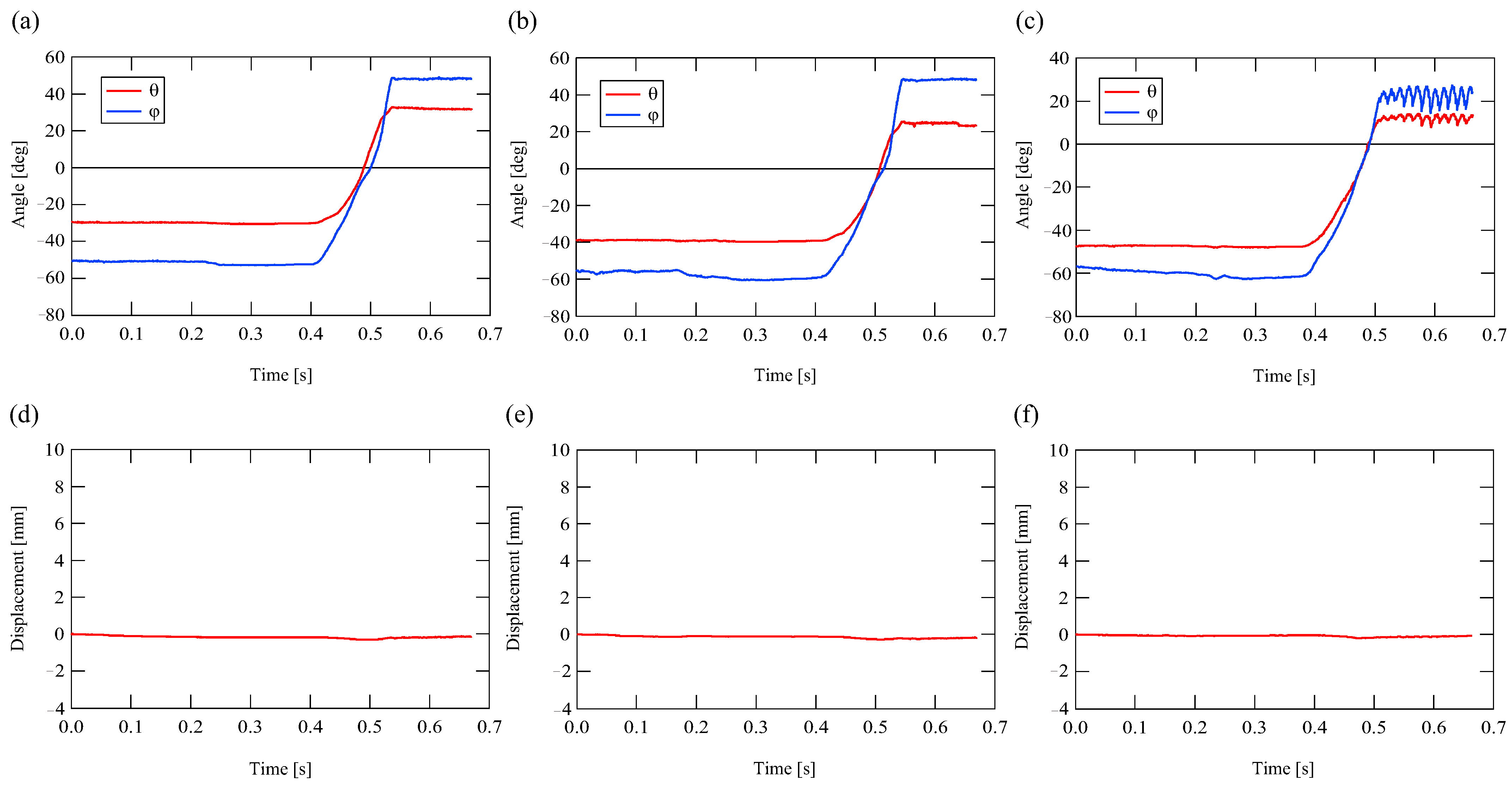
5. Experimental Results
5.1. Experimental Apparatus and Procedure
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| weight of the head | |
| weight of the first link | |
| weight of the second link | |
| moment of inertia of the first link about the center of gravity | |
| moment of inertia of the second link about the center of gravity | |
| original length of the head spring | |
| length of the first link | |
| length of the second link | |
| distance from the top to the center of gravity of the first link | |
| distance from the top to the center of gravity of the second link | |
| spring constant of the head | |
| rotation stiffness of the first link without shoulder contact | |
| rotation stiffness of the first link with shoulder contact | |
| rotation stiffness of the second link | |
| damping of the head | |
| damping of the first link | |
| damping of the second link | |
| a | amplitude of the oscillator |
| frequency of the oscillator | |
| initial compression of the head spring | |
| angle of the first link | |
| angle of the second link | |
| displacement along the y-axis of the tip of the wiper blade | |
| angle of shoulder contact | |
| coefficient of dynamic friction | |
| maximum static friction | |
| y-direction coordinate of the tip after transition from the slip state to the stick state | |
| N | normal force acting on the tip |
| f | friction force acting on the tip |
Appendix A. Process of Deriving the Equations of Motion
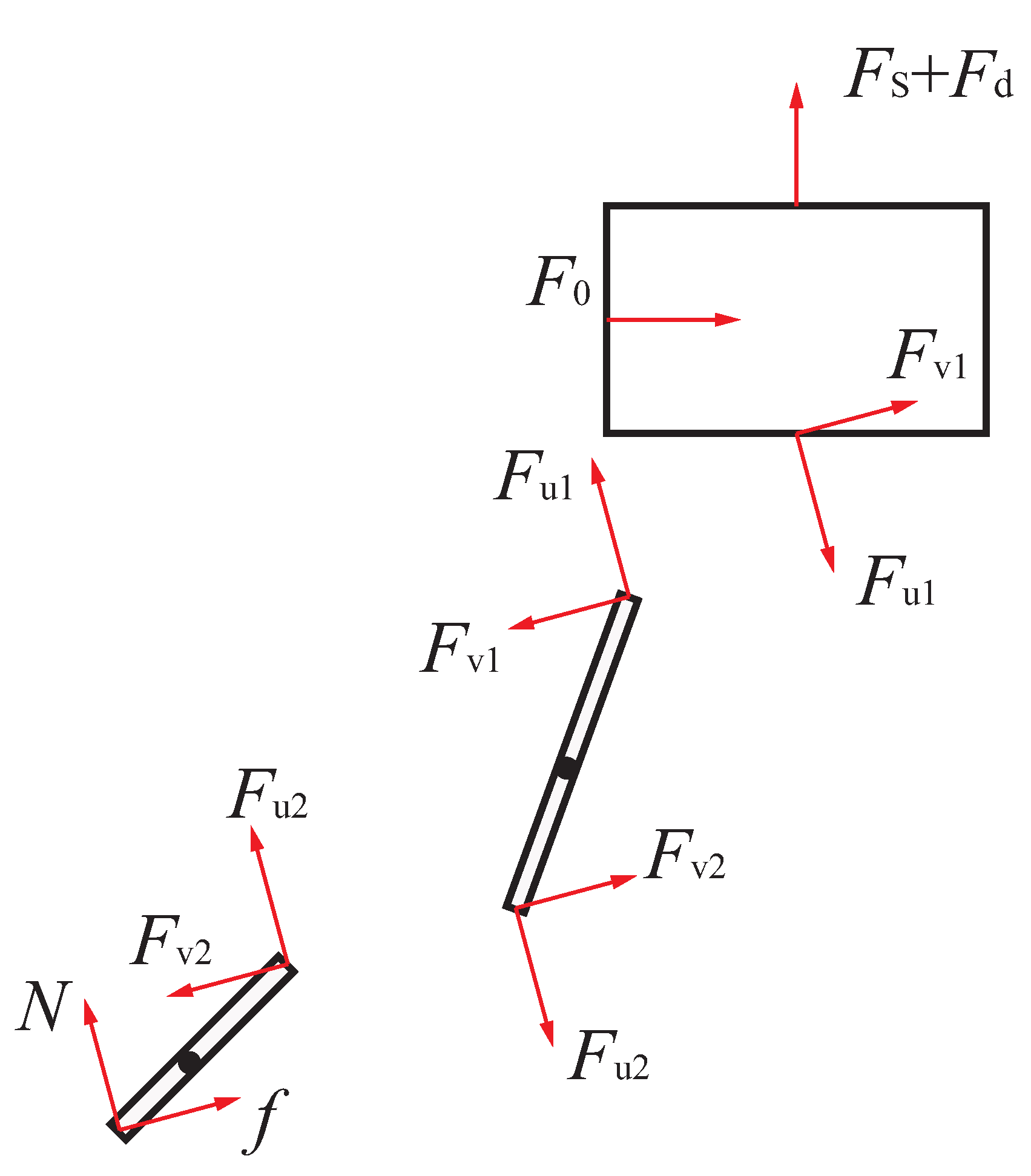
Appendix B. Elements of Matrices B and Q
Appendix C. Experimental Identification of the Parameters Expressing the Stiffness and Damping in the Analytical Model

References
- Grenouillat, R.; Leblanc, C. Simulation of chatter vibrations for wiper systems. SAE Tech. Paper. 2002. [Google Scholar] [CrossRef]
- Awang, I.M.; Abd Ghani, B.; Abd Rahman, R.; Zain, M.Z.M. Complex eigenvalue analysis of windscreen wiper chatter noise and its suppression by structural modifications. Int. J. Veh. Struct. Syst. 2009, 1, 24–29. [Google Scholar] [CrossRef]
- Lancioni, G.; Lenci, S.; Galvanetto, U. Dynamics of windscreen wiper blades: Squeal noise, reversal noise and chattering. Int. J. Non-Linear Mech. 2016, 80, 132–143. [Google Scholar] [CrossRef]
- Okura, S.; Sekiguchi, T.; Oya, T. Dynamic analysis of blade reversal behavior in a windshield wiper system. SAE Trans. 2000, 109, 183–192. [Google Scholar]
- Zolfagharian, A.; Zain, M.M.; AbuBakar, A.R.; Hussein, M. Particle swarm optimization approach on flexible structure at wiper blade system. Proc. World Acad. Sci. Eng. Technol. 2011, 18, 97–102. [Google Scholar]
- Koenen, A.; Sanon, A. Tribological and vibroacoustic behavior of a contact between rubber and glass (application to wiper blade). Tribol. Int. 2007, 40, 1484–1491. [Google Scholar] [CrossRef]
- Leine, R.I.; Nijmeijer, H. Dynamics and Bifurcations of Non-Smooth Mechanical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 18, pp. 39–46. [Google Scholar]
- Nakano, K. Two dimensionless parameters controlling the occurrence of stick-slip motion in a 1-DOF system with Coulomb friction. Tribol. Lett. 2006, 24, 91–98. [Google Scholar] [CrossRef]
- Bódai, G.; Goda, T.J. Friction force measurement at windscreen wiper/glass contact. Tribol. Lett. 2012, 45, 515–523. [Google Scholar] [CrossRef]
- Le Rouzic, J.; Le Bot, A.; Perret-Liaudet, J.; Guibert, M.; Rusanov, A.; Douminge, L.; Bretagnol, F.; Mazuyer, D. Friction-induced vibration by Stribeck’s law: Application to wiper blade squeal noise. Tribol. Lett. 2013, 49, 563–572. [Google Scholar] [CrossRef]
- Reddyhoff, T.; Dobre, O.; Le Rouzic, J.; Gotzen, N.A.; Parton, H.; Dini, D. Friction induced vibration in windscreen wiper contacts. J. Vib. Acoust. 2015, 137, 041009. [Google Scholar] [CrossRef]
- Unno, M.; Shibata, A.; Yabuno, H.; Yanagisawa, D.; Nakano, T. Analysis of the behavior of a wiper blade around the reversal in consideration of dynamic and static friction. J. Sound Vib. 2017, 393, 76–91. [Google Scholar] [CrossRef]
- Deleau, F.; Mazuyer, D.; Koenen, A. Sliding friction at elastomer/glass contact: Influence of the wetting conditions and instability analysis. Tribol. Int. 2009, 42, 149–159. [Google Scholar] [CrossRef]
- Bódai, G.; Goda, T.J. Sliding friction of wiper blade: Measurement, FE modeling and mixed friction simulation. Tribol. Int. 2014, 70, 63–74. [Google Scholar] [CrossRef]
- Chevennement-Roux, C.; Dreher, T.; Alliot, P.; Aubry, E.; Lainé, J.P.; Jézéquel, L. Flexible wiper system dynamic instabilities: Modelling and experimental validation. Exp. Mech. 2007, 47, 201–210. [Google Scholar] [CrossRef]
- Min, D.; Jeong, S.; Yoo, H.H.; Kang, H.; Park, J. Experimental investigation of vehicle wiper blade’s squeal noise generation due to windscreen waviness. Tribol. Int. 2014, 80, 191–197. [Google Scholar] [CrossRef]
- Mohamad, S.M.; Othman, N.; Sharif, I.; Zain, M.M.; Bakar, A.A. Dynamic behaviour and characteristics of rubber blade car performance. Int. J. Automot. Mech. Eng. 2019, 16, 6437–6452. [Google Scholar] [CrossRef]
- Lee, C.E.; Kim, H.K. Analysis of the Cross-Sectional Shape and Wiping Angle of a Wiper Blade. SAE Int. J. Mater. Manuf. 2020, 13, 183–194. [Google Scholar] [CrossRef]
- Chen, T.J.; Hong, Y.J. Geometric Analysis of the Vibration of Rubber Wiper Blade. Taiwan. J. Math. 2021, 25, 491–516. [Google Scholar] [CrossRef]
- Baumgarte, J. Stabilization of constraints and integrals of motion in dynamical systems. Comput. Methods Appl. Mech. Eng. 1972, 1, 1–16. [Google Scholar] [CrossRef]
- Turner, J.D. On the simulation of discontinuous functions. J. Appl. Mech. 2001, 68, 751–757. [Google Scholar] [CrossRef]


| Parameter | Value | Units |
|---|---|---|
| a | ||
| 2 × | ||
| A | ||
| B | 5 | |
| E | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Yabuno, H.; Kamiyama, K. Dynamic Analysis of a Wiper Blade in Consideration of Attack Angle and Clarification of the Jumping Phenomenon. Appl. Sci. 2022, 12, 4112. https://doi.org/10.3390/app12094112
Zhao Z, Yabuno H, Kamiyama K. Dynamic Analysis of a Wiper Blade in Consideration of Attack Angle and Clarification of the Jumping Phenomenon. Applied Sciences. 2022; 12(9):4112. https://doi.org/10.3390/app12094112
Chicago/Turabian StyleZhao, Zihan, Hiroshi Yabuno, and Katsuya Kamiyama. 2022. "Dynamic Analysis of a Wiper Blade in Consideration of Attack Angle and Clarification of the Jumping Phenomenon" Applied Sciences 12, no. 9: 4112. https://doi.org/10.3390/app12094112
APA StyleZhao, Z., Yabuno, H., & Kamiyama, K. (2022). Dynamic Analysis of a Wiper Blade in Consideration of Attack Angle and Clarification of the Jumping Phenomenon. Applied Sciences, 12(9), 4112. https://doi.org/10.3390/app12094112






