Numerical Study of Partial Dam–Break Flow with Arbitrary Dam Gate Location Using VOF Method
Abstract
:1. Introduction
2. Numerical Model
3. Results and Discussions
3.1. Mesh Sensitivity and Comparison 2D and 3D Numerical Solutions
3.2. Effect of Initial Water Stage, Breach Size and Position of Dam Gate on Hydraulic Characteristics
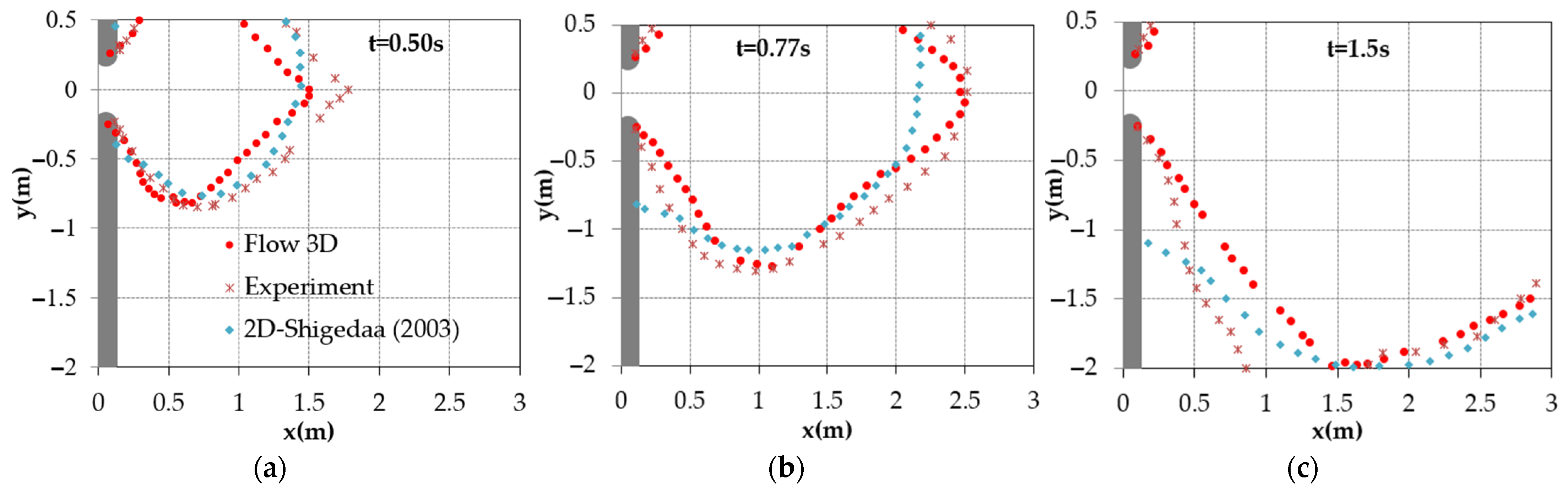
3.2.1. Dynamics and Structure of Dam–Break Wave Inside Reservoir
3.2.2. Peak Discharge of Outflow Hydrograph
4. Conclusions
- -
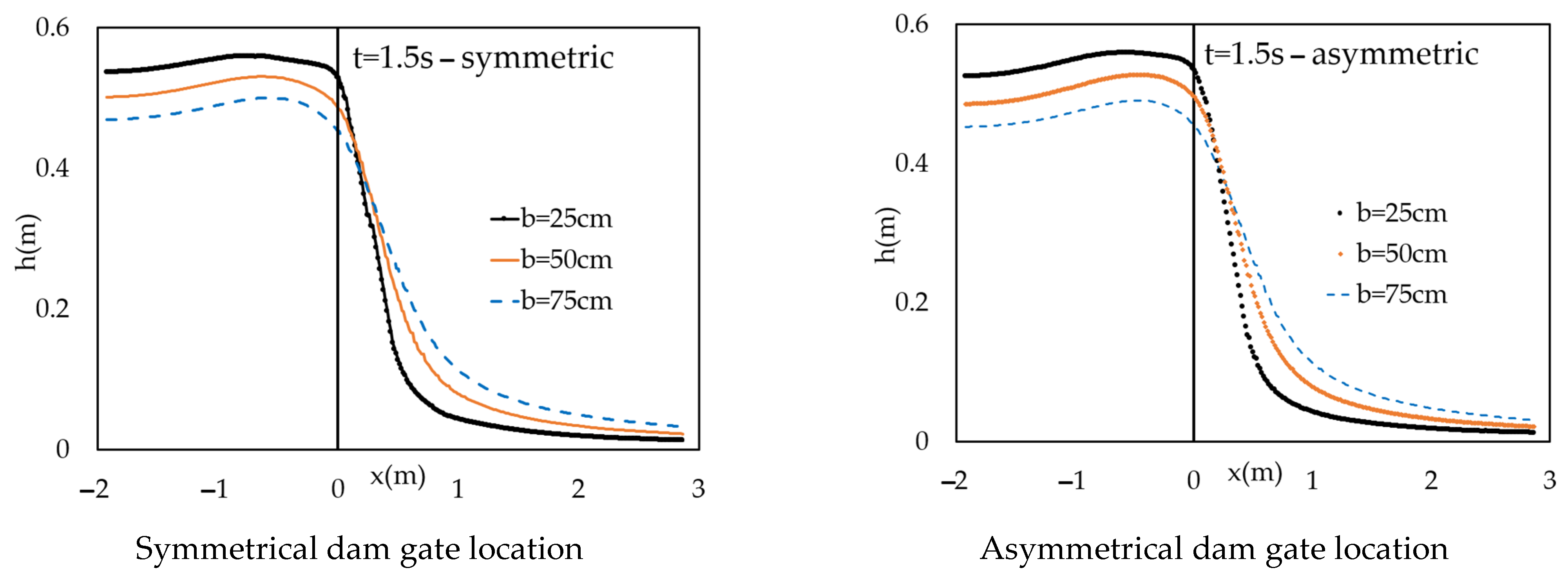
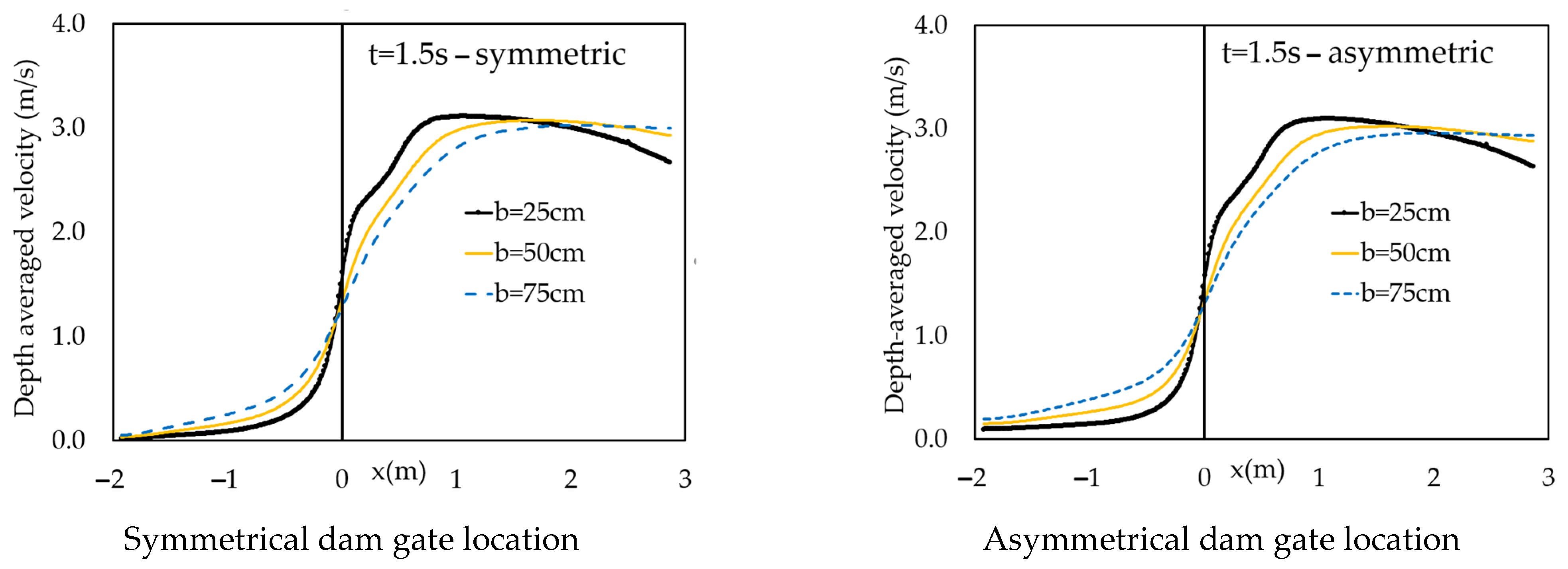
- Increasing breach size causes reducing water depth profile at the central line of the dam gate on a reservoir. The opposite trend is observed in depth–average velocity hydrographs.
- -
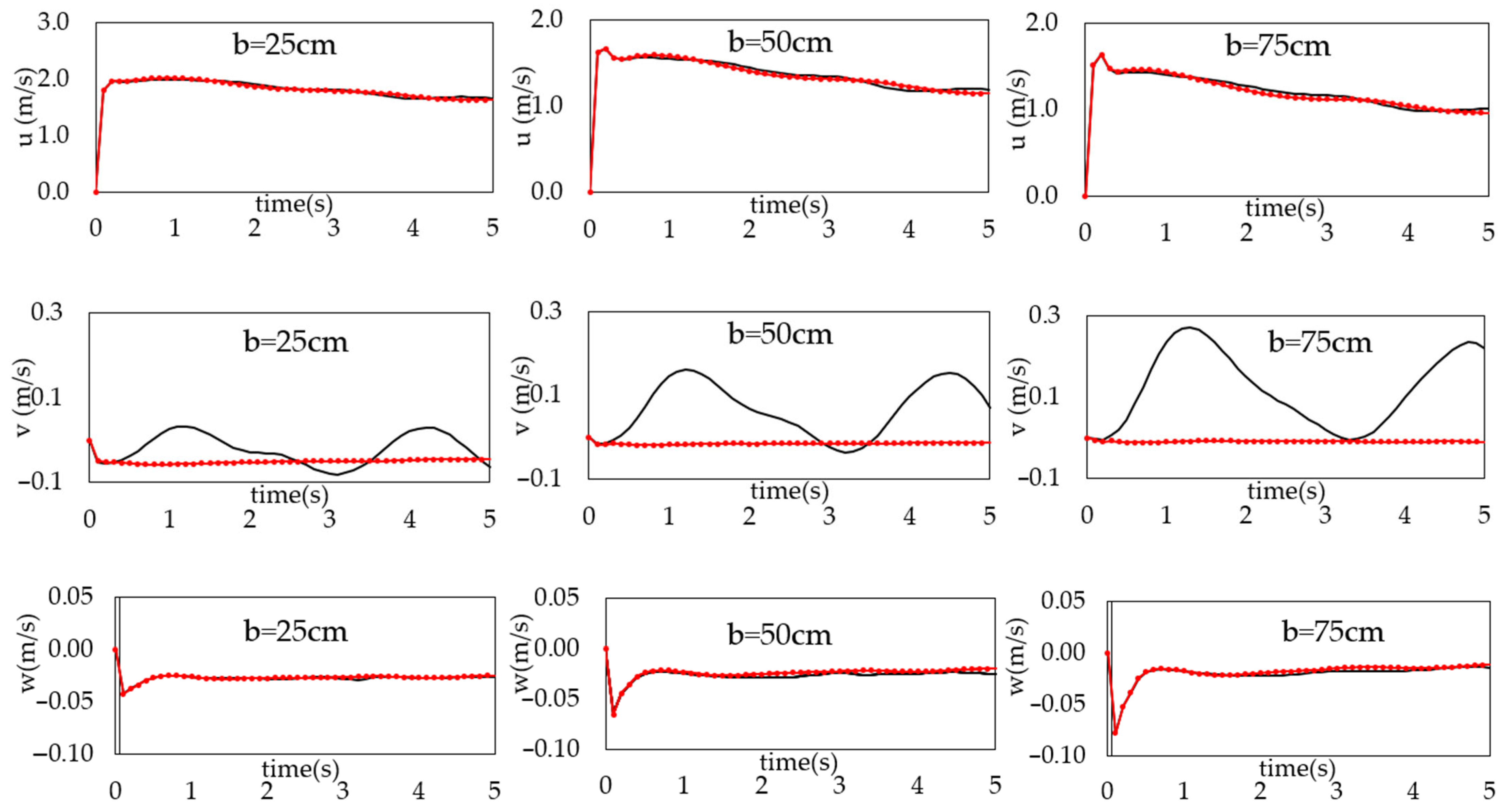
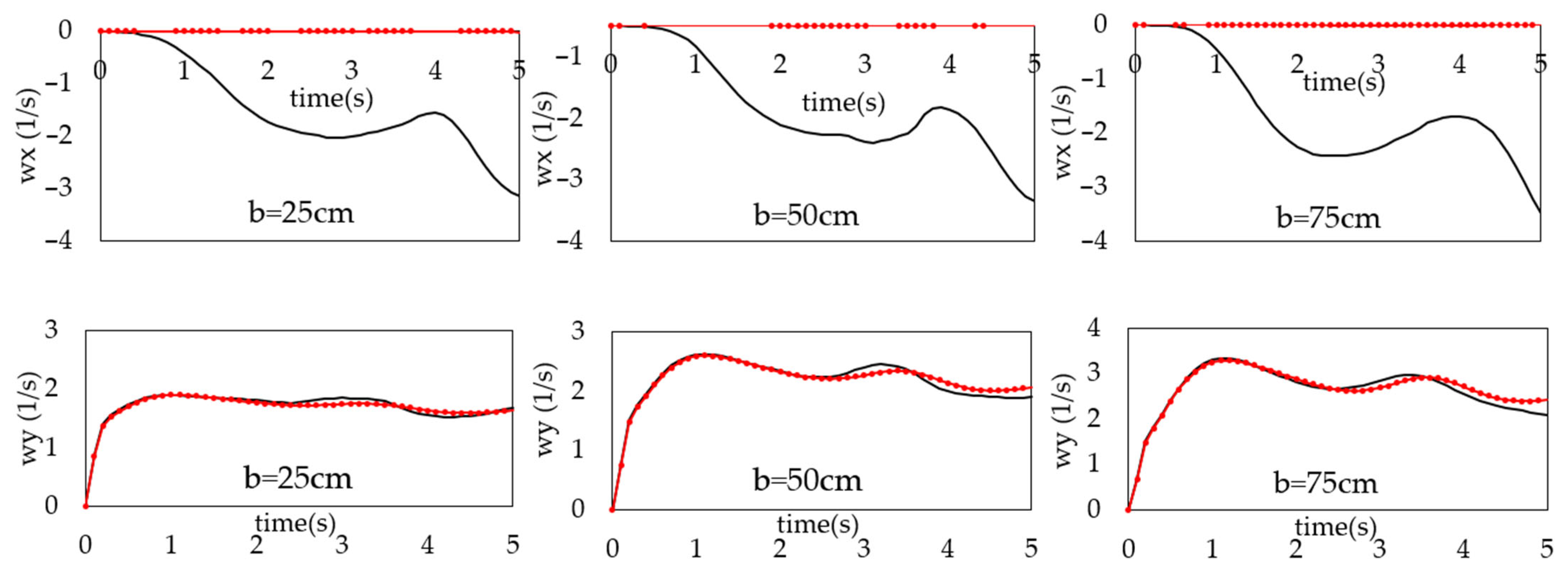
- Velocity and vorticity components in x and z directions are independent of the position of dam gate. In contrast, components v and wy in the y axis vanished when the reservoir outlet was at the central line of the dam.
- -
- Streamline patterns exhibit the movement of fluid particles at certain times. In early stage, not all fluid elements move to the reservoir mouth when breach size is small.
- -
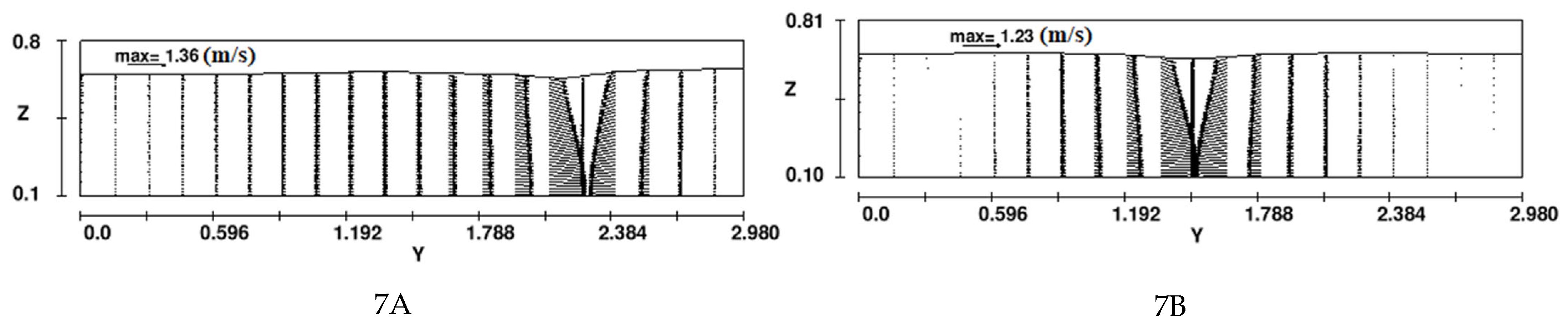
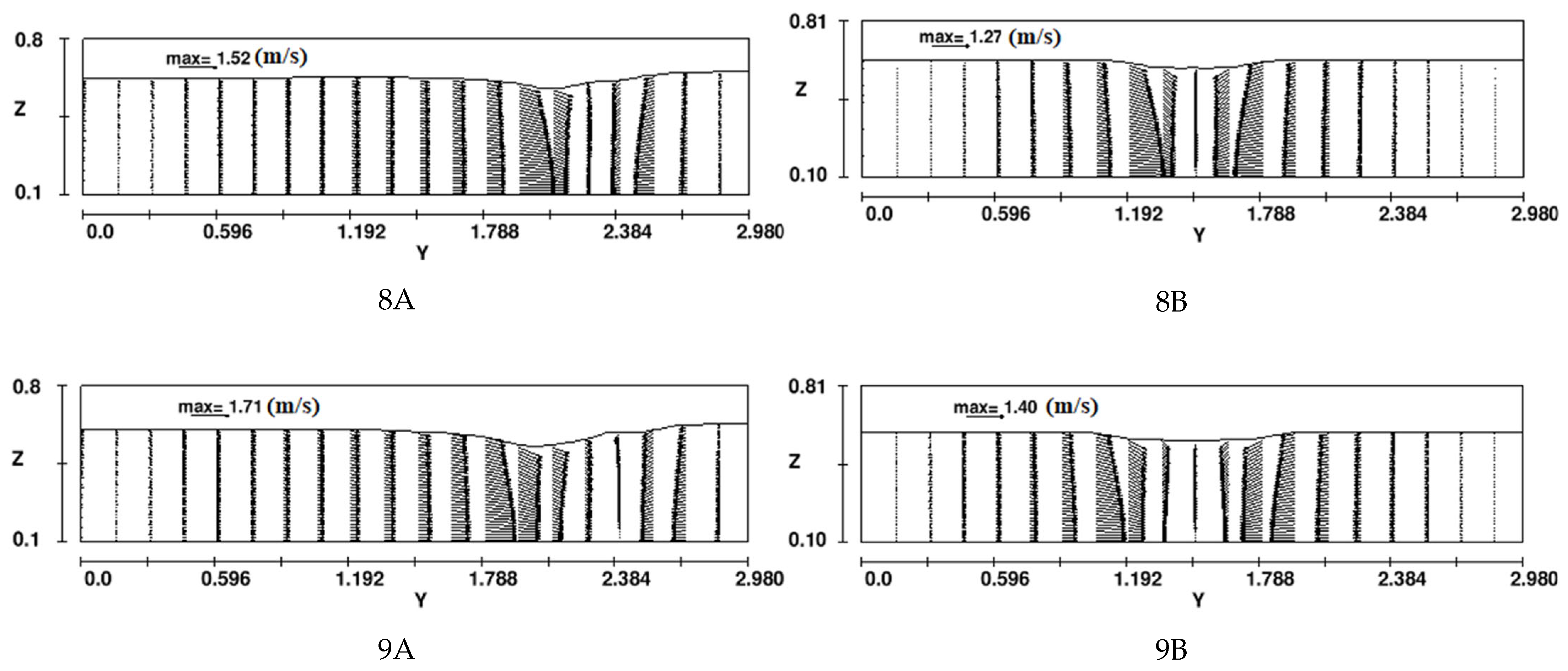
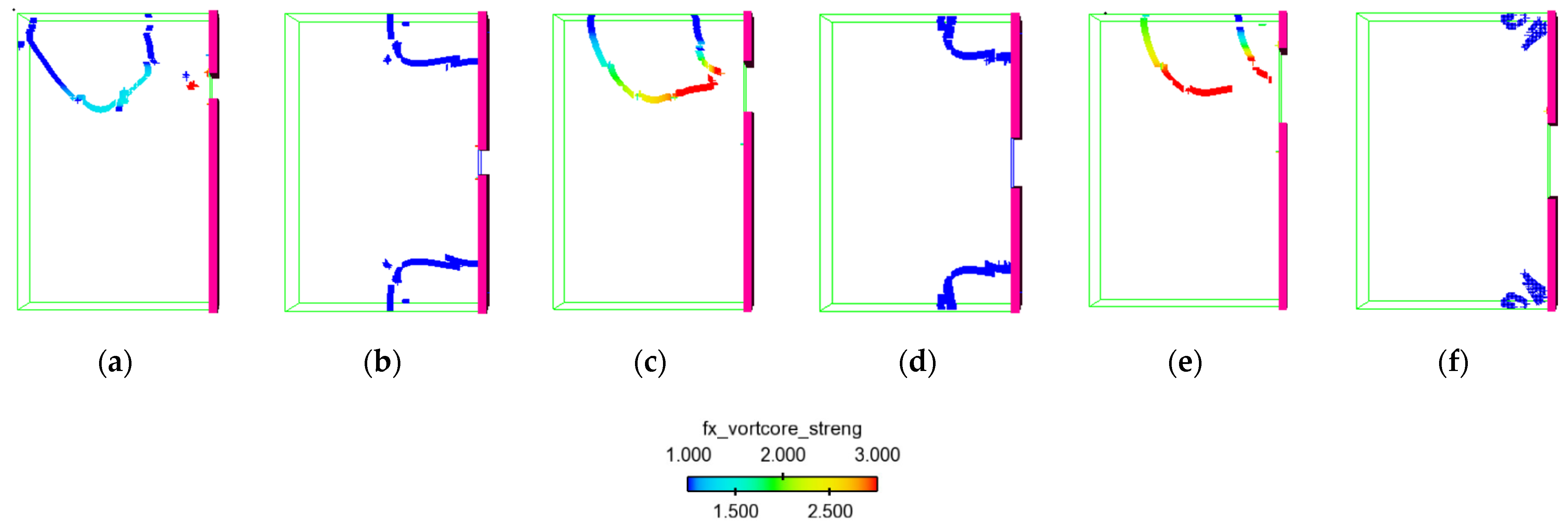
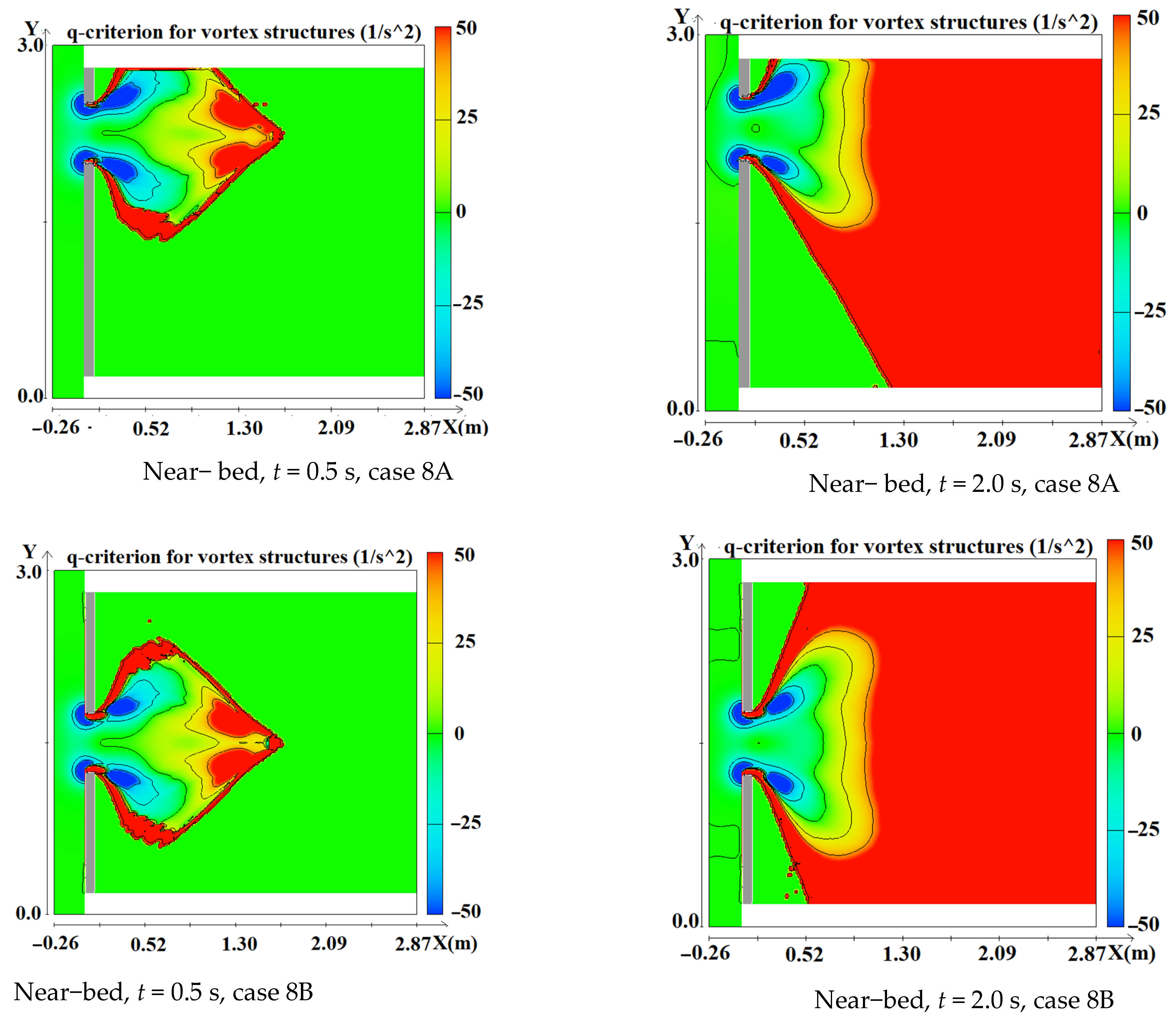
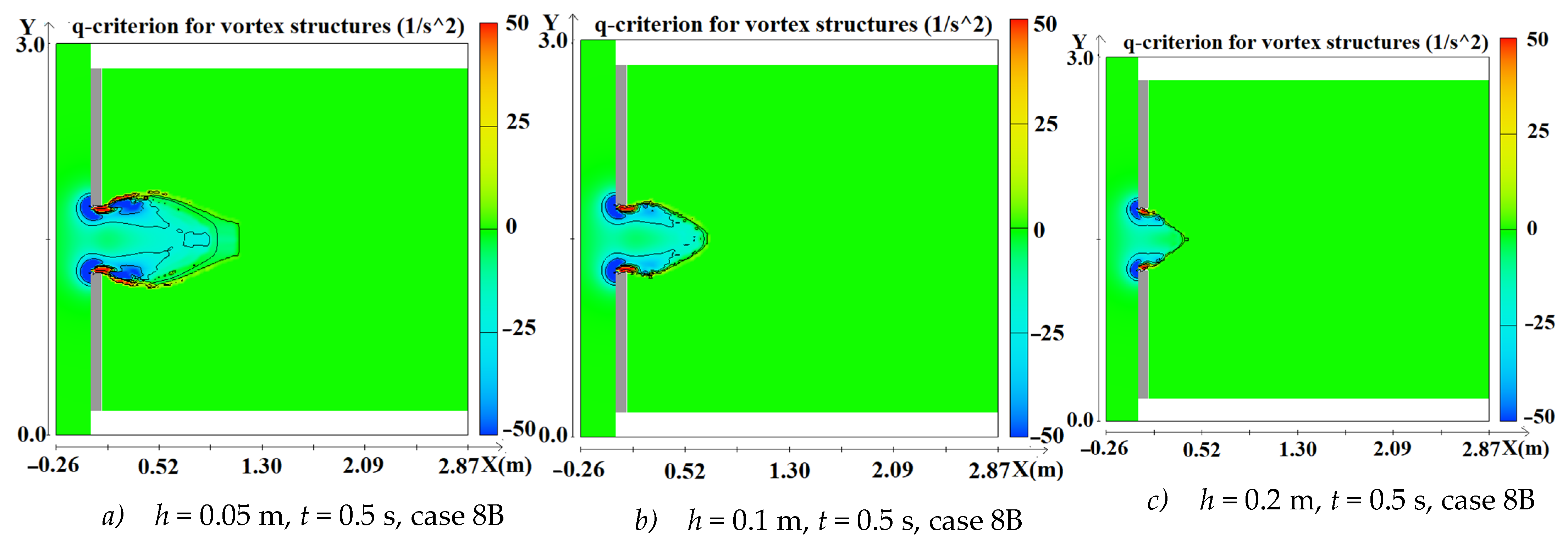
- Some sophisticated hydraulic factors indicating swirling flow are involved in the time series of q–criterion and vortex core mapping. In the case of symmetrical reservoir outlet, breach width increases, vortex core area at both corners near the dam site decreases, which means vorticity is weak. In contrast, stronger swirling flow appeared near the top right corner of the reservoir when a broken block is asymmetrically placed.
- -
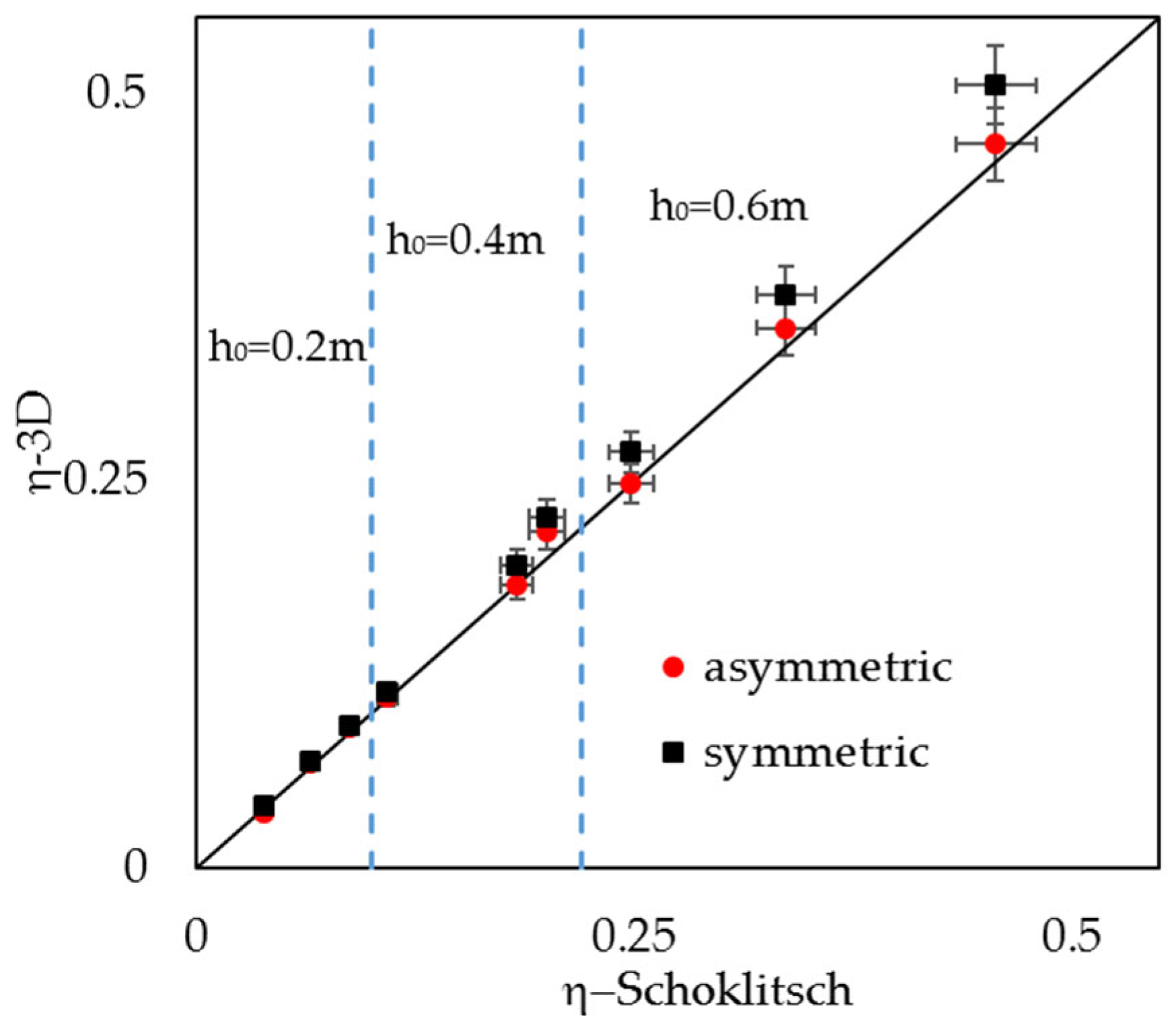
- Normal peak discharge does not only depend on initial water stage, and dam breach ratio. It is also influenced by location of dam gate. The reservoir’s initial water stage is greater, and maximum flow rate released by symmetrical breach location is more notable, than those released by the asymmetrical case.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fraccarollo, L.; Toro, E.F. Experimental and numerical assessment of the shallow water model for two–dimensional dam–break type problems. J. Hydraul. Res. 1995, 33, 843–864. [Google Scholar] [CrossRef]
- Aureli, F.; Mignosa, P.; Tomirotti, M. Numerical simulation and experimental verification of Dam–Break flows with shocks. J. Hydraul. Res. 2000, 38, 197–206. [Google Scholar] [CrossRef]
- Proust, S.; Berni, C.; Boudou, M.; Chiaverini, A.; Dupuis, V.; André, J.-B.F.; Paquier, M.L.; Guillen–Ludena, S.; Lopez, D. Predicting the flow in the floodplains with evolving land occupations during extreme flood events (FlowRes ANR project). E3S Web Conf. 2016, 7, 04004. [Google Scholar] [CrossRef] [Green Version]
- Aureli, F.; Maranzoni, A.; Mignosa, P.; Ziveri, C. Dam–Break Flows: Acquisition of Experimental Data through an Imaging Technique and 2D Numerical Modeling. J. Hydraul. Eng. 2008, 134, 1089–1101. [Google Scholar] [CrossRef]
- Aureli, F.; Maranzoni, A.; Mignosa, P.; Ziveri, C. An image processing technique for measuring free surface of dam–break flows. Exp. Fluids 2010, 50, 665–675. [Google Scholar] [CrossRef]
- Aureli, F.; Maranzoni, A.; Mignosa, P. A semi–analytical method for predicting the outflow hydrograph due to dam–break in natural valleys. Adv. Water Resour. 2014, 63, 38–44. [Google Scholar] [CrossRef]
- Soares–Frazão, S.; Zech, Y. Experimental study of dam–break flow against an isolated obstacle. J. Hydraul. Res. 2007, 45, 27–36. [Google Scholar] [CrossRef]
- Soares–Frazão, S.; Zech, Y. Dam–break flow through an idealised city. J. Hydraul. Res. 2008, 46, 648–658. [Google Scholar] [CrossRef] [Green Version]
- Lobovský, L.; Botia–Vera, E.; Castellana, F.; Mas–Soler, J.; Souto–Iglesias, A. Experimental investigation of dynamic pressure loads during dam–break. J. Fluids Struct. 2014, 48, 407–434. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Liu, H. An experimental study of the maximum run–up height under dambreak flow on the initial dry–bed. J. Ocean Univ. China 2017, 16, 697–702. [Google Scholar] [CrossRef]
- Schoklitsch, A. On waves created by dam breaches (in German). Sitz. Der Kais. Akad. Der Wiss. Wien 1917, 126, 1489–1514. [Google Scholar]
- Waterway Experiment Station (WES). Floods resulting from suddenly breached dams. Misc paper no 2–374. Rep 1: Conditions of minimum resistance. Rep. prepared for U.S. Army Corps of Engineers, Vicksburg, MS, USA, 1960. [Google Scholar]
- Zhang, X.; Pirker, S.; Saeedipour, M. Numerical investigation of particle motion at the steel—slag interface in continuous casting using VOF method and dynamic overset grids. Exp. Comput. Multiph. Flow 2022, 1–14. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Xiao, J.; Jordan, T. Large eddy simulation of turbulent flow using the parallel computational fluid dynamics code GASFLOW–MPI. Nucl. Eng. Technol. 2017, 49, 1310–1317. [Google Scholar] [CrossRef]
- Yu, S.; Lim, J.; Cho, I.; Han, J. Inerting Strategy for a Demonstration–Scale Hot Cell Facility Based on Experiences from Pilot–Scale Argon Cell Facility Operation and CFD Analysis. Sci. Technol. Nucl. Install. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Shige–eda, M.; Akiyama, J. Numerical and Experimental Study on Two–Dimensional Flood Flows with and without Structures. J. Hydraul. Eng. 2003, 129, 817–821. [Google Scholar] [CrossRef]
- Khankandi, F.A.; Tahershamsi, A.; Soares–Frazão, S. Experimental investigation of reservoir geometry effect on dam–break flow. J. Hydraul. Res. 2012, 50, 376–387. [Google Scholar] [CrossRef]
- Hiền, L.T.T.; Hiền, N.T. Đánh giá ảnh hưởng của dòng chảy vỡ đập khi có và không có vật cản bằng mô hình toán hai chiều. processings of the Hội Nghị Cơ Học Thủy Khí Lần Thứ 21, Quy Nhon, Vietnam, 19–21 July 2018. (In Vietnamese). [Google Scholar]
- Pilotti, M.; Tomirotti, M.; Valerio, G.; Bacchi, B. Simplified Method for the Characterization of the Hydrograph following a Sudden Partial Dam–break. J. Hydraul. Eng. 2010, 136, 693–704. [Google Scholar] [CrossRef]
- Ozmen–Cagatay, H.; Kocaman, S. Dam–break flows during initial stage using SWE and RANS approaches. J. Hydraul. Res. 2010, 48, 603–611. [Google Scholar] [CrossRef]
- Hien, L.T.T.; Van Chien, N. Investigate Impact Force of Dam–Break Flow against Structures by Both 2D and 3D Numerical Simulations. Water 2021, 13, 344. [Google Scholar] [CrossRef]
- Aureli, F.; Dazzi, A.; Maranzoni, A.; Mignosa, P.; Vacondio, R. Experimental and numerical evaluation of the force due to the impact of a dam–break wave on a structure. Adv. Water Resour 2015, 76, 29–42. [Google Scholar] [CrossRef]
- Larocque, L.A.; Imran, J.; Chaudhry, M.H. 3D numerical simulation of partial breach dam–break flow using the LES and k–ϵ turbulence models. J. Hydraul. Res. 2013, 51, 145–157. [Google Scholar] [CrossRef]
- Biscarini, C.; Di Francesco, S.; Manciola, P. CFD modelling approach for dam–break flow studies. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 6759–6793. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Yang, W.; Qin, S.; Li, Q.; Yang, B. Numerical study on characteristics of dam–break wave. Ocean Eng. 2018, 159, 358–371. [Google Scholar] [CrossRef]
- Saghi, H.; Lakzian, E. Effects of using obstacles on the dam–break flow based on entropy generation analysis. Eur. Phys. J. Plus 2019, 134, 237. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Nsom, B.; Gohari, S.; Banejad, H. A comprehensive study on dam–break flow over dry and wet beds. Ocean Eng. 2019, 188, 106279. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Nsom, B.; Bahmanpouri, F.; Dehrashid, F.A.; Adeli, A. Numerical Study of the Dynamics and Structure of a Partial Dam–Break Flow Using the VOF Method. Water Resour. Manag. 2021, 35, 1513–1528. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, J.; Li, T.; Yang, J. A simplified mathematical model for the dam–breach hydrograph for three reservoir geometries following a sudden full dam–break. Nat. Hazards 2020, 102.3, 1515–1540. [Google Scholar] [CrossRef]
- Tsakiris, G.; Spiliotis, M. Dam– Breach Hydrograph Modelling: An Innovative Semi– Analytical Approach. Water Resour. Manag. 2012, 27, 1751–1762. [Google Scholar] [CrossRef]
- Kaurav, R.; Mohapatra, P.K. Studying the Peak Discharge through a Planar Dam Breach. J. Hydraul. Eng. 2019, 145, 06019010. [Google Scholar] [CrossRef]
- Lee, K.-H. Simulation of Dam–Breach Outflow Hydrographs Using Water Level Variations. Water Resour. Manag. 2019, 33, 3781–3797. [Google Scholar] [CrossRef]
- Flow–3D; Version 12.0; User Manual; Flow Science Inc.: Santa Fe, NM, USA, 2020.
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics. 1985, 39(1), 201–225. [Google Scholar] [CrossRef]
- Ketabdari, M.J.; Saghi, H. Large Eddy Simulation of Laminar and Turbulent Flow on Collocated and Staggered Grids. ISRN Mech. Eng. 2011, 2011, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Wea. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
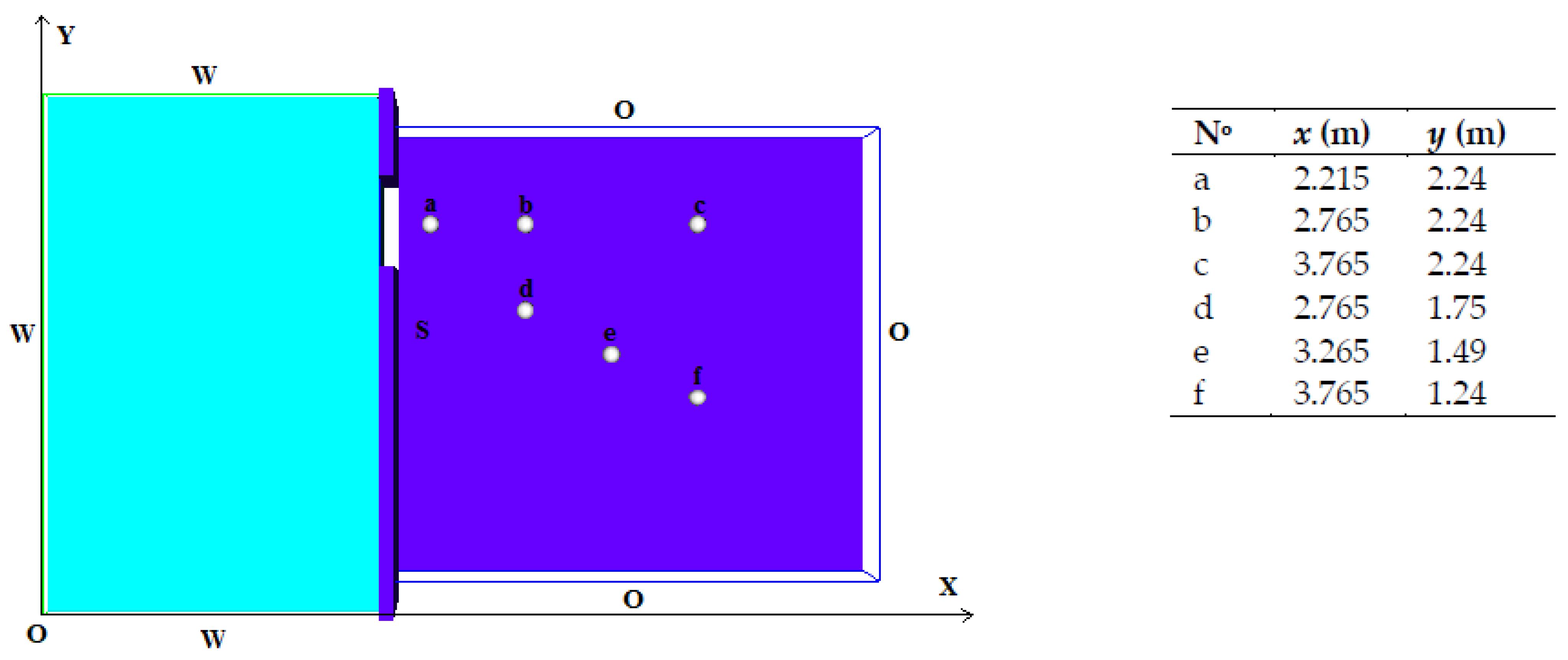
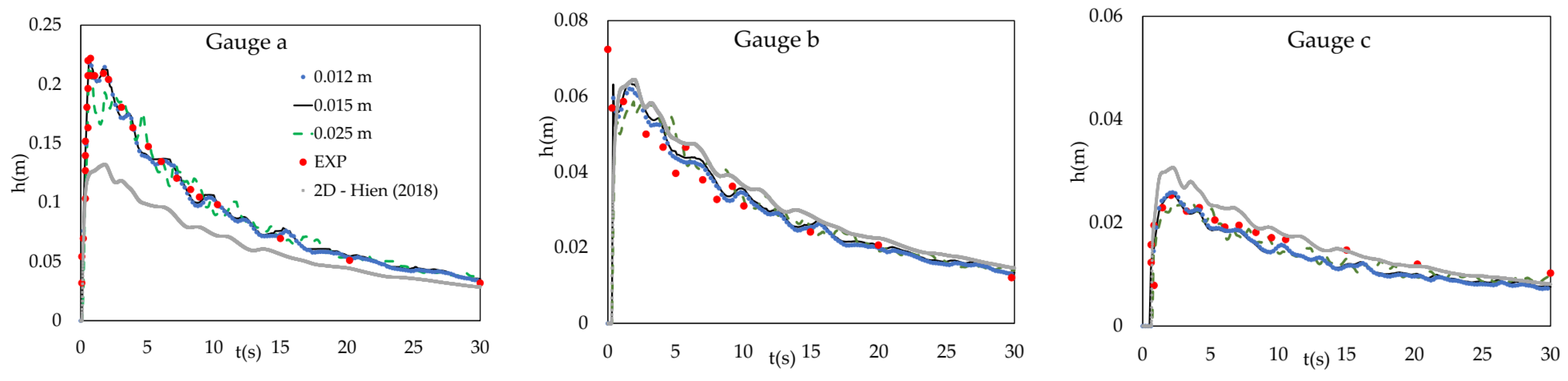






| Model Mesh Size Δx × Δy × Δz (m3) | Mesh Quality | Number of Cells (–) | Time Step (s) | Dam–Break Total Time (s) | CPU Time(h) |
|---|---|---|---|---|---|
| 0.025 × 0.025 × 0.025 | Coarse | 510,328 | 0.0020 | 30 | 2.2 |
| 0.015 × 0.015 × 0.015 | Fine | 2,183,656 | 0.0013 | 30 | 4.9 |
| 0.012 × 0.012 × 0.012 | Finest | 4,239,769 | 0.0010 | 30 | 8.1 |
| Gauge | a | b | c | |||||||||
| Model | 3D | 2D | 3D | 2D | 3D | 2D | ||||||
| Mesh | 0.025 | 0.015 | 0.012 | 0.015 | 0.025 | 0.015 | 0.012 | 0.015 | 0.025 | 0.015 | 0.012 | 0.015 |
| h | 0.129 | 0.092 | 0.066 | 0.296 | 0.406 | 0.391 | 0.389 | 0.389 | 0.323 | 0.159 | 0.264 | 0.376 |
| u | 0.285 | 0.264 | 0.228 | 0.699 | 0.091 | 0.057 | 0.076 | 0.105 | 0.165 | 0.102 | 0.125 | 0.133 |
| v | 0.373 | 0.360 | 0.474 | 0.584 | 0.609 | 0.481 | 0.658 | 0.914 | 0.318 | 0.301 | 0.335 | 0.393 |
| Gauge | d | e | f | |||||||||
| Model | 3D | 2D | 3D | 2D | 3D | 2D | ||||||
| Mesh | 0.025 | 0.015 | 0.012 | 0.015 | 0.025 | 0.015 | 0.012 | 0.015 | 0.025 | 0.015 | 0.012 | 0.015 |
| h | 0.412 | 0.114 | 0.276 | 0.269 | 0.006 | 0.358 | 0.295 | 0.331 | 0.314 | 0.239 | 0.293 | 0.304 |
| u | 0.375 | 0.217 | 0.203 | 0.277 | 0.113 | 0.069 | 0.064 | 0.081 | 0.094 | 0.083 | 0.093 | 0.082 |
| v | 0.415 | 0.245 | 0.226 | 0.211 | 0.243 | 0.218 | 0.218 | 0.382 | 0.141 | 0.110 | 0.122 | 0.250 |
| Case | Initial Water Level (h0) (cm) | Opening Width (b) (cm) and b/B | Dam Gate Position | |
|---|---|---|---|---|
| A | B | |||
| 1 | 20 | 25 (0.083) | Asymmetric | Centrer of dam |
| 2 | 20 | 50 (0.166) | Asymmetric | Centrer of dam |
| 3 | 20 | 75 (0.249) | Asymmetric | Centrer of dam |
| 4 | 40 | 25 (0.083) | Asymmetric | Centrer of dam |
| 5 | 40 | 50 (0.166) | Asymmetric | Centrer of dam |
| 6 | 40 | 75 (0.249) | Asymmetric | Centrer of dam |
| 7 | 60 | 25 (0.083) | Asymmetric | Centrer of dam |
| 8 | 60 | 50 (0.166) | Asymmetric | Centrer of dam |
| 9 | 60 | 75 (0.249) | Asymmetric | Centrer of dam |
| N° | h0 (cm) | b/B (–) | η–Schoklitsch (–) | η–3D, A (–) | η–3D, B (–) |
|---|---|---|---|---|---|
| 1 | 20 | 0.084 | 0.5505 | 0.5140 | 0.5720 |
| 2 | 20 | 0.168 | 0.4629 | 0.4899 | 0.4924 |
| 3 | 20 | 0.251 | 0.4183 | 0.4363 | 0.4379 |
| 4 | 40 | 0.084 | 0.5505 | 0.5568 | 0.5785 |
| 5 | 40 | 0.168 | 0.4629 | 0.4626 | 0.4947 |
| 6 | 40 | 0.251 | 0.4183 | 0.4185 | 0.4531 |
| 7 | 60 | 0.084 | 0.5505 | 0.5975 | 0.6239 |
| 8 | 60 | 0.168 | 0.4629 | 0.4801 | 0.5095 |
| 9 | 60 | 0.251 | 0.4183 | 0.4291 | 0.4638 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.T.H.; Nguyen, V.C. Numerical Study of Partial Dam–Break Flow with Arbitrary Dam Gate Location Using VOF Method. Appl. Sci. 2022, 12, 3884. https://doi.org/10.3390/app12083884
Le TTH, Nguyen VC. Numerical Study of Partial Dam–Break Flow with Arbitrary Dam Gate Location Using VOF Method. Applied Sciences. 2022; 12(8):3884. https://doi.org/10.3390/app12083884
Chicago/Turabian StyleLe, Thi Thu Hien, and Van Chien Nguyen. 2022. "Numerical Study of Partial Dam–Break Flow with Arbitrary Dam Gate Location Using VOF Method" Applied Sciences 12, no. 8: 3884. https://doi.org/10.3390/app12083884
APA StyleLe, T. T. H., & Nguyen, V. C. (2022). Numerical Study of Partial Dam–Break Flow with Arbitrary Dam Gate Location Using VOF Method. Applied Sciences, 12(8), 3884. https://doi.org/10.3390/app12083884






