Modeling and Simulation of Household Appliances Power Consumption
Abstract
:Featured Application
Abstract
1. Introduction
2. Methodology
2.1. Continuous Power Consumption Household Appliances
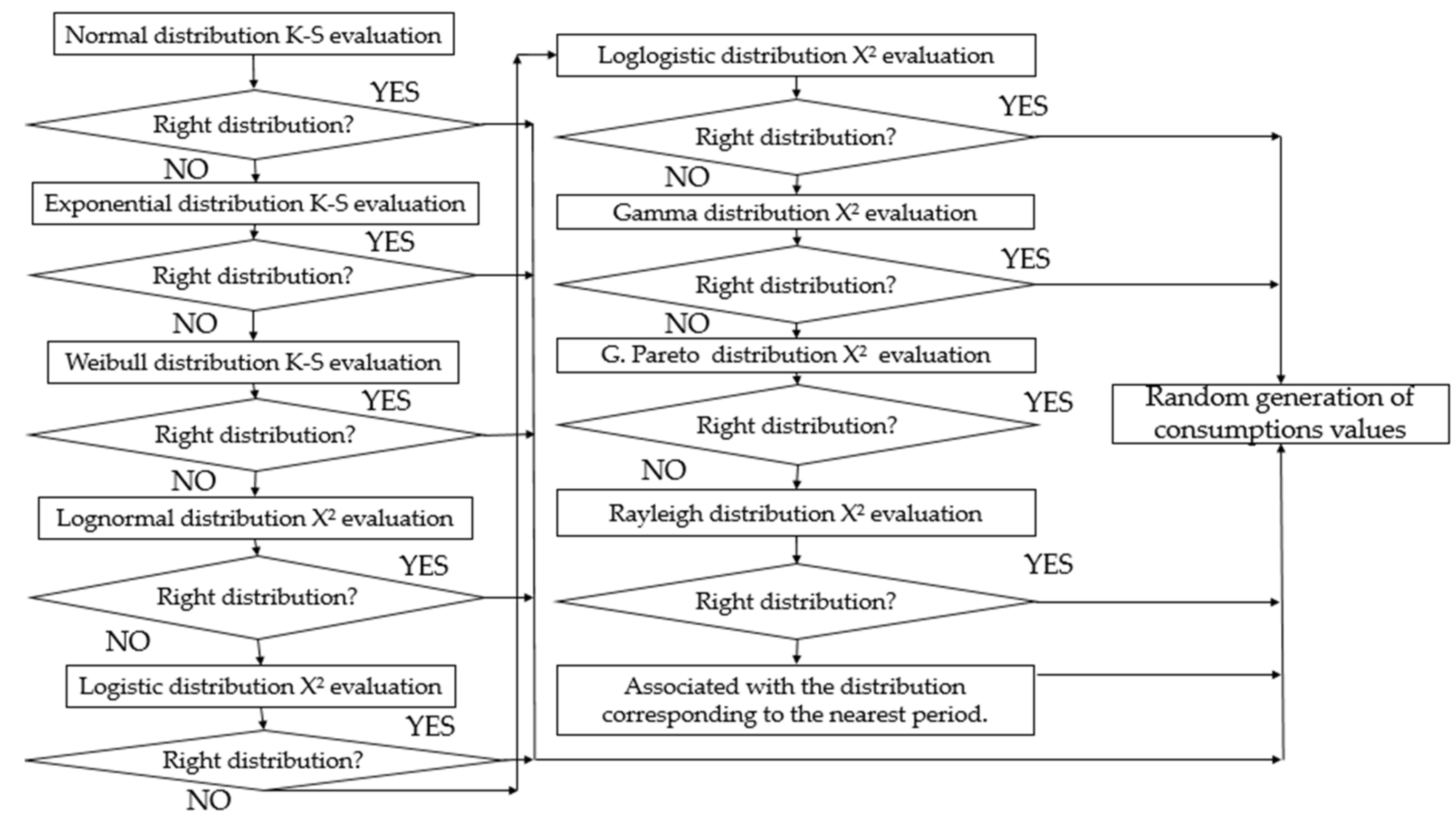
2.2. Discontinuous Power Consumption Household Appliances
- Simulation of the number of power consumptions of each element, where the probability of each integer value is based on the ratio of the previous count.
- If the above-simulated value is greater than or equal to 1, the duration of each count and its start time are simulated, also based on the data previously collected.
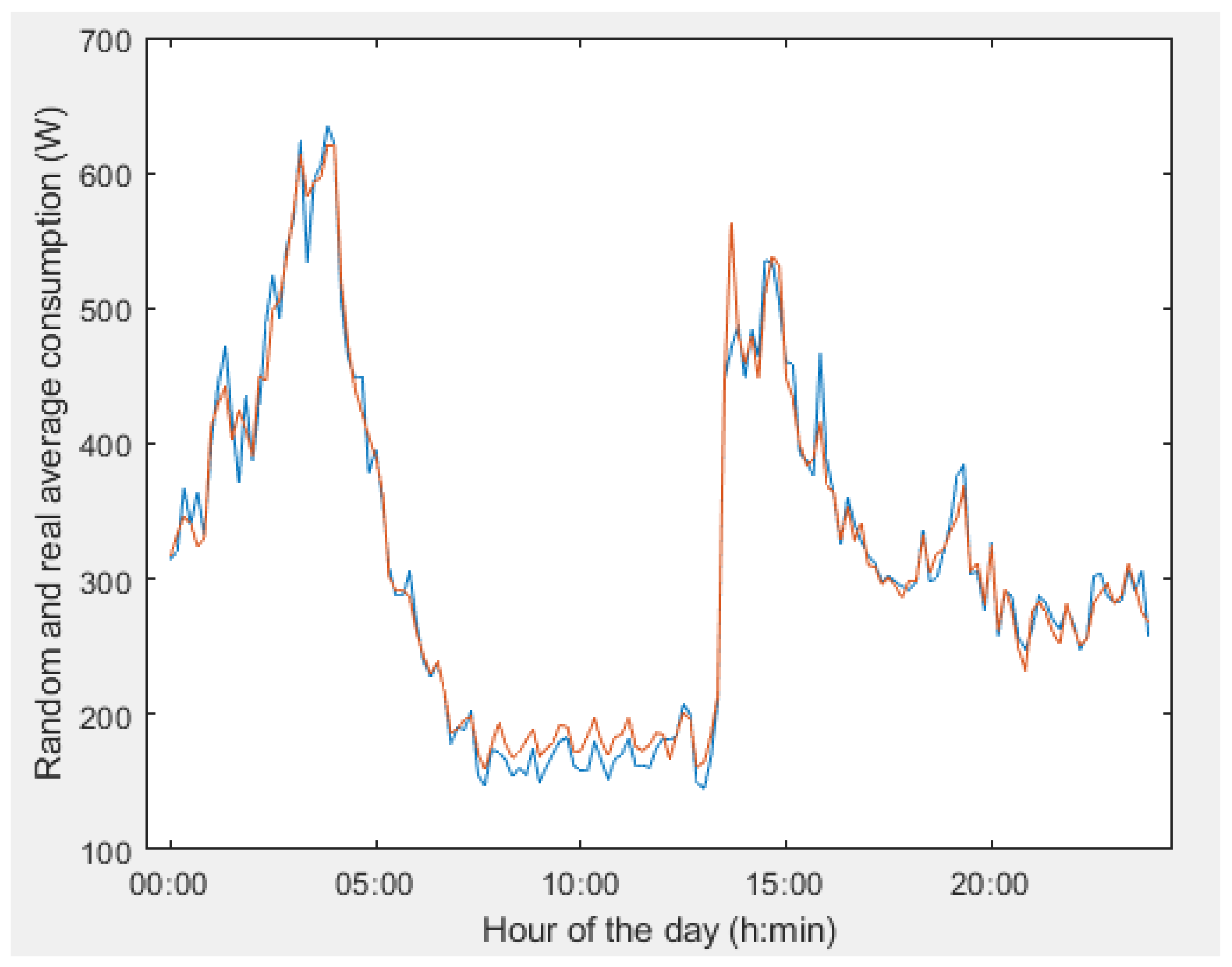
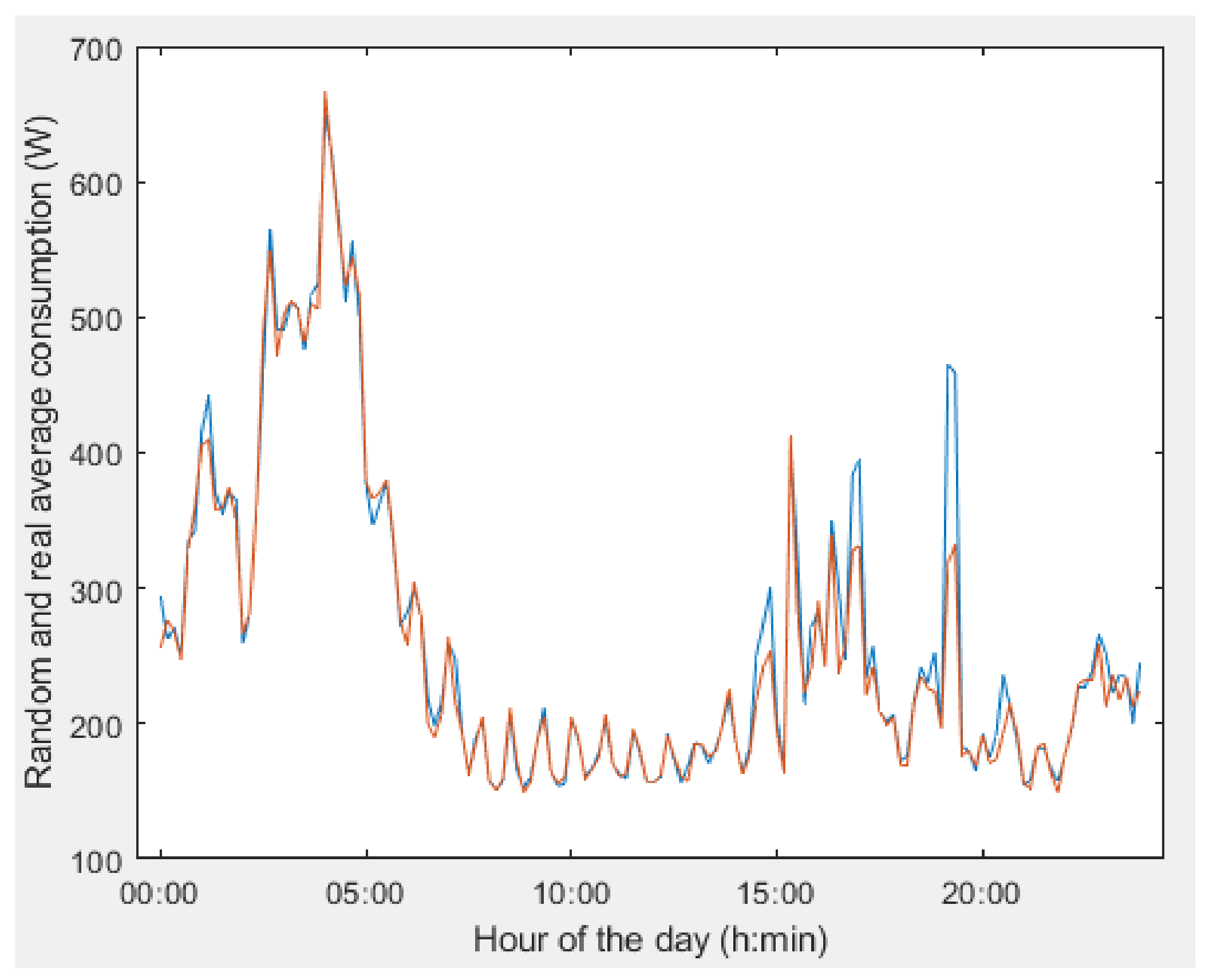
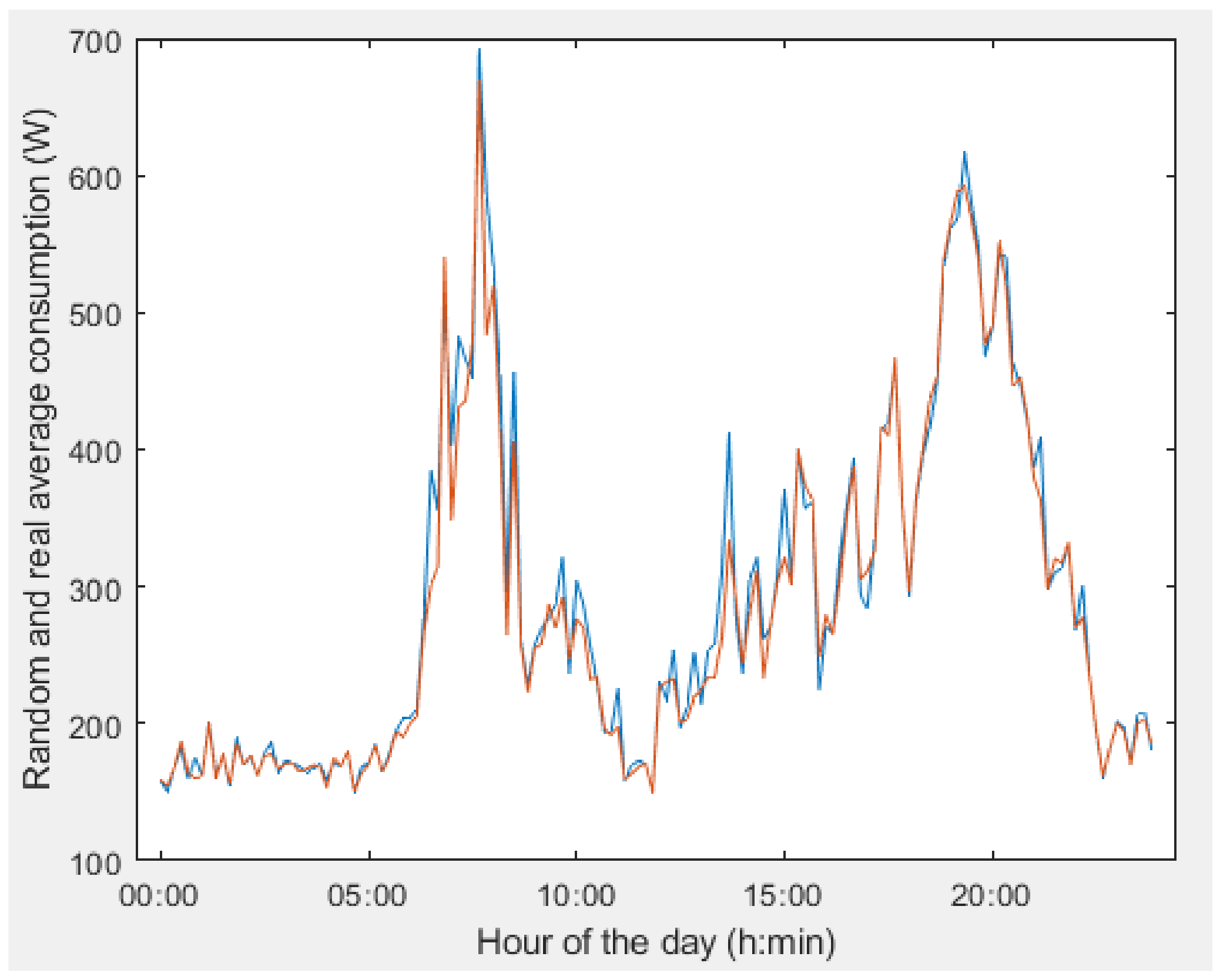
- Simulation of 300 sets of random consumptions according to the duration of the consumptions and their associated distribution, comparing their average value with the average of the real values.
- Calculation of the percentage of error by Equation (16).
3. Case study
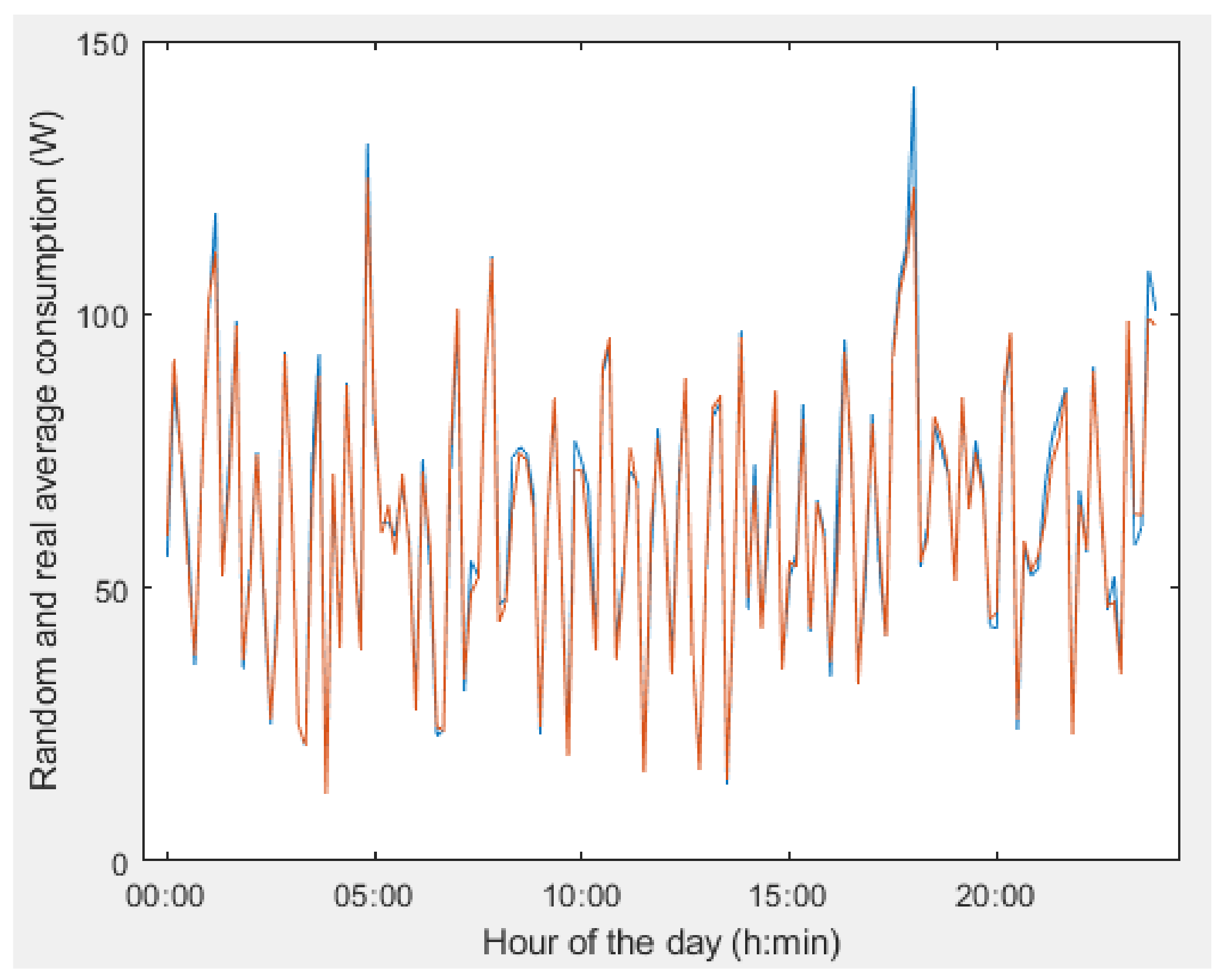
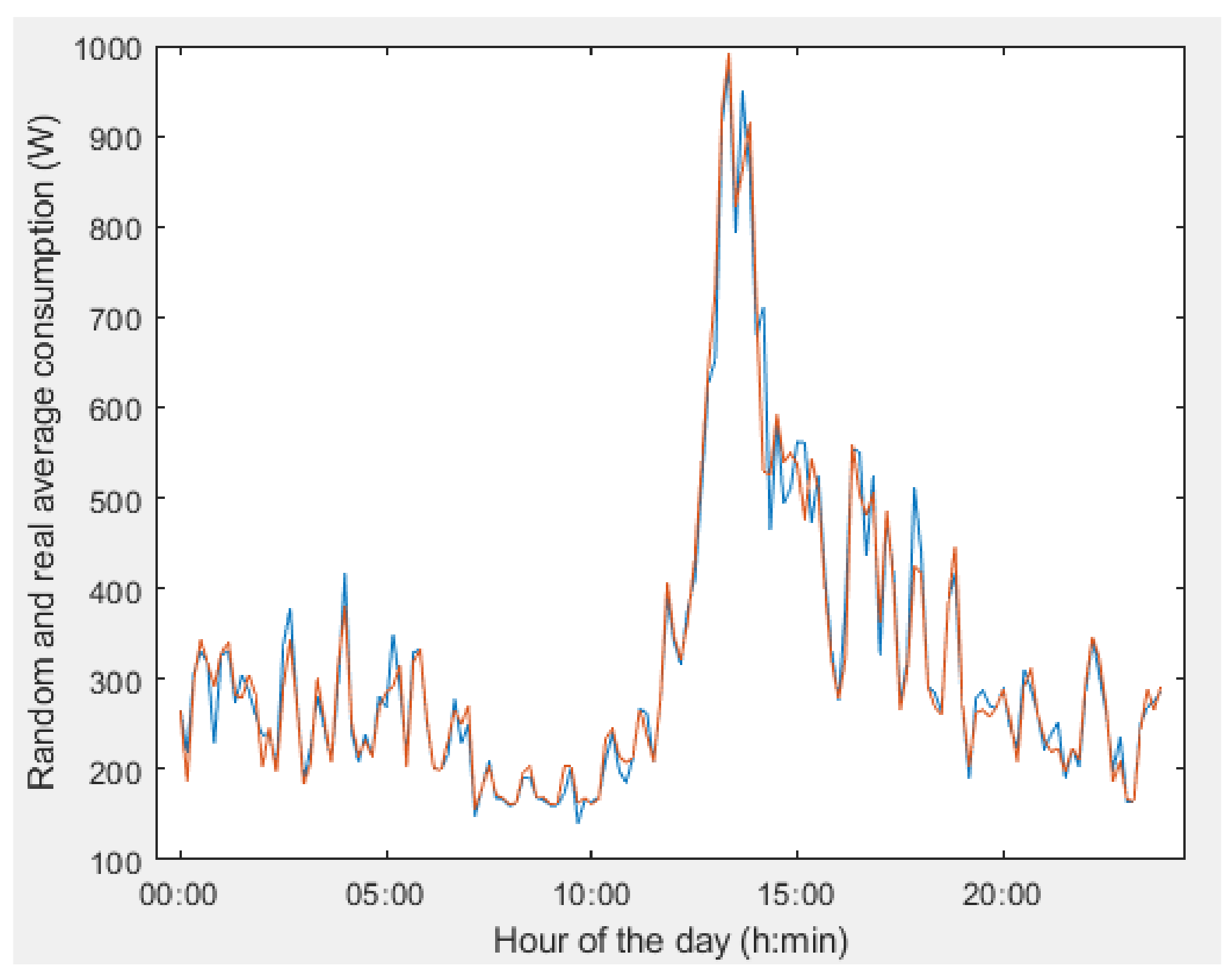
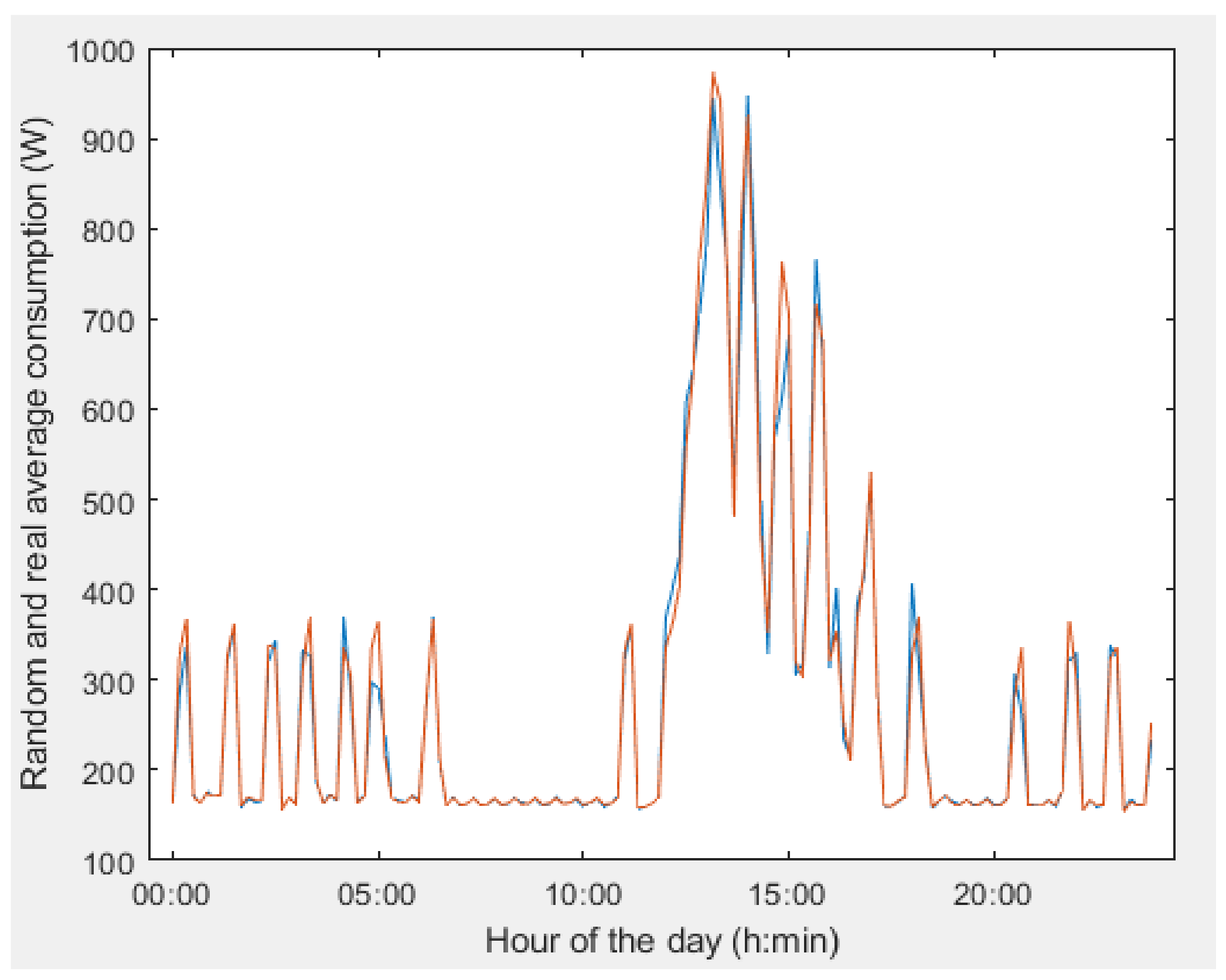
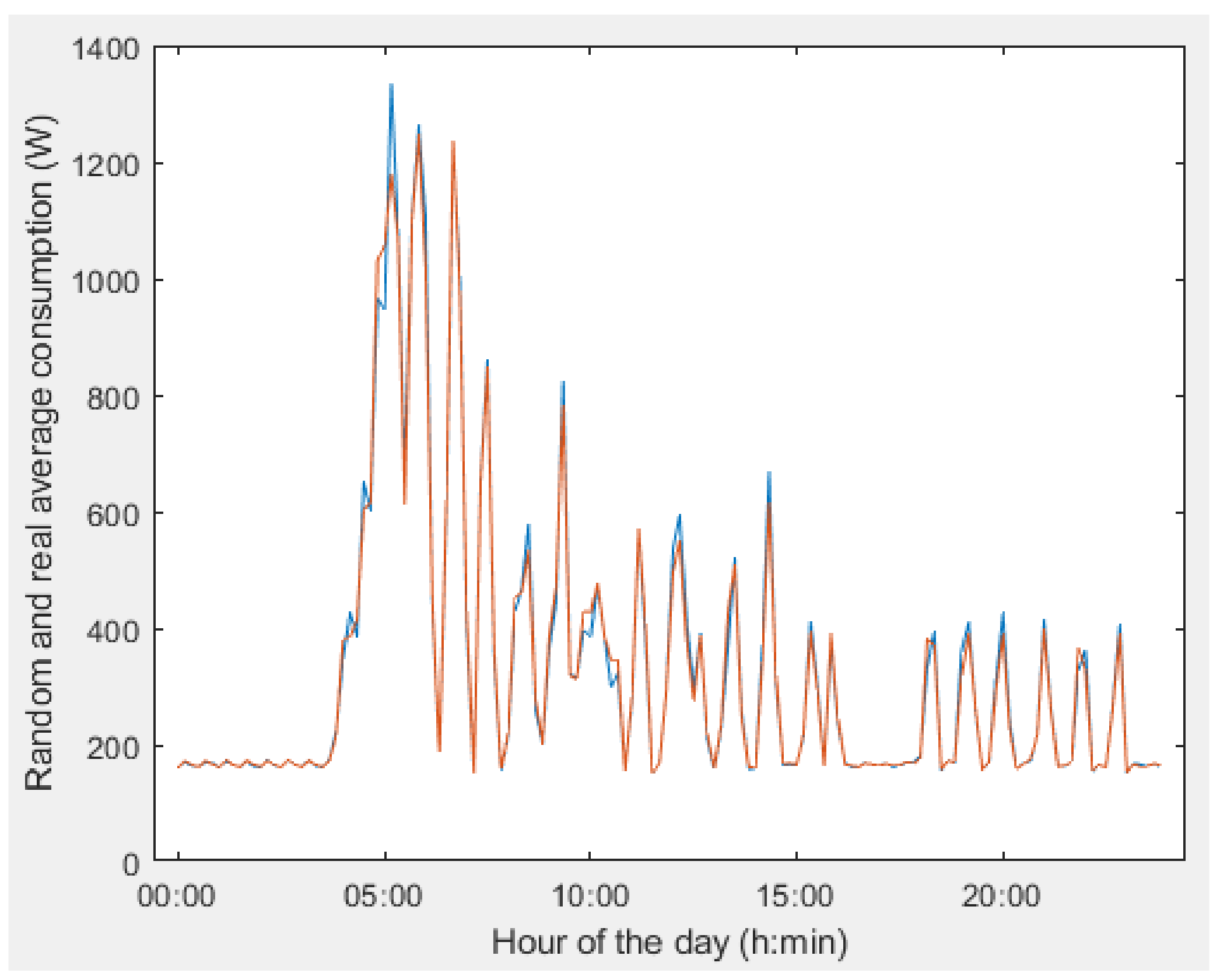
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Symbols and Acronyms
| μ | Mean |
| σ | Standard deviation |
| Normal cumulative distribution function | |
| Observed cumulative frequency | |
| Probability density function | |
| Upper difference between the observed cumulative frequency and normal cumulative Distribution | |
| Lower difference between the observed cumulative frequency and normal cumulative distribution | |
| Maximum difference between the observed cumulative frequency and normal cumulative distribution | |
| Maximum tabulated difference between the observed cumulative frequency and normal cumulative distribution | |
| Coefficient of significance | |
| Tabulated expression which determines | |
| Expected frequency | |
| Observed frequency | |
| α | Level of significance |
| n | Number of samples |
| λ | Rate parameter |
| β | Scale factor |
| α | Shape factor |
| μl | Location factor |
| λa | Skewness shape factor |
| αd | Distribution shape factor |
| X2 | Chi square |
| X2α(k-r-1) | Tabulated chi square |
| DR | Demand Response |
| HVAC | Heating, ventilating and air condition |
| SVM | Support-vector machines |
| POE | Post Occupancy Evaluation |
References
- Avila, M.; Méndez, J.; Ponce, P.; Peffer, T.; Meier, A.; Molina, A. Energy Management System Based on a Gamified Application for Households. Energies 2021, 14, 3445. [Google Scholar] [CrossRef]
- Guo, A.H. Research and Exploration on Green Design of Household Electrical Appliances. Adv. Mater. Res. 2014, 945–949, 531–534. [Google Scholar] [CrossRef]
- Lokeshgupta, B.; Sivasubramani, S. Dynamic Economic and Emission Dispatch with Renewable Energy Integration Under Uncertainties and Demand-Side Management. Electr. Eng. 2022, 1–12. [Google Scholar] [CrossRef]
- Kott, M. The electricity consumption in Polish households. In Proceedings of the 2015 Modern Electric Power Systems (MEPS), Proceedings of the International Conference on Modern Electric Power Systems, Wroclaw, Poland, 6–9 July 2015; IEEE: New York, NY, USA, 2016; pp. 1–5. [Google Scholar]
- Fattoruso, G.; De Vito, S.; Di Palma, C.; Di Francia, G. Innovative System and Method for Monitoring Energy Efficiency in Buildings. In Sensors; Springer: New York, NY, USA, 2013; Volume 162, pp. 523–527. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Afsharchi, M.; Khodayifar, S. Demand Response Management in Smart Homes Using Robust Optimization. Electr. Power Components Syst. 2020, 48, 817–832. [Google Scholar] [CrossRef]
- Chauhan, R.K.; Chauhan, K.; Badar, A.Q. Optimization of electrical energy waste in house using smart appliances management System-A case study. J. Build. Eng. 2021, 46, 103595. [Google Scholar] [CrossRef]
- Villanueva, D.; Cordeiro, M.; Feijóo, A.; Míguez, E.; Fernández, A. Effects of Adding Batteries in Household Installations: Savings, Efficiency and Emissions. Appl. Sci. 2020, 10, 5891. [Google Scholar] [CrossRef]
- Mazzeo, D.; Baglivo, C.; Matera, N.; Congedo, P.M.; Oliveti, G. A novel energy-economic-environmental multi-criteria decision-making in the optimization of a hybrid renewable system. Sustain. Cities Soc. 2020, 52, 101780. [Google Scholar] [CrossRef]
- Toader, C.; Postolache, P.; Golovanov, N.; Porumb, R.; Mircea, I.; Mircea, P.-M. Power quality impact of energy-efficient electric domestic appliances. In Proceedings of the International Conference on Applied and Theoretical Electricity, Craiova, Romania, 23–25 October 2014; IEEE: New York, NY, USA, 2014; pp. 1–8. [Google Scholar]
- Amin, A.; Kem, O.; Gallegos, P.; Chervet, P.; Ksontini, F.; Mourshed, M. Demand response in buildings: Unlocking energy flexibility through district-level electro-thermal simulation. Appl. Energy 2021, 305, 117836. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, N.; Wang, Y.; Yan, G. Identifying Fridge Consumption Non-intrusively. In Proceedings of the 3rd IEEE Conference on Energy Internet and Energy System Integration: Ubiquitous Energy Network Connecting Everything, Changsha, China, 8–10 November 2019; IEEE: New York, NY, USA, 2020; pp. 2770–2775. [Google Scholar]
- Liu, T.; Jin, L.; Zhong, C.; Xue, F. Study of thermal sensation prediction model based on support vector classification (SVC) algorithm with data preprocessing. J. Build. Eng. 2021, 48, 103919. [Google Scholar] [CrossRef]
- Colmenar-Santos, A.; Muñoz-Gómez, A.-M.; Rosales-Asensio, E.; Fernandez Aznar, G.; Galan-Hernandez, N. Adaptive model predictive control for electricity management in the household sector. Int. J. Electr. Power Energy Syst. 2022, 137, 107831. [Google Scholar] [CrossRef]
- Lankeshwara, G.; Sharma, R.; Yan, R.; Saha, T.K. Control algorithms to mitigate the effect of uncertainties in residential demand management. Appl. Energy 2021, 306, 117971. [Google Scholar] [CrossRef]
- Lee, S.-J.; Song, S.-Y. Determinants of residential end-use energy: Effects of buildings, sociodemographics, and household appliances. Energy Build. 2021, 257, 111782. [Google Scholar] [CrossRef]
- Hecht, C.; Sprake, D.; Vagapov, Y.; Anuchin, A. Domestic demand-side management: Analysis of microgrid with renewable energy sources using historical load data. Electr. Eng. 2021, 103, 1791–1806. [Google Scholar] [CrossRef]
- Lee, Y.; Yoon, Y.; Moon, H. Occupant behavior detection from environmental data and appliance electricity consumptions using machine learning. In Proceedings of the 16th Conference of the International Society of Indoor Air Quality and Climate: Creative and Smart Solutions for Better Built Environments, Indoor Air 2020, Virtual, Online, 1 November 2020; ISIAQ: Herndon, VA, USA, 2020. [Google Scholar]
- Liang, R.; Ding, W.; Zandi, Y.; Rahimi, A.; Pourkhorshidi, S.; Khadimallah, M.A. Buildings’ internal heat gains prediction using artificial intelligence methods. Energy Build. 2021, 258, 111794. [Google Scholar] [CrossRef]
- Hussein, N.; Hesham, A.; Rashawn, M. States and power consumption estimation for NILM. In Proceedings of the 14th International Conference on Computer Engineering and Systems, Cairo, Egypt, 17 December 2019; IEEE: New York, NY, USA, 2020; pp. 275–281. [Google Scholar]
- Wenninger, M.; Stecher, D.; Schmidt, J. SVM-based segmentation of home appliance energy measurements. In Proceedings of the 18th IEEE International Conference on Machine Learning and Applications, Boca Raton, FL, USA, 16–19 December 2019; IEEE: New York, NY, USA, 2020; pp. 1666–1670. [Google Scholar]
- Yu, C.; Du, J.; Pan, W. Improving accuracy in building energy simulation via evaluating occupant behaviors: A case study in Hong Kong. Energy Build. 2019, 202, 109373. [Google Scholar] [CrossRef]
- Parvin, K.; Al-Shetwi, A.Q.; Hannan, M.A.; Jern, K.P. Modelling of Home Appliances Using Fuzzy Controller in Achieving Energy Consumption and Cost Reduction. Electron. Electr. Eng. 2021, 27, 15–25. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, M.; Gao, C.; Wang, X.; Ampimah, B.C. A new interactive real-time pricing mechanism of demand response based on an evaluation model. Appl. Energy 2021, 295, 117052. [Google Scholar] [CrossRef]
- Waseem, M.; Lin, Z.; Liu, S.; Zhang, Z.; Aziz, T.; Khan, D. Fuzzy compromised solution-based novel home appliances scheduling and demand response with optimal dispatch of distributed energy resources. Appl. Energy 2021, 290, 116761. [Google Scholar] [CrossRef]
- Mutluer, M. Analysis and Design Optimization of Permanent Magnet Motor with External Rotor for Direct Driven Mixer. J. Electr. Eng. Technol. 2021, 16, 1527–1538. [Google Scholar] [CrossRef]
- Mota, F.P.; Steffens, C.R.; Adamatti, D.F.; Botelho, S.S.D.C.; Rosa, V. A persuasive multi-agent simulator to improve electrical energy consumption. J. Simul. 2021, 1–15. [Google Scholar] [CrossRef]
- Xie, X.; Chen, D. Data-driven dynamic harmonic model for modern household appliances. Appl. Energy 2022, 312, 118759. [Google Scholar] [CrossRef]
- Dorahaki, S.; Rashidinejad, M.; Ardestani, S.F.F.; Abdollahi, A.; Salehizadeh, M.R. A home energy management model considering energy storage and smart flexible appliances: A modified time-driven prospect theory approach. J. Energy Storage 2022, 48, 104049. [Google Scholar] [CrossRef]
- McKenna, E.; Few, J.; Webborn, E.; Anderson, B.; Elam, S.; Shipworth, D.; Cooper, A.; Pullinger, M.; Oreszczyn, T. Explaining daily energy demand in British housing using linked smart meter and socio-technical data in a bottom-up statistical model. Energy Build. 2022, 258, 111845. [Google Scholar] [CrossRef]
- Toosty, N.T.; Hagishima, A.; Bari, W.; Zaki, S.A. Behavioural changes in air-conditioner use owing to the COVID-19 movement control order in Malaysia. Sustain. Prod. Consum. 2022, 30, 608–622. [Google Scholar] [CrossRef]
- Tehrani, M.; Nazar, M.S.; Shafie-Khah, M.; Catalao, J.P.S. Demand Response Program Integrated With Electrical Energy Storage Systems for Residential Consumers. IEEE Syst. J. 2022, 1–12. [Google Scholar] [CrossRef]
- Gong, H.; Jones, E.S.; Alden, R.; Frye, A.G.; Colliver, D.; Ionel, D.M. Virtual Power Plant Control for Large Residential Communities Using HVAC Systems for Energy Storage. IEEE Trans. Ind. Appl. 2021, 58, 622–633. [Google Scholar] [CrossRef]
- Yan, L.; Liu, M. Predicting household air conditioners’ on/off state considering occupants’ preference diversity: A study in Chongqing, China. Energy Build. 2021, 253, 1–17. [Google Scholar] [CrossRef]
- Nishimwe, A.M.R.; Reiter, S. Estimation, analysis and mapping of electricity consumption of a regional building stock in a temperate climate in Europe. Energy Build. 2021, 253, 111535. [Google Scholar] [CrossRef]
- Dongre, P.; Aldrees, A.; Gračanin, D. Clustering appliance energy consumption data for occupant energy-behavior modeling. BuildSys 2021. In Proceedings of the 2021 ACM International Conference on Systems for Energy-Efficient Built Environments, Coimbra, Portugal, 17–18 November 2021; ACM: New York, NY, USA, 2021; pp. 290–293. [Google Scholar]
- Liu, H.; Sun, H.; Mo, H.; Liu, J. Analysis and modeling of air conditioner usage behavior in residential buildings using monitoring data during hot and humid season. Energy Build. 2021, 250, 111297. [Google Scholar] [CrossRef]
- Hua, Y.; Xie, Q.; Hui, H.; Ding, Y.; Wang, W.; Qin, H.; Shentu, X.; Cui, J. Collaborative voltage regulation by increasing/decreasing the operating power of aggregated air conditioners considering participation priority. Electr. Power Syst. Res. 2021, 199, 107420. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, X.; Lu, X.; Jing, J.; Gao, C. Inverter air conditioner load modeling and operational control for demand response. Dianli Xitong Baohu yu Kongzhi/Power Syst. Prot. Control 2021, 49, 132–140. [Google Scholar]
- Barrella, R.; Cosin, A.; Arenas, E.; Linares, J.I.; Romero, J.C.; Centeno, E. Modeling and analysis of electricity consumption in Spanish vulnerable households. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Li, P.; Liu, Z.; Sun, P.; Yang, B. Research on Optimal Control Strategy of Household Electricity Load. In Proceedings of the 3rd Asia Energy and Electrical Engineering Symposium, Chengdu, China, 26–29 March 2021; IEEE: New York, NY, USA, 2021; pp. 765–771. [Google Scholar]
- Karamalian, D.; Moradian, M.; Heydari, S. Residential Energy Management Using Hierarchical Delay in Home Appliance. J. Electr. Syst. 2021, 17, 77–89. [Google Scholar]
- Makonin, S.; Wang, Z.J.; Tumpach, C. RAE: The Rainforest Automation Energy Dataset for Smart Grid Meter Data Analysis. Data 2018, 3, 8. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Kumar, A.; Shankhwar, A.K.; Verma, A.; Kumar, V. Modelling of metereological drought in the foothills of Central Himalayas: A case study in Uttarakhand State, India. Ain Shams Eng. J. 2022, 13, 1–14. [Google Scholar] [CrossRef]
- Babichev, S.; Yasinska-Damri, L.; Liakh, I.; Durnyak, B. Comparison Analysis of Gene Expression Profiles Proximity Metrics. Symmetry 2021, 13, 1812. [Google Scholar] [CrossRef]




| A | |||
|---|---|---|---|
| Model | 0.1 | 0.05 | 0.01 |
| General | 1.224 | 1.358 | 1.628 |
| Normal | 0.819 | 0.895 | 1.035 |
| Exponential | 0.990 | 1.094 | 1.308 |
| Weibull n = 10 | 0.760 | 0.819 | 0.944 |
| Weibull n = 20 | 0.779 | 0.843 | 0.973 |
| Weibull n = 50 | 0.790 | 0.856 | 0.988 |
| 0.803 | 0.874 | 1.007 | |
| Distribution | k(n) |
|---|---|
| General | |
| Normal | |
| Exponential | |
| Weibull |
| Appliance | Type of Consumption | Type of Days | Amount of Data |
|---|---|---|---|
| Lightning | Continuous | Working days | 45 |
| Saturdays | 9 | ||
| Sundays | 9 | ||
| Refrigerator | Continuous | Working days | 45 |
| Saturdays | 9 | ||
| Sundays | 9 | ||
| HVAC | Continuous | Working days | 45 |
| Saturdays | 9 | ||
| Sundays | 9 | ||
| Dryer | Occasional | Working days | 45 |
| Washing machine | Occasional | Working days | 45 |
| Dishwasher | Occasional | Working days | 45 |
| Appliance | Type of Day | Duration | Error |
|---|---|---|---|
| Lightning | Working day | All day | 3.81% |
| Saturdays | All day | 4.26% | |
| Sundays | All day | 4.27% | |
| Refrigerator | Working day | All day | 3.91% |
| Saturdays | All day | 3.33% | |
| Sundays | All day | 3.61% | |
| HVAC | Working day | All day | 5.55% |
| Saturdays | All day | 4.72% | |
| Sundays | All day | 4.03% | |
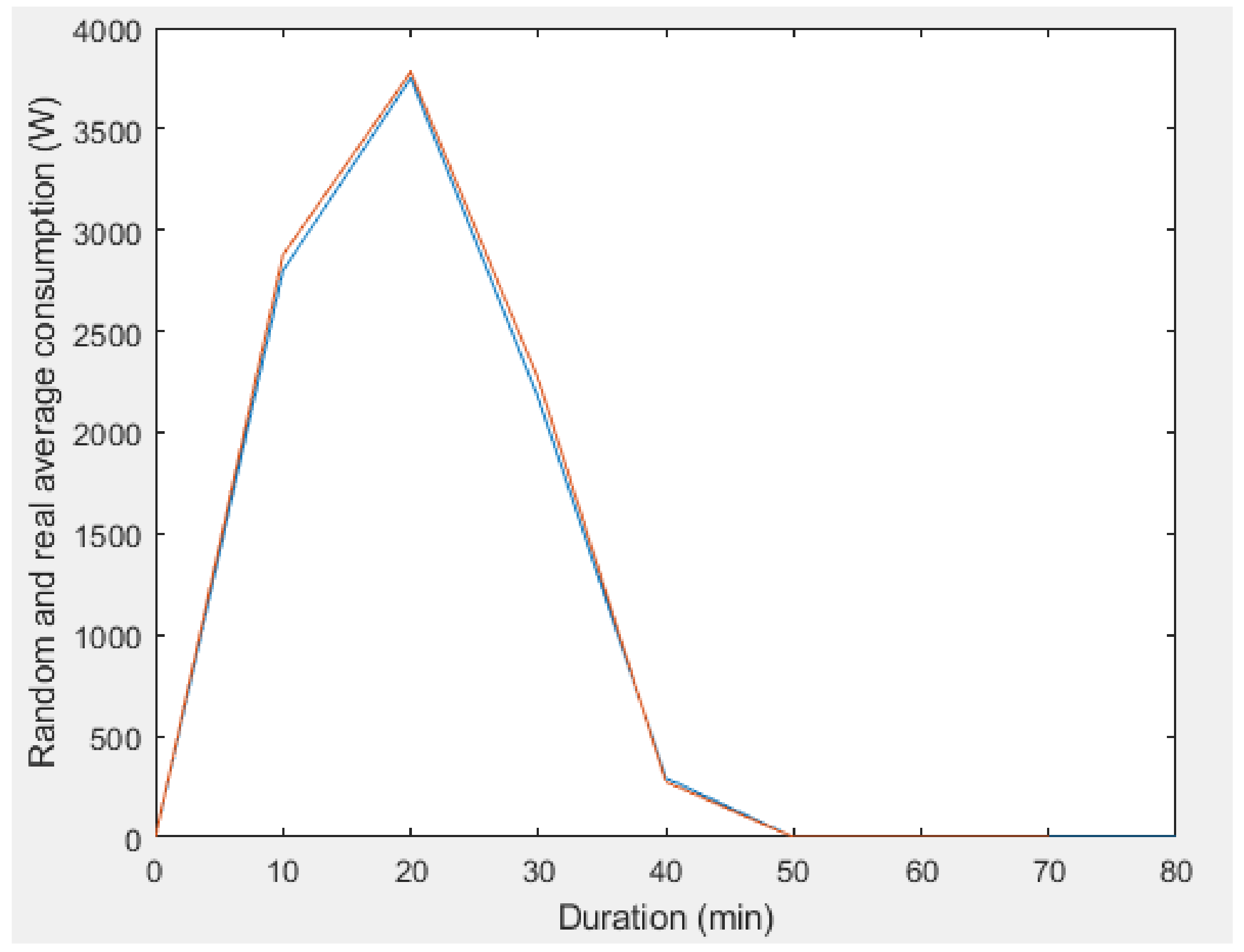
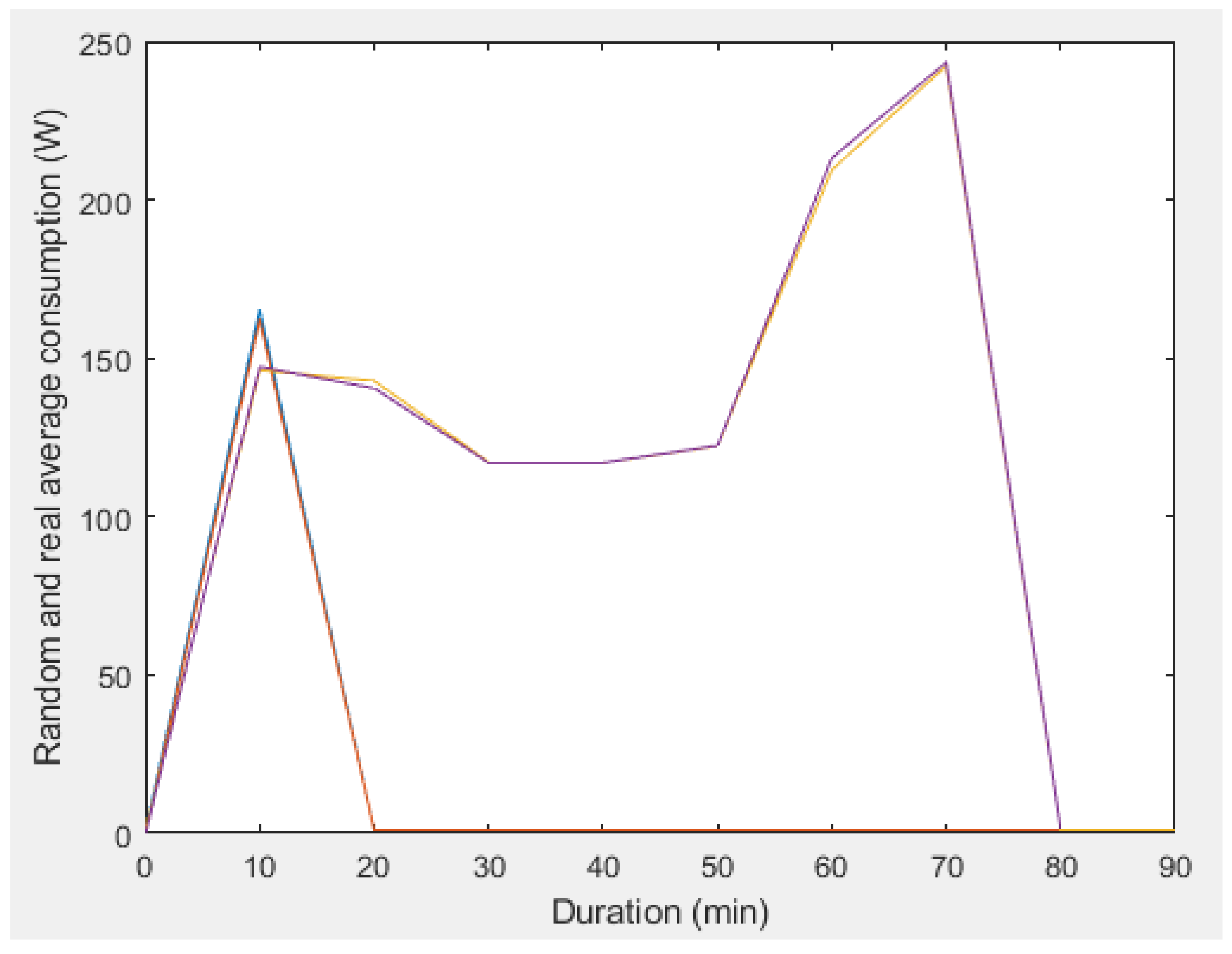
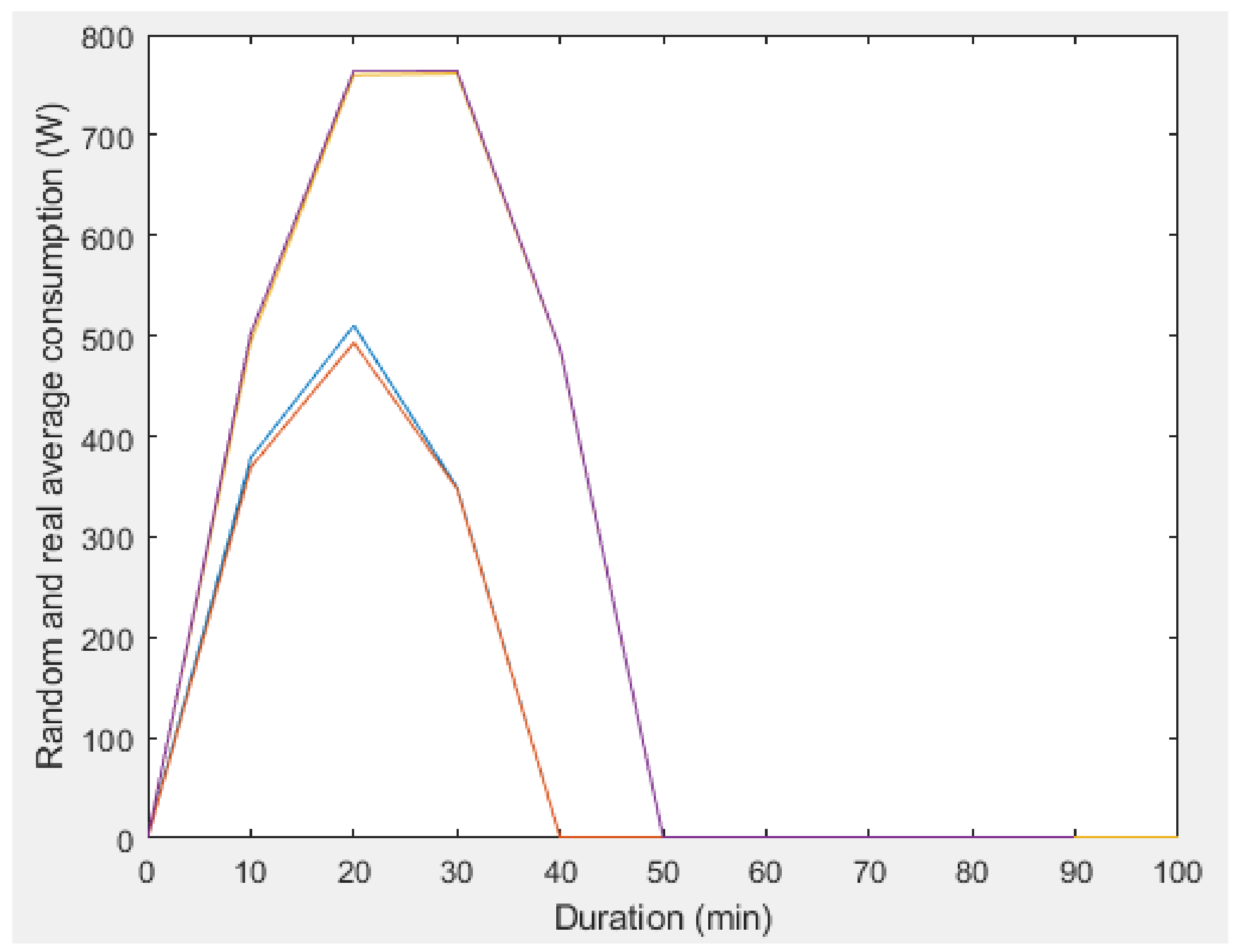
| Dryer | Working days | 40 min | 1.17% |
| Washing machine | Working days | 10 min | 1.04% |
| 70 min | 0.78% | ||
| Dishwasher | Working days | 30 min | 2.33% |
| 40 min | 0.78% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villanueva, D.; San-Facundo, D.; Miguez-García, E.; Fernández-Otero, A. Modeling and Simulation of Household Appliances Power Consumption. Appl. Sci. 2022, 12, 3689. https://doi.org/10.3390/app12073689
Villanueva D, San-Facundo D, Miguez-García E, Fernández-Otero A. Modeling and Simulation of Household Appliances Power Consumption. Applied Sciences. 2022; 12(7):3689. https://doi.org/10.3390/app12073689
Chicago/Turabian StyleVillanueva, Daniel, Diego San-Facundo, Edelmiro Miguez-García, and Antonio Fernández-Otero. 2022. "Modeling and Simulation of Household Appliances Power Consumption" Applied Sciences 12, no. 7: 3689. https://doi.org/10.3390/app12073689
APA StyleVillanueva, D., San-Facundo, D., Miguez-García, E., & Fernández-Otero, A. (2022). Modeling and Simulation of Household Appliances Power Consumption. Applied Sciences, 12(7), 3689. https://doi.org/10.3390/app12073689







