Abstract
This study examines various factors and conditions that are related with the performance of reinforcement learning, and defines a multi-agent DQN system (N-DQN) model to improve them. N-DQN model is implemented in this paper with examples of maze finding and ping-pong as examples of delayed reward system, where delayed reward occurs, which makes general DQN learning difficult to apply. The implemented N-DQN shows about 3.5 times higher learning performance compared to the Q-Learning algorithm in the reward-sparse environment in the performance evaluation, and compared to DQN, it shows about 1.1 times faster goal achievement speed. In addition, through the implementation of the prioritized experience replay and the implementation of the reward acquisition section segmentation policy, such a problem as positive-bias of the existing reinforcement learning models seldom or never occurred. However, according to the characteristics of the architecture that uses many numbers of actors in parallel, the need for additional research on light-weighting the system for further performance improvement has raised. This paper describes in detail the structure of the proposed multi-agent N_DQN architecture, the contents of various algorithms used, and the specification for its implementation.
1. Introduction
Reinforcement learning is an algorithm that makes autonomous decision-making in the direction of maximizing the value expected in the future by defining the environment to be applied as the state, behavior, and expected reward. Unlike other techniques such as supervised learning, since reinforcement learning recognizes the state of data and makes decisions, it is the more effective in solving the problem of choosing the optimal policy at every moment. In addition, it has the advantage of being able to proceed with learning by judging the environment and situation by oneself without the need for prior knowledge on complex problems [1].
However, this does not mean that reinforcement learning with these strengths can be applied to all fields and problems. A variety of unpredictable and abrupt variables may occur in certain fields and systems, and they use high-dimensional data with an unpredictable number of cases. In a specific environment like this, a clear limitation of reinforcement learning is revealed [2].
As an example, the most commonly used Q-Learning algorithm in reinforcement learning has a decision-making structure that evaluates the Q-value of an action and selects the action with the highest value when performing the learning in the environment based on the Markov Decision Process (MDP) theory [3]. It is a learning paradigm with learning by rewards/penalties with some interesting applications, so as to maximize numerical performance measures that express a long-term objective. This decision-making structure is most similar to the basic philosophy of reinforcement learning, but when this structure is applied to an environment with poor regularity, it has been found that the learning ability is significantly deteriorated [2].
Setting up the goal of multi-agent reinforcement learning is a difficult task, which incorporates the stability of the learning dynamics of the agent on the one hand, and the adaptation to the changing behavior of the other agents on the other hand. The goals typically formulate conditions for static games, in terms of strategies and rewards. Several factors that directly affect the performance of reinforcement learning are suggested, various studies and attempts are being made to improve the learning performance in many applications. An environment in which rewards occur frequently means an environment in which there is a high probability of achieving a goal even through unlearned actions, and conversely, an environment in which rewards do not occur frequently means that the probability of obtaining a defined reward in an irregular and anomalous environment is low. In such an environment where rewards are low, many problems arise in performing learning.
If the agent knows enough facts about its environment, the corresponding logical approach allows him to formulate plans that are guaranteed to work. Such an organization of the functioning of the agent is very convenient. Unfortunately, agents almost never have access to all the necessary information about their environment. Therefore, agents must act under conditions of uncertainty, which makes applying the traditional Q learning algorithm difficult to sparse reward environment. Episodes acquired by each actor performing actions are stored and shared in the replay buffer, and in this process, various reinforcement learning improvement factors such as prioritized experience replay and segmentation of reward acquisition sections are applied. This study further expands the hierarchical structure into multi-agent HDQN to further utilize the strengths of HDQN, meaning that the proposed structure adds multi-layers of neural networks on HDQN.
Therefore, this paper intends to tackle this delayed reward environment using multi-agent N-DQN. Similarly, this paper also attempts to improve the reinforcement learning performance by examining these issues through various experiments focusing on various factors and conditions that affect performance. Multi-agent N-DQN model is presented and implemented in this paper. N-DQN is a concept that applies and extends the structure of HDQN [3], layering several actors, and has a structure in which tasks are performed simultaneously/parallelly through policy-based behavior management.
Specifically in this paper, the multi-agent N-DQN model is proposed in Section 3, which improves the existing Q-Learning and Deep Q-Networks (DQN) algorithms. We explain the used technology and performance improvement factors. In addition, as a work to prove this, performance evaluation is performed by implementing N-DQN, Q-Learning, and DQN in two environments with different characteristics, and the results are compared and analyzed in Section 4 and Section 5. These experimental results are intended to examine what potentiality the N-DQN model might have in solving the limitations of reinforcement learning in delayed reward system. At last, conclusions and future research issues are dealt with in Section 6.
2. Related Works
2.1. Q-Learning
Q-Learning is one of the most representative algorithms for reinforcement learning based on MDP [4]. Q-Learning evaluates the Q-value of an action while learning and selects the action with the highest value. Equation (1) means this Q-Learning algorithm. At each time t, the actor performs an action () in a state () and transits to a new state (), and as a result of this, it obtains a reward (), which repeats using the weighted sum of the old value and the new information.
However, since Q-Learning uses the same values for both evaluating and selecting each action, there is a problem in that the future value of the present action of the highest value is overestimated. That is, excessively good Q-values are continuously selected, forming a positive bias in learning, and as learning progresses, a vicious cycle occurs [5]. This phenomenon is a chronic problem that has occurred in general function estimation even before the introduction of deep learning.
To solve this problem, researchers at Google’s DeepMind and MIT devised a hierarchical-DQN (HDQN) model that parallelly processes multiple reinforcement learning models. This means a structure in which learning is performed by being layering into top-level and lower-level, as shown in Table 1. In the HDQN model, the top-level and the lower-level have different purposes. The lower level is not intended to achieve a final goal, but has a unique purpose that is valid at that point. Conversely, the top-level collects the results generated in the lower-level and performs learning based on the policy. The mechanism of this hierarchical structure was found to increase the possibility of efficient learning even in a complex and irregular environment. Therefore, this study further expands the hierarchical structure into multi-agent HDQN which is shown in Figure 1 to further utilize the strengths of HDQN. It is intended to define a H-DQN model that stratifies multiple neural networks, and simultaneously performs actions in parallel based on policies.

Table 1.
Basic rules of the maze game.
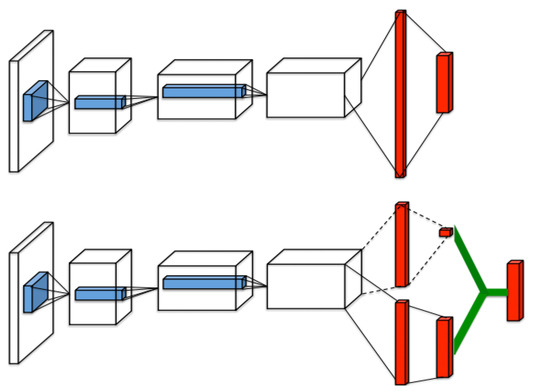
Figure 1.
The structure of H-DQN.
2.2. Maze Finding
The maze game is a game that moves the actor (  ) from the starting point of the maze to the ending point as shown in Figure 2. The actor can move in only four directions (up/down/left/right) by default, and there is an intuitive rule that walls cannot pass. In this process, the actor is considered to have the best performance in the order of the least amount of time or steps required to reach the destination. Even before reinforcement learning emerged and was studied, there were various studies to automatically perform maze finding [1]. In general, it is implemented in a way that heuristics are applied to recursive functions, etc., and rather than implementing a mechanism to find the destination all at once, the problem was solved by finding the optimal path and weight in repeated experiences [1].
) from the starting point of the maze to the ending point as shown in Figure 2. The actor can move in only four directions (up/down/left/right) by default, and there is an intuitive rule that walls cannot pass. In this process, the actor is considered to have the best performance in the order of the least amount of time or steps required to reach the destination. Even before reinforcement learning emerged and was studied, there were various studies to automatically perform maze finding [1]. In general, it is implemented in a way that heuristics are applied to recursive functions, etc., and rather than implementing a mechanism to find the destination all at once, the problem was solved by finding the optimal path and weight in repeated experiences [1].
 ) from the starting point of the maze to the ending point as shown in Figure 2. The actor can move in only four directions (up/down/left/right) by default, and there is an intuitive rule that walls cannot pass. In this process, the actor is considered to have the best performance in the order of the least amount of time or steps required to reach the destination. Even before reinforcement learning emerged and was studied, there were various studies to automatically perform maze finding [1]. In general, it is implemented in a way that heuristics are applied to recursive functions, etc., and rather than implementing a mechanism to find the destination all at once, the problem was solved by finding the optimal path and weight in repeated experiences [1].
) from the starting point of the maze to the ending point as shown in Figure 2. The actor can move in only four directions (up/down/left/right) by default, and there is an intuitive rule that walls cannot pass. In this process, the actor is considered to have the best performance in the order of the least amount of time or steps required to reach the destination. Even before reinforcement learning emerged and was studied, there were various studies to automatically perform maze finding [1]. In general, it is implemented in a way that heuristics are applied to recursive functions, etc., and rather than implementing a mechanism to find the destination all at once, the problem was solved by finding the optimal path and weight in repeated experiences [1].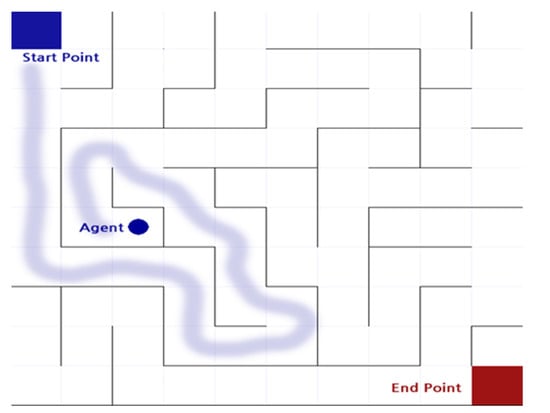
Figure 2.
The maze game implemented through Python.
Therefore, when applying reinforcement learning to the maze game, this problem-solving method is also applied. In other words, it is to find and learn the optimal weight from the learning data (Episode) generated during repeated training of the actor. To perform intuitive experiments, this study implemented the maze game environment through Python by implementing a reinforcement learning model with such a direction, and the rules applied in the game are defined in Table 1.
2.3. The Ping-Pong Game
The ping-pong game is a game where the actor tracks and hits the ball ( 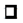 ) through the movement of the actor’s paddle (
) through the movement of the actor’s paddle ( 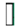 ), and the ball is sent to a space where the ball cannot be received by the opponent’s paddle as shown in Figure 3. The actor can basically perform one of five actions (top/bottom/left/right/nothing), and the movement is limited to a movement of up/down. The left/right action can be triggered when the ball hits the paddle and pushes the ball strongly in the opponent’s direction. The ball advances through the laws of physics when hitting and is refracted when it touches the top/bottom of the game screen. Therefore, it is important for the actor to strike the ball in a position that the opponent cannot receive while considering these laws of physics. Table 2 shows the rules of the ping-pong game. In applying reinforcement learning to the ping-pong game, both the position of the actor paddle, the position of the ball, and the position of the opponent’s paddle should be considered. It is predicted that, when various objects move like this, the value of the previously performed learning data may be lowered according to the movement of the object. To implement and experiment with a reinforcement learning model with such a direction we implemented using Python, and the opponent’s paddle operates by the rule-based algorithm with heuristics. Therefore, the content of performance evaluation means a confrontation structure between reinforcement learning and rule-based heuristics.
), and the ball is sent to a space where the ball cannot be received by the opponent’s paddle as shown in Figure 3. The actor can basically perform one of five actions (top/bottom/left/right/nothing), and the movement is limited to a movement of up/down. The left/right action can be triggered when the ball hits the paddle and pushes the ball strongly in the opponent’s direction. The ball advances through the laws of physics when hitting and is refracted when it touches the top/bottom of the game screen. Therefore, it is important for the actor to strike the ball in a position that the opponent cannot receive while considering these laws of physics. Table 2 shows the rules of the ping-pong game. In applying reinforcement learning to the ping-pong game, both the position of the actor paddle, the position of the ball, and the position of the opponent’s paddle should be considered. It is predicted that, when various objects move like this, the value of the previously performed learning data may be lowered according to the movement of the object. To implement and experiment with a reinforcement learning model with such a direction we implemented using Python, and the opponent’s paddle operates by the rule-based algorithm with heuristics. Therefore, the content of performance evaluation means a confrontation structure between reinforcement learning and rule-based heuristics.
 ) through the movement of the actor’s paddle (
) through the movement of the actor’s paddle (  ), and the ball is sent to a space where the ball cannot be received by the opponent’s paddle as shown in Figure 3. The actor can basically perform one of five actions (top/bottom/left/right/nothing), and the movement is limited to a movement of up/down. The left/right action can be triggered when the ball hits the paddle and pushes the ball strongly in the opponent’s direction. The ball advances through the laws of physics when hitting and is refracted when it touches the top/bottom of the game screen. Therefore, it is important for the actor to strike the ball in a position that the opponent cannot receive while considering these laws of physics. Table 2 shows the rules of the ping-pong game. In applying reinforcement learning to the ping-pong game, both the position of the actor paddle, the position of the ball, and the position of the opponent’s paddle should be considered. It is predicted that, when various objects move like this, the value of the previously performed learning data may be lowered according to the movement of the object. To implement and experiment with a reinforcement learning model with such a direction we implemented using Python, and the opponent’s paddle operates by the rule-based algorithm with heuristics. Therefore, the content of performance evaluation means a confrontation structure between reinforcement learning and rule-based heuristics.
), and the ball is sent to a space where the ball cannot be received by the opponent’s paddle as shown in Figure 3. The actor can basically perform one of five actions (top/bottom/left/right/nothing), and the movement is limited to a movement of up/down. The left/right action can be triggered when the ball hits the paddle and pushes the ball strongly in the opponent’s direction. The ball advances through the laws of physics when hitting and is refracted when it touches the top/bottom of the game screen. Therefore, it is important for the actor to strike the ball in a position that the opponent cannot receive while considering these laws of physics. Table 2 shows the rules of the ping-pong game. In applying reinforcement learning to the ping-pong game, both the position of the actor paddle, the position of the ball, and the position of the opponent’s paddle should be considered. It is predicted that, when various objects move like this, the value of the previously performed learning data may be lowered according to the movement of the object. To implement and experiment with a reinforcement learning model with such a direction we implemented using Python, and the opponent’s paddle operates by the rule-based algorithm with heuristics. Therefore, the content of performance evaluation means a confrontation structure between reinforcement learning and rule-based heuristics.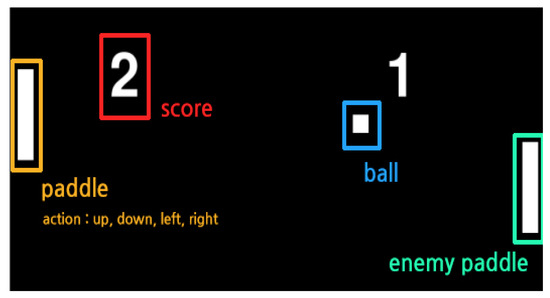
Figure 3.
The ping-pong game implemented through Python.

Table 2.
Basic rules of the ping-pong game.
2.4. Multi-Agent System and Reinforcement Learning
A multi-agent system is a group of autonomous, interacting entities sharing a common environment, which they perceive with sensors and upon which they act with actuators. Multi-agent systems are finding applications in a variety of domains including robotic teams, distributed control, resource management, collaborative decision support systems, data mining, etc.
Because of the distributed nature of the multi-agent solution, such as the speedup made possible by parallel computation, multiple reinforcement learning agents can harness new benefits from sharing experience, e.g., by communication, teaching, or imitation. When one or more agents fail in a multi-agent system, the remaining agents can take over some of their tasks. This implies that multi-agent reinforcement learning is inherently robust. Furthermore, by design most multi-agent systems also allow the easy insertion of new agents into the system, leading to a high degree of scalability.
However, multi-agent reinforcement learning algorithms are typically applied to small problems only, like static games and small grid-worlds. Therefore, it is unclear whether these algorithms scale up to realistic multi-agent problems, where the state and action spaces are large or even continuous. The discrete state-action space grows exponentially in the number of state and action variables (dimensions). Because basic reinforcement learning algorithms like Q-learning estimate values for each possible discrete state or state-action pair, this growth leads directly to an exponential increase of their computational complexity.
3. Proposed Multi-Agent N-DQN
3.1. Proposed Architecture
As shown in Figure 4, the N-DQN uses several neural networks (  ) in parallel and has a kind of HDQN-like architecture. In addition, by establishing a policy to control action and learning, each action of several neural networks is controlled. The reward and experience according to the action are shared in one memory, and the best data is selected and prioritized for learning.
) in parallel and has a kind of HDQN-like architecture. In addition, by establishing a policy to control action and learning, each action of several neural networks is controlled. The reward and experience according to the action are shared in one memory, and the best data is selected and prioritized for learning.
 ) in parallel and has a kind of HDQN-like architecture. In addition, by establishing a policy to control action and learning, each action of several neural networks is controlled. The reward and experience according to the action are shared in one memory, and the best data is selected and prioritized for learning.
) in parallel and has a kind of HDQN-like architecture. In addition, by establishing a policy to control action and learning, each action of several neural networks is controlled. The reward and experience according to the action are shared in one memory, and the best data is selected and prioritized for learning.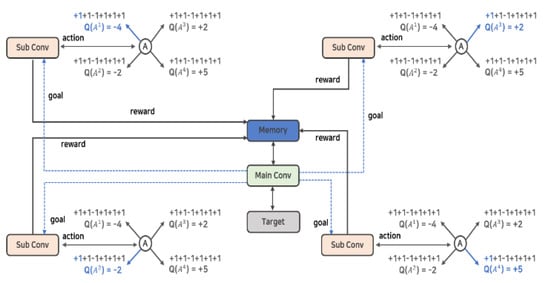
Figure 4.
Architecture of the proposed multi-agent N-DQN.
3.1.1. Hierarchization and Policy
N-DQN is defined by being largely divided into a main layer and a sublayer. First, the sublayer is defined as an actor that actually performs an action, obtains rewards and experiences, and stores them in memory, and the main layer extracts better data from the learning data (Episode). It controls the behavior of the sublayers through policies, while managing actual learning. Looking at the example in Figure 4, each of the four sublayers (  ) can perform four types of actions. At this time, the sublayer is implemented to perform the action that has not been performed before and without overlapping with other sublayers’ actions by the policy established by the main layer (
) can perform four types of actions. At this time, the sublayer is implemented to perform the action that has not been performed before and without overlapping with other sublayers’ actions by the policy established by the main layer (  ). This implementation policy is to increase learning efficiency by efficiently creating episodes in contrast to the existing reinforcement learning algorithms, and it can be implemented as in Algorithm 1.
). This implementation policy is to increase learning efficiency by efficiently creating episodes in contrast to the existing reinforcement learning algorithms, and it can be implemented as in Algorithm 1.
 ) can perform four types of actions. At this time, the sublayer is implemented to perform the action that has not been performed before and without overlapping with other sublayers’ actions by the policy established by the main layer (
) can perform four types of actions. At this time, the sublayer is implemented to perform the action that has not been performed before and without overlapping with other sublayers’ actions by the policy established by the main layer (  ). This implementation policy is to increase learning efficiency by efficiently creating episodes in contrast to the existing reinforcement learning algorithms, and it can be implemented as in Algorithm 1.
). This implementation policy is to increase learning efficiency by efficiently creating episodes in contrast to the existing reinforcement learning algorithms, and it can be implemented as in Algorithm 1.Algorithm 1 refers to the process in which each sublayer (  ) takes a non-overlapping action through the history queue H created by the main layer (
) takes a non-overlapping action through the history queue H created by the main layer (  ). History queue H stores state and action records for all episodes stored in the existing replay buffer. Therefore, each sublayer can verify the redundancy of its current target action by checking the history queue H. The existing Q-Learning and DQN algorithms perform random actions to acquire learning data that has not been performed [3]. This is implemented as a process (e-greedy) in which a random number is generated, an action is performed when it is lower
than the threshold, and the process of gradually lowering the value of the threshold is repeatedly performed. Because these procedures rely on random probabilities, their clarity and efficiency are poor [6]. However, multi agent N-DQN does not rely only on random probability through Algorithm 1, but it performs verification and by actively intervening in the creation of learning data through policy, the efficiency of learning can be increased.
). History queue H stores state and action records for all episodes stored in the existing replay buffer. Therefore, each sublayer can verify the redundancy of its current target action by checking the history queue H. The existing Q-Learning and DQN algorithms perform random actions to acquire learning data that has not been performed [3]. This is implemented as a process (e-greedy) in which a random number is generated, an action is performed when it is lower
than the threshold, and the process of gradually lowering the value of the threshold is repeatedly performed. Because these procedures rely on random probabilities, their clarity and efficiency are poor [6]. However, multi agent N-DQN does not rely only on random probability through Algorithm 1, but it performs verification and by actively intervening in the creation of learning data through policy, the efficiency of learning can be increased.
 ) takes a non-overlapping action through the history queue H created by the main layer (
) takes a non-overlapping action through the history queue H created by the main layer (  ). History queue H stores state and action records for all episodes stored in the existing replay buffer. Therefore, each sublayer can verify the redundancy of its current target action by checking the history queue H. The existing Q-Learning and DQN algorithms perform random actions to acquire learning data that has not been performed [3]. This is implemented as a process (e-greedy) in which a random number is generated, an action is performed when it is lower
than the threshold, and the process of gradually lowering the value of the threshold is repeatedly performed. Because these procedures rely on random probabilities, their clarity and efficiency are poor [6]. However, multi agent N-DQN does not rely only on random probability through Algorithm 1, but it performs verification and by actively intervening in the creation of learning data through policy, the efficiency of learning can be increased.
). History queue H stores state and action records for all episodes stored in the existing replay buffer. Therefore, each sublayer can verify the redundancy of its current target action by checking the history queue H. The existing Q-Learning and DQN algorithms perform random actions to acquire learning data that has not been performed [3]. This is implemented as a process (e-greedy) in which a random number is generated, an action is performed when it is lower
than the threshold, and the process of gradually lowering the value of the threshold is repeatedly performed. Because these procedures rely on random probabilities, their clarity and efficiency are poor [6]. However, multi agent N-DQN does not rely only on random probability through Algorithm 1, but it performs verification and by actively intervening in the creation of learning data through policy, the efficiency of learning can be increased.The main layer also creates and executes policies related to rewards to enhance the efficiency of learning. In Figure 4, the main layer presents a goal to the sublayer. This is a result from the fact that one of the factors that directly affects the performance of reinforcement learning comes from the frequency of occurrence of rewards [7]. Reinforcement learning is characterized by a significant change in learning difficulty according to the frequency and probability of rewards according to an action [7].
To solve this problem, N-DQN establishes a policy that divides and subdivides the reward acquisition period. Specifically, learning is performed for a certain period of time (time, step), and in an environment where reward acquisition occurs little, the principal of NDQN is to enable the gradual learning by subdividing the reward acquisition section based on the episode, which includes all information such as action, reward, and status. This series of processes is shown in Algorithm 2. It refers to the process in which an immediate reward is given by checking the subdivided reward acquisition period. It has information about the predefined reward acquisition period in the form of a list, and the reward value corresponding to each period is also maintained. Using these values, while taking a random action at every step and calculating the reward for it, eventually after checking whether it corresponds to reward acquisition, an additional reward is given to the immediate reward.
| Algorithm 1: Action Control Policy | |
| 1 | Input: number of sublayer N, current states, target action a |
| 2 | Initialize: shared replay memory D to size N ∗ n |
| 3 | Initialize: N action-value function Q with random weights |
| 4 | Initialize: episode history queue H to size N ∗ n |
| 5 | Copy data to H from D For 1, N do For state in H do if state = s then For action in state.action do if action != a then do action else break else do action |
| Algorithm 2: Reward Policy | |
| 1 | Input: current state s, immediate reward r |
| 2 | Initialize: list of lethal state L, dict of reward P |
| 3 | Initialize: the number of reward point K After do action Before return immediate reward r |
| 4 | For k in range (0, K) if s = L[k] then return r += P[L[k]] else return r |
3.1.2. Parallel Processing and Memory Sharing
Actors in the sublayers performs actions simultaneously in parallel and the system is implemented to share the result (episode) information in one replay buffer. To implement such parallel processing and shared structure, this study referred to the parallel processing structure using Apache Spark [8,9,10]. Figure 5 shows the parallel processing structure applied to N-DQN. The example used in the figure shows a structure in which two actors (Sub Conv) are processed in parallel through the Apache Spark library, and it is actually based on the research results showing that the performance is better than a single processing.
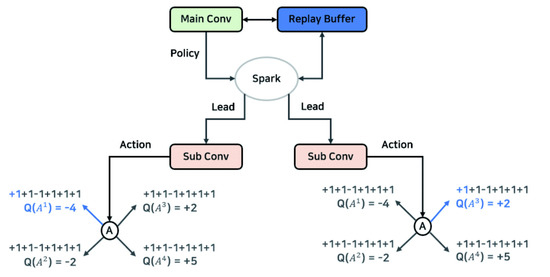
Figure 5.
Structure of parallel processing through Spark.
Each episode result obtained by the actor performing parallel processing can be shared and stored in the replay buffer. Due to this, the speed of data accumulation in the buffer is improved in proportion to the number of actors. After that, the main layer efficiently selects and learns data from the rapidly accumulated replay buffer. Algorithm 3 is a specification for implementing the structure of sharing experience, which is one of the characteristics of N-DQN. Each actor (  ) obtains the value of n number of action-value function Q and stores the result in the shared replay buffer. As such, the learning data shared by several actors enables collecting data faster than a general reinforcement learning algorithm.
) obtains the value of n number of action-value function Q and stores the result in the shared replay buffer. As such, the learning data shared by several actors enables collecting data faster than a general reinforcement learning algorithm.
 ) obtains the value of n number of action-value function Q and stores the result in the shared replay buffer. As such, the learning data shared by several actors enables collecting data faster than a general reinforcement learning algorithm.
) obtains the value of n number of action-value function Q and stores the result in the shared replay buffer. As such, the learning data shared by several actors enables collecting data faster than a general reinforcement learning algorithm.
| Algorithm 3: N-DQN Experience Sharing | |
| 1 | Procedure: training |
| 2 | Initialize: shared replay memory D to size N ∗ n |
| 3 | Initialize: N action-value function Q with random weights |
| 4 | Loop: episode = 1, M do Initialize state s1 For t = 1, T do For each Qn do With probability ϵ select random action at otherwise select at = argmaxa Qn(st, a; θi) Execute action at in emulator and observe rt and st+1 Store transition (st, at, rt, st+1) in D End For Sample a minibatch of transitions (sj, aj, rj, sj+1) from D Set yj: = rj For terminal sj+1 rj + γmax_(a^′) Qn(sj+1, a′; θi) For non-terminal sj+1 Perform a gradient step on (yj − Qn(sj, aj; θi))2 with respect to θ end For |
| 5 | End Loop |
3.1.3. Training Policy
In general, the reinforcement learning algorithm stores data in the replay buffer to remove the dependence between data, and then performs learning by selecting it randomly [6]. However, not all data stored in the replay buffer have the same value. Exceptions may occur depending on the environment, but in general, a specific experience may have a more important value [11]. Various studies have been conducted to prioritize or classify the importance of learning data according to these characteristics, and of them, the most representative technology is the prioritized experience replay [11].
Because the N-DQN utilizes many actors according to the characteristics of the architecture, the accumulation speed of experience is faster than the general DQN. Therefore, the mechanism for determining the value of experience by implementing prioritized experience replay based on this architecture is a factor that greatly affects learning performance. The importance of experience is proportional to the amount that can be learned from the current state through the experience. These quantitative values can be obtained through the difference between the TD target defined as a TD-error and the actual V(S). It is generally defined as Equation (2).
The quantitative value obtained through Equation (2) is implemented by creating a probability distribution based on the size of TD-error as in Algorithm 4 and extracting a value from the distribution. We can simply use the TD-error value, but it is known that using the probability distribution shows better results [4,12,13,14].
| Algorithm 4: Prioritized Experience Replay | |
| 1. | Input: minibatch k, step-size n, replay period K and size N, exponents α and β, budget T and N action-value function Q |
| 2. | Initialize replay memory H = θ, Δ = 0, = 1 |
| 3. | Observe and choose ~ () |
| 4. | for t = 1 to T do Observe for p = 1 to N do Store transition ( in H with maximal priority = end for if t then for j = 1 to k do Sample transition j ~ P(j) = Compute sampling weight Compute TD-error = Update transition priority Gather weight-change Δ Δ + end for Update weights Δ, reset Δ = 0 From time to time copy weights into target NN end if for p = 1 to N do Choose action ∼ () end for end for |
4. Evaluation Results and Analysis with Maze Finding
4.1. Environment
Figure 6 refers to the structure for performing reinforcement learning in the maze game environment. The principle that the action at each state is performed is diagrammed.
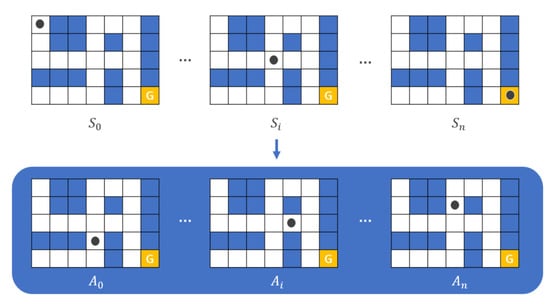
Figure 6.
Visualization of reinforcement learning of maze game.
4.2. Training Features
The state is defined as the actor’s current position coordinates (x/y) in the game. The actor is implemented to acquire information again each time an action is performed because the location changes in real time according to the action. Action is defined as the direct movement of an Actor. The actor can take one of the following actions (up/down/left/right) and cannot pass through blocked walls. Reward is defined as checking how close the state’s location information is to the goal in proportion to the number of cells. Also, when reaching the goal, it is implemented to obtain a reward with a high weight. Table 3 shows the object of learning in the maze game.

Table 3.
Object of learning in the maze game.
4.3. Implement and Performance Evaluation
4.3.1. N-DQN-Based Implementation
Four sublayers and one main layer were used between the implementation of reinforcement learning in the maze game environment through N-DQN. The learning algorithm is based on the DQN and includes the structure and functions of the architecture described in Chapter 3. Figure 7 means the reward policy applied to the maze game. While performing learning and exploration for a certain period, it establishes a policy to subdivide the reward acquisition periods based on the time taken in each state and the number of steps to reach the goal. In the reward, the sum of the rewards until the game is finished is calculated and weighted by additionally implementing Equation (3), which is discounted by a factor of y at each stage. In addition to this process, the stage in which the reward rapidly deteriorates is identified based on the state. The identified stage as such is given a negative reward to the weight.
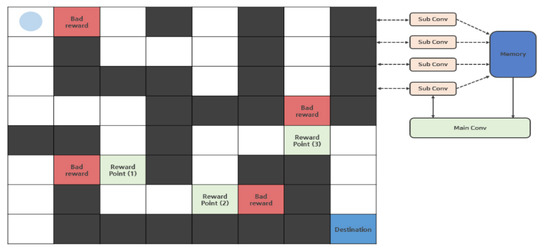
Figure 7.
N-DQN’s reward acquisition policy.
4.3.2. Performance Evaluation and Discussion
In this section, to evaluate the performance of the proposed multi-agent N-DQN model, we compare and examine our results with Q-Learning and DQN algorithm under the same environments and conditions. Figure 8 is the result of applying Q-Learning to a 5 × 5 maze environment. In conclusion, Q-Learning solved the problem within the targeted 400 steps, and it took less than 50 steps and showed good learning efficiency. In a maze of small size, there is a high probability of achieving a goal even by unlearned actions. For this reason, the simple storage method using Q-table shows higher efficiency than other models using Q-network. Figure 9 is the result of applying DQN to a 5 × 5 maze environment. In conclusion, the DQN algorithm failed to solve the problem within the targeted 400 steps. The goal was successfully resolved in the result of additionally performing the number of targeted steps by adding 25% (100 steps) compared to the previous one to check the possibility of a logic error occurring between implementations.
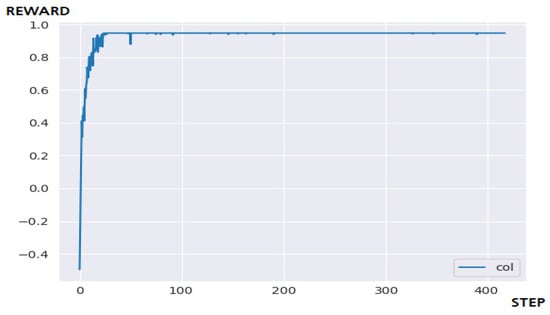
Figure 8.
The result of a 5 × 5 maze game through Q-Learning.
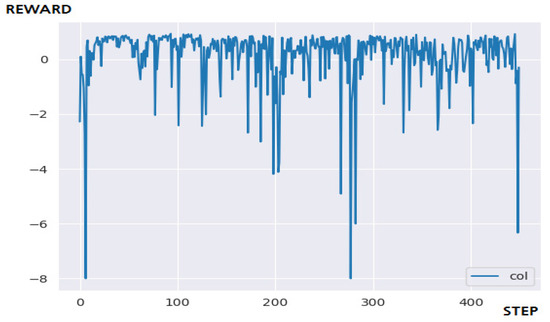
Figure 9.
The result of a 5 × 5 maze game through DQN.
These experimental results suggest that the cause of failure is that the process of selecting a learning sample from the replay buffer has randomness, and so the learning efficiency is not good [6]. Additional implementations of algorithms that improve learning efficiency, or sequential removal of the oldest data from the replay buffer, will also significantly improve performance. Figure 10 is the result of applying N-DQN to a 5 × 5 maze environment. In conclusion, the N-DQN solved the problem within the targeted 400 steps, and it shows stable performance after about 100 steps. Unlike DQN, since various performance improvement factors are implemented, the learning efficiency is very outstanding. However, problems with high H/W or resource occupancy occurring in parallelization of sublayers are identified. Q-Learning managed to solve the problem with the fewest steps and time. The 5 × 5 sized maze does not have many episodes, and there is a high probability of obtaining a reward even for an unlearned action. In other words, it was judged that the difficulty of learning was too easy to draw a conclusion, so an additional experiment was conducted by further expanding the size of the maze. Table 4 summarizes 5 × 5 learning results.
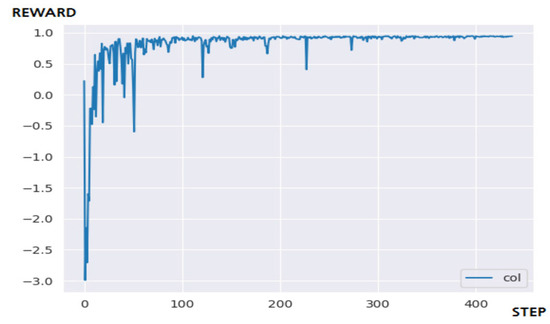
Figure 10.
The result of 5 × 5 maze game through N-DQN.

Table 4.
Summary of 5 × 5 learning results.
Figure 11 shows the result of applying Q-Learning to a 10 × 10 maze environment. Q-Learning failed to solve the problem within the targeted 700 steps. However, if the number of learning steps was increased, it showed an upward curve to an extent that it is enough to reach the goal. In fact, it was confirmed that the goal was achieved from the result of performing about 1200 steps of learning by increasing the goal value by 1.7 times.
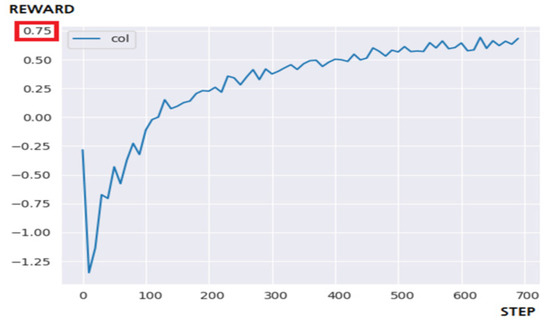
Figure 11.
Result of 10 × 10 maze through Q-Learning.
Figure 12 is the result of applying the DQN to a 10 × 10 maze environment. The DQN failed to solve the problem within the targeted steps as in the case of the 5 × 5 maze. This shows that it sometimes resulted in good performance curves in several experiments, but it is judged to be a factor of luck. Learning efficiency started to appear when 1400 learning steps were performed, when doubling the number of learning steps. From the result of observing the actor’s movement through rendering to consider the cause of the performance degradation, it was confirmed that when entering the wrong section of the maze, it was not possible to get out and performed an inefficient action. Therefore, a large amount and number of state and actions occurs in episodes, and the performance of learning is greatly reduced.
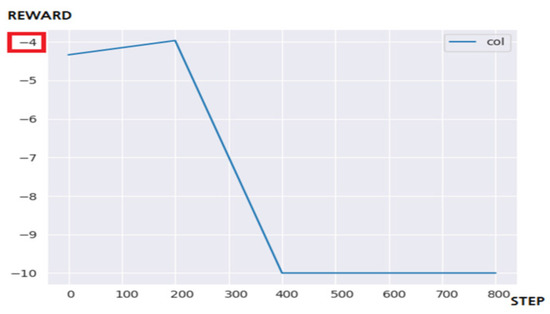
Figure 12.
The result of a 10 × 10 maze game through DQN.
Figure 13 is the result of applying the N-DQN to a 10 × 10 maze environment. The N-DQN succeeded in solving the problem within the targeted 700 steps, and it showed consistent and stable learning efficiency. When about 400 steps have passed, learning at a certain level or more has already been completed. These results are most influenced by policies that control learning and action [15]. By implementing prioritized experience replay and polices of subdividing the reward acquisition stage, the positive-bias problem of the existing reinforcement learning hardly occurred, and it is estimated that the problem of lowering learning efficiency in the reward-sparse environment has also been improved. However, as before, it shows a very high share of hardware resources due to the nature of the architecture that uses a large number of actors in parallel. This can be greatly improved by turning off the rendering responsible for the visualization of the game screen.
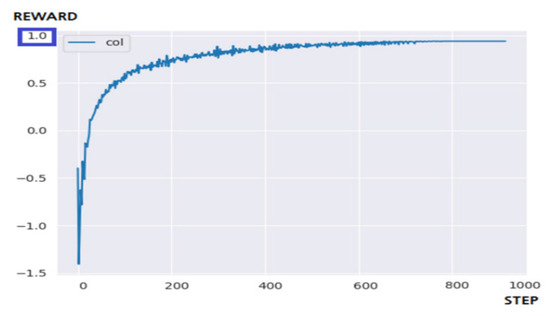
Figure 13.
The result of a 10 × 10 maze game through N-DQN.
Table 5 is a summary of the experimental results. Only the N-DQN solved the problem within the targeted stage, and compared to the DQN, it showed about 10% faster performance speed. In terms of learning efficiency, the reward value of 0.75 obtained through 700 steps by Q-Learning was obtained through about 200 steps by N-DQN. This means a performance difference of about 3.5 times. Even when the reward was delayed, the N-DQN model showed stable learning performance.

Table 5.
Summary of 10 × 10 learning results.
5. Evaluation Results and Analysis with Ping-Pong
In this section, we have implemented a ping-pong game to verify the performance of our multi-agent N-DQN [16].
5.1. Environment
Figure 14 refers to the structure for performing reinforcement learning in the ping-pong game.
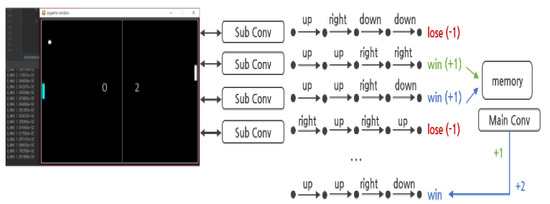
Figure 14.
Visualization of the ping-pong game through reinforcement learning.
5.2. Training Features
State is defined in the game as the current position coordinates of the actor’s paddle and the current position of the ball. The actor’s paddles and balls change their positions in real time according to actions, so it is implemented to acquire information again every time an action is performed. Action is defined as a direct movement of the actor’s paddle. The actor takes one of the four actions up/down/left/right. Because the player wins the round if the opponent’s paddle fails to receive the ball, a high-weighted reward is given. On the other hand, because the player loses the round if the actor’s paddle misses the ball, reward is given negatively. Table 6 shows the objects of leaning in the maze game.

Table 6.
Objects of learning in the maze game.
5.3. Implement and Performance Evaluation
5.3.1. N-DQN-Based Implementation
In order to implement the reinforcement learning in the ping-pong game environment through N-DQN, four sublayers and one main layer were used. Figure 14 shows this hierarchical structure and architecture. The learning algorithm was based on the DQN, and it includes the structure and functions of the architecture described in Section 3. As a pre-preparation process for reinforcement learning, the game is divided into frames and processed in gray scale [17]. It is based on the research results that this process affects the recognition rate [17,18].
After that, after adjusting the image frame to the size of 80 × 80, four frames are stacked to form an 80 × 80 × 4 array. The neural network has a structure of a total of three layers as shown in Figure 15, and the last hidden layer consists of 256 fully connected ReLUs. Among the implementations of the learning algorithm, the most common structure is utilized based on the DQN algorithm. When performing an action in a given state through a function defined as a Q-value as shown in Equation (4) below, the maximum expected value is approximated and used [6].
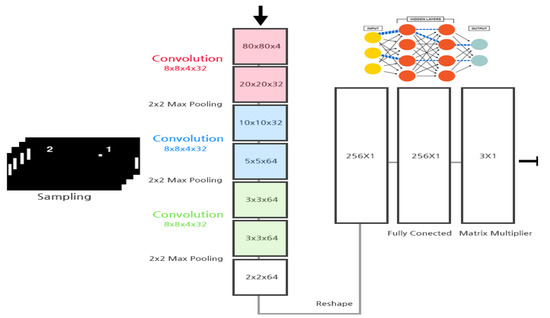
Figure 15.
The structure of the implemented artificial neural network.
The learning structure defined by Equation (3) can be implemented in the same way as Algorithm 5. The code of the algorithm was written based on DQN. As the ball and the opponent’s paddle move organically, the value of the future value brought by each action of the actor paddle may be lowered. To solve this problem, we implemented a centralized critic policy that individualizes objects is necessary [19,20].
| Algorithm 5: PING-PONG Game’s DQN Training | |
| 1. | Procedure: training |
| 2. | Initialize: replay memory D to size N |
| 3. | Initialize: action-value function Q with random weights |
| 4. | Loop: episode = 1, M do Initialize state s_1 for t = 1, T do With probability ϵ select random action a_t otherwise select a_t = argmax_a Q(s_t,a; θ_i) Execute action a_t in emulator and observe r_t and s_(t + 1) Store transition (s_t,a_t,r_t,s_(t + 1)) in D Sample a minibatch of transitions (s_j,a_j,r_j,s_(j + 1)) from D Set y_j:= r_j for terminal s_(j + 1) r_j + γ*max_(a^′ ) Q(s_(j + 1),a′; θ_i) for non-terminal s_(j + 1) Perform a gradient step on (y_j-Q(s_j,_j; θ_i))^2 with respect to θ end for |
| 5. | End Loop |
To maximize the learning efficiency, segmentation of the reward acquisition structure is also applied. A policy to subdivide the reward acquisition period is established based on the time taken in each state after performing learning and exploration for a certain period, and the number of steps to reach the goal. The sum of the rewards until the game is finished in the reward is calculated, and weighting by implementing Equation (5), which is discounted by a factor of y at each stage added. This has the purpose of carrying out the goal in the shortest period, which is consistent with the segmenting of the reward acquisition structure.
5.3.2. Performance Evaluation and Discussion
To evaluate the performance of the N-DQN architecture proposed in this paper, we compare our result against DQN algorithm, with the same environments and conditions.
Figure 16 is the result of applying the DQN algorithm [21,22,23,24] to the ping-pong game environment. In conclusion, although the application of reinforcement learning that guarantees a certain level of performance through many training steps was successful, there are often intervals in which the performance deteriorates. It shows inefficient performance because it relies on randomness in the process of exploring and creating new episodes.
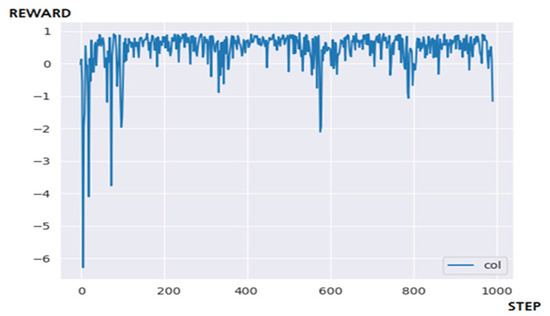
Figure 16.
The result of the ping-pong game through DQN.
Figure 17 is the result of applying N-DQN to the ping-pong game environment. In conclusion, it succeeded in applying reinforcement learning that guarantees a certain level and compared with the performance result of the DQN algorithm [25,26,27,28], it responds more flexibly to the new episode pattern. Also, there is almost no positive-bias problem. However, it did not significantly reduce the number of steps required for learning than expected, and it failed to completely exclude the section where the performance deteriorated. We still need to find a better solution to this and for the time being, for further performance improvement, adding heuristics to the reward structure can be a solution [29,30].
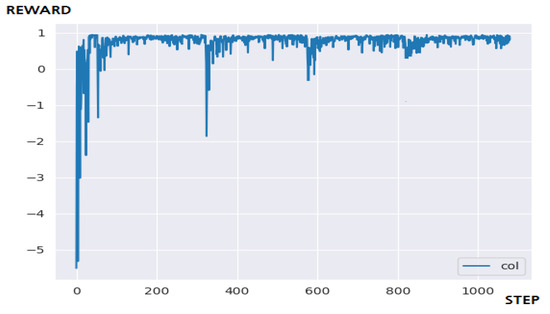
Figure 17.
The result of the ping-pong game through N-DQN.
6. Conclusions and Future Research
Since the agent does not have enough knowledge on its environment, the corresponding logical approach allows him to formulate plans that are not guaranteed to work. Agents almost never have access to all the necessary information about their environment in a delayed reward system such as games. Therefore, agents must act under conditions of uncertainty, which makes applying the traditional Q learning algorithm difficult to sparse reward environment.
In this study, we suggest and implement multi-agent N-DQN model to improve reinforcement learning by focusing on various factors and conditions that affect the performance of reinforcement learning, especially for the delayed reward systems, which are not easy to apply with general Q-learning [21,22,23,24]. The N-DQN has a structure in which multiple neural networks are layered by applying and extending the structure of HDQN so that NDQN can perform actions based on policies simultaneously in parallel. In addition, several additional ideas and technologies such as prioritized experience replay and subdivision of reward policies were adopted to improve the performance. The N-DQN, which has many factors of performance improvement, showed better results in the same environment than general reinforcement learning algorithms in actual performance evaluation.
The N-DQN shows about 3.5 times higher learning performance compared to the Q-Learning algorithm in the reward-sparse environment, and compared to the DQN, it showed about 1.1 times faster goal achievement speed. In addition, through the implementation of prioritized experience replay and the implementation of the reward acquisition period segmentation policy, the positive-bias of the existing reinforcement learning hardly occurred, and several problems of lowering learning efficiency were also improved. We have showed our implementation result with maze finding and ping-pong games.
According to the characteristics of the architecture that use many numbers of actors in parallel, the need for additional research on light-weighting the system for further performance improvement has been raised. It is because the multi-agent N-DQN shows a higher H/W share than general reinforcement learning models. [9] Consequently, a separate interest in studying multi-agent simulation and interaction of agents is an extension of the autonomy of agents by endowing them with the ability to draw logical conclusions and make decisions. According to these characteristics, we may think of two different directions for future research. One is more for parallel processing the agents, which implies more sophisticated algorithm for the distributed agents how to interact each other to expedite the learning speed. The other is to work on the weight reduction of the neural network structure to find a better solution (i.e., movement in the example games). We also have a plan to do some experiments on control systems in smart factory environment, which will prove that the model is suitable for self-learning in practical applications [31,32,33,34]. Because of the characteristics of the policy-based system, some heuristics are used in proving those rules. Hence, the system performance may depend on those heuristics. This is more like a basic XAI (Explainable AI) problem. The system presented in the paper is for delayed reward system, so it may need to make some modifications to the algorithm for non-delayed reward systems.
Funding
This work was partially supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (2020R1A2C11013921320682073250103) and partially supported by the MIST (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2022-2017-0-01633) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This paper was supported by Konkuk University in 2020.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef] [Green Version]
- Boyan, J.A.; Moore, A.W. Generalization in reinforcement learning: Safely approximating the value function. Adv. Neural Inf. Process. Syst. 1995, 369–376. [Google Scholar]
- Kulkarni, T.D.; Narasimhan, K.; Saeedi, A.; Tenenbaum, J. Hierarchical deep reinforcement learning: Integrating temporal abstraction and intrinsic motivation. Adv. Neural Inf. Inf. Process. Syst. 2016, 3675–3683. [Google Scholar]
- Hasselt, H.V. Double Q-learning. Adv. Neural Inf. Process. Syst. 2010, 2613–2621. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Sutton, R.S. Generalization in reinforcement learning: Successful examples using sparse coarse coding. Adv. Neural Inf. Process. Syst. 1996, 8, 1038–1044. [Google Scholar]
- Queyrel, M. Multithreading to Construct Neural Networks 2018. Available online: https://www.slideshare.net/altoros/multithreading-to-construct-neural-networks (accessed on 14 January 2019).
- Purkaitl, N. How to Train Your Neural Networks in Parallel with Keras and ApacheSpark 2018. Available online: https://towardsdatascience.com/how-to-train-your-neural-networks-in-parallel-with-keras-and-apache-spark-ea8a3f48cae6 (accessed on 15 January 2019).
- Lifeomic/Sparkflow. 2018. Available online: https://github.com/lifeomic/sparkflow (accessed on 15 January 2019).
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling network architectures for deep reinforcement learning. arXiv 2015, arXiv:1511.06581. [Google Scholar]
- Tesauro, G. Temporal difference learning and TD-Gammon. Commun. ACM 1995, 38, 58–68. [Google Scholar] [CrossRef]
- O’Doherty, J.P.; Dayan, P.; Friston, K.; Critchley, H.; Dolan, R.J. Temporal difference models and reward-related learning in the human brain. Neuron 2003, 38, 329–337. [Google Scholar] [CrossRef] [Green Version]
- Lyu, S. Prioritized Experience Replay. 2018. Available online: https://lyusungwon.github.io/reinforcement-learning/2018/03/20/preplay.html (accessed on 11 January 2019).
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Adv. Neural Inf. Process. Syst. 2000, 12, 1057–1063. [Google Scholar]
- Tijsma, A.D.; Drugan, M.M.; Wiering, M.A. Comparing exploration strategies for Q-learning in random stochastic mazes. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Saravanan, C. Color image to grayscale image conversion. In Proceedings of the 2010 Second International Conference on Computer Engineering and Applications, Bali Island, Indonesia, 19–21 March 2010. [Google Scholar]
- Kanan, C.; Cottrell, G.W. Color-to-Grayscale: Does the method matter in image recognition? PLoS ONE 2012, 7, e29740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foerster, J.N.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual multi-agent policy gradients. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, O.P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6379–6390. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the Thirtieth AAAI Conference Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. Int. Conf. Mach. Learn. 2016, 48, 1928–1937. [Google Scholar]
- Osband, I.; Blundell, C.; Pritzel, A.; van Roy, B. Deep exploration via bootstrapped DQN. Adv. Neural Inf. Process. Syst. 2016, 29, 4026–4034. [Google Scholar]
- Oh, J.; Guo, X.; Lee, H.; Lewis, R.L.; Singh, S. Action-conditional video prediction using deep networks in atari games. Adv. Neural Inf. Process. Syst. 2015, 28, 2863–2871. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Wiering, M.A.; van Hasselt, H. Ensemble algorithms in reinforcement learning. IEEE Trans. Syst. Man Cybern. 2008, 38, 930–936. [Google Scholar] [CrossRef] [Green Version]
- Rolls, E.T.; McCabe, C.; Redoute, J. Expected value, reward outcome, and temporal difference error representations in a probabilistic decision task. Cereb. Cortex 2007, 18, 652–663. [Google Scholar] [CrossRef]
- Moore, A.W.; Atkeson, C.G. Prioritized sweeping: Reinforcement learning with less data and less time. Mach. Learn. 1993, 13, 103–130. [Google Scholar] [CrossRef] [Green Version]
- Dayan, P.; Hinton, G.E. Feudal reinforcement learning. Adv. Neural Inf. Process. Syst. 1993, 5, 271–278. [Google Scholar]
- Tesauro, G. Practical issues in temporal difference learning. Adv. Neural Inf. Process. Syst. 1992, 4, 259–266. [Google Scholar]
- Abul, O.; Polat, F.; Alhajj, R. Multiagent reinforcement learning using function approximation. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2000, 4, 485–497. [Google Scholar] [CrossRef]
- Bus¸oniu, L.; De Schutter, B.; Babuska, R. Multiagent reinforcement learning with adaptive state focus. In Proceedings of the 17th Belgian-Dutch Conference on Artificial Intelligence (BNAIC-05), Brussels, Belgium, 17–18 October 2005; pp. 35–42. [Google Scholar]
- Castaño, F.; Haber, R.E.; Mohammed, W.M.; Nejman, M.; Villalonga, A.; Martinez Lastra, J.L. Quality monitoring of complex manufacturing systems on the basis of model driven approach. Smart Struct. Syst. 2020, 26, 495–506. [Google Scholar] [CrossRef]
- Beruvides, G.; Juanes, C.; Castaño, F.; Haber, R.E. A self-learning strategy for artificial cognitive control systems. In Proceedings of the 2015 IEEE International Conference on Industrial Informatics, INDIN, Cambridge, UK, 22–24 July 2015; pp. 1180–1185. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).