Structural Stress Characteristics and Joint Deformation of Shield Tunnels Crossing Active Faults
Abstract
:1. Introduction
2. Numerical Modeling
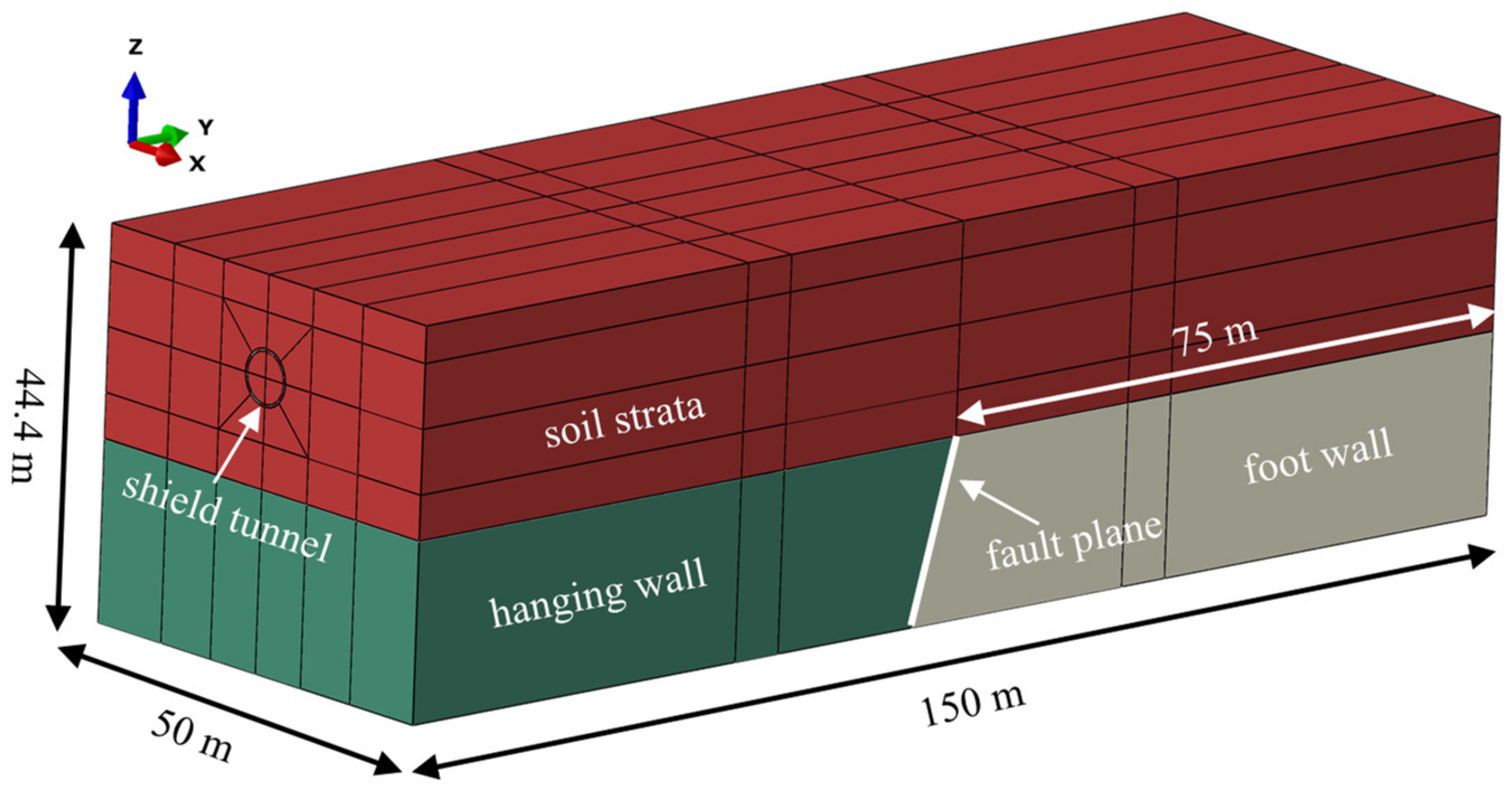
2.1. Engineering Background
2.2. Overview of Numerical Models
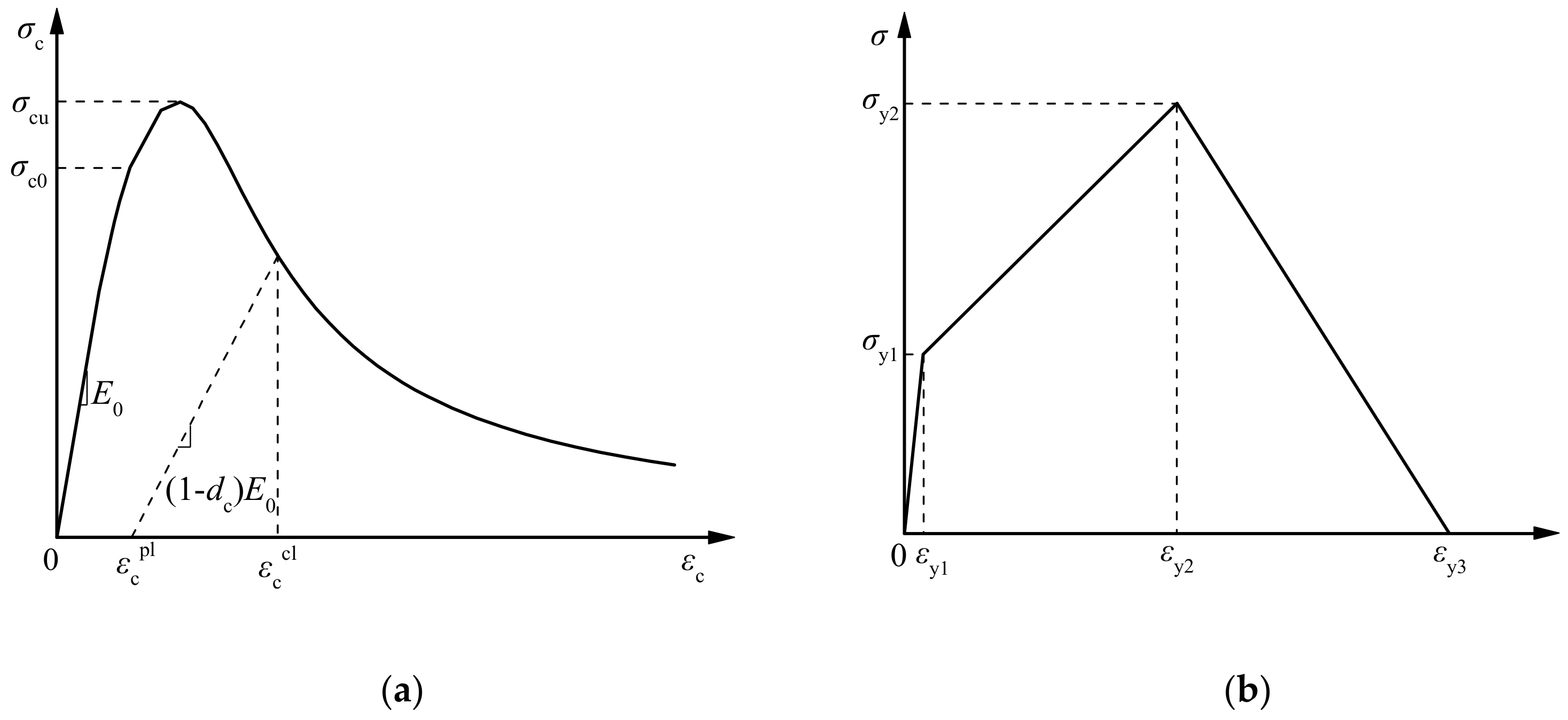
2.3. Constitutive Model and Contact Settings
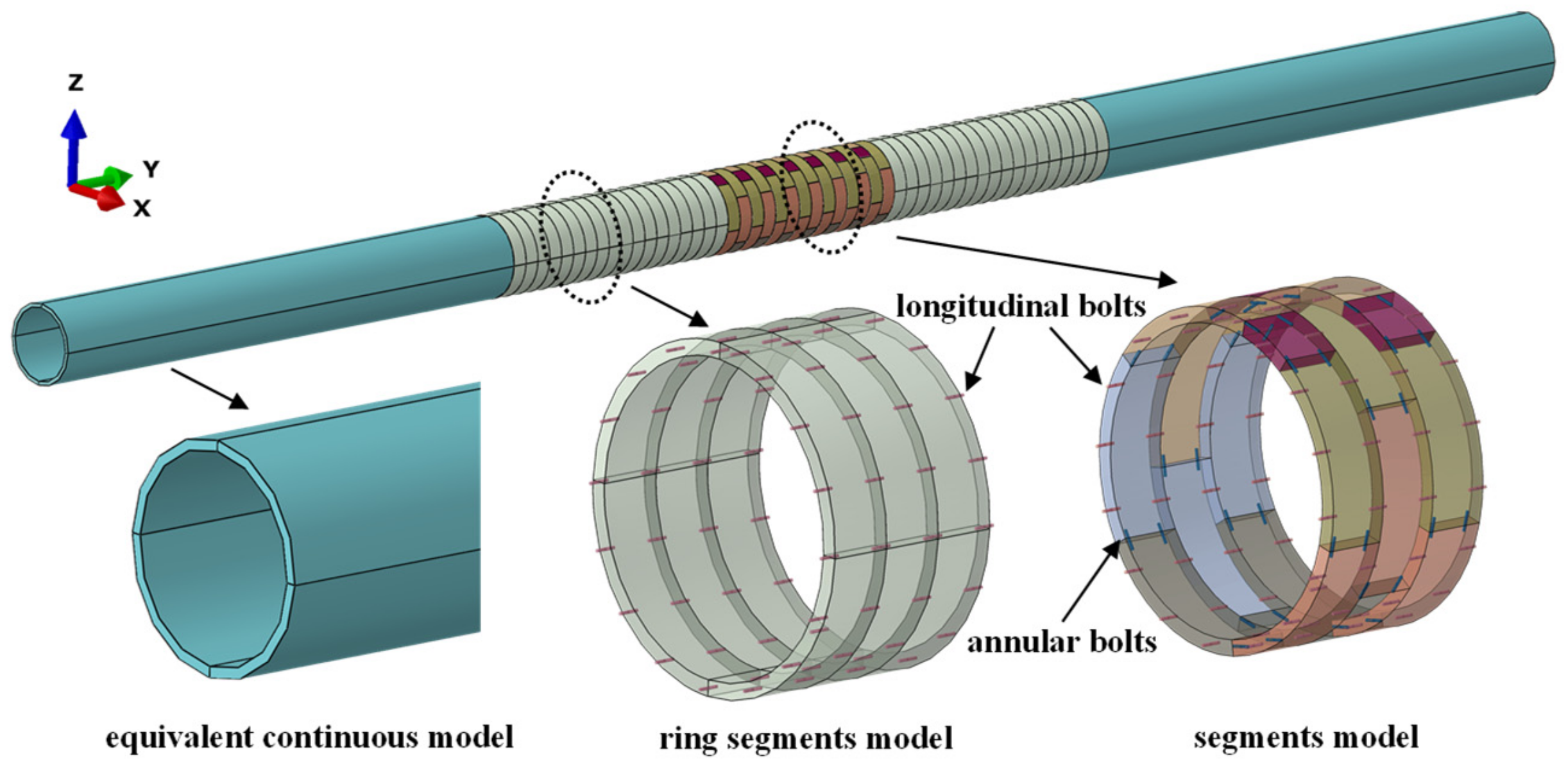
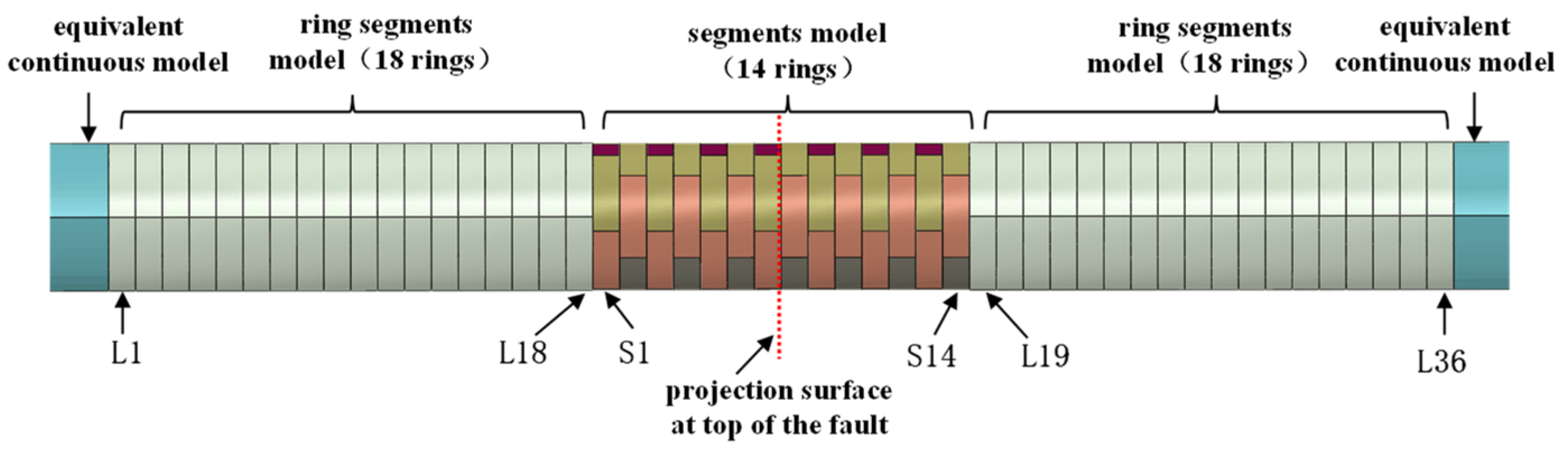
2.4. Segmental Tunnel Simulation
2.5. Boundary Conditions and Simulation of Fault Movement
3. Analysis of Segmental Tunnel Influenced by Fault Movement
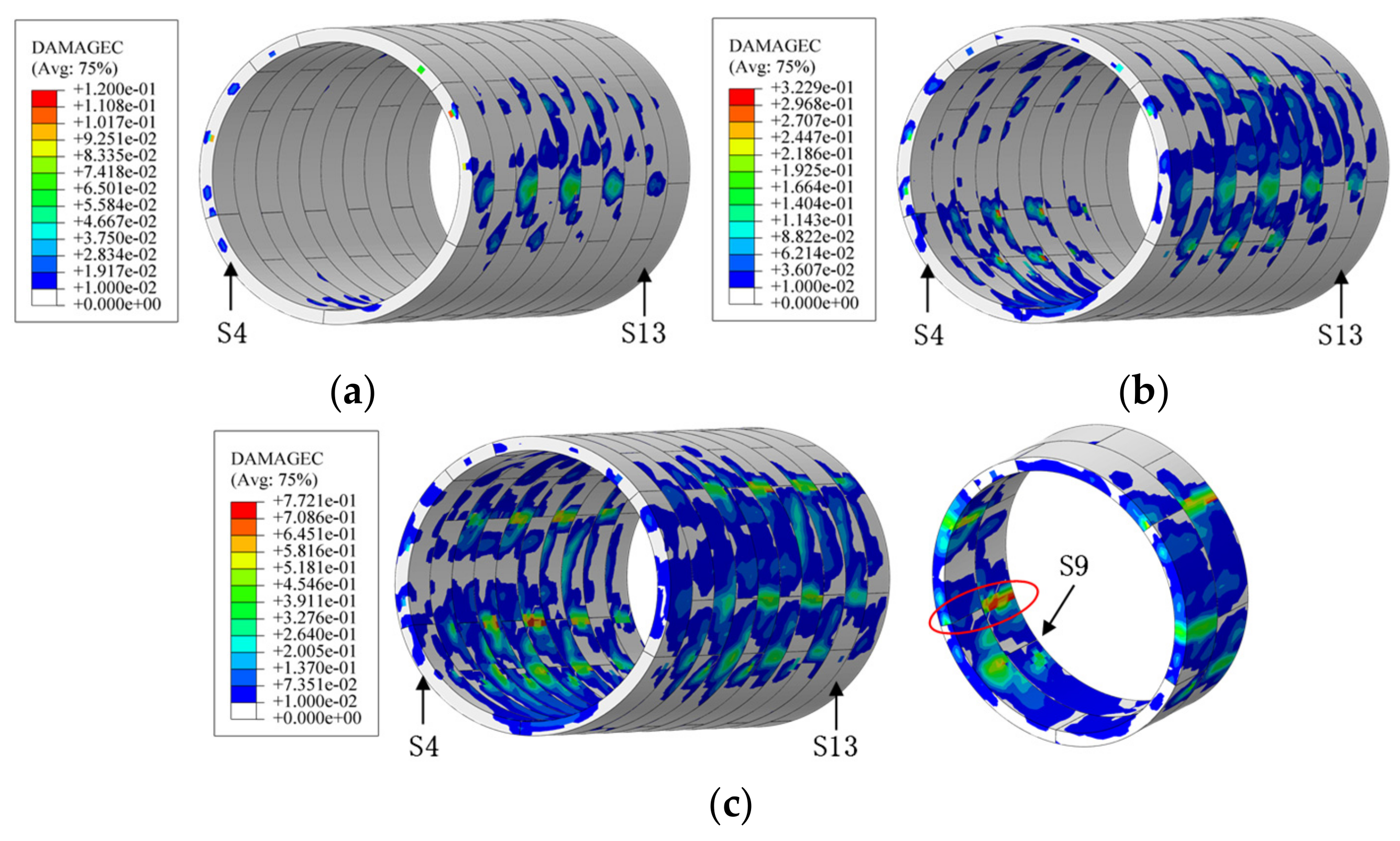
3.1. Mechanical Response of Segmental Tunnel
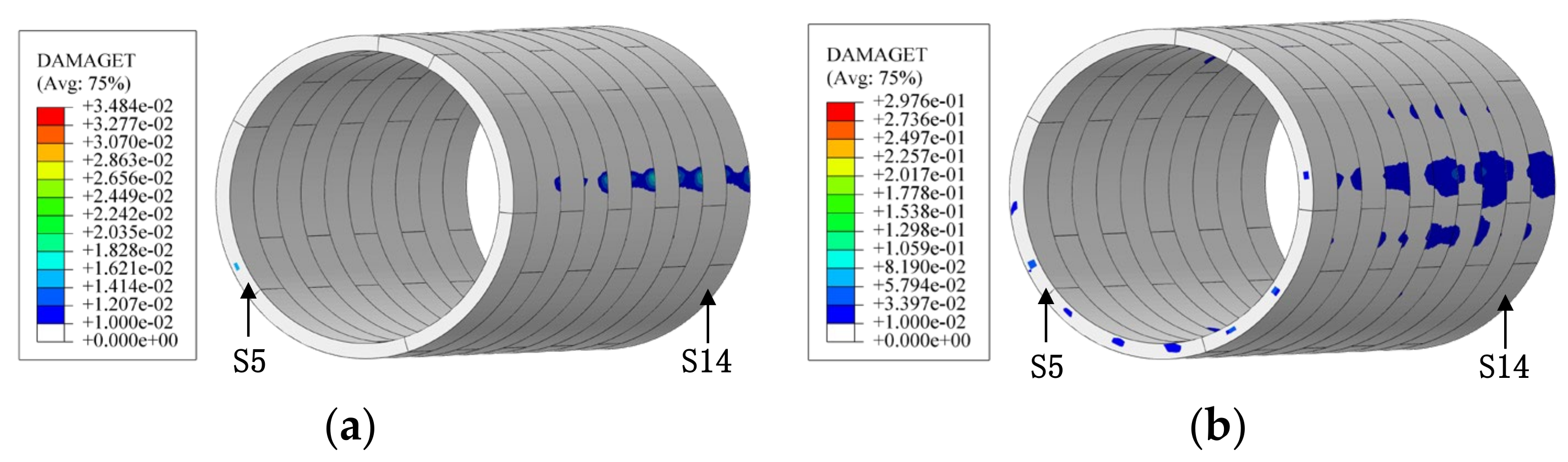
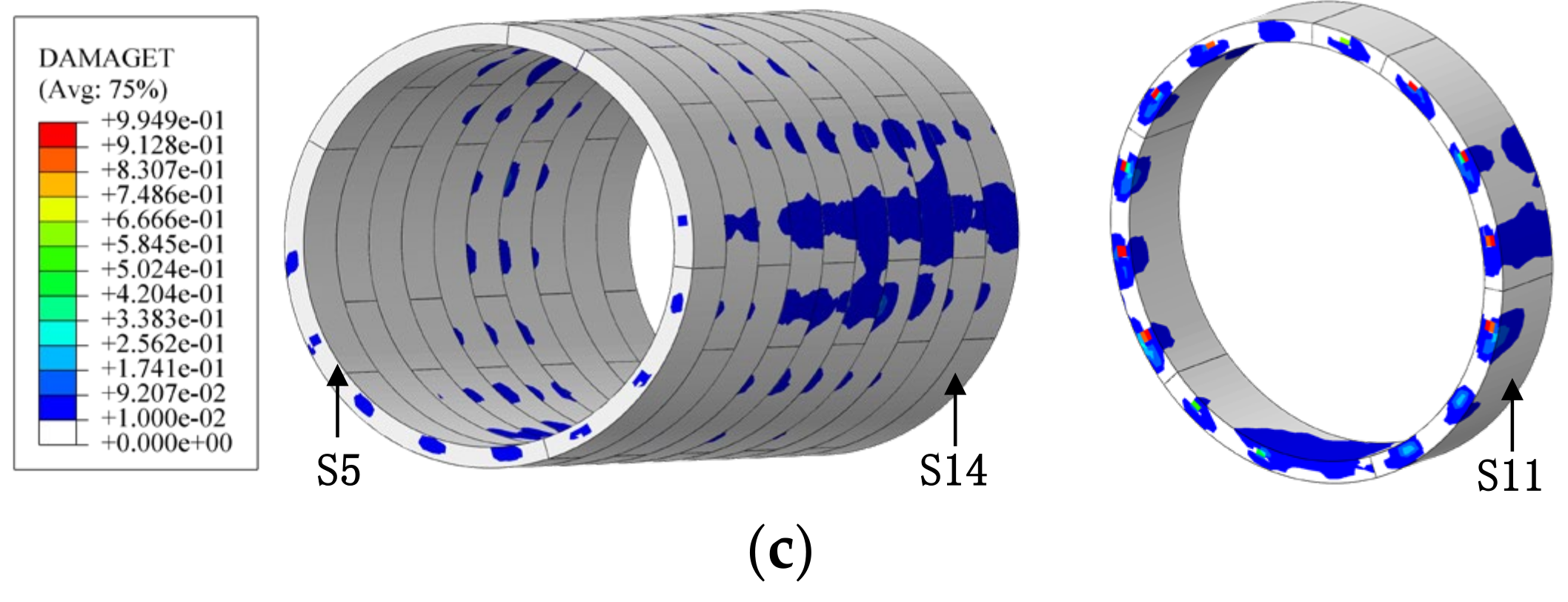
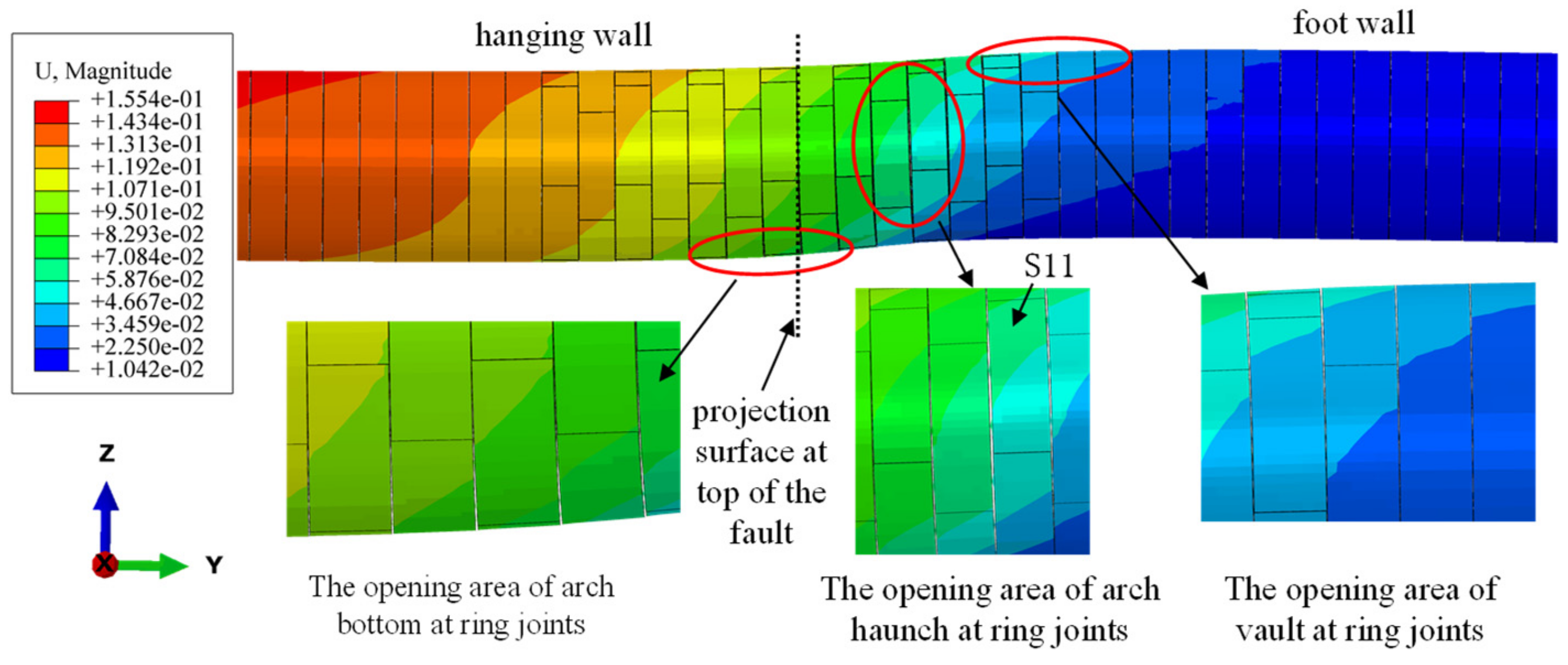
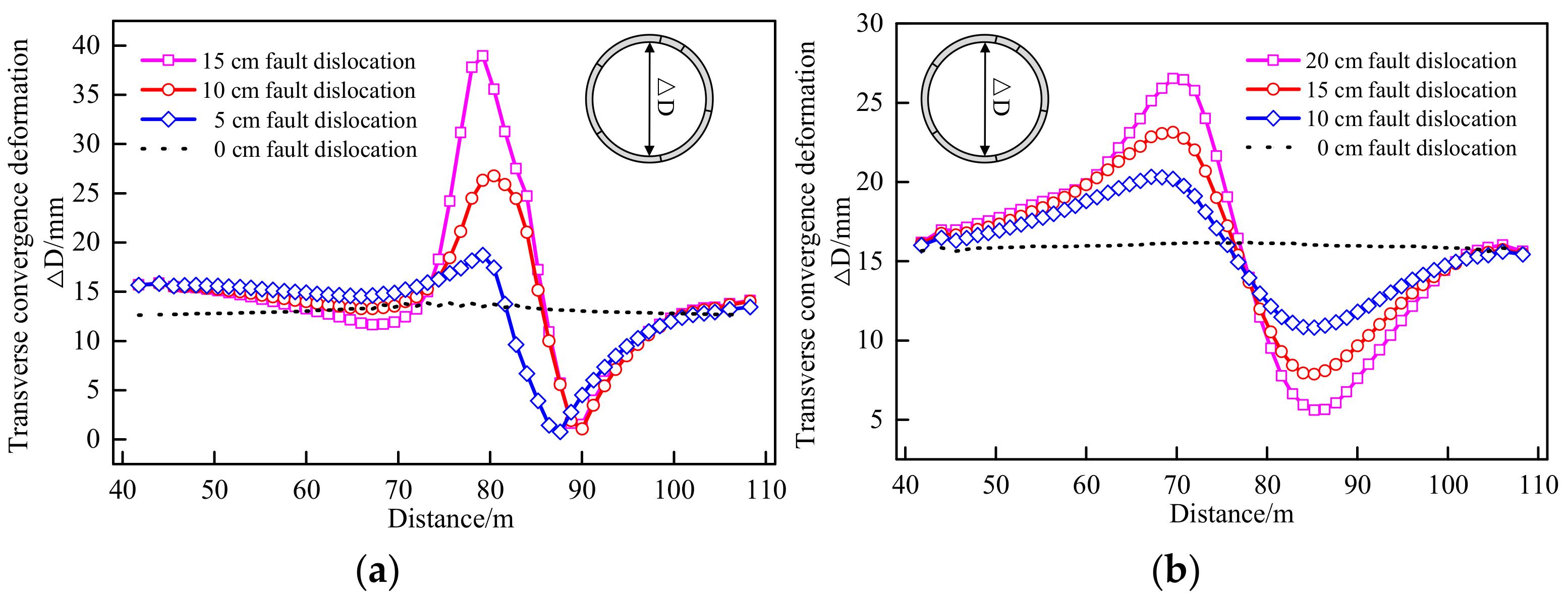
3.2. Deformation of Segmental Lining and Joints
4. Parametric Study and -Discussions
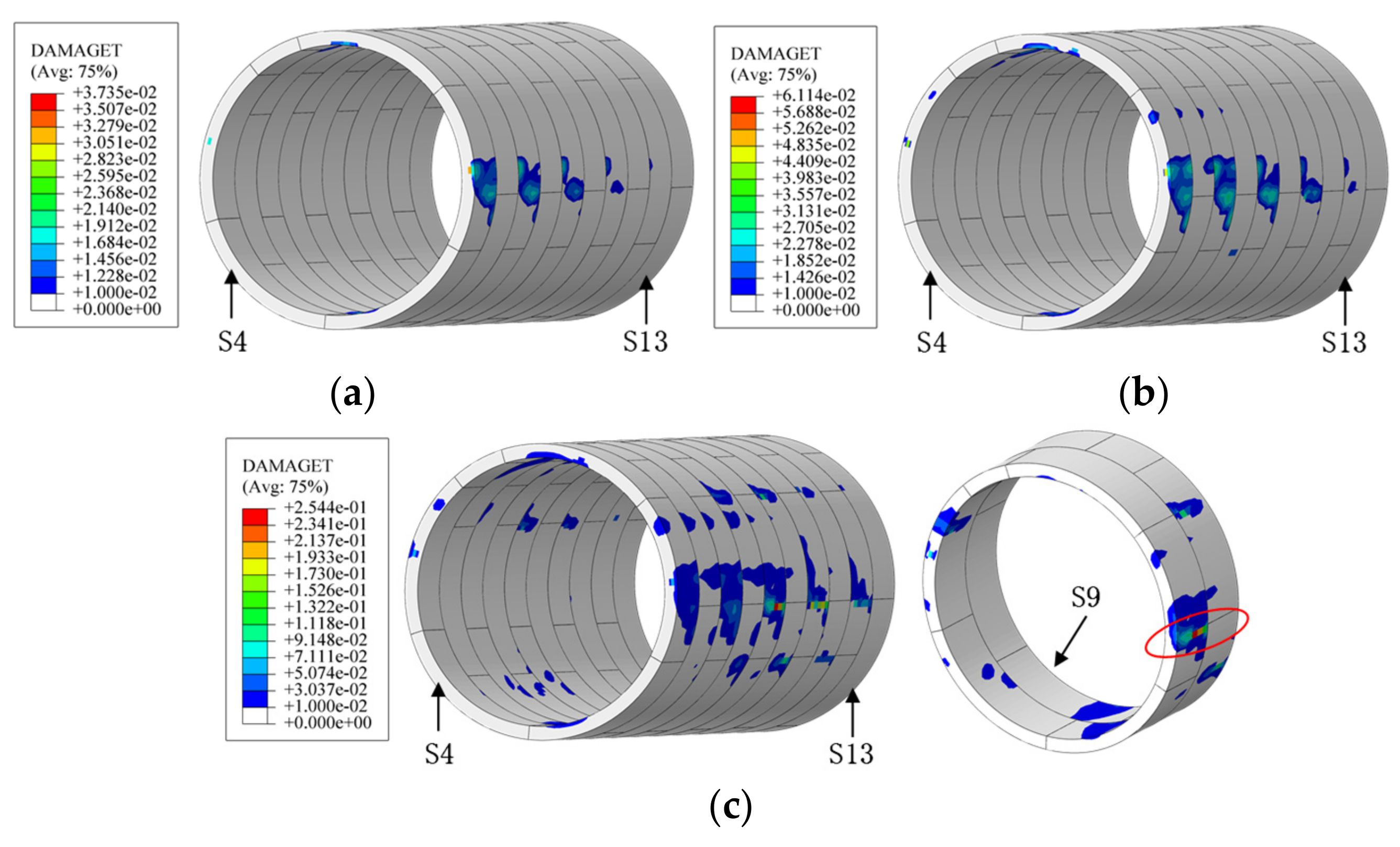
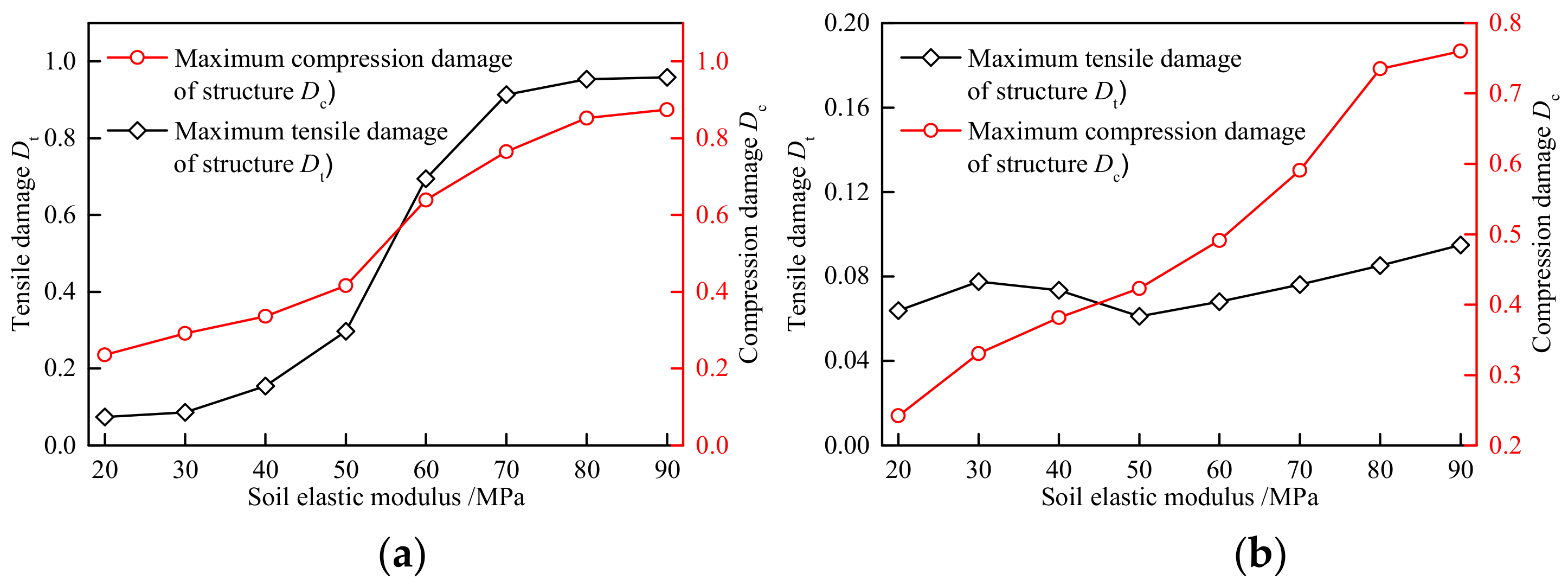
4.1. Elastic Modulus of Stratum Influence on Tunnel Behavior
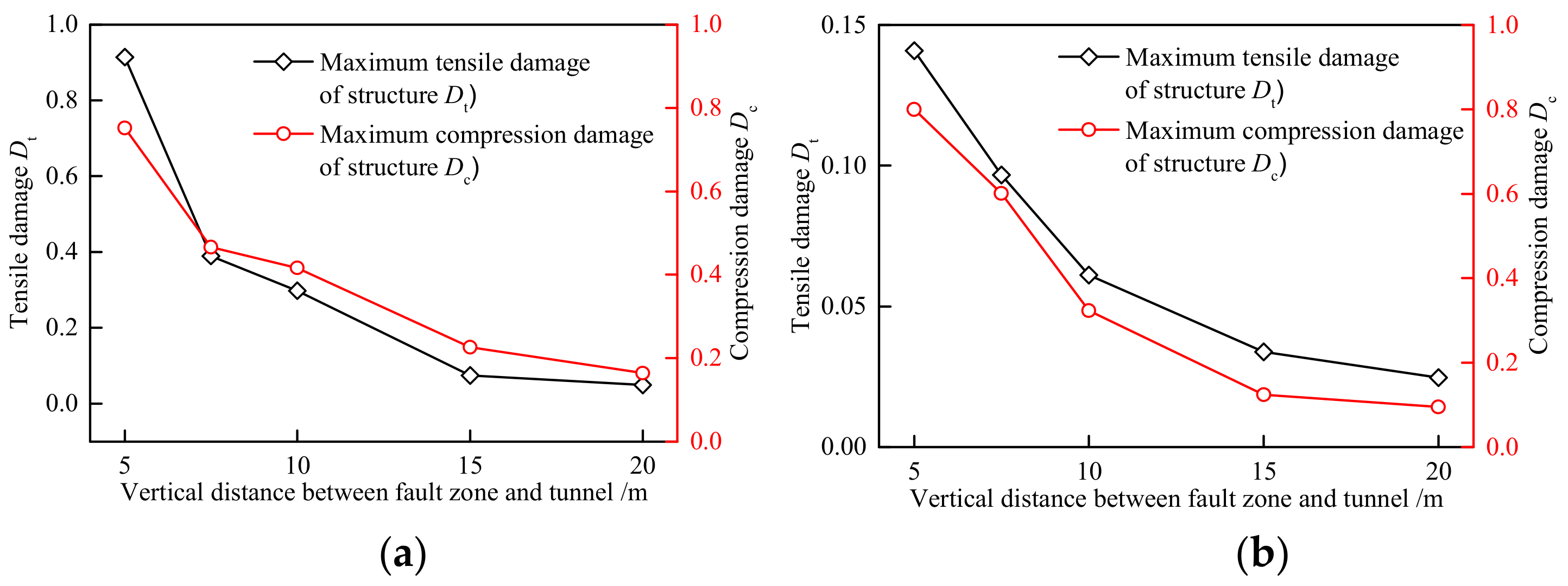
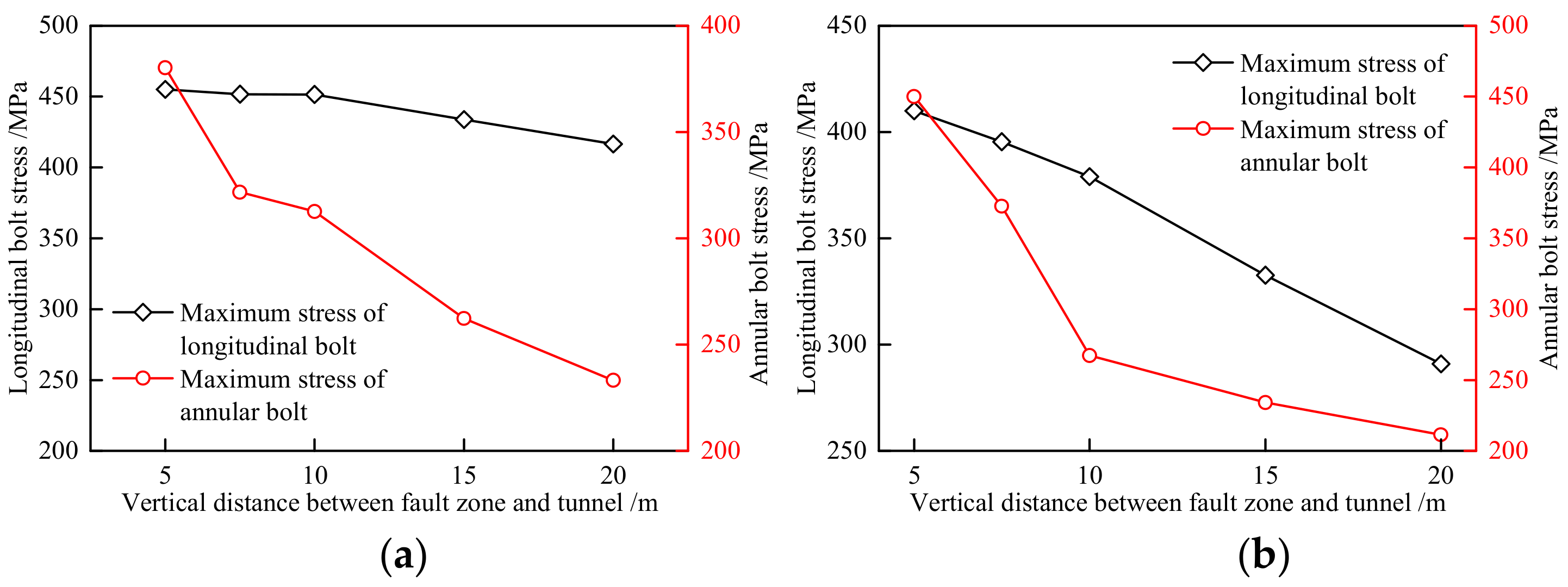
4.2. Vertical Distance between Fault Zone and Tunnel
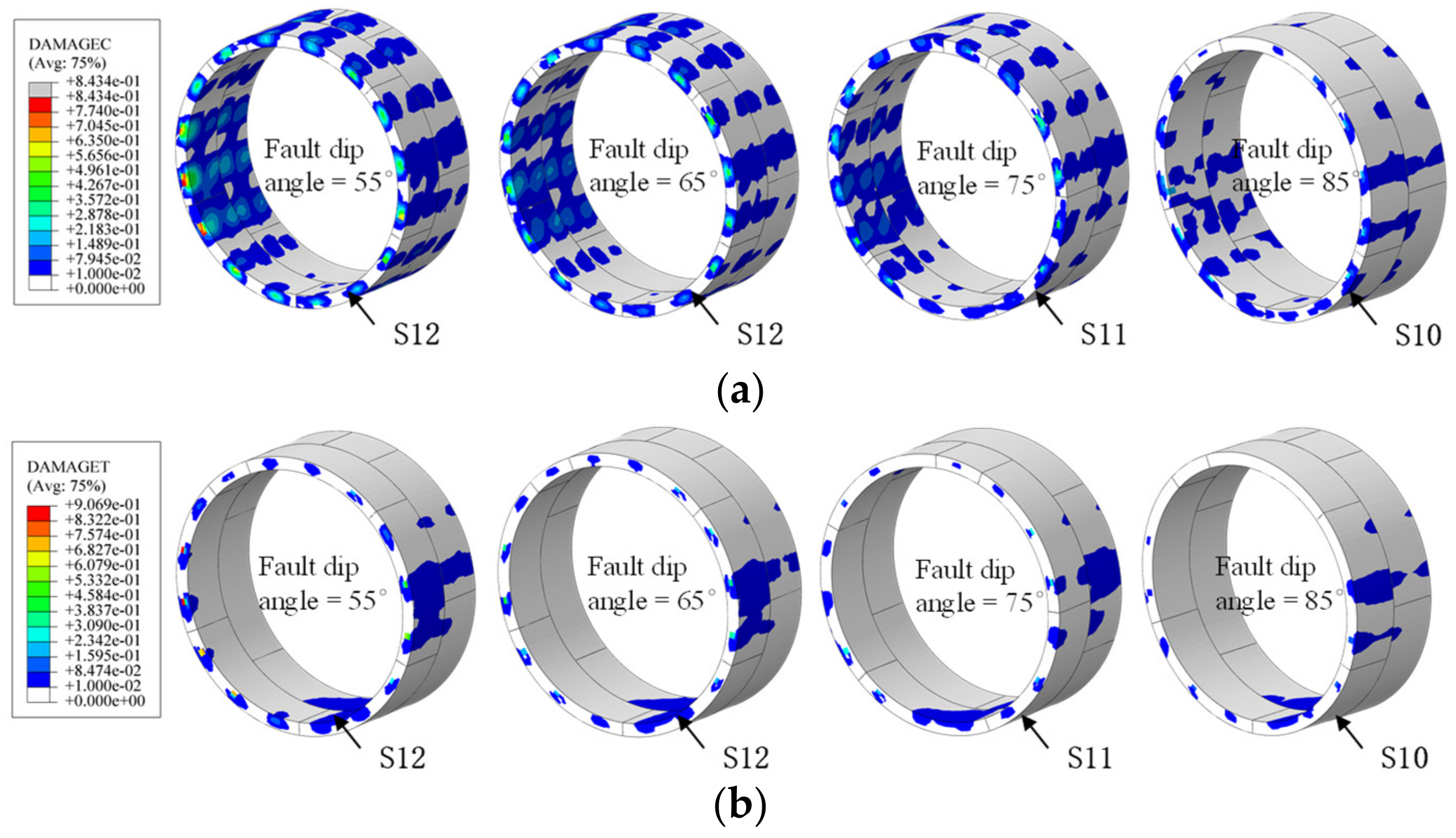
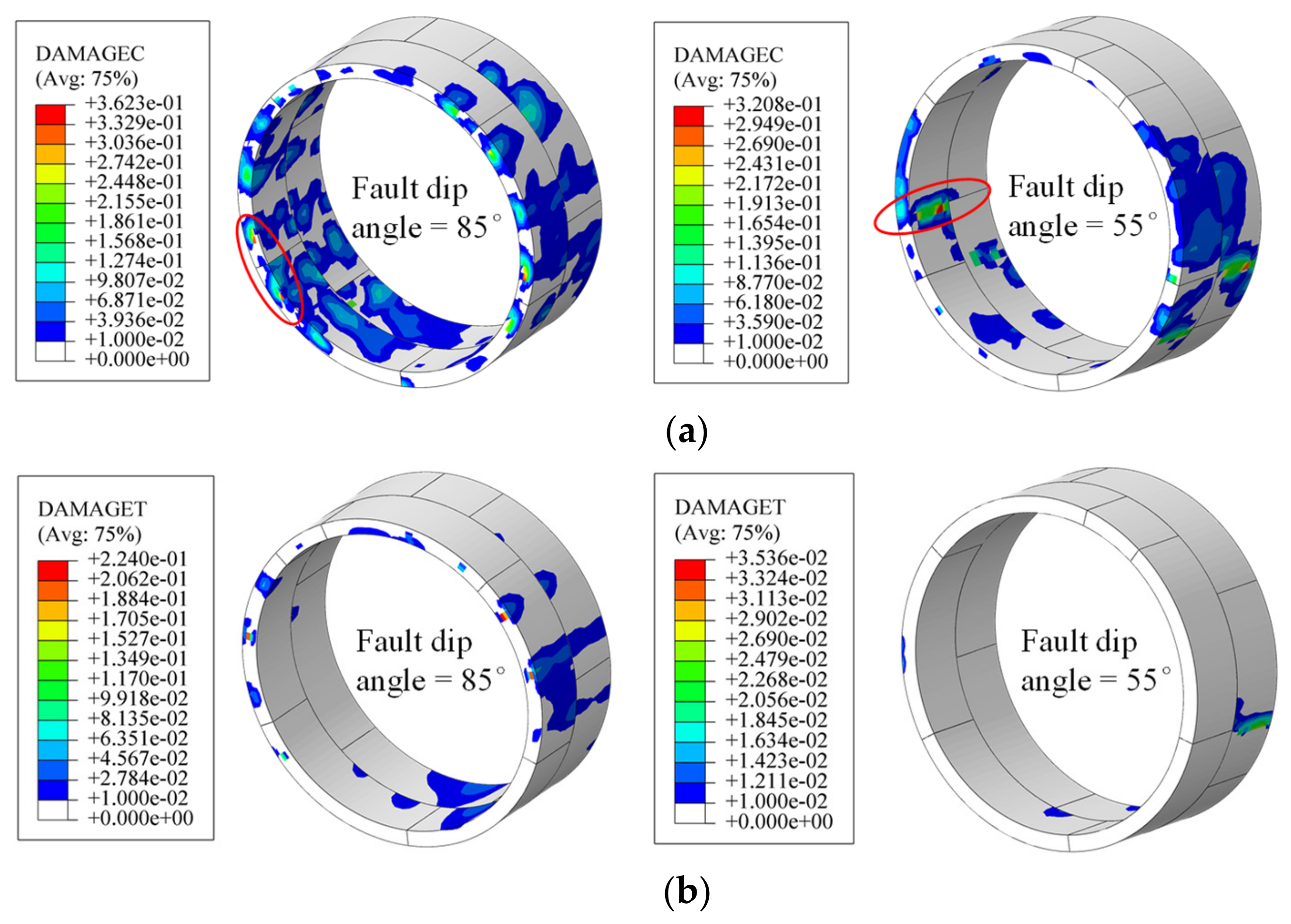
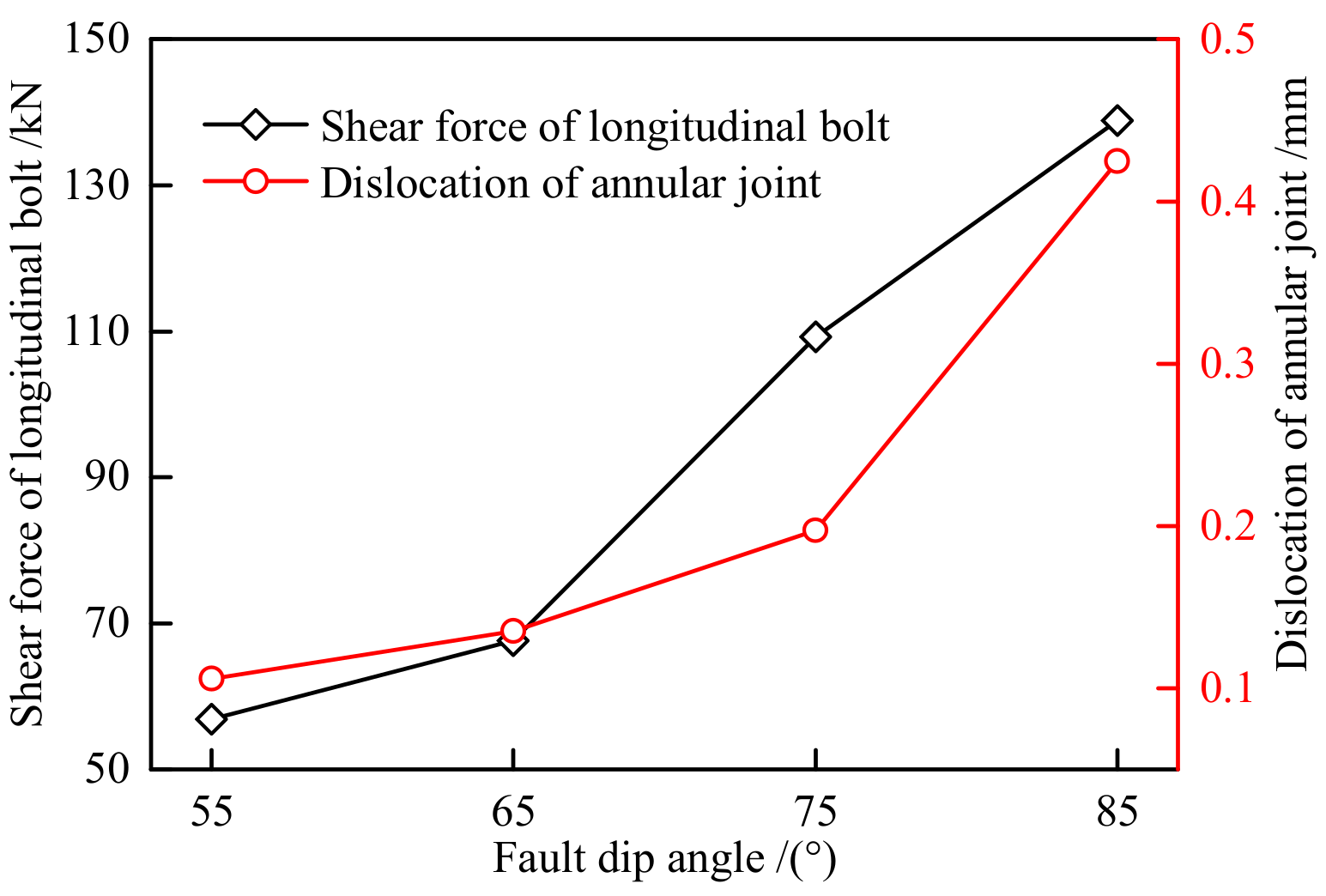
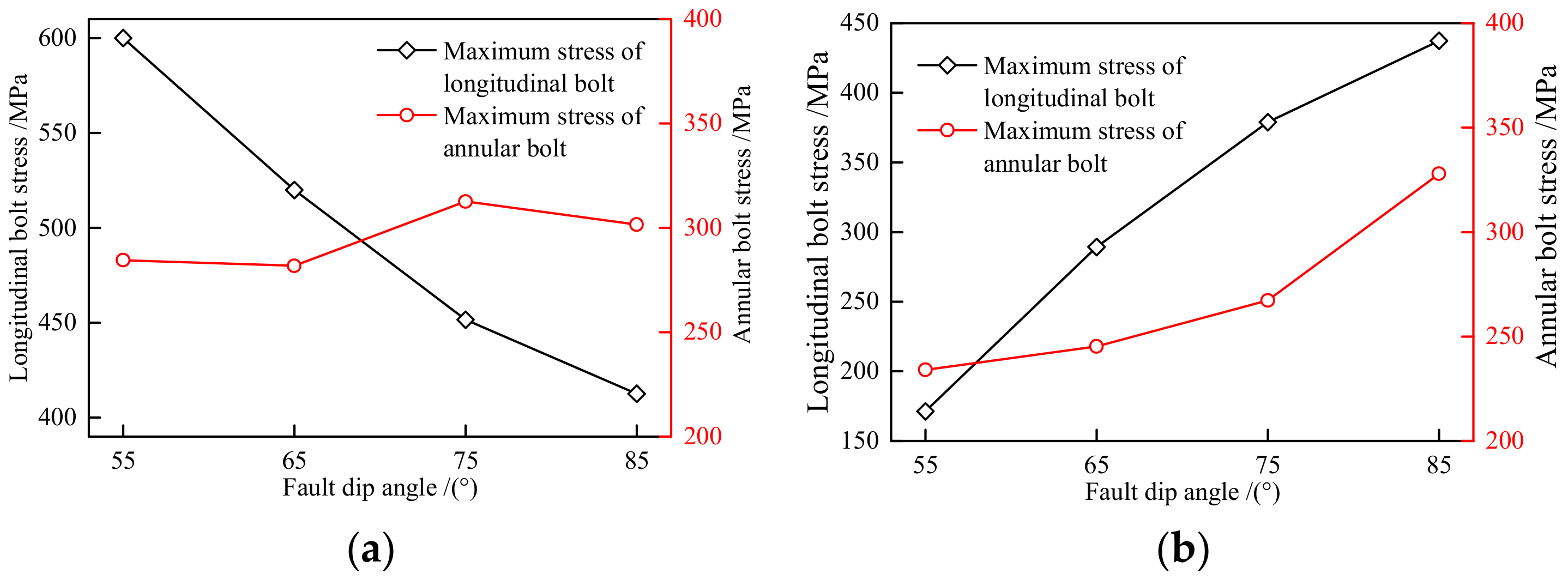
4.3. Fault Dip Influence on Tunnel Behavior
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, Q.P.; Peng, J.M.; Ng, C.W.; Shi, J.W.; Chen, X.X. Centrifuge and numerical modeling of tunnel intersected by normal fault rupture in sand. Comput. Geotech. 2019, 106, 108–116. [Google Scholar] [CrossRef]
- Wang, H.R.; Zhong, Z.L.; Zhao, M.; Wang, Z.; Zhao, X.; Du, X. Model experimental study of the influence of strike-slip fault dislocation on tunnel. J. Beijing Univ. Technol. 2021, 47, 691–701. [Google Scholar] [CrossRef]
- Wang, D.Y.; Cui, G.Y.; Yuan, J.X. Model tests on effect of dislocation reducing measures of stick-slip fault of tunnels. Chin. J. Geotech. Eng. 2018, 40, 1515–1521. [Google Scholar] [CrossRef]
- Wang, T.Q.; Cui, Z.; Sheng, Q.; Ning, B.K.; Ma, Y.L.N.; Zhou, G.X. Model experimental test and numerical analysis of the influence of a strike-slip fault on a tunnel project. IOP Conf. Ser. Earth Environ. Sci. 2020, 570, 032019. [Google Scholar] [CrossRef]
- Shahidi, A.R.; Vafaeian, M. Analysis of longitudinal profile of the tunnels in the active faulted zone and designing the flexible lining (for Koohrang-III tunnel). Tunn. Undergr. Space Technol. 2005, 20, 213–221. [Google Scholar] [CrossRef]
- Han, X.; Li, W. Numerical Analysis on the Structure Type and Mechanical Response of Tunnel Crossing Active Reverse Fault. Geofluids 2021, 2021, 5513042. [Google Scholar] [CrossRef]
- An, S.; Tao, L.J.; Bian, J.; Han, X.; Wu, X. Damage Analysis on Subway Tunnel Structure under Effect of Reverse Fault Dis-location. J. Hunan Univ. (Nat. Sci.) 2020, 47, 147–156. [Google Scholar] [CrossRef]
- Ranjbarnia, M.; Zaheri, M.; Dias, D. Three-dimensional finite difference analysis of shallow sprayed concrete tunnels crossing a reverse fault or a normal fault: A parametric study. Front. Struct. Civ. Eng. 2020, 14, 998–1011. [Google Scholar] [CrossRef]
- Liu, X.Z.; Li, X.F.; Sang, Y.L.; Lin, L. Experimental study on normal fault rupture propagation in loose strata and its impact on mountain tunnels. Tunn. Undergr. Space Technol. 2015, 49, 417–425. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, Z.Q.; Yi, Z.W. Model experimental study of the influence of normal fault with stick-slip dislocation on subway tunnel structure. Rock Soil Mech. 2019, 47, 3037–3044, 3053. [Google Scholar] [CrossRef]
- Sabagh, M.; Ghalandarzadeh, A. Centrifugal modeling of continuous shallow tunnels at active normal faults intersection. Transp. Geotech. 2020, 22, 100325. [Google Scholar] [CrossRef]
- Yao, C.; He, C.; Takemura, J.; Feng, K.; Guo, D.; Huang, X. Active length of a continuous pipe or tunnel subjected to reverse faulting. Soil Dyn. Earthq. Eng. 2021, 148, 106825. [Google Scholar] [CrossRef]
- Yan, G.; Shen, Y.; Gao, B.; Zheng, Q.; Fan, K.; Huang, H. Experimental study of stick-slip fault crossing segmental tunnels with joints. Rock Soil Mech. 2019, 40, 4450–4458. [Google Scholar] [CrossRef]
- Cui, G.Y.; Wang, X.L. Model Test Study on the Antibreaking Technology of Reducing Dislocation Layer for Subway Interval Tunnel of the Stick-Slip Fracture. Adv. Civ. Eng. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Shen, Y.S.; Wang, Z.Z.; Yu, J.; Zhang, X.; Gao, B. Shaking table test on flexible joints of mountain tunnels passing through normal fault. Tunn. Undergr. Space Technol. 2020, 98, 103299. [Google Scholar] [CrossRef]
- Kanik, M. Evaluation of the limitations of RMR89 system for preliminary support selection in weak rock class. Comput. Geotech. 2019, 115, 103159. [Google Scholar] [CrossRef]
- Alnmr, A. Material Models to Study the Effect of Fines in Sandy Soils Based on Experimental and Numerical Results. Acta Tech. Jaurinensis 2021, 14, 651–680. [Google Scholar] [CrossRef]
- Sabagh, M.; Ghalandarzadeh, A. Numerical modelings of continuous shallow tunnels subject to reverse faulting and its verification through a centrifuge. Comput. Geotech. 2020, 128, 103813. [Google Scholar] [CrossRef]
- Guo, X.Y.; Geng, P.; Ding, T.; Wang, Q.; Yang, Q.; He, Y. Mechanical behavior of tunnel under stick-slip action of reverse fault. J. Vib. Shock. 2021, 40, 249–258. [Google Scholar] [CrossRef]
- Zhong, Z.; Wang, Z.; Zhao, M.; Du, X. Structural damage assessment of mountain tunnels in fault fracture zone subjected to multiple strike-slip fault movement. Tunn. Undergr. Space Technol. 2020, 104, 103527. [Google Scholar] [CrossRef]
- She, F.T.; Li, Y.P.; Li, T.; Wang, S. Mechanical properties of split-tunnel-linning structure caused by buried ground fissuse propagation. China Earthq. Eng. J. 2020, 40, 684–691. [Google Scholar] [CrossRef]
- An, S.; Tao, L.J.; Han, X.C.; Zhang, Y. Application of two-level design method on subway tunnel crossing active fault: A case study on Urumqi subway tunnel intersected by reverse fault dislocation. Bull. Eng. Geol. Environ. 2021, 80, 3871–3884. [Google Scholar] [CrossRef]
- Zhao, K.; Chen, W.; Yang, D.; Zhao, W.; Wang, S.; Song, W. Mechanical tests and engineering applicability of fibre plastic concrete used in tunnel design in active fault zones. Tunn. Undergr. Space Technol. 2019, 88, 200–208. [Google Scholar] [CrossRef]
- Zaheri, M.; Ranjbarnia, M.; Dias, D.; Oreste, P. Performance of segmental and shotcrete linings in shallow tunnels crossing a transverse strike-slip faulting. Transp. Geotech. 2020, 23, 100333. [Google Scholar] [CrossRef]
- Kiani, M.; Akhlaghi, T.; Ghalandarzadeh, A. Experimental modeling of segmental shallow tunnels in alluvial affected by normal faults. Tunn. Undergr. Space Technol. 2016, 51, 108–119. [Google Scholar] [CrossRef]
- Hu, Z.P.; Peng, J.B.; Wang, Q.Y.; Zhu, Q.D.; Zhao, Z.R. Modeling test research on failure mechanism of shieldtunnel crossing ground fissure with 60°. Chin. J. Rock Mech. Eng. 2010, 29, 176–183. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=YSLX201001022&DbName=CJFQ2010 (accessed on 22 February 2022).
- Hu, Z.P.; Peng, J.B.; Huang, Q.B.; Wang, Q.Y. Physical modeling test on shield tunnel crossing ground fissure with 30°. J. Chang. Univ. (Nat. Sci. Ed.) 2009, 29, 63–68. [Google Scholar] [CrossRef]
- Li, H.Y.; Li, X.G.; Ma, M.Z.; Liu, H.; Yang, Y. Model experimental study on influence of buried fault dislocation on shield tunnel. J. Zhejiang Univ. (Eng. Sci.) 2022, 56, 1–9. Available online: https://kns.cnki.net/kcms/detail/33.1245.T.20220105.1431.011.html (accessed on 22 February 2022).
- Liang, J.W.; Wu, Z.Q.; Xin, Y.; Ba, Z. Seismic counter- measures of shield tunnel under fault movement. Earthq. Eng. Eng. Vib. 2020, 40, 1–11. [Google Scholar] [CrossRef]
- Lunardi, P.; Cassani, G.; Canzoneri, A.; Carriero, F.; Bomben, G. Passage of a precast segmental lining tunnel through an active fault-Special segments and details-Thessaloniki metro. In Proceedings of the World Tunnel Congress 2017–Surface Challenges–Underground Solutions; JSCE: Bergen, Norway, 1966; pp. 37–44. Available online: https://www.rocksoil.com/pdf/269.pdf (accessed on 22 February 2022).
- Keskin, İ.; Ahmed, M.Y.; Taher, N.R.; Gör, M.; Abdulsamad, B.Z. An evaluation on effects of surface explosion on underground tunnel; availability of ABAQUS Finite element method. Tunn. Undergr. Space Technol. 2022, 120, 104306. [Google Scholar] [CrossRef]
- Liu, X.Z.; Cai, G.Y.; Yang, F.; Sang, Y.L.; Wu, J.X. Structural Bearing Behavior and Deformation Controlling Indicators for Staggered Jointed Shield Tunnel Lining in Fractured Surrounding Rock. China J. Highw. Transp. 2017, 30, 57–65. [Google Scholar] [CrossRef]
- GB 50010-2010 Code for Design of Concrete Structures; China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Shen, X.P.; Wang, C.Y.; Zhou, L. A Damage Plastic Constitutive Model for Reinforced Concrete and Its Engi-neering Application. Eng. Mech. 2007, 24, 122–128. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, Z.Q.; Qing, C. Research on Influence upon Tunnel Structure of Metro Line 1 in Urumqi Forced by Normal Fault Dislocation. China Railw. Sci. 2019, 40, 54–63. [Google Scholar] [CrossRef]
- Shiba, Y.; Kawashima, K.; Obinata, N.; Kano, T. An evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analyses. Doboku Gakkai Ronbunshu 1988, 398, 319–327. [Google Scholar] [CrossRef]











| Materials | Gravity Density (kN•m−3) | Elastic Modulus (MPa) | Poisson Ratio | Angle of Internal Friction (°) | Cohesive Force (kPa) | Yield Stress (MPa) | Ultimate Stress (MPa) |
|---|---|---|---|---|---|---|---|
| Soil | 2080 | 50 | 0.2 | 35 | 20 | - | - |
| Rock stratum | 2720 | 8 × 104 | 0.2 | 40 | 500 | - | - |
| Bolts | 7800 | 170 × 103 (after reduction) [32] | 0.2 | - | - | 480 | 600 |
| Tensile Strain | Tensile Damage Factor | |
|---|---|---|
| 0 | 0 | 0 |
| εy1 | 0.0001 | 0 |
| εy2 | 0.002 | 0.1 |
| εy3 | 0.0078 | 0.9 |
| Position | Contact Surface Parameters | Remark |
|---|---|---|
| Fault dislocation surface | Normal direction is hard contact, tangential friction coefficient is 0.1 | Sliding and inseparable |
| Tunnel-strata | Normal direction is hard contact, tangential friction coefficient is 0.4 | Separable |
| Segment-segment | Normal direction is hard contact, tangential friction coefficient is 0.6 | Separable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Li, X.; Yang, Y.; Liu, Y.; Ma, M. Structural Stress Characteristics and Joint Deformation of Shield Tunnels Crossing Active Faults. Appl. Sci. 2022, 12, 3229. https://doi.org/10.3390/app12073229
Li H, Li X, Yang Y, Liu Y, Ma M. Structural Stress Characteristics and Joint Deformation of Shield Tunnels Crossing Active Faults. Applied Sciences. 2022; 12(7):3229. https://doi.org/10.3390/app12073229
Chicago/Turabian StyleLi, Hanyuan, Xinggao Li, Yi Yang, Yang Liu, and Mingzhe Ma. 2022. "Structural Stress Characteristics and Joint Deformation of Shield Tunnels Crossing Active Faults" Applied Sciences 12, no. 7: 3229. https://doi.org/10.3390/app12073229
APA StyleLi, H., Li, X., Yang, Y., Liu, Y., & Ma, M. (2022). Structural Stress Characteristics and Joint Deformation of Shield Tunnels Crossing Active Faults. Applied Sciences, 12(7), 3229. https://doi.org/10.3390/app12073229






