Calculation of View Factors for Building Simulations with an Open-Source Raytracing Tool
Abstract
:1. Introduction
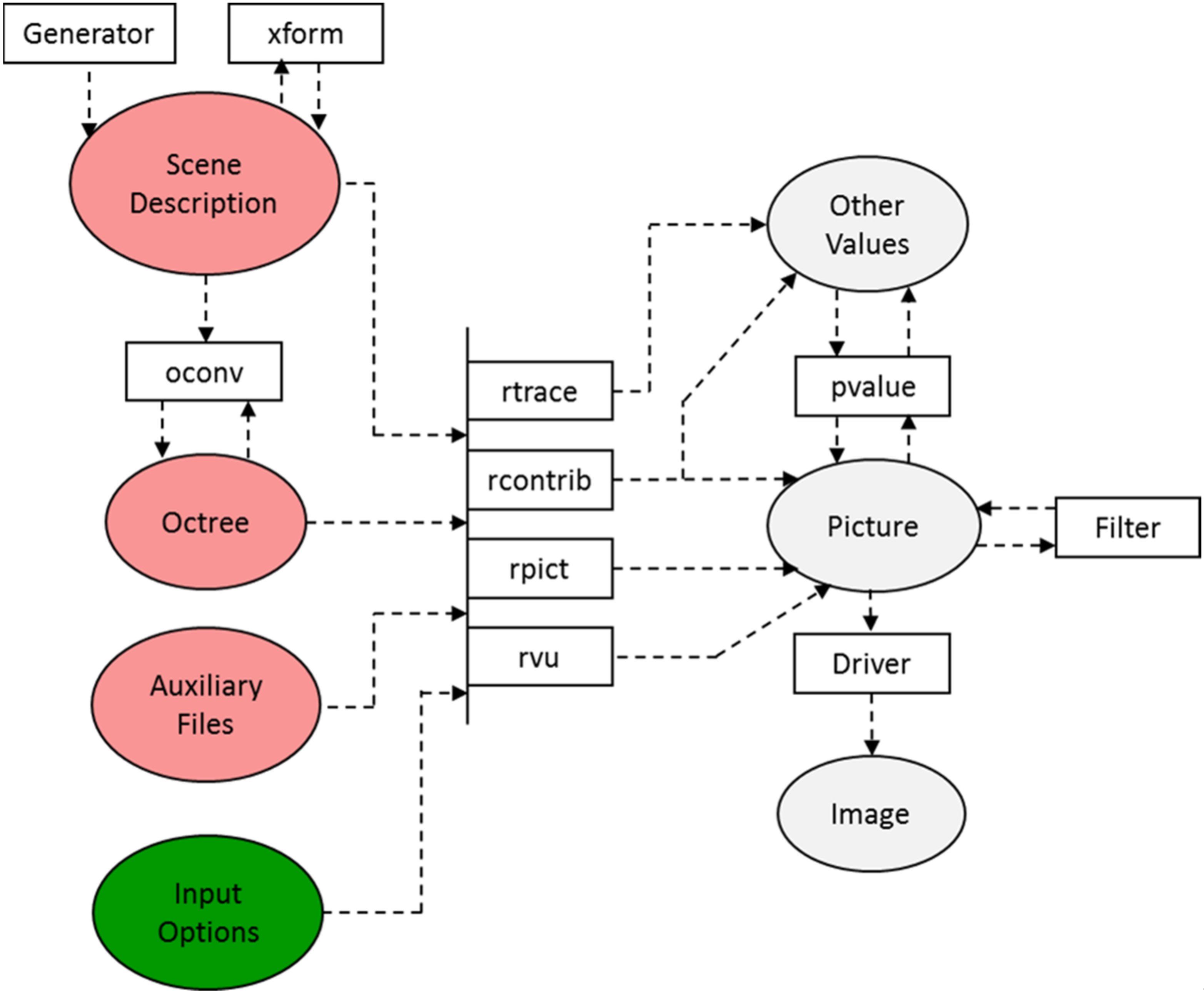
2. RADIANCE: Theoretical Basis and General Calculation Methodology
2.1. Introduction and Background
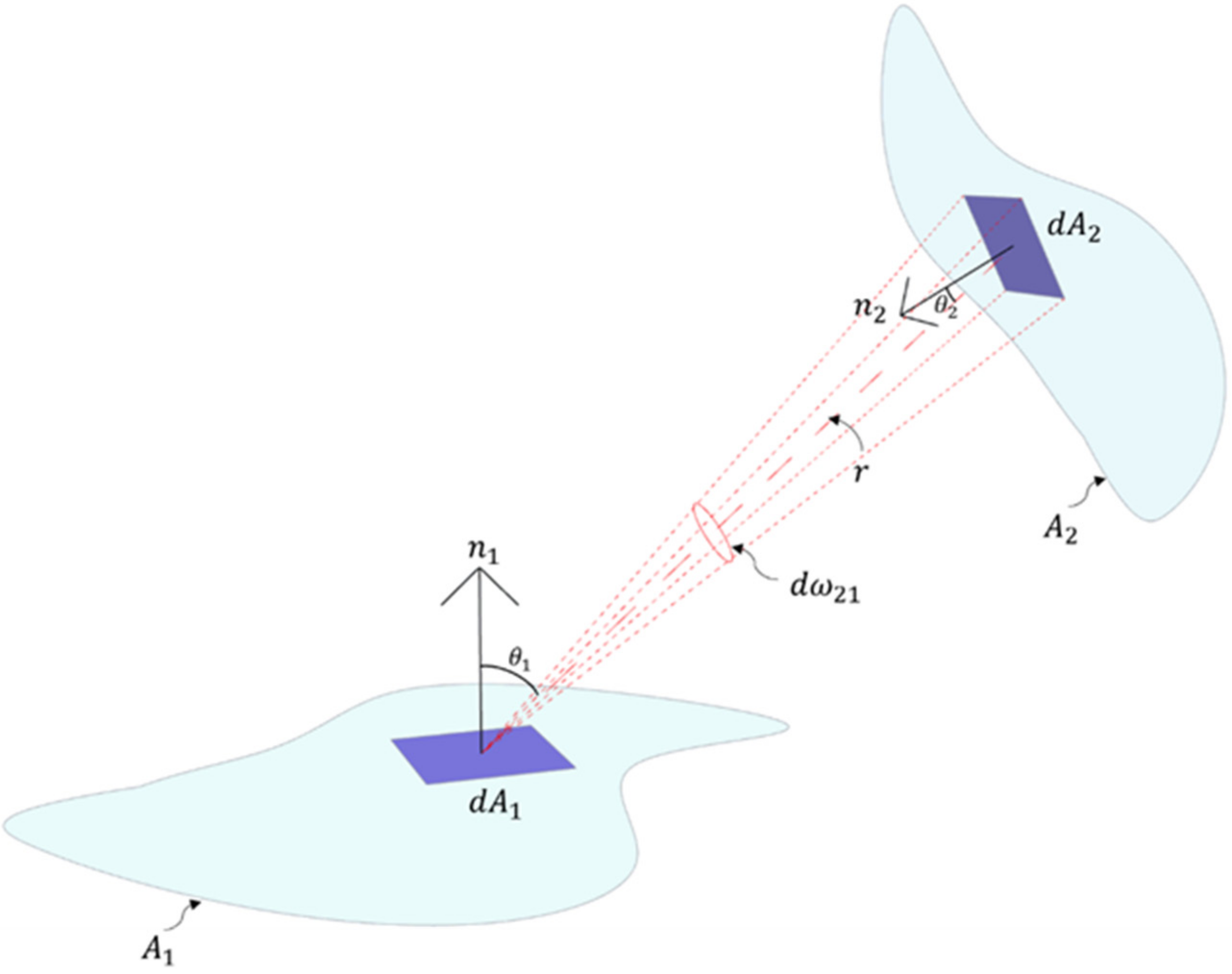
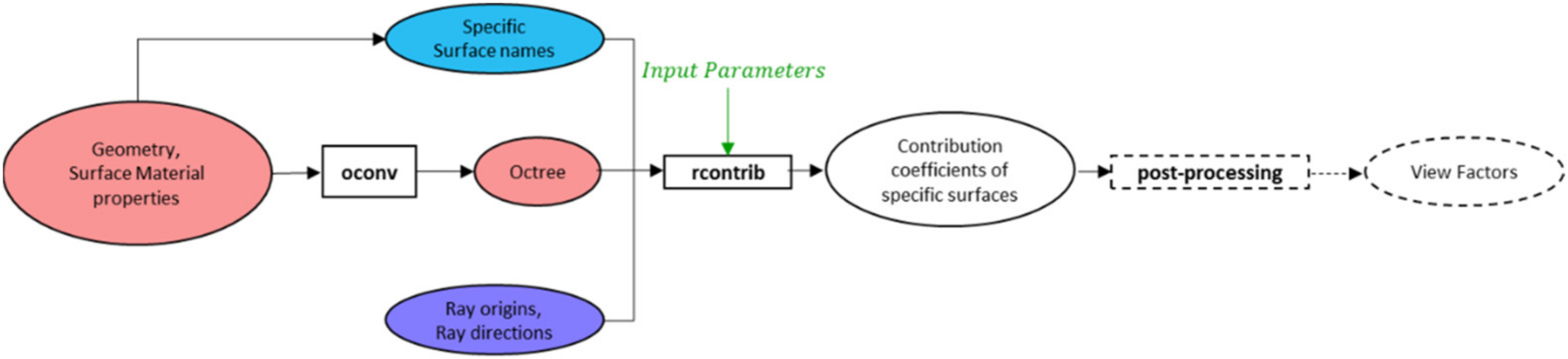
2.2. Calculating View Factors
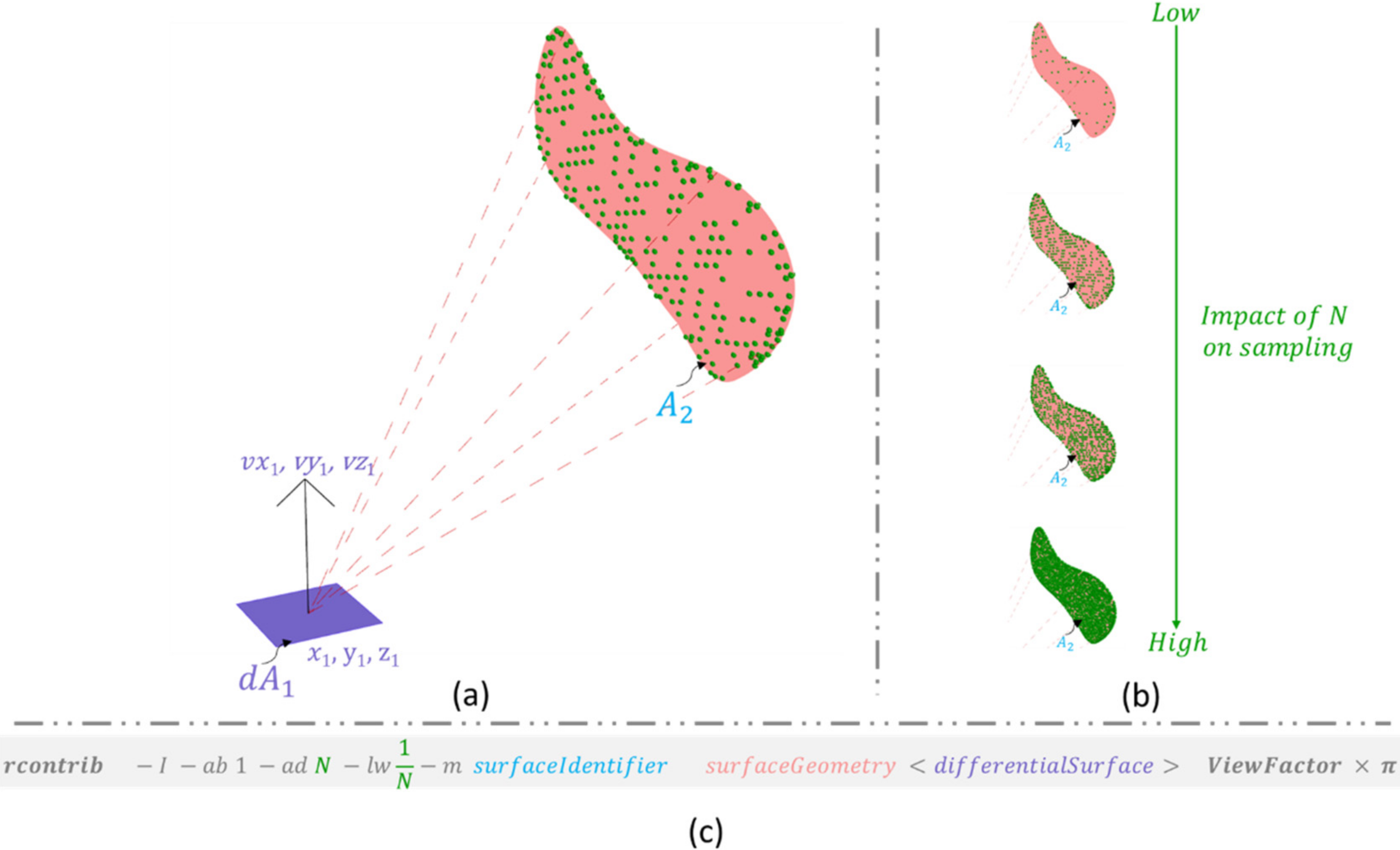
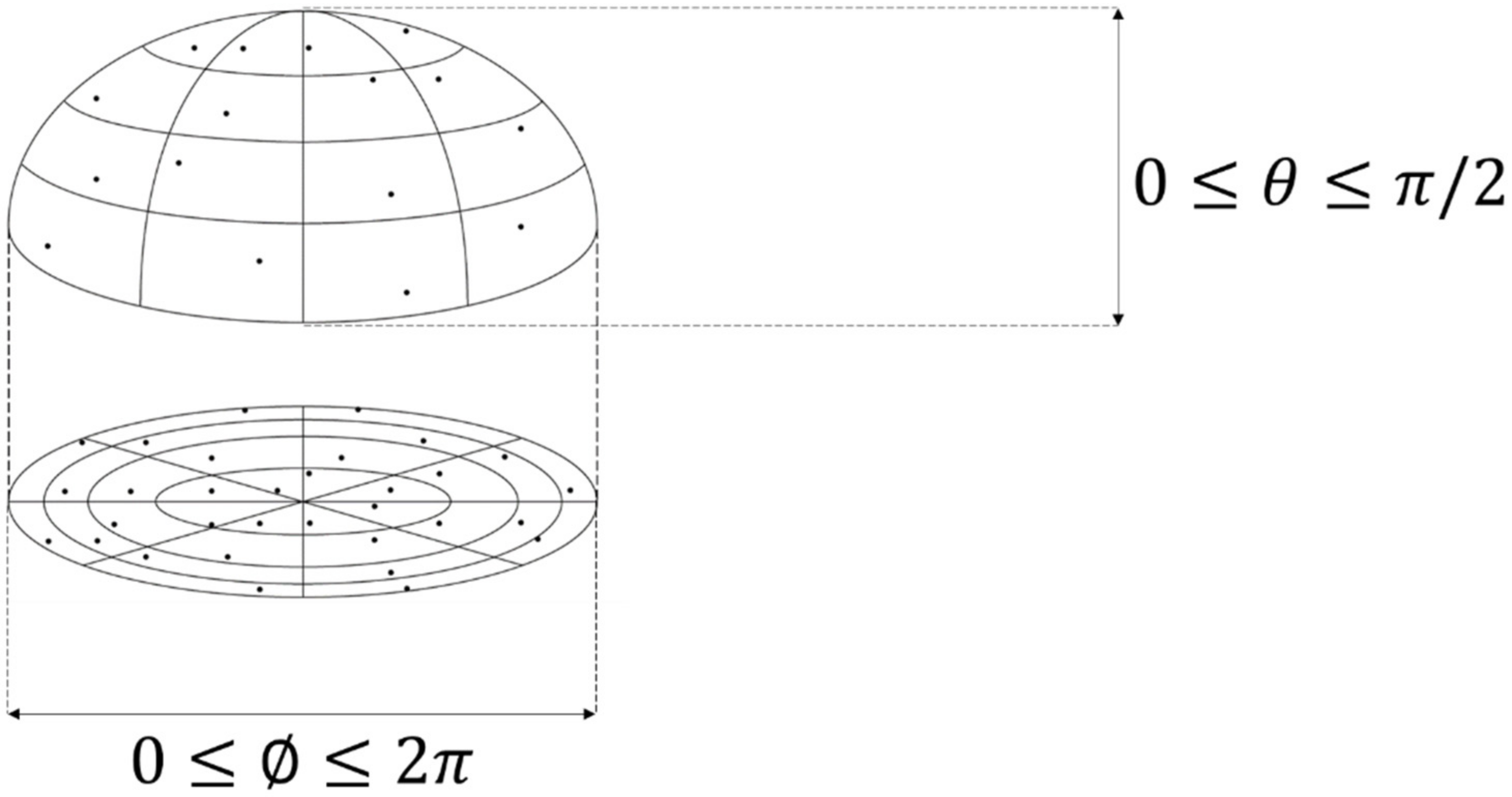
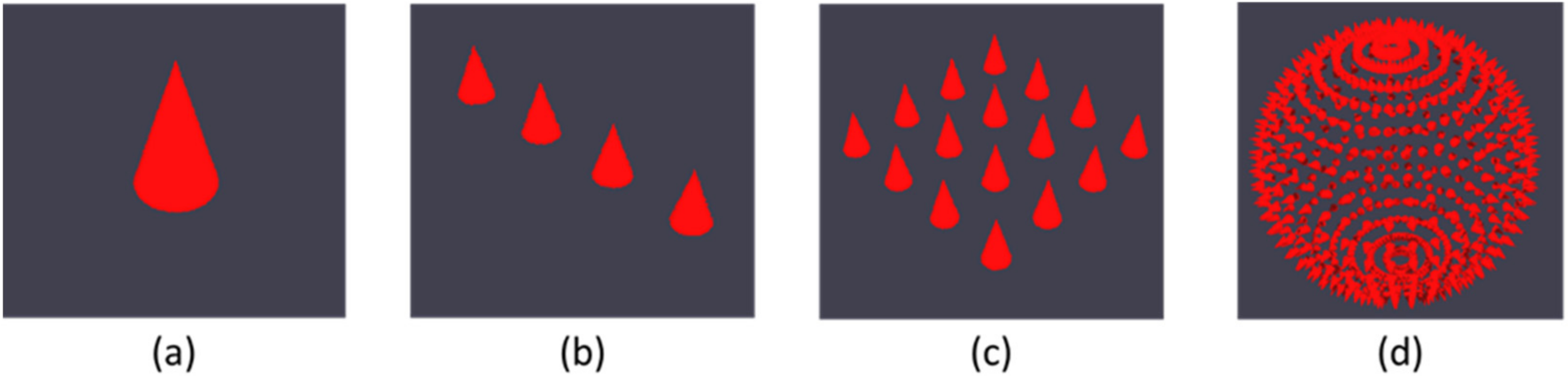
- For a given infinitesimal area dA1, N rays are stochastically mapped over a hemispherical basis as shown in Figure 4. The approach for randomly mapping these rays is based on the methodology proposed by Shirley and Chiu [26]. For the random sampling to converge, such that the results from two independent ray tracing processes are numerically within a tolerance range of less than 1%, a large number of samples is required.
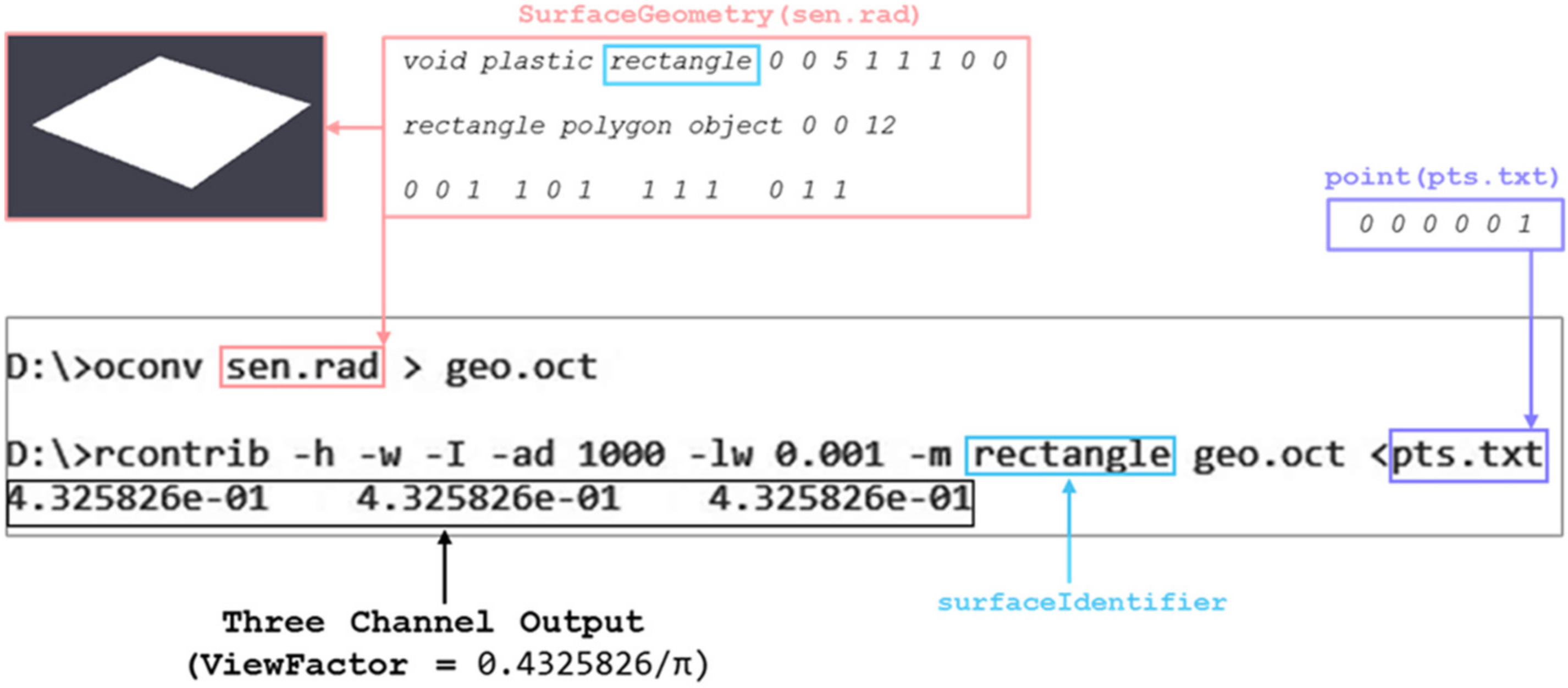
- For each ray that strikes the geometry of the surface(s) identified through “surfaceIdentifier”, a contribution is added. The contribution of a single ray will be equal to π/N, where the presence of the value of π is owing to the use of irradiance integral.
- The sum of all ray contributions to the surface identified through the surface identifier constitutes the fraction of the total hemispherical basis viewed by the infinitesimal area. This fraction constitutes an approximation of the view factor. As explained through Figure 3c, the output generated through RADIANCE is the approximate view factor multiplied by a factor of π.
2.3. Specifying Inputs and Interpreting Outputs
3. Validation of RADIANCE Generated Results against Analytical Solutions
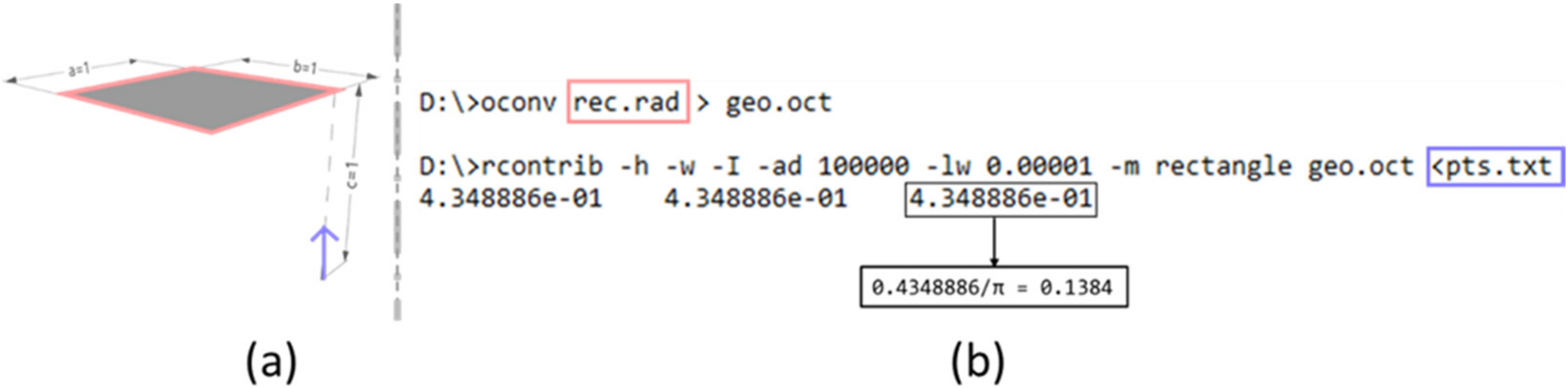
3.1. Differential Element to Finite Parallel Rectangle
3.2. Differential Element to Rectangle in a Plane at 90° to Plane of Element
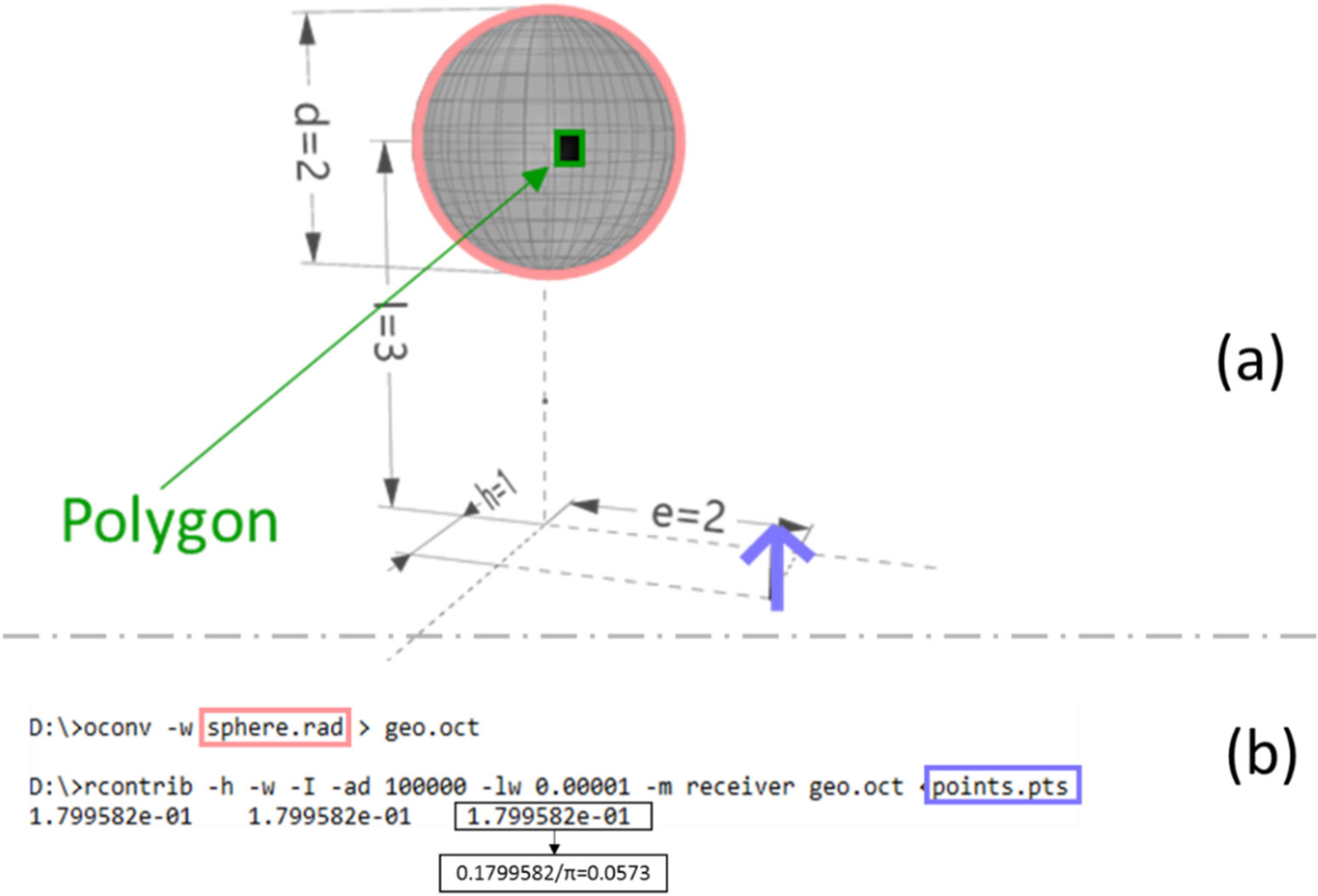
3.3. Element in a Plane to a Sphere
3.4. Energy Balance
4. View Factors for Complex Shapes and Obstructions
4.1. Complex Shapes with Curvature
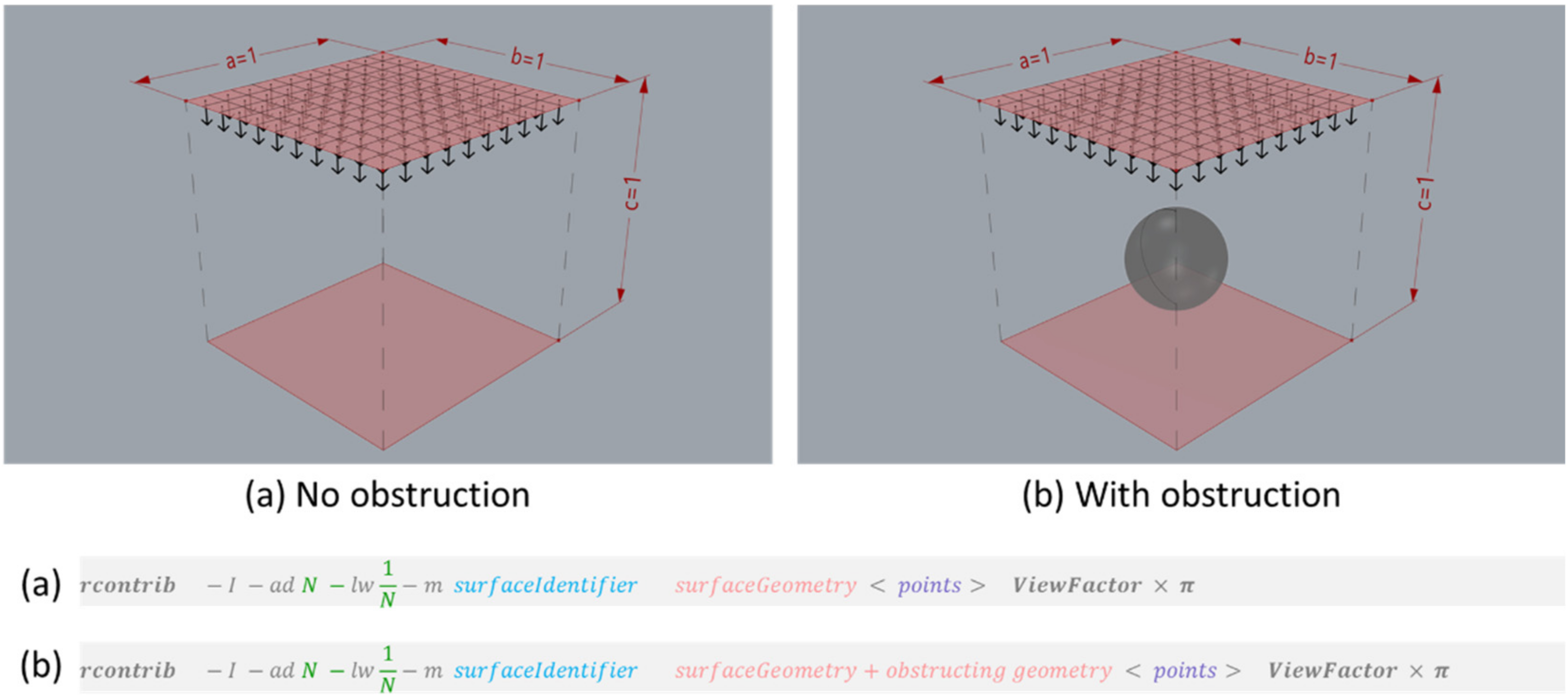
4.2. Incorporating Obstructions
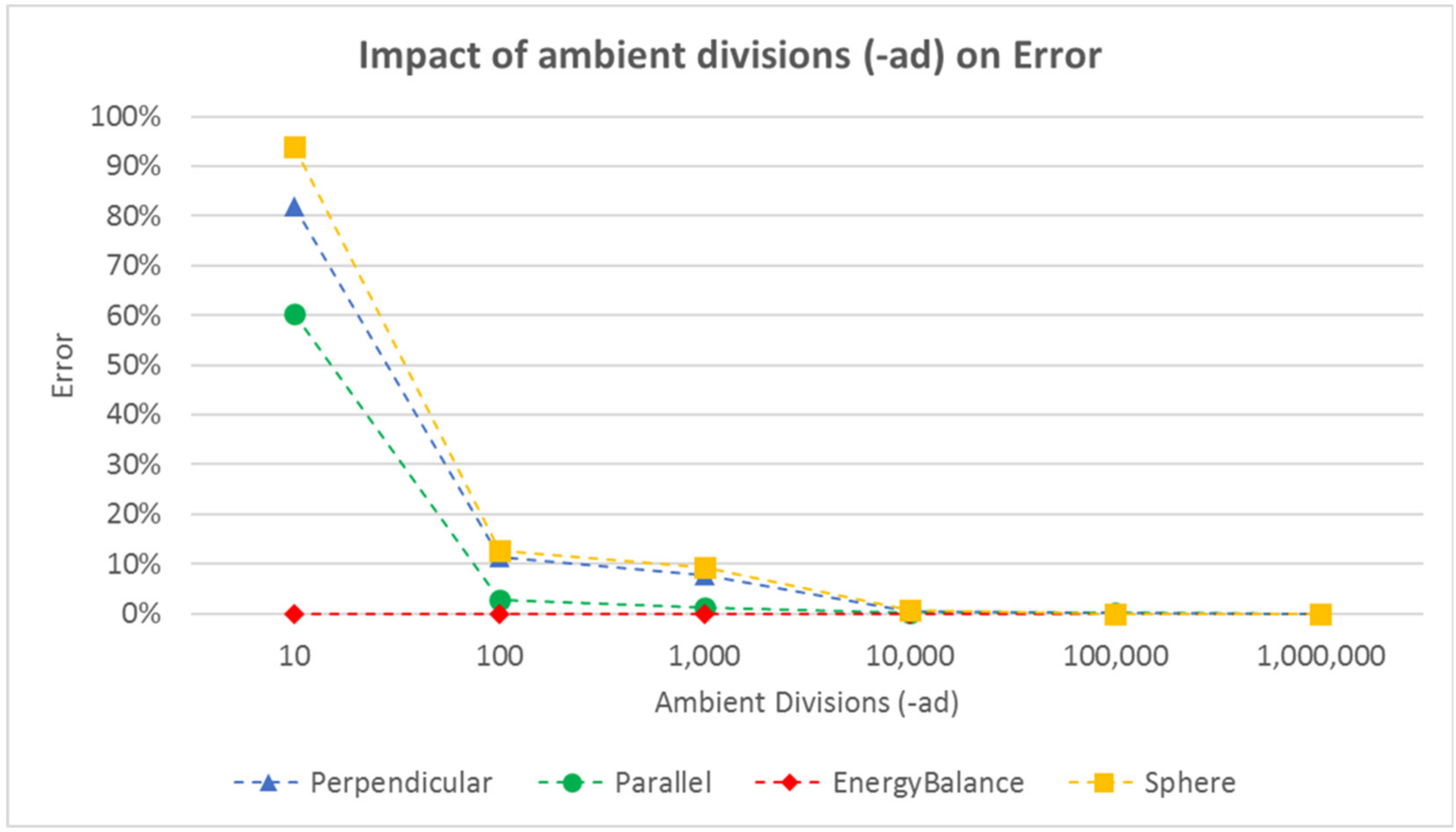
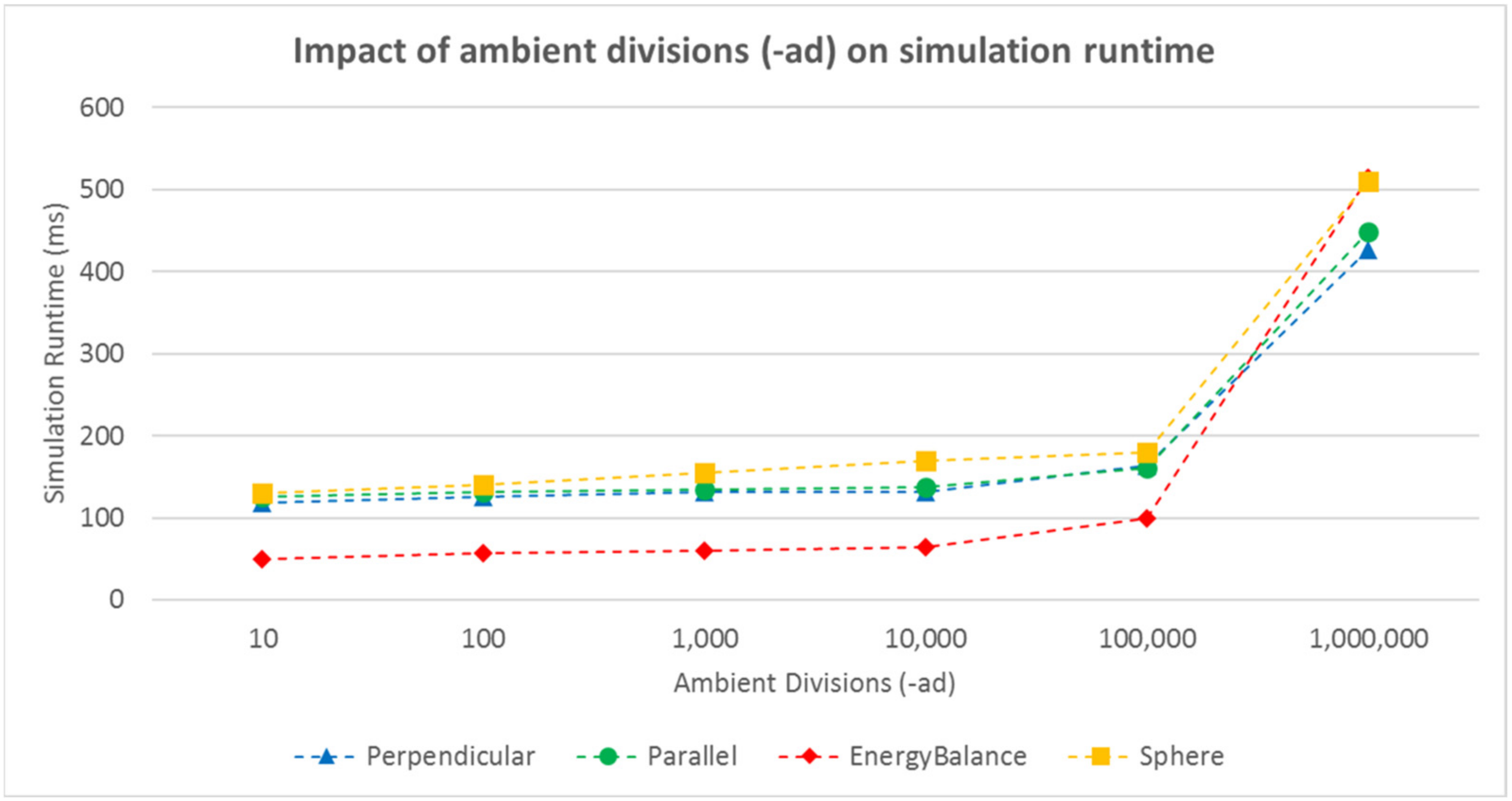
5. Impact of Calculation Parameters on Accuracy, Repeatability of Results, and Runtime
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Two arbitrarily oriented surfaces | |
| Differential surface elements of A1 and A2 respectively. | |
| F12 | Diffuse view factor from surface A1 to A2. |
| Diffuse view factor from surface dA1 to dA2. | |
| The angle between the surface-normal of dA1 and the line connecting dA1 and dA2 | |
| The angle between the surface-normal of dA2 and the line connecting dA1 and dA2 | |
| Distance between surfaces dA1 and dA2 | |
| θ | Polar angle measured from the surface normal. |
| φ | Azimuthal angle. |
| Reflected radiance in W/(sr*m2), | |
| Emitted radiance in W/(sr*m2) | |
| Incident radiance in W/(sr*m2), | |
| Bidirectional reflectance-transmittance distribution function in sr−1 | |
| Indirect irradiance in W/m2 | |
| oconv | RADIANCE program that is used for creating an octree structure. |
| rcontrib | RADIANCE program that is used for raytracing. |
| -I | rcontrib option that assigns irradiance mode of calculation. |
| -ad | rcontrib option that specifies the number of ambient divisions. |
| -ab | rcontrib option that specifies the number of ambient bounces. |
| -lw | rcontrib option to specify the limit weight parameter. |
| -m | rcontrib option to specify the modifier of the finite surface whose view factor is to be calculated. |
| -w | rcontrib option to turn off warnings. |
| -h | rcontrib option to turn off the header. This enables only the result of the calculation being generated as the output. |
References
- Cengel, Y. Heat and Mass Transfer: Fundamentals and Applications; McGraw-Hill Higher Education: New York, NY, USA, 2015; ISBN 9780072458930. [Google Scholar]
- Hensen, J.L.M.; Lamberts, R. Building Performance Simulation for Design and Operation, 2nd ed.; Routledge: London, UK, 2019; ISBN 9781138392199. [Google Scholar]
- Gupta, M.K.; Bumtariya, K.J.; Shukla, H.; Patel, P.; Khan, Z. Methods for Evaluation of Radiation View Factor: A Review. Mater. Today Proc. 2017, 4, 1236–1243. [Google Scholar] [CrossRef]
- Howell, J.R.; Menguc, M.P.; Siegel, R. Thermal Radiation Heat Transfer; CRC Press: Boca Raton, FL, USA, 2010; ISBN 9781439894552. [Google Scholar]
- Spencer, S.N. The Hemisphere Radiosity Method: A Tale of Two Algorithms. In Photorealism in Computer Graphics; Bouatouch, K., Bouville, C., Eds.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 127–135. [Google Scholar]
- Cohen, M.F.; Greenberg, D.P. The hemi-cube: A radiosity solution for complex environments. ACM SIGGRAPH Comput. Graph. 1985, 19, 31–40. [Google Scholar] [CrossRef]
- Walton, G. Calculation of Obstructed View Factors by Adaptive Integration; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2002. [Google Scholar]
- Howell, J.R. Application of Monte Carlo to Heat Transfer Problems. Adv. Heat Transfer 1969, 5, 1–54. [Google Scholar] [CrossRef]
- Hien, V.D.; Chirarattananon, S. Triangular Subdivision for the Computation of Form Factors. LEUKOS 2005, 2, 41–59. [Google Scholar] [CrossRef]
- Vujičić, M.R.; Lavery, N.P.; Brown, S.G.R. View factor calculation using the Monte Carlo method and numerical sensitivity. Commun. Numer. Methods Eng. 2005, 22, 197–203. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Saboonchi, A. View factor calculation using the Monte Carlo method for a 3D strip element to circular cylinder. Int. Commun. Heat Mass Transf. 2011, 38, 821–826. [Google Scholar] [CrossRef]
- He, F.; Shi, J.; Zhou, L.; Li, W.; Li, X. Monte Carlo calculation of view factors between some complex surfaces: Rectangular plane and parallel cylinder, rectangular plane and torus, especially cold-rolled strip and W-shaped radiant tube in continuous annealing furnace. Int. J. Therm. Sci. 2018, 134, 465–474. [Google Scholar] [CrossRef]
- MacFarlane, J. VISRAD—A 3-D view factor code and design tool for high-energy density physics experiments. J. Quant. Spectrosc. Radiat. Transf. 2003, 81, 287–300. [Google Scholar] [CrossRef] [Green Version]
- Maltby, J.D.; Zeeb, C.N.; Dolaghan, J.; Burns, P.J. User’s Manual for MONT2D-Version 2.6 and MONT3D-Version 2.3; Colorado State University: Fort Collins, CO, USA, 1994. [Google Scholar]
- Ward, G.J.; Rubinstein, F.M.; Clear, R.D. A ray tracing solution for diffuse interreflection. ACM SIGGRAPH Comput. Graph. 1988, 22, 85–92. [Google Scholar] [CrossRef]
- Ward, G.J.; Rubinstein, F.M. A New Technique for Computer Simulation of Illuminated Spaces. J. Illum. Eng. Soc. 1988, 17, 80–91. [Google Scholar] [CrossRef]
- Ward, G.; Rubinstein, F.; Grynberg, A. Luminance in computer-aided lighting design. In Proceedings of the 1st Building Simulation Conference, Vancouver, BC, Canada, 23–24 June 1989. [Google Scholar]
- Ward, G.J.; Heckbert, P.S. Irradiance gradients. In Proceedings of the Third Eurographics Workshop on Rendering, Bristol, UK, 17–20 May 1992. [Google Scholar]
- Grynberg, A. Validation of Radiance. LBNL. 1989. Available online: https://eta-publications.lbl.gov/sites/default/files/lbid-1575.pdf (accessed on 20 February 2022).
- Mardaljevic, J. Validation of a lighting simulation program under real sky conditions. Light. Res. Technol. 1995, 27, 181–188. [Google Scholar] [CrossRef]
- McNeil, A.; Lee, E.S. A validation of the Radiance three-phase simulation method for modelling annual daylight performance of optically complex fenestration systems. J. Build. Perform. Simul. 2013, 6, 24–37. [Google Scholar] [CrossRef]
- Lee, E.S.; Geisler-Moroder, D.; Ward, G. Modeling the direct sun component in buildings using matrix algebraic approaches: Methods and validation. Sol. Energy 2018, 160, 380–395. [Google Scholar] [CrossRef] [Green Version]
- Ward, G.; Shakespeare, R.; Ehrlich, C.; Mardaljevic, J.; Phillips, E.; Apian-Bennewitz, P. Rendering with Radiance: The Art and Science of Lighting Visualization; Morgan Kaufmann: San Francisco, CA, USA, 1998; ISBN 0974538108. [Google Scholar]
- Ward, G.; Mistrick, R.; Lee, E.S.; McNeil, A.; Jonsson, J. Simulating the Daylight Performance of Complex Fenestration Systems Using Bidirectional Scattering Distribution Functions within Radiance. LEUKOS 2011, 7, 241–261. [Google Scholar] [CrossRef] [Green Version]
- LBNL. Rcontrib. 2016. Available online: https://www.radiance-online.org/learning/documentation/manual-pages/pdfs/rfluxmtx.pdf (accessed on 20 February 2022).
- Shirley, P.; Chiu, K. A Low Distortion Map Between Disk and Square. J. Graph. Tools 1997, 2, 45–52. [Google Scholar] [CrossRef]
- Glassner, A.S. Space subdivision for fast ray tracing. IEEE Comput. Graph. Appl. 1984, 4, 15–24. [Google Scholar] [CrossRef]
- Ward, G.J. The RADIANCE lighting simulation and rendering system. In Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques—SIGGRAPH ’94, Orlando, FL, USA, 24–29 July 1994; pp. 459–472. [Google Scholar]
- Ward, G. Radiance File Formats. 1997. Available online: https://floyd.lbl.gov/radiance/refer/filefmts.pdf (accessed on 20 February 2022).
- Konstantinos, M.P. Desktop Radiance: A New Tool for Computer-Aided Daylighting Design. ACADIA Q. 2000, 19, 2. [Google Scholar]
- Bleicher, T. su2rad—Radiance Exporter for SketchUp. In Proceedings of the 7th International Radiance Workshop, Fribourg, Switzerland, 30–31 October 2008. Available online: https://www.radiance-online.org:447/radiance-workshop7/Content/Bleicher/su2rad.pdf (accessed on 20 February 2022).
- Roudsari, M.; Pak, M. Ladybug: A Parametric Environmental Plugin for Grasshopper to Help Designers Create an Environmentally-Conscious Design. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambery, France, 25–28 August 2013. [Google Scholar]
- Hamilton, D.C.; Morgan, W. Radiant-Interchange Configuration Factors. NASA. 1952. Available online: https://ntrs.nasa.gov/citations/19930083529 (accessed on 20 February 2022).
- Howell, J.R. A Catalog of Radiation Transfer Configuration Factors. 2001. Available online: http://www.thermalradiation.net/indexCat.html (accessed on 20 February 2022).
- Naraghi, M.H.N. Radiative View Factors from Spherical Segments to Planar Surfaces. J. Thermophys. Heat Transf. 1988, 2, 373–375. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subramaniam, S.; Hoffmann, S.; Thyageswaran, S.; Ward, G. Calculation of View Factors for Building Simulations with an Open-Source Raytracing Tool. Appl. Sci. 2022, 12, 2768. https://doi.org/10.3390/app12062768
Subramaniam S, Hoffmann S, Thyageswaran S, Ward G. Calculation of View Factors for Building Simulations with an Open-Source Raytracing Tool. Applied Sciences. 2022; 12(6):2768. https://doi.org/10.3390/app12062768
Chicago/Turabian StyleSubramaniam, Sarith, Sabine Hoffmann, Sridhar Thyageswaran, and Greg Ward. 2022. "Calculation of View Factors for Building Simulations with an Open-Source Raytracing Tool" Applied Sciences 12, no. 6: 2768. https://doi.org/10.3390/app12062768
APA StyleSubramaniam, S., Hoffmann, S., Thyageswaran, S., & Ward, G. (2022). Calculation of View Factors for Building Simulations with an Open-Source Raytracing Tool. Applied Sciences, 12(6), 2768. https://doi.org/10.3390/app12062768




