A Fuzzy Logic Reinforcement Learning Control with Spring-Damper Device for Space Robot Capturing Satellite
Abstract
:1. Introduction
2. Structure of the SDD and Buffer Compliance Strategy
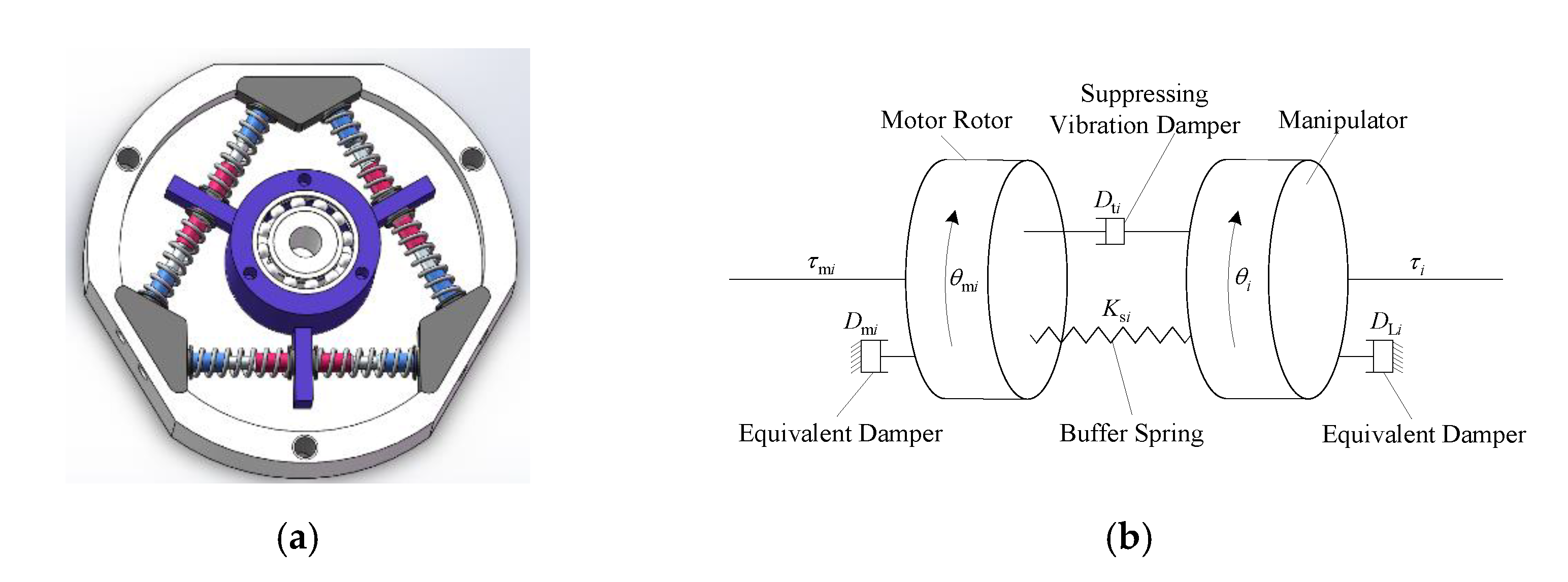
2.1. Structure of the SDD
2.2. Buffer Compliance Strategy
3. Dynamic Modeling and Impact Analysis
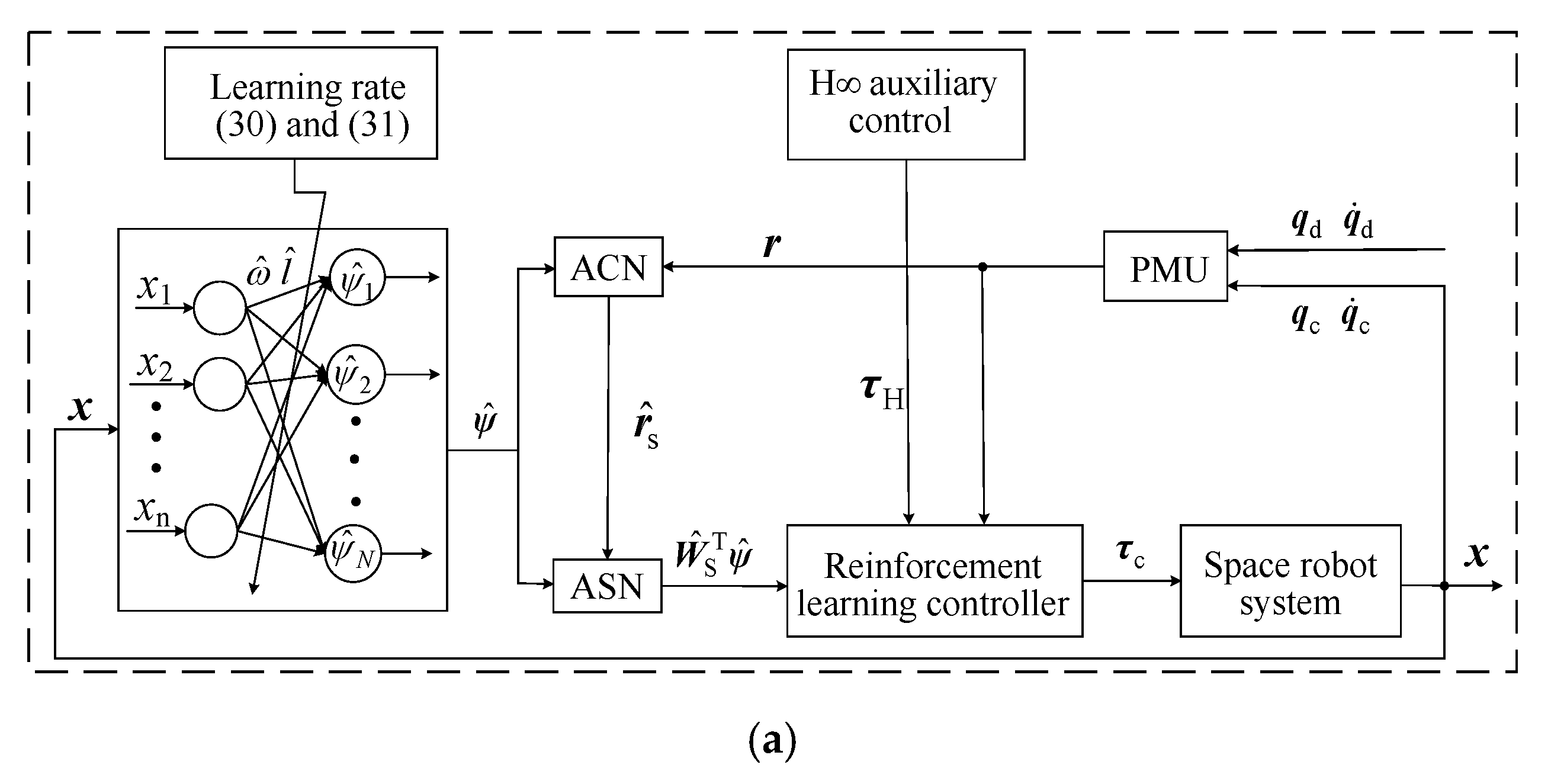
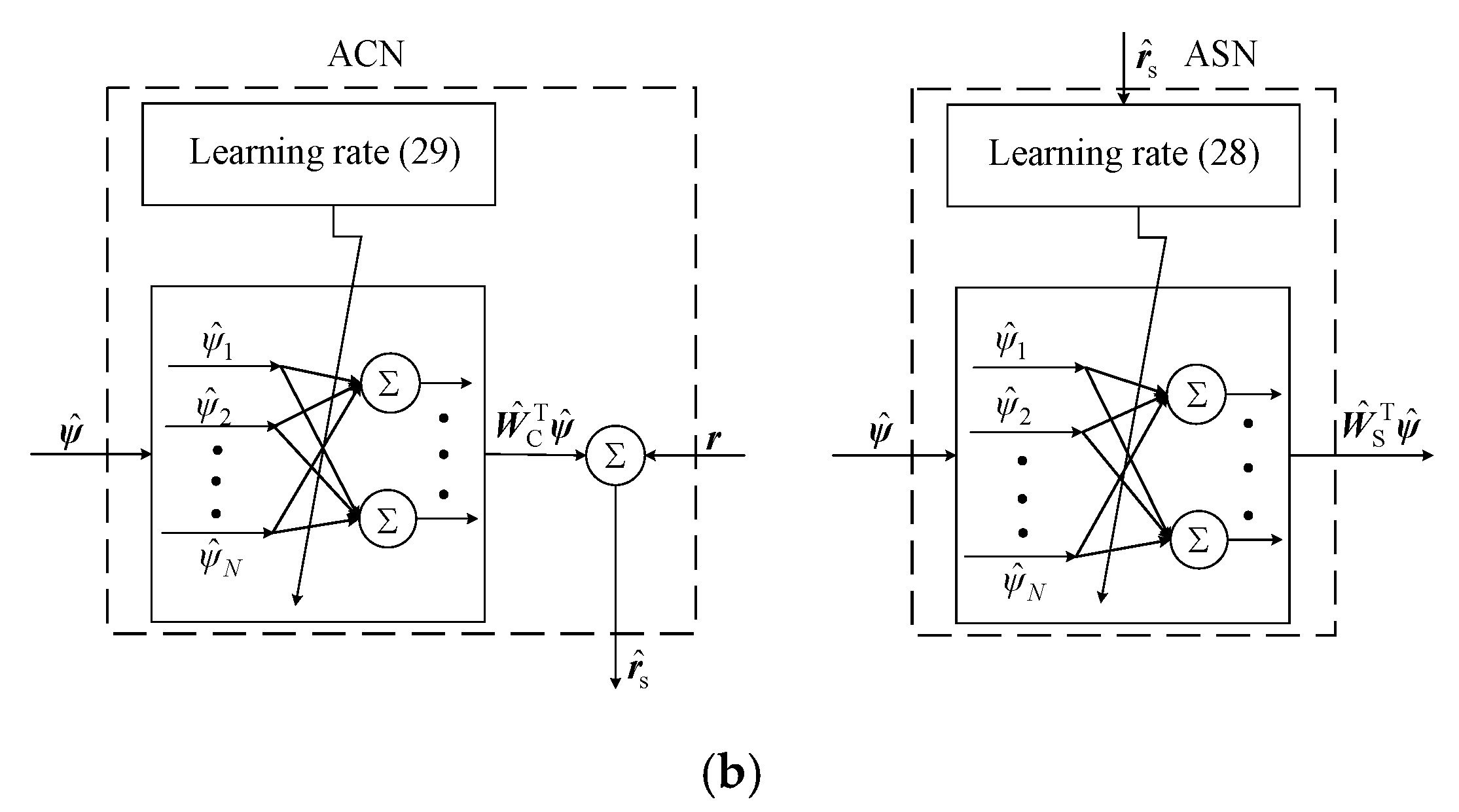
4. Design of Controller
5. Simulation Results
5.1. Simulation of Impact Resistance of the SDD
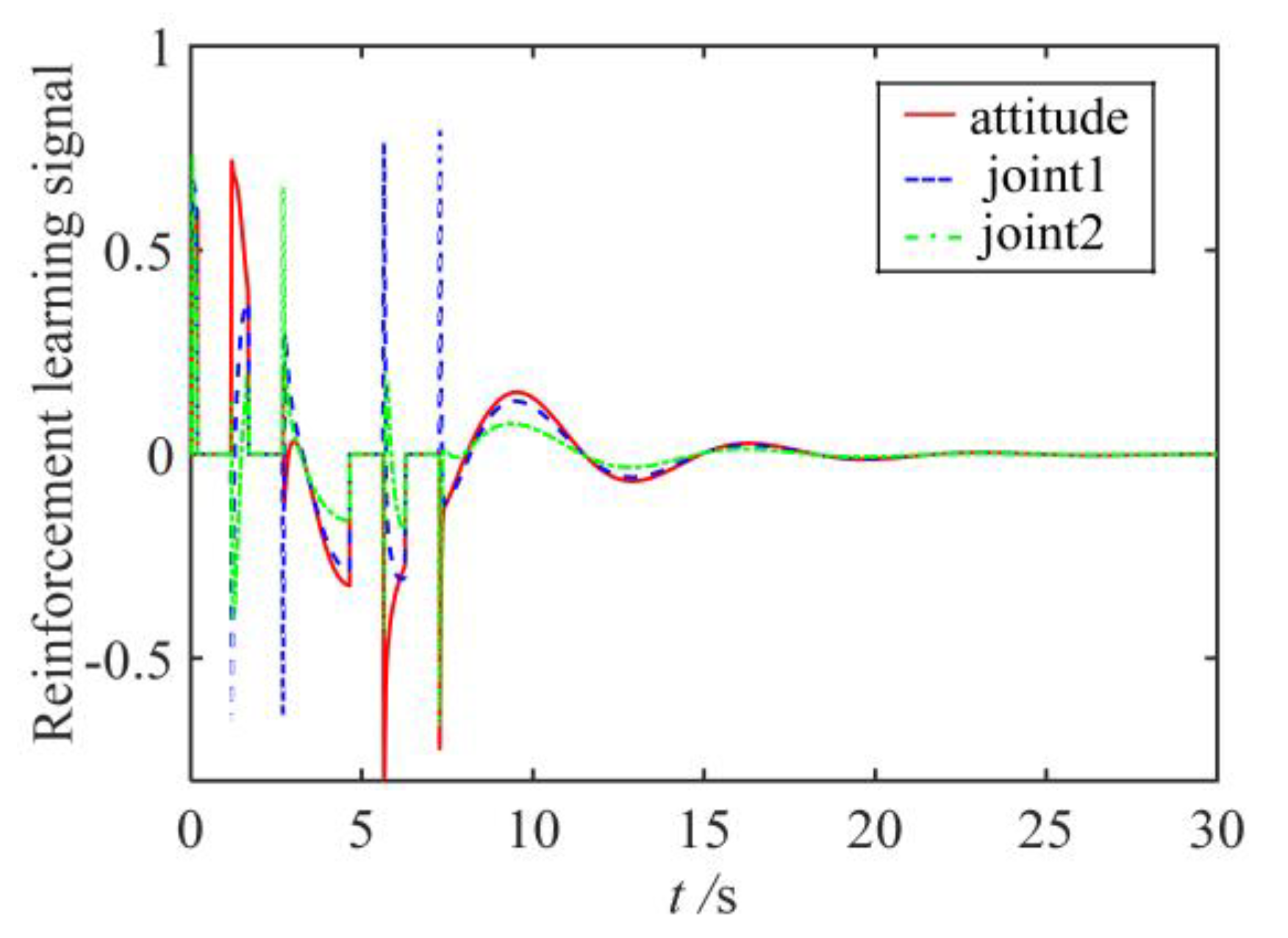
5.2. Buffer Compliance Control Strategy Performance Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, X.; Ai, H.; Chen, L. Repetitive learning sliding mode stabilization control for a flexible-base, flexible-link and flexible-joint space robot capturing a satellite. Appl. Sci. 2021, 11, 8077. [Google Scholar] [CrossRef]
- He, J.; Zheng, H.; Gao, F.; Zhang, H. Dynamics and control of a 7-DOF hybrid manipulator for capturing a non-cooperative target in space. Mech. Machine Theory 2019, 140, 83–103. [Google Scholar] [CrossRef]
- Ai, H.; Zhu, A.; Wang, J.; Yu, X.; Chen, L. Buffer Compliance Control of Space Robots Capturing a Non-Cooperative Spacecraft Based on Reinforcement Learning. Appl. Sci. 2021, 11, 5783. [Google Scholar] [CrossRef]
- Meng, Q.; Liang, J.; Ma, O. Identification of all the inertial parameters of a non-cooperative object in orbit. Aerosp. Sci. Technol. 2019, 91, 571–582. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Chen, Y.; Cai, G. Dynamics and control of space robot considering joint friction. Acta Astronaut. 2015, 111, 1–18. [Google Scholar] [CrossRef]
- Li, M.; Guo, W.; Lin, R.; Wu, C. An efficient motion generation method for redundant humanoid robot arms based on motion continuity. Adv. Robot. 2018, 32, 1185–1196. [Google Scholar] [CrossRef]
- Fu, X.; Ai, H.; Chen, L. Integrated Fixed Time Sliding Mode Control for Motion and Vibration of Space Robot with Fully Flexible Base–Link–Joint. Appl. Sci. 2021, 11, 11685. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Chen, Y.; Cai, G.; Wang, X. Dynamics and control of capture of a floating rigid body by a spacecraft robotic arm. Multibody Syst. Dyn. 2015, 33, 315–332. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, L. Mechanical analysis and calm control of dual-arm space robot for capturing a satellite. Chin. J. Theor. Appl. Mech. 2016, 48, 832–842. (In Chinese) [Google Scholar]
- Uyama, N.; Hirano, D.; Nakanishi, H.; Nagaoka, K.; Yoshida, K. Impedance-based contact control of a free-flying space robot with respect to coefficient of restitution. IEEE/SICE Int. Symp. Syst. Integr. 2012, 1196–1201. [Google Scholar] [CrossRef]
- Dimitrov, D.; Yoshida, K. Utilization of the bias momentum approach for capturing a tumbling satellite. IEEE/RSJ Int. Conf. Intell. Robot. Syst. 2004, 3333–3338. [Google Scholar] [CrossRef]
- Yoshida, K.; Nakanishi, H.; Ueno, H.; Inaba, N. Dynamics control and impedance matching for robotic capture of a non-cooperative satellite. Adv. Robot. 2004, 2, 175–198. [Google Scholar] [CrossRef]
- Dong, Q.; Chen, L. Composite control of robust stabilization and adaptive vibration suppression of flexible space manipulator capturing a satellite. Robot 2014, 36, 342–348. (In Chinese) [Google Scholar]
- Sariyildiz, E.; Chen, G.; Yu, H. An acceleration-based robust motion controller design for a novel series elastic actuator. IEEE Trans. Ind. Electron. 2016, 63, 1900–1910. [Google Scholar] [CrossRef]
- Li, X.; Pan, Y.; Chen, G.; Yu, H. Continuous tracking control for a compliant actuator with two-stage stiffness. IEEE Trans. Autom. Sci. Eng. 2018, 15, 57–66. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, Z.; Yao, B. Decoupled torque control of series elastic actuator with adaptive robust compensation of time-varying load-side dynamics. IEEE Trans. Ind. Electron. 2019, 67, 5604–5614. [Google Scholar] [CrossRef]
- Irmscher, C.; Woschke, E.; May, E.; Daniel, C. Design, Optimization and testing of a compact, inexpensive elastic element for series elastic actuators. Med. Eng. Phys. 2018, 52, 84–89. [Google Scholar] [CrossRef]
- Keppler, M.; Lakatos, D.; Ott, C.; Albu-Schaffer, A. Elastic structure preserving (EPS) control for compliantly actuated robots. IEEE Trans. Robot. 2018, 34, 317–335. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.; Sun, N.; Fang, Y. Adaptive fuzzy control for a class of mimo underactuated systems with plant uncertainties and actuator deadzones: Design and experiments. IEEE Trans. Cybern. 2021, 99, 1–14. [Google Scholar] [CrossRef]
- Sun, L.; Li, M.; Wang, M.; Yin, W.; Sun, N.; Liu, J. Continuous finite-time output torque control approach for series elastic actuator. Mech. Syst. Signal Processing 2020, 139, 105853. [Google Scholar] [CrossRef]
- Wang, M.; Sun, L.; Yin, W.; Dong, S.; Liu, J. Continuous robust control for series elastic actuator with unknown payload parameters and external disturbances. IEEE/CAA J. Autom. Sin. 2017, 4, 620–627. [Google Scholar] [CrossRef]
- Ai, H.; Chen, L. Buffer and compliant dynamic surface control of space robot capturing satellite based on compliant mechanism. Chin. J. Theor. Appl. Mech. 2020, 52, 975–984. (In Chinese) [Google Scholar]
- Liu, S.; Wu, L.; Lu, Z. Impact dynamics and control of a flexible dual-arm space robot capturing an object. Appl. Math. Comput. 2007, 185, 1149–1159. [Google Scholar] [CrossRef]
- Huang, X.; Duan, G. Attitude control and structure robust control allocation for combined spacecraft. Control. Theory Appl. 2018, 35, 1447–1457. (In Chinese) [Google Scholar]
- Luo, J.; Wei, C.; Dai, H.; Yin, Z. Robust inertia-free attitude takeover control of post capture combined spacecraft with guaranteed prescribed performance. ISA Trans. 2018, 74, 28–44. [Google Scholar] [CrossRef]
- Gangapersaud, R.; Liu, G.; De Ruiter, A. Detumbling of a non-cooperative target with unknown inertial parameters using a space robot. Adv. Space Res. 2019, 63, 3900–3915. [Google Scholar] [CrossRef]
- Sands, T. Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). J. Mar. Sci. Eng. 2020, 8, 578. [Google Scholar] [CrossRef]
- Ai, H.; Chen, L. Passivity-based neural network H∞ avoidance compliant control of space robot capturing spacecraft. Opt. Precis. Eng. 2020, 28, 717–726. (In Chinese) [Google Scholar] [CrossRef]
- Chen, Z.; Gao, F. Time-optimal trajectory planning method for six-legged robots under actuator constraints. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 095440621983307. [Google Scholar] [CrossRef]
- Hu, Y.; Si, B. A reinforcement learning neural network for robotic manipulator control. Neural Comput. 2018, 30, 1983–2004. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Liu, J.; Huang, Z.; Peng, Y.; Pu, H.; Ding, L. Adaptive impedance control of human-robot cooperation using reinforcement learning. IEEE Trans. Ind. Electron. 2017, 64, 8013–8022. [Google Scholar] [CrossRef]
- Leottau, D.; Ruiz-Del-Solar, J.; Babuška, R. Decentralized reinforcement learning of robot behaviors. Artif. Intell. 2018, 256, 130–159. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T. Student-t policy in reinforcement learning to acquire global optimum of robot control. Appl. Intell. 2019, 49, 4335–4347. [Google Scholar] [CrossRef]
- Tai, L.; Liu, M. Mobile robots exploration through cnn-based reinforcement learning. Robot. Biomim. 2016, 3, 24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.C. A self-learning rule-based controller employing approximate reasoning and neural net concepts. Int. J. Intell. Syst. 1991, 6, 71–93. [Google Scholar] [CrossRef]
- Bustamante, C.; Gadea, E.; Horsfield, A.; Todorov, T.; González Lebrero, M.; Scherlis, D. Dissipative equation of motion for electromagnetic radiation in quantum dynamics. Phys. Rev. Lett. 2021, 126, 087401. [Google Scholar] [CrossRef]
- Chang, Y.; Chen, B. A nonlinear adaptive H∞ tracking control design in robotic systems via neural networks. IEEE Trans. Control. Syst. Technol. 1997, 5, 13–29. [Google Scholar] [CrossRef]
- Lin, C.; Wang, S. An adaptive H∞ controller design for bank-to-turn missiles using ridge Gaussian neural networks. IEEE Trans. Neural Netw. 2004, 15, 1507–1516. [Google Scholar] [CrossRef]












| Initial Velocity of Satellite/ (m/s, m/s, rad/s) | Max Impact Torque without SDD/ (N·m) | Max Impact Torque with SDD/ (N·m) | Percentage Reduction/ (%) |
|---|---|---|---|
| [0.1, 0.1, 0.15]T | 226.68 | 133.27 | 41.21 |
| [0.1, 0, 0]T | 78.38 | 38.78 | 50.52 |
| [0, 0.1, 0]T [0, 0, 0.15]T | 34.17 117.33 | 15.67 66.09 | 54.14 43.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, A.; Ai, H.; Chen, L. A Fuzzy Logic Reinforcement Learning Control with Spring-Damper Device for Space Robot Capturing Satellite. Appl. Sci. 2022, 12, 2662. https://doi.org/10.3390/app12052662
Zhu A, Ai H, Chen L. A Fuzzy Logic Reinforcement Learning Control with Spring-Damper Device for Space Robot Capturing Satellite. Applied Sciences. 2022; 12(5):2662. https://doi.org/10.3390/app12052662
Chicago/Turabian StyleZhu, An, Haiping Ai, and Li Chen. 2022. "A Fuzzy Logic Reinforcement Learning Control with Spring-Damper Device for Space Robot Capturing Satellite" Applied Sciences 12, no. 5: 2662. https://doi.org/10.3390/app12052662
APA StyleZhu, A., Ai, H., & Chen, L. (2022). A Fuzzy Logic Reinforcement Learning Control with Spring-Damper Device for Space Robot Capturing Satellite. Applied Sciences, 12(5), 2662. https://doi.org/10.3390/app12052662






