Dynamics of Submersion of a «Diving Buoy» with Account of Hull Compression and Depth-Wise Variation of Water Density
Abstract
:1. Introduction
2. Mathematical Model
3. Analytical and Numerical Solutions
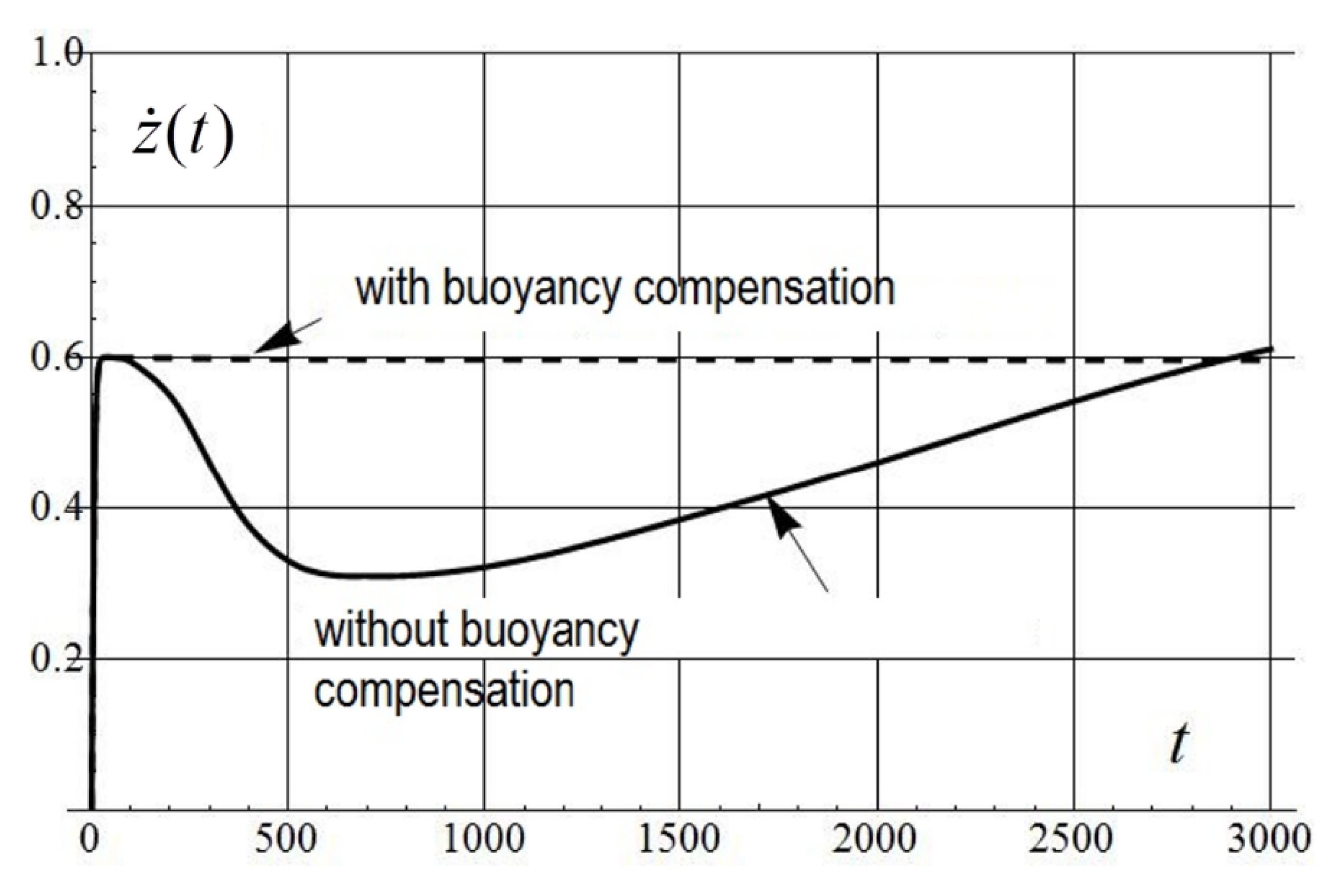
3.1. Case of Constant Density and Incompressible Hull
3.2. Case of Variable Density and Compressible Hull
4. Conclusions
Funding
Conflicts of Interest
References
- Simonetti, P.J. SLOCUM: A long Endurance Ocean Profiler Powered by Thermocline Driven Engine. Sea Technol. 1998, 39, 17–21. [Google Scholar]
- Davis, R.E.; Sherman, J.T.; Dufour, J. Profiling ALACEs and other advances in autonomous subsurface floats. J. Atmos. Ocean. Technol. 2001, 18, 982–993. [Google Scholar] [CrossRef]
- D’Asaro, E.A. Performance of Autonomous Lagrangian floats. J. Atmos. Ocean. Technol. 2003, 20, 896–911. [Google Scholar] [CrossRef] [Green Version]
- Sherman, J.; Davis, R.E.; Owens, W.B.; Valdes, J. The autonomous underwater glider “Spray”. IEEE Ocean. Eng. 2001, 26, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, G.; Davis, R.E.; Erickesen, C.C.; Jones, C.P. Autonomous buoyancy driven underwater gliders. In Technology and Applications of Autonomous Underwater Gliders; Taylor & Francis: London, UK, 2002. [Google Scholar]
- Jenkins, S.A.; Humphreys, D.E.; Sherman, J.; Osse, J.; Jones, C.; Leonard, N.; Graver, J.; Bachmayer, R.; Clem, T.; Carroll, P. Underwater Glider System Study. Scripps Inst. Oceanogr. Tech. Rep. 2003, 53, 6. [Google Scholar]
- Bachmayer, R.; Leonard, N.E.; Graver, J.G.; Fiorelli, E.; Bhatta, P.; Paley, D. Underwater gliders: Recent developments and future applications. In Proceedings of the 2004 International Symposium on Underwater Technology (IEEE Cat. No.04EX869), Taipei, Taiwan, 20–23 April 2004. [Google Scholar]
- Jones, C.; Webb, D.; Glenn, S.; Schogield, O.; Kerfoot, J.; Kohut, J.; Aragon, D.; Haldeman, C.; Haskin, T.; Kahl, A.; et al. Slocum Glider-Expanding the Capabilities; UUSR: Moscow, Russia, 2011. [Google Scholar]
- Rozhdestvensky, K.V. A View on the Development of Underwater Gliders. In Proceedings of the Plenary Presentation at a Society of Underwater Technology Technical Conference, Shanghai, China, 2 September 2013. [Google Scholar]
- Lee, C.M.; Rudnick, D.L. Chapter Underwater Gliders. In Observing the Oceans in Real Time; Venkatesan, R., Ed.; Springer International Publishing AG: Berlin/Heidelberg, Germany, 2018; 322p. [Google Scholar]
- Than, K. James Cameron Completes Record-Breaking Mariana Trench Dive. National Geographic News, 25 March 2021. [Google Scholar]
- Janes, N. Design of a Buoyancy Engine for an Underwater Vehicle; National Research Council of Canada, Institute for Ocean Technology, Laboratory Memorandum LM-2004-12: St. John’s, NL, Canada, 2004. [Google Scholar]
- Yang, Y.; Liu, Y.; Zhang, H.; Zhang, L. Dynamic modeling and motion control strategy for deep-sea hybrid-driven underwater gliders considering hull deformation and sea water density variation. Ocean Eng. 2017, 143, 66–78. [Google Scholar] [CrossRef]
- Song, Y.; Ye, H.; Wang, Y.; Niu, W.; Wan, X.; Ma, M. Energy Consumption Modeling for Underwater Gliders Considering Ocean Currents and Sea Water Density Variation. J. Mar. Sci. Eng. 2021, 9, 1164. [Google Scholar] [CrossRef]
- Zhou, H.; Fu, J.; Liu, C.; Yao, B.; Lian, L. Dynamic modeling and endurance enhancement analysis of deep-sea gliders with a hybrid buoyancy regulating system. Ocean Eng. 2020, 217, 108146. [Google Scholar] [CrossRef]
- Xie, X.; Wang, Y.; Yang, S.; Luo, C.; Chen, J. An Optimal Buoyancy Compensation System for Deep-sea Gliders based on GA. In Proceedings of the Global Oceans: Singapore-U.S. Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, M.; Yang, S.; Wang, Y.; Liang, Y.; Wang, S.; Zhang, L. Optimization design of neutrally buoyant hull for underwater gliders. J. Ocean. Eng. 2020, 209, 107512. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, Y.; Wang, S.; Wang, Y. A Bionic Flexible-bodied Underwater Glider with Neutral Buoyancy. J. Bionic Eng. 2021, 18, 1073–1085. [Google Scholar] [CrossRef]
- Dologlonyan, A.V.; Sukhov, A.K. Evaluation of immersion/floating time of marine diving buoys with the help of approximate model. Environ. Control. Syst. 2018, 14, 27–32. [Google Scholar] [CrossRef]
- Krasnodubets, L.A.; Zaburdaev, V.I.; Alchakov, V.V. Control of marine buoys-profilers as a method of enhancing representativeness of thermokhaline measurements. Models of motions. Mar. Hydrophys. J. 2021, 4, 69–79. [Google Scholar]


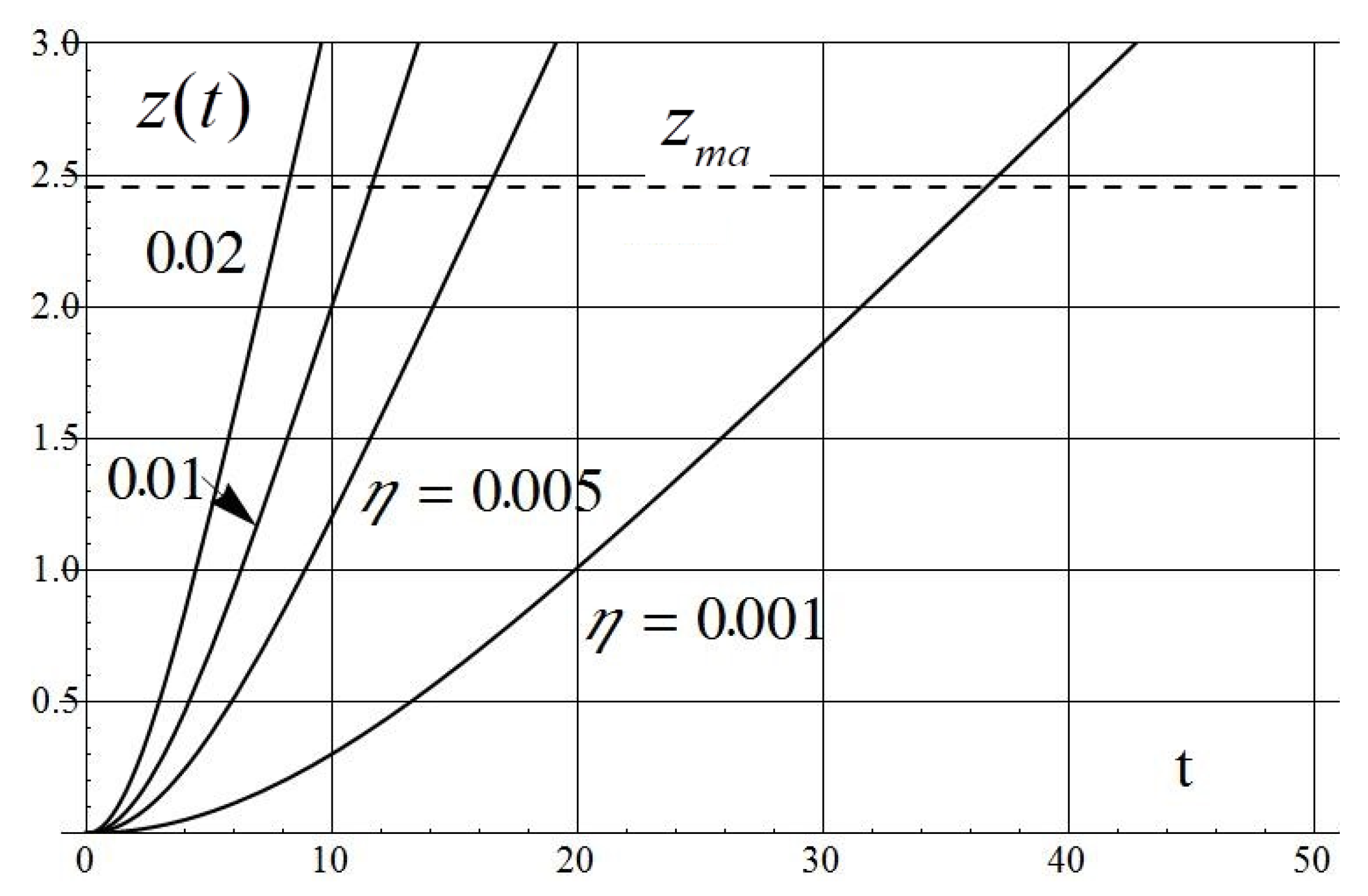
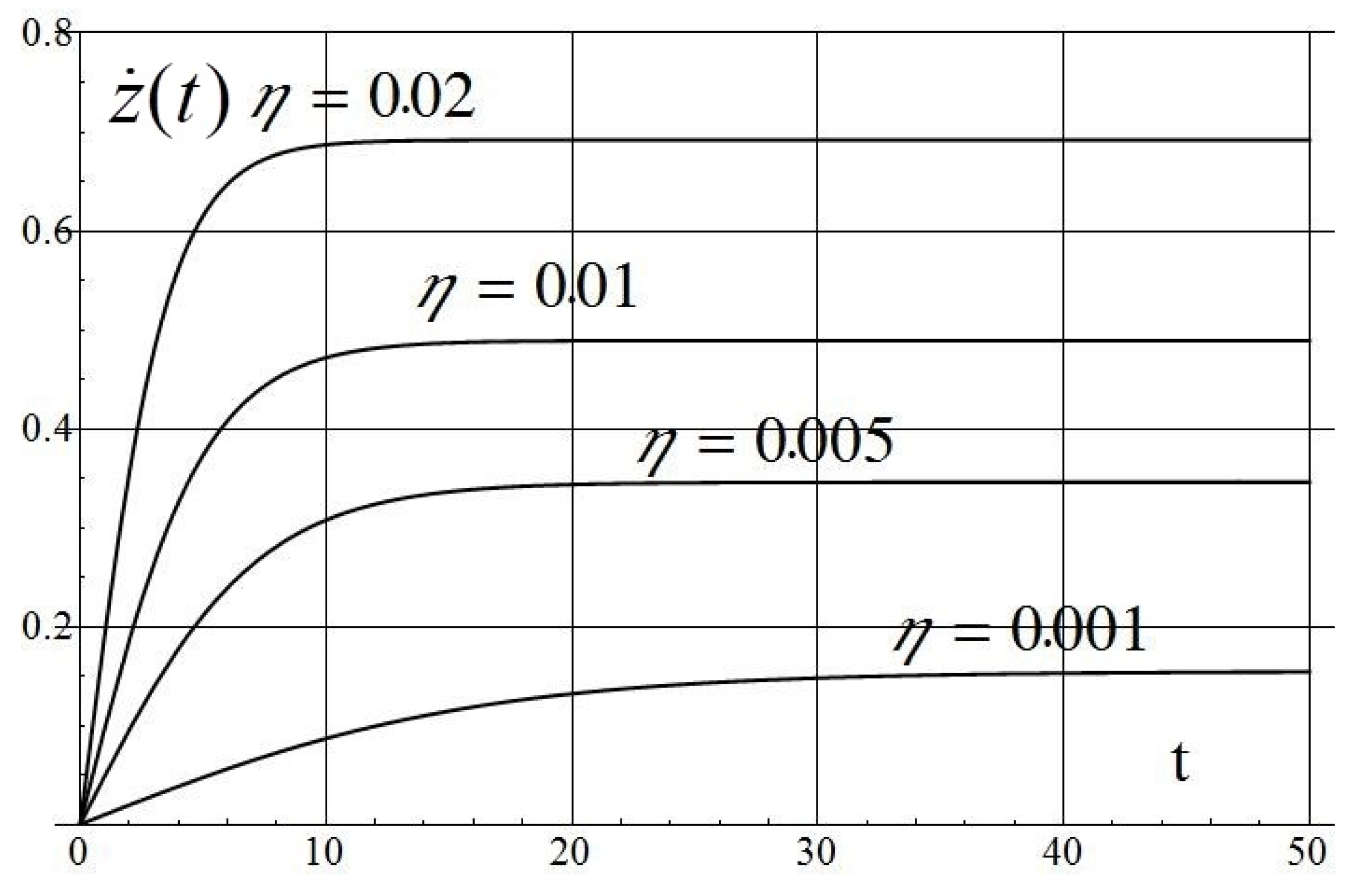
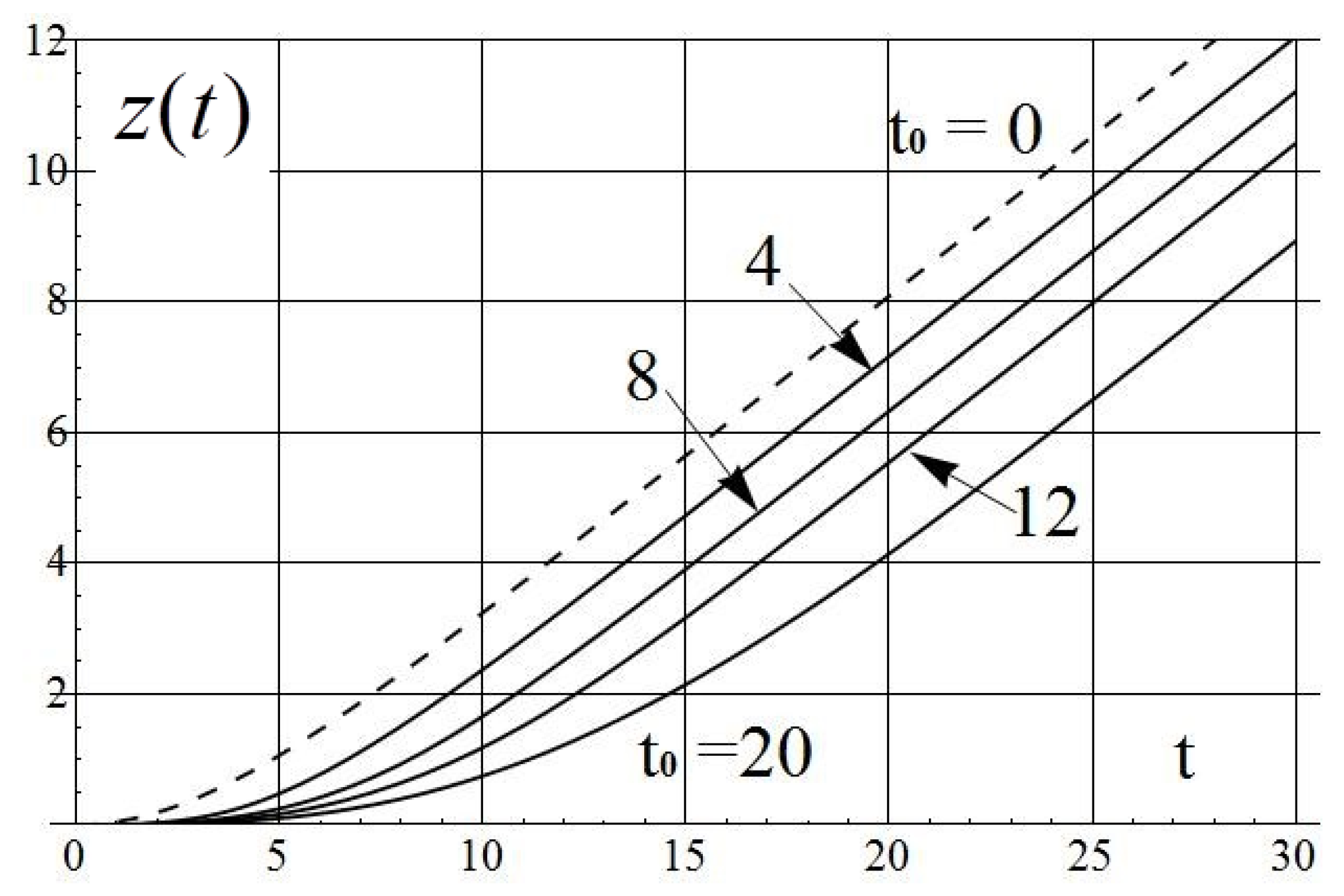


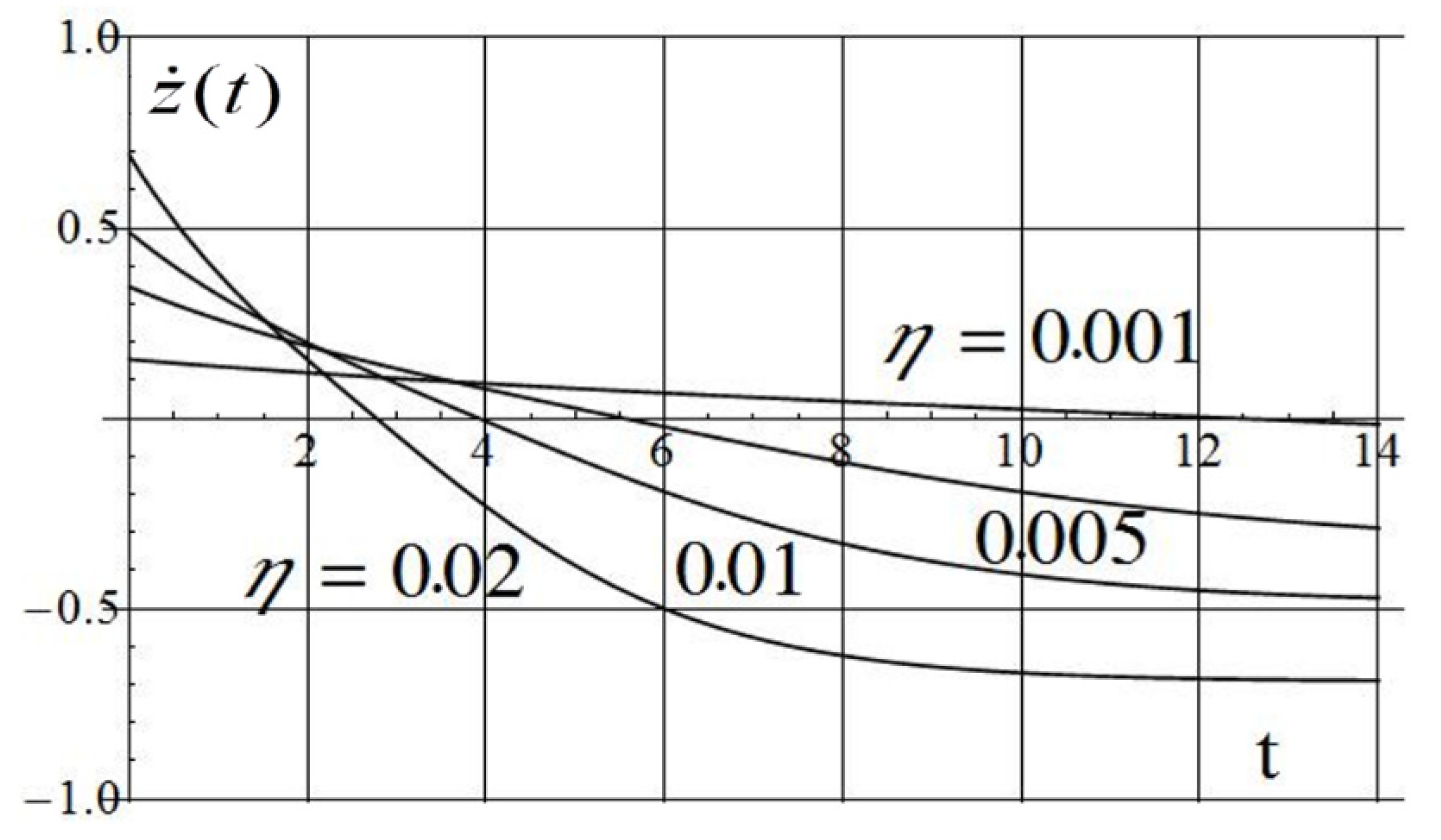

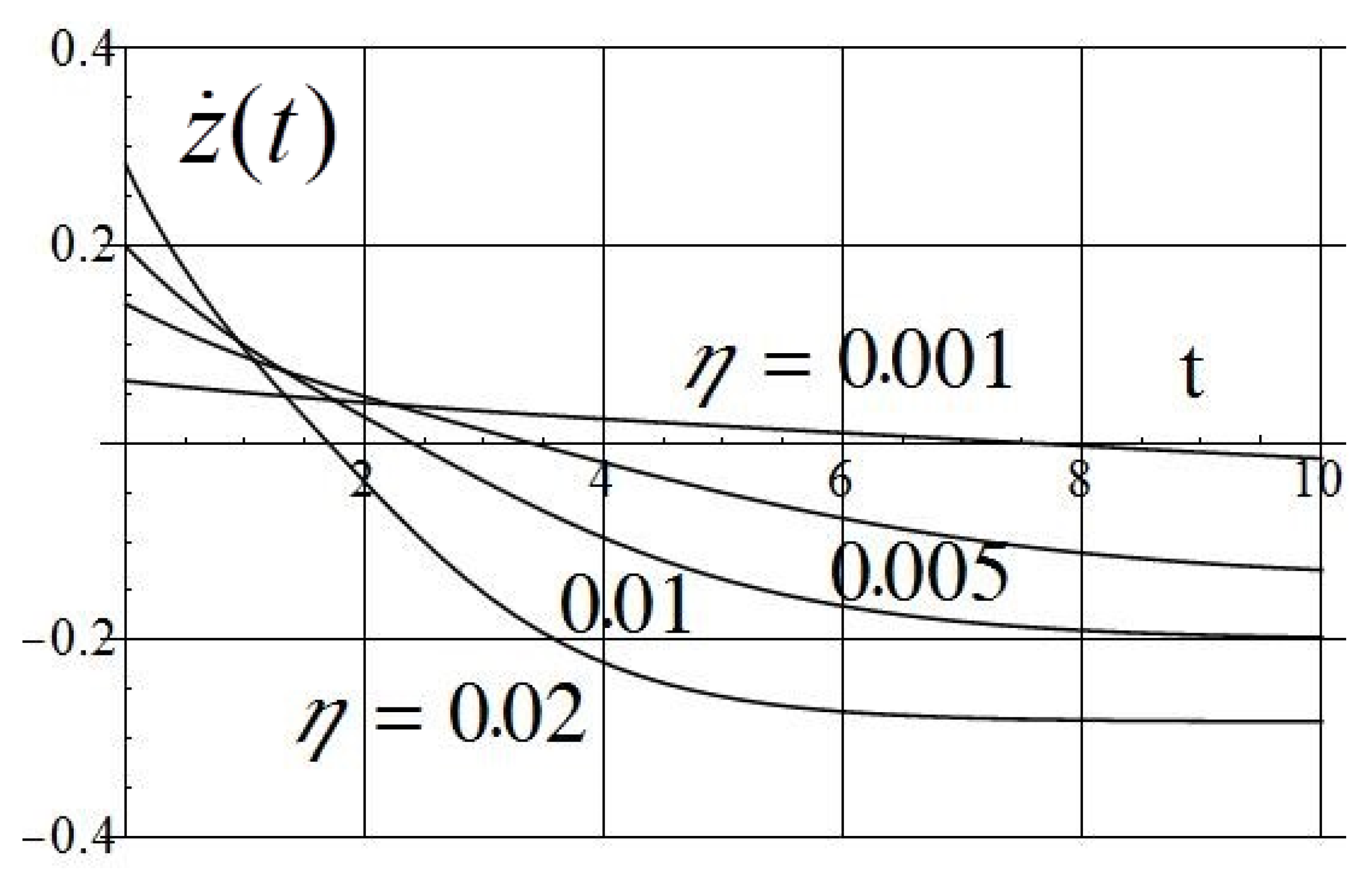
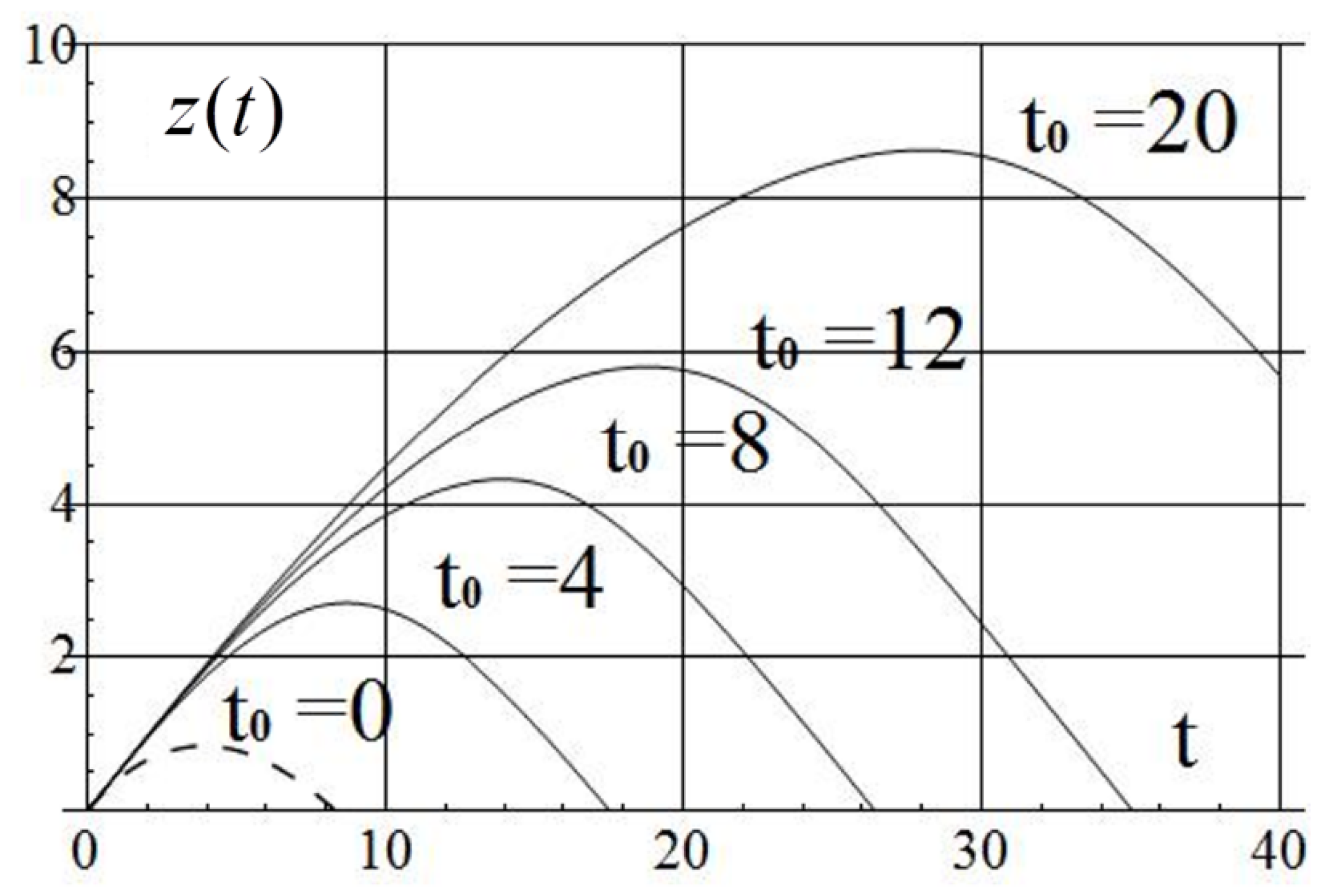
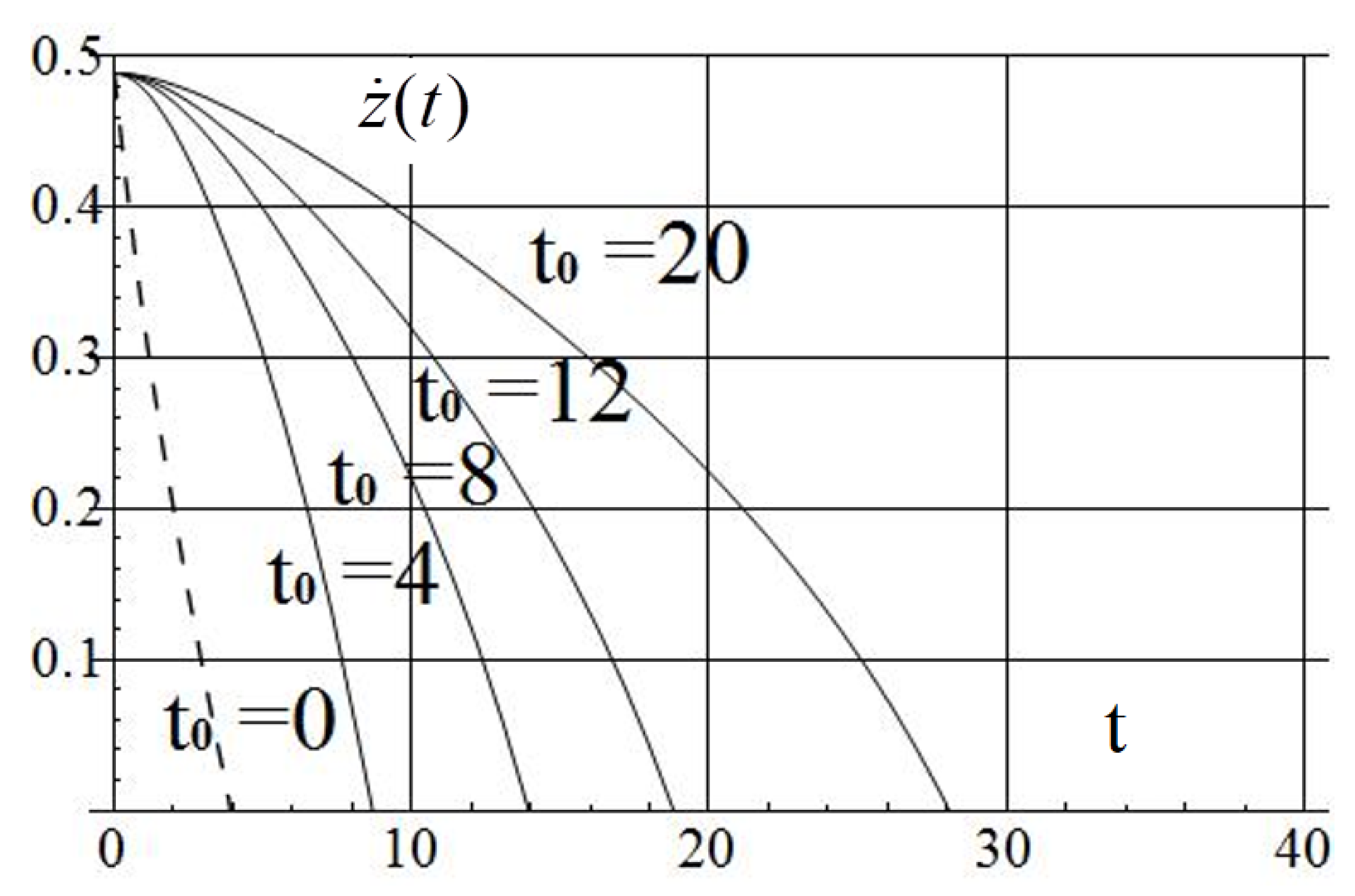
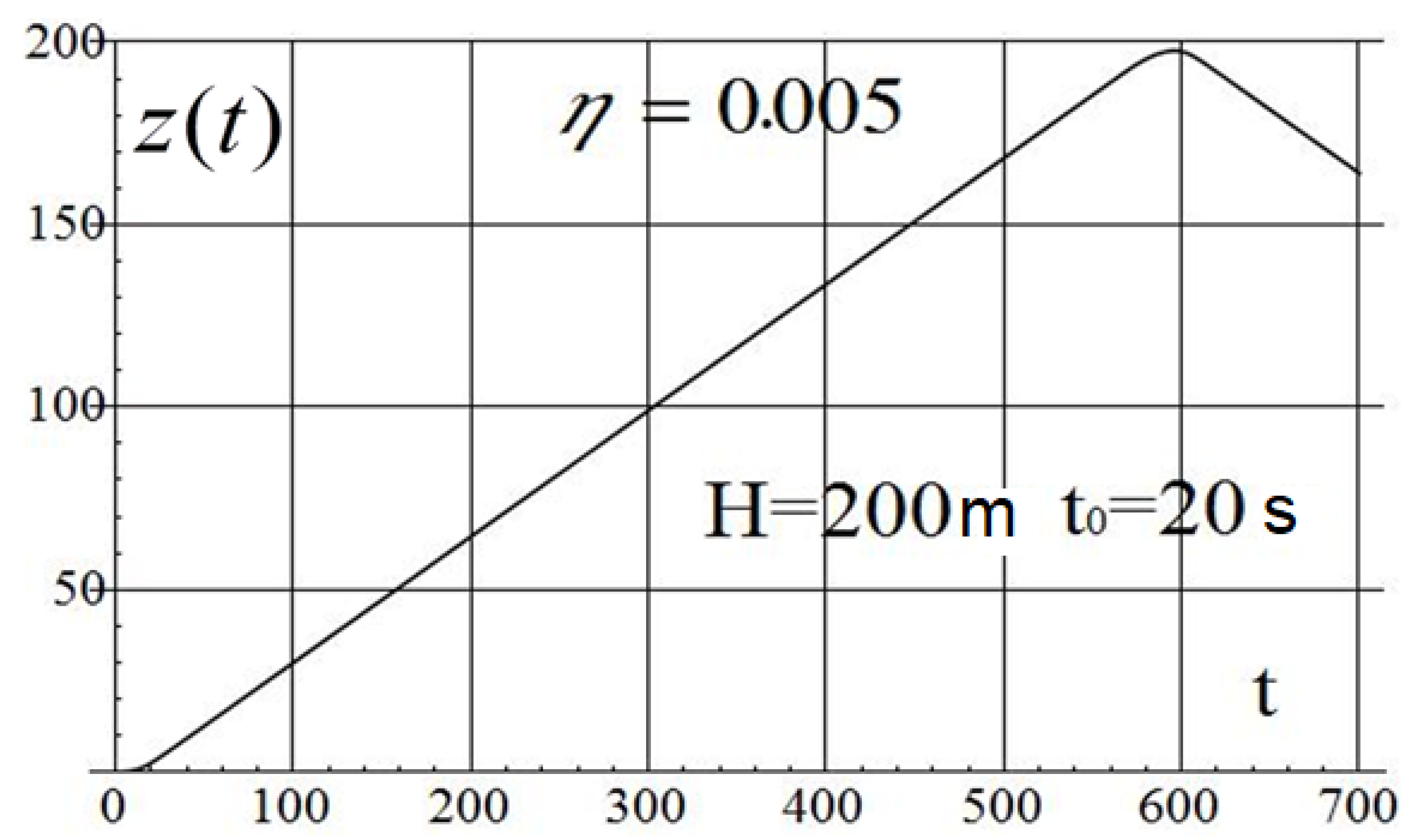

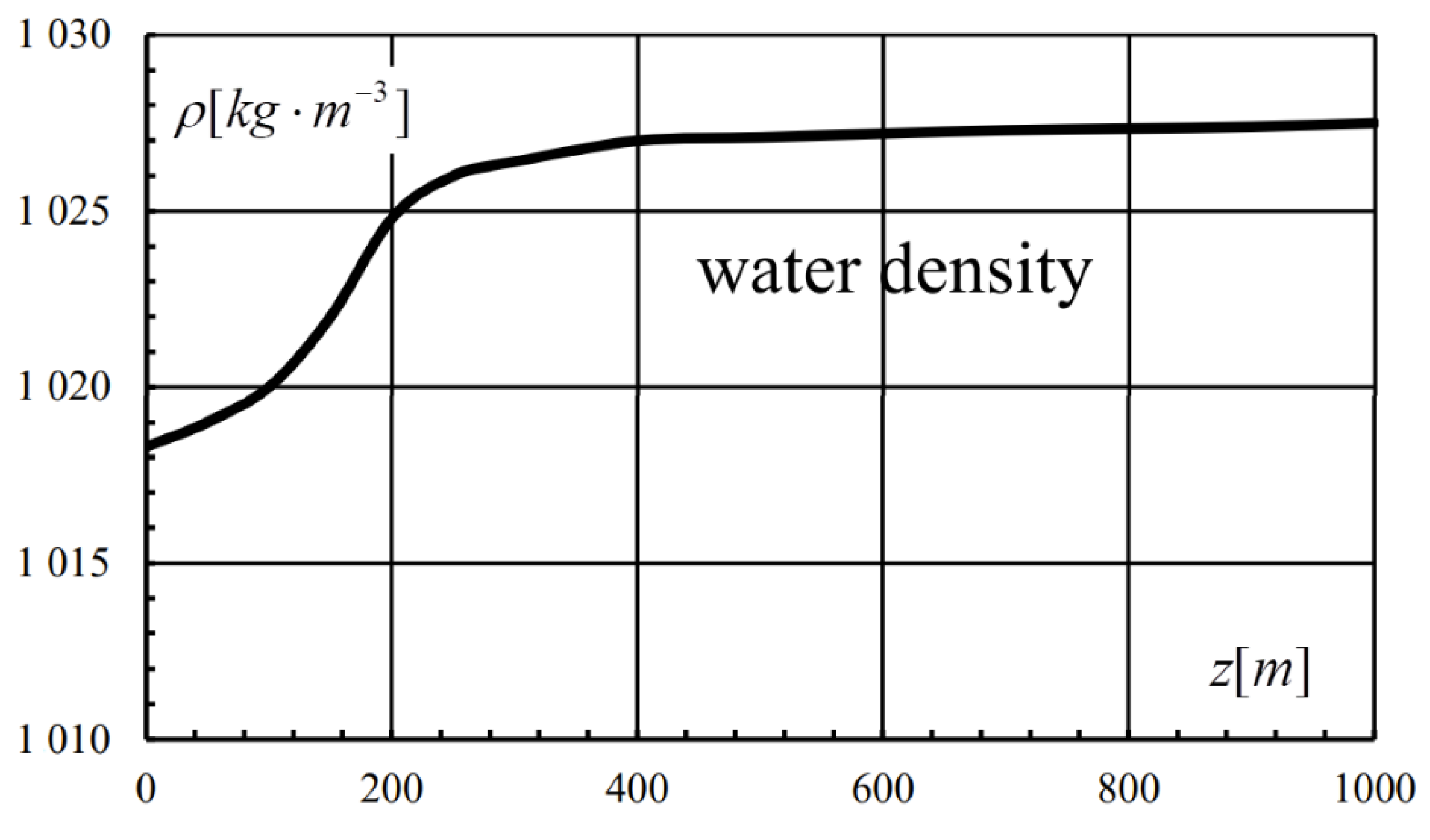
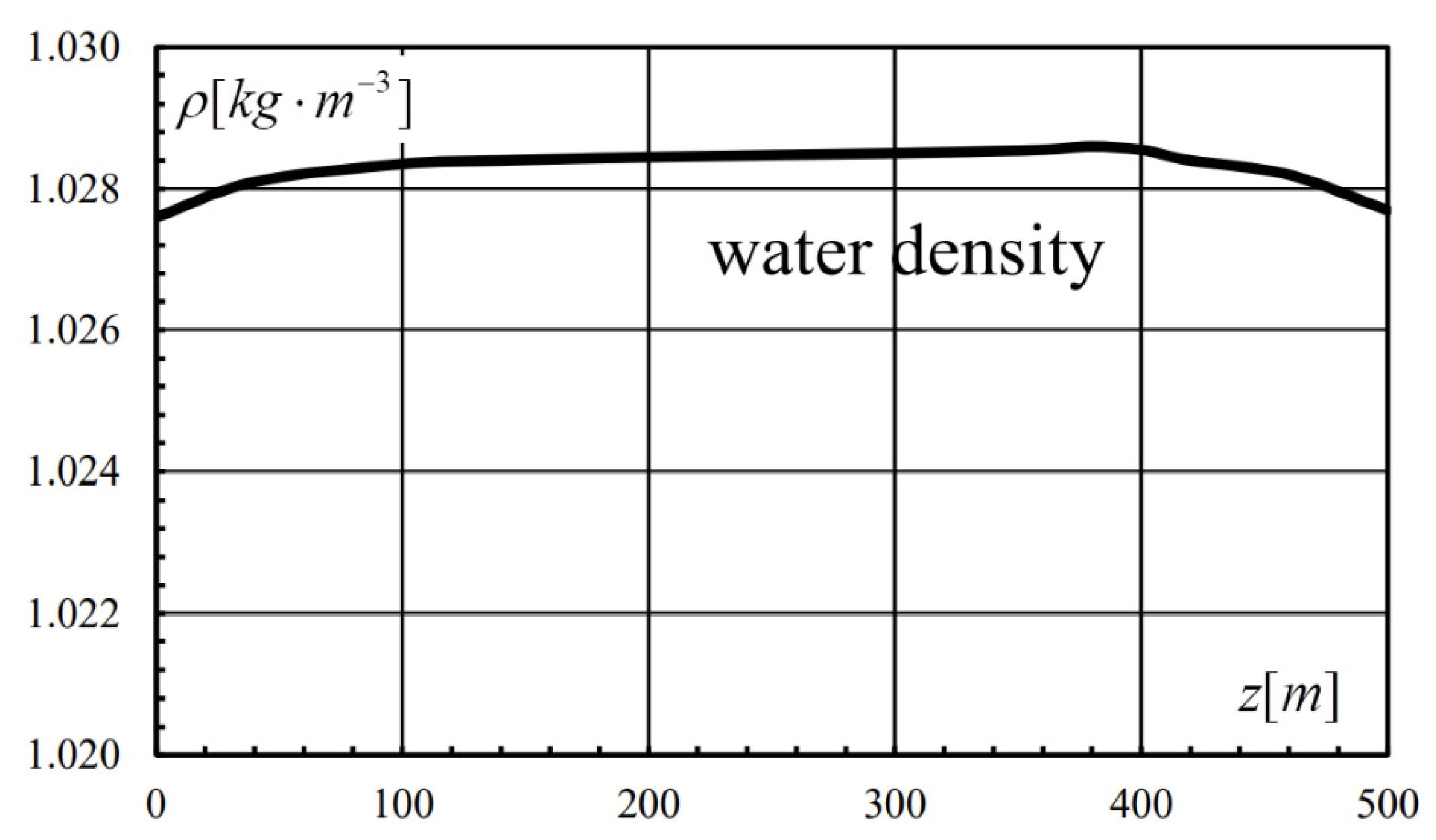

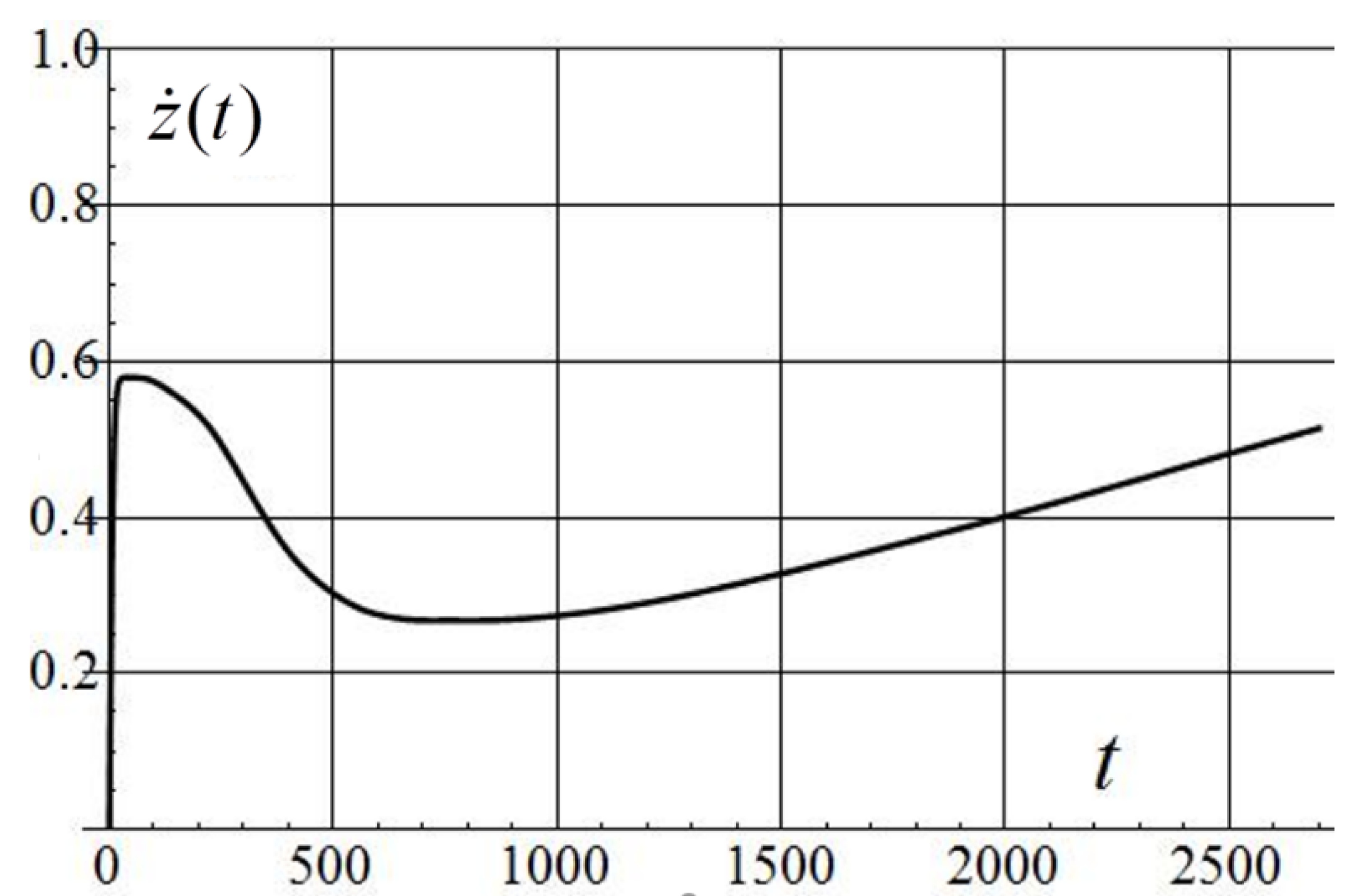
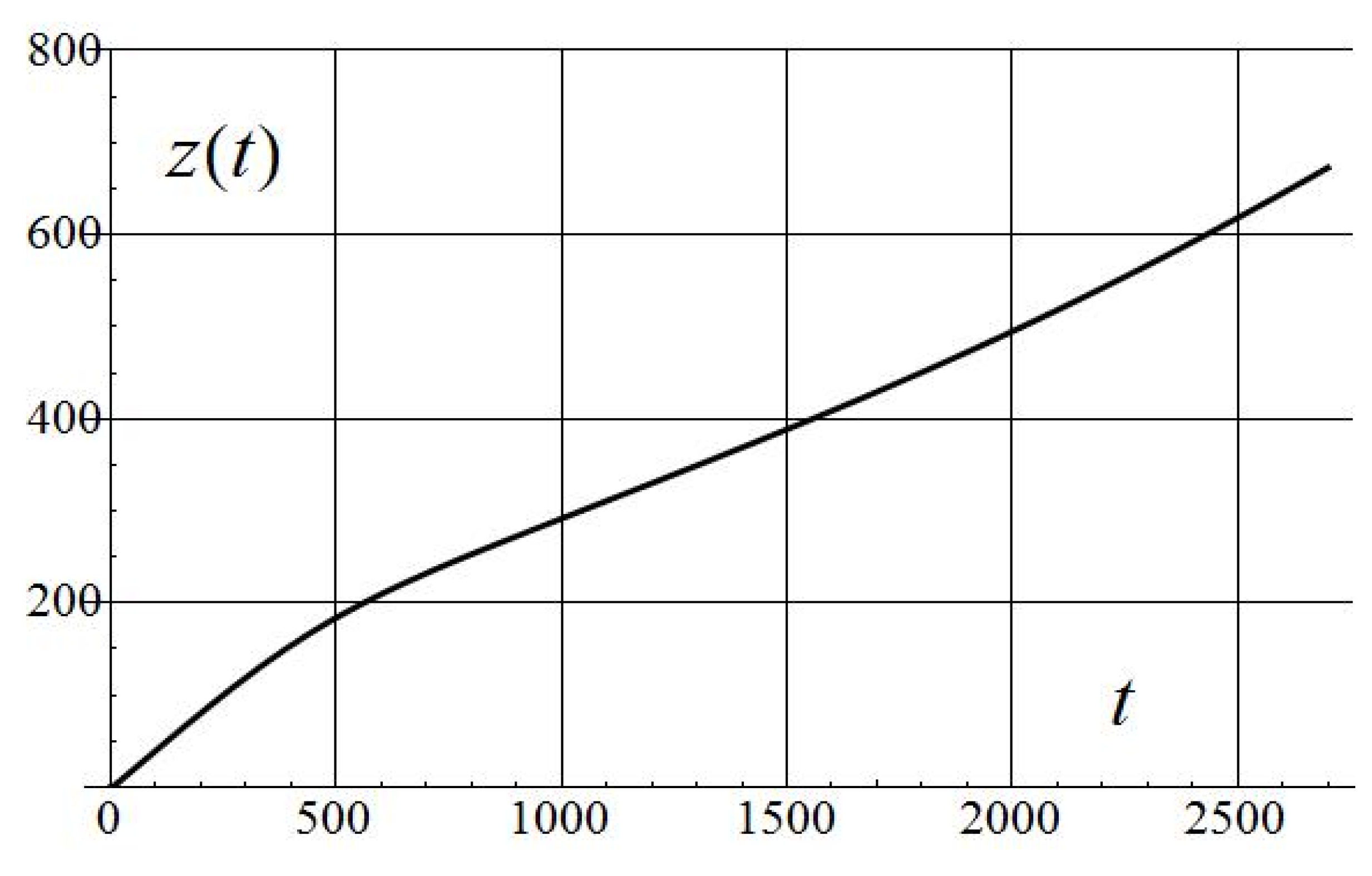
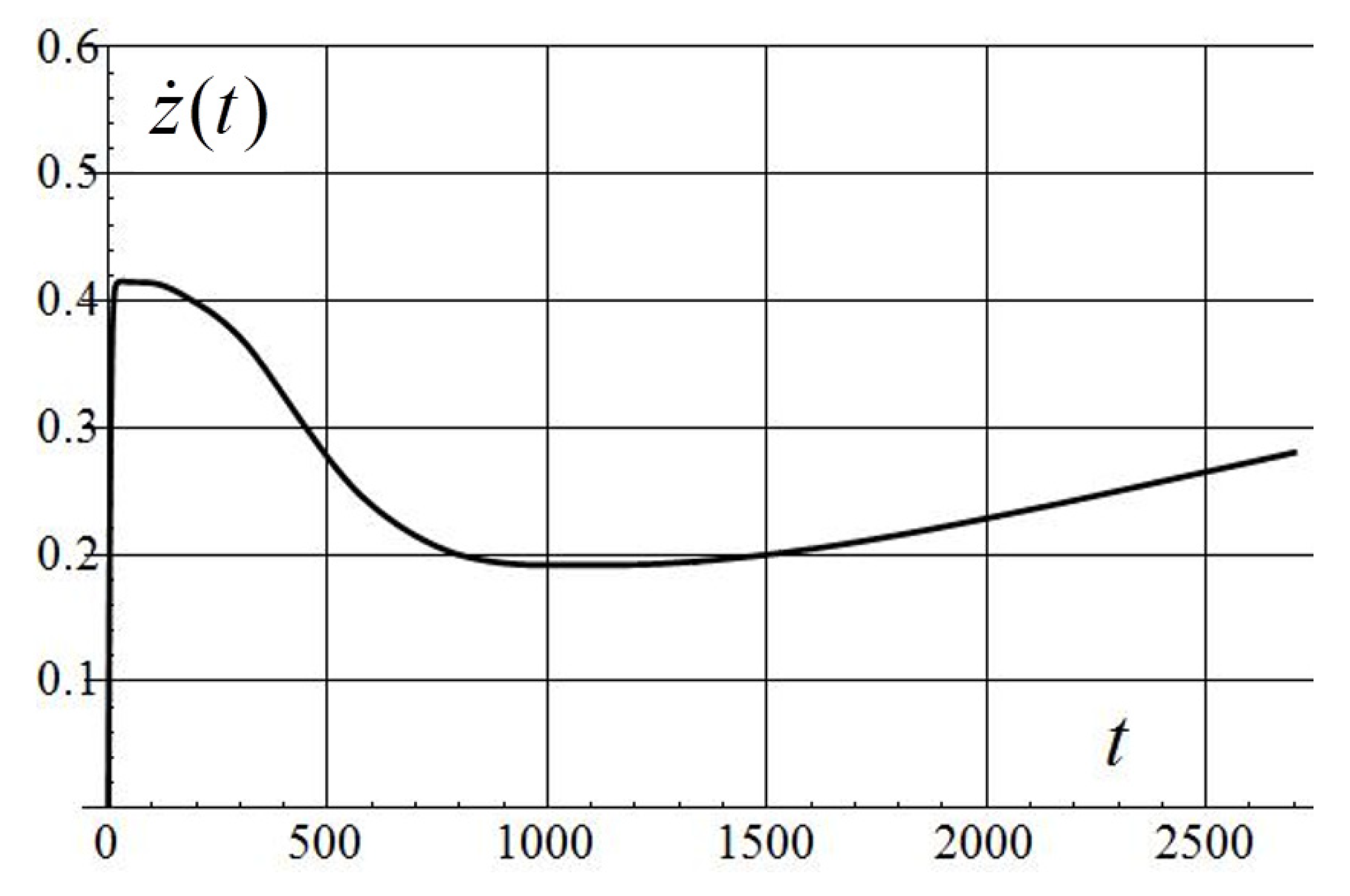
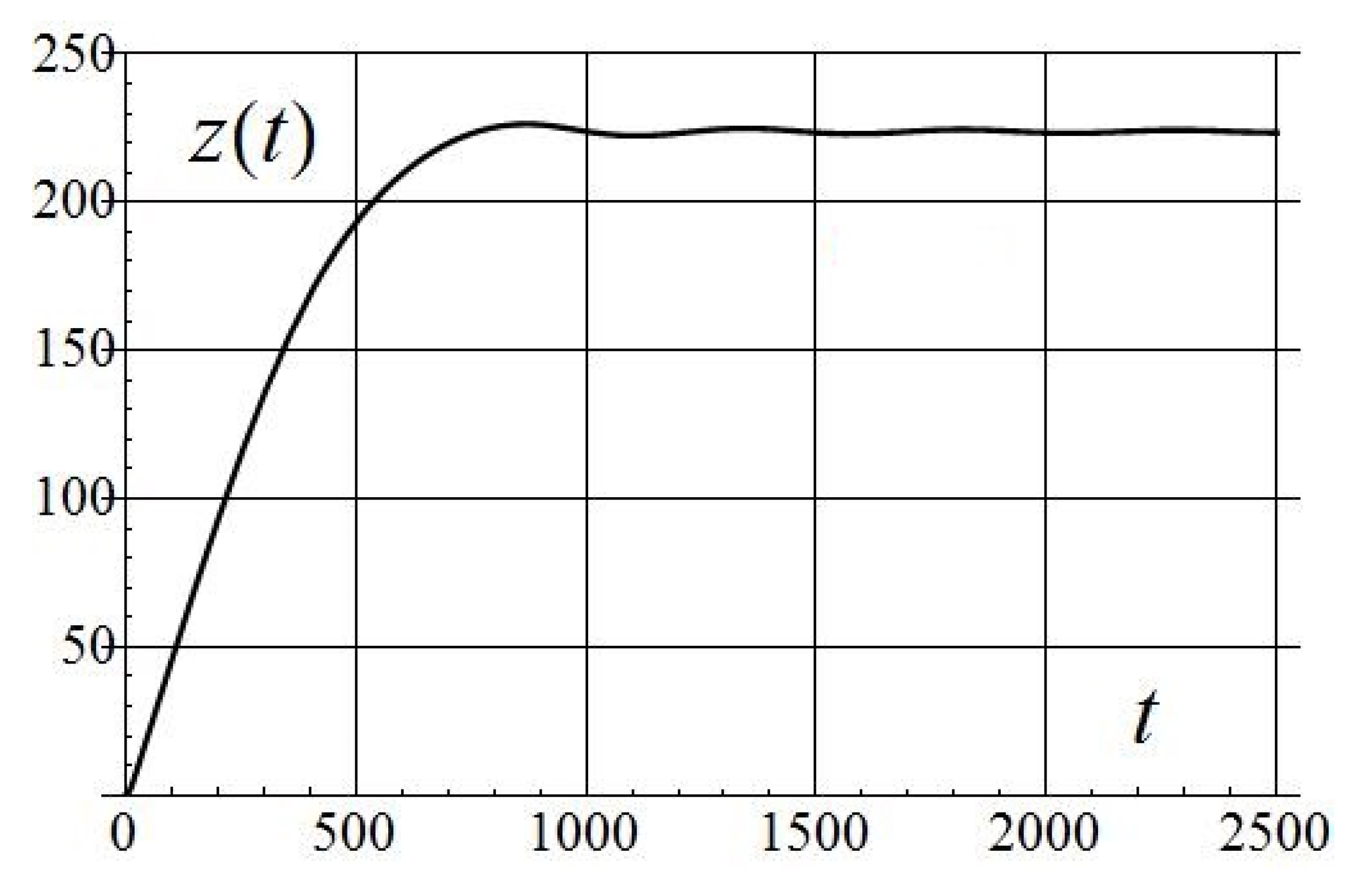
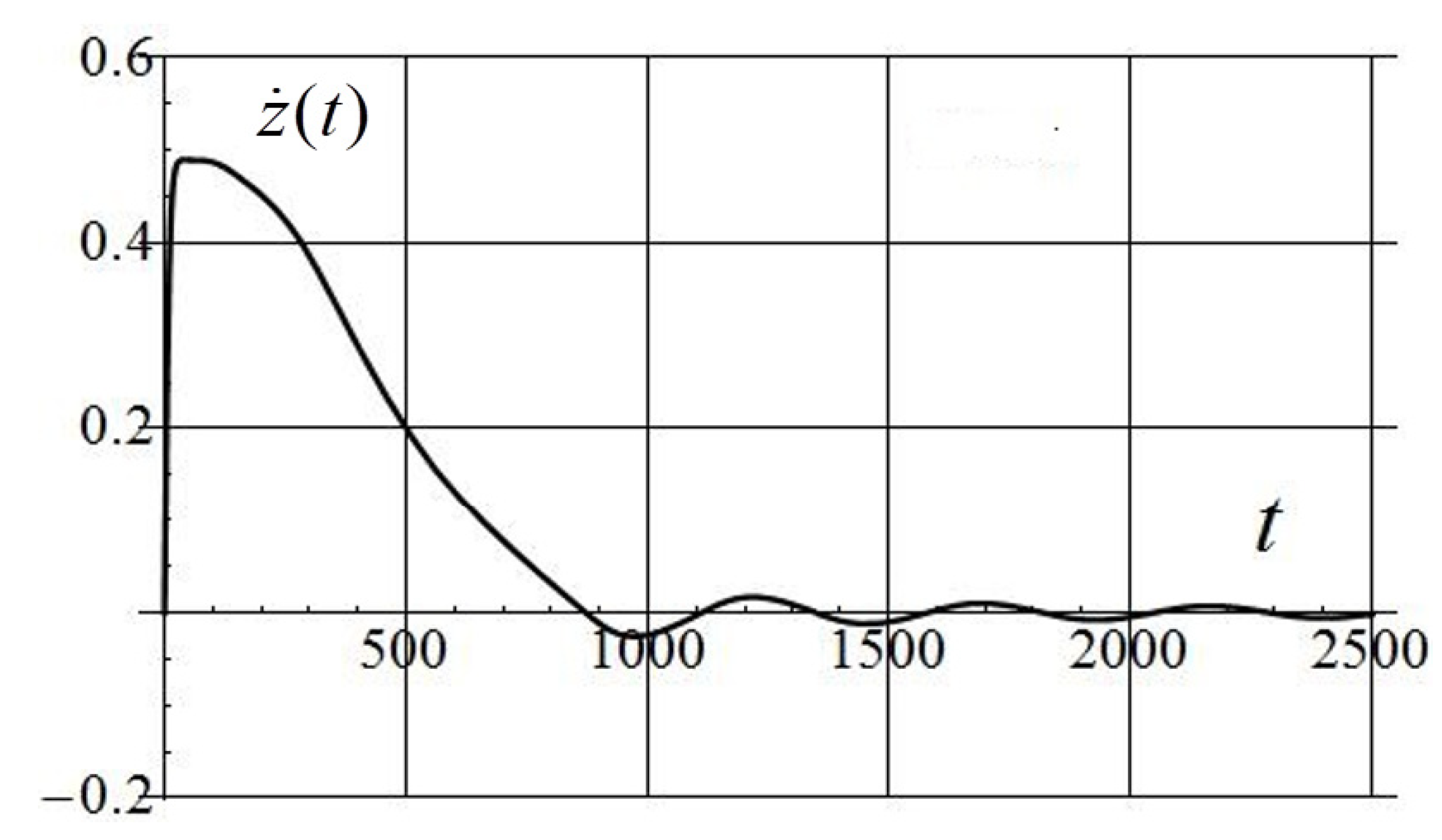
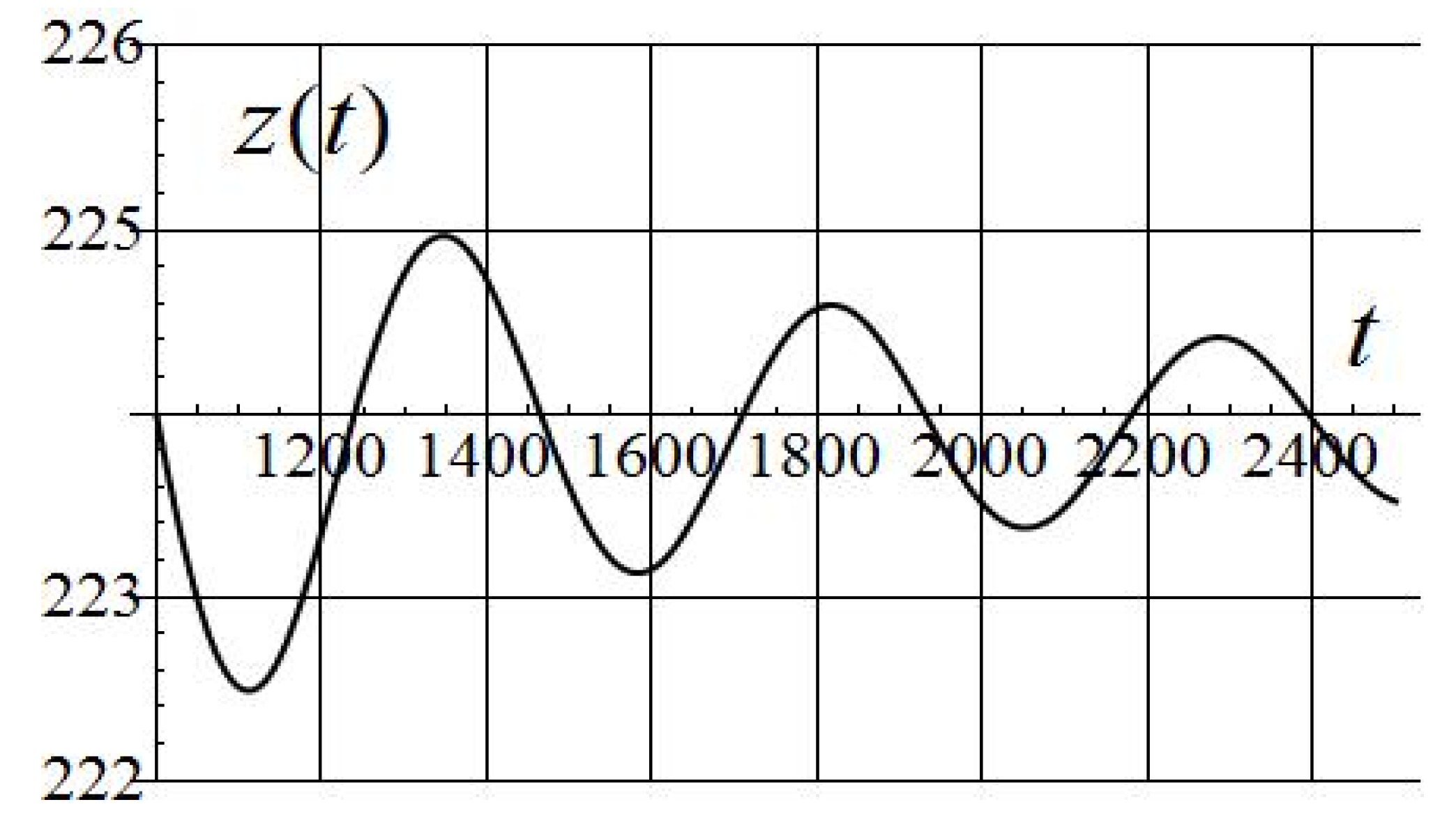

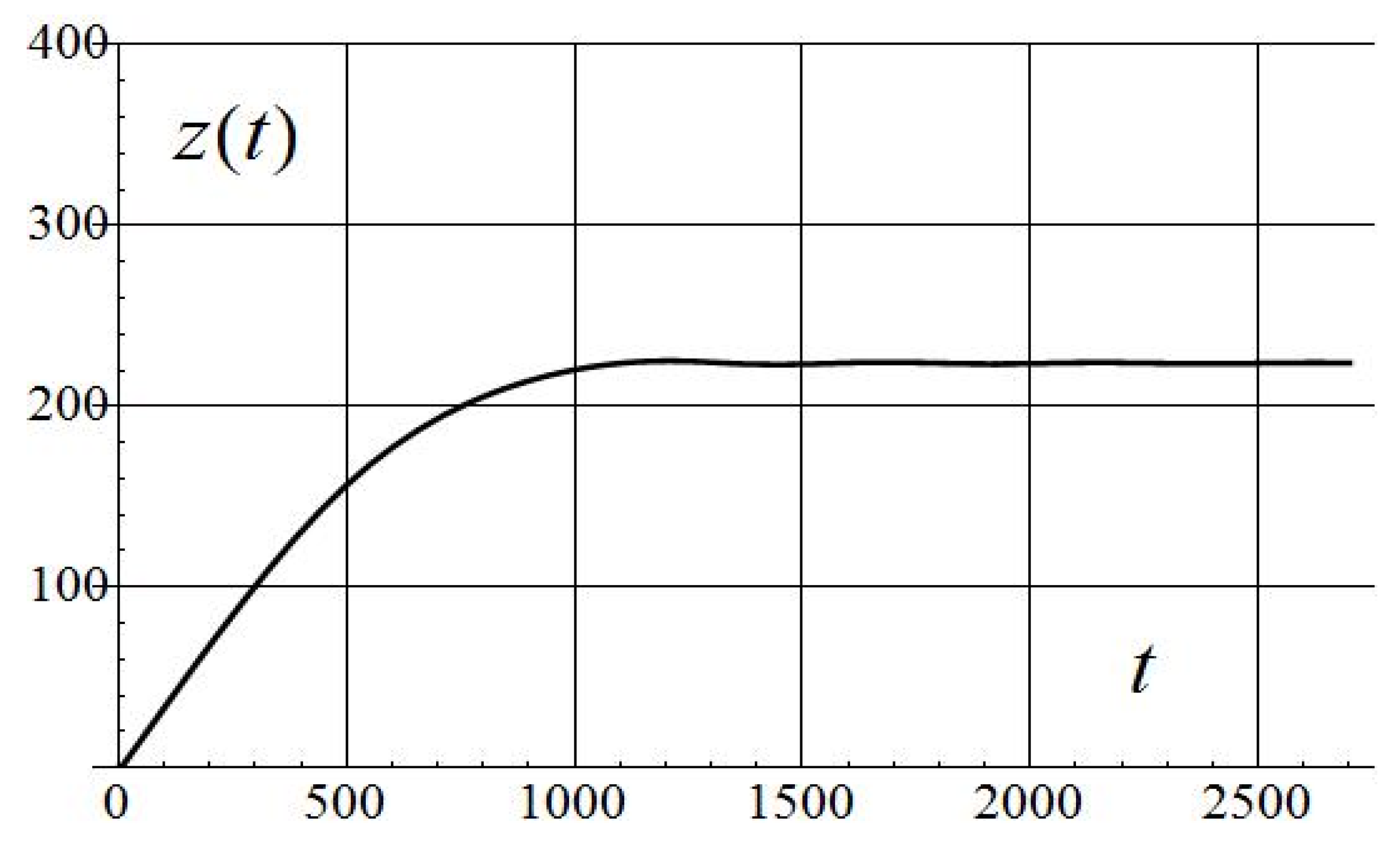

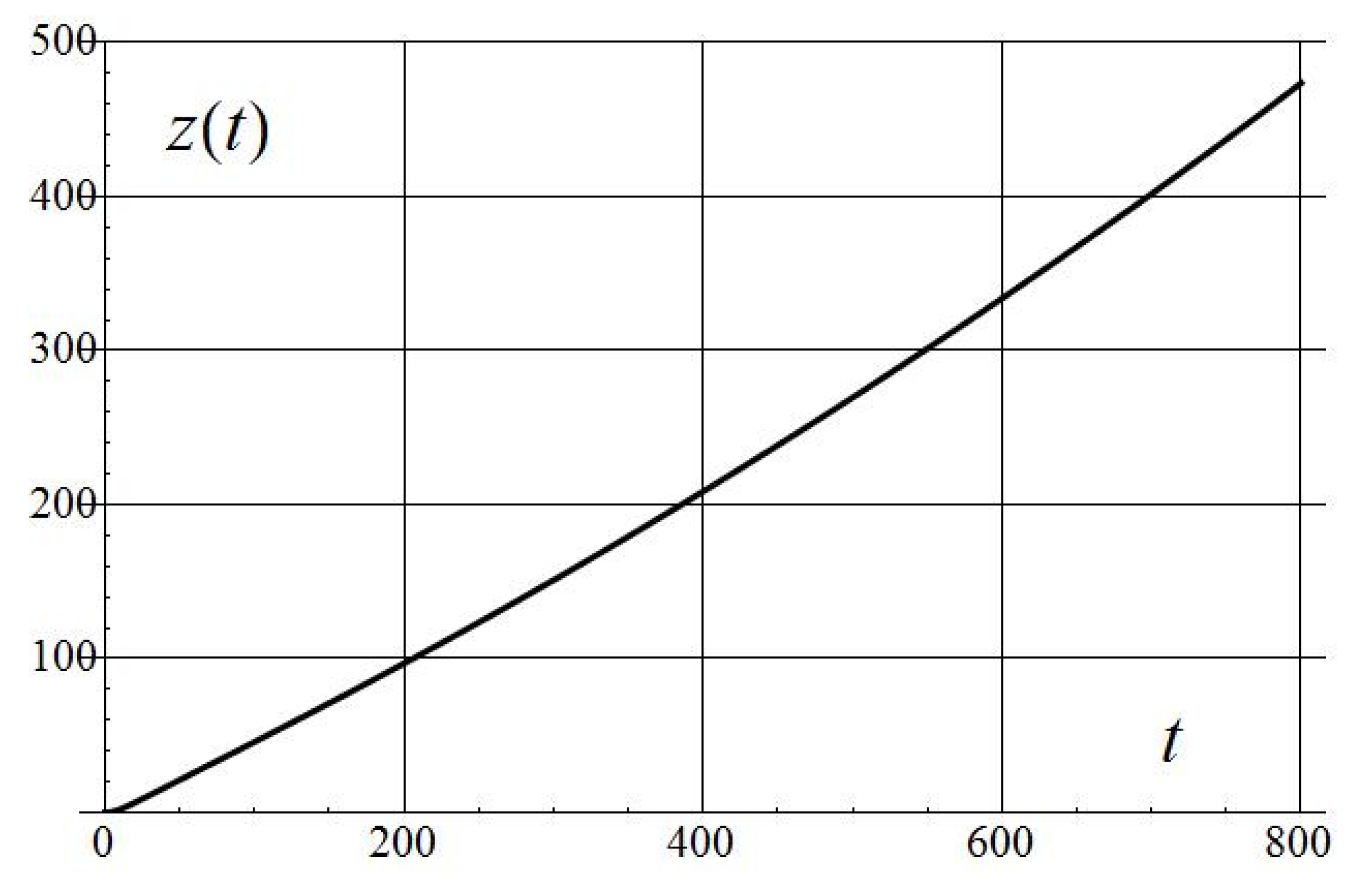
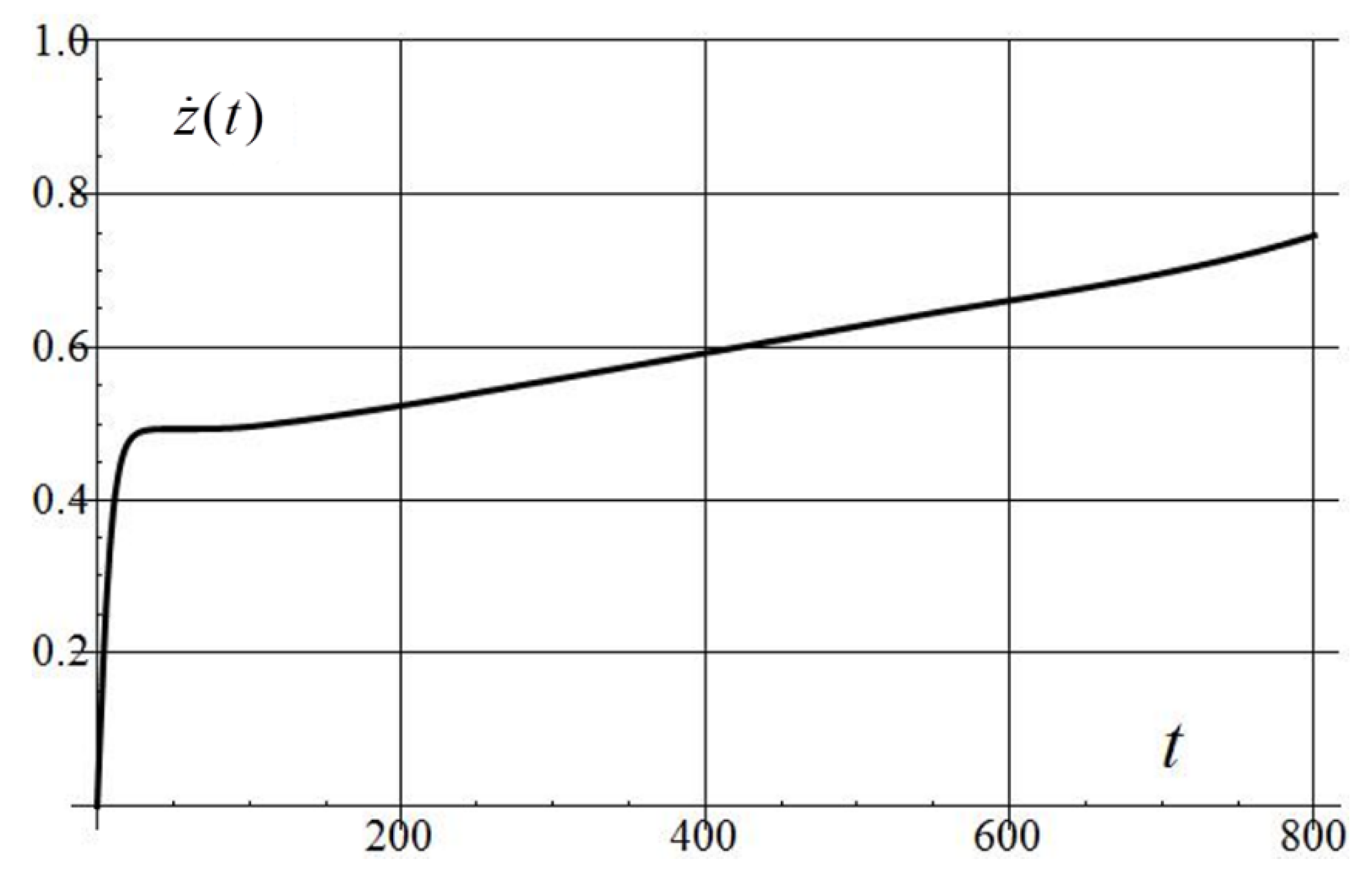
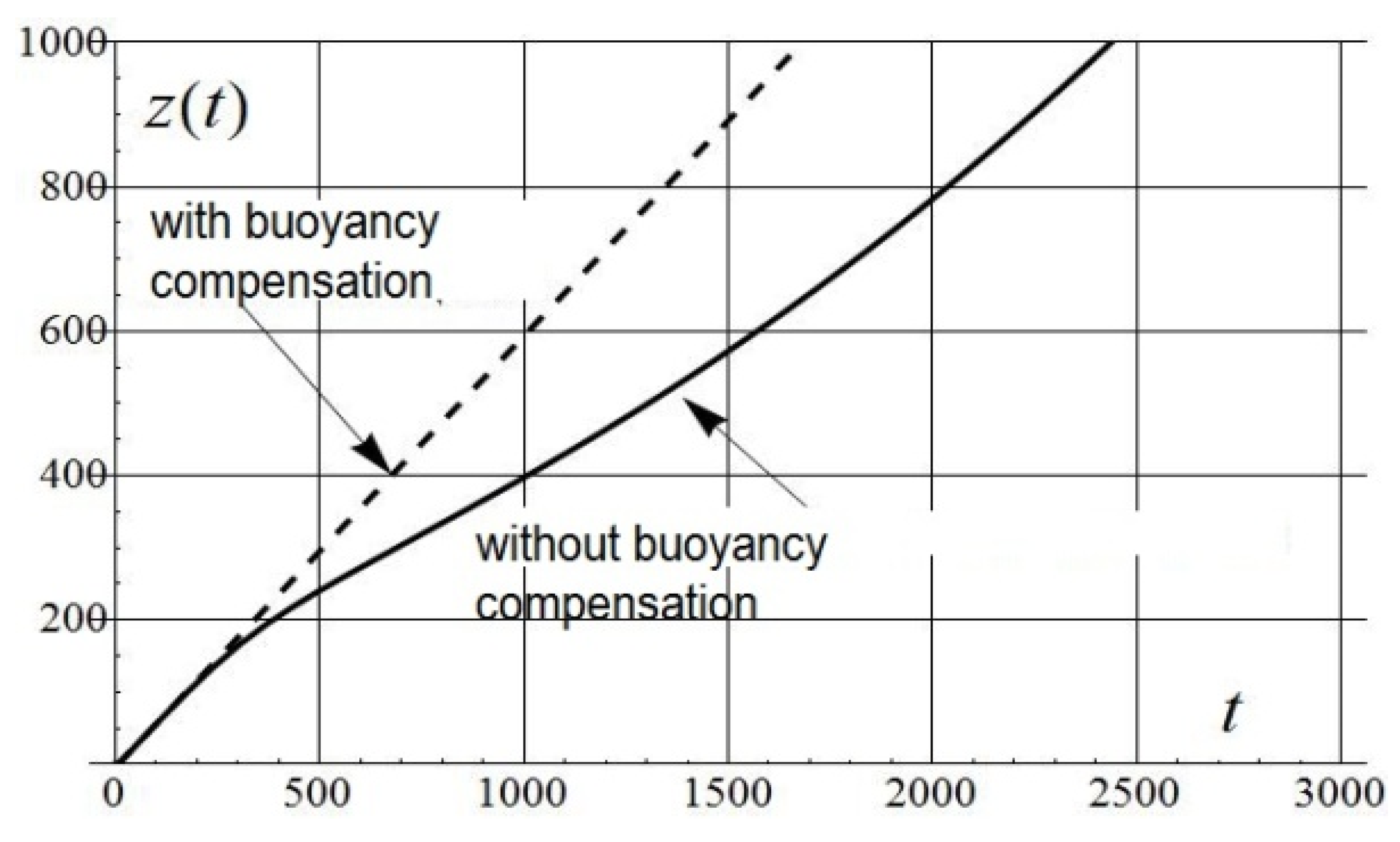
| 0.001 | 29.7 | 1.5 | 0.21 | 41.4 | 5.83 | 917 | 988/16 |
| 0.005 | 28.4 | 6.3 | 0.49 | 43.2 | 10.2 | 375 | 447/7.5 |
| 0.01 | 27.5 | 9.8 | 0.69 | 30.2 | 13.2 | 257 | 315/5.2 |
| 0.02 | 25.1 | 13.1 | 0.98 | 28.1 | 17.3 | 173 | 226/3.8 |
| 0.03 | 23.7 | 15.4 | 1.2 | 27.0 | 20.4 | 137 | 188/3.1 |
| 0.05 | 22.4 | 19.0 | 1.55 | 26.0 | 25.2 | 100 | 148/2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozhdestvensky, K. Dynamics of Submersion of a «Diving Buoy» with Account of Hull Compression and Depth-Wise Variation of Water Density. Appl. Sci. 2022, 12, 2651. https://doi.org/10.3390/app12052651
Rozhdestvensky K. Dynamics of Submersion of a «Diving Buoy» with Account of Hull Compression and Depth-Wise Variation of Water Density. Applied Sciences. 2022; 12(5):2651. https://doi.org/10.3390/app12052651
Chicago/Turabian StyleRozhdestvensky, Kirill. 2022. "Dynamics of Submersion of a «Diving Buoy» with Account of Hull Compression and Depth-Wise Variation of Water Density" Applied Sciences 12, no. 5: 2651. https://doi.org/10.3390/app12052651
APA StyleRozhdestvensky, K. (2022). Dynamics of Submersion of a «Diving Buoy» with Account of Hull Compression and Depth-Wise Variation of Water Density. Applied Sciences, 12(5), 2651. https://doi.org/10.3390/app12052651





