Microstructured Phononic Crystal Isolates from Ultrasonic Mechanical Vibrations
Abstract
:1. Introduction
2. Design of 3D Phononic Crystals
3. Fabrication and Characterization of the Phononic Crystal
3.1. Material and Writing Procedure
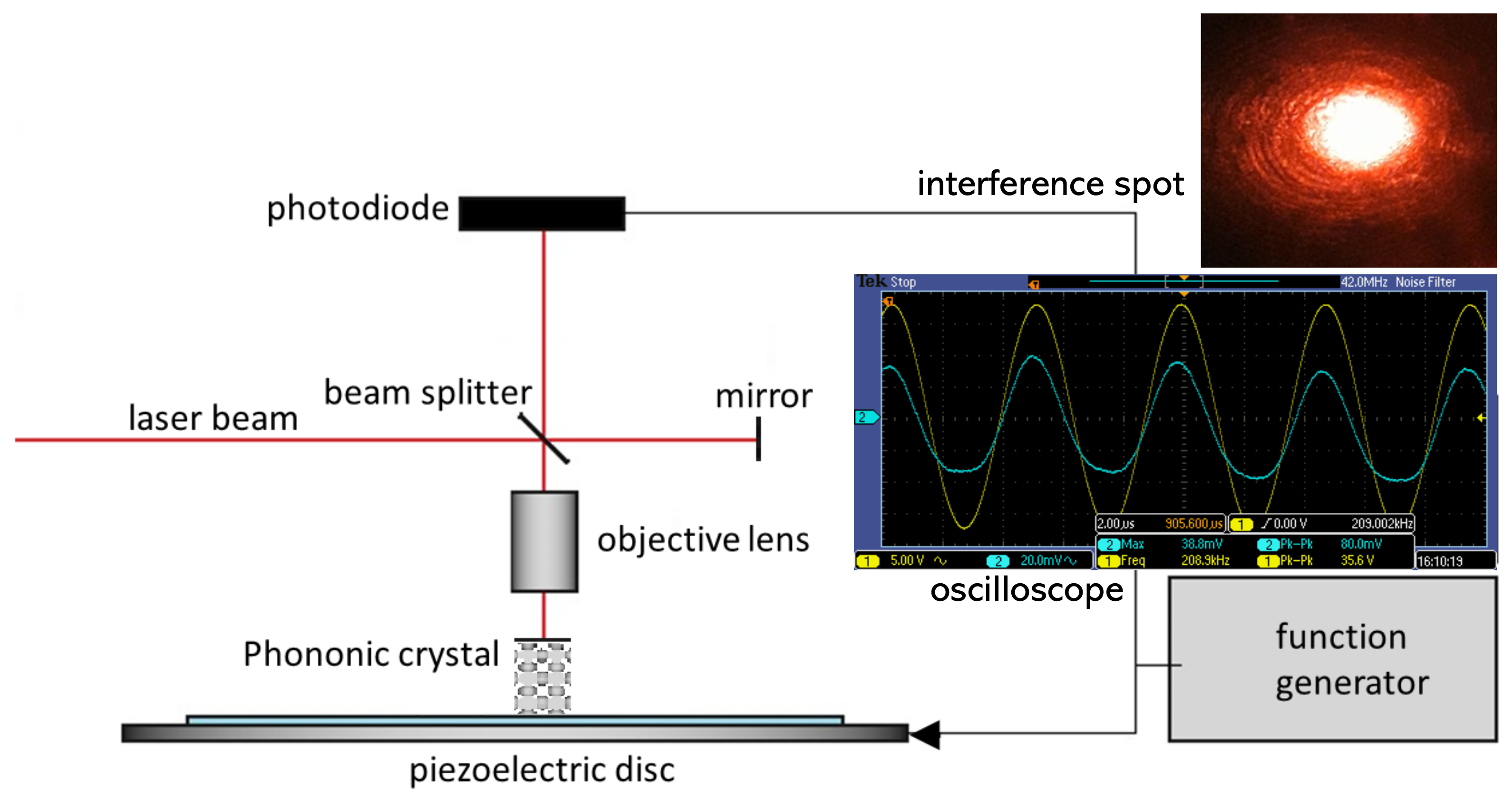
3.2. Experimental Set-Up
4. Results
4.1. Phononic Microstructures
4.2. Oscillation Measurements
5. Discussion
6. Conclusions
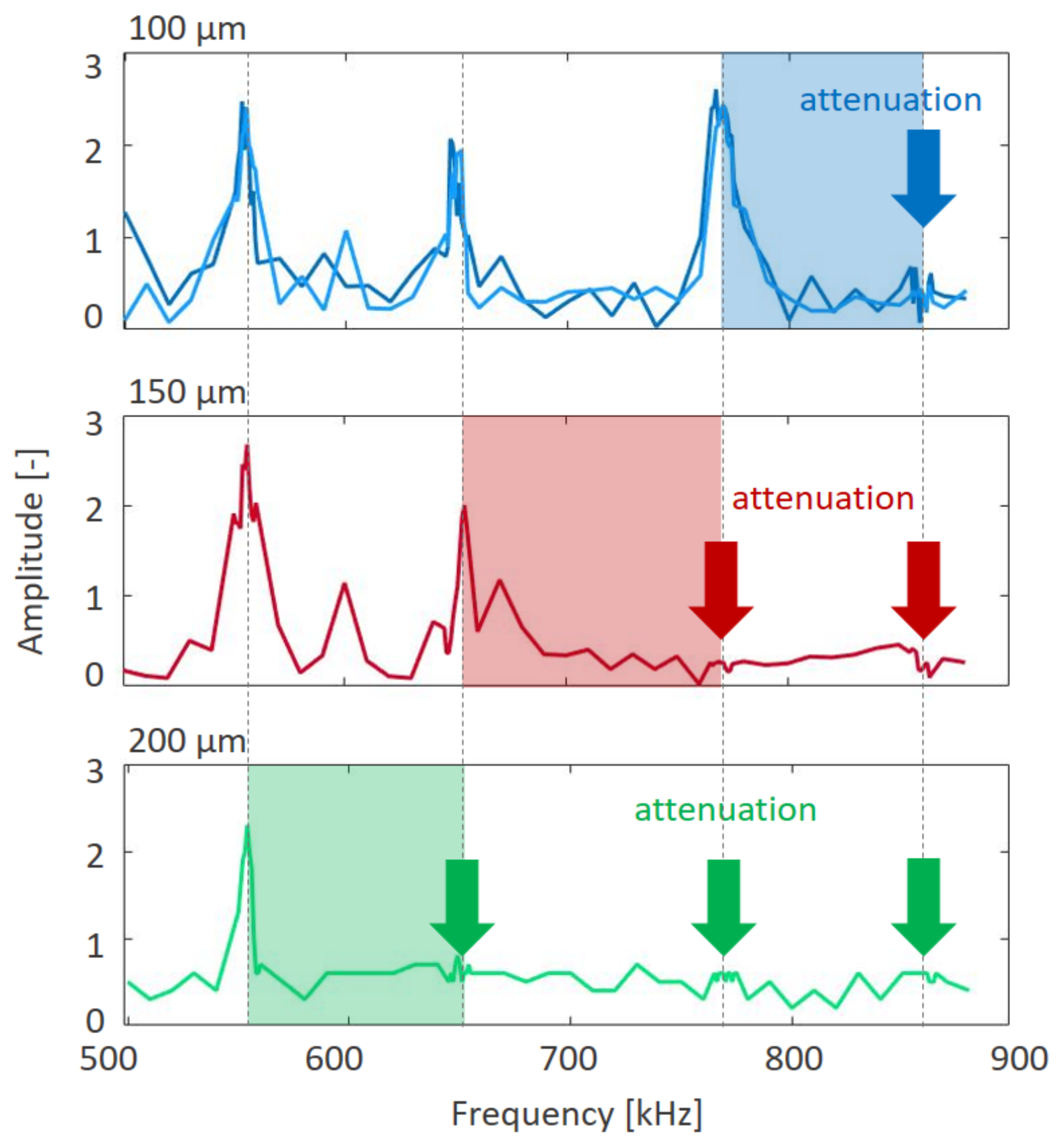
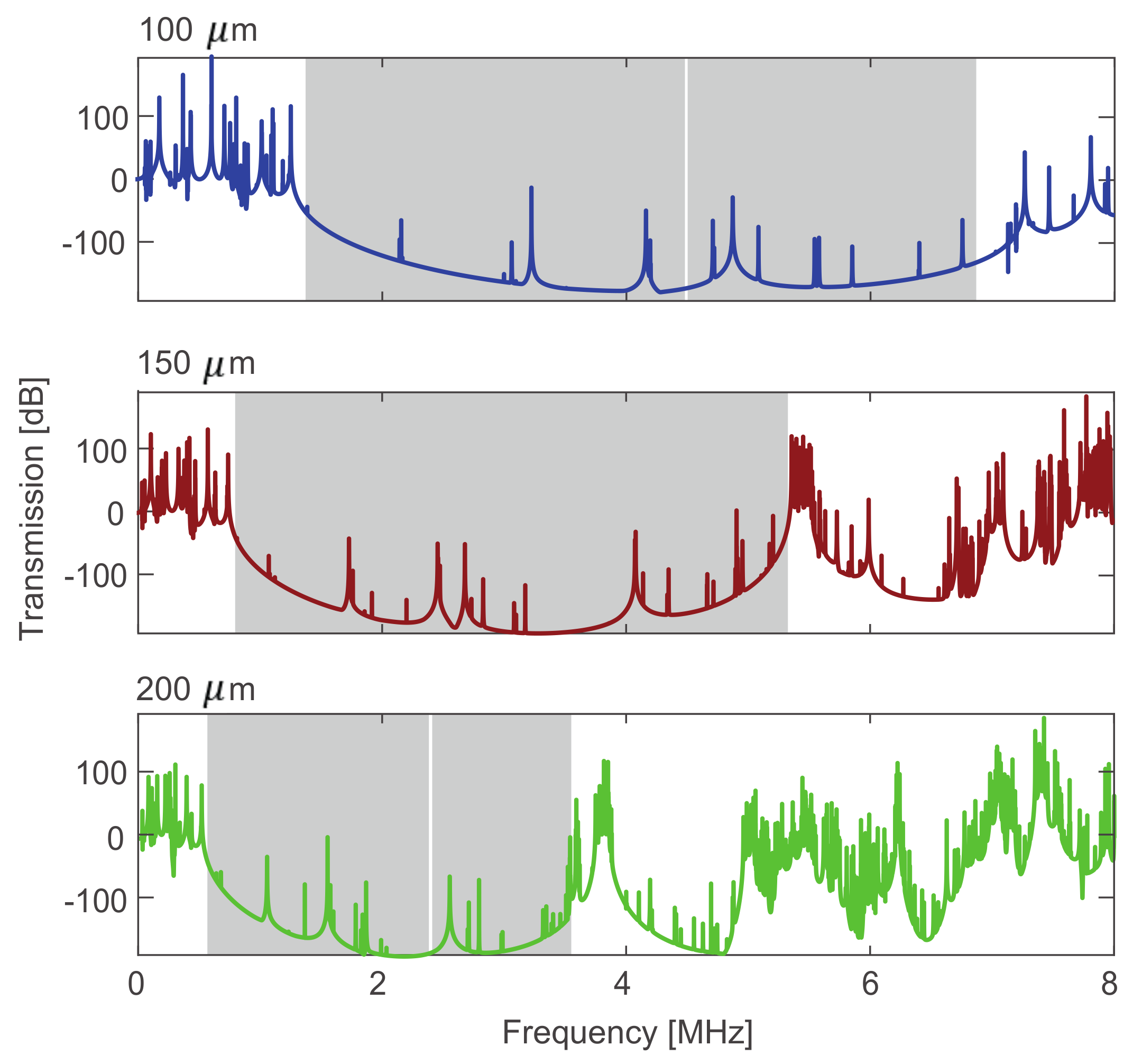
- three prototypes made by a 2 × 2 × 3 periodic repetition of unit cells of 100, 150 and 200 µm width were fabricated through the 2PP technique, numerically simulated in COMSOL Multiphysics and experimentally tested through a Michelson interferometer;
- a good agreement between theoretical predictions based on dispersion analyses of the ideally periodic material, attenuation analyses of the designed metastructures and experimental results on the fabricated metastructures was achieved;
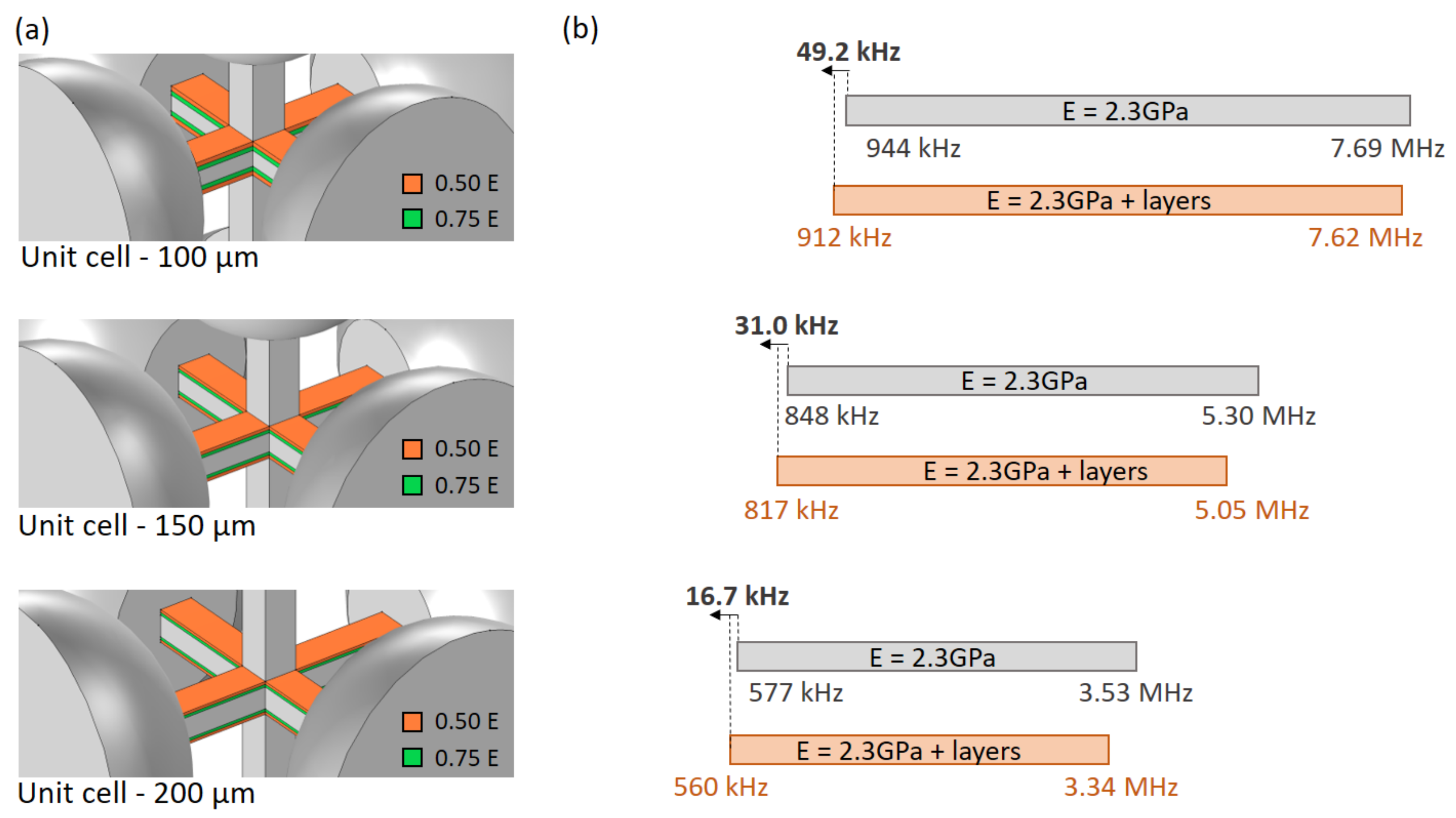
- the influence of the layered structure obtained by 2PP on the elastic properties of the polymerized material was highlighted and simulated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2PP | Two-Photon Polymerization |
| MEMS | Micro Electro Mechanical Systems |
| IBZ | Irreducible Brillouin Zone |
References
- Corigliano, A.; Ardito, R.; Comi, C.; Frangi, A.; Ghisi, A.; Mariani, S. Mechanics of Microsystems; Wiley: Hoboken, NJ, USA, 2018; ISBN 978-1-119-05383-5. [Google Scholar]
- Zega, V.; Silva, P.; Geers, M.; Kouznetsova, V. Experimental proof of emergent subharmonic attenuation zones in a nonlinear locally resonant metamaterial. Sci. Rep. 2020, 10, 12041. [Google Scholar] [CrossRef] [PubMed]
- Fronk, M.D.; Leamy, M.J. Internally resonant wave energy exchange in weakly nonlinear lattices and metamaterials. Phys. Rev. E 2019, 100, 032213. [Google Scholar] [CrossRef]
- Jiao, W.; Gonella, S. Intermodal and Subwavelength Energy Trapping in Nonlinear Metamaterial Waveguides. Phys. Rev. Appl. 2018, 10, 024006. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Torrent, D.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Simultaneous control of the S0 and A0 Lamb modes by graded phononic crystal plates. J. Appl. Phys. 2015, 117, 244904. [Google Scholar] [CrossRef]
- Tol, S.; Degertekin, F.L.; Erturk, A. Phononic crystal Luneburg lens for omnidirectional elastic wave focusing and energy harvesting. Appl. Phys. Lett. 2017, 111, 013503. [Google Scholar] [CrossRef]
- Zhao, L.; Lai, C.; Yu, M. Modified structural Luneburg lens for broadband focusing and collimation. Mech. Syst. Signal Process. 2020, 144, 106868. [Google Scholar] [CrossRef]
- Chaplain, G.J.; Craster, R.V. Flat lensing by graded line meta-arrays. Phys. Rev. B 2019, 99, 220102. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Guo, H.; Wang, T. A review of acoustic metamaterials and phononic crystals. Crystals 2020, 10, 305. [Google Scholar] [CrossRef]
- Vasileiadis, T.; Varghese, J.; Babacic, V.; Gomis-Bresco, J.; Navarro Urrios, D.; Graczykowski, B. Progress and perspectives on phononic crystals. J. Appl. Phys. 2021, 129, 160901. [Google Scholar] [CrossRef]
- He, J.; He, X.; Dong, T.; Wang, S.; Fu, M.; Zhang, Y. Recent progress and applications of terahertz metamaterials. J. Phys. Appl. Phys. 2021, 55, 123002. [Google Scholar] [CrossRef]
- Seshia, A.A.; Palaniapan, M.; Roessig, T.A.; Howe, R.T.; Gooch, R.W.; Schimert, T.R.; Montague, S. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromech. Syst. 2002, 11, 784–793. [Google Scholar] [CrossRef] [Green Version]
- Liewald, J.; Kuhlmann, B.; Balslink, T.; Trächtler, M.; Dienger, M.; Manoli, Y. 100 kHz MEMS Vibratory Gyroscope. J. Microelectromech. Syst. 2013, 22, 1115–1125. [Google Scholar] [CrossRef]
- Agarwal, M.; Park, K.K.; Hopcroft, M.; Chandorkar, S.; Candler, R.N.; Kim, B.; Melamud, R.; Yama, G.; Murmann, B.; Kenny, T.W. Effects of Mechanical Vibrations and Bias Voltage Noise on Phase Noise of MEMS Resonator Based Oscillators. In Proceedings of the 19th IEEE International Conference on Micro Electro Mechanical Systems, Istanbul, Turkey, 22–26 January 2006; pp. 154–157. [Google Scholar]
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration-induced errors in MEMS tuning fork gyroscopes. Sens. Actuators A Phys. 2012, 180, 32–44. [Google Scholar] [CrossRef]
- Yoon, S.W.; Lee, S.; Perkins, N.C.; Najafi, K. Analysis and wafer-level design of a high-order silicon vibration isolator for resonating MEMS devices. J. Micromech. Microeng. 2010, 21, 015017. [Google Scholar] [CrossRef]
- Kim, S.J.; Dean, R.; Flowers, G.; Chen, C. Active Vibration Control and Isolation for Micromachined Devices. J. Mech. Des. 2009, 131, 657–664. [Google Scholar] [CrossRef]
- Yao, Z.; Zega, V.; Su, Y.; Zhou, Y.; Ren, J.; Zhang, J.; Corigliano, A. Design, Fabrication and Experimental Validation of a Metaplate for Vibration Isolation in MEMS. J. Microelectromech. Syst. 2020, 29, 1401–1410. [Google Scholar] [CrossRef]
- Lee, H.K.; Melamud, R.; Chandorkar, S.; Salvia, J.; Yoneoka, S.; Kenny, T.W. Stable Operation of MEMS Oscillators Far Above the Critical Vibration Amplitude in the Nonlinear Regime. J. Microelectromech. Syst. 2011, 20, 1228–1230. [Google Scholar] [CrossRef]
- Jaakkola, A.; Prunnila, M.; Pensala, T.; Dekker, J.; Pekko, P. Design Rules for Temperature Compensated Degenerately n-Type-Doped Silicon MEMS Resonators. J. Microelectromech. Syst. 2015, 24, 1832–1839. [Google Scholar] [CrossRef]
- Van Beek, J.T.M.; Puers, R. A review of MEMS oscillators for frequency reference and timing applications. J. Micromech. Microeng. 2011, 22, 013001. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Belloni, E.; Ardito, R.; Braghin, F.; Corigliano, A. Mechanical low-frequency filter via modes separation in 3D periodic structures. Appl. Phys. Lett. 2017, 111, 231902. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Zega, V.; Ardito, R.; Corigliano, A. 3D auxetic single material periodic structure with ultra-wide tunable bandgap. Sci. Rep. 2018, 8, 2262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, L.; Yang, Y.; James, G.K.; Ankit, S. 3-D phononic crystals with ultra-wide band gaps. Sci. Rep. 2017, 7, 43407. [Google Scholar]
- Li, W.; Meng, F.; Li, Y.; Huang, X. Topological design of 3D phononic crystals for ultra-wide omnidirectional bandgaps. Struct. Multidisc. Optim. 2019, 60, 2405–2415. [Google Scholar] [CrossRef]
- Fang, X.; Wen, J.; Bonello, B.; Yin, J.; Yu, D. Ultra-low and ultra-broad-band nonlinear acoustic metamaterials. Nat. Commun. 2017, 8, 1288. [Google Scholar] [CrossRef]
- Bortot, E.; Amir, O.; Shmuel, G. Topology optimization of dielectric elastomers for wide tunable band gaps. Int. J. Solids Struct. 2018, 143, 262–273. [Google Scholar] [CrossRef]
- Bonnecaze, R.T.; Rodin, G.J.; Sigmund, O.; Søndergaard Jensen, J. Systematic design of phononic bandgap materials and structures by topology optimization. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 1001–1019. [Google Scholar]
- Han, X.K.; Zhang, Z. Topological Optimization of Phononic Crystal Thin Plate by a Genetic Algorithm. Sci. Rep. 2019, 9, 8331. [Google Scholar] [CrossRef] [Green Version]
- D’Alessandro, L.; Bahr, B.; Daniel, L.; Weinstein, D.; Ardito, R. BESO approach to topology optimization of GaN phononic crystals. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece, 5–10 June 2016; pp. 3583–3595. [Google Scholar]
- Meng, F.; Huang, X.; Jia, B. Bi-directional evolutionary optimization for photonic band gap structures. J. Comput. Phys. 2015, 302, 393–404. [Google Scholar] [CrossRef]
- Sharma, A.; Kosta, M.; Shmuel, G.; Amir, O. Gradient-based topology optimization of soft dielectrics as tunable phononic crystals. Compos. Struct. 2022, 280, 114846. [Google Scholar] [CrossRef]
- Olsson, R.H.; Ziaei-Moayyed, M.; Kim, B.; Reinke, C.; Su, M.F.; Hopkins, P.; Soliman, Y.M.; Goettler, D.F.; Leseman, Z.C.; El-Kady, I. Micro and nano fabricated phononic crystals: Technology and applications. In Proceedings of the 2011 IEEE International Ultrasonics Symposium, Orlando, FL, USA, 18–21 October 2011; pp. 983–988. [Google Scholar]
- Olsson, R.H.; El-Kady, I. Microfabricated phononic crystal devices and applications. Meas. Sci. Technol. 2008, 20, 012002. [Google Scholar] [CrossRef]
- Feng, D.; Jiang, W.; Xu, D.; Xiong, B.; Wang, Y. Micro-silicon phononic crystal with locally resonant theory. Appl. Phys. Lett. 2017, 110, 171902. [Google Scholar] [CrossRef]
- Cang, Y.; Jin, Y.; Djafari-Rouhani, B.; Fytas, G. Fundamentals, progress and perspectives on high-frequency phononic crystals. J. Phys. Appl. Phys. 2022, 55, 193002. [Google Scholar] [CrossRef]
- Maruo, S.; Kawata, S. Two-photon absorbed photopolymerization for three-dimensional microfabrication. In Proceedings of the IEEE The Tenth Annual International Workshop on Micro Electro Mechanical Systems, Nagoya, Japan, 26–30 January 1997; pp. 169–174. [Google Scholar]
- Farsari, M.; Vamvakaki, M.; Chichkov, B.N. Multiphoton polymerization of hybrid materials. J. Opt. 2010, 12, 124001. [Google Scholar] [CrossRef]
- Baldacchini, T. Three-Dimensional Microfabrication Using Two-Photon Polymerization; William Andrew: Norwich, NY, USA, 2015. [Google Scholar]
- Valdevit, L.; Bauer, J. Fabrication of 3D micro-/nanoarchitected materials. In Three-Dimensional Microfabrication Using Two-Photon Polymerization; William Andrew: Norwich, NY, USA, 2019; pp. 541–576. [Google Scholar]
- D’Alessandro, L.; Belloni, E.; Ardito, R.; Corigliano, A.; Braghin, F. Modeling and experimental verification of an ultra-wide bandgap in 3D phononic crystal. Appl. Phys. Lett. 2016, 109, 221907. [Google Scholar] [CrossRef] [Green Version]
- Brillouin, L. Wave Propagation in Periodic Structures; Dover Publications: Mignola, NY, USA, 1953. [Google Scholar]
- Srikantha Phani, A.; Woodhouse, J.; Fleck, N. Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 2006, 119, 1995–2005. [Google Scholar] [CrossRef] [Green Version]
- Pertoldi, L.; Zega, V.; Comi, C.; Osellame, R. Dynamic mechanical characterization of two-photon-polymerized SZ2080 photoresist. J. Appl. Phys. 2020, 128, 175102. [Google Scholar] [CrossRef]
- Flamourakis, G.; Spanos, I.; Vangelatos, Z.; Manganas, P.; Papadimitriou, L.; Grigoropoulos, C.; Ranella, A.; Farsari, M. Laser-made 3D Auxetic Metamaterial Scaffolds for Tissue Engineering Applications. Macromol. Mater. Eng. 2020, 305, 2000238. [Google Scholar] [CrossRef]
- Wang, G.; Wen, X.; Wen, J.; Shao, L.; Liu, Y. Two-dimensional locally resonant phononic crystals with binary structures. Phys. Rev. Lett. 2004, 93, 154302. [Google Scholar] [CrossRef]
- Comi, C.; Marigo, J.J. Homogenization Approach and Bloch-Floquet Theory for Band-Gap Prediction in 2D Locally Resonant Metamaterials. J. Elast. 2020, 139, 61–90. [Google Scholar] [CrossRef] [Green Version]
- Hong, Z.; Ye, P.; Loy, D.A.; Liang, R. Three-dimensional printing of glass micro-optics. Optica 2021, 8, 904–910. [Google Scholar] [CrossRef]
- Ma, Z.C.; Zhang, Y.L.; Han, B.; Chen, Q.D.; Sun, H.B. Femtosecond-Laser Direct Writing of Metallic Micro/Nanostructures: From Fabrication Strategies to Future Applications. Small Methods 2018, 2, 1700413. [Google Scholar] [CrossRef]
- Gonzalez-Hernandez, D.; Varapnickas, S.; Merkininkaitė, G.; Čiburys, A.; Gailevičius, D.; Šakirzanovas, S.; Juodkazis, S.; Malinauskas, M. Laser 3D Printing of Inorganic Free-Form Micro-Optics. Photonics 2021, 8, 577. [Google Scholar] [CrossRef]


| Cell Size a | Beam Squared Cross Section | Beam Length (x-/y-Axis) | Beam Length (z-Axis) |
|---|---|---|---|
| 100 µm | 7.5 µm | 44 µm | 48 µm |
| 150 µm | 10 µm | 70 µm | 76 µm |
| 200 µm | 12 µm | 98 µm | 106 µm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zega, V.; Pertoldi, L.; Zandrini, T.; Osellame, R.; Comi, C.; Corigliano, A. Microstructured Phononic Crystal Isolates from Ultrasonic Mechanical Vibrations. Appl. Sci. 2022, 12, 2499. https://doi.org/10.3390/app12052499
Zega V, Pertoldi L, Zandrini T, Osellame R, Comi C, Corigliano A. Microstructured Phononic Crystal Isolates from Ultrasonic Mechanical Vibrations. Applied Sciences. 2022; 12(5):2499. https://doi.org/10.3390/app12052499
Chicago/Turabian StyleZega, Valentina, Luca Pertoldi, Tommaso Zandrini, Roberto Osellame, Claudia Comi, and Alberto Corigliano. 2022. "Microstructured Phononic Crystal Isolates from Ultrasonic Mechanical Vibrations" Applied Sciences 12, no. 5: 2499. https://doi.org/10.3390/app12052499
APA StyleZega, V., Pertoldi, L., Zandrini, T., Osellame, R., Comi, C., & Corigliano, A. (2022). Microstructured Phononic Crystal Isolates from Ultrasonic Mechanical Vibrations. Applied Sciences, 12(5), 2499. https://doi.org/10.3390/app12052499










