Non-Linear Analysis of Structures Utilizing Load-Discretization of Stiffness Matrix Method with Coordinate Update
Abstract
:1. Introduction
2. Review the Literature of the Studies
2.1. Dynamic Relaxation Method (DRM)
2.2. Non-Linear Approach by Kwan
3. Establishing the Proposed Approach
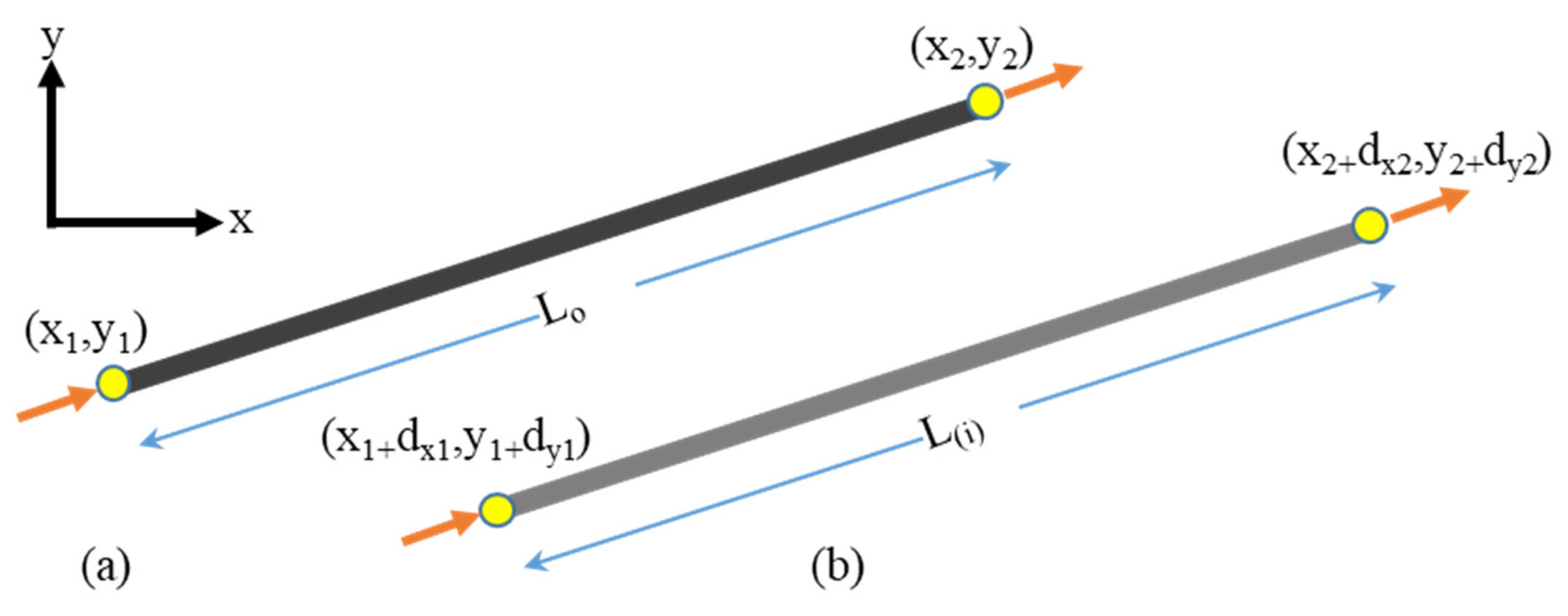
3.1. Formulation of the Technique
3.2. Stiffness Matrix Establishment
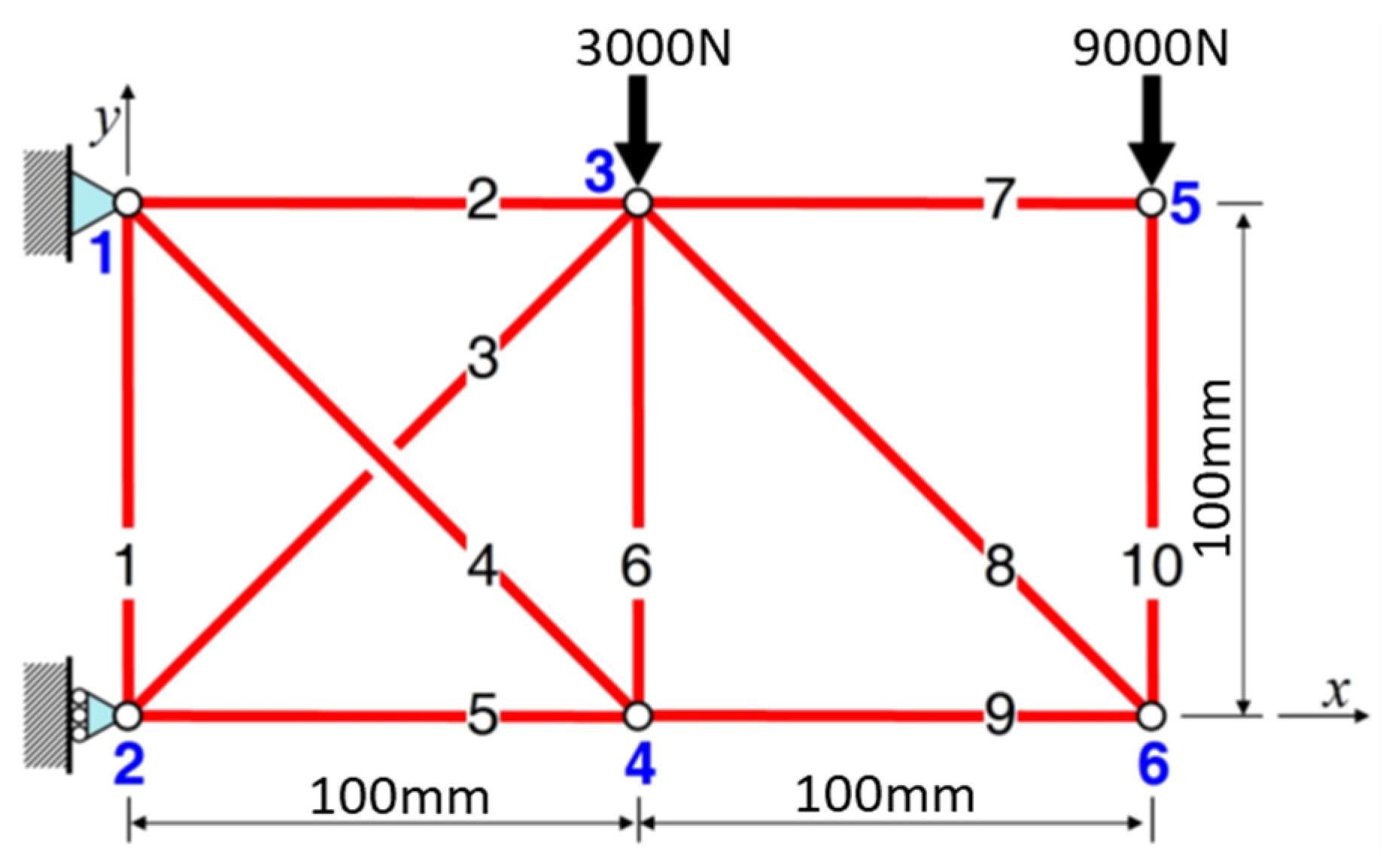
4. An Example for Illustrating the Technique
5. Results and Discussion
5.1. Structure 1
5.2. Structure 2
5.3. Structure 3
5.4. Structure 4
6. Conclusions
- ➢
- The results of the proposed technique are in good agreement with the non-linear techniques’ ones, with a slight discrepancy, while the dissimilarity between of the nodal displacements of SM and the quoted non-linear methods is 228%;
- ➢
- It can be concluded that the proposed technique is accurate and applicable for geometrically non-linear structures;
- ➢
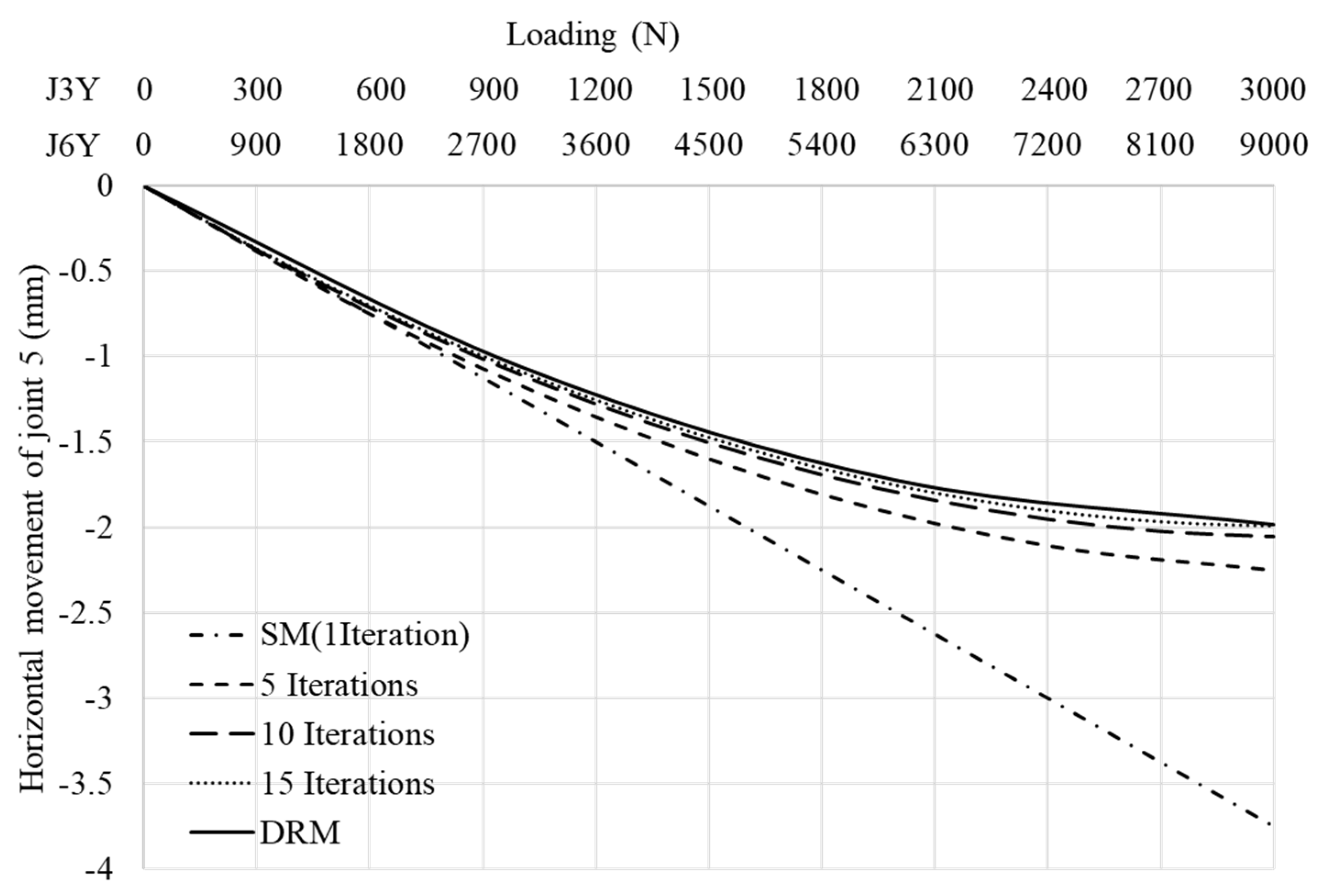
- The accuracy of the technique is enhanced by increasing the number of iterations; however, the number of iterations could be assumed to be 15 to get reasonable results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saeed, N.M.; Kwan, A.S.K. Shape morphing and adjustment of pantographic morphing aerofoil section structure. Smart Struct. Syst. 2019, 24, 193–207. [Google Scholar] [CrossRef]
- Przemieniecki, J.S. Theory of Matrix Structural Analysis; Courier Corporation: North Chelmsford, MA, USA, 1985; Available online: https://books.google.fr/books?id=Jd6i0k4wvtQC (accessed on 18 December 2021).
- Skelton, R.E.; De Oliveira, M.C. Tensegrity Systems; Springer: Berlin/Heidelberg, Germany, 2013; Volume 1, Available online: https://www.researchgate.net/profile/Robert_Skelton3/publication/252773301_Controllable_tensegrity_a_new_class_of_smart_structures/links/56aa247708ae7f592f0f208b.pdf (accessed on 1 January 2022).
- Przemieniecki, J.S. Discrete-element methods for stability analysis of complex structures. Aeronaut. J. 1968, 72, 1077–1086. [Google Scholar] [CrossRef]
- Deng, H.; Kwan, A.S.K. Unified classification of stability of pin-jointed bar assemblies. Int. J. Solids Struct. 2005, 42, 4393–4413. [Google Scholar] [CrossRef]
- Calladine, C.R.; Pellegrino, S. First-order infinitesimal mechanisms. Int. J. Solids Struct. 1991, 27, 505–515. [Google Scholar] [CrossRef]
- Skorpen, S.A.; Dekker, N.W. The application and interpretation of linear finite element analysis results in the design and detailing of hogging moment regions in reinforced concrete flat plates. J. S. Afr. Inst. Civ. Eng. 2014, 56, 77–92. [Google Scholar]
- Guest, S.D. The stiffness of prestressed frameworks: A unifying approach. Int. J. Solids Struct. 2006, 43, 842–854. [Google Scholar] [CrossRef] [Green Version]
- Guest, S.D. The stiffness of tensegrity structures. IMA J. Appl. Math. 2011, 76, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.Y.; Ohsaki, M. Adaptive force density method for form-finding problem of tensegrity structures. Int. J. Solids Struct. 2006, 43, 5658–5673. [Google Scholar] [CrossRef] [Green Version]
- Azadi, M.; Behzadipour, S.; Faulkner, G. Antagonistic variable stiffness elements. Mech. Mach. Theory 2009, 44, 1746–1758. [Google Scholar] [CrossRef]
- Xia, J.-W.; Wu, X.-S. Evaluating the stiffness of cable-bar tensile structures based on subspaces of zero elastic stiffness and demand stiffness. Eng. Struct. 2020, 206, 110167. [Google Scholar] [CrossRef]
- Przemieniecki, J.S.; Denke, P.H. Joining of complex substructures by the matrix force method. J. Aircr. 1966, 3, 236–243. [Google Scholar] [CrossRef]
- Pellegrino, S. Structural computations with the singular value decomposition of the equilibrium matrix. Int. J. Solids Struct. 1993, 30, 3025–3035. [Google Scholar] [CrossRef]
- Pellegrino, S.; Calladine, C.R. Matrix analysis of statically and kinematically indeterminate frameworks. Int. J. Solids Struct. 1986, 22, 409–428. [Google Scholar] [CrossRef]
- Ma, Q.; Ohsaki, M.; Chen, Z.; Yan, X. Step-by-step unbalanced force iteration method for cable-strut structure with irregular shape. Eng. Struct. 2018, 177, 331–344. [Google Scholar] [CrossRef] [Green Version]
- Jenkins, J.A.; Seitz, T.B.; Przemieniecki, J.S. Large deflections of diamond-shaped frames. Int. J. Solids Struct. 1966, 2, 591–603. [Google Scholar] [CrossRef]
- Kwan, A.S.K. A new approach to geometric nonlinearity of cable structures. Comput. Struct. 1998, 67, 243–252. [Google Scholar] [CrossRef]
- Vaezzadeh, A.; Ahmadizadeh, M. Three-dimensional nonlinear dynamic analysis of slack cable structures. In Proceedings of the 13th International Conference on Steel, Space and Composite Structures, Perth, Australia, 31 January–2 February 2018; pp. 1–10. [Google Scholar]
- Barnes, M.R. Form-finding and analysis of prestressed nets and membranes. Comput. Struct. 1988, 30, 685–695. [Google Scholar] [CrossRef]
- Lewis, J.W. A comparative study of numerical methods for the solution of pretensioned cable networks. In Proceedings of the International Conference on the Design and Construction of Non-Conventional Structures, Edinburgh, UK, 8–10 December 1987; pp. 27–33. [Google Scholar]
- Rezaiee, P.M.; Taghavian, H.M. Nonlinear analysis of truss structures using dynamic relaxation. Int. J. Eng. 2006, 19, 11–22. [Google Scholar]
- Rezaiee, P.M.; Alamatian, J. The dynamic relaxation method using new formulation for fictitious mass and damping. Struct. Eng. Mech. 2010, 11, 109. [Google Scholar] [CrossRef] [Green Version]
- Rushton, K.R. Large deflexion of variable-thickness plates. Int. J. Mech. Sci. 1968, 10, 723–735. [Google Scholar] [CrossRef]
- Lewis, W.J.; Jones, M.S.; Rushton, K.R. Dynamic relaxation analysis of the non-linear static response of pretensioned cable roofs. Comput. Struct. 1984, 18, 989–997. [Google Scholar] [CrossRef]
- Krishna, P. Cable-Suspended Roofs; McGraw-Hill Companies: New York, NY, USA, 1978. [Google Scholar]
- Stefanou, G.D.; Moossavi, E.; Bishop, S.; Koliopoulos, P. Conjugate gradients method for calculating the response of large cable nets to static loads. Comput. Struct. 1993, 49, 843–848. [Google Scholar] [CrossRef]
- Zhang, L.C.; Kadkhodayan, M.; Mai, Y.-W. Development of the maDR method. Comput. Struct. 1994, 52, 1–8. [Google Scholar] [CrossRef]
- Nikishkov, G.P. Introduction to the Finite Element Method; University of Aizu: Aizuwakamatsu, Japan, 2004; Available online: https://www.iitg.ac.in/mech/documents/128/introfem.pdf (accessed on 18 December 2021).
- Manguri, A.A.; Saeed, N.M. An Approximate Linear Analysis of Structures Using Incremental Loading of Force Method. UKH J. Sci. Eng. Struct. 2020, 4, 37–44. [Google Scholar] [CrossRef]
- Saeed, N.M. Prestress and Deformation Control in Flexible Structures. Ph.D. Thesis, Cardiff University, Cardiff, UK, December 2014. [Google Scholar]
- Saeed, N.M.; Kwan, A.S.K. Simultaneous displacement and internal force prescription in shape control of pin-jointed assemblies. AIAA J. 2016, 54, 2499–2506. [Google Scholar] [CrossRef]
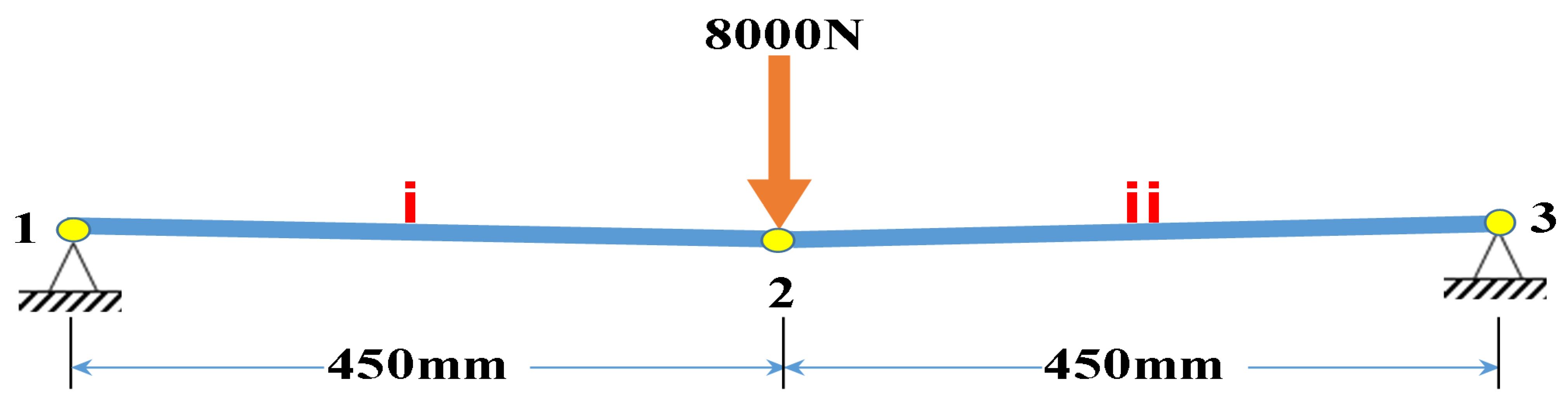

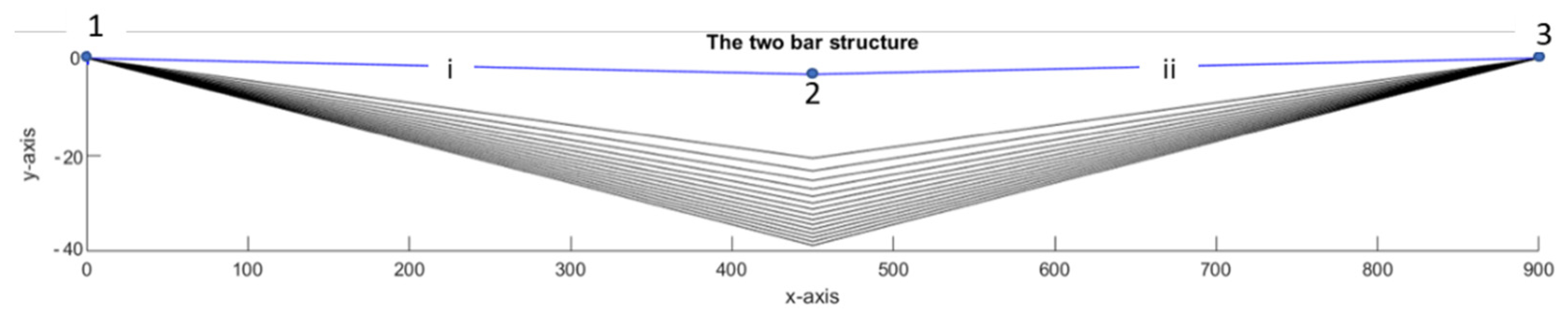
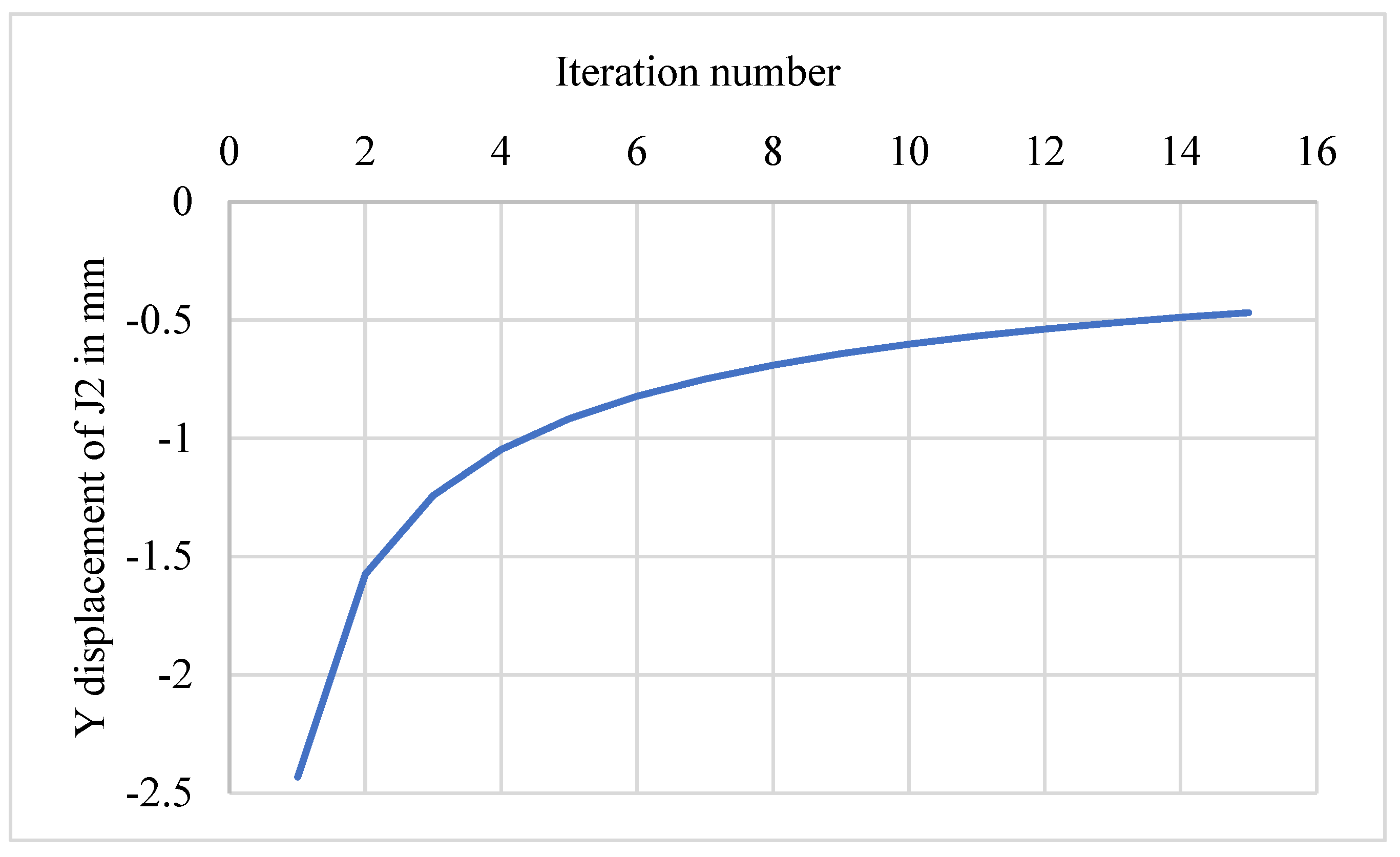

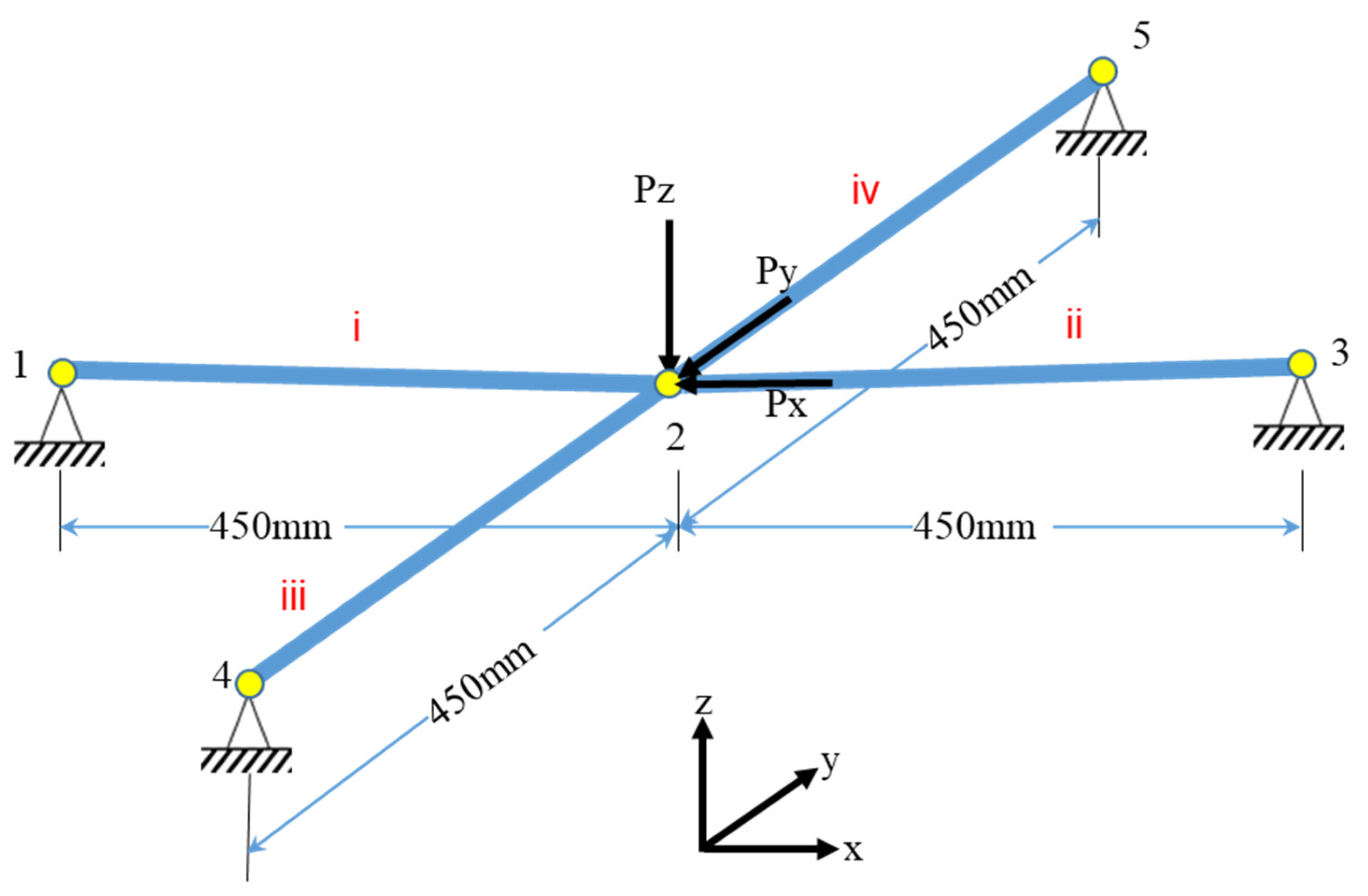
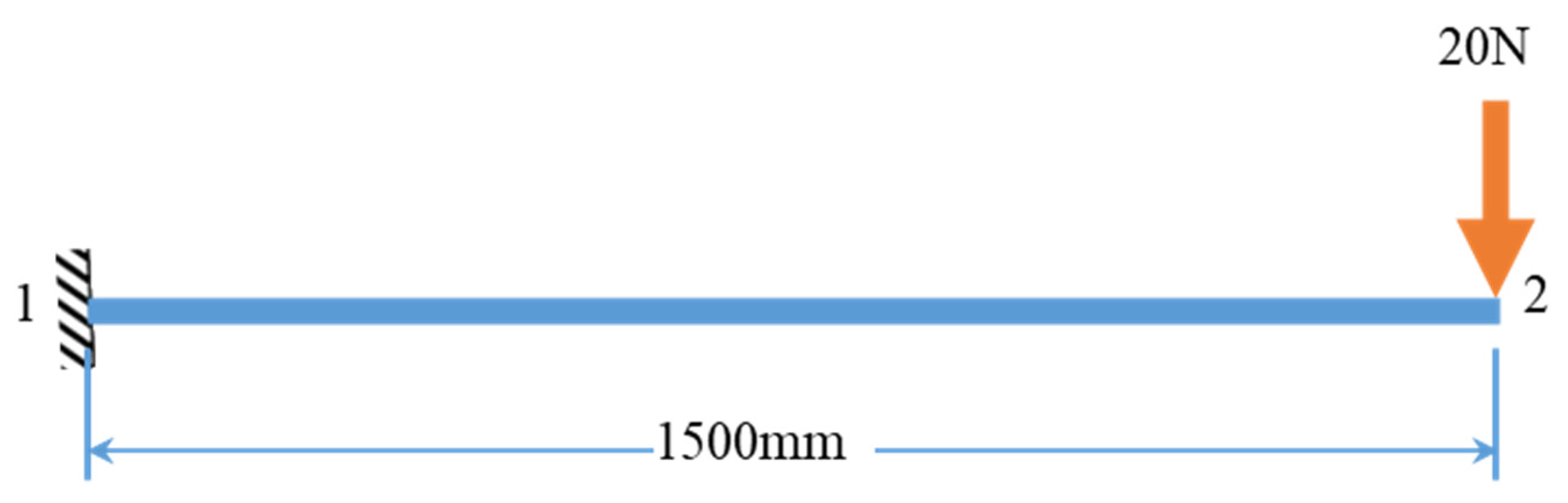
| Iterations | y-Coordinates of J2 mm | Load N | Vertical Displacement of J2 mm |
|---|---|---|---|
| 1 | −10 | 533.33 | −2.4318 |
| 2 | −12.4318 | 533.33 | −1.5741 |
| 3 | −14.0059 | 533.33 | −1.2406 |
| 4 | −15.2465 | 533.33 | −1.0472 |
| 5 | −16.2936 | 533.33 | −0.9171 |
| 6 | −17.2107 | 533.33 | −0.8222 |
| 7 | −18.0329 | 533.33 | −0.7491 |
| 8 | −18.7820 | 533.33 | −0.6906 |
| 9 | −19.4726 | 533.33 | −0.6427 |
| 10 | −20.1153 | 533.33 | −0.6024 |
| 11 | −20.7176 | 533.33 | −0.5679 |
| 12 | −21.2856 | 533.33 | −0.5381 |
| 13 | −21.8237 | 533.33 | −0.5120 |
| 14 | −22.3357 | 533.33 | −0.4889 |
| 15 | −22.8246 | 533.33 | −0.4682 |
| Total | 8000 | −13.2929 | |
| Methods | Joint | SM (mm) | Current Study (mm) | Kwan (1998) (mm) | Lewis et al., (1984) (mm) |
|---|---|---|---|---|---|
| Downward displacement (mm) | 2 | −36.4770 | −12.9887 | −11.1120 | −11.1168 |
| Displacement of Joint (2) | SM (mm) | Current Study (mm) | Kwan (1998) (mm) | Lewis et al., (1984) (mm) |
|---|---|---|---|---|
| x | −0.03 | −0.03 | −0.03 | −0.03 |
| Y | −0.03 | −0.03 | −0.03 | −0.03 |
| Z | −36.47 | −12.87 | −11.11 | −11.11 |
| Joint | Direction | Methods | |||
|---|---|---|---|---|---|
| SM (mm) | Curren Study (mm) | Kwan (1998) (mm) | Lewis et al., (1984) (mm) | ||
| 5 | x | 3.75 | 1.989 | 1.99 | 1.988 |
| y | −27.857 | −28.144 | −27.61 | −28.221 | |
| 6 | x | −6 | −7.601 | −7.54 | −7.812 |
| y | −25.607 | −25.487 | −24.95 | −25.510 | |
| Methods | ||||
|---|---|---|---|---|
| Joint | Direction | SM (mm) | Current Study (mm) | Lewis et al., (1984) (mm) |
| 2 | X | 0 | −6.05 | −6.01 |
| Y | −135 | −134.64 | −134.05 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeed, N.; Manguri, A.; Szczepanski, M.; Jankowski, R. Non-Linear Analysis of Structures Utilizing Load-Discretization of Stiffness Matrix Method with Coordinate Update. Appl. Sci. 2022, 12, 2394. https://doi.org/10.3390/app12052394
Saeed N, Manguri A, Szczepanski M, Jankowski R. Non-Linear Analysis of Structures Utilizing Load-Discretization of Stiffness Matrix Method with Coordinate Update. Applied Sciences. 2022; 12(5):2394. https://doi.org/10.3390/app12052394
Chicago/Turabian StyleSaeed, Najmadeen, Ahmed Manguri, Marcin Szczepanski, and Robert Jankowski. 2022. "Non-Linear Analysis of Structures Utilizing Load-Discretization of Stiffness Matrix Method with Coordinate Update" Applied Sciences 12, no. 5: 2394. https://doi.org/10.3390/app12052394
APA StyleSaeed, N., Manguri, A., Szczepanski, M., & Jankowski, R. (2022). Non-Linear Analysis of Structures Utilizing Load-Discretization of Stiffness Matrix Method with Coordinate Update. Applied Sciences, 12(5), 2394. https://doi.org/10.3390/app12052394