Thirty executions are carried out to evaluate the metaheuristic algorithm performance (DE/RAND/1/BIN, GA, PSO, MUMSA) for each constraint-handling technique (FR, SR, C, PF, NCH). The acronyms given by the sixteen algorithms are related to the algorithms’ acronym, followed by the constraint-handling technique through a dash. For instance, in the case of algorithms related to the DE/RAND/1/BIN, the acronyms are expressed as R1B-FR, R1B-SR, R1B-C, and R1B-PF.
The results obtained by each algorithm consider the thirty best objective function values obtained through the thirty executions (one value per each execution). This set of values conforms to one sample for the statistical analysis described in this section for a particular algorithm.
In this section, the samples of all algorithms are analyzed by using descriptive statistics, confidence intervals, and inferential statistics.
4.2.1. Descriptive Statistics
The samples related to thirty executions of algorithms are analyzed by using descriptive statistics metrics, such as the mean, the media, the standard deviation (std), and the maximum (max) and minimum (min) values of the objective function. In addition, the number of Non-Feasible Solutions (NFS) at the end of the optimization process through the thirty executions is also included to know whether the constraint-handling technique shows some issue to leave the infeasible region.
Study case 1:
Table 5 shows the descriptive statistics of samples for study case 1 using trajectory 1 in the synthesis process. The columns are related to the analyzed algorithm, the descriptive statistics metrics, and the NFS for each sample. Boldface indicates the minimum value for each column. According to the results in
Table 5, all metaheuristic algorithms find feasible solutions through the thirty executions (see NFS metric). R1B-NCH, R1B-SR, and R1B-PF obtain the three best solutions in that order (see column “min”). R1B-NCH gives the best algorithm performance finding solutions. The obtained solution in R1B-SR and R1B-PF presents an increment of
and
, respectively, with respect to R1B-NCH (see column “min”). In addition, the mean and minimum results are less in R1B-NCH than other algorithms, and the standard deviation, the median, and maximum values present an average behavior.
Table 6 shows the descriptive statistics of the samples for study case 1 using trajectory 2 in the synthesis process. The columns of such tables contain the same terms explained above. In this analysis, the R1B-NCH algorithm reliability is studied under trajectory changes to be followed by the four–bar linkage mechanism. According to the results in
Table 6, all metaheuristic algorithms find feasible solutions (see “NFS” column). MUMSA-
C, R1B-FR, and R1B-NCH obtain the three best solutions in that order. In spite of R1B-NCH presenting the third position, the difference with respect to the MUMSA-
C is minimal at around
(see “min” column). Moreover, the R1B-NCH algorithm has the best mean value, indicating the consistency of results through different executions. The standard deviation, the median, the maximum, and minimum values of the objective function have average performance in the R1B-NCH with respect to other algorithms.
Study case 2:
Table 7 shows the descriptive statistics for study case 2 using trajectory 1 in the synthesis process. The columns of such tables contain the same terms explained above. According to the results in
Table 7, all metaheuristic algorithms find feasible solutions except for the PSO-FR and R1B-SR algorithm (see “NFS” column). R1B-NCH, MUMSA-FR, and MUMSA-
C obtain the three best solutions (see “min” column). R1B-NCH gives the best algorithm performance finding solutions due to the mean, the median, and the min value of the best objective function being less than other algorithms. The standard deviation and the maximum value of the objective function also present a lower value than the average in the proposal.
Table 8 shows the descriptive statistics for study case 2 using trajectory 2 in the synthesis process. The columns of such tables contain the same terms explained above. In this analysis, the R1B-NCH algorithm reliability is studied under a trajectory change in the cam–linkage mechanism. According to the results in
Table 8, all metaheuristic algorithms find feasible solutions except for PSO-FR, R1B-SR, and PSO-
C (see “NFS” column). MUMSA-FR, R1B-NCH, and MUMSA-SR obtain the three best solutions in that order. The R1B-NCH presents a very slight increment of around
with respect to the obtained result given in MUMSA-FR (see “min” column). The R1B-NCH also obtains the best values in the mean, the standard deviation, the median, and the maximum value of the objective function.
It is observed in
Table 5,
Table 6,
Table 7 and
Table 8 that the R1B-NCH presents an outstanding mean performance (see “mean” columns) in the search for solutions through study cases in spite of presenting changes in the optimization problems (rehabilitation trajectories) where the algorithm setting and the NCH technique were tuned and trained, respectively.
However, descriptive statistics cannot estimate the best algorithm behaviors for future executions. Therefore, the analysis of results by
confidence intervals and inferential statistics [
56] is carried out in the next section.
4.2.2. Confidence Intervals and Inferential Statistics
This section confirms the best algorithm behavior to solve each study case considered in this work. The best algorithm behavior is obtained by analyzing the sample (thirty best values of the objective function) obtained in each algorithm execution by
confidence intervals [
61] and using the non-parametric Friedman test [
56].
The
Confidence Interval (CI) [
61] is a range of values for a selected sample of a study, where, with a
confidence, the interval contains the population’s true mean. Therefore, the confidence interval values closest to zero indicate the most promising algorithm due to the high probability that the mean behavior of the algorithm is inside such interval. Moreover, in what follows, for each study case, the use of inferential statistics through the Friedman test of the algorithm samples with the best CI will confirm the algorithm performance.
Study case 1:
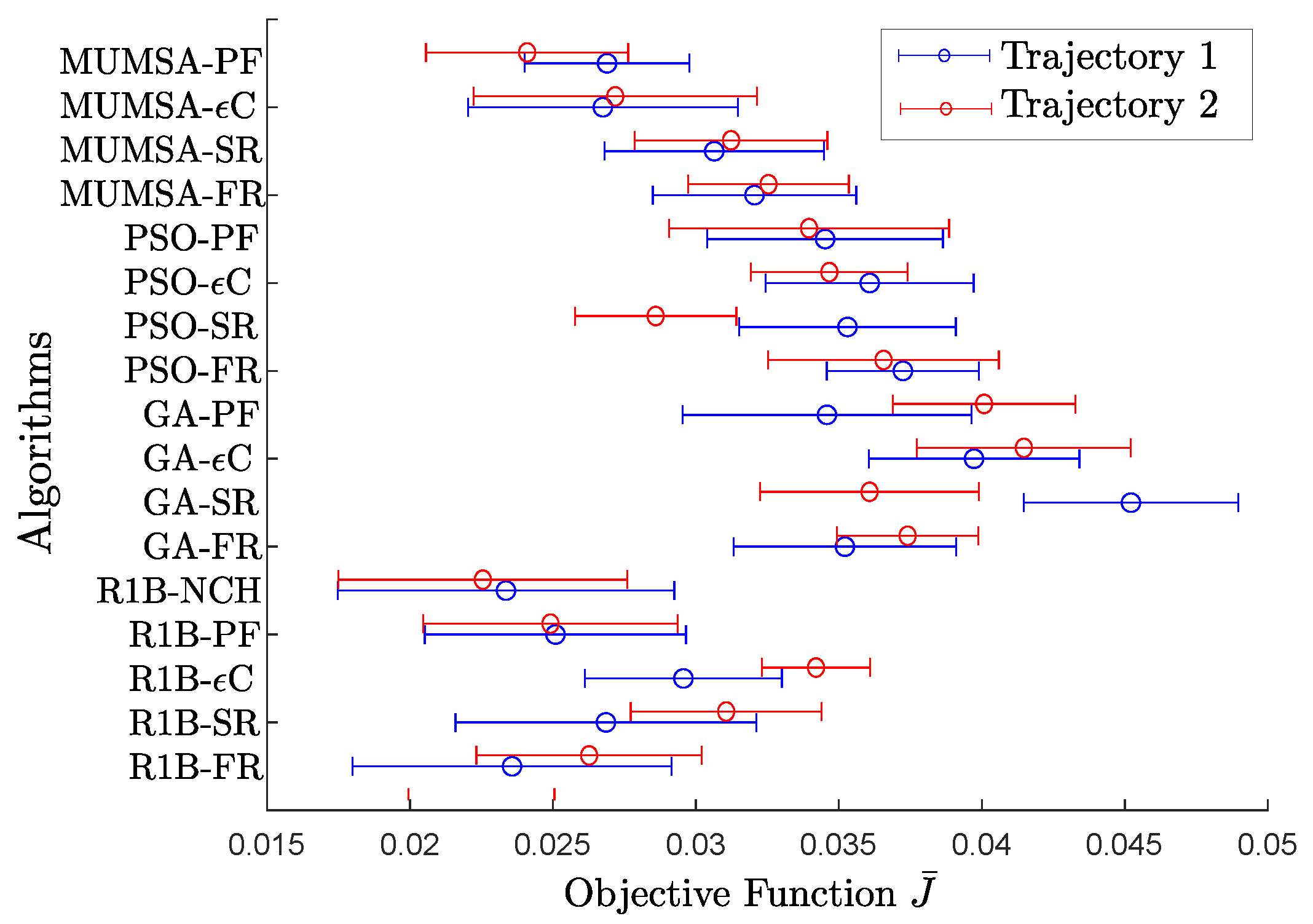
Table 9 shows the confidence interval values obtained by each algorithm for study case 1 using both trajectories, and
Figure 7 shows its graphical representation. It is observed that the R1B-NCH, the R1B-PF, and the MUMSA-PF have confidence intervals closer to zero (to the left) for trajectory 1. The R1B-NCH presents the confidence interval lower limit value closest to zero, and its confidence interval upper limit does not exceed the MUMSA-PF confidence interval upper limit. The results using trajectory 2 show that R1B-FR, R1B-PF, and R1B-NCH have confidence intervals closer to zero. The R1B-NCH presents the confidence interval lower limit value closest to zero, and the upper limit does not exceed the confidence interval upper limit of R1B-FR.
The
-confidence Friedman test is carried out in those three outstanding algorithms per each trajectory, i.e., in R1B-NCH, R1B-PF, and MUMSA-PF for trajectory 1; and, in R1B-FR, R1B-PF, and R1B-NCH for trajectory 2. According to the Friedman test in those groups of three algorithms, there is no statistically significant difference in the comparisons because the returned
p-value is greater than
. It is also confirmed in the multiple comparisons with the Bonferroni post-hoc error correction method of the Friedman test given in
Table 10 that the associated
p-value is greater than
, indicating the no confirmation of the superiority of one algorithm in the comparison. In this paper, a tie is declared in the comparison when that situation occurs. Thus, in all comparisons presented in
Table 10, the algorithms draw.
In the mechanism synthesis problem, it is common to obtain the optimal solution by setting different (usually thirty) executions to the same problem [
47]. However, there may be significant differences among the best solutions obtained through different executions, and the most promising solution obtained by the optimizer in the mechanism synthesis problem is given through the best solution among executions [
62].
Then, to know whether the proposed R1B-NCH empirically presents a high probability of finding the best results in the kinematic synthesis problem for lower limb rehabilitation, the following is defined: As the confidence interval indicates whether these executions are repeated in several tests, the proportion of calculated confidence intervals that is included the population’s true mean value would tend toward ; then, the confidence interval closest to zero will indicate the population’s true mean value is closer to the reduction of the objective function, and, hence, it is assumed that this interval presents a high probability of granting the best solution (minimum value) through thirty executions of the algorithm (executions commonly used for finding the best solution in the mechanism synthesis problem).
In order to verify the previous assumption, the other four sets of thirty executions are performed for the two groups of three algorithms (R1B-NCH, R1B-PF, and MUMSA-PF for trajectory 1; and R1B-FR, R1B-PF, and R1B-NCH for trajectory 2). In
Table 11, the minimum values from the thirty executions per set are displayed. It is observed that, in each column related to the set of data for the corresponding trajectories, the minimum value, marked in boldface, is obtained by the proposed R1B-NCH.
According to this analysis for study case 1, it is observed that the R1B-NCH algorithm presents a high probability to find the best solution through thirty executions of the algorithm in the mechanism synthesis problem for lower limb rehabilitation.
Study case 2:
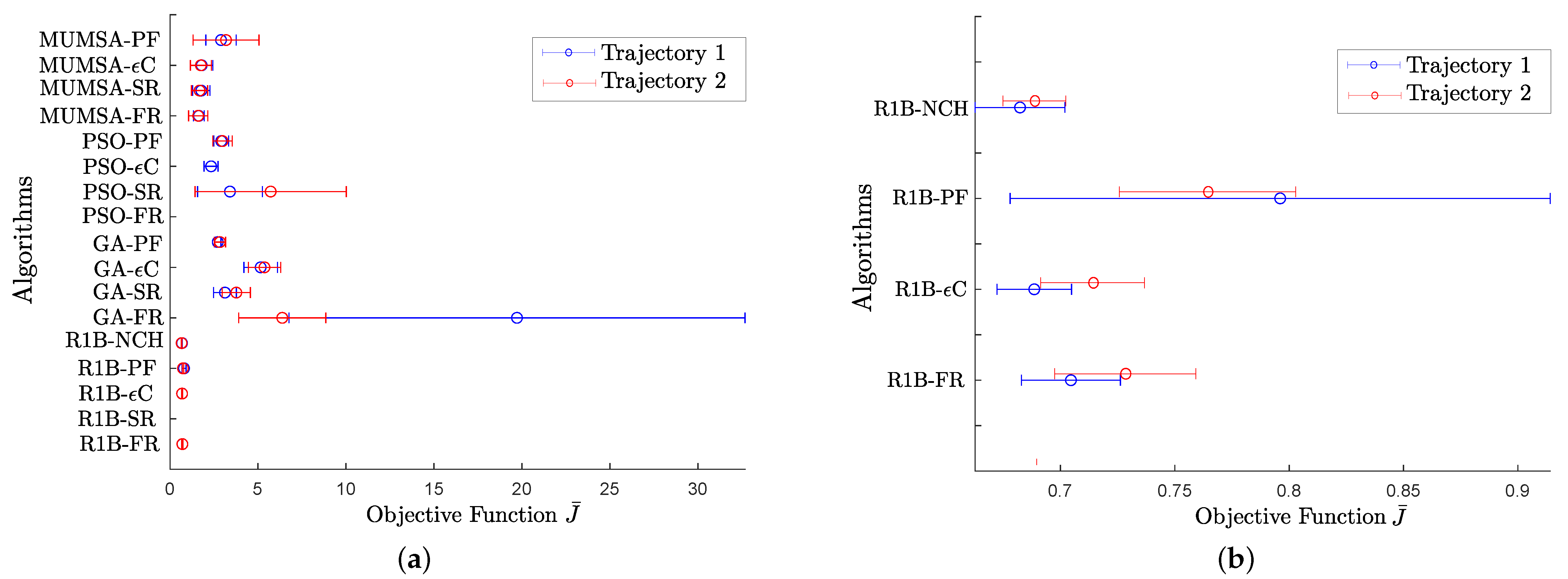
Table 12 shows the confidence intervals obtained by each algorithm for study case 2 using both trajectories.
Figure 8a shows the graphical representation of the confidence interval, and
Figure 8b shows the close-up view of the confidence intervals closer to zero. According to the results for both trajectories, R1B-FR, R1B-
C, and R1B-NCH have confidence intervals closer to zero, where R1B-NCH presents the confidence interval lower limit value closest to zero and its upper limit does not exceed the R1B-
C confidence interval upper limit.
The
-confidence Friedman test is performed in those three outstanding algorithms, i.e., in R1B-FR, R1B-
C, and R1B-NCH for both trajectories. According to the Friedman test in those groups of three algorithms, there exist a statistically significant difference among them in both trajectories because the
p-value associated is less than the proposed significance level. Hence, to determine if one algorithm outperforms the other, inferential statistics given by the Friedman test for multiple comparisons with the Bonferroni post-hoc error correction method is carried out for finding the accurate pairwise comparisons. In
Table 13, such tests are given, and in boldface, the winner in the comparison is highlighted. According to the number of wins, the results indicate that R1B-NCH is the most promising optimizer in the optimal synthesis for the study case 2 in both trajectories because it wins in all comparisons.
In order to empirically confirm the superiority of the proposed R1B-NCH, to obtain the optimal solution by setting different (usually thirty) executions to the same problem, other four sets of thirty executions are performed for the two groups of three algorithms (R1B-FR, R1B-
C, and R1B-NCH for both trajectories). In
Table 14, the minimum values from the thirty executions per set are displayed. It is observed that, in each column, the minimum value, marked in boldface, is given by the expected algorithm (based on
Table 13), i.e., the proposed R1B-NCH. Note that these boldface values cannot be reached by the other algorithms (R1B-FR and R1B-
C), confirming the statistical analysis presented above.
4.2.3. Overall Evaluation of the Proposed NCH through Study Cases
The overall evaluation of the most promising algorithms given in
Section 4.2.2 is discussed next.
In the first study case and according to
Table 10, the most promising algorithms considering both trajectories are: R1B-NCH, R1B-PF, MUMSA-PF, and R1B-FR. In that case, all algorithms draw with each other. Thus, each algorithm presents two draws. In the second study case and according to
Table 13, the most promising algorithms are: R1B-NCH, R1B-EC, and R1B-FR. In such a case, the R1B-NCH wins four times, and the R1B-EC wins one time. With this information, a summary of the number of wins and draws for both study cases, and trajectories are presented in
Table 15. According to this table, the overall evaluation of the most promising algorithms is analyzed, and it is confirmed that the most promising one is the proposed R1B-NCH because it wins and draws four times. The next best behaviors of the algorithms to solve the synthesis problem are related to R1B-PF and R1B-FR in that order.
Then, the NCH technique increases the exploration and exploitation capabilities in the ED/RAND/1/BIN algorithm to solve the considered mechanism synthesis problems. The obtained solution (mechanism) could improve the lower limb rehabilitation machine.
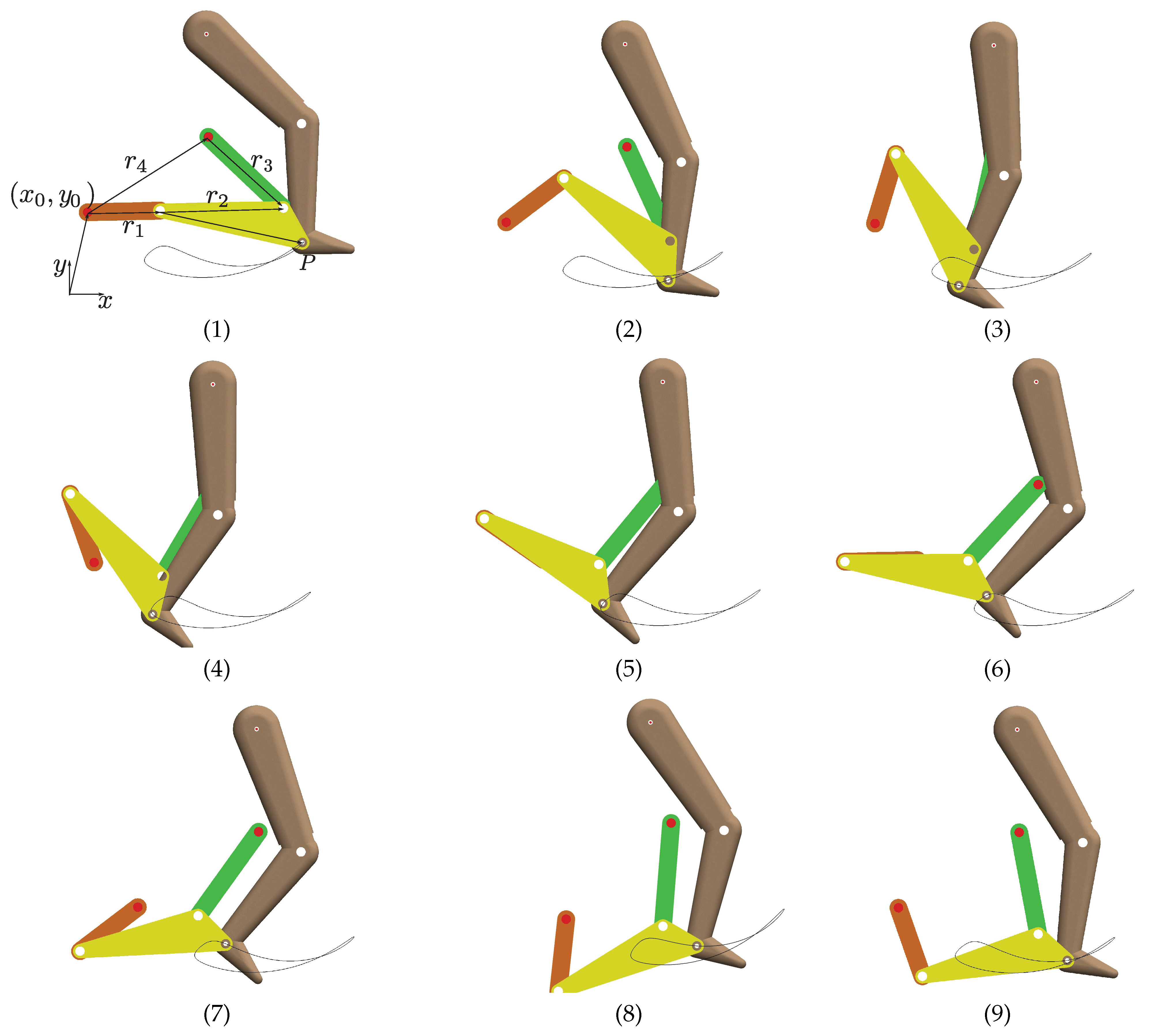
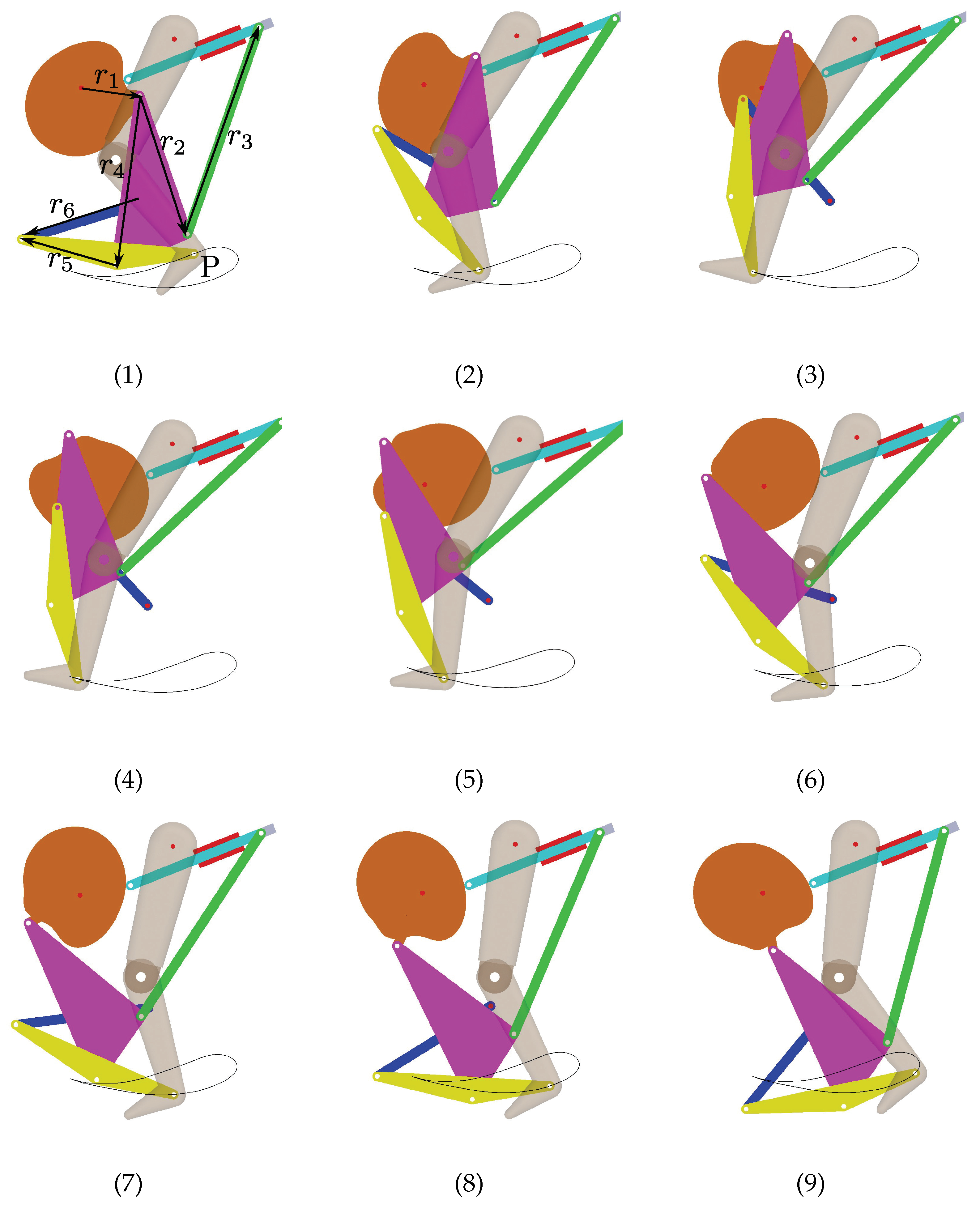
Finally, the best solutions obtained by the R1B-NCH algorithm for each study case are displayed in
Table 16 and
Table 17. In order to validate the obtained mechanism for rehabilitation purposes, the Computer-Aided Design (CAD) of the mechanism in different phases of the crank movement is shown in
Figure 9 and
Figure 10. Through the figure sequences given by the number 1 to the sequence number 9, it is observed that the coupler point of the mechanism in both figures can provide the proposed rehabilitation routine showing in a continuous line. Furthermore, if we fixed the human ankle joint in the coupler point of the mechanism, the mechanism can reproduce the natural movement of the leg, as is shown in those figures.