Simple and Robust Log-Likelihood Ratio Calculation of Coded MPSK Signals in Wireless Sensor Networks for Healthcare
Abstract
:1. Introduction
- As a benchmark, the optimal bit LLR under a phase noncoherent channel is first given. For this scheme, both zero-order Bessel function and perfect instantaneous fading amplitude is involved. Thus, we propose a simple calculation configuration without CSI, which greatly simplifies the optimal scheme.
- The optimal bit LLR under a Rayleigh fading channel is also given, wherein we assume that the statistical characteristic of the fading amplitude is available. In this context, the variance estimation for both additive white Gaussian noise (AWGN) and the statistical characteristic of the fading amplitude is involved, and extensive exponential operation is also unavoidable. A simple calculation scheme is then developed.
- We find that the decision statistic is exactly the same under both phase noncoherent channels and the Rayleigh fading channel when no coding is considered, and no contribution from the fade amplitude and the variance of the AWGN noise is observed in this decision statistic. We also find that the CSI can be perfectly avoided in the bit LLR calculation when channel coding is considered if the approximation is ingeniously designed and implemented to the optimal LLR.
- In order to verify the desirable properties of our proposed simple schemes, the characteristics of the receiver are studied from many aspects with extensive simulations.
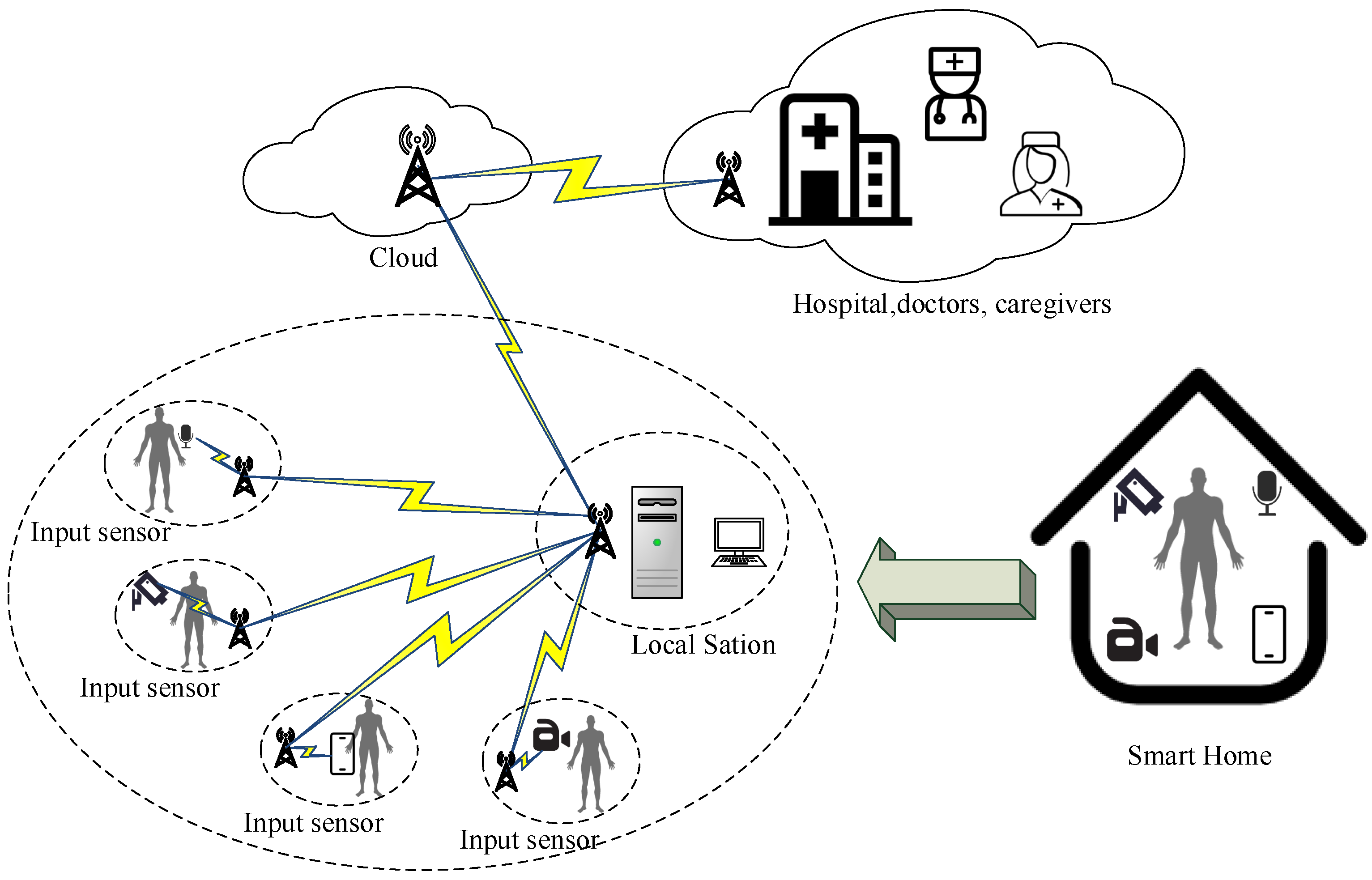
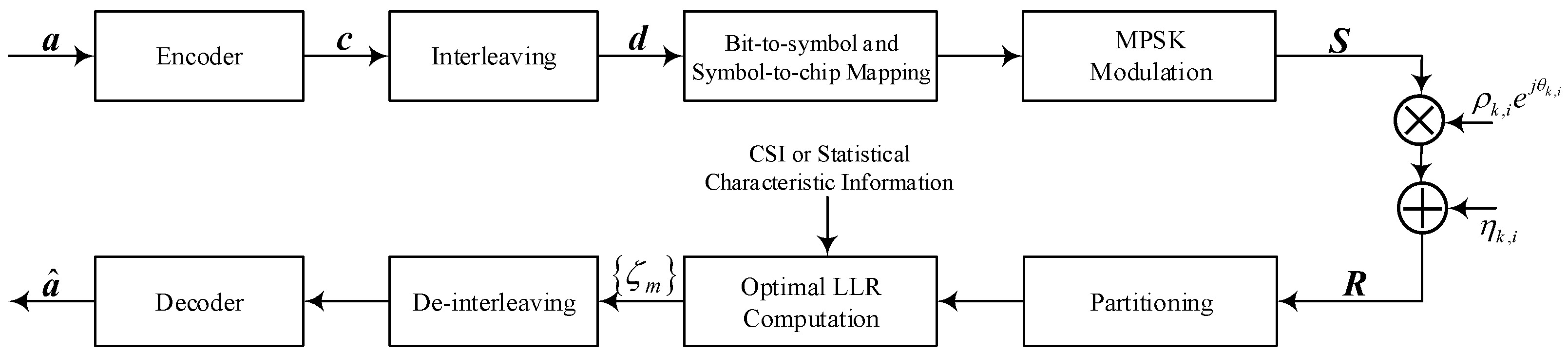
2. System Mode
3. LLR Calculation under Phase Noncoherent Channel
4. LLR Calculation under Rayleigh Fading Channel
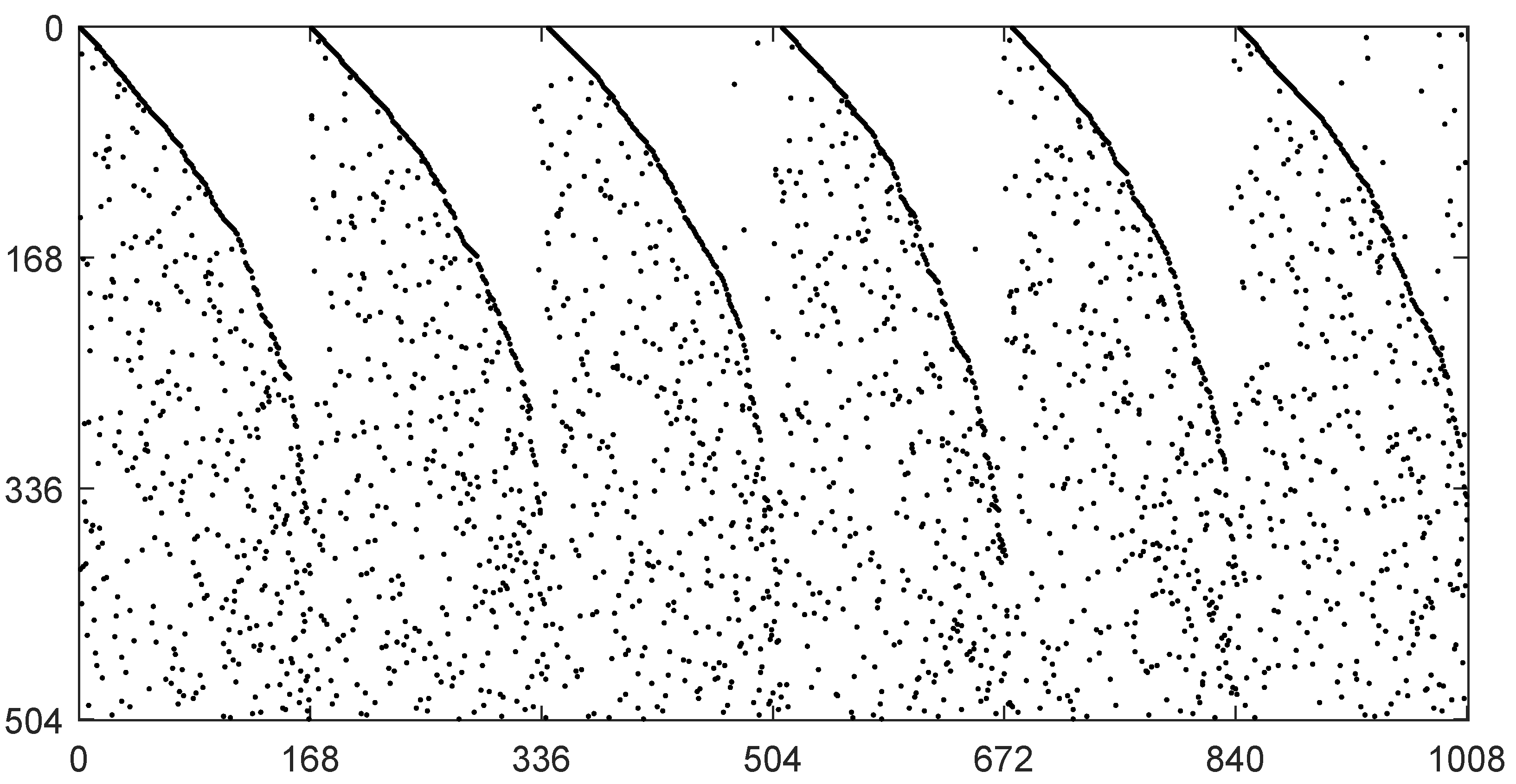
5. Numerical Results and Discussion
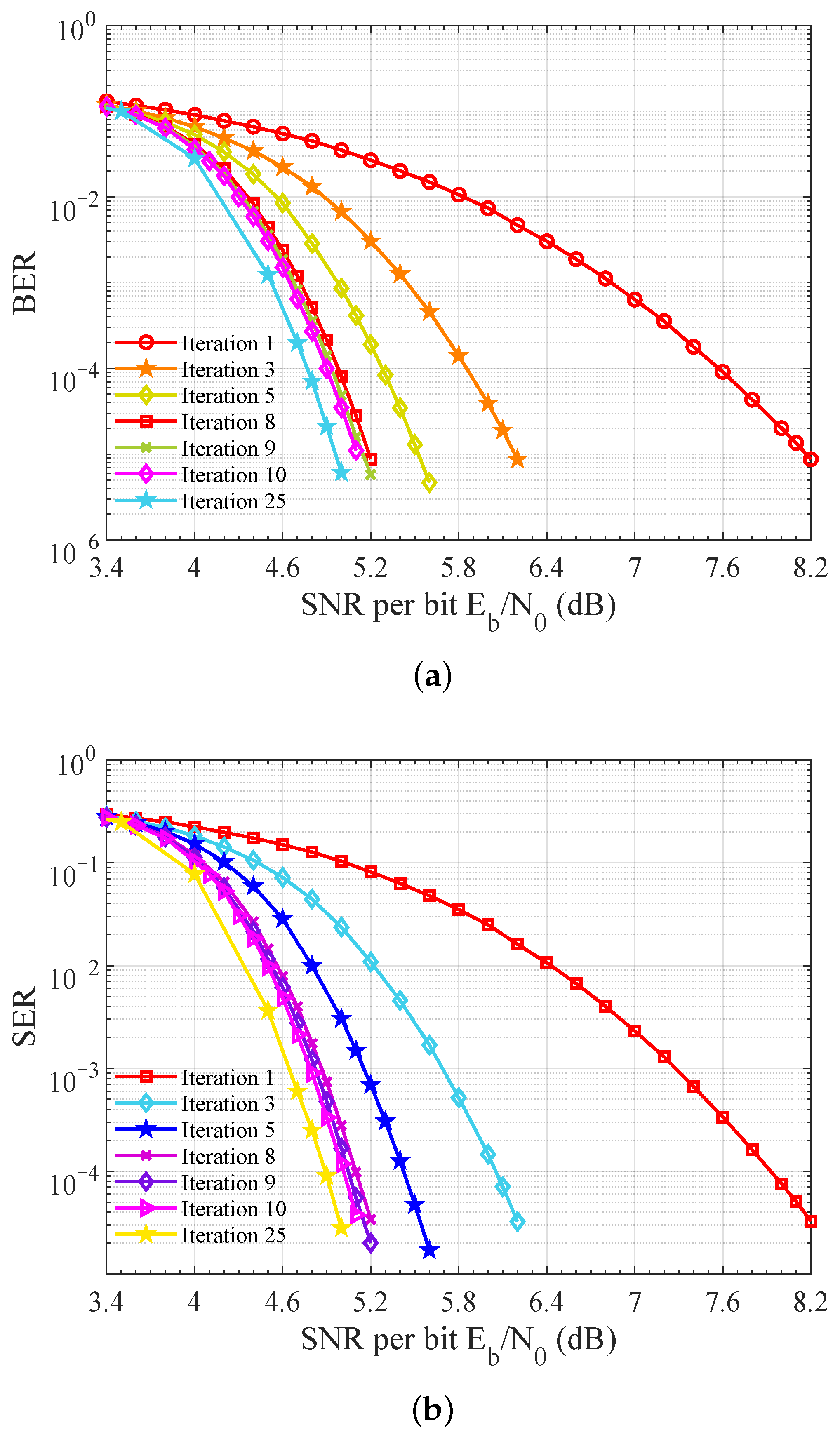
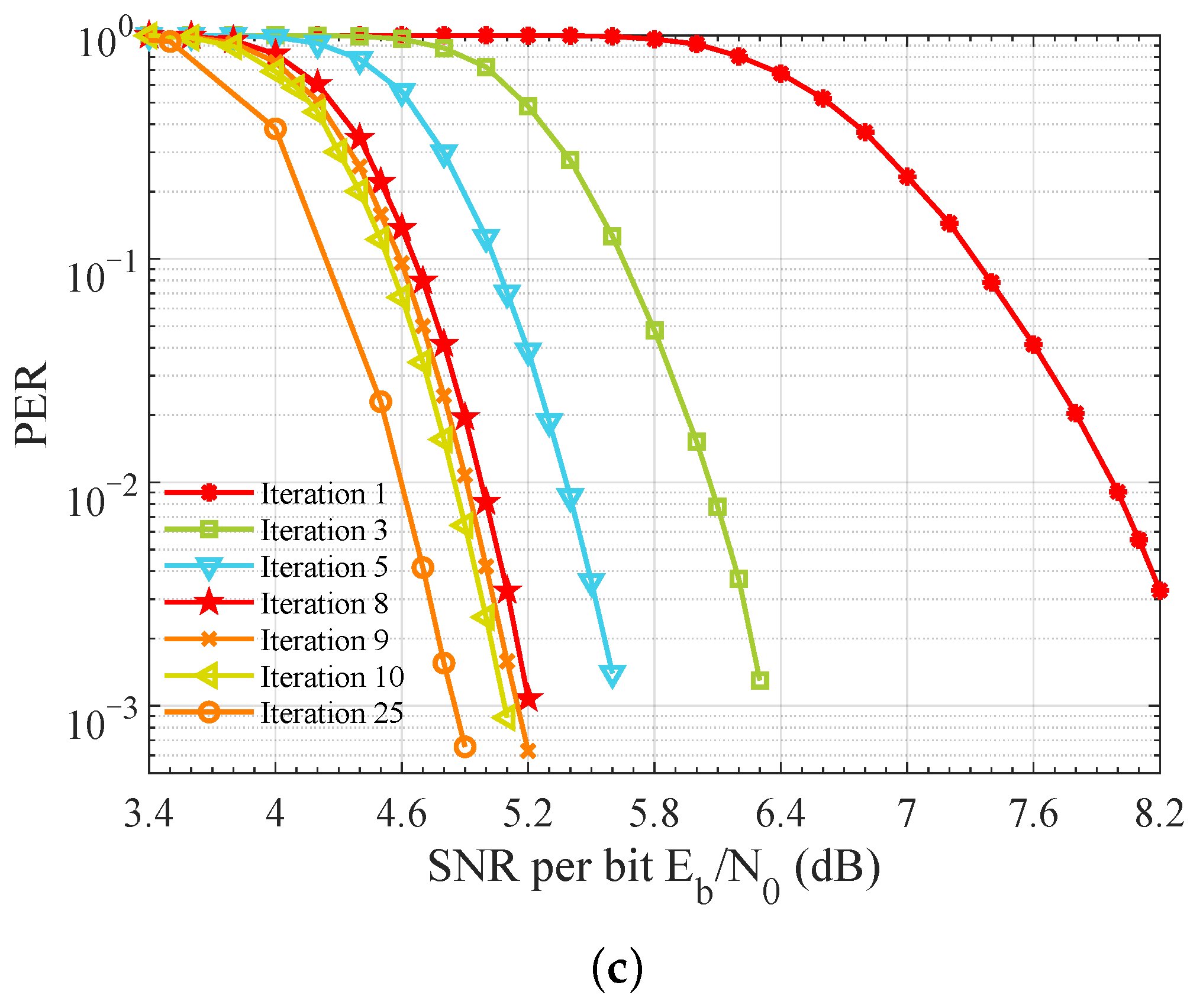
5.1. The Influence of the Maximum Iteration Number on Detection Performance
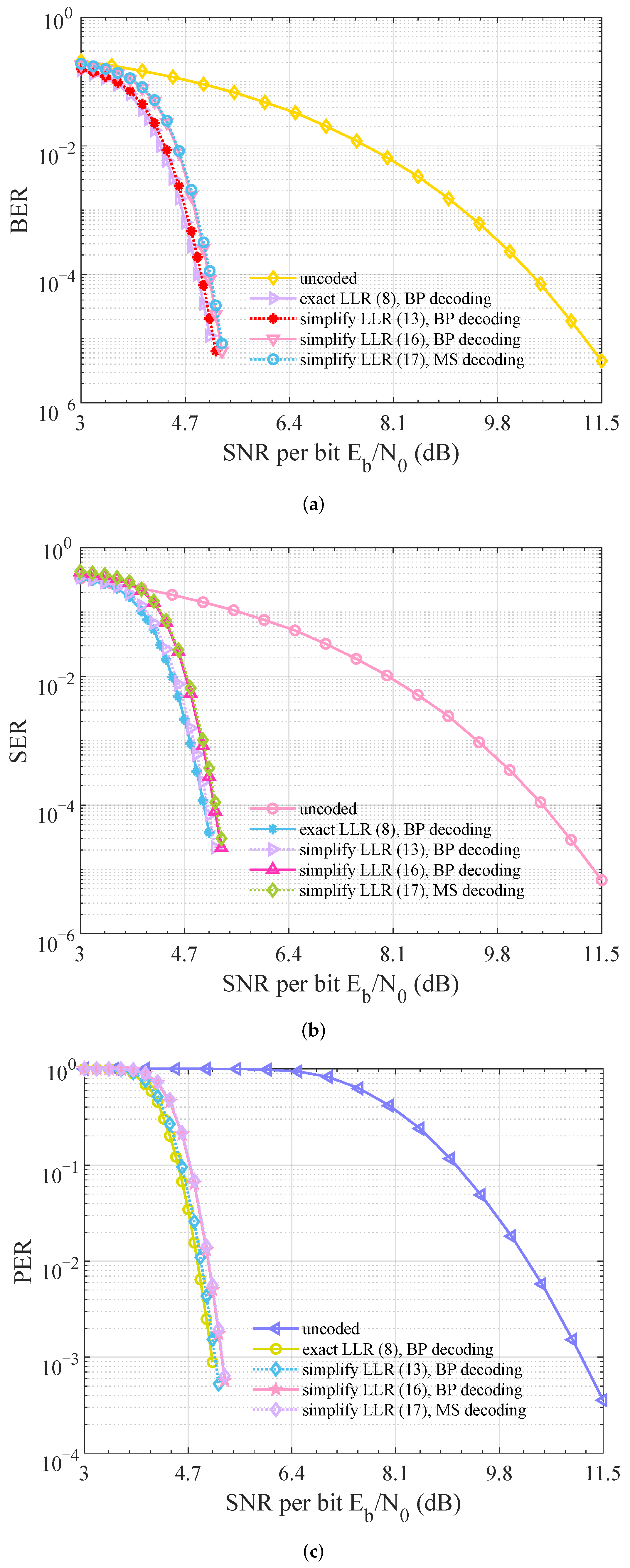
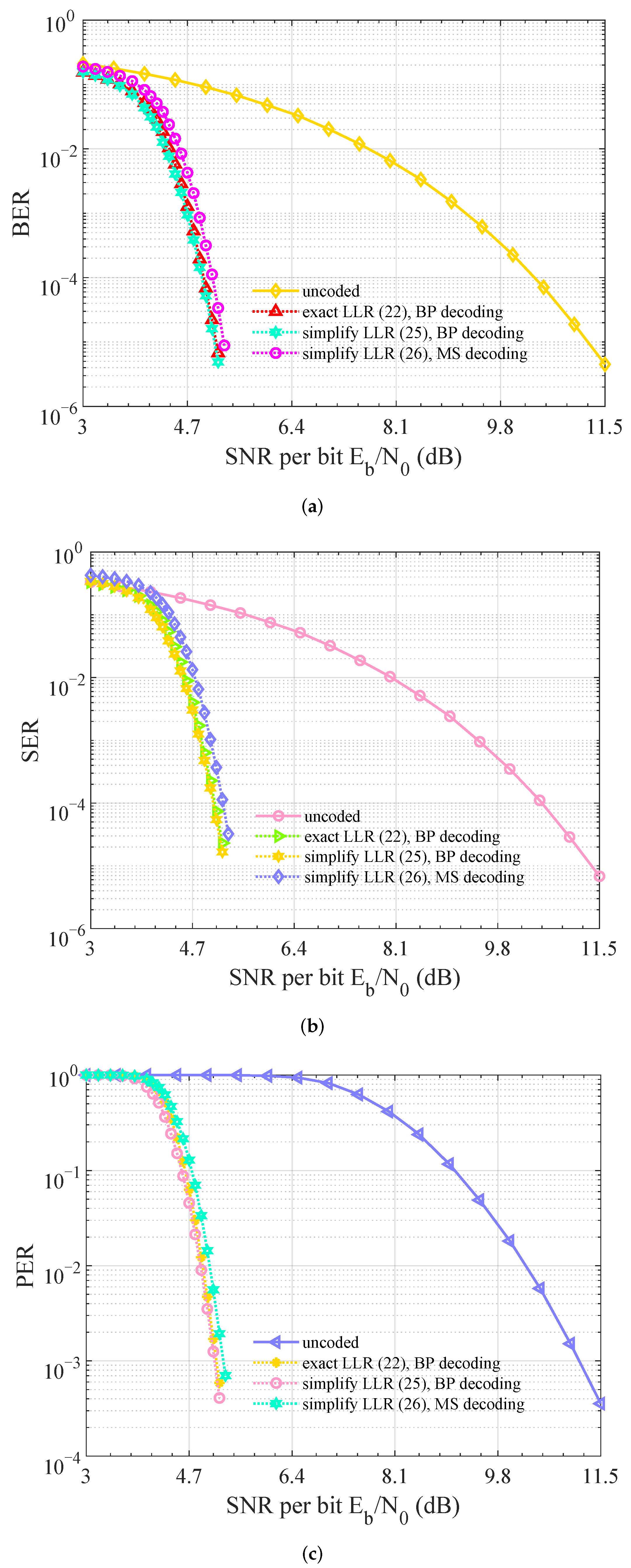
5.2. Detection Performance under Phase Noncoherent Channel
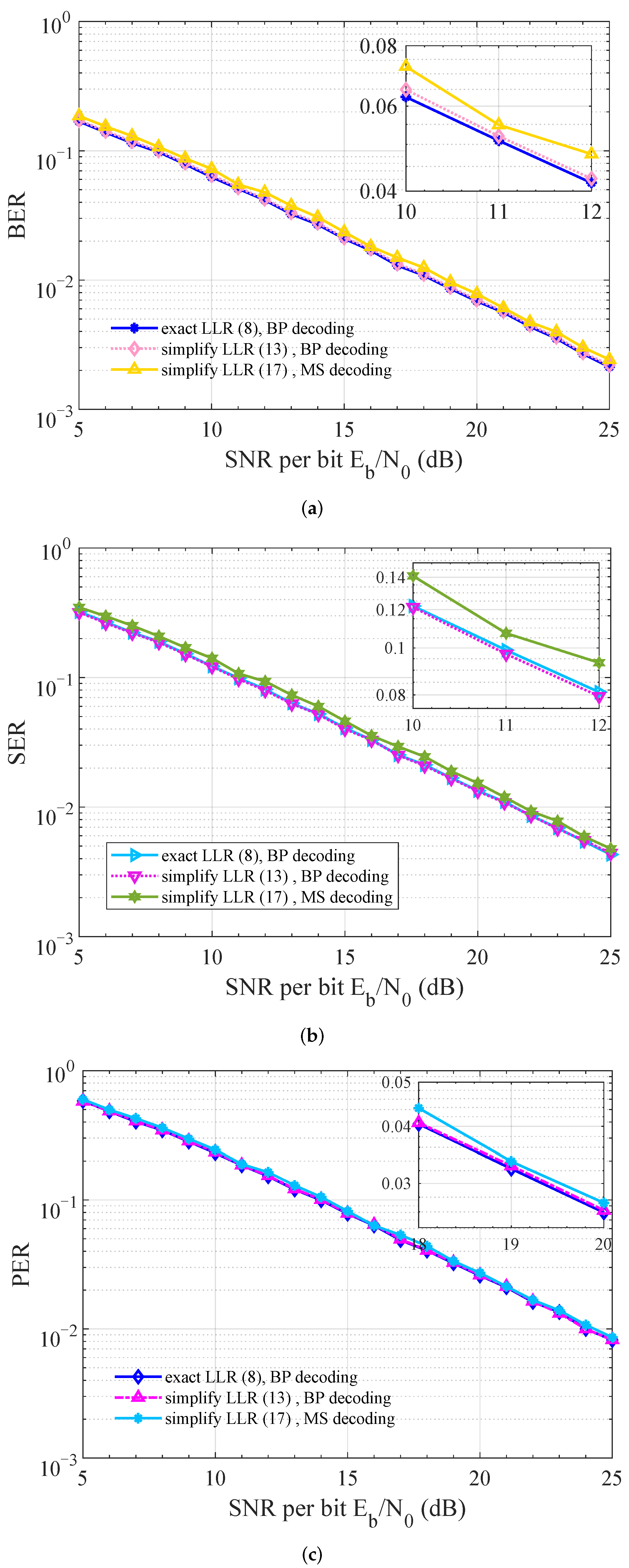
5.3. Detection Performance under Rayleigh Fading Channel
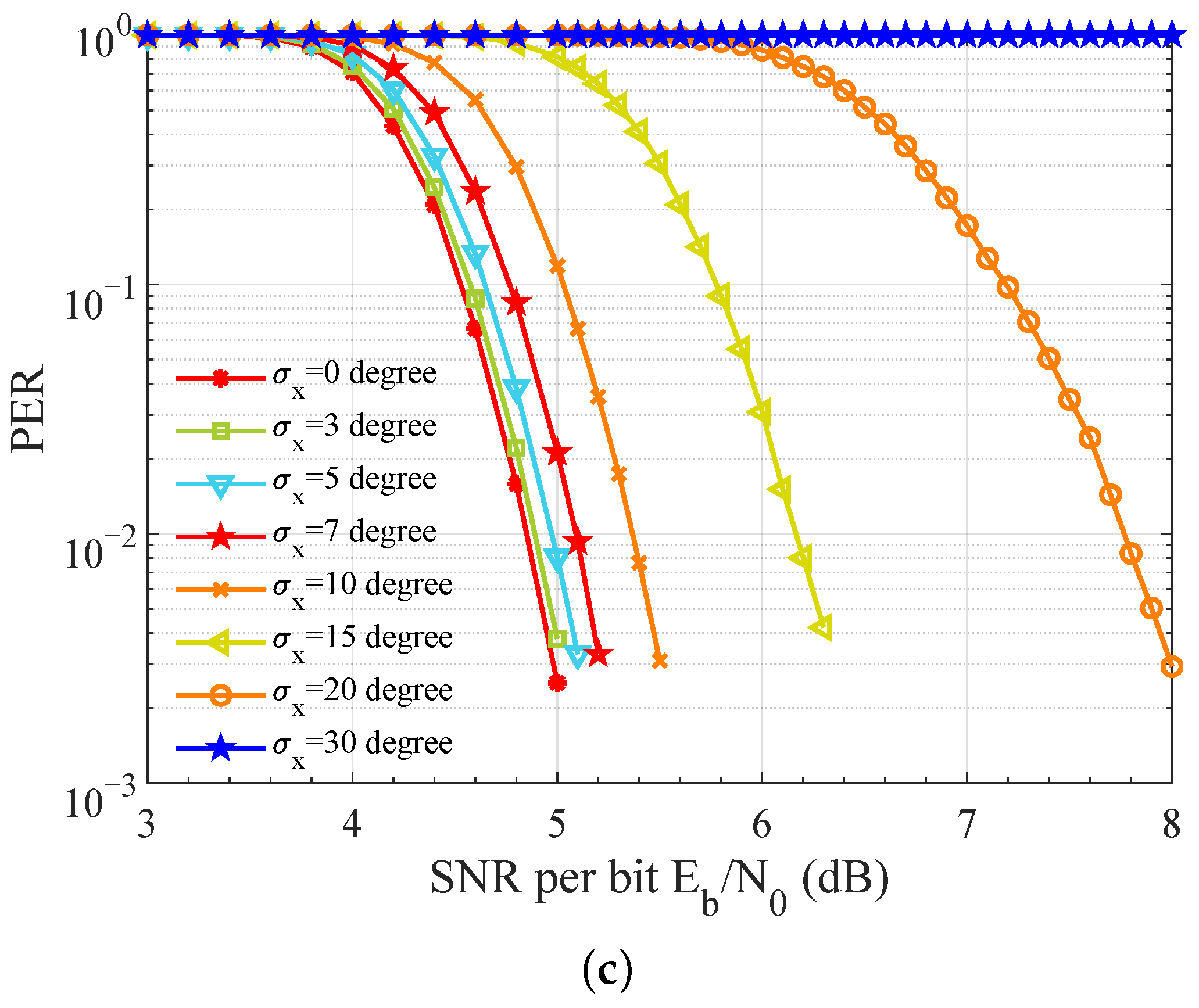
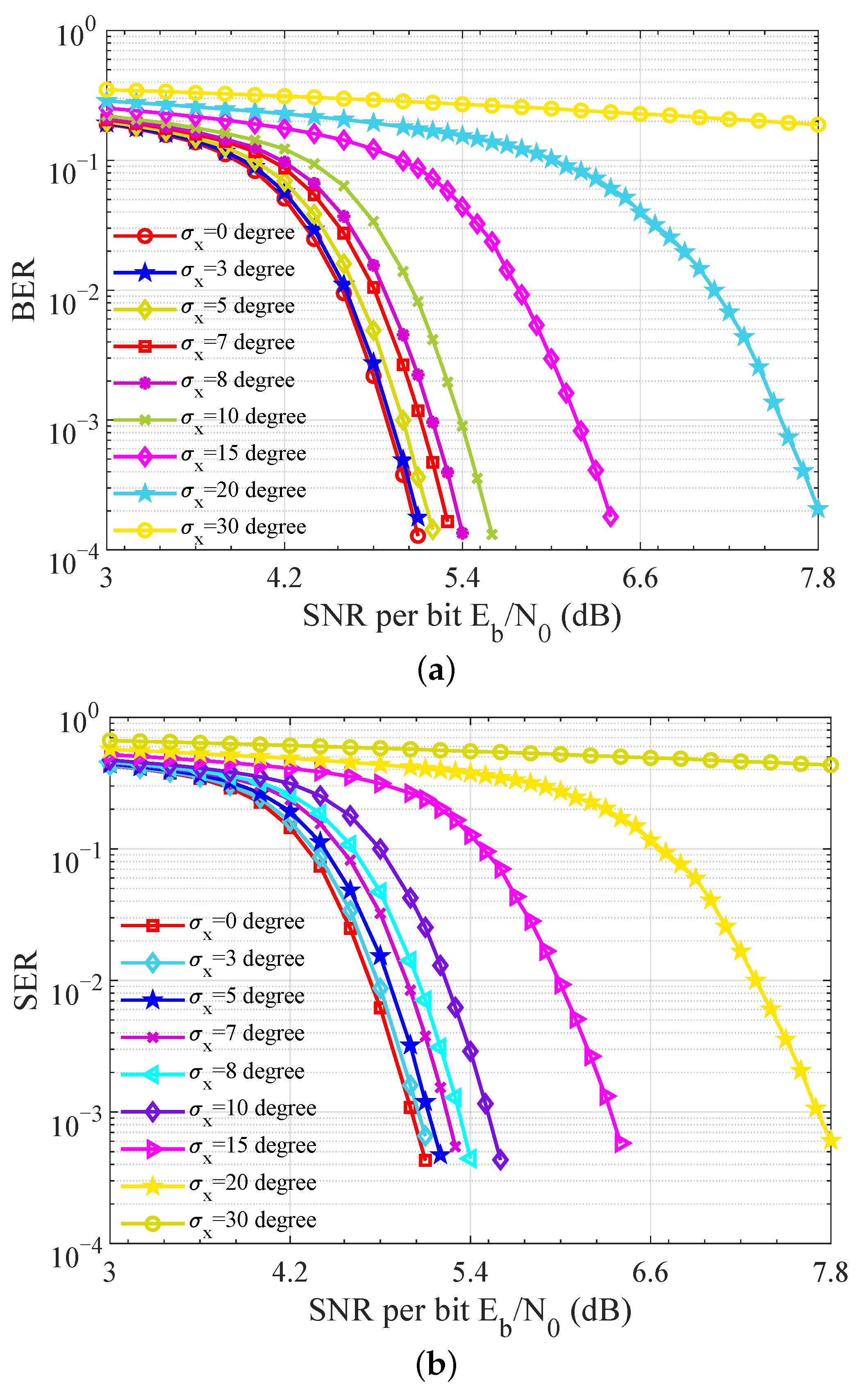
5.4. Variance Robustness
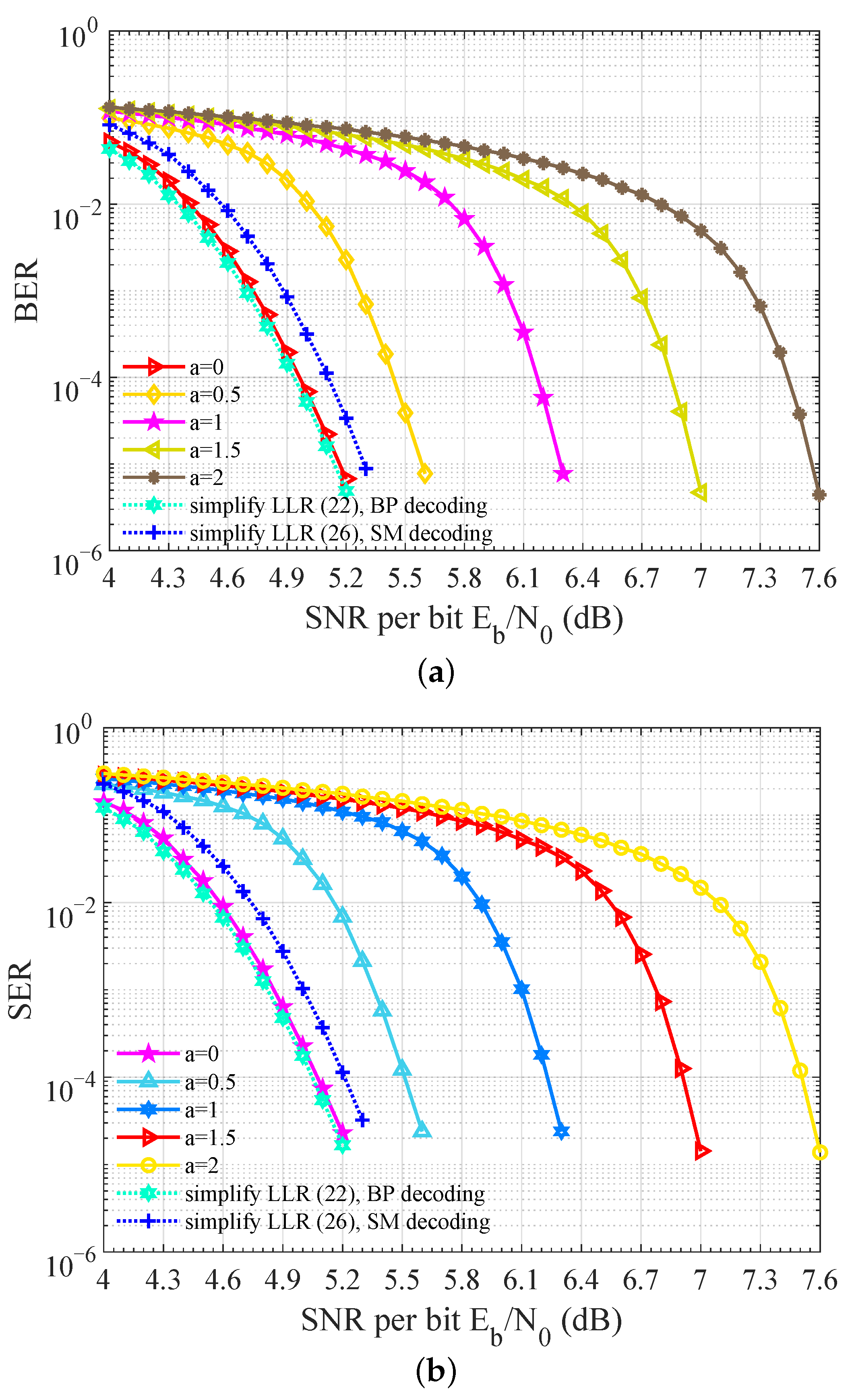
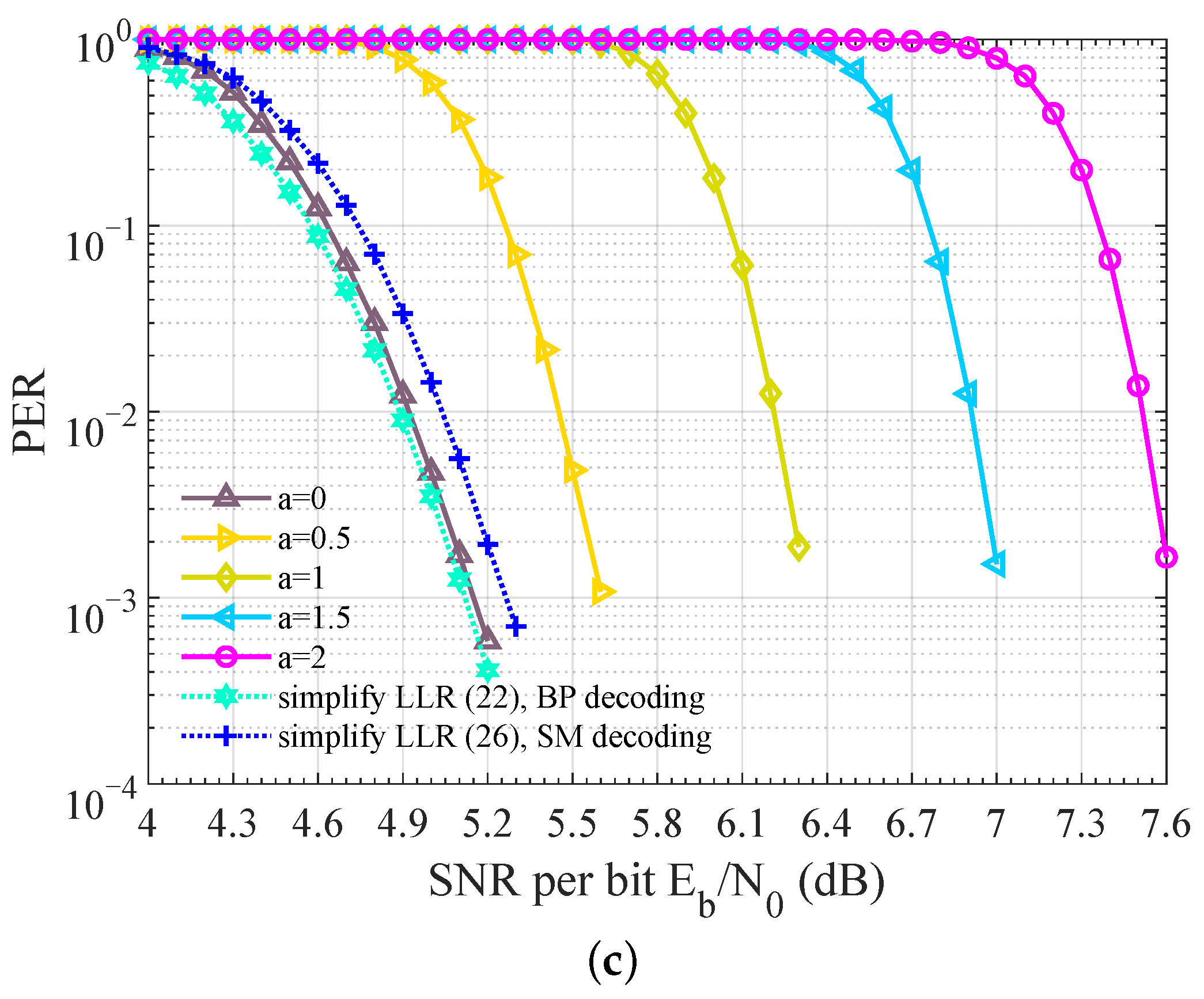
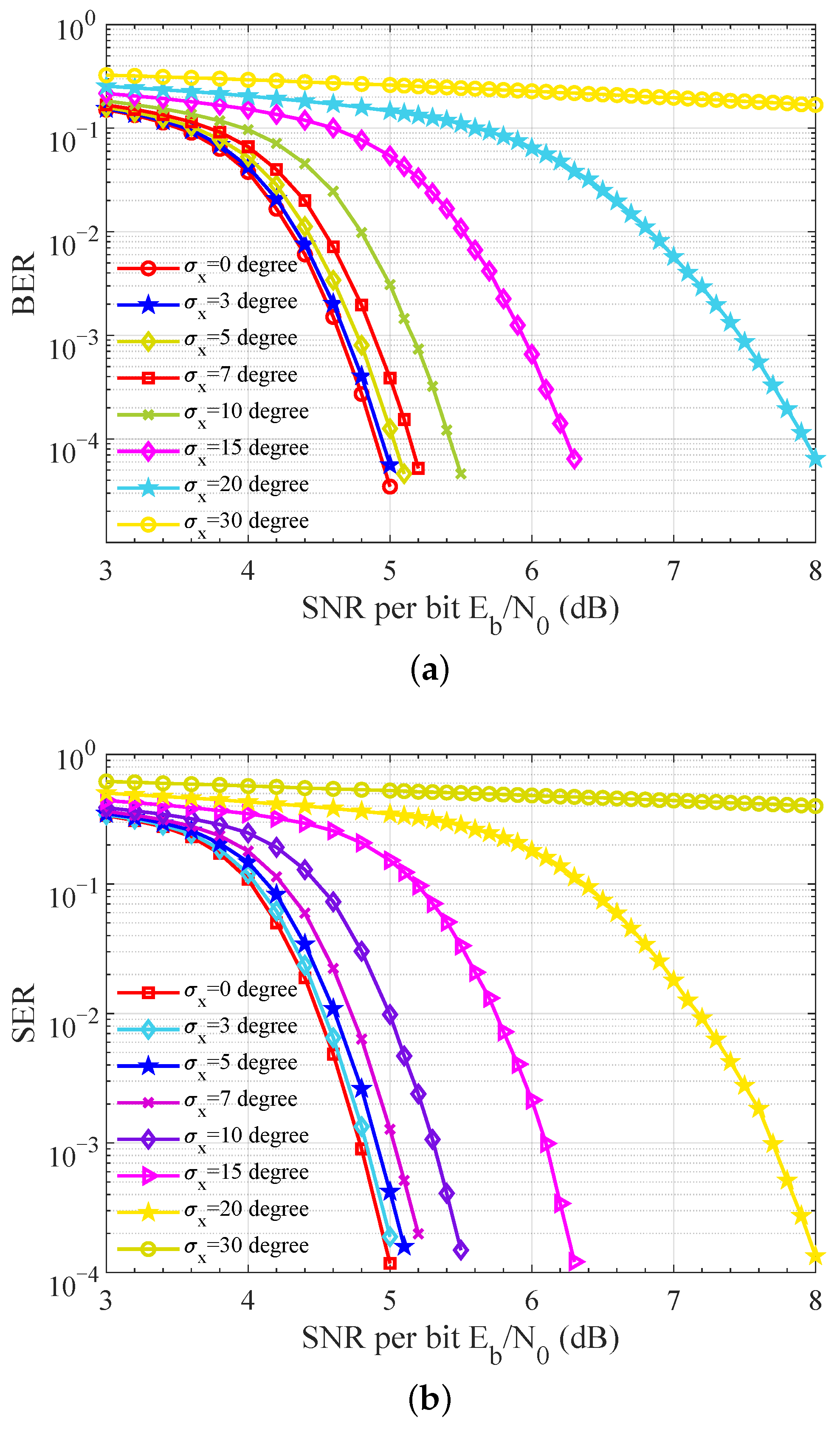
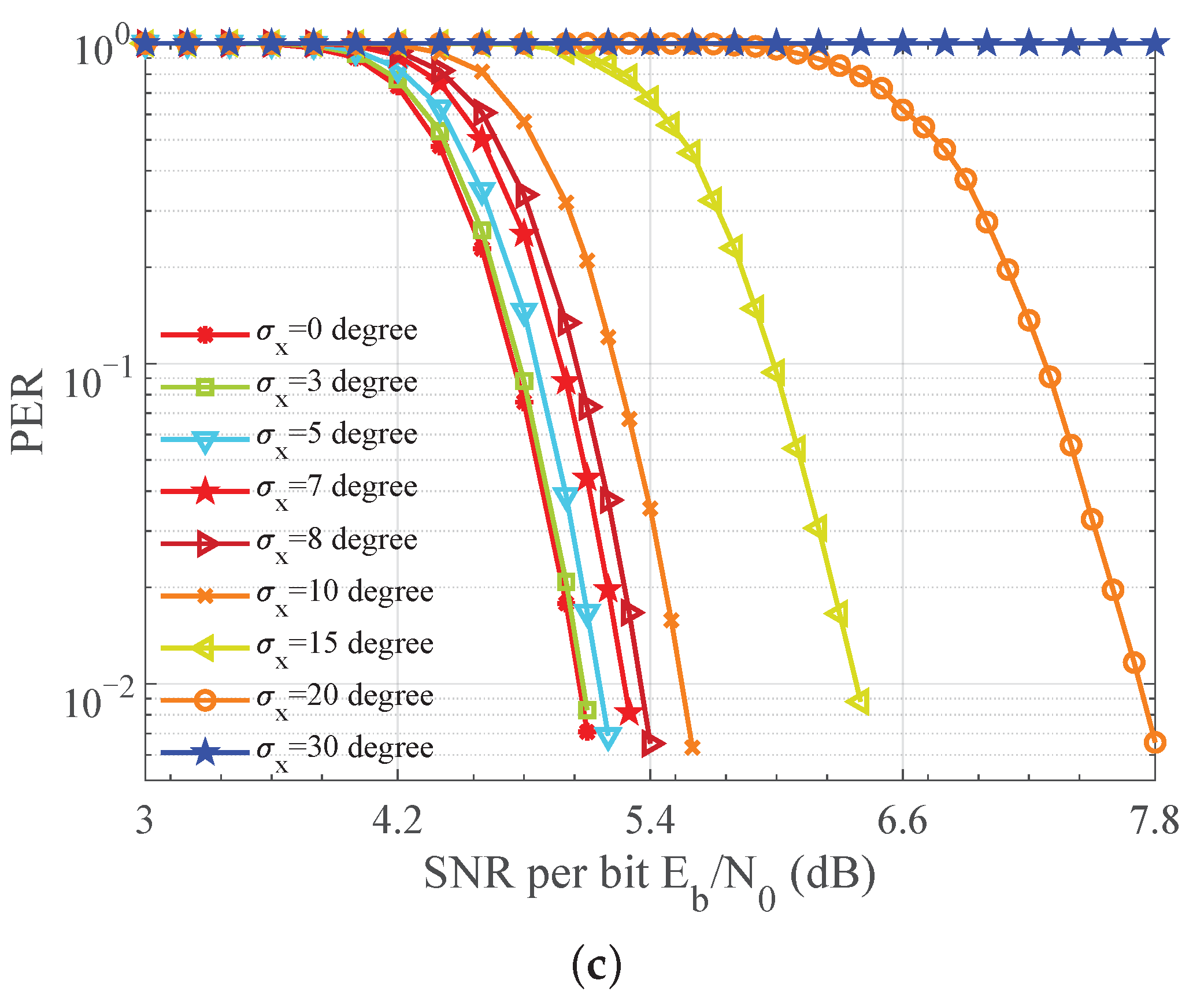
5.5. CPO Robustness
5.6. Complexity Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walther, J.; Jong, C.D. Technology for More Effective Healthcare. IEEE Multimed. 2009, 16, 5–7. [Google Scholar] [CrossRef]
- Torres, C.; Fried, J.C.; Rose, K.; Manjunath, B.S. A Multiview Multimodal System for Monitoring Patient Sleep. IEEE Trans. Multimed. 2018, 20, 3057–3068. [Google Scholar] [CrossRef] [Green Version]
- Kirsal Ever, Y. Secure-Anonymous User Authentication Scheme for e-Healthcare Application Using Wireless Medical Sensor Networks. IEEE Syst. J. 2019, 13, 456–467. [Google Scholar] [CrossRef]
- Muhammed, T.; Mehmood, R.; Albeshri, A.; Katib, I. UbeHealth: A Personalized Ubiquitous Cloud and Edge-Enabled Networked Healthcare System for Smart Cities. IEEE Access 2018, 6, 32258–32285. [Google Scholar] [CrossRef]
- Alhussein, M.; Muhammad, G. Voice Pathology Detection Using Deep Learning on Mobile Healthcare Framework. IEEE Access 2018, 6, 41034–41041. [Google Scholar] [CrossRef]
- Alemdar, H.; Ersoy, C. Wireless sensor networks for healthcare: A survey. Comput. Netw. 2010, 54, 2688–2710. [Google Scholar] [CrossRef]
- Ramgopal, K. Applications of wireless sensor networks in healthcare. In IoT and WSN Applications for Modern Agricultural Advancements: Emerging Research and Opportunities; IGI Global: Hershey, PA, USA, 2020; pp. 8–40. [Google Scholar]
- Djedouboum, A.C.; Abba Ari, A.A.; Gueroui, A.M.; Mohamadou, A.; Aliouat, Z. Big Data Collection in Large-Scale Wireless Sensor Networks. Sensors 2018, 18, 4474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, P.; Kumari, S.; Sharma, V.; Sangaiah, A.K.; Wei, J.; Li, X. A certificateless aggregate signature scheme for healthcare wireless sensor network. Sustain. Comput. Inform. Syst. 2018, 18, 80–89. [Google Scholar] [CrossRef]
- Ayyildiz, C.; Erdem, H.E.; Dirikgil, T.; Dugenci, O.; Kocak, T.; Altun, F.; Gungor, V.C. Structure health monitoring using wireless sensor networks on structural elements. Ad Hoc Netw. 2019, 82, 68–76. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef] [Green Version]
- Ko, J.; Lu, C.; Srivastava, M.B.; Stankovic, J.A.; Terzis, A.; Welsh, M. Wireless Sensor Networks for Healthcare. Proc. IEEE 2010, 98, 1947–1960. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.P.; Amgoth, T.; Annavarapu, C.S.R. Machine learning algorithms for wireless sensor networks: A survey. Inf. Fusion 2019, 49, 1–25. [Google Scholar] [CrossRef]
- IEEE 802.15.4-2015 Standard; IEEE Standard for Low-Rate Wireless Networks. IEEE Press: New York, NY, USA, 2016.
- ISO/IEC/IEEE Standard 802.15.4-2018; Information Technology-Telecommunications and Information Exchange between Systems-Local and Metropolitan Area Networks-Specific Requirements-Part 15-4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (WPANs). IEEE Press: New York, NY, USA, 2018.
- Li, Q.; Du, P.; Bi, G. Generalized soft decision metric generation for MPSK/MQAM without noise variance knowledge. In Proceedings of the 14th IEEE Proceedings on Personal, Indoor and Mobile Radio Communications (PIMRC 2003), Beijing, China, 7–10 September 2003; pp. 1027–1030. [Google Scholar]
- Yuan, H.; Kam, P. The LLR Metric for q-ary LDPC Codes with MPSK Modulation over Rayleigh Channels with Imperfect CSI. IEEE Trans. Commun. 2012, 60, 1793–1799. [Google Scholar] [CrossRef]
- Cao, S.; Kam, P.-Y.; Yu, C. Pilot-Aided Log-Likelihood Ratio for LDPC Coded MPSK-OFDM Transmission. IEEE Photonics Technol. Lett. 2013, 25, 594–597. [Google Scholar] [CrossRef]
- Jeon, H.J.; Demeechai, T.; Lee, W.G.; Kim, D.H.; Chang, T.G. IEEE 802.15.4 BPSK receiver architecture based on a new efficient detection scheme. IEEE Trans. Signal Process. 2016, 58, 4711–4719. [Google Scholar] [CrossRef]
- Zhang, G.; Wen, H.; Wang, L.; Song, L.; Tang, J.; Liao, R. Simple and robust near-optimal single differential detection scheme for IEEE 802.15. 4 BPSK receivers. IET Commun. 2019, 13, 186–197. [Google Scholar] [CrossRef]
- Zhang, G.; Wen, H.; Wang, L.; Zeng, X.; Tang, J.; Liao, R.; Song, L. Multiple symbol differential detection scheme for IEEE 802.15. 4 BPSK receivers. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2018, 101, 1975–1979. [Google Scholar] [CrossRef]
- Zhang, G.; Wen, H.; Wang, L.; Xie, P.; Song, L.; Tang, J.; Liao, R. Simple adaptive single differential coherence detection of BPSK signals in IEEE 802.15. 4 wireless sensor networks. Sensors 2018, 18, 52. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Han, C.; Ji, B.; Shi, C.; Xie, P.; Yang, L. A new multiple-symbol differential detection strategy for error-floor elimination of IEEE 802.15.4 BPSK receivers impaired by carrier frequency offset. Wirel. Commun. Mob. Comput. 2019, 2019, 5409612. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, D.; Song, L.; Wu, H.; Xie, P.; Ji, B.; Wen, H. Simple non-coherent detection scheme for IEEE 802.15. 4 BPSK receivers. Electron. Lett. 2017, 53, 628–629. [Google Scholar] [CrossRef]
- Park, D.; Park, C.S.; Lee, K. Simple design of detector in the presence of frequency offset for IEEE 802.15.4 LR-WPANs. IEEE Trans. Circuits Syst. II Express Briefs 2009, 56, 330–334. [Google Scholar] [CrossRef]
- Zhang, G.; Shi, C.; Han, C.; Li, X.; Wang, D.; Rabie, K.; Kharel, R. Implementation-friendly and energy-efficient symbol-by-symbol detection scheme for IEEE 802.15. 4 O-QPSK receivers. IEEE Access 2020, 8, 158402–158415. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, G.; Li, H.; Han, C.; Tang, J.; Wen, H.; Wang, L.; Wang, D. Reduced-complexity multiple-symbol detection of O-QPSK signals in smart metering utility networks. Electronics 2020, 9, 2049. [Google Scholar] [CrossRef]
- Divsalar, D.; Simon, M.K. Multiple-symbol differential detection of MPSK. IEEE Trans. Commun. 1990, 38, 300–308. [Google Scholar] [CrossRef]
- Hagenauer, J.; Offer, E.; Papke, L. Iterative decoding of binary block and convolutional codes. IEEE Trans. Inf. Theory 1996, 42, 429–445. [Google Scholar] [CrossRef] [Green Version]
- Motedayen-Aval, I.; Anastasopoulos, A. Polynomial-complexity noncoherent symbol-by-symbol detection with application to adaptive iterative decoding of turbo-like codes. IEEE Trans. Commun. 2003, 51, 197–207. [Google Scholar] [CrossRef]
- Xi, D. Bessel Function; Higher Education Press: Beijing, China, 1998. [Google Scholar]
- Van Tress, H.L.; Bell, K.L.; Zhi, T. Part I: Detection, Estimation and Filtering Theory. In Detection Estimation and Modulation Theory; Wiley: Hoboken, NJ, USA, 2012; pp. 1–176. [Google Scholar]
- Lin, S.; Costello, D.J. Error Control Coding: Fundamentals and Applications; Prentise-Hall Publisher: Hemel Hempstead, UK, 1983; pp. 1–720. [Google Scholar]
- ZZhang, G.; Wen, H.; Pu, J.; Tang, J. Build-in wiretap channel I with feedback and LDPC codes by soft decision decoding. IET Commun. 2017, 11, 1808–1814. [Google Scholar] [CrossRef]



| Spreading Sequence | Chip Phases for | |
|---|---|---|
| 0000 | ||
| 1000 | ||
| 0100 | ||
| 1100 | ||
| 0010 | ||
| 1010 | ||
| 0110 | ||
| 1110 | ||
| 0001 | ||
| 1001 | ||
| 0101 | ||
| 1101 | ||
| 0011 | ||
| 1011 | ||
| 0111 | ||
| 1111 |
| Parameter | Detailed Description |
|---|---|
| Channel condition | phase noncoherent or Rayleigh fading |
| Power of the complex AWGN | |
| Timing synchronization | Perfect |
| LDPC code | PEGReg (1008, 504) |
| Code rate | 0.5 |
| Degree distribution | (3, 6) |
| Data modulation | MPSK |
| Symbols | 16-ary orthogonal |
| Payload length of PPDU (bits) | 504 |
| Spreading factor | 16 |
| Chip rate (Mchip/s) | 1 |
| Symbol rate (ks/s) | 62.5 |
| Binary data rate (kb/s) | 250 |
| Carrier frequency (MHz) | 786 |
| fading phase (rads) | Uniform distribution in |
| PN length | 16 |
| fading amplitude | Rayleigh distribution |
| Scheme | CSI | Re | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (8) | 1156 | 1016 | 64 | 1024 | 64 | 4 | 64 | ✓ | \ | \ |
| (16) | 1024 | 990 | 64 | 1024 | 8 | \ | \ | \ | \ | \ |
| Scheme | CSI | Re | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (21) | 4164 | 3000 | 2048 | 1024 | 5120 | \ | \ | \ | 64 | \ |
| (23) | 64 | 990 | 64 | 64 | 64 | \ | \ | \ | \ | \ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, B.; Ma, C.; Li, H.; Zhang, G.; Han, C. Simple and Robust Log-Likelihood Ratio Calculation of Coded MPSK Signals in Wireless Sensor Networks for Healthcare. Appl. Sci. 2022, 12, 2330. https://doi.org/10.3390/app12052330
Xie B, Ma C, Li H, Zhang G, Han C. Simple and Robust Log-Likelihood Ratio Calculation of Coded MPSK Signals in Wireless Sensor Networks for Healthcare. Applied Sciences. 2022; 12(5):2330. https://doi.org/10.3390/app12052330
Chicago/Turabian StyleXie, Bo, Congfang Ma, Haiqiong Li, Gaoyuan Zhang, and Congzheng Han. 2022. "Simple and Robust Log-Likelihood Ratio Calculation of Coded MPSK Signals in Wireless Sensor Networks for Healthcare" Applied Sciences 12, no. 5: 2330. https://doi.org/10.3390/app12052330
APA StyleXie, B., Ma, C., Li, H., Zhang, G., & Han, C. (2022). Simple and Robust Log-Likelihood Ratio Calculation of Coded MPSK Signals in Wireless Sensor Networks for Healthcare. Applied Sciences, 12(5), 2330. https://doi.org/10.3390/app12052330







