Boolean Masking for Arithmetic Additions at Arbitrary Order in Hardware
Abstract
:1. Introduction
Contribution
- A Kogge–Stone adder with a latency of -cycles.
- A Sklansky adder with the same latency but reduced area and randomness requirements.
- A Brent–Kung adder which trades off higher latency for an even lower logic area requirement and requires less randomness.
2. Preliminaries
2.1. Notation
2.2. Parallel Prefix Adders
2.3. Masking Countermeasures
Threshold Implementation
Probe-Isolating Non-Interference and Hardware Private Circuits
3. Boolean Masking for Addition Circuits
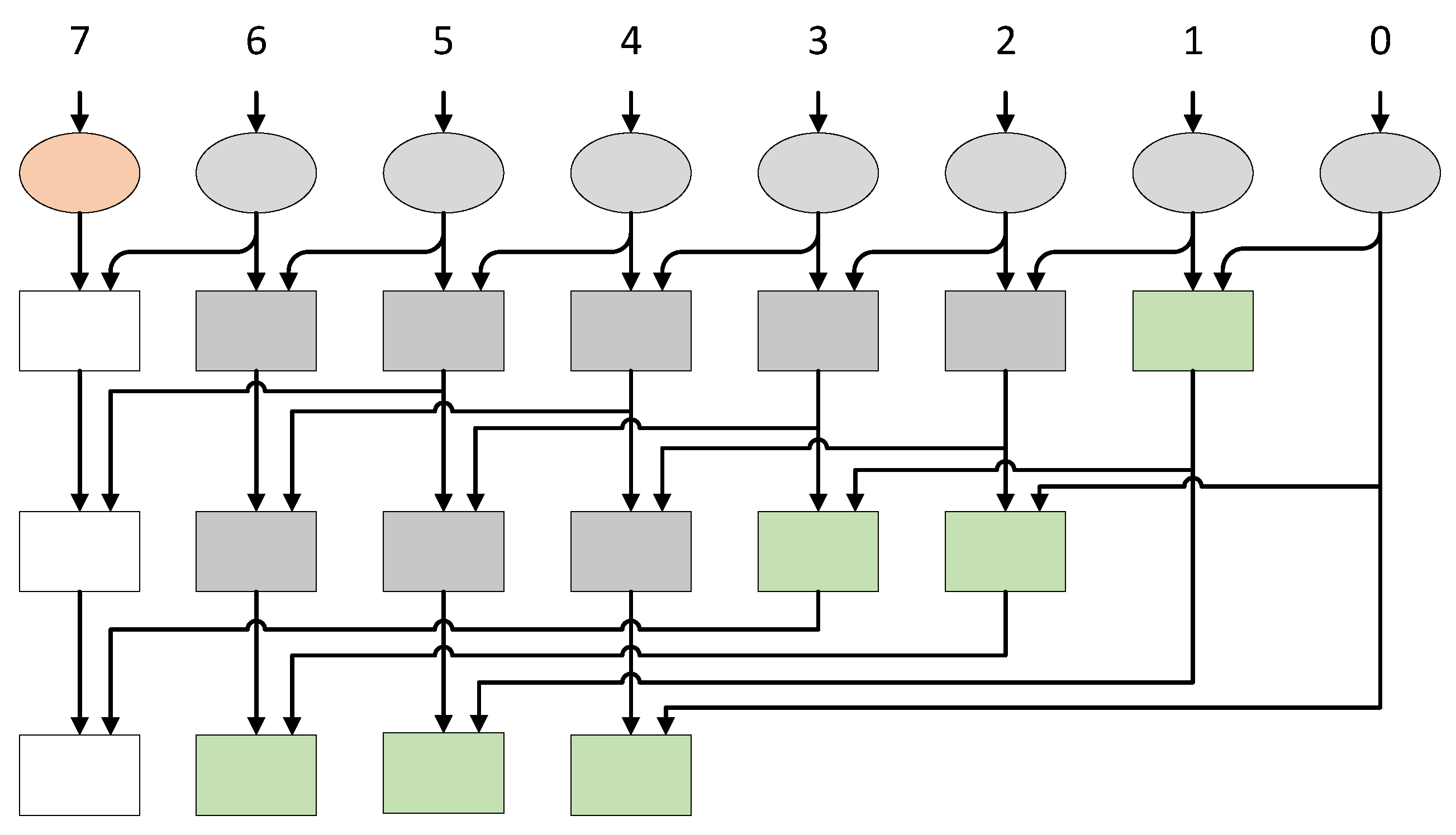
3.1. Kogge–Stone Adder (KSA)
Masking KSAs
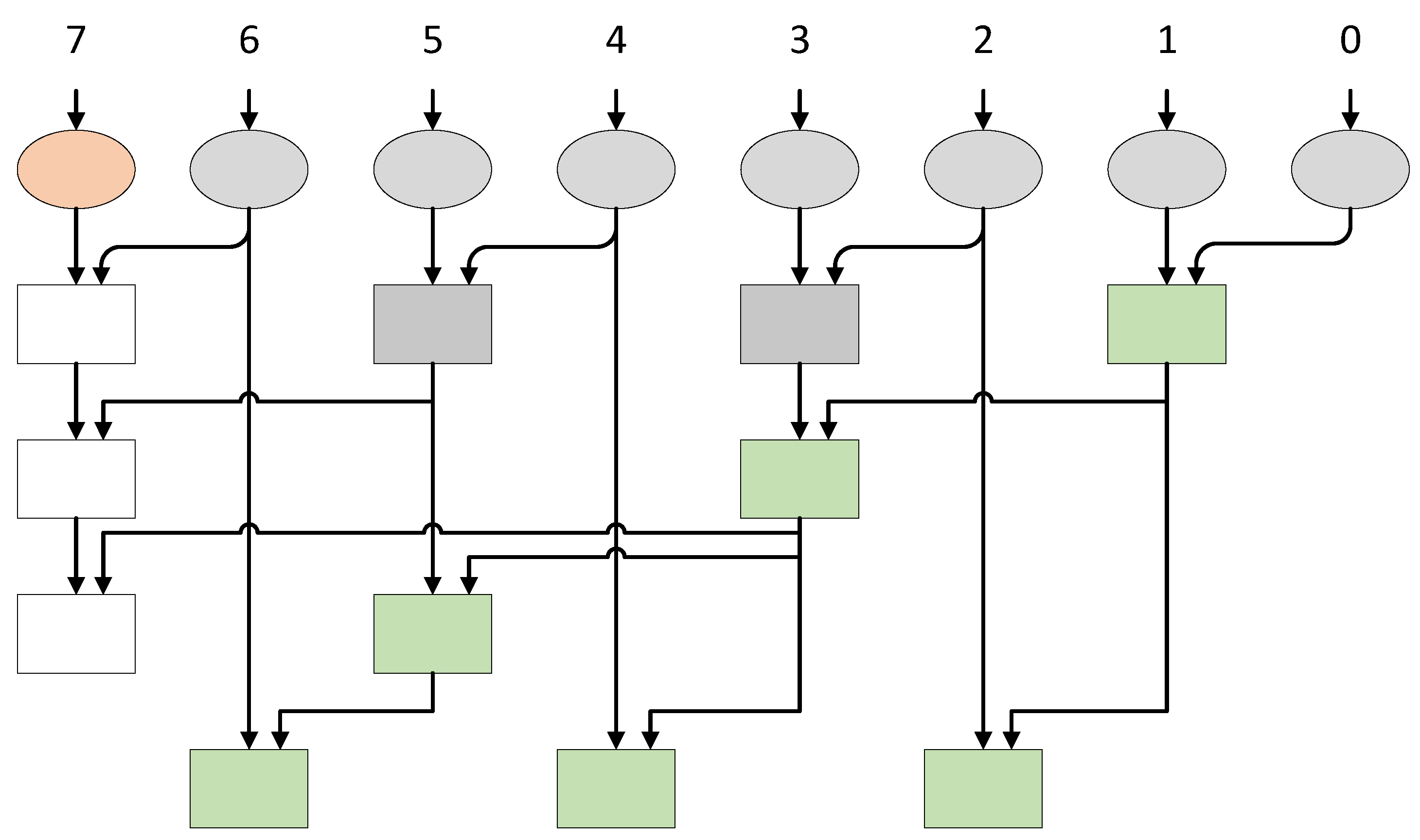
3.2. Sklansky Adder (SA)
Masking SAs
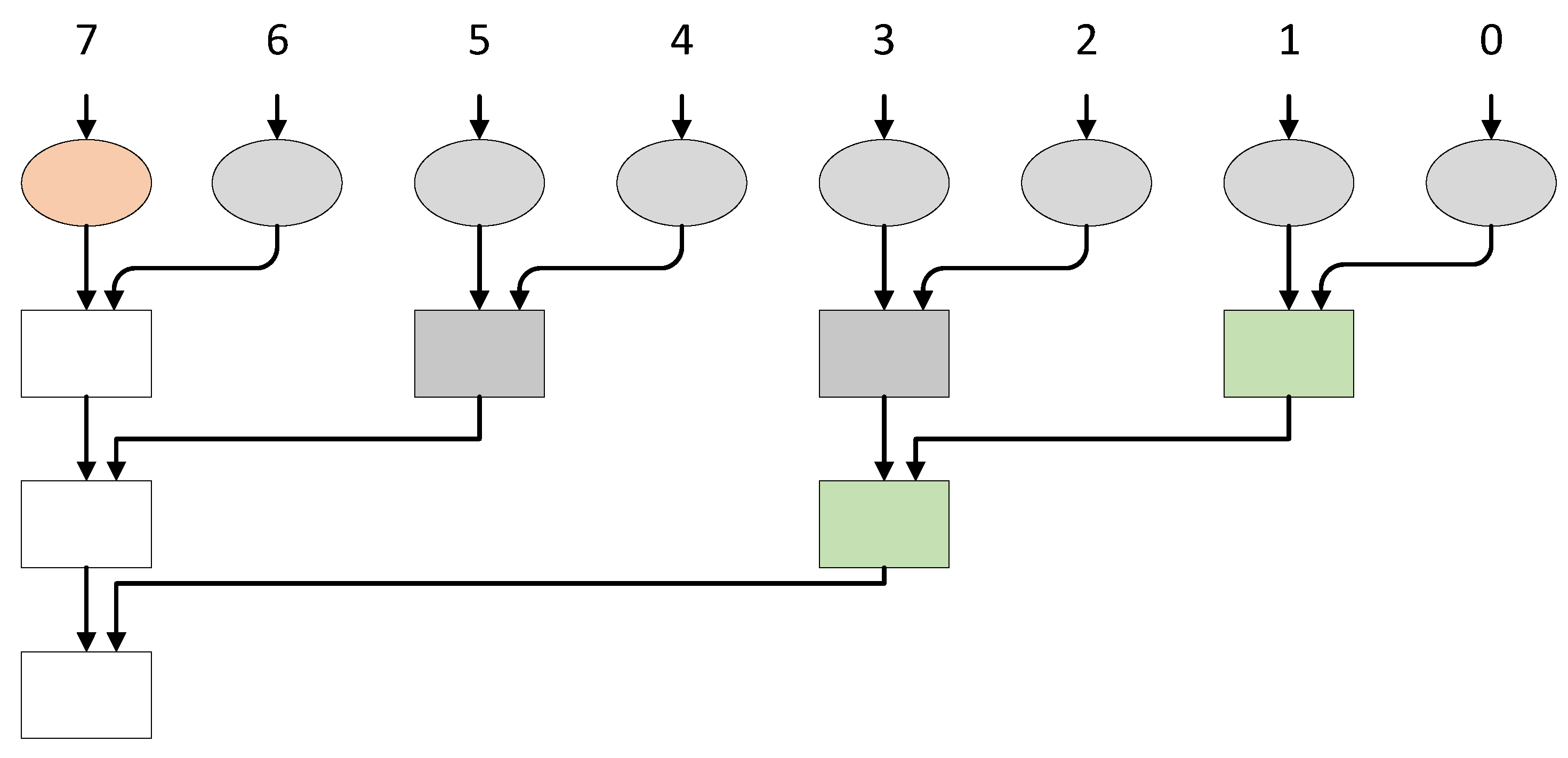
3.3. Brent–Kung Adder (BKA)
Masking BKAs
4. Implementation Results and Discussion
4.1. TI Implementations
4.2. HPC2 Implementations
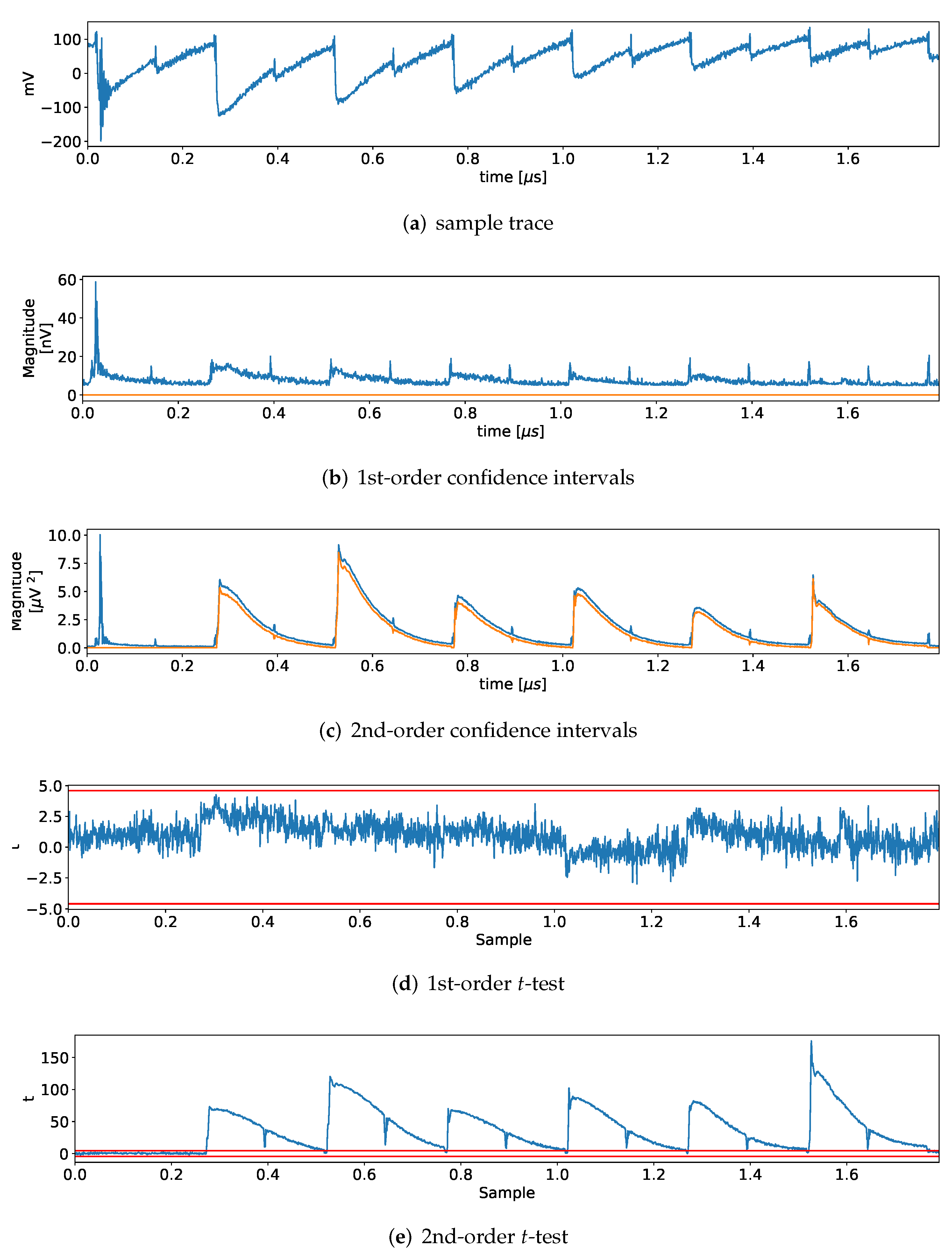
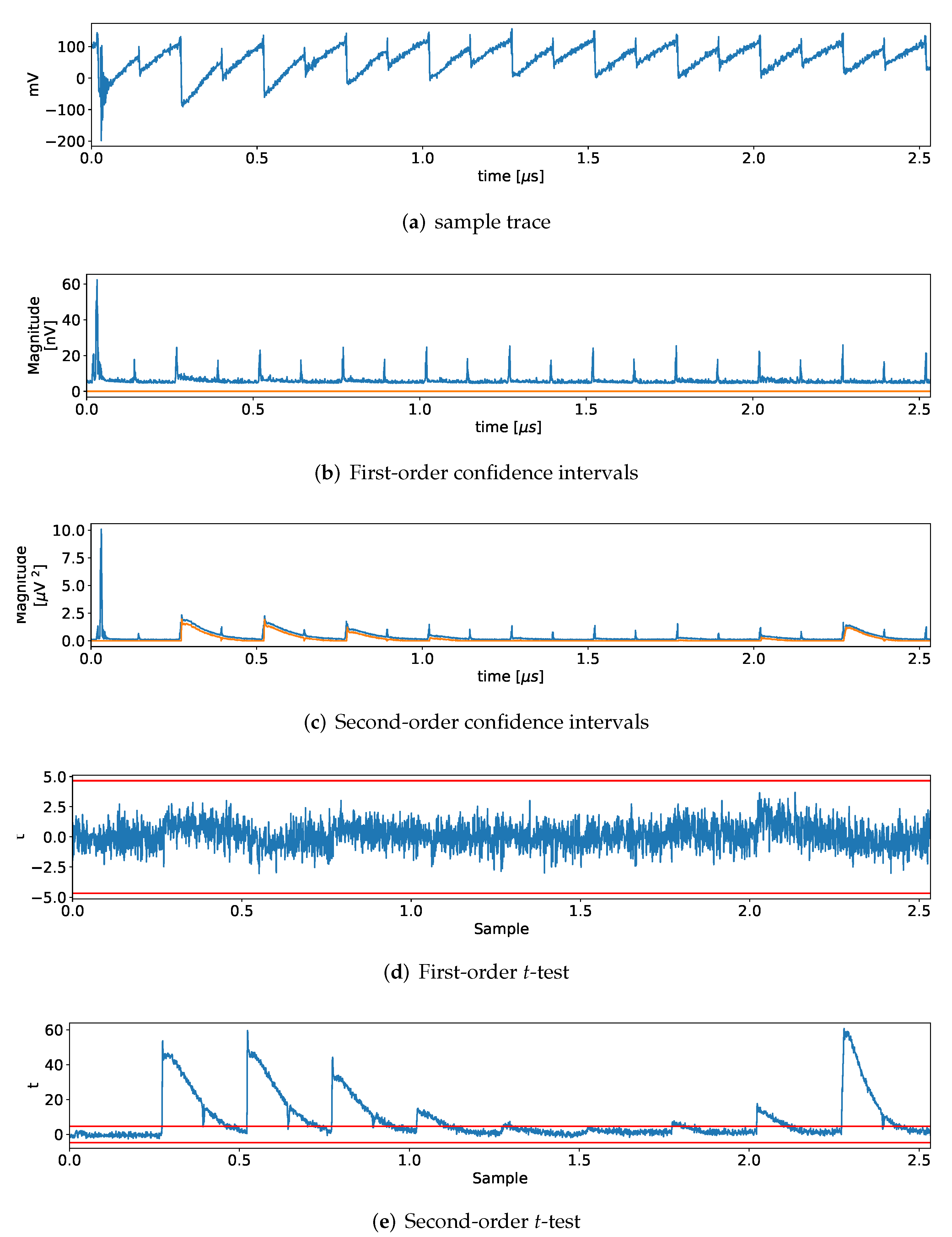
5. Side-Channel Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Cassiers, G.; Grégoire, B.; Levi, I.; Standaert, F. Hardware Private Circuits: From Trivial Composition to Full Verification. IEEE Trans. Comput. 2020, 2020, 185. [Google Scholar] [CrossRef]
- Schneider, T.; Moradi, A.; Güneysu, T. Arithmetic Addition over Boolean Masking-Towards First- and Second-Order Resistance in Hardware. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9092, pp. 559–578. [Google Scholar]
- Reparaz, O. A note on the security of Higher-Order Threshold Implementations. IACR Cryptology ePrint Archive. 2015. Available online: https://eprint.iacr.org/2015/001 (accessed on 12 February 2022).
- Duc, A.; Faust, S.; Standaert, F. Making Masking Security Proofs Concrete-Or How to Evaluate the Security of Any Leaking Device. EUROCRYPT (1). In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9056, pp. 401–429. [Google Scholar]
- Reparaz, O.; Bilgin, B.; Nikova, S.; Gierlichs, B.; Verbauwhede, I. Consolidating Masking Schemes. CRYPTO (1). In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9215, pp. 764–783. [Google Scholar]
- Groß, H.; Mangard, S.; Korak, T. Domain-Oriented Masking: Compact Masked Hardware Implementations with Arbitrary Protection Order. In Proceedings of the ACM Workshop on Theory of Implementation Security, TIS@CCS 2016, Vienna, Austria, 24 October 2016; Bilgin, B., Nikova, S., Rijmen, V., Eds.; ACM: New York, NY, USA, 2016; p. 3. [Google Scholar] [CrossRef]
- Nikova, S.; Rechberger, C.; Rijmen, V. Threshold Implementations Against Side-Channel Attacks and Glitches. ICICS. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4307, pp. 529–545. [Google Scholar]
- Bilgin, B.; Gierlichs, B.; Nikova, S.; Nikov, V.; Rijmen, V. Higher-Order Threshold Implementations. In Advances in Cryptology–ASIACRYPT 2014; Sarkar, P., Iwata, T., Eds.; Number 8874 in Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; pp. 326–343. [Google Scholar] [CrossRef] [Green Version]
- Ishai, Y.; Sahai, A.; Wagner, D. Private Circuits: Securing Hardware against Probing Attacks. In Proceedings of the 23rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2003; Advances in Cryptology-CRYPTO 2003. Springer: Berlin, Heidelberg, Germany, 2003; pp. 463–481. [Google Scholar]
- Coron, J.; Prouff, E.; Rivain, M.; Roche, T. Higher-Order Side Channel Security and Mask Refreshing. FSE. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8424, pp. 410–424. [Google Scholar]
- Barthe, G.; Belaïd, S.; Dupressoir, F.; Fouque, P.; Grégoire, B.; Strub, P.; Zucchini, R. Strong Non-Interference and Type-Directed Higher-Order Masking; CCS; ACM: New York, NY, USA, 2016; pp. 116–129. [Google Scholar]
- Cassiers, G.; Standaert, F. Trivially and Efficiently Composing Masked Gadgets With Probe Isolating Non-Interference. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2542–2555. [Google Scholar] [CrossRef]
- Cassiers, G. “fullVerif”. Available online: https://github.com/cassiersg/fullverif (accessed on 30 September 2021).
- Kogge, P.M.; Stone, H.S. A Parallel Algorithm for the Efficient Solution of a General Class of Recurrence Equations. IEEE Trans. Comput. 1973, 22, 786–793. [Google Scholar] [CrossRef]
- Sklansky, J. Conditional-Sum Addition Logic. IRE Trans. Electron. Comput. 1960, 9, 226–231. [Google Scholar] [CrossRef]
- Brent, R.P.; Kung, H.T. A Regular Layout for Parallel Adders. IEEE Trans. Comput. 1982, 31, 260–264. [Google Scholar] [CrossRef]
- Goodwill, G.; Jun, B.; Jaffe, J.; Rohatgi, P. A testing methodology for side channel resistance validation. In Proceedings of the NIST Non-Invasive Attack Testing Workshop, Nara, Japan, 26–27 September 2011; NIST CSRS: Gaithersburg, MD, USA, 2011. [Google Scholar]
- Schneider, T.; Moradi, A. Leakage Assessment Methodology-A Clear Roadmap for Side-Channel Evaluations. CHES. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9293, pp. 495–513. [Google Scholar]
- Cassiers, G.; Standaert, F. Provably Secure Hardware Masking in the Transition- and Glitch-Robust Probing Model: Better Safe than Sorry. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2021, 2021, 136–158. [Google Scholar] [CrossRef]
- Knichel, D.; Moradi, A.; Müller, N.; Sasdrich, P. Automated Generation of Masked Hardware. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2022, 2022, 589–629. [Google Scholar] [CrossRef]
- Müller, N.; Knichel, D.; Sasdrich, P.; Moradi, A. Transitional Leakage in Theory and Practice-Unveiling Security Flaws in Masked Circuits. IACR Cryptology ePrint Archive. 2022, p. 23. Available online: https://eprint.iacr.org/2022/023 (accessed on 12 February 2022).
- Side-Channel AttacK User Reference Architecture. Available online: http://satoh.cs.uec.ac.jp/SAKURA/index.html (accessed on 12 February 2022).
- Bache, F.; Plump, C.; Güneysu, T. Confident leakage assessment-A side-channel evaluation framework based on confidence intervals. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 1117–1122. [Google Scholar]

| Function | |||||
|---|---|---|---|---|---|
| AND | 1 | 0 | 1 | 1 | 0 |
| XOR | 0 | 1 | 1 | 0 | 1 |
| Kogge–Stone | n | n | |||
| Sklansky | n | n | |||
| Brent–Kung | n | n |
| Kogge–Stone | Sklansky | Brent–Kung | |
|---|---|---|---|
| AND | |||
| XOR |
| Design | LUTs | Flip-Flops | Freq. (MHz) | Latency | Rand. (Bit) |
|---|---|---|---|---|---|
| TI KSA [2] | 937 | 1330 | 62 | 6 | 32 |
| TI KSA | 873 | 1416 | 228 | 6 | 31 |
| 1st-order HPC2-KSA | 2936 | 3981 | 176 | 12 | 249 |
| 2nd-order HPC2-KSA | 3915 | 8001 | 148 | 12 | 747 |
| TI SA | 579 | 1416 | 174 | 6 | 41 |
| 1st-order HPC2-SA | 1801 | 3166 | 153 | 12 | 119 |
| 2nd-order HPC2-SA | 1994 | 5979 | 128 | 12 | 357 |
| TI BKA | 487 | 2352 | 280 | 9 | 31 |
| 1st-order HPC2-BKA | 1588 | 4317 | 173 | 18 | 74 |
| 2nd-order HPC2-BKA | 1666 | 7122 | 158 | 18 | 222 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bache, F.; Güneysu, T. Boolean Masking for Arithmetic Additions at Arbitrary Order in Hardware. Appl. Sci. 2022, 12, 2274. https://doi.org/10.3390/app12052274
Bache F, Güneysu T. Boolean Masking for Arithmetic Additions at Arbitrary Order in Hardware. Applied Sciences. 2022; 12(5):2274. https://doi.org/10.3390/app12052274
Chicago/Turabian StyleBache, Florian, and Tim Güneysu. 2022. "Boolean Masking for Arithmetic Additions at Arbitrary Order in Hardware" Applied Sciences 12, no. 5: 2274. https://doi.org/10.3390/app12052274
APA StyleBache, F., & Güneysu, T. (2022). Boolean Masking for Arithmetic Additions at Arbitrary Order in Hardware. Applied Sciences, 12(5), 2274. https://doi.org/10.3390/app12052274






