Geochemical Association Rules of Elements Mined Using Clustered Events of Spatial Autocorrelation: A Case Study in the Chahanwusu River Area, Qinghai Province, China
Abstract
:1. Introduction
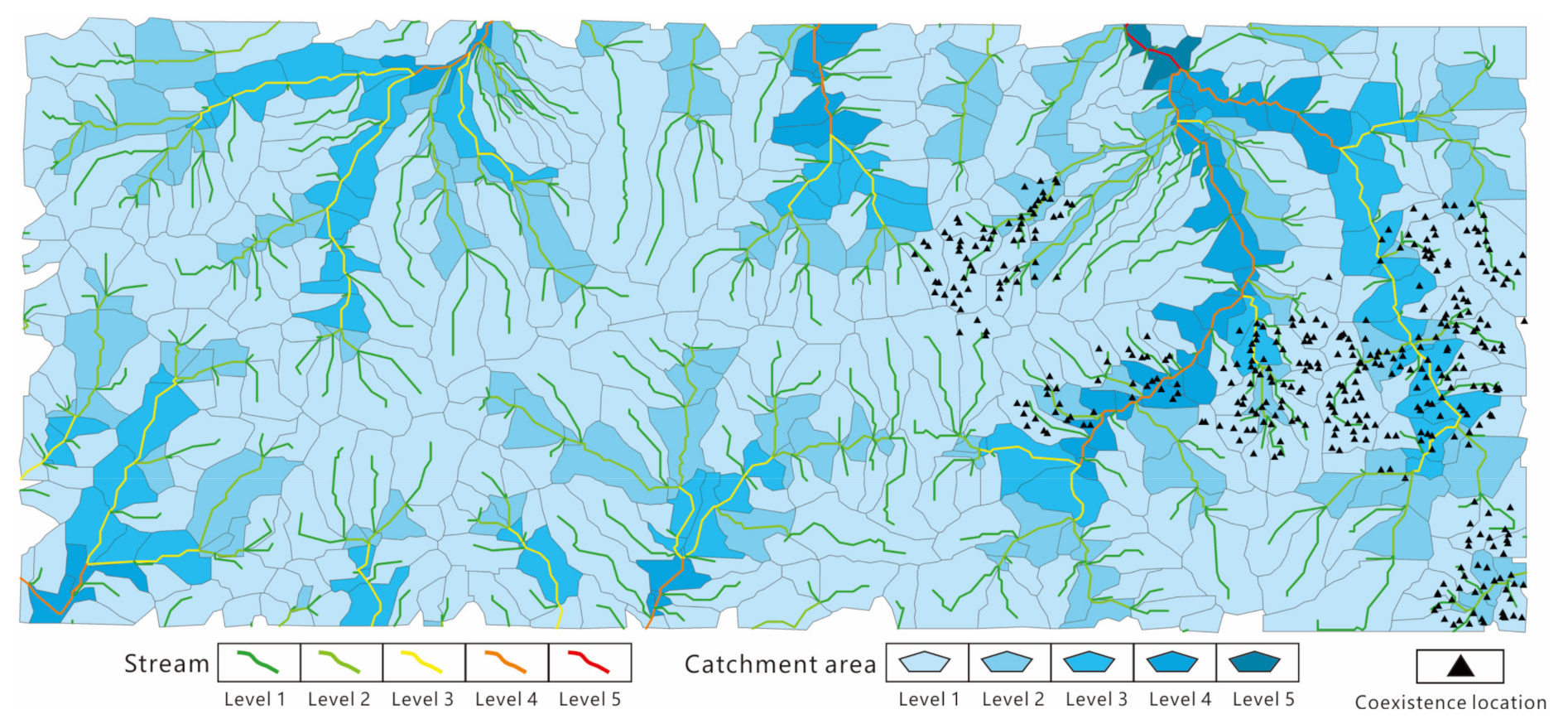
2. Study Area and Data
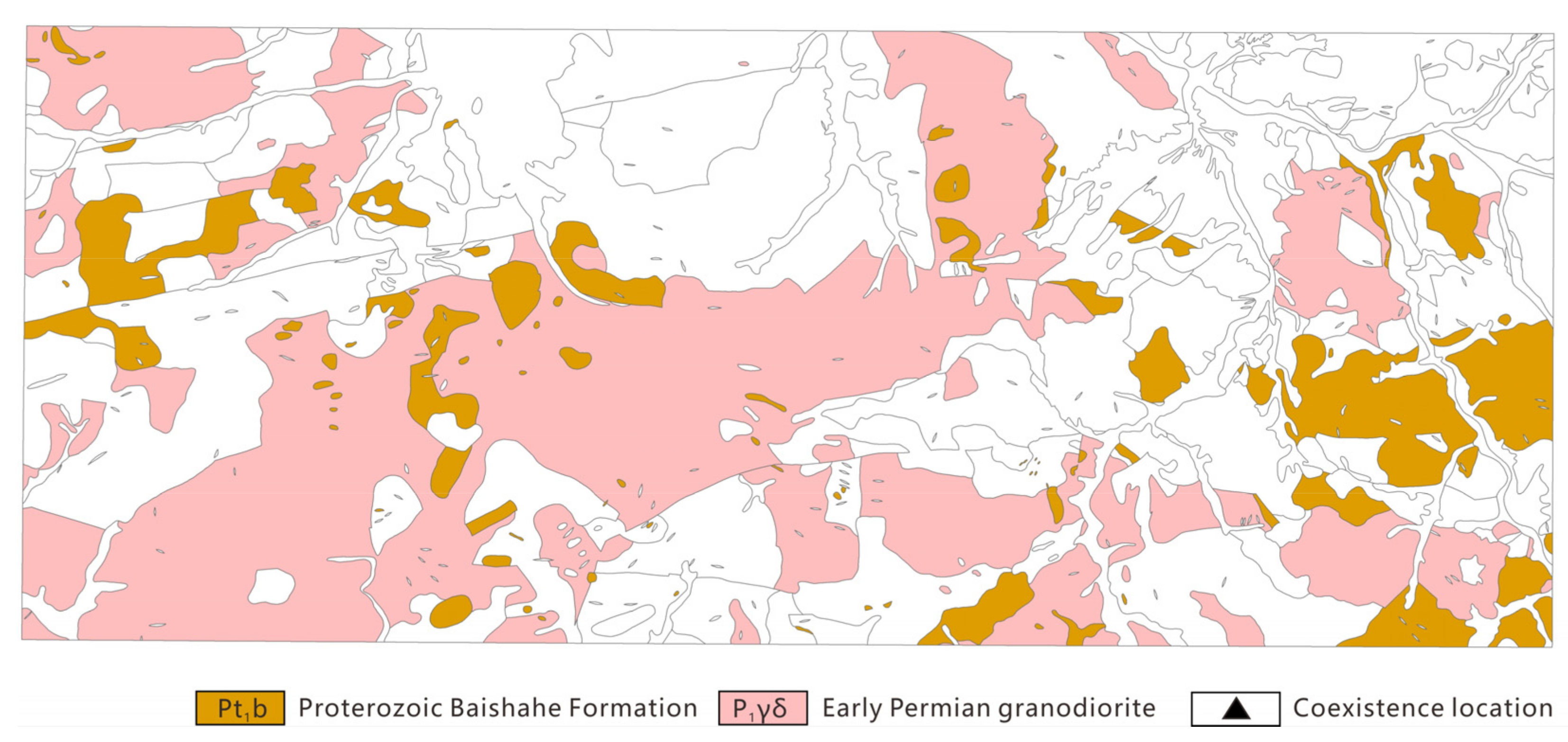
2.1. Geological Background
2.2. Geochemical Data
3. Methods
3.1. Spatial Autocorrelation
3.1.1. Univariate Spatial Autocorrelation
3.1.2. Multivariate Spatial Cross Correlation
3.2. Association Rule Mining and Apriori Algorithm
4. Results and Discussion
4.1. Spatial Autocorrelation of Elements
4.1.1. Univariate Spatial Autocorrelation of Individual Elements
4.1.2. Bivariate Spatial Cross Correlation between Two Elements
4.2. Association Rules among Multiple Elements
4.2.1. Association Rule Mining
4.2.2. Comparison with Bivariate Spatial Cross Correlation
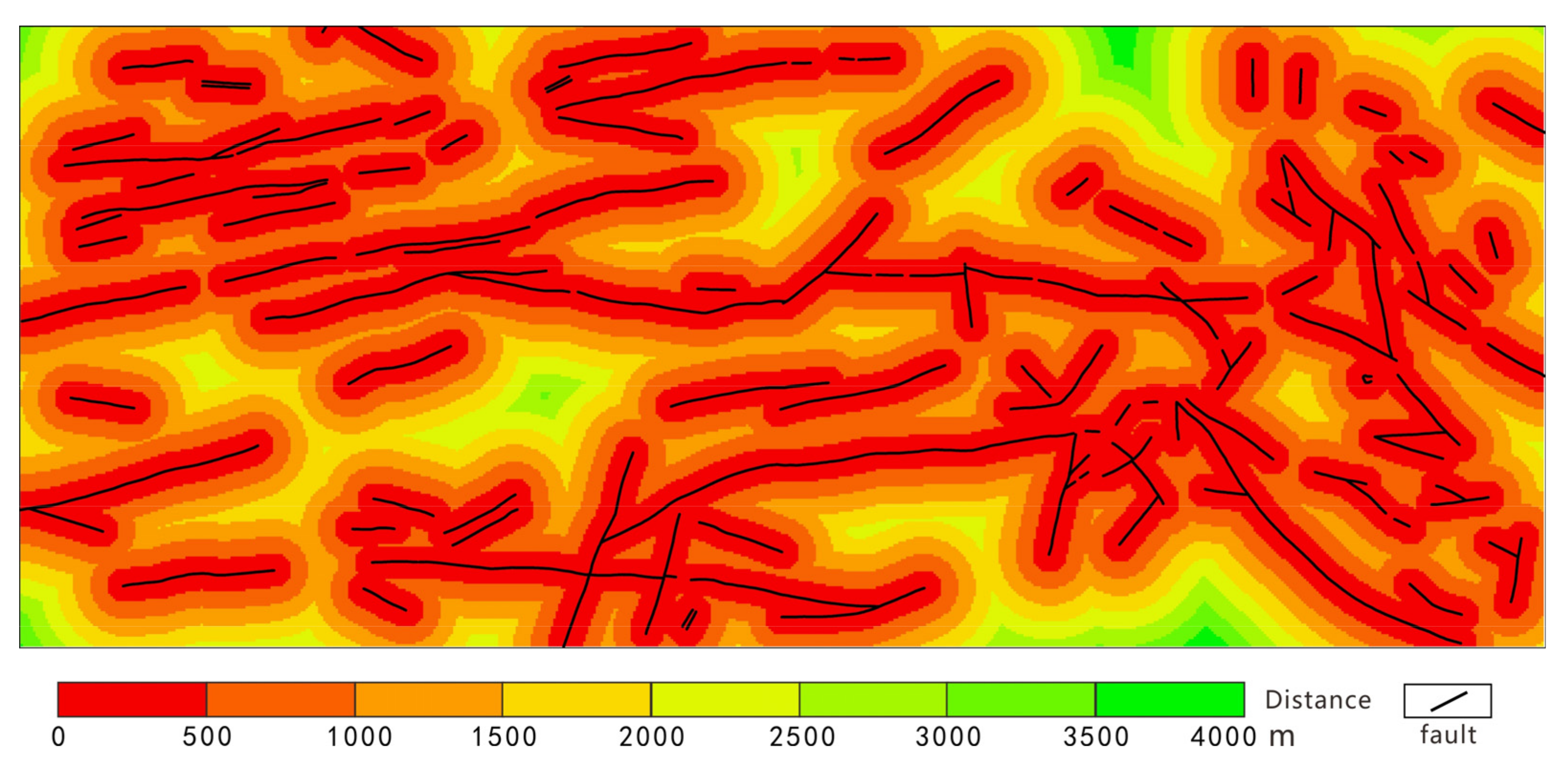
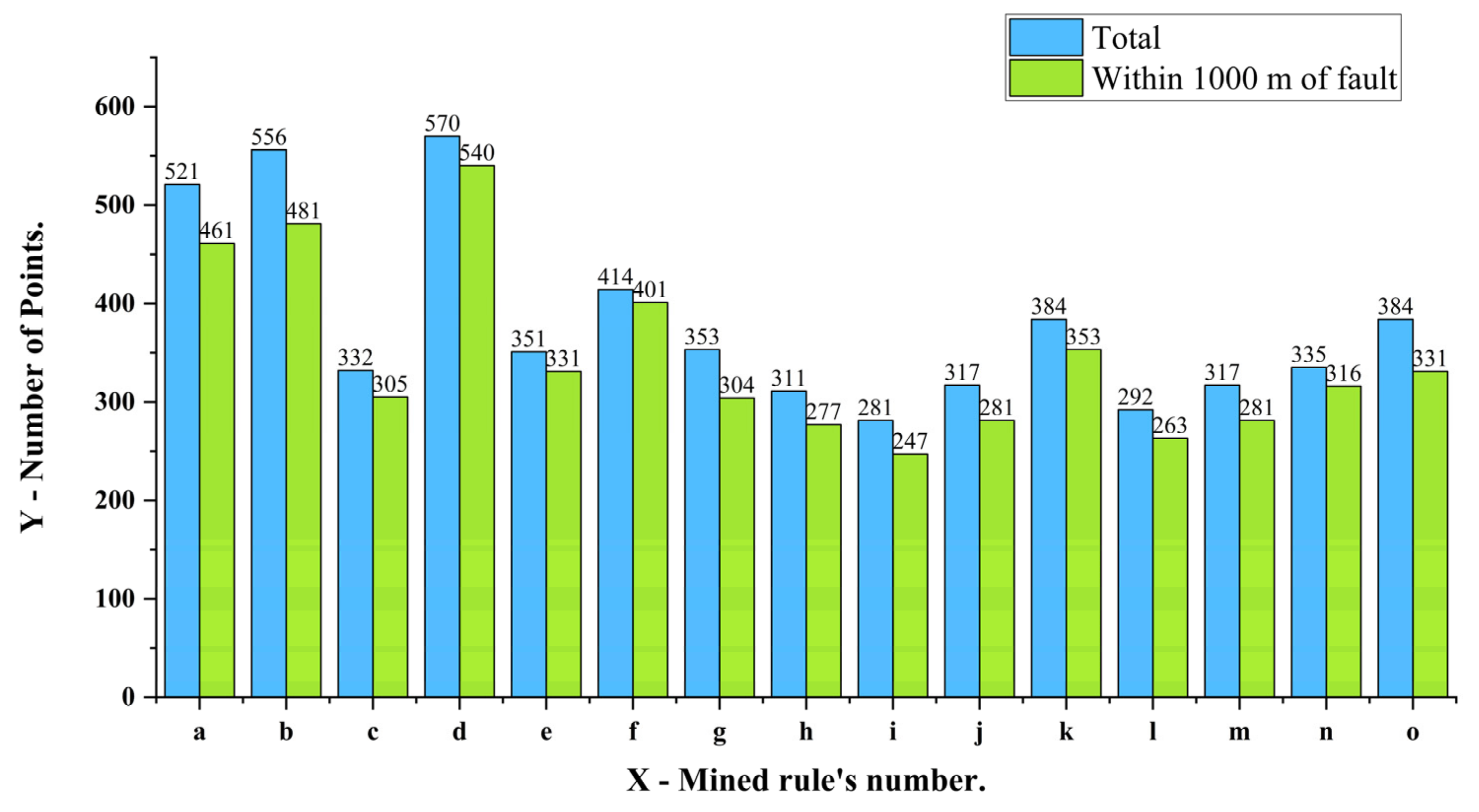
4.2.3. Controls of Geological Features
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korobova, E.M.; Romanov, S.L. A Chernobyl 137Cs contamination study as an example for the spatial structure of geochemical fields and modeling of the geochemical field structure. Chemom. Intell. Lab. Syst. 2009, 99, 1–8. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Huang, A.; Lu, H.; Cheng, Q. Geochemical field and its roles on the 3D prediction of concealed ore-bodies. Acta Petrol. Sin. 2018, 34, 352–362. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Geary, R.C. The Contiguity Ratio and Statistical Mapping. Inc. Stat. 1954, 5, 115–146. [Google Scholar] [CrossRef]
- Cliff, A.D.; Ord, J.K. The Problem of Spatial Autocorrelation. Reg. Sci. 1969, 1, 26–55. [Google Scholar]
- Cliff, A.D.; Ord, J.K. Evaluating the percentage points of a spatial autocorrelation coefficient. Geogr. Anal. 1971, 3, 51–62. [Google Scholar] [CrossRef]
- Cliff, A.D.; Ord, J.K. Spatial Processes: Models & Applications; Taylor & Francis: Oxford, UK, 1981. [Google Scholar]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 127–145. [Google Scholar]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Boots, B.; Okabe, A. Local statistical spatial analysis: Inventory and prospect. Int. J. Geogr. Inf. Sci. 2007, 21, 355–375. [Google Scholar] [CrossRef]
- Anselin, L. A local indicator of multivariate spatial association: Extending Geary’s C. Geogr. Anal. 2019, 51, 133–150. [Google Scholar] [CrossRef]
- Goovaerts, P.; Jacquez, G.M. Accounting for regional background and population size in the detection of spatial clusters and outliers using geostatistical filtering and spatial neutral models: The case of lung cancer in Long Island, New York. Int. J. Health Geogr. 2004, 3, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McLaughlin, C.C.; Boscoe, F.P. Effects of randomization methods on statistical inference in disease cluster detection. Health Place 2007, 13, 152–163. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Wang, S.; Wang, H.; Liang, Y.; Chen, S.; Wu, K.; Yang, Z.; Li, C.; Chang, Y.; Zhan, Y. Detection of Geochemical Element Assemblage Anomalies Using a Local Correlation Approach. J. Earth Sci. 2021, 32, 408–414. [Google Scholar] [CrossRef]
- Xiao, G.; Hu, Y.; Li, N.; Yang, D. Spatial autocorrelation analysis of monitoring data of heavy metals in rice in China. Food Control 2018, 89, 32–37. [Google Scholar] [CrossRef]
- Bivand, R.S.; Wong, D.W. Comparing implementations of global and local indicators of spatial association. Test 2018, 27, 716–748. [Google Scholar] [CrossRef]
- Cheng, Q. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas. J. Geochem. Explor. 2012, 122, 55–70. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Geochemical Anomaly and Mineral Prospectivity Mapping in GIS; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Zuo, R.; Xiong, Y. Geodata science and geochemical mapping. J. Geochem. Explor. 2019, 209, 106431. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y.; Xiao, F. Identification of multi-element geochemical anomalies using unsupervised machine learning algorithms: A case study from Ag–Pb–Zn deposits in north-western Zhejiang, China. Appl. Geochem. 2020, 120, 104679. [Google Scholar] [CrossRef]
- Taylor, R.; Steven, T. Definition of mineral resource potential. Econ. Geol. 1983, 78, 1268–1270. [Google Scholar] [CrossRef]
- Wang, L.; Wu, X.; Zhang, B.; Li, X.; Huang, A.; Meng, F.; Dai, P. Recognition of Significant Surface Soil Geochemical Anomalies Via Weighted 3D Shortest-Distance Field of Subsurface Orebodies: A Case Study in the Hongtoushan Copper Mine, NE China. Nat. Resour. Res. 2019, 28, 587–607. [Google Scholar] [CrossRef]
- Hawkes, H.E.; Webb, J.S. Geochemistry in mineral exploration. Soil Sci. 1963, 95, 283. [Google Scholar] [CrossRef]
- Sinclair, A. Selection of threshold values in geochemical data using probability graphs. J. Geochem. Explor. 1974, 3, 129–149. [Google Scholar] [CrossRef]
- Govett, G.; Goodfellow, W.; Chapman, R.; Chork, C. Exploration geochemistry—distribution of elements and recognition of anomalies. J. Int. Assoc. Math. Geol. 1975, 7, 415–446. [Google Scholar] [CrossRef]
- El-Makky, A.M. Statistical analyses of La, Ce, Nd, Y, Nb, Ti, P, and Zr in bedrocks and their significance in geochemical exploration at the Um Garayat Gold mine area, Eastern Desert, Egypt. Nat. Resour. Res. 2011, 20, 157. [Google Scholar] [CrossRef]
- Ravani, P.; Barrett, B.J.; Parfrey, P.S. Longitudinal Studies 2: Modeling Data Using Multivariate Analysis. Methods Mol. Biol. Clifton NJ 2021, 2249, 103–124. [Google Scholar]
- Cox, D.R.; Snell, E.J. Analysis of Binary Data; Routledge: London, UK, 2018. [Google Scholar]
- Cioci, A.C.; Cioci, A.L.; Mantero, A.M.; Parreco, J.P.; Yeh, D.D.; Rattan, R. Advanced statistics: Multiple logistic regression, Cox proportional hazards, and propensity scores. Surg. Infect. 2021, 22, 604–610. [Google Scholar] [CrossRef]
- Agterberg, F.P. Computer programs for mineral exploration. Science 1989, 245, 76–81. [Google Scholar] [CrossRef]
- Cheng, Q.; Agterberg, F. Fuzzy weights of evidence method and its application in mineral potential mapping. Nat. Resour. Res. 1999, 8, 27–35. [Google Scholar] [CrossRef]
- Goyes-Penafiel, P.; Hernandez-Rojas, A. Double landslide susceptibility assessment based on artificial neural networks and weights of evidence. Bol. Geol. 2021, 43, 173–191. [Google Scholar]
- Cheng, Q.; Agterberg, F.; Ballantyne, S. The separation of geochemical anomalies from background by fractal methods. J. Geochem. Explor. 1994, 51, 109–130. [Google Scholar] [CrossRef]
- Cheng, Q.; Xu, Y.; Grunsky, E. Integrated spatial and spectrum method for geochemical anomaly separation. Nat. Resour. Res. 2000, 9, 43–52. [Google Scholar] [CrossRef]
- Cheng, Q. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China. Ore Geol. Rev. 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical modelling of spatial uncertainty using p-field simulation with conditional probability fields. Int. J. Geogr. Inf. Sci. 2002, 16, 167–178. [Google Scholar] [CrossRef]
- Naik, M.R.; Barik, M.; Prasad, K.; Kumar, A.; Verma, A.K.; Sahoo, S.K.; Jha, V.; Sahoo, N.K. Hydro-geochemical analysis based on entropy and geostatistics model for delineation of anthropogenic ground water pollution for health risks assessment of Dhenkanal district, India. Ecotoxicology 2021, 2, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Zuo, R.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Xiong, J.; Li, J.; Cheng, W.; Wang, N.; Guo, L. A GIS-based support vector machine model for flash flood vulnerability assessment and mapping in China. ISPRS Int. J. Geo-Inf. 2019, 8, 297. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Galiano, V.; Chica-Olmo, M.; Chica-Rivas, M. Predictive modelling of gold potential with the integration of multisource information based on random forest: A case study on the Rodalquilar area, Southern Spain. Int. J. Geogr. Inf. Sci. 2014, 28, 1336–1354. [Google Scholar] [CrossRef]
- Zhang, B.; Li, M.; Li, W.; Jiang, Z.; Khan, U.; Wang, L.; Wang, F. Machine learning strategies for lithostratigraphic classification based on geochemical sampling data: A case study in the area of the Chahanwusu River, Qinghai Province, China. J. Cent. South Univ. 2021, 28, 1422–1447. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.J.M. Classifiers for Modeling of Mineral Potential; Wiley-Blackwell: Hoboken, NJ, USA, 2008. [Google Scholar]
- Porwal, A.; Carranza, E.J.M.; Hale, M. Bayesian network classifiers for mineral potential mapping. Comput. Geosci. 2006, 32, 1–16. [Google Scholar] [CrossRef]
- Klüppelberg, C.; Krali, M. Estimating an extreme Bayesian network via scalings. J. Multivar. Anal. 2021, 181, 104672. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R. Recognition of geochemical anomalies using a deep autoencoder network. Comput. Geosci. 2016, 86, 75–82. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Liu, X.; Ren, Z. A study of geochemical exploration spational cluster identification based on local spatial autocorrelation. Geophys. Geochem. Explor. 2014, 38, 370–376. [Google Scholar]
- Wang, H.; Cheng, Q.; Zuo, R. Spatial characteristics of geochemical patterns related to Fe mineralization in the southwestern Fujian province (China). J. Geochem. Explor. 2015, 148, 259–269. [Google Scholar] [CrossRef]
- Ji, B.; Zhou, T.; Yuan, F.; Zhang, D.; Liu, L.; Liu, G. A method for identifying geochemical anomalies based on spatial autocorrelation. Sci. Surv. Mapp. 2017, 42, 24–27. [Google Scholar]
- Sadeghi, M.; Morris, G.A.; Carranza, E.J.M.; Ladenberger, A.; Andersson, M. Rare earth element distribution and mineralization in Sweden: An application of principal component analysis to FOREGS soil geochemistry. J. Geochem. Explor. 2013, 133, 160–175. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, R. Quantifying the Distribution Characteristics of Geochemical Elements and Identifying Their Associations in Southwestern Fujian Province, China. Minerals 2020, 10, 183. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.-S.; Li, Y. Extension of local association rules mining algorithm based on apriori algorithm. In Proceedings of the 2014 5th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 27–29 June 2014; pp. 340–343. [Google Scholar]
- Zhang, X. Study of an improved Apriori algorithm for data mining of association rules. In Proceedings of the International Conference on Applied Science & Engineering Innovation, Jinan, China, 30–31 August 2015. [Google Scholar]
- Xu, T.; Dong, X. Mining frequent patterns with multiple minimum supports using basic Apriori. In Proceedings of the 2013 Ninth International Conference on Natural Computation (ICNC), Shenyang, China, 23–25 July 2013; pp. 957–961. [Google Scholar]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Philip, S.Y. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, R.; Imieliński, T.; Swami, A. Mining association rules between sets of items in large databases. In Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, Washington, DC, USA, 25–28 May 1993; pp. 207–216. [Google Scholar]
- Liu, X.; Zhou, Y. Application of association rule algorithm in studying abnormal elemental associations in the Pangxidong area in western Guangdong Province, China. Earth Sci. Front. 2019, 26, 57–71. [Google Scholar]
- Qinghai Geological Survey Institute. Comprehensive Survey Report of 1:50000 Regional Mineral Geology, Stream Sediment Geochemistry and High-Precision Magnetic Survey in the Chahanwusu River Area, Dulan County, Qinghai Province; Qinghai Geological Survey Institute: Xining, China, 2008; pp. 254–273. [Google Scholar]
- Chou, Y.H. Spatial pattern and spatial autocorrelation. In Proceedings of the International Conference on Spatial Information Theory, Semmering, Austria, 21–23 September 1995; pp. 365–376. [Google Scholar]
- Buja, A.; Cook, D.; Swayne, D.F. Interactive high-dimensional data visualization. J. Comput. Graph. Stat. 1996, 5, 78–99. [Google Scholar]
- Anselin, L.; Syabri, I.; Smirnov, O. Visualizing multivariate spatial correlation with dynamically linked windows. In Proceedings of the Proceedings, CSISS Workshop on New Tools for Spatial Data Analysis, Santa Barbara, CA, USA, 22–26 July 2002. [Google Scholar]
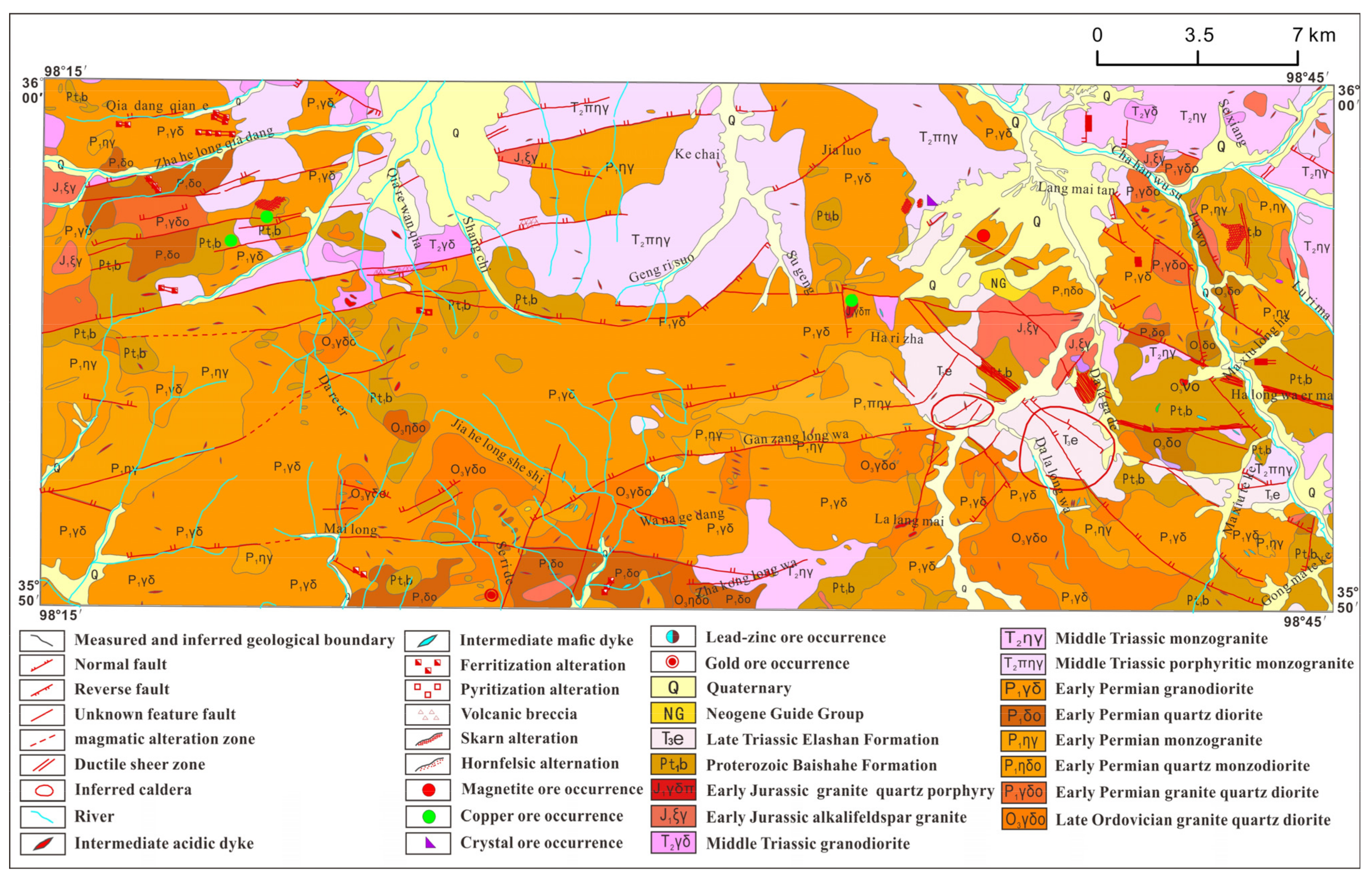

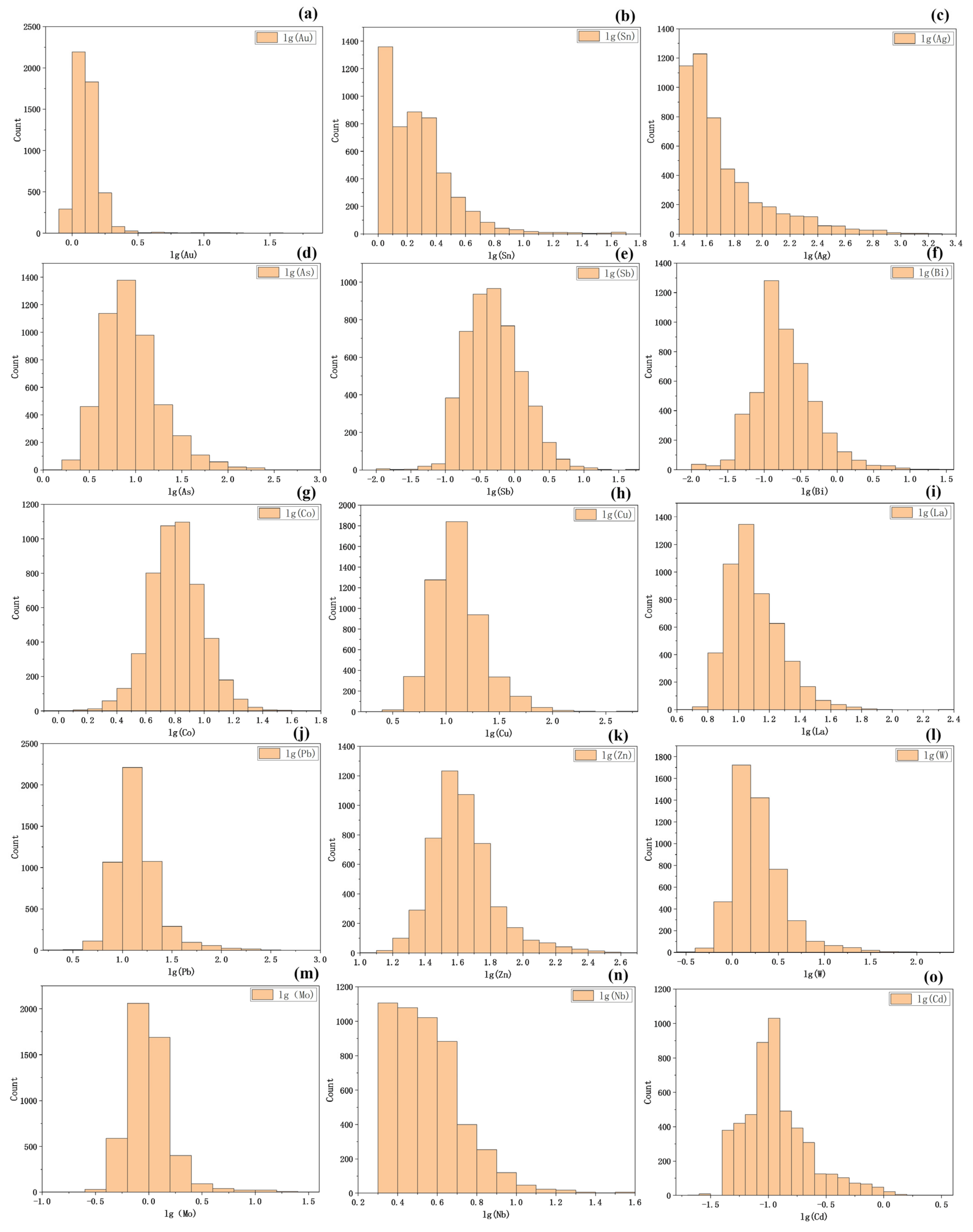
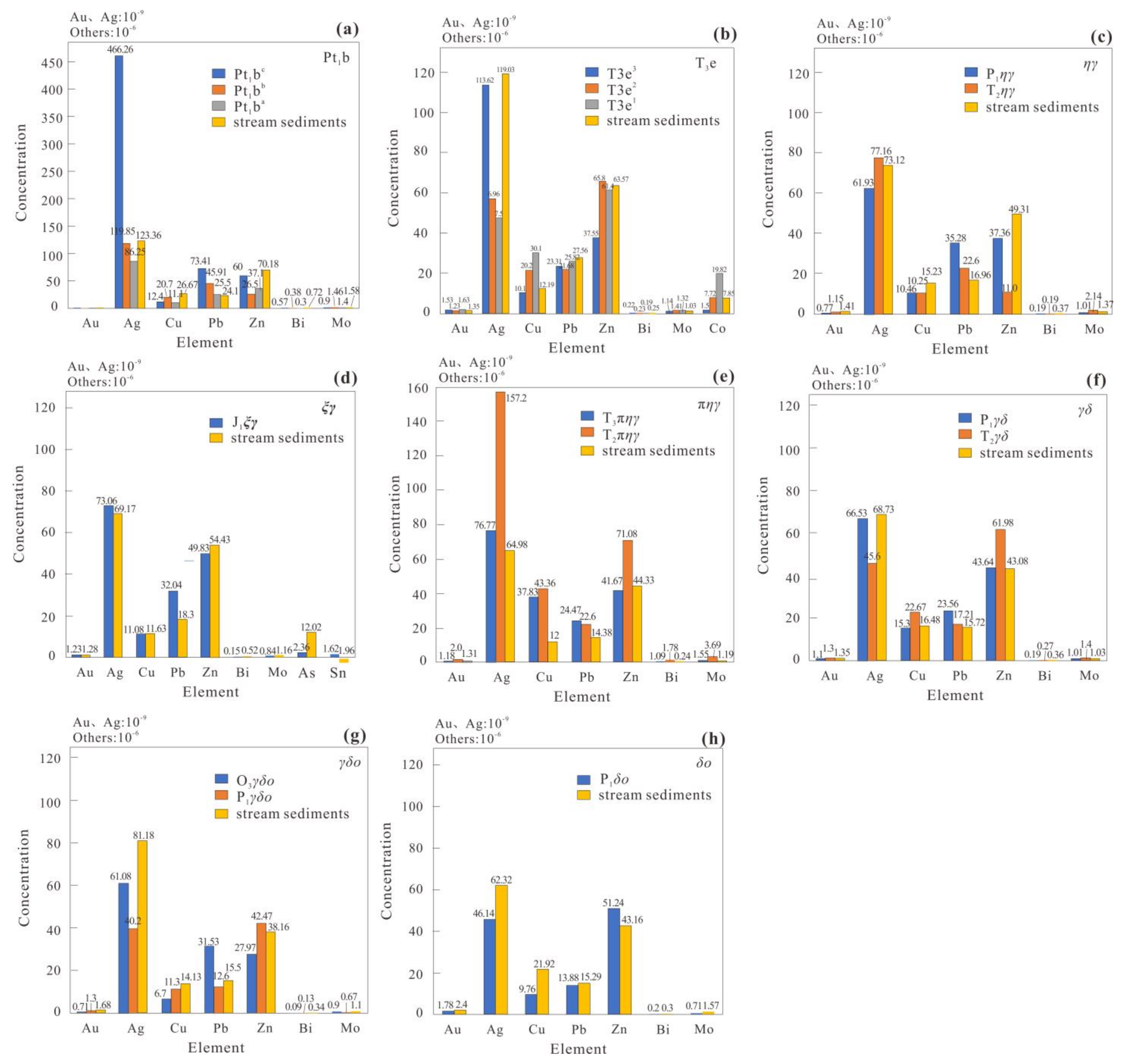
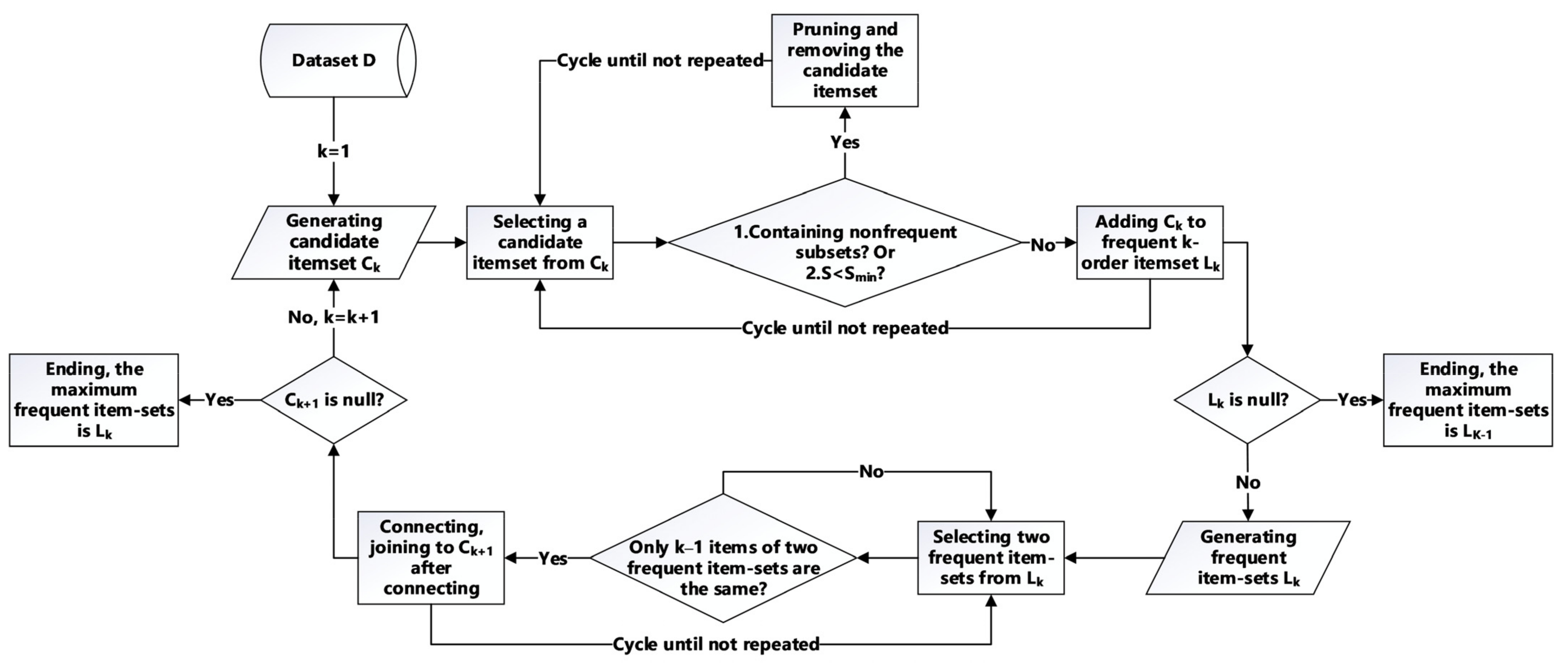












| Element | Mean | Median | Standard Deviation | Skewness | Kurtosis | Coefficient of Variation |
|---|---|---|---|---|---|---|
| Au | 1.42 | 1.20 | 1.81 | 25.07 | 793.15 | 1.27 |
| Sn | 2.31 | 1.70 | 3.21 | 10.35 | 134.68 | 1.39 |
| Ag | 76.31 | 41.00 | 117.35 | 6.77 | 67.02 | 1.54 |
| As | 13.07 | 8.10 | 21.89 | 13.21 | 303.48 | 1.68 |
| Sb | 0.82 | 0.47 | 1.45 | 14.56 | 372.59 | 1.88 |
| Bi | 0.37 | 0.17 | 1.00 | 13.68 | 256.65 | 2.50 |
| Co | 7.07 | 6.40 | 3.44 | 3.07 | 24.09 | 0.48 |
| Cu | 16.05 | 12.10 | 20.44 | 15.15 | 330.62 | 1.27 |
| La | 13.73 | 12.00 | 8.30 | 8.99 | 192.65 | 0.61 |
| Pb | 17.00 | 12.80 | 21.29 | 13.35 | 314.69 | 1.25 |
| Zn | 48.29 | 40.40 | 32.06 | 4.27 | 27.61 | 0.66 |
| W | 2.74 | 1.70 | 5.99 | 18.99 | 528.95 | 2.22 |
| Mo | 1.20 | 0.96 | 1.36 | 9.31 | 117.22 | 1.17 |
| Nb | 3.93 | 3.30 | 2.26 | 4.53 | 37.90 | 0.59 |
| Cd | 0.15 | 0.10 | 0.18 | 5.28 | 49.30 | 0.85 |
| Spatial Autocorrelation Statistics | Calculation Formula | Remarks | References |
|---|---|---|---|
| global Moran’s I | The range of is [−1, 1], < 0 indicates negative spacial autocorrelation, > 0 indicates positive spacial autocorrelation, and tends to 0 indicates spatial random distribution. | [4,6,7,8] | |
| global Geary’s C | The range of is [0, 2] > 1 indicates indicates negative spatial autocorrelation, < 1 indicates positive spatial autocorrelation, and tends to 1 indicates spatial random distribution. | [5,6,8] | |
| global Getis–Ord’s G | < mathematical expectation (ME) indicates low value clustered, > ME indicates high value clustered, and tends to ME indicates spatial random distribution. | [9] | |
| local Moran’s I | < 0 indicates negative spatial autocorrelation, > 0 indicates positive spatial auto-correlation, and tends to 0 indicates spatial random distribution. | [9] | |
| local Geary’s C | < 0 indicates negative spatial autocorrelation, and > 0 indicates positive spatial autocorrelation, and tends to 0 indicates spatial random distribution. | [11] | |
| local Getis–Ord’s G | < 0 indicates negative spatial autocorrelation, > 0 indicates positive spatial autocorrelation, and tends to 0 indicates spatial random distribution. | [9] |
| Variable | Global Moran’s I | Global Geary’s C | Global Getis–Ord’s G | ||||
|---|---|---|---|---|---|---|---|
| I | p-Value (×10−16) | C | p-Value (×10−16) | G | p-Value (×10−16) | E(G) (×10−9) | |
| log10(Au) | 0.059 | <2.2 | 0.949 | <2.2 | 0.009 | <2.2 | 5.1 |
| log10(Sn) | 0.439 | <2.2 | 0.563 | <2.2 | 0.014 | <2.2 | 6.7 |
| log10(Ag) | 0.430 | <2.2 | 0.570 | <2.2 | 0.013 | <2.2 | 9.0 |
| log10(As) | 0.451 | <2.2 | 0.551 | <2.2 | 0.012 | <2.2 | 11.0 |
| log10(Sb) | 0.608 | <2.2 | 0.394 | <2.2 | 0.014 | <2.2 | 13.0 |
| log10(Bi) | 0.438 | <2.2 | 0.564 | <2.2 | 0.019 | <2.2 | 52.0 |
| log10(Co) | 0.423 | <2.2 | 0.578 | <2.2 | 0.009 | <2.2 | 0.6 |
| log10(Cu) | 0.468 | <2.2 | 0.535 | <2.2 | 0.012 | <2.2 | 5.3 |
| log10(La) | 0.259 | <2.2 | 0.740 | <2.2 | 0.009 | <2.2 | 0.9 |
| log10(Pb) | 0.500 | <2.2 | 0.500 | <2.2 | 0.011 | <2.2 | 5.1 |
| log10(Zn) | 0.530 | <2.2 | 0.468 | <2.2 | 0.010 | <2.2 | 1.1 |
| log10(W) | 0.365 | <2.2 | 0.638 | <2.2 | 0.015 | <2.2 | 24.0 |
| log10(Mo) | 0.430 | <2.2 | 0.572 | <2.2 | 0.012 | <2.2 | 4.0 |
| log10(Nb) | 0.181 | <2.2 | 0.817 | <2.2 | 0.009 | <2.2 | 0.8 |
| log10(Cd) | 0.459 | <2.2 | 0.539 | <2.2 | 0.012 | <2.2 | 4.0 |
| Element/log10() | Au | Sn | Ag | As | Sb | Bi | Co | Cu | La | Pb | Zn | W | Mo | Nb | Cd |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Au | 0.06 | 0.03 | 0.03 | 0.03 | 0.03 | 0.01 | −0.03 | 0.00 | 0.01 | 0.02 | −0.02 | 0.01 | −0.02 | −0.01 | 0.02 |
| Sn | 0.03 | 0.44 | 0.28 | 0.27 | 0.20 | 0.30 | 0.15 | 0.29 | −0.03 | 0.29 | 0.15 | 0.19 | 0.08 | −0.03 | 0.30 |
| Ag | 0.03 | 0.28 | 0.43 | 0.31 | 0.26 | 0.25 | 0.15 | 0.26 | 0.01 | 0.36 | 0.30 | 0.22 | 0.14 | 0.02 | 0.34 |
| As | 0.03 | 0.27 | 0.31 | 0.45 | 0.35 | 0.22 | 0.19 | 0.22 | −0.02 | 0.34 | 0.26 | 0.16 | 0.09 | 0.02 | 0.33 |
| Sb | 0.03 | 0.20 | 0.26 | 0.35 | 0.61 | 0.15 | 0.11 | 0.10 | 0.04 | 0.32 | 0.26 | 0.12 | −0.01 | 0.00 | 0.30 |
| Bi | 0.01 | 0.30 | 0.25 | 0.22 | 0.15 | 0.44 | 0.18 | 0.36 | −0.06 | 0.28 | 0.21 | 0.27 | 0.23 | 0.03 | 0.24 |
| Co | −0.03 | 0.15 | 0.15 | 0.19 | 0.11 | 0.18 | 0.42 | 0.31 | −0.15 | 0.20 | 0.22 | 0.15 | 0.15 | 0.01 | 0.16 |
| Cu | 0.00 | 0.29 | 0.26 | 0.22 | 0.10 | 0.36 | 0.31 | 0.47 | −0.13 | 0.26 | 0.22 | 0.29 | 0.27 | 0.04 | 0.23 |
| La | 0.01 | −0.03 | 0.01 | −0.02 | 0.04 | −0.06 | −0.15 | −0.13 | 0.26 | 0.06 | 0.06 | −0.02 | −0.01 | 0.07 | 0.04 |
| Pb | 0.02 | 0.29 | 0.36 | 0.34 | 0.32 | 0.28 | 0.20 | 0.26 | 0.06 | 0.50 | 0.42 | 0.23 | 0.16 | 0.05 | 0.43 |
| Zn | −0.02 | 0.15 | 0.30 | 0.26 | 0.26 | 0.21 | 0.22 | 0.22 | 0.06 | 0.42 | 0.53 | 0.22 | 0.21 | 0.22 | 0.36 |
| W | 0.01 | 0.19 | 0.22 | 0.16 | 0.12 | 0.27 | 0.15 | 0.29 | −0.02 | 0.23 | 0.22 | 0.37 | 0.32 | 0.07 | 0.19 |
| Mo | −0.02 | 0.08 | 0.14 | 0.09 | −0.01 | 0.23 | 0.15 | 0.27 | −0.01 | 0.16 | 0.21 | 0.32 | 0.43 | 0.10 | 0.11 |
| Nb | −0.01 | −0.03 | 0.02 | 0.02 | 0.00 | 0.03 | 0.01 | 0.04 | 0.07 | 0.05 | 0.22 | 0.07 | 0.10 | 0.18 | 0.03 |
| Cd | 0.02 | 0.30 | 0.34 | 0.33 | 0.30 | 0.24 | 0.16 | 0.23 | 0.04 | 0.43 | 0.36 | 0.19 | 0.11 | 0.03 | 0.46 |
| Positive Correlation | |
|---|---|
| = 0.43 | Pb-Cd |
| = 0.42 | Pb-Zn |
| = 0.36 | Ag-Pb, Cu-Bi, Zn-Cd |
| = 0.35 | As-Sb |
| = 0.34 | Ag-Cd, Pb-As |
| = 0.33 | As-Cd |
| = 0.32 | Pb-Sb, Mo-W |
| = 0.31 | Ag-As, Cu-Co |
| = 0.30 | Sn-Bi, Sn-Cd, Ag-Zn, Sb-Cd |
| Negative Correlation | |
|---|---|
| = −0.13 | La-Co |
| = −0.15 | La-Cu |
(Point) | (Au) | (Sn) | (Ag) | (As) | (Sb) | (Bi) | (Co) | (Cu) | (La) | (Pb) | (Zn) | (W) | (Mo) | (Nb) | (Cd) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | HL | HH | HH | HH | HH | HH | HH | HH | HH | HH | |||||
| 2 | LL | HH | HH | HL | |||||||||||
| 3 | HH | LH | HH | LH | HH | ||||||||||
| 4 | HH | HH | HH | HH | LH | HH | |||||||||
| 5 | LL | LL | LL | LL | LL | LL | HH | LL | LL | ||||||
| 6 | LL | LL | LL | LL | LL | LL | LL | LL | LL | LL | LL | ||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 4959 | HH | HH | HH | HH | HH | HH | HH | LH | HH | HH | HH | HH | HH |
| Element | Insignificant | High–High | Low–Low | Low–High | High–Low |
|---|---|---|---|---|---|
| Au | 4023 | 113 | 466 | 163 | 194 |
| Sn | 2584 | 300 | 1786 | 190 | 99 |
| Ag | 1706 | 560 | 2286 | 336 | 71 |
| As | 1931 | 521 | 2137 | 259 | 111 |
| Sb | 1192 | 867 | 2509 | 305 | 86 |
| Bi | 2352 | 351 | 1973 | 194 | 89 |
| Co | 1810 | 981 | 1613 | 327 | 228 |
| Cu | 2036 | 570 | 2044 | 169 | 140 |
| La | 2025 | 659 | 1529 | 417 | 329 |
| Pb | 3740 | 65 | 796 | 315 | 43 |
| Zn | 1662 | 793 | 2049 | 200 | 255 |
| W | 2442 | 332 | 1874 | 193 | 118 |
| Mo | 2289 | 414 | 1952 | 128 | 176 |
| Nb | 2749 | 478 | 1132 | 329 | 271 |
| Cd | 2054 | 556 | 1927 | 303 | 119 |
| ID | Association Rules | Support Degree | Confidence |
|---|---|---|---|
| a | {As (HH)} ⇒ {Sb (HH)} | 0.076 | 0.73 |
| b | {Cd (HH)} ⇒ {Zn (HH)} | 0.090 | 0.81 |
| c | {W (HH)} ⇒ {Cu (HH)} | 0.051 | 0.76 |
| d | {Cu (HH)} ⇒ {Co (HH)} | 0.089 | 0.77 |
| e | {Bi (HH)} ⇒ {Cu (HH)} | 0.059 | 0.83 |
| f | {Mo (HH)} ⇒ {Sb (LL)} | 0.065 | 0.77 |
| g | {Zn (HH), Ag (HH)} ⇒ {Cd (HH)} | 0.058 | 0.81 |
| h | {Cd (HH), Ag (HH)} ⇒ {Zn (HH)} | 0.058 | 0.92 |
| i | {Cd (HH), As (HH)} ⇒ {Zn (HH)} | 0.053 | 0.93 |
| j | {As (HH), Zn (HH)} ⇒ {Cd (HH)} | 0.053 | 0.82 |
| k | {Zn (HH), Sb (HH)} ⇒ {Cd (HH)} | 0.055 | 0.71 |
| l | {Cd (HH), Sb (HH)} ⇒ {Zn (HH)} | 0.055 | 0.93 |
| m | {Zn (HH), As (HH)} ⇒ {Sb (HH)} | 0.052 | 0.82 |
| n | {Cu (HH), La (LL)} ⇒ {Co (HH)} | 0.052 | 0.76 |
| o | {Co (HH), Sb (LL)} ⇒ {La (LL)} | 0.056 | 0.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Jiang, Z.; Chen, Y.; Cheng, N.; Khan, U.; Deng, J. Geochemical Association Rules of Elements Mined Using Clustered Events of Spatial Autocorrelation: A Case Study in the Chahanwusu River Area, Qinghai Province, China. Appl. Sci. 2022, 12, 2247. https://doi.org/10.3390/app12042247
Zhang B, Jiang Z, Chen Y, Cheng N, Khan U, Deng J. Geochemical Association Rules of Elements Mined Using Clustered Events of Spatial Autocorrelation: A Case Study in the Chahanwusu River Area, Qinghai Province, China. Applied Sciences. 2022; 12(4):2247. https://doi.org/10.3390/app12042247
Chicago/Turabian StyleZhang, Baoyi, Zhengwen Jiang, Yiru Chen, Nanwei Cheng, Umair Khan, and Jiqiu Deng. 2022. "Geochemical Association Rules of Elements Mined Using Clustered Events of Spatial Autocorrelation: A Case Study in the Chahanwusu River Area, Qinghai Province, China" Applied Sciences 12, no. 4: 2247. https://doi.org/10.3390/app12042247
APA StyleZhang, B., Jiang, Z., Chen, Y., Cheng, N., Khan, U., & Deng, J. (2022). Geochemical Association Rules of Elements Mined Using Clustered Events of Spatial Autocorrelation: A Case Study in the Chahanwusu River Area, Qinghai Province, China. Applied Sciences, 12(4), 2247. https://doi.org/10.3390/app12042247







